平行四边形分类讨论问题

平行四边形分类讨论问题

上海市松江区中考

如图1，已知抛物线y ＝－x 2＋bx ＋c 经过A (0, 1)、B (4, 3)两点． （1）求抛物线的解析式； （2）求tan ∠ABO 的值；

（3）过点B 作BC ⊥x 轴，垂足为C ，在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ，交抛物线于点M ，若四边形MNCB 为平行四边形，求点M 的坐标．

图1

（1）将A (0, 1)、B (4, 3)分别代入y ＝－x 2＋bx ＋c ，得

1,164 3.

c b c =??

-++=? 解得9

2b =，c ＝1． 所以抛物线的解析式是29

1

2

y x x =-+

+． （2）在Rt △BOC 中，OC ＝4，BC ＝3，所以OB ＝5． 如图2，过点A 作AH ⊥OB ，垂足为H ．

在Rt △AOH 中，OA ＝1，4sin sin 5

AOH OBC ∠=∠=，

所以4

sin 5

AH OA AOH =?∠=

． 图2 所以35OH =，22

5

BH OB OH =-=．

在Rt △ABH 中，4222

tan 5511AH ABO BH ∠==÷=．

（3）直线AB 的解析式为1

12y x =+．

设点M 的坐标为29(,1)2x x x -++，点N 的坐标为1

(,1)2

x x +，

那么2291

(1)(1)422

MN x x x x x =-++-+=-+．

当四边形MNCB 是平行四边形时，MN ＝BC ＝3．

解方程－x 2＋4x ＝3，得x ＝1或x ＝3．

因为x ＝3在对称轴的右侧（如图4），所以符合题意的点M 的坐标为9

(1,)2

（如图3）．

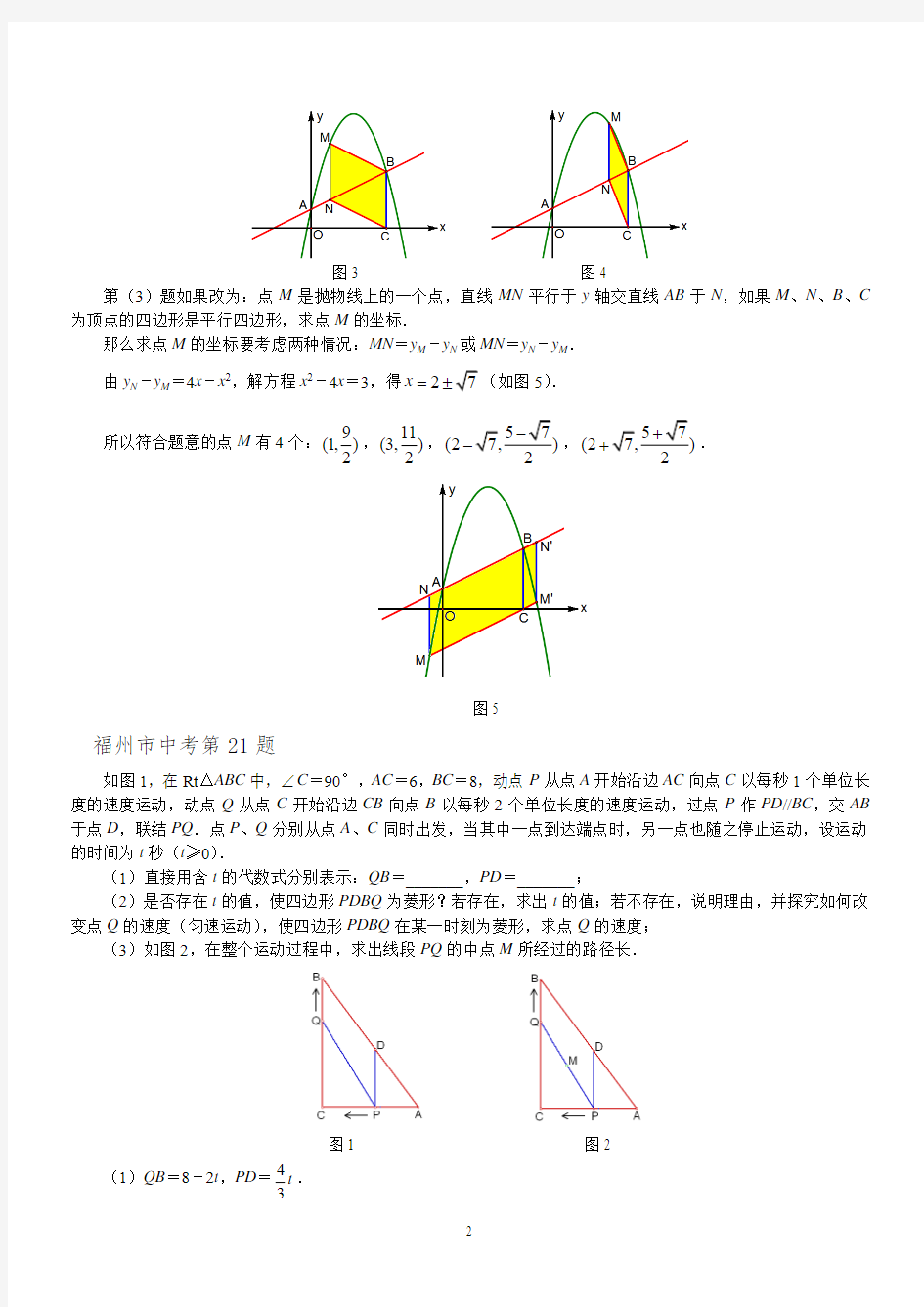
图3 图4

第（3）题如果改为：点M 是抛物线上的一个点，直线MN 平行于y 轴交直线AB 于N ，如果M 、N 、B 、C 为顶点的四边形是平行四边形，求点M 的坐标．

那么求点M 的坐标要考虑两种情况：MN ＝y M －y N 或MN ＝y N －y M ．

由y N －y M ＝4x －x 2，解方程x 2－4x ＝3，得2x =（如图5）．

所以符合题意的点M 有4个：9

(1,)2，11

(3,

)2

，(2，(2+．

图5

福州市中考第21题

如图1，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8，动点P 从点A 开始沿边AC 向点C 以每秒1个单位长

度的速度运动，动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动，过点P 作PD //BC ，交AB 于点D ，联结PQ ．点P 、Q 分别从点A 、C 同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t 秒（t ≥0）．

（1）直接用含t 的代数式分别表示：QB ＝_______，PD ＝_______；

（2）是否存在t 的值，使四边形PDBQ 为菱形？若存在，求出t 的值；若不存在，说明理由，并探究如何改变点Q 的速度（匀速运动），使四边形PDBQ 在某一时刻为菱形，求点Q 的速度；

（3）如图2，在整个运动过程中，求出线段PQ 的中点M 所经过的路径长．

图1 图2

（1）QB ＝8－2t ，PD ＝4

3

t ．

（2）如图3，作∠ABC 的平分线交CA 于P ，过点P 作PQ //AB 交BC 于Q ，那么四边形PDBQ 是菱形． 过点P 作PE ⊥AB ，垂足为E ，那么BE ＝BC ＝8． 在Rt △ABC 中，AC ＝6，BC ＝8，所以AB ＝10． 图3

在Rt △APE 中，23cos 5AE A AP t =

==，所以10

3

t =． 当PQ //AB 时，

CQ CP CB CA =，即10

638

6

CQ -

=

．解得329CQ =．

所以点Q 的运动速度为

321016

9315

÷=． （3）以C 为原点建立直角坐标系．

如图4，当t ＝0时，PQ 的中点就是AC 的中点E (3，0)． 如图5，当t ＝4时，PQ 的中点就是PB 的中点F (1，4)． 直线EF 的解析式是y ＝－2x ＋6．

如图6，PQ 的中点M 的坐标可以表示为（62t -，t ）．经验证，点M （62

t

-，t ）在直线EF 上．

所以PQ 的中点M 的运动路径长就是线段EF 的长，EF

＝

图4 图5 图6

第（3）题求点M 的运动路径还有一种通用的方法是设二次函数： 当t ＝2时，PQ 的中点为(2，2)．

设点M 的运动路径的解析式为y ＝ax 2＋bx ＋c ，代入E (3，0)、F (1，4)和(2，2)，

得930,4,42 2.a b c a b c a b c ++=??++=??++=?

解得a ＝0，b ＝－2，c ＝6． 所以点M 的运动路径的解析式为y ＝－2x ＋6．

烟台市中考第26题

如图1，在平面直角坐标系中，已知矩形ABCD 的三个顶点B (1, 0)、C (3, 0)、D (3, 4)．以A 为顶点的抛物线y ＝ax 2＋bx ＋c 过点C ．动点P 从点A 出发，沿线段AB 向点B 运动，同时动点Q 从点C 出发，沿线段CD 向点D 运动．点P 、Q 的运动速度均为每秒1个单位，运动时间为t 秒．过点P 作PE ⊥AB 交AC 于点E ．

（1）直接写出点A 的坐标，并求出抛物线的解析式；

（2）过点E 作EF ⊥AD 于F ，交抛物线于点G ，当t 为何值时，△ACG 的面积最大？最大值为多少？

（3）在动点P 、Q 运动的过程中，当t 为何值时，在矩形ABCD 内（包括边界）存在点H ，使以C 、Q 、E 、H 为顶点的四边形为菱形？请直接写出t 的值．

（1）A (1, 4)．因为抛物线的顶点为A ，设抛物线的解析式为y ＝a (x －1)2＋4， 代入点C (3, 0)，可得a ＝－1．

所以抛物线的解析式为y ＝－(x －1)2＋4＝－x 2＋2x ＋3．

（2）因为PE //BC ，所以

2AP AB PE BC ==．因此11

22PE AP t ==． 所以点E 的横坐标为1

12

t +．

将112x t =+代入抛物线的解析式，y ＝－(x －1)2＋4＝21

44

t -．

所以点G 的纵坐标为2144t -．于是得到2211

(4)(4)44GE t t t t =---=-+．

因此22111

()(2)1244

ACG AGE CGE S S S GE AF DF t t t ???=+=+=-+=--+．

所以当t ＝1时，△ACG 面积的最大值为1．

（3）20

13

t =或20t =-

第（3）题的解题思路是这样的：

因为FE //QC ，FE ＝QC ，所以四边形FECQ 是平行四边形．再构造点F 关于PE 轴对称的点H ′，那么四边形EH ′CQ 也是平行四边形．

再根据FQ ＝CQ 列关于t 的方程，检验四边形FECQ 是否为菱形，根据EQ ＝CQ 列关于t 的方程，检验四边形EH ′CQ 是否为菱形．

1(1,4)2E t t +-，1

(1,4)2

F t +，(3,)Q t ，(3,0)C ．

如图2，当FQ ＝CQ 时，FQ 2＝CQ 2，因此2221

(2)(4)2

t t t -+-=．

整理，得240800t t -+=．解得120t =-，220t =+．

如图3，当EQ ＝CQ 时，EQ 2＝CQ 2，因此2221

(2)(42)2

t t t -+-=．

整理，得213728000t t -+=．(1320)(40)0t t --=．所以120

13

t =

，240t =（舍去）．

图2 图3

【2013·浙江温州·24题】如图，在平面直角坐标系轴，直线AB与x轴、y轴分别交于点A（6，0）、B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上一动点，连接CD、DE，以CD、DE为边作平行四边形CDEF。

（1）当0＜m＜8时，求CE的长（用含m的代数式表示）；

（2）当m=3时，是否存在点D，使平行四边形CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；

（3）点D在整个运动过程中，若存在唯一的位置，使得平行四边形CDEF为矩形，请求出所有满足条件的m 的值。

解：（1）∵CE⊥AB ∴∠BEC=∠BOA=90°

∵∠CEB=∠ABO

∴△BEC∽△AOB ∴CE CB OA AB

=

∵OA=6，OB=8，OC=m

∴

=10，CB=8-m

∴CE=3

5

(8-m)

（2）存在。

∵m=3 ∴CB=5，CE=3 ∴BE=4

∵F在y轴上∴DE∥OB

∴OD OA

BE AB

=∴OD=

12

5

∴点D坐标为（12

5

，0）

（3）①当0＜m＜8时，以CE为直径作⊙P，当⊙P

与x轴相切于点D时，平行四边形CDEF为矩形，如

图a。此时，PC=PD=

1

2

CE=

3

10

(8-m)

过点P作PQ⊥y轴于Q，易证得△PQC∽△BOA

∴

CQ PC

OA AB

=∴CQ=

9

50

(8-m)

∴OQ=OC+CQ=m+

9

50

(8-m)

易证四边形ODPQ为矩形，则OQ=PD=PC

∴m+

9

50

(8-m)=310(8-m)，得m=67

② 当m ≥8时，OQ ＞PC ，不存在满足条件的m 。 ③ 当m=0时，点C 与点O 重合，如图b ，显然满足条件。

④ 当m ＜0，且点E 与点A 重合时，以CE 为直径作⊙P 必过点O ，当点D 与点O 重合时，平行四边形CDEF 为矩形，如图c 。

∵∠BAC=90°，AO ⊥BC

∴OA 2=OB ·OC(射影定理) ∴OC=9

2

∴m=-

92

⑤ 当m ＜0，且点E 与点A 不重合时，当⊙P 与x 轴相切于点D 时，平行四边形CDEF 为矩形，如图d 。 与①同理可得，CQ=

9

50(8-m)，OC=-m ∴OQ=OC -CQ=-m -9

50

(8-m) ∵OQ=PD=PC ∴-m -9

50

(8-m)=310(8-m)

解得m=96

13

-

综上所述，m=67或0或-92或96

13

-

【2013·浙江义乌·24题】如图1，已知y =

6

x

(x ＞0)图象上一点P ，PA ⊥x 轴于点A （a ，0），点B 坐标为（0，b ）（b ＞0），动点M 是y 轴正半轴上B 点上方的点，动点N 在射线AP 上，过点B 作AB 的垂线，交射线AP 于点D ，交直线MN 于点Q ，连接AQ ，取AQ 的中点为C 。

（1）如图2，连接BP ，求△PAB 的面积；

（2）当点Q 在线段BD 上时，若四边形BQNC 时菱形，面积为P 点的坐标；

（3）当点Q 在射线BD 上时，且a =3，b =1，若以点B 、C 、N 、Q 为顶点的四边形是平行四边形，求这个平行四边形的周长。

解：（1）由题意可得，OA=a ，AP=

6

a

∴S △PAB =12AP ·OA=12·6

a

·a =3

（2）∵DB ⊥AB ∴∠ABQ=90°

∵C 是AQ 的中点 ∴BC=CQ=AC ∵四边形BQNC 是菱形 ∴BC=BQ=CN=QN ∴BC=BQ=CQ=CN=QN

∴△

BCQ 、△NCQ 是等边三角形 ∴∠AQB=60° ∴∠BAQ=30° ∵菱形BQNC

的面积为

∴BC=BQ=2，AQ=4 ∴∵

BQ=NQ ，∠AQB=∠AQN=60°，AQ=AQ ∴△ABQ ≌△ANQ ∴∠NAQ=∠BAQ=30° ∴∠BAO=30° ∴OA=

2

AB=3，即a =3 ∵点P 在y =

6

x

图象上，PA ⊥x 轴 ∴点P 坐标为（3，2） （3）易证△ABD

∽△BOA ，则

BD AB

OA

OB

= ∵OA=3，OB=1 ∴① 当Q 在线段BD 上时，如图3a 。 ∵四边形BCNQ 是平行四边形

∴CN ∥QD ，CN=BQ ∵C 是AQ 的中点

∴N 是AD 的中点 ∴CN=12

QD ∴BQ=12(BD -BQ) ∴BQ=1

3

∴

∴BC=

2

∴C □BCNQ

② 当Q 在线段BD 的延长线上时，如图3b 。 ∵BC=CQ=

12

AQ ∴平行四边形BCQN 是菱形 ∴AQ=2CQ=2BN ∵BN ∥AQ ∴1

2

BD BN DQ AQ == ∴DQ=2BD

∴

∴

∴

∴C □BCQN

故，该平行四边形的周长为

O C D

y

P B

F

y

x

P Q

A

(E)

F

O

C

D

y

x

P

B

O

C

F

y

x

P Q

A

(E)

F

O

C

D

x P

B

O C

E

A D y

x

P

Q

【2013·浙江嘉兴&舟山·24题与y 轴的交点为B ，连结AB ，AC ⊥AB ，交y 轴于点C ，延长CA 到点D ，使AD=AC ，连结BD 。作AE ∥x 轴，DE ∥y 轴。

（1）当m=2时，求点B 的坐标； （2）求DE 的长？

（3）①设点D 的坐标为（x ，y ），求y 关于x 的函数关系式？②过点D 作AB 的平行线，与第(3)①题确定的函数图象的另一个交点为P ，当m 为何值时，以A 、B 、D 、

P 为顶点的四边形是平行四边形？

解：（1）∵点B 是抛物线与y 轴的交点

∵m=2

∴点B 坐标为（0，2） （2）延长EA 交y 轴于F

∵DE ∥y 轴，AC=AD ∴DE=CF

，B （0，m ） ，AF ⊥BC ∴AF 2

=BF ·CF(射影定理) ∴CF=4，即DE=4

（3）①∵点D 的坐标为（x ，y ），DE=4

∴点E 的坐标为（x ，y -4）

211

4162

y x x =-

++ ②（i ）当四边形ABDP 为平行四边形时，如图右侧。

过点P 作PH ⊥DE 于H ，易证△PDH ≌△ABF ∴则点

3

2

m+4

即m 2-∵当m=0时，点A 、B 重合，故舍去 ∴m=8

(ii) 当四边形ABPD 为平行四边形时，如图左侧。

同理可得PH=AF=AE=-m ，则点P 坐标为（m ，m+4） 即m 2+∴m=-8

故，当m=±8时，以A 、B 、D 、P

为顶点的四边形是平行四边形