对数公式及对数函数的总结

对数的定义
①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.
②负数和零没有对数。③对数式与指数式的互化:log (0,1,0)x
a x N a N a a N =?=>≠>。
常用对数与自然对数
常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). 对数函数及其性质
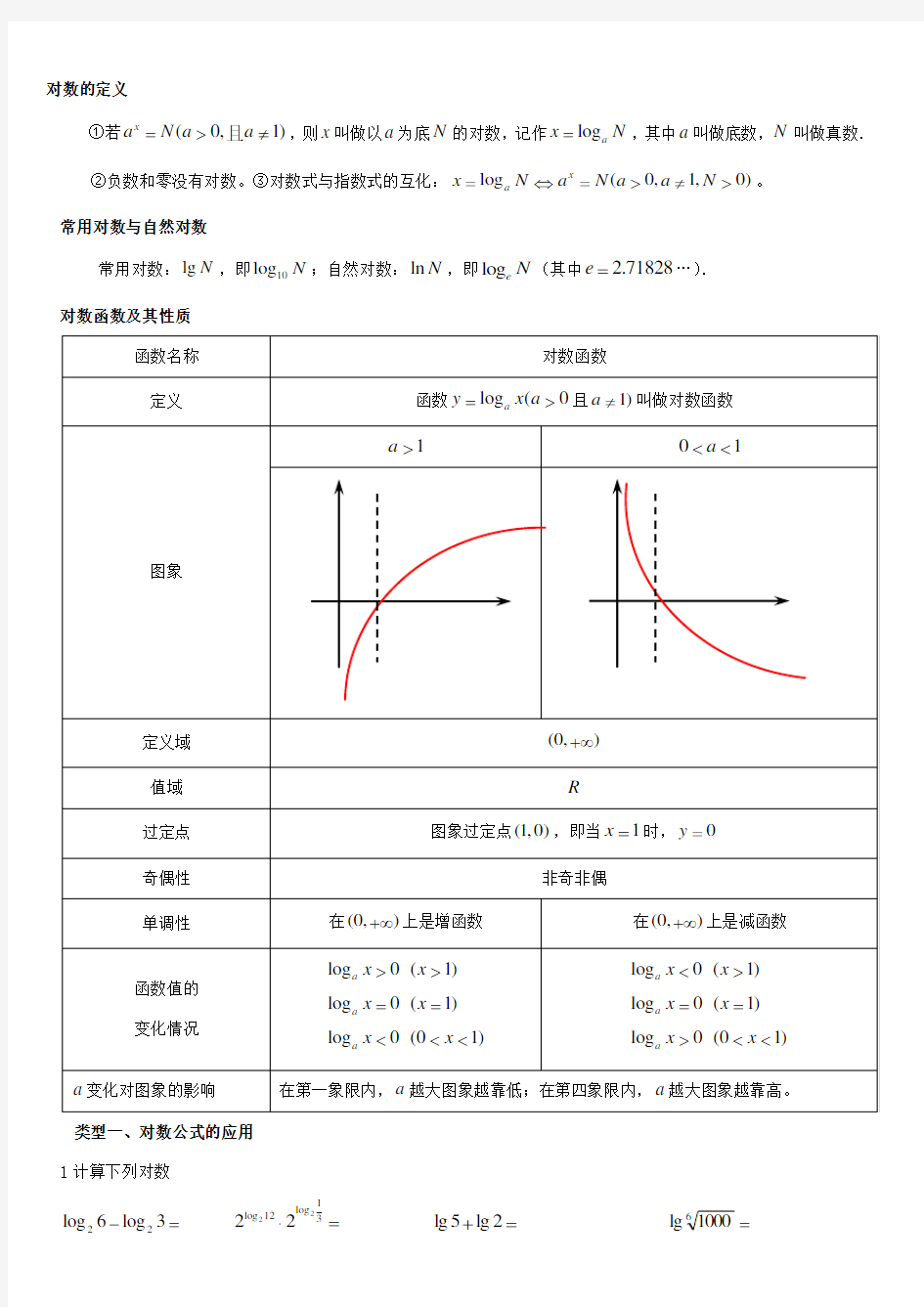
类型一、对数公式的应用 1计算下列对数
=-3log 6log 22 =?3
1log 12
log 2
22
2
=+2lg 5lg =61000lg
=+64log 128log 22 =?)24(log 432 =++)2log 2)(log 3log 3(log 9384
=++3log 23log 2242 =?16log 27log 32 =+-2log 90log 5log 333
=++c b a 842log log log =+++200
199lg 43lg 32lg
Λ =++32log 8log 8log 842 =+25.0log 10log 255 =-64log 325log 225 =)))65536(log (log (log log 2222
2 解对数的值:
18lg 7lg 37
lg
214lg -+- 0
-1
1
3
341log 2log 8??
-? ???
的值0 提示:对数公式的运算
如果0,1,0,0a a M N >≠>>,那么
(1)加法:log log log ()a a a M N MN += (2)减法:log log log a a a
M
M N N
-= (3)数乘:log log ()n
a a n M M n R =∈ (4)log a
N a N = (5)log log (0,)b n a a n
M M b n R b
=≠∈
(6)换底公式:log log (0,1)log b a b N
N b b a
=
>≠且 (7)1log log =?a b b a (8)a b b a log 1log =
类型二、求下列函数的定义域问题 1函数)13lg(13)(2
++-=
x x
x x f 的定义域是)1,31
(-
2设()x x x f -+=22lg
,则??
?
??+??? ??x f x f 22的定义域为 ()()4,11,4Y --
3
函数()f x = ]1,0()0,1(Y - )
提示:(1)分式函数,分母不为0,如0,1
≠=
x x
y 。 (2) 二次根式函数,被开方数大于等于0,0,≥=
x x y 。
(3)对数函数,真数大于0,0,log >=x x y a 。 类型三、对数函数中的单调性问题
1函数2
()lg(43)f x x x =-+的单调递增区间为( )1,(-∞ ) 2函数)152ln()(2--=x x x f 的单调递增区间是 ),5(+∞
3函数)23(log 2
5.0+-=x x y 的递增区间是( )1,(-∞ )
4已知,则的最小值为( -2 )
5若函数2
2log ()y x ax a =---
在区间(,1-∞上是增函数,a
的取值范围。[2-
6不等式1)12(log 3≤-x 的解集为 ]2,2
1(
7设函数()()()22log 4log 2f x x x =?,且x 满足241740x x -+≤,求()f x 的最大值。12.
提示:(1)在对数函数中x x f a log )(=中,当1>a ,)(x f 在其定义域上是增函数;当01>>a ,)(x f 在其定义域上是减函数。
(2)在复合函数)(log )(x g x f a =中,函数的单调性复合同增异减。 类型四、对数函数中的大小比较
1已知log 4log 4m n <,比较m ,n 的大小。01m n <<<
2已知4log ,3log ,2log 543===c b a ,比较c b a ,,的大小关系 a b c >> 3设,则c b a ,,的大小关系
4若0>>b a ,10< a c c > 5若1>a ,且y a x a a y a x log log -<---,则x 与y 之间的大小关系是( )0>>y x 提示:在b y a log =比较大小题型中,当1>a ,???<>>>>00101y x y x ;当01>>a ,? ??>>><>00101 y x y x 。 类型五、对数函数求值问题 1已知函数x x f lg )(=,若1)(=ab f ,则=+)()(2 2b f a f 2 2解方程08log 9log log )(log 3222 2=?--x x 8=x 或4 1= x 3已知1>>b a ,若2 5log log = +a b b a ,a b b a =,则a ,b 。 2,4==b a 4已知函数2log log )(32+-=x b x a x f ,若4)2014 1 ( =f ,则)2014(f 的值为_____0___. 提示:在对数函数求值过程中,主要用到对数公式 类型六、对数函数中的分段函数问题 1设函数()( )12 32 2log 1 2x e x f x x x -? ,,则()()2f f 的值为( 2 ) 2已知21()0()2log 0x x f x x x ??=??>?,, ,, ≤则21(8)(log )4f f +=___7________. 3已知函数满足:当4≥x ,则=;当4 提示:分段函数中涉及到对数公式,需要注意函数的定义域问题 类型七、对数函数中含参数问题 1若11 12 log <-a a ,则a 的取值范围是 ()4+∞, . 2 若关于x 的方程4)lg()lg(2 =?ax ax 的所有解都大于1,求a 的取值范围。)100 1, 0( 3函数)00(log )(≠>=a a x x f a 且,当),2[+∞∈x 时,1|)(|≥x f ,则a 的取值范围是( 2112 1 ≤<<≤a a 或 ) 4设1a >,函数()log a f x x =在区间[,2]a a 上的最大值与最小值之差为 1 2 ,则a = 4 提示:对数函数中有参数以及求参数的取值范围,需要考虑对数函数的单调性,综合性很强。 类型八、对数函数中的图像问题 1当1a >时,函数x x f a log )(=和x a x f )1()(-=的图象只可能是( ) 2函数x x x x f 2log )(= 的大致图象是( ) 3图2-2-2中的曲线是对数函数x y a log =的图象,已知a 取10 1 ,53,34,3四个值。则相应4321,,,c c c c 的a 值依 次为( 5 3 ,101, 3,34 ) 提示:函数的图像题型,先看奇偶性再看单调性,然后用特指排除。 类型九、对数函数中的奇偶性问题 1若函数)2(log )(2 2a x x x f a ++=是奇函数,则=a 2 2 。 2若函数)ln()(2x a x x x f ++=为偶函数,则=a 1 3若函数()( ) ax e x f x ++=1ln 3是偶函数,则=a ____3 2 -________. 4 若函数m x x f a +=log )(是偶函数,且在]4,2[上最大值为2,则m a +的值 2 提示:偶函数必有)()(x f x f =-,然后求参数。 类型十、对数函数中的绝对值问题 1 已知函数x x f ln )(=,若)()(b f a f =,求b a +的取值范围),2(+∞ 2已知函数)1lg()(+=x x f ,若b a ≠且)()(b f a f =,则b a +的取值范围是 0+∞(,) 3已知函数x x f lg )(=,若b a <<0,且)()(b f a f =,则b a 2+的取值范围是(3,)+∞ 提示:已知对数函数x x f a log )(=的图像,只需要把x 轴下方的图像翻到x 轴上方。如果当)()(b f a f =,且 b a <,必有1,10>< 类型十一、对数函数中的综合问题 1若函数)1(log )(++=x a x f a x 在]1,0[上的最大值和最小值之和为a ,则a 的值为( 2 ) 2 若42log (34)log a b +=a b +的最小值为( 7+) 3设点P 在曲线x e y 2 1= 上,点 Q 在曲线)2ln(x y =上,则PQ 的最小值为( )1ln 2- ) 4已知两个函数x x f a log )(=,x a x g =)(,(1)若)()()(x g x f x h +=,在]4,1[的最大值为18,求a 值;(2)对任意的]4,1[∈x 时,)()(x g x f ≤,求a 的取值范围。 【答案】(1)2=a ;(2)),2[)1,0(+∞∈Y a 。 提示:对数函数中可以和不等式,单调性,导数等进行综合,解答中需要多个知识点相结合多种考虑。 习题 类型一、关于对数公式的应用 1求下列各式中的x 的值: (1)313x = ;(2)64 1 4x =;(3)92x =; (4)1255x 2=;(5)171x 2=-;(6))4(lg )100(log )9(log 32?? 2化简下列各式: (1)51lg 5lg 32lg 4-+;(2) 5 36lg 27lg 321240 lg 9lg 21 1+--+ ;(3)3lg 70lg 7 3lg -+;(4)120lg 5lg 2lg 2-+ (5)4log 3log 54)5 1 ()41(+ (6) 2 log 2 log 4 log 7 101.03 17 10 3 -+(7)6 lg 3log 2log 100492575-+ (8)3 1 log 27 log 12 log 25 945 3 2 +- (9))2log 2(log )3log 3(log 9384+?+; (10)6log ]18log 2log )3log 1[(46626??+- (11) 3 log 9 log 28 3设25a b m ==,且 11 2a b +=,则m = 4计算 31 10 2 log 8)8 3 3()32()23(3 64log 3--+-++-的值 2. 5计算:( ) ) 310 log 23 0.02717lg 6lg 0.02- - +-的值 25 3 6计算:( )2 20 2 3 1lg 2lg5lg 200.0273-?? ++ +? ??? g 的值 102 7 计算:]1)2(log )41 )[(log 5lg 2(lg 14 12 1 -++-= -1 8计算:3 log 1 5log 15log 5log 52 333- -的值是(0 ) 9计算: 2 log 3 log 3log 2log )3log 2(log 32232 23-- +的值是( 2 ) 10已知z y x ,,为正数,且1243==y x ,求使 y x 1 1+的值。1 11已知lg a ,lg b 是方程22410x x -+=的两个根,则2 (lg )a b 的值是( 2 ) 12已知48a =,296m n ==,且 112+=b m n ,则1.2a 与0.8b 的大小关系____1.20.8>a b ___ 13设方程02102 =+-x x 的两个根分别为βα,,求2 224)(log βαβαβα-+-的值2 1 14已知)2lg(2lg lg y x y x -=+,求y x 2 log 的值。4 15实数)(,,c b c b a <,且)1lg()1lg()1lg(2-++=-c a b ,15,2=+++=c b a c a b ,求c b a ,,的值。1,5,9 16已知n m ,为正整数,0>a 且1≠a ,且n m n m m m a a a a a log log )1 11(log )11(log log +=-+++++ +Λ, 求n m ,的值。22.m n ??? =, = 类型二、对数函数的应用 1函数)1(log )(2 1-= x x f 的定义域是_]2,1(___. 2函数x x f 6log 21)(-=的定义域为 ]6,0( . 3函数4)(log )(2-=x x f 的定义域是( ),16[+∞) 4函数()()lg 43 x f x x -=-的定义域_)4,3()3,(Y -∞_。 5若,则的定义域为( ) 6函数) 34(log 1 )(5.0-= x x f 的定义域是(]1,43()7求函数)23(log 1log )(33-+=x x x f 的定义 域.),1()1,0(+∞Y 8函数234)1lg()(x x x x f --++=的定义域为( ]1,1( ) 9函数x x x x f )2ln()(2++-=的定义域是()2,0()0,1(Y -)10函数) 23(log 25)(2 --=x x x f a 的定义域是 (]5,1()1,32 (Y ) 11函数)86(log )(2)12(+-=-x x x f x 的定义域是( ),4()2,1()1,2 1(+∞Y Y ) 12函数]4)[(log log )(5.02-=x x f 的定义域是( )16 1 , 0( ) 13函数)(x f 的定义域是]2,1[-,则函数)(log 2x f 的定义域是_____]4,2 1[__. 14 函数141log )(5.0--= x x x f 的定义域是( )2 1 ,41()41,0(Y ) 15函数)416(log )()1(x x x f -=+的定义域是( )2,0()0,1(Y -) 16函数??? ? ??+-=-112log )()13(x x x f x 的定义域是 (),3 2()32 ,21[+∞Y ) 17函数()()2log 5x y x -=-的定义域是( ()()2,33,5? ) 18已知函数x x f 2 1log 2)(=的值域为]1,1[-,则函数)(x f 的定义域是( ]2,2 2 [ ) 19函数)2(log 2 5.0+=x y 的值域是( ]1,(--∞ ) 20函数)5(2log 5≥+=x x y 的值域是( ),2 5[+∞ ) 21函数x x f 2log )(=在]2,4 1[上的值域是( ]1,2[- ) 22函数)1(3log 2≥+=x x y 的值域是( ),3[+∞ ) 23函数)43(log 2+=x y 的值域是( ),2(+∞ ). 24函数)64(log 22++=x x y 的值域是( ),1[+∞ ). 25函数)64(log 22 1++=x x y 的值域是( ]1,(--∞ ). 26函数() 2 3log 2y x x =-的单调减区间是( (),0-∞ ) 27若函数)1,0( )(log )(3 ≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是 )1,4 3 [ 28已知函数)22(log )(2 2+-=x x x f ,使)(x f 是单调增函数的x 值的区间是( ),1[+∞ ) 29如果函数x a x f )3()(-=与x x g a log )(=的增减性相同,则a 的取值范围是___)2,1(_____. 30函数)124(log 23 1++-=x x y 的单调递减区间是__)2,2(-______. 31函数)32(log 2 3--=x x y 是单调增函数的区间是( ),3(+∞ ) 32函数]1)1[(log )(+-=x a x f a 在定义域上( A ) A .是增函数 B .是减函数 C .先增后减 D .先减后增 33已知10,10<<< 3(log <-x b a ,则x 的取值范围是__)4,3(______. 34设偶函数||log )(b x x f a +=在),0(+∞上单调递减,则)2(-b f 与)1(+a f 的大小关系是( A ) A. )1()2(+=-a f b f B. )1()2(+>-a f b f C. )1()2(+<-a f b f D. 不能确定 35函数||lg x y =( B ) A. 是偶函数,在区间)0,(-∞上单调递增 B. 是偶函数,在区间)0,(-∞上单调递减 C. 是奇函数,在区间),0(+∞上单调递增 D. 是奇函数,在区间),0(+∞上单调递减 36已知函数,若,求的取值范围; 37设2 ()lg( )1f x a x =+-是奇函数,则使()0f x <的x 的取值范围是((1,0)- ) 38若02log 2log < 130的大小关系是( 3log 1log 33 130>> ) 40如果02log 2log >>b a ,那么下面不等关系式中正确的是( 1>>b a ) 41设6log ,2 1 log ,2log 53 3===c b a ,则c b a ,,的大小关系( b a c >> ) 42若0a b >>,且1ab =,则下列不等式成立的是C (A )()21log 2a b a a b b + <<+ (B )()21log 2a b a b a b <+<+ (C )()21log 2 a b a a b b + <+< (D )()21log 2a b a b a b +<+< 43若13(1)ln 2ln ln x e a x b x c x -∈===,, ,,,则c b a ,,的大小关系(b 44若0.5 2a =,πlog 3b =,22π log sin 5 c =,则c b a ,,的大小关系( a b c >> ) 45设则c b a ,,的大小关系 46设均为正数,且,,.则c b a ,,的大小关系( ) 47已知324log 0.3 log 3.4 log 3.6 15,5 ,,5a b c ?? === ? ?? 则c b a ,,的大小关系 a c b >> 48若l n 2l n 3l n 5 ,,235 a b c = ==,则c b a ,,的大小关系 49已知5log ,4log ,3log 432===c b a ,比较c b a ,,的大小关系c b a >> 50若d x <<1,令)(log log log )(log 2 2x c x b x a d d d d ===,,,则c b a ,,的大小关系( c a b >> ) 51已知,00 ln e )(>≤?? ?=x x x x g x 则)]31([g g =___3 1 _____. 52已知函数()13 log 02 0x x x f x x >??=??≤?,,,若()12f a >,则实数a 的取值范围是( 1 ?- ?? ) 53已知函数,若,则( ) 54函数()()( )()2 2332log 12x x f x x x -? x f x ?≥????,, ( +),则)3log 2(2+f =____124____. 56已知732log [log (log )]0x =,那么1 2 x = 57设函数,( 9 ) 58已知函数???>+-≤-=-1 )1(log 122)(21x x x x f x ,且3)(-=a f ,则)6(a f -=-7 4 59已知函数13 33,1()log ,01x x f x x x ?-≥?=?< ???5log ,913 . 60已知函数???>≤=-1 log 12)(81x x x x f x ,若41 )(=x f ,求x 的值. 61函数224 log ([2,4])log y x x x =+∈的最大值是_5_____. 62若41 2x log 3= ,则=x _____9 1________. 63若)1(log )(3-=x x f ,使2)(=a f ,那么=a ______10_______. 64若12)1(log )(3++-=x x x f ,使5)(=a f ,那么=a ____2_________. 65已知函数x x f 5log )(=,求)5()325( )3(f f f -+的值. 2 3 66已知函数 )1(log )(2+=x x f ,若()1,f α=则α= 1 67对数函数的图象过点(8,3),则此函数的解析式为___x x f 2log )(=_____. 68设0>a 且1≠a ,函数x y a log =和x y a 1 log =的图象关于( A ) A .x 轴对称 B .y 轴对称 C .y =x 对称 D .原点对称 69已知函数x a x x f -+=1log )(2的图象关于原点对称,则实数a 的值为___1_____. 70已知函数x x a x a x x f --+-+=221log )(2的图象关于原点对称,则实数a 的值为_____1___. 71函数?? ? ??-+=112lg x y 的图象关于( 原点 )对称 72若12log 74等比数列{}n a 的各项均为正数,且564718a a a a +=,则3132310log log log a a a +++=L ( 10 ) 75已知函数()f x 是奇函数,当0x >时,()()0,1x f x a a a =>≠且,且21log 34f ? ?=- ?? ?, 则a 点的值为) 76函数()f x 的图象关于y 轴对称,且对任意x R ∈都有()()3f x f x +=-,若当3 5 2 2x ??∈ ???,时,()12x f x ??= ???, 则()2017f =( 1 4- ) 77 函数()y f x =的图象与函数3log (0)y x x =>的图象关于直线y x =对称,则 ()f x =__x y 3=__________。 78设x x f a log )(=(0>a 且1≠a ),若1)()()(21=+++n x f x f x f Λ(+ ∈R x i ,n i ,,2,1Λ=),则 )()()(3 3231n x f x f x f +++Λ的值等于____3____。 79将函数2log y x =的图象向左平移一个单位,得到图象C 1,再将C 1向上平移一个单位得到图象C 2,则C 2的解析式为________。)1(log 12+=-x y 80已知1x 是方程2008lg =x x 的根,2x 是方程200810=?x x 的根,求12x x 的值.2008 81设常数1a >,实数x 、y 满足log 2log log 3a x x x a y ++=-,若y ,则x 的值为( 1 8 ) 82已知对数函数 ()log (0a f x x a =>,且1)a ≠在区间上的最大值与最小值之积为,则a = ( 2 ) 83若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a 的值为____4 2 ____. 84若函数)1(log )(>=a x x f a 在区间]4,[a a 上的最大值是最小值的3倍,则a 的值为( 2 ) 85若函数)1(log )(>=a x x f a 在区间]47,[2+a a 上的最大值是最小值的差为a 2,则a 的值为( 2 ) 86 若函数)01y a a = >≠且的定义域和值域都是[]0,1,则548log log 65 a a += 3 87已知函数x x f 2 1log )(=,当][2 a a x ,∈时,函数的最大值比最小值大3,则实数a 的值8 88若函数)1(log )(++=x a x f a x 在]1,0[上的最大值和最小值之和为a ,则a 的值为( 2 1 ) 89若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a 的值为____ 4 2 ____. 90函数 )1(log >+=a a x y x a 在]2,1[上的最大值与最小值之差为 2 3a ,求x x a a -+在]2,2[-上的最小值为2 91若x 满足 ,求()f x =最大值和最小值。2 4 3 92设函数()()2 1f x x aIn x =++有两个极值点12x x 、,且12x x <,求a 的取值范围,)2 1,0( 93若函数)12lg(2 ++=x ax y 的值域为R ,则实数a 的取值范围为___]1,0[____。 94若函数)34(log )(2 2++=kx kx x f 的定义域为R ,则实数k 的取值范围是________。?? ????43,0 95函数x y a log =在),2[+∞上恒有1>y ,则a 取值范围是___)2,1()1,2 1(Y _____. 96已知?? ?≥<--=1log 14)6()(x x x a x a x f a 是R 上的增函数,求a 的取值范围.)6,56 [ 97已知?????≥<--=22log 2 2)3 2()(x x x a x a x f a 是R 上的减函数,求a 的取值范围.)32,81[ 98已知函数)2(log ax y a -=在]1,0[上是x 的减函数,则a 的取值范围是( )2,1( ) 99已知函数)3(log )(ax x f a -=,当]2,0[∈x 时,函数)(x f 恒有意义,求实数a 的取值范围。)2 3,1()1,0(Y 100若不等式0log 2 ≤-x x a 在??? ??∈21, 0x 内恒成立,则a 的取值范围是( )1,16 1 [ 101函数)53(log )(2 5.0+-=ax x x f 在),1[+∞-上是减函数,求实数a 的取值范围. 102当2 10≤ log 4<,则a 的取值范围是()1,22( ) 103已知函数24 3 log 1≤ ,则实数a 的取值范围是( ]23,43( ) 104如果2)2(log )(2 ≥+=x x x f a 的解集为),2[]4,(+∞--∞Y ,则实数a 的值是( 2 ) 105函数)(log )(2 3a ax x x f -+=的定义域是R ,则实数a 的取值范围是__)2,2(-_ 106函数)1(log 22)(2--=x x f x ,若6)(≥a f ,则实数a 的取值范围是____),2[+∞_________. 107已知x x x f a -+=33log )(,其定义域为)3,3(-,试判断)(x f 的奇偶性并证明. 108判断下列函数的奇偶性: (1)x x x f +-=11lg )( (2))1ln()(2x x x f -+= (3))1ln()(2x x x x f ++= 109试比较2 2 lg )(lg x x 与的大小。 110函数3)2(log ++=x y a 的图象过定点__)3,1(-______. 111函数3)2(log --=x y a 的图象过定点___)3,3(-_____ 112函数1)3(log +-=x y a 的图象过定点__)1,2(______ 112函数2)3(log 2 ++-=-x a a x y 的图象过定点___)3,2()0,1(-_____ 113使1)(log 2+<-x x 成立x 的取值范围 114函数)(log 2log )(22c x x x f +-=,其中0>c ,若对任意),0(+∞∈x ,有1)(≤x f ,则c 的取值范围是_8 1≥ c 115设10< x a a a x f ,则使0)( 116函数2()log (2x 1),(a 0,a 1)a a f x x =+->≠且的图象必过的定点坐标为__(1,1)___. 117已知函数满足:且.( B ) A.若,则 B.若,则 C.若,则 D.若,则 118函数的值域为 (),0-∞ . 119已知函数()f x =,若ax x f ≥)(,则的取值范围是[2,0]- 120函数??? ??>+-≤<=062 1100lg )(x x x x x f 若c b a ,,均不相等,且)()()(c f b f a f ==,则abc 的取值范围是)12,10( 121设函数)(x f y =的图像与a x y +=2关于直线x y -=对称,且1)4()2(=+-f f ,则=a 2 122已知函数()()21 02 x f x x e x =+-<与()()2ln g x x x a =++的图象上存在关于y 轴对称的点, 则a 的取值范围是( (-∞ ) 123已知两条直线1l :m y =和2l :)0(1 28 >+= m m y ,1l 与函数x y 2log =的图象从左至右相交于点B A 、, 2l 与函数x y 2log =的图象从左至右相交于点D C ,,记线段AC 和BD 在x 轴上的投影长度分别为b a ,,当m 变化时,求b a 的最小值.28 124若1x 满足522=+x x , 2x 满足5)1(log 222=-+x x ,则1x +2x = 2 7 125函数x y )3 1(=的图象与函数x y 3log -=的图象关于直线_____x y =________对称. 126函数()? ??>+-≤-=1,341 ,442x x x x x x f 的图象和函数()x x g 2log =的图象的交点个数是( 3 ) 127当1>a 时,在同一坐标系中,函数x a y -=与x y a log =的图象是( ) 128已知x x f lg )(=,则|)1(|x f y -=的图象( ) 129函数x x f 2log 1)(+=与1 2 )(+-=x x g 在同一直角坐标系下的图象大致是( c ) 130函数|1|| |ln --=x e y x 的图象大致是( D ) 131已知0>a ,且1≠a ,函数x a y =与)(log x y a -=的图象只能是图中的( ) 132已知函数1 ()ln(1)f x x x =+-;则()y f x =的图像大致为( ) 133已知函数,函数(,且) (1)求函数的定义域 (2)求使函数)()(x f x g y -=的值为负数的的取值范围: 答案:当时,的取值范围是;当时,的取值范围是. 134已知函数()log (2)log (3),a a f x x x =++-其中01a <<. (1)求函数()f x 的定义域;)3,2(- (2)若函数()f x 的最小值为-4,求a 的值.5 a ∴= 135已知函数2()log (1)f x x =+,2()log (31)g x x =+. (1)求出使()()g x f x ≥成立的x 的取值范围;0x ≥ (2)在(1)的范围内求()()y g x f x =-的最小值.当0x =时,min 1u =,从而min 0y = 136已知函数2 42)1lg()1lg()(x x x x x f -+++-= (1)求函数)(x f 的定义域;)1,1(-. (2)判断函数)(x f 的奇偶性; (3)求函数)(x f 的值域]0,(-∞ 137已知函数2 ()(lg 2)lg f x x a x b =+++满足(1)2f -=-,且对于任意的x R ∈,恒有()2f x x ≥成立. (1)求实数a ,b 的值;即10b =,100a = (2)解不等式()5f x x <+.{}|41x x -<< 138已知函数. (1)设,函数的定义域为, 求的最大值;4 (2)当时,求使的的取值范围. 139已知函数2()log ()(1)f x g x k x =+-. (1)若2(log )1g x x =+,且()f x 为偶函数,求实数k 的值;12 k = (2)当1k =,2 ()(1)g x ax a x a =+++时,若函数()f x 的值域为R ,求实数a 的取值范围.[]0,1 140已知R a ∈,函数()f x =21log ()a x +. (1)当 1a =时,解不等式1)(>x f ; (2)若关于x 的方程()f x +2 2log ()x =0的解集中恰有一个元素,求a 的值;0a =或14 - . (3)设0>a ,若对任意t ∈1[,1]2 ,函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围.),3 2[+∞ 141设函数 (1)求的定义域; (2)时,求使的所有值. 142已知x x x f a -+=11log )()1,0(≠>a a 。 (1)求)(x f 的定义域;)1,1(-(2)判断)(x f 的奇偶性;奇函数(3)求使0)(>x f 的x 的取值范围。故当1>a 时,)1,0(∈x ;当10< f x f 2lo g )1 (1)(?+=。 (1)求函数)(x f 的解析式;x x x f 2 22log 1log 1)(++= (2)求)2(f 的值;1(3)解方程)2()(f x f =。1=x 或2=x 。 144已知函数)(log )(x a a a x f -=(1>a )。 (1)求)(x f 的定义域、)1,(-∞值域;)1,(-∞(2)判断)(x f 的单调性;所以函数)(log )(x a a a x f -=在) 1,(-∞上是减函数; 145已知函数)2lg()(2 m x x x f +-=(R m ∈,且为常数)。 (1)求这个函数的定义域;(2)函数)x (f 的图象有无平行于y 轴的对称轴? (3)函数)(x f 的定义域与值域能否同时为实数集R ?证明你的结论。 146已知函数)35(log )42(log 3231x y x y -=+=,. (1)分别求这两个函数的定义域; (2)求使21y y =的x 的值; (3)求使21y y >的x 值的集合. 147已知函数)1lg()(2x x x f -+= (1)求函数的定义域; (2)证明:)(x f 是减函数. 指数函数及对数函数重难点 根式的概念: ①定义:若一个数的n 次方等于),1(* ∈>N n n a 且,则这个数称a 的n 次方根.即,若 a x n =,则x 称a 的n 次方根)1*∈>N n n 且, 1)当n 为奇数时,n a 的次方根记作n a ; 2)当n 为偶数时,负数a 没有n 次方根,而正数a 有两个n 次方根且互为相反数,记作 )0(>±a a n . ②性质:1)a a n n =)(; 2)当n 为奇数时,a a n n =; 3)当n 为偶数时,???<-≥==) 0() 0(||a a a a a a n 幂的有关概念: ①规定:1)∈???=n a a a a n ( N * , 2))0(10 ≠=a a , n 个 3)∈=-p a a p p (1 Q ,4)m a a a n m n m ,0(>=、∈n N * 且)1>n ②性质:1)r a a a a s r s r ,0(>=?+、∈s Q ), 2)r a a a s r s r ,0()(>=?、∈s Q ), 3)∈>>?=?r b a b a b a r r r ,0,0()( Q ) (注)上述性质对r 、∈s R 均适用. 例 求值 (1) 3 28 (2)2 125 - (3)()5 21- (4)() 43 8116- 例.用分数指数幂表示下列分式(其中各式字母均为正数) (1)43a a ? (2)a a a (3)32 )(b a - (4)43 )(b a + (5)32 2b a ab + (6)42 33 )(b a + 例.化简求值 (1)0 121 32322510002.08 27)()()()(-+--+---- (2)2 11 5 3125.05 25 .231 1.0)32(256) 027.0(?? ????+-+-????? ?-- (3)=?÷ ?--3133 73 32 9a a a a (4)21 1511336622263a b a b a b ??????-÷- ??? ??????? = (5)6323 1.512??= 指数函数的定义: ①定义:函数)1,0(≠>=a a a y x 且称指数函数, 1)函数的定义域为R , 2)函数的值域为),0(+∞, 3)当10<a 时函数为增函数. 提问:在下列的关系式中,哪些不是指数函数,为什么? (1)2 2 x y += (2)(2)x y =- (3)2x y =- (4)x y π= (5)2y x = (6)2 4y x = (7)x y x = (8)(1)x y a =- (a >1,且2a ≠) 例:比较下列各题中的个值的大小 (1)1.72.5 与 1.7 3 ( 2 )0.1 0.8 -与0.2 0.8 - ( 3 ) 1.70.3 与 0.93.1 例:已知指数函数()x f x a =(a >0且a ≠1)的图象过点(3,π),求 (0),(1),(3)f f f -的值. 思考:已知0.7 0.9 0.8 0.8,0.8, 1.2,a b c ===按大小顺序排列,,a b c . 例 如图为指数函数x x x x d y c y b y a y ====)4(,)3(,)2(,)1(,则 d c b a ,,,与1的大小关系为 O x y a d c b 专题:对数函数知识点总结 1.对数函数的定义: 一般地,函数 x y a log =( )叫做对数函数 .定义域是 2. 对数函数的性质为 思考:函数log a y x =与函数x y a =)10(≠>a a 且的定义域、值域之间有什么关系? ___________________________________________________________________________ 对数函数的图象与指数函数的图象关于_______________对称。 一般的,函数y=a x 与y=log a x (a>0且a ≠1)互称相对应的反函数,它们的图象关于直线y=x 对称 y=f(x)存在反函数,一般将反函数记作y=f -1 (x) 如:f(x)=2x ,则f -1 (x)=log 2x,二者的定义域与值域对调,且图象关 于直线y=x 对称 函数与其反函数的定义域与值域对调,且它们的图象关于直线y=x 对称 专题应用练习 一、求下列函数的定义域 (1)0.2log (4);y x =-; (2)log 1a y x =- (0,1).a a >≠; (3)2(21)log (23)x y x x -=-++ (4)2log (43)y x =- (5) y=lg 1 1 -x (6) y=x 3log =log(5x-1)(7x-2)的定义域是________________ = )8lg(2x - 的定义域是_______________ 3.求函数2log (21)y x =+的定义域___________ 4.函数y=13 log (21)x -的定义域是 5.函数y =log 2(32-4x )的定义域是 ,值域是 . 6.函数5log (23)x y x -=-的定义域____________ 7.求函数2 log ()(0,1)a y x x a a =->≠的定义域和值域。 8.求下列函数的定义域、值域: (1)2log (3)y x =+; (2)2 2log (3)y x =-; (3)2log (47)a y x x =-+(0a >且1a ≠). 9.函数f (x )=x 1 ln (432322+--++-x x x x )定义域 10.设f(x)=lg x x -+22,则f )2 ()2(x f x +的定义域为 11.函数f(x)=)1(lo g 1 |2|2---x x 的定义域为 12.函数f(x)= 2 29)2(1x x x g --的定义域为 ; 13.函数f (x )= x 1 ln (432322+--++-x x x x )的定义域为 14 2 2 2 log log log y x =的定义域是 1. 设f (x )=lg(ax 2 -2x +a ), (1) 如果f (x )的定义域是(-∞, +∞),求a 的取值围; (2) 如果f (x )的值域是(-∞, +∞),求a 的取值围. 15.已知函数)32(log )(22 1+-=ax x x f (1)若函数的定义域为R ,数a 的取值围 (2)若函数的值域为R ,数a 的取值围 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数y a y x x a ==,l o g 在a >1及01<≠01且叫指数函数。 定义域为R ,底数是常数,指数是自变量。 为什么要求函数y a x =中的a 必须a a >≠01且。 因为若a <0时,()y x =-4,当x = 14 时,函数值不存在。 a =0,y x =0,当x ≤0,函数值不存在。 a =1时,y x =1对一切x 虽有意义,函数值恒为1,但 y x =1的反函数不存在, 因为要求函数y a x =中的 a a >≠01且。 1、对三个指数函数y y y x x x ==?? ?? ?=21210,,的图象的 认识。 图象特征与函数性质: 对图象的进一步认识,(通过三个函数相互关系的比较): ①所有指数函数的图象交叉相交于点(0,1),如y x =2和y x =10相交于()01,,当x >0时,y x =10的图象在y x =2的图象的上方,当x <0,刚好相反,故有10222>及10222--<。 ②y x =2与y x =?? ? ? ?12的图象关于y 轴对称。 ③通过y x =2,y x =10,y x =?? ? ? ?12三个函数图象,可以画出任意一个函数y a x =(a a >≠01且)的 示意图,如y x =3的图象,一定位于y x =2和y x =10两个图象的中间,且过点()01,,从而y x =?? ? ? ? 13也由 关于y 轴的对称性,可得y x =?? ? ? ?13的示意图,即通过有限个函数的图象进一步认识无限个函数的图象。 2、对数: 定义:如果a N a a b =>≠()01且,那么数b 就叫做以a 为底的对数,记作b N a =l o g (a 是底数,N 是真数,log a N 是对数式。) 由于N a b =>0 故log a N 中N 必须大于0。 当N 为零的负数时对数不存在。 (1)对数式与指数式的互化。 由于对数是新学的,常常把不熟悉的对数式转化为指数式解决问题,如: 求lo g .032524?? ? ? ? 分析:对于初学者来说,对上述问题一般是束手无策,若将它写成log .032524?? ? ? ?=x ,再改写为指数式就比较好办。 解:设log .032524?? ? ? ?=x 专题:对数函数知识点总结 1.对数函数的定义: 一般地,函数 x y a log =( )叫做对数函数 .定义域是 2. 对数函数的性质为 思考:函数log a y x =与函数x y a =)10(≠>a a 且的定义域、值域之间有什么关系? ___________________________________________________________________________ 对数函数的图象与指数函数的图象关于_______________对称。 | 一般的,函数y=a x 与y=log a x (a>0且a ≠1)互称相对应的反函数,它们的图象关于直线y=x 对称 y=f(x)存在反函数,一般将反函数记作y=f -1 (x) 如:f(x)=2x ,则f -1 (x)=log 2x,二者的定义域与值域对调,且图象关 于直线y=x 对称 函数与其反函数的定义域与值域对调,且它们的图象关于直线y=x 对称 专题应用练习 一、求下列函数的定义域 (1)0.2log (4);y x =-; (2 )log a y =(0,1).a a >≠; (3)2 (21)log (23)x y x x -=-++ (4 )y = ? (5) y=lg 1 1 -x (6) y=x 3log =log(5x-1)(7x-2)的定义域是________________ = )8lg(2x - 的定义域是_______________ 3.求函数2log (21)y x =+的定义域___________ 4.函数 的定义域是 5.函数y =log 2(32-4x )的定义域是 ,值域是 . 6.函数5log (23)x y x -=-的定义域____________ { 7.求函数2 log ()(0,1)a y x x a a =->≠的定义域和值域。 8.求下列函数的定义域、值域: (1)2log (3)y x =+; (2)2 2log (3)y x =-; (3)2log (47)a y x x =-+(0a >且1a ≠). 9.函数f (x )=x 1 ln (432322+--++-x x x x )定义域 10.设f(x)=lg x x -+22,则f )2 ()2(x f x +的定义域为 对数 导读:本文是关于对数,希望能帮助到您! 教学目标 1.理解对数的概念,掌握对数的运算性质. (1) 了解对数式的由来和含义,清楚对数式中各字母的取值范围及与指数式之间的关系.能认识到指数与对数运算之间的互逆关系. (2) 会利用指数式的运算推导对数运算性质和法则,能用符号语言和文字语言描述对数运算法则,并能利用运算性质完成简单的对数运算. (3) 能根据概念进行指数与对数之间的互化. 2.通过对数概念的学习和对数运算法则的探究及证明,培养学生从特殊到一般的概括思维能力,渗透化归的思想,培养学生的逻辑思维能力. 3.通过对数概念的学习,培养学生对立统一,相互联系,相互转化的思想.通过对数运算法则的探究,使学生善于发现问题,揭示数学规律从而调动学生思维的积极参与,培养学生分析问题,解决问题的能力及大胆探索,实事求是的科学精神. 教学建议 教材分析 (1) 对数既是一个重要的概念,又是一种重要的运算,而且它是与指数概念紧密相连的.它们是对同一关系从不同角度的刻 画,表示为当时,.所以指数式中的底数,指数,幂与对数式中的底数,对数,真数的关系可以表示如下: (2) 本节的教学重点是对数的定义和运算性质,难点是对数的概念. 对数首先作为一种运算,由引出的,在这个式子中已知一个数和它的指数求幂的运算就是指数运算,而已知一个数和它的幂求指数就是对数运算(而已知指数和幂求这个数的运算就是开方运算),所以从方程角度来看待的话,这个式子有三个量,知二求一.恰好可以构成以上三种运算,所以引入对数运算是很自然的,也是很重要的,也就完成了对的全面认识.此外对数作为一种运算除了认识运算符号“”以外,更重要的是把握运算法则,以便正确完成各种运算,由于对数与指数在概念上相通,使得对数法则的推导应借助指数运算法则来完成,脱到过程又加深了指对关系的认识,自然应成为本节的重点,特别予以关注.对数运算的符号的认识与理解是学生认识对数的一个障碍,其实与+,等符号一样表示一种运算,不过对数运算的符号写在前面,学生不习惯,所以在认识上感到有些困难. 教法建议 (1)对于对数概念的学习,一定要紧紧抓住与指数之间的关系,首先从指数式中理解底数和真数的要求,其次对于对数的性质及零和负数没有对数的理解也可以通过指数式来证明,验证.同时在关系的指导下完成指数式和对数式的互化. 对数公式的运用 1.对数的概念 如果a(a>0,且a≠1)的b次幂等于N,即a b=N,那么数b叫做以a为底N的对数,记作:log a N=b,其中a叫做对数的底数,N叫做真数. 由定义知: ①负数和零没有对数; ②a>0且a≠1,N>0; ③log a1=0,log a a=1,a logaN=N(对数恒等式),log a a b=b。 特别地,以10为底的对数叫常用对数,记作log10N,简记为lgN; 以无理数e(e=2.718 28…)为底的对数叫做自然对数,记作log e N,简记为lnN. 2.对数式与指数式的互化 式子名称a b=N 指数式a b=N(底数)(指数)(幂值) 对数式log a N=b(底数) (真数) (对数) 3.对数的运算性质 如果a>0,a≠1,M>0,N>0,那么 (1)log a(MN)=log a M+log a N. (2)log a(M/N)=log a M-log a N. (3)log a M n=nlog a M(n∈R). 问:①公式中为什么要加条件a>0,a≠1,M>0,N>0? ②log a a n=? (n∈R) ③对数式与指数式的比较.(学生填表) 式子a b=N,log a N=b名称:a—幂的底数b—N— a—对数的底数b—N— 运算性质: a m·a n=a m+n a m÷a n= a m-n (a>0且a≠1,n∈R) log a MN=log a M+log a N log a MN= log a M n= (n∈R) (a>0,a≠1,M>0,N>0) 难点疑点突破 对数定义中,为什么要规定a>0,,且a≠1? 理由如下: ①a<0,则N的某些值不存在,例如log-28=? ②若a=0,则N≠0时b不存在;N=0时b不惟一,可以为任何正数? ③若a=1时,则N≠1时b不存在;N=1时b也不惟一,可以为任何正数? 为了避免上述各种情况,所以规定对数式的底是一个不等于1的正数? 指数函数和对数函数 1、指数函数: 定义:函数() y a a a x =>≠01且叫指数函数。 定义域为R ,底数是常数,指数是自变量。 为什么要求函数y a x =中的a 必须a a >≠01且。 因为若a <0时,()y x =-4,当x = 1 4 时,函数值不存在。 a =0,y x =0,当x ≤0,函数值不存在。 a =1时,y x =1对一切x 虽有意义,函数值恒为1,但y x =1的反函数不存在, 因为要求函数y a x =中的a a >≠01且。 1、对三个指数函数y y y x x x ==?? ? ? ?=21210,,的图象的认识。 对图象的进一步认识,(通过三个函数相互关系的比较): ①所有指数函数的图象交叉相交于点(0,1),如y x =2和y x =10相交于()01,, 当x >0时,y x =10的图象在y x =2的图象的上方,当x <0,刚好相反,故有102 2 2 >及1022 2--<。 ②y x =2与y x =?? ?? ?12的图象关于y 轴对称。 ③通过y x =2,y x =10,y x =?? ?? ?12三个函数图象,可以画出任意一个函数y a x =(a a >≠01且)的示意图,如y x =3的图象,一定位于y x =2和y x =10两个图象的中 间,且过点()01,,从而y x =?? ???13也由关于y 轴的对称性,可得y x =?? ? ? ?13的示意图,即 通过有限个函数的图象进一步认识无限个函数的图象。 2、对数: 定义:如果a N a a b =>≠()01且,那么数b 就叫做以a 为底的对数,记作b N a =log (a 是底数,N 是真数,log a N 是对数式。) 由于N a b =>0故log a N 中N 必须大于0。 当N 为零的负数时对数不存在。 (1)对数式与指数式的互化。 由于对数是新学的,常常把不熟悉的对数式转化为指数式解决问题,如: 求log .032524?? ? ? ? 分析:对于初学者来说,对上述问题一般是束手无策,若将它写成log .032524?? ? ? ?=x 再改写为指数式就比较好办。解:设log .032524?? ? ? ?=x 则即∴即032524 8258251 2 5241 212 032.log .x x x = ?? ???=?? ???=- ?? ?? ?=- - 评述:由对数式化为指数式可以解决问题,反之由指数式化为对数式也能解决问题,因此必须因题而异。如求35x =中的x ,化为对数式x =log 35即成。 (2)对数恒等式: 由a N b N b a ==()log ()12 将(2)代入(1)得a N a N log = 运用对数恒等式时要注意此式的特点,不能乱用,特别是注意转化时必须幂的底数和 对数的底数相同。 计算: () 313 2 -log 解:原式==?? ?? ?-=3 131 2 222 13 1 3 log log 。 (3)对数的性质: 1对数的概念 如果a(a>0,且a≠1)的b次幂等于N,即ab=N,那么数b叫做以a为底N的对数,记作:logaN=b,其中a叫做对数的底数,N叫做真数. 由定义知: ①负数和零没有对数; ②a>0且a≠1,N>0; ③loga1=0,logaa=1,alogaN=N,logaab=b. 特别地,以10为底的对数叫常用对数,记作log10N,简记为lgN;以无理数e(e=2.718 28…)为底的对数叫做自然对数,记作logeN,简记为lnN. 2对数式与指数式的互化 式子名称abN指数式ab=N(底数)(指数)(幂值)对数式logaN=b(底数)(对数)(真数) 3对数的运算性质 如果a>0,a≠1,M>0,N>0,那么 (1)loga(MN)=logaM+logaN. (2)logaMN=logaM-logaN. (3)logaMn=nlogaM (n∈R). 问:①公式中为什么要加条件a>0,a≠1,M>0,N>0? ②logaan=? (n∈R) ③对数式与指数式的比较.(学生填表) 式子ab=NlogaN=b名称a—幂的底数 b— N—a—对数的底数 b— N—运 算 性 质am?an=am+n am÷an= (am)n= (a>0且a≠1,n∈R)logaMN=logaM+logaN logaMN= logaMn=(n∈R) (a>0,a≠1,M>0,N>0) 难点疑点突破 对数定义中,为什么要规定a>0,,且a≠1? 理由如下: ①若a<0,则N的某些值不存在,例如log-28 ②若a=0,则N≠0时b不存在;N=0时b不惟一,可以为任何正数 ③若a=1时,则N≠1时b不存在;N=1时b也不惟一,可以为任何正数 为了避免上述各种情况,所以规定对数式的底是一个不等于1的正数 解题方法技巧 1 高一数学必修一对数及对数函数知识点总 结 数学是学习和研究现代科学技术必不可少的基本工具。以下是查字典数学网为大家整理的高一数学必修一对数及 对数函数知识点,希望可以解决您所遇到的相关问题,加油,查字典数学网一直陪伴您。 对数定义 如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底N的对数,记作x=logaN。其中,a叫做对数的底数,N叫做真数。 注: 1.以10为底的对数叫做常用对数,并记为lg。 2.称以无理数e(e=2.71828...)为底的对数称为自然对数,并记为ln。 3.零没有对数。 4.在实数范围内,负数无对数。在复数范围内,负数是有对数的。 对数公式 0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。/p p其中x 是自变量,函数的定义域是(0,+∞)。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定, 同样适用于对数函数。/p p对数函数性质/p p align=" center="" img="" /> 定义域求解:对数函数y=logax的定义域是{x丨x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意大于0以外,还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需同时满足x>0且x≠1和2x-1>0,得到x>1/2且x≠1,即其定义域为{x丨x>1/2且x≠1} 值域:实数集R,显然对数函数无界。 定点:函数图像恒过定点(1,0)。 单调性:a>1时,在定义域上为单调增函数; 奇偶性:非奇非偶函数 周期性:不是周期函数 对称性:无 最值:无 零点:x=1 注意:负数和0没有对数。 两句经典话:底真同对数正,底真异对数负。 要练说,得练听。听是说的前提,听得准确,才有条件正确模仿,才能不断地掌握高一级水平的语言。我在教学中,注意听说结合,训练幼儿听的能力,课堂上,我特别重视教师的语言,我对幼儿说话,注意声音清楚,高低起伏,抑扬有致,富有吸引力,这样能引起幼儿的注意。当我发现有的幼 对数及对数函数 1、对数的基本概念 (1)一般地,如果a (1,0≠>a a )的b 次幂等于N ,就是N a b =,那么数b 叫做以a 为底N 的对 数, 记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式 (2)常用对数:N 10log ,记作N lg ; 自然对数N e log (e =2.71828…),记作N ln . (3)指数式与对数式的关系:log x a a N x N =?=(0>a ,且1≠a ,0N >) (4)对数恒等式: 2、对数的性质 (1)负数和零没有对数,即0>N ; (2)1的对数是零,即01log =a ; (3)底的对数等于1,即1log =a a 3、对数的运算性质 (1)如果a >0,a ≠1,M >0,N >0,那么 ①N M MN a a a log log )(log +=; ②N M N M a a a log log log -=; ③M n M a n a log log = (2)换底公式: 推论:① b N N b log 1log = ; ② ; ③ 1log log =?a b b a 4、对数函数的定义: 函数 叫做对数函数,其中x 是自变量 (1)研究对数函数的图象与性质: 由于对数函数 与指数函数 互为反函数,所以 的图像和 的图像关于直线 对称。 (2)复习)10(≠>=a a a y x 且的图象和性质 ()010log >≠>=N a a N a N a ,且b N N a a b log log log = b m n b a n a m log log =a y log x =(a 0a 1)>≠且a y log x =x y a =a y log x =x y a =y x = 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数 y a y x x a ==,log 在a >1及01<≠01且叫指数函数。 定义域为R ,底数是常数,指数是自变量。 为什么要求函数y a x =中的a 必须a a >≠01且。 因为若a <0时,()y x =-4,当x =1 4 时,函数值不存在。 a =0,y x =0,当x ≤0,函数值不存在。 a =1时,y x =1对一切x 虽有意义,函数值恒为1, 但y x =1的反函数不存在,因为要求函数y a x =中的a a >≠01且。 1、对三个指数函数y y y x x x ==?? ? ? ?=21210,,的图 象的认识。 对图象的进一步认识,(通过三个函数相互关系的比较): ①所有指数函数的图象交叉相交于点(0,1),如y x =2和y x =10相交于()01,,当x >0 时,y x =10的图象在y x =2的图象的上方,当x <0,刚好相反,故有10222>及 10222--<。 ②y x =2与y x =?? ?? ?12的图象关于y 轴对称。 ③通过y x =2,y x =10,y x =?? ?? ?12三个函数图象,可以画出任意一个函数y a x =(a a >≠01且)的示意图,如y x =3的图象,一定位于y x =2和y x =10两个图象的中 间,且过点()01,,从而y x =?? ???13也由关于y 轴的对称性,可得y x =?? ? ? ?13的示意图,即 通过有限个函数的图象进一步认识无限个函数的图象。 2、对数: 定义:如果a N a a b =>≠()01且,那么数b 就叫做以a 为底的对数,记作b N a =log (a 是底数,N 是真数,log a N 是对数式。) 由于N a b =>0故log a N 中N 必须大于0。 当N 为零的负数时对数不存在。 (1)对数式与指数式的互化。 (2)对数恒等式: 由a N b N b a ==()log ()12 将(2)代入(1)得a N a N log = 运用对数恒等式时要注意此式的特点,不能乱用,特别是注意转化时必须幂的底数和对数的底数相同。 计算: () 313 2 -log 解:原式==?? ?? ?-=3 131 2 222 13 1 3 log log 。 (3)对数的性质: ①负数和零没有对数; ②1的对数是零; ③底数的对数等于1。 (4)对数的运算法则: ①()()log log log a a a MN M N M N R =+∈+ , ②()log log log a a a M N M N M N R =-∈+ , ③()()log log a n a N n N N R =∈+ ④()log log a n a N n N N R =∈+ 1 对数的运算法则 教学目标 1.理解并掌握对数性质及运算法则,能初步运用对数的性质和运算法则解题. 2.通过法则的探究与推导,培养学生从特殊到一般的概括思想,渗透化归思想及逻辑思维能力.3.通过法则探究,激发学生学习的积极性.培养大胆探索,实事求是的科学精神. 教学重点是对数的运算法则及推导和应用难点是法则的探究与证明. 一. 引入新课 我们前面学习了对数的概念,那么什么叫对数呢?通过下面的题目来回答这个问题 如果看到这个式子会有何联想? 由学生回答(1)(2) (3)(4). 也就要求学生以后看到对数符号能联想四件事.从式子中,可以总结出从概念上讲,对数与指数就是一码事,从运算上讲它们互为逆运算的关系.既然是一种运算,自然就应有相应的运算法则,所以我们今天重点研究对数的运算法则. 二.对数的运算法则(板书) 对数与指数是互为逆运算的,自然应把握两者的关系及已知的指数运算法则来探求对数的运算法则,所以我们有必要先回顾一下指数的运算法则. 由学生回答后教师让学生看:,,. 然后直接提出课题:若是 否成立? 由学生讨论并举出实例说明其不成立(如可以举而 ),教师在肯定结论的正确性的同时再提出 可提示学生利用刚才的反例,把5改写成应为,而32 =2,还可以让学生再找几个例子, .之后让学生大胆说出发现有什么规律? 由学生回答应有成立. 现在它只是一个猜想,要保证其对任意都成立,需要给出相应的证明,怎么证呢? 你学过哪些与之相关的证明依据呢? 学生经过思考后找出可以利用对数概念,性质及与指数的关系,再找学生提出证明的基本思路,即对数问题先化成指数问题,再利用指数运算法则求解.找学生试说证明过程,教师可适当提示,然后板书. 证明:设则,由指数运算法则 得, 即.(板书) 法则出来以后,要求学生能从以下几方面去认识: (1) 公式成立的条件是什么?(由学生指出.注意是每个真数都大于零,每个对数式都有意义为使用前提条件). 高考指数函数和对数函数 一.基础知识 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方 根,其中n >1,且n ∈N * . 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,? ??<≥-==)0()0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: )1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1 *>∈>= = -n N n m a a a a n m n m n m 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3) s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 注意:指数函数的底数的取值范围,底数不能是负数、零和1. 注意:利用函数的单调性,结合图象还可以看出: (1)在[a ,b]上,)1a 0a (a )x (f x ≠>=且值域是)] b (f ),a (f [ 或)]a (f ),b (f [; (2)若0x ≠,则1)x (f ≠;)x (f 取遍所有正数当且仅当R x ∈; (3)对于指数函数)1a 0a (a )x (f x ≠>=且,总有a )1(f =; 二、对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明:○1 注意底数的限制0>a ,且1≠a ; ○ 2 x N N a a x =?=log ; ○ 3 注意对数的书写格式. 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . 指数式与对数式的互化 幂值 真数 对数 (二)对数的运算性质 如果0>a ,且1≠a ,0>M ,0>N ,那么:○1 M a (log ·=)N M a log +N a log ;○ 2 =N M a log M a log -N a log ; ○ 3 n a M log n =M a log )(R n ∈. 注意:换底公式 a b b c c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ;0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log =;(2)a b b a log 1log =. (二)对数函数 1、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对 对数函数公式的推导(全) 由指数函数 (01)n a a a b >≠=且,可推知:log a n b =,从而: ()log a b a b =对数恒等式 性质1、log ()log log a a a MN M N =+ <证法1> 由于m n m n a a a +?= 设 ,m n M a N a == 则: log a M m = l o g a N n = m n MN a += 于是: ()log log log a a a M N MN m n =+=+ <证法2> log log log a a a M N M N M N M N a a a =?=?对数恒等式 即: log log log a a a MN M N a a +=由于指数函数是单调函数,故: log ()log log a a a MN M N =+ 性质2、log log log M a a a N M N =- <证明> log log log log log M M N a a a a N a M N a M M N N a a a -== =对数恒等式 由于指数函数是单调函数,故:log log log M a a a N M N =- 性质3、log log ()(0,1)log b b a N N a b b >≠= 换底公式 特例:1log log a b b a = <证明> 由对数恒等式可知:log log a b N N N a b ==,log b a a b = log log log log a b b a N a N a N b b ???→==?? log log log b b a N a N N b b ?→== 由于指数函数是单调函数,故:log log log b b a N a N =? 故:log log log b b a N N a = 性质4、log log n a a M n M = 特例:1 log log n a a n M M = 对数函数 知识点一:对数函数的概念 1.定义:函数0(log >=a x y a ,且)1≠a 叫做对数函数.其中x 是自变量,函数的定义域是(0, +∞),值域为),(+∞-∞.它是指数函数x a y = )10(≠>a a 且的反函数. 注意: ○ 1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:x y 2log 2=,5 log 5 x y = 都不是对数函数,而只能称其为对数型函数. ○ 2 两个常用对数: (1)常用对数 简记为: lgN (以10为底) (2)自然对数 简记为: lnN (以e 为底) 例1、求下列函数的定义域、值域: (1)4 121 2 - = --x y ( 2))52(log 2 2++=x x y (3))54(log 2 3 1++-=x x y (4))(log 2x x y a --= 知识点二:对数函数的图象 方法一:由于对数函数是指数函数的反函数,所以对数函数的图象只须由相应的指数函数图象作关于x y =的对称图形,即可获得。 同样:也分1>a 与10< (3) x y 3log =(4) x y 3 1log = 思考:函数x y 2log =与y =3log x 与y 函数的相同性质和不同性质. 相同性质: 不同性质: 例2、作出下列对数函数的图象: 知识点三:对数函数的性质 由对数函数的图象,观察得出对数函数的性质. 思考:底数a 是如何影响函数 x y a log =的.(学生独立思考,师生共同总结) 规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大. 例3、比较下列各组数中两个值的大小: 对数运算和对数函数 对数的定义 ①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数。③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =?=>≠>。 常用对数与自然对数 常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). 对数函数及其性质 类型一、对数公式的应用 1计算下列对数 =-3log 6log 22 =?3 1log 12 log 2 22 2 =+2lg 5lg =61000lg =+64log 128log 22 =?)24(log 432 =++)2log 2)(log 3log 3(log 9384 =++3log 23log 2242 =?16log 27log 32 =+-2log 90log 5log 333 =++c b a 842log log log =+++200 199lg 43lg 32lg Λ =++32log 8log 8log 842 =+25.0log 10log 255 =-64log 325log 225 =)))65536(log (log (log log 2222 2 解对数的值: 18lg 7lg 37lg 214lg -+- 0 =-+-1)21 (2lg 225lg -1 1 3 341log 2log 8?? -? ??? 的值0 提示:对数公式的运算 如果0,1,0,0a a M N >≠>>,那么 (1)加法:log log log ()a a a M N MN += (2)减法:log log log a a a M M N N -= (3)数乘:log log ()n a a n M M n R =∈ (4)log a N a N = (5)log log (0,)b n a a n M M b n R b =≠∈ (6)换底公式:log log (0,1)log b a b N N b b a = >≠且 (7)1log log =?a b b a (8)a b b a log 1log = 类型二、求下列函数的定义域问题 1函数)13lg(13)(2 ++-= x x x x f 的定义域是)1,31 (- 2设()x x x f -+=22lg ,则?? ? ??+??? ??x f x f 22的定义域为 ()()4,11,4Y -- 3 函数()f x = ]1,0()0,1(Y - ) 提示:(1)分式函数,分母不为0,如0,1 ≠= x x y 。 (2) 二次根式函数,被开方数大于等于0,0,≥= x x y 。 (3)对数函数,真数大于0,0,log >=x x y a 。 类型三、对数函数中的单调性问题 指数函数与对数函数知识点总结 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N *. 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,???<≥-==)0()0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: ) 1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1*>∈>= = - n N n m a a a a n m n m n m 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3) s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 注意:指数函数的底数的取值范围,底数不能是负数、零和1. 2、指数函数的图象和性质 注意:利用函数的单调性,结合图象还可以看出: (1)在[a ,b]上,)1a 0a (a )x (f x ≠>=且值域是)]b (f ),a (f [或 )]a (f ),b (f [; (2)若0x ≠,则1)x (f ≠;)x (f 取遍所有正数当且仅当 R x ∈; (3)对于指数函数)1a 0a (a )x (f x ≠>=且,总有a )1(f =; 二、对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数,记作: N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明:○1 注意底数的限制0>a ,且1≠a ; ○ 2 x N N a a x =?=log ; ○ 3 注意对数的书写格式. 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . 指数与指数幂的运算 【学习目标】 1.理解有理指数幂的含义,掌握幂的运算. 2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点. 3.理解对数的概念及其运算性质. 4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指 数型函数、对数型函数进行变形处理. 5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质. 6.知道指数函数与对数函数 互为反函数(a >0,a ≠1). 【要点梳理】 要点一、幂的概念及运算性质 1.整数指数幂的概念及运算性质 2.分数指数幂的概念及运算性质 为避免讨论,我们约定a>0,n ,m ∈N * ,且 m n 为既约分数,分数指数幂可如下定义: 1 n a = m m n a == -1m n m n a a = 3.运算法则 当a >0,b >0时有: (1)n m n m a a a +=?; (2)() mn n m a a =; (3)()0≠>=-a n m a a a n m n m ,; (4)()m m m b a ab =. 要点诠释: (1)根式问题常利用指数幂的意义与运算性质,将根式转化为分数指数幂运算; (2)根式运算中常出现乘方与开方并存,要注意两者的顺序何时可以交换、何时不能交换.如 244 2)4()4(-≠-; (3)幂指数不能随便约分.如2 14 2)4()4(-≠-. 要点二、根式的概念和运算法则 1.n 次方根的定义: 若x n =y(n ∈N * ,n>1,y ∈R),则x 称为y 的n 次方根,即x=n y . n 为奇数时, y 的奇次方根有一个,是负数,记为n y ;零的奇次方根为零,记为00=n ; n 为偶数时,正数y 的偶次方根有两个,记为;负数没有偶次方根;零的偶次方根为零,0=. 2.两个等式 (1)当1n >且* n N ∈时, n a =;指数对数概念及运算公式
专题:对数函数知识点总结及类型题归纳
对数指数函数公式全集
专题:对数函数知识点总结及类型题归纳
对数
对数公式的运算
高中对数函数公式
对数公式总结
高一数学必修一对数及对数函数知识点总结
对数及对数函数知识点总结及题型分析
指数、对数函数公式
对数的运算法则
高考学生指数与对数函数知识点小结及典型例题
对数公式的推导(全)
对数函数知识点总结
(完整版)对数公式及对数函数的总结
指数与对数函数知识点总结
指数、对数、幂函数总结归纳
