正17边形尺规作图法(高斯原创againDo整理)

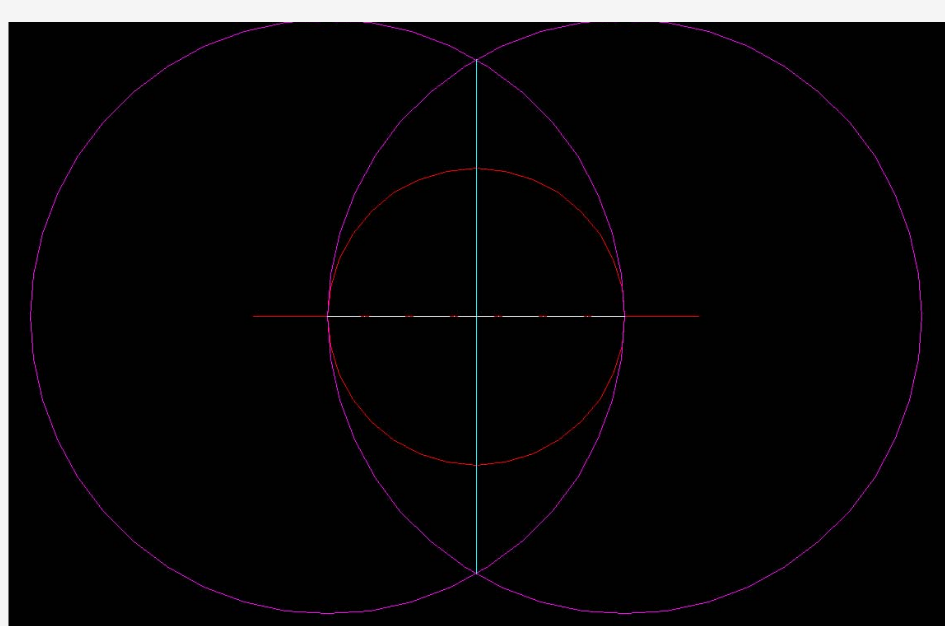
尺规作图专题详尽归纳
考点名称:尺规作图 【学习目标】 1.了解什么是尺规作图. 2.学会用尺规作图法完成下列五种基本作图:(1)画一条线段等于已知线段;(2)画一个角等于已知角;(3)画线段的垂直平分线;(4)过已知点画已知直线的垂线;(5)画角平分线.3.了解五种基本作图的理由. 4.学会使用精练、准确的作图语言叙述画图过程. 5.学会利用基本作图画三角形等较简单的图形. 6.通过画图认识图形的本质,体会图形的内在美. 【基础知识精讲】 1.尺规作图: ①定义:限定只用直尺和圆规来完成的画图,称为尺规作图. 注意:这里所指的直尺是没有刻度的直尺,由于免去了度量,因此,用尺规作图法画出的图形的精确度更高,它在工程绘图等领域应用比较广泛. ②步骤:(1)根据给出的条件和求作的图形,写出已知和求作部分;(2)分析作图的方法和过程;(3)用直尺和圆规进行作图; (4)写出作法步骤,即作法。(根据题目要求来定是否需要写出作法) 2.尺规作图中的最基本、最常用的作图称为基本作图.任何尺规作图的步骤均可分解为以下五种. 3.基本作图共有五种: (1)画一条线段等于已知线段. 如图24-4-1,已知线段DE. 求作:一条线段等于已知线段. 作法:①先画射线AB. ②然后用圆规在射线AB上截取AC=MN. 线段AC就是所要作的线段. (2)作一个角等于已知角. 如图24-4-2,已知∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB. 作法:①作射线O′A′; ②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D. ③以点O′为圆心,以OC长为半径作弧,交O′A′于C′. ④以点C′为圆心,以CD为半径作弧,交前弧于D′. ⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角. (3)作线段的垂直平分线. 如图24-4-3,已知线段AB. 求作:线段AB的垂直平分线. 作法:①分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C和D. ②作直线CD. 直线CD就是线段AB的垂直平分线. 注意:直线CD与线段AB的交点,就是AB的中点. (4)经过一点作已知直线的垂线. a.经过已知直线上的一点作这条直线的垂线,如图24-4-4. 已知:直线AB和AB上一点C, 求作:AB的垂线,使它经过点C. 作法:作平角ACB的平分线CF. 直线CF就是所求的垂线,如图24-4-4. b.经过已知直线外一点作这条直线的垂线. 如图24-4-5,已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
解读高斯正十七边形的作法(下)
解读高斯正十七边形的作法 正十七边形的尺规作法: 步骤1:在平面直角坐标系xOy 中作单位圆O 步骤2:在x 轴负半轴上取点N ,使|ON|= 41,易知|NB|=417,以N 为圆心,NB 为半径作弧,交x 轴于F 、F’,易知|OF|= 2a ,|OF’|=2b 步骤3:此时|FB|=122+?? ? ??a =242+a ,以F 为圆心,|FB|为半径作弧,交x 轴正半轴于G ,此时|OG|=2 422++a a =c 步骤4:.类似地,|F’B|=122 +?? ? ??b =242+b ,以F’为圆心,|F’B|为半径作弧,交x 轴正半轴于点G’,此时|OG’|=2422++b b =e 步骤5:以|CG’|为直径作圆,交y 轴正半轴于点H ,易知OH 2=1·e
步骤6:以H 为圆心, 21|OG|为半径作弧,交x 轴正半轴于点K ,则有|OK|=222OH OG -??? ??=222e c -?? ? ??=242e c -步骤7:以K 为圆心,|KH|=2 1|OG|为半径作弧,交x 轴正半轴于点L ,则|OL|=2 42e c c -+步骤8:取OL 的中点M ,则|OM|=4 42e c c -+=cos 172π步骤9:过点M 作y 轴的并行线交单位圆O 于两点A 2和A 17,则Α为正十七边形的第一个顶点,A 2为第二个顶点,A 17为第十七个顶点,从而作出正十七边形。 正十七边形边长的表达式 在上面得到的一系列等式: a =2171+-, b =2171--, c =242++a a ,e =2 42++b b ,cos 172π=4 42e c c -+中,依次求出c =4 17234171-++-,
中考尺规作图专题
中考专题复习:尺规作图 最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。 五种基本作图: 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 5、过一点作已知直线的垂线; 专题训练: 1.已知:线段a,b 求作:△ABC,使AB=a,BC=b,AC=2a.(尺规作图,不写作法,保留作图痕迹) 分析:首先画线段AC=2a,再以A为圆心,a长为半径画弧,再以C为圆心,b长为半径画弧,两弧交于点B, 连接AB、BC即可. 解:如图所示:△ABC即为所求. , 点评:此题主要考查了作图,关键是掌握作一条线段等于已知线段的方法. 2.如图(1),已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形). 分析:根据两直线平行的性质,同位角相等或内错角相等,故作一个角∠ECD=∠EFB即可. 作法:如图(2). 图(1)图(2) (1)过点C作直线EF,交AB于点F; (2)以点F为圆心,以任意长为半径作弧,交FB于点P,交EF于点Q; (3)以点C为圆心,以FP为半径作弧,交CE于M点; (4)以点M为圆心,以PQ为半径作弧,交前弧于点D; (5)过点D作直线CD,CD就是所求的直线. 3.已知:∠AOB,求作:∠A′O′B′=∠AOB(用尺规作图,保留作图痕迹,不写步骤). 分析:(1)作射线O′B′; (2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D; (3)以O′为圆心,以OC的长为半径画弧,交O′A′于点C′; (4)以点D′为圆心,以CD的长为半径画弧,交前弧于点C′; (5)过C′作射线O′A′. 则∠A′O′B′就是所求作的角. 解:∠A′O′B′就是所求作的角. 4.画出∠AOB的角平分线(要求:尺规作图,不写作图过程保留作图痕迹). 分析:以点O为圆心,以任意长为半径画弧,与边OA、OB分别相交于点M、N,再以点M、N为圆心,以大 于1/2 MN长为半径,画弧,在∠AOB内部相交于点C,作射线OC即为∠AOB的平分线. 解:如图所示,OC即为所求作的∠AOB的平分线. 5.尺规作图:线段MN的垂直平分线(不写作法,保留作图痕迹) 分析:分别以M、N点为圆心,以大于1/2 MN的长为半径作弧,两弧相交于A,B两点;作直线AB,AB即 为线段AB的垂直平分线. 解:如图所示:AB即为所求. 6.经过已知直线外一点作这条直线的垂线“的尺规作图过程: 已知:直线l和l外一点P.求作:直线l的垂线,使它经过点P.
尺规作图学习知识归纳
考点名称:尺规作图 尺规作图:是指限定用没有刻度的直尺和圆规来完成的画图。一把没有刻度的直尺看似不能做什么,画一个圆又不知道它的半径,画线段又没有精确的长度。 其实尺规作图的用处很大,比如单用圆规找出一个圆的圆心,量度一个角的角度,等等。运用尺规作图可以画出与某个角相等的角,十分方便。 尺规作图的中基本作图: 作一条线段等于已知线段; 作一个角等于已知角; 作线段的垂直平分线; 作已知角的角平分线; 过一点作已知直线的垂线。 还有: 已知一角、一边做等腰三角形 已知两角、一边做三角形 已知一角、两边做三角形 依据公理: 还可以根据已知条件作三角形,一般分为已知三边作三角形,已知两边及夹角作三角形,已知两角及夹边作三角形等,作图的依据是全等三角形的判定定理:SSS,SAS,ASA等。注意: 保留全部的作图痕迹,包括基本作图的操作程序,只有保留作图痕迹,才能反映出作图的操作是否合理。
尺规作图方法: 任何尺规作图的步骤均可分解为以下五种方法: ·通过两个已知点可作一直线。 ·已知圆心和半径可作一个圆。 ·若两已知直线相交,可求其交点。 ·若已知直线和一已知圆相交,可求其交点。 ·若两已知圆相交,可求其交点。 【学习目标】 1.了解什么是尺规作图. 2.学会用尺规作图法完成下列五种基本作图:(1)画一条线段等于已知线段;(2)画一个角等于已知角;(3)画线段的垂直平分线;(4)过已知点画已知直线的垂线;(5)画角平分线.3.了解五种基本作图的理由. 4.学会使用精练、准确的作图语言叙述画图过程. 5.学会利用基本作图画三角形等较简单的图形. 6.通过画图认识图形的本质,体会图形的内在美. 【基础知识精讲】 1.尺规作图: 限定只用直尺和圆规来完成的画图,称为尺规作图. 注意:这里所指的直尺是没有刻度的直尺,由于免去了度量,因此,用尺规作图法画出的图形的精确度更高,它在工程绘图等领域应用比较广泛.
尺规作图专题
尺规作图专题 1、尺规作图的定义所谓尺规作图,就是只准有限次地使用没有刻度的直尺和圆规进行作图。最早提出几何作 图要有尺规限制的是古希腊的哲学家安那萨哥拉斯。他因政治上的纠葛,被关进监狱,并被处死刑。传说,在监狱里,他思考化圆为方以及其它有关问题,用来打发令人苦恼的无所事事的生活。他不可能用规范的作图工具,只能用一根绳子画图,用随便找来的破木棍、竹片之类作直尺,当然这些“尺”上就不可能有刻度。另外,对他来说,时间是不多了。因此他很自然地想到要有限次地使用尺规解决问题。后来以理论形式具体明确这个规定的是欧几里得,他在《几何原本》中对作图作了三条规定(公设)。由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来。 2、尺规作图的要求 ①直尺必须没有刻度,可以无限长,且只能使用直尺的固定一侧。只可以用它来将两个点连在一起,不可 以在上画刻度。 ②圆规可以开至无限宽,但上面亦不能有刻度。它只可以拉开成你之前构造过的长度或一个任意的长度. 3、尺规作图的三大不能为问题 古希腊人说的直尺,指的是没有刻度的直尺。他们在大量的画图经历中感觉到,似乎只用直尺、圆规这两种作图工具就能画出各种满足要求的几何图形,因而,古希腊人就规定,作图时只能有限次地使用直尺和圆规这两种工具来进行,并称之为尺规作图法。漫长的作图实践,按尺规作图的要求,人们作出了大量符合给定条件的图形,即便一些较为复杂的作图问题,独具匠心地经过有限步骤也能作出来。到了大约公元前 6 世纪到 4 世纪之间,古希腊人遇到了令他们百思不得其解的三个作图问题。 ①三等分角问题:将任一个给定的角三等分。 ②立方倍积问题:求作一个正方体的棱长,使这个正方体的体积是已知正方体 体积的二倍。 ③化圆为方问题:求作一个正方形,使它的面积和已知圆的面积相等。这就是著名的古代几何作图三大难题,它 们在《几何原本》问世之前就提出了, 随着几何知识的传播,后来便广泛留传于世。 4、初中几个最基本的尺规作图 一.已知一线段 1. 作已知线段的中点 2. 作已知线段的垂线 3. 作已知线段的垂直平分线 4. 过一点作已知直线的垂线 5. 作已知线段的三等分点 6. 过直线外一点作已知直线的平行线 二.已知一角 1. 作一角与已知角相等 2. 作已知角的角平分线 1
高斯与正十七边形
高斯与正十七边形 数学就象一棵美丽的星球,他那博大精深、简明透彻的数学美就是他的引力场。许许多多人类的精英被他的引力所吸引,投入他的怀抱为他献出了自己毕生的精力。被誉为“数学王子”的伟大数学家高斯就是其中之一。 高斯是个数学天才,幼年时巧妙地计算1+2+3+…+100为101×50=5050的故事几乎尽人皆知。其实,学生日期的高斯不仅数学成绩优异,而且各科成绩都名列前茅。小学毕业后,高斯考了文科学校。由于他古典文学成绩突出,入学后直接上了二年级。两年以后高斯又升入了高中哲学班。 15岁时,高斯在一位公爵的资助下上了大学-卡罗琳学院。在那里,他掌握了希腊文、拉丁文、法文、英文有丹麦文,又学会了代数、几何、微积分。语言学和数学是他最喜爱的两门课程。 18岁时,高斯进入了哥廷根大学深造。这时,高斯面临着一个非常痛苦的选择:是把语言学作为自己的终生事业?还是把数学作为自己的终生事业?两棵下不了决心进行最后的选择。 后来,一次数学研究上的突破改变了两个引力场的均衡。高斯终于下定决心,飞向了数学之星。 事情是这样的,尺规作图是几何学的重要内容之一,从古希腊开始,人们一直认为正多边形是最美的图形,因此,用尺规作图法能够作出哪些正多边形,历来就是一个极具魅力的问 题。到高斯的时代,人们已经解决了边数是n 23?、n 24?、n 25?、n 253??(=n 0,1, 2,3……)的正多边形的尺规作图问题。但是,还没有人能作出正7边形、正11边形、正17边形等等。很多人认为,当边数是大于5的素数时,那样的正多边形是不可以用尺规作图完成的。 高斯一直对正多边形尺规作图问题非常着迷。经过持久地,如醉如痴的思考与画图,于1796年3月30日,19岁的高斯出人意料地作出了正17边形。并且,他把正多边形作图问题与高次方程联系起来,彻底解决了哪些正多边形能作出,哪些正多边形不能作出。他证明 了一切边数形如122+t (=t 0,1,2,3,……)的正多边形都只可以作出,而边数为7、11、14,……的正多边形是作不出的。 正17边形作图问题不仅震撼了数学界,也震撼了高斯自己的心灵。他再也无法控制自己,在数学美的巨大引力的作用下,飞向了自己理想的星球-他选择了数学。 从此,高斯的数学成就象喷泉一样涌了出来。他在几乎所有的数学学科中留下了自己的光辉成就,成为伟大的数学家。 高斯直到晚年还十分欣赏使自己走上数学之路的正17边形,对数学美的赞叹与追求伴高斯渡过了他的一生。高斯逝世后,人们按照他的遗嘱,在他的雕像下面建立了一座正17边枎的底座,用他非常欣赏的《李尔王》中的诗句赞美道:“你,自然,我的女神,我要为你的规律而献身”。
尺规作图题专题复习
320国道 . 5 题 . 学习必备 欢迎下载 一、尺规基本作图归纳 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作角的平分线; 4、作线段的中垂线; 5、已知三边,两边和其夹角或两角和其夹边作三角形; 6、已知底边和底边上的高作等腰三角形; 7、过直线上一点作直线的垂线; 8、过直线外一点作直线的垂线. 题 1、如图,有一破残的轮片,现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计一种方案,确定 这个圆形零件的半径. 2、 如图:107 国道 OA 和 320 国道 OB 在某市相交于点 O,在∠AOB 的内部有工厂 C 和 D,现要修建一个货站 P ,使 P 到 OA 、OB 的距离相等且 PC=PD ,用尺规作出货站 P 的位置(不写作法,保留作图痕迹,写出结论) A D A 107国道 C C B O B 3、 三条公路两两相交,交点分别为 A ,B ,C ,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加 油站地址有几种情况? B A A O A C B C 4、 过点 C 作一条线平行于 AB ; 5、过不在同一直线上的三点 A 、B 、C 作圆 O ; 6、过直线外一点 A 作圆 O 的切线。 二、几何画图:1 只利用一把有刻度的直尺,用度量的方法,按下列要求画图: 1)画等腰三角形 ABC 的对称轴: 2)画∠AOB 的对称轴 2 有一个未知圆心的圆形工件.现只允许用一块三角板(注:不允许用三角板上的刻度)画出该工件表面上的一条直径 并定出圆心.要求在图上保留画图痕迹,写出画法. 3 某校有一个正方形的花坛,现要将它分成形状和面积都相同的四块种上不同颜色的花卉,请你帮助设计至少三种不同 的方案,分别画在下面正方形图形上(用尺规作图或画图均可,但要尽可能准确些、美观些) 4 某村一块若干亩土地的图形是ΔABC ,现决定把这块土地平均分给四位“花农”种植,请你帮他们分一分,提供至少两 种分法。要求:画出图形,并简要说明分法。 5.如图所示,在正方形网格上有一个三角形 ABC.①作△ABC 关于直线 MN 的对称图形(不写作法); ②若网格上的最小正方形的边长为 △1.求 ABC 的面积. M P A A 甲 乙 丙 丁 C C B D Q B C A B 6 题 7 题 N 6 如图,方格纸中每个小方格都是边长为 1 的正方形,我们把以格点连线为边的多边形称为“格点多边形” 如图(一) 中四边形 ABCD 就是一个“格点四边形”. ①求图中四边形 ABCD 的面积;②在图中方格纸上画一个格点△EFG ,使△EFG 的面积等于四边形 ABCD 的面积且为
尺规作图方法大全(正式)
尺规作图 【知识回顾】 1、 尺规作图的定义: 尺规作图是指用没有刻度的直尺和圆规作图。最基本 一些复杂的尺规作图都是由基本作图组成的。 2、 五种基本作图: ,最常用的尺规作图,通常称基本作图。 (1)题目一:作一条线段等于已知线段。 已知 如图,线段 a . 求作 线段 AB, 使 AB = a . 作法 (1) 作射线AP (2) 在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。 (2) 题目二:作已知线段的中点。 已知 如图,线段 MN. 求作 点 0,使MO=N (即0是MN 的中点). 作法 |M N (1: 分别以M N 为圆心,大于 5 1、作一条线段等于已知线段; 、作一个角等于已知角; 、作已知线段的垂直平分线; 、作已知角的角平分线; 、过一点作已知直线的垂 线; (2) 则点 (3) 已知: 求作: 作法: (1) 的相同线段为半径画弧, 两弧相交于P, Q 连接PQ 交MN 于0. 0就是所求作的MN 的中点。 题目三:作已知角的角平分线。 如图,/ AOB 射线0P,使/ AOP=Z BOP (即卩0P 平分/ N AOB 。 以0为圆心,任意长度为半径画弧, 分别交OA 0B 于 M, N; 分别以M N 为圆心,大于 [的线 为半径画弧,两弧交/ AOB 内于P; (3) 作射线0P 则射线0P 就是/ AOB 的角平分线。 (4) 题目四:作一个角等于已知角。 已知:如图,/ AOB 求作:/ A O B',使 A ' O B' =/AOB (2)
作法: (1) 作射线O' A ; (2) 以O 为圆心,任意长度为半径画弧,交 OA 于M 交OB 于N; (3) 以O 为圆心,以 OM 的长为半径画弧,交 O A '于M ; (4) 以M 为圆心,以MN 的长为半径画弧,交前弧于 N'; (5) 连接O N'并延长到B '。 则/ A O' B '就是所求作的角。 (5)题目五:经过直线上一点做已知直线的垂线。 已知:如图,P 是直线 AB 上一点。 求作:直线 CD,是CD 经过点P,且CD 丄ABo A P B 作法: (1)以P 为圆心,任意长为半径画弧,交 AB 于M N; 1 (2) 分别以M N 为圆心,大于-MN 的长为半径画弧,两弧交于点 Q; 2 (3) 过D Q 作直线CD 则直线CD 是求作的直线。 * P (6)题目六:经过直线外一点作已知直线的垂线 已知:如图,直线 AB 及外一 点P o 求作: 直线CD,使CD 经过点P, 且 CDL ABo A B 作法: (1) 以P 为圆心,任意长为半径画弧,交 AB 于M N 1; a 1 (2) 分别以M N 圆心,大于-MN 长度的 2 (3) 过P 、Q 作直线CD 0 则直线CD 就是所求作的直线。 (5)题目七:已知三边作三角形。 已知:如图,线段 a , b , c. 求作:△ ABC 使 AB = c , AC = b , BC = a. 作法: (1) 作线段AB = c ; (2) 以A 为圆心,以b 为半径作弧, 以B 为 圆心,以a 为半径作弧与 前弧相交于C; (3) 连接 AC, BG 则厶ABC 就是所求作的三角形。 题目八:已知两边及夹角作三角形。 已知:如图,线段 m n ,/ a . 求作:△ ABC 使/ A=Z : , AB=m AC=n. 半为半径画弧,两弧交于点 Q c n
初中尺规作图详细讲解含图)
初中数学尺规作图讲解初等平面几何研究的对象,仅限于直线、圆以及由它们(或一部分)所组成的图形,因此作图的工具,习 惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法,叫做尺规作图法.最简单的尺规作图 有如下三条: ⑴经过两已知点可以画一条直线; ⑵已知圆心和半径可以作一圆; ⑶两已知直线;一已知直线和一已知圆;或两已知圆,如果相交,可以求出交点; 以上三条,叫做作图公法.用直尺可以画出第一条公法所说的直线;用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点.一个作图题,不管多么复杂,如果能反复应用上述三条作图公法,经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题;否则,就称为尺规作图不能问题. 历史上,最著名的尺规作图不能问题是: ⑴三等分角问题:三等分一个任意角; ⑵倍立方问题:作一个立方体,使它的体积是已知立方体的体积的两倍; ⑶化圆为方问题:作一个正方形,使它的面积等于已知圆的面积. 这三个问题后被称为“几何作图三大问题”.直至1837年,万芝尔(Pierre Laurent Wantzel)首先证明三等分角问题和立方倍积问题属尺规作图不能问题;1882年,德国数学家林德曼(Ferdinand Lindemann)证明π是一个超越数(即π是一个不满足任何整系数代数方程的实数),由此即可推得根号π(即当圆半径1 r=时所求正方形的边长)不可能用尺规作出,从而也就证明了化圆为方问题是一个尺规作图不能问题. 若干著名的尺规作图已知是不可能的,而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此,仍有很多业余爱好者尝试这些不可能的题目,当中以化圆为方及三等分任意角最受注意.数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书. 还有另外两个著名问题: ⑴正多边形作法 ·只使用直尺和圆规,作正五边形. ·只使用直尺和圆规,作正六边形. ·只使用直尺和圆规,作正七边形——这个看上去非常简单的题目,曾经使许多著名数学家都束手无策,因为正七边形是不能由尺规作出的. ·只使用直尺和圆规,作正九边形,此图也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的. ·问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积,解 决了两千年来悬而未决的难题. ⑵四等分圆周 只准许使用圆规,将一个已知圆心的圆周4等分.这个问题传言是拿破仑·波拿巴出的,向全法国数学家的挑战. 尺规作图的相关延伸: 用生锈圆规(即半径固定的圆规)作图 1.只用直尺及生锈圆规作正五边形 2.生锈圆规作图,已知两点A、B,找出一点C使得AB BC CA ==. 3.已知两点A、B,只用半径固定的圆规,求作C使C是线段AB的中点. 4.尺规作图,是古希腊人按“尽可能简单”这个思想出发的,能更简洁的表达吗?顺着这思路就有了更简洁的表达.10世纪时,有数学家提出用直尺和半径固定的圆规作图. 1672年,有人证明:如果把“作直线”解释为“作出直线上的2点”,那么凡是尺规能作的,单用圆规也能作出!从已知点作出新点的几种情况:两弧交点、
尺规作图方法大全
a M 七年级数学期末复习资料(七) 尺规作图 【知识回顾】 1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。 2、五种基本作图: 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段。 已知:如图,线段a . 求作:线段AB ,使AB = a . 作法: (1) 作射线AP ; (2) 在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。 (2)题目二:作已知线段的中点。 已知:如图,线段MN. 求作:点O ,使MO=NO (即O 是MN 的中点). 作法: (1)分别以M 、N 为圆心,大于 的相同线段为半径画弧, 两弧相交于P ,Q ; (2)连接PQ 交MN 于O . 则点O 就是所求作的MN的中点。 (3)题目三:作已知角的角平分线。 已知:如图,∠AOB , 求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。 作法: (1)以O 为圆心,任意长度为半径画弧, 分别交OA ,OB 于M ,N ; (2)分别以M 、N为圆心,大于 的线段长 为半径画弧,两弧交∠AOB 内于P; (3) 作射线OP 。 则射线OP 就是∠AOB 的角平分线。
③ ② ① P B A P (4)题目四:作一个角等于已知角。 已知:如图,∠AOB 。 求作:∠A ’O ’B ’,使A ’O ’B ’=∠AOB 作法: (1)作射线O ’A ’; (2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ; (3)以O ’为圆心,以OM 的长为半径画弧,交O ’A ’于M ’; (4)以M ’为圆心,以MN 的长为半径画弧,交前弧于N ’; (5)连接O ’N ’并延长到B ’。 则∠A ’O ’B ’就是所求作的角。 (5)题目五:经过直线上一点做已知直线的垂线。 已知:如图,P 是直线AB 上一点。 求作:直线CD ,是CD 经过点P ,且CD ⊥AB 。 作法: (1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ; (2)分别以M 、N 为圆心,大于 MN 2 1 的长为半径画弧,两弧交于点Q ; (3)过D 、Q 作直线CD 。 则直线CD 是求作的直线。 (6)题目六:经过直线外一点作已知直线的垂线 已知:如图,直线AB 及外一点P 。 求作:直线CD ,使CD 经过点P , 且CD ⊥AB 。
正十七边形做法及证明.
步骤一: 给一圆O,作两垂直的直径OA、OB, 作C点使OC=1/4OB, 作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度 步骤二: 作AE中点M,并以M为圆心作一圆过A点, 此圆交OB于F点,再以D为圆心,作一圆 过F点,此圆交直线OA于G4和G6两点。 步骤三: 过G4作OA垂直线交圆O于P4, 过G6作OA垂直线交圆O于P6, 则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点。 正十七边形的尺规作图存在之证明:
设正17边形中心角为a,则17a=360度,即16a=360度-a 故sin16a=-sina,而 sin16a=2sin8acos8a=22sin4acos4acos8a=2 4 sinacosacos2acos4acos8a 因sina不等于0,两边除之有: 16cosacos2acos4acos8a=-1 又由2cosacos2a=cosa+cos3a等,有 2(cosa+cos2a+…+cos8a=-1 注意到 cos15a=cos2a,cos12a=cos5a,令 x=cosa+cos2a+cos4a+cos8№a y=cos3a+cos5a+cos6a+cos7a 有: x+y=-1/2 又xy=(cosa+cos2a+cos4a+cos8a(cos3a+cos5a+cos6a+cos7a =1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a 经计算知xy=-1 又有 x=(-1+根号17/4,y=(-1-根号17/4 其次再设:x1=cosa+cos4a,x2=cos2a+cos8a y1=cos3a+cos5a,y2=cos6a+cos7a 故有x1+x2=(-1+根号17/4 y1+y2=(-1-根号17/4 最后,由cosa+cos4a=x1,cosacos4a=(y1/2 可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出
初中数学专题尺规作图(含答案)
第28课时尺规作图 ◆考点聚焦 1.掌握基本作图,尺规作图的要求与步骤. 2.利用基本作图工具画三角形、四边形、圆以及简单几何体的三视图,?对简单的作图能叙述作法. 3.运用基本作图、结合相关的数学知识(平移、旋转、对称、?位似)等进行简单的图案设计. 4.运用基本作图解决实际问题. ◆备考兵法 1.熟练掌握基本作图. 2.在画几何体的三视图时,要注意其要求,?即“长对正”“高平齐”“宽相等”. 3.认真分析题意,善于把实际问题转化为基本作图. ◆识记巩固 1.尺规作图的定义:_____________. 2.基本作图包括:_______,_______,________,________,_______.3.三角形三边的垂直平分线的交点叫三角形的外心,?三角形三内角平分线的交点叫三角形的内心,外心到三角形的_______的距离相等,内心到三角形_______的距离相等.识记巩固参考答案: 1.限定只能使用圆规和没有刻度的直尺作图 2.作线段作角作线段的垂直平分线过一点作已知直线的垂线作角平分线 3.顶点三边 ◆典例解析 例1 (2008,新疆建设兵团) (1)请用两种不同的方法,用尺规在所给的两个矩形中各作一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上.(保留作图痕迹)
(2)写出你的作法. 解析(1)所作菱形如图①,②所示. 说明:作法相同的图形视为同一种,例如类似图③,?图④的图形视图与图②是同一种. ①② ③④ (2)图①的作法:作矩形A1B1C1D1四条边的中点E1,F1,G1,H1,连结H1E1,E1F1,G1F1,G1H1. 四边形E1F1G1H1即为菱形. 图②的作法:在B2C2上取一点E2,使E2C2>A2E2且E2不与B2重合,连结A2E2.以A2为圆心,A2E2为半径画弧,交A2D2于H2; 以E2为圆心,A2E2为半径画弧,交B2C2于F2; 连结H2F2,则四边形A2E2F2H2为菱形. 例2 如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画∠AOB的平分线(请保留画图痕迹).
尺规作图方法大全正式
B P A a O Q P N M O N M B P A N M B O A ① A'A' N' O' B' M'O' A' N' M'M'O' 尺规作图 【知识回顾】 1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。 2、五种基本作图: 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段。 已知:如图,线段a . 求作:线段AB ,使AB = a . 作法: (1) 作射线AP ; (2) 在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。 (2)题目二:作已知线段的中点。 已知:如图,线段MN. 求作:点O ,使MO=NO (即O 是MN 的中点). 作法: (1)分别以M 、N 为圆心,大于 的相同线段为半径画弧, 两弧相交于P ,Q ; (2)连接PQ 交MN 于O . 则点O 就是所求作的MN的中点。 (3)题目三:作已知角的角平分线。 已知:如图,∠AOB , 求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。 作法: (1)以O 为圆心,任意长度为半径画弧, 分别交OA ,OB 于M ,N ; (2)分别以M 、N为圆心,大于 的线段长 为半径画弧,两弧交∠AOB 内于P; (3) 作射线OP 。 则射线OP 就是∠AOB 的角平分线。 (4)题目四:作一个角等于已知角。 已知:如图,∠AOB 。 求作:∠A ’O ’B ’,使A ’O ’B ’=∠AOB 作法: (1)作射线O ’A ’;
17边形画法
步骤一: 给一圆O,作两垂直的半径OA、OB, 作C点使OC=1/4OB, 作D点使∠OCD=1/4∠OCA, 作AO延长线上E点使得∠DCE=45度。 步骤二: 作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点, 再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。 步骤三: 过G4作OA垂直线交圆O于P4, 过G6作OA垂直线交圆O于P6, 则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。 连接P4P6,以1/2弧P4P6为半径,在圆上不断截取,即可在此圆上截出正十七边形的所有顶点。 正十七边形的尺规作图存在之证明: 设正17边形中心角为a,则17a=360度,即16a=360度-a
故sin16a=-sina,而 sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a 因sina不等于0,两边除之有: 16cosacos2acos4acos8a=-1 又由2cosacos2a=cosa+cos3a等,有 2(cosa+cos2a+…+cos8a)=-1 注意到cos15a=cos2a,cos12a=cos5a,令 x=cosa+cos2a+cos4a+cos8№a y=cos3a+cos5a+cos6a+cos7a 有: x+y=-1/2 又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a) =1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a) 经计算知xy=-1 又有 x=(-1+根号17)/4,y=(-1-根号17)/4 其次再设:x1=cosa+cos4a,x2=cos2a+cos8a y1=cos3a+cos5a,y2=cos6a+cos7a 故有x1+x2=(-1+根号17)/4 y1+y2=(-1-根号17)/4 最后,由cosa+cos4a=x1,cosacos4a=(y1)/2 可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出
初中尺规作图详细讲解(含图)
初中数学尺规作图讲解 初等平面几何研究的对象,仅限于直线、圆以及由它们(或一部分)所组成的图形,因此作图的工具,习惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法,叫做尺规作图法.最简单的尺规作图有如下三条: ⑴ 经过两已知点可以画一条直线; ⑵ 已知圆心和半径可以作一圆; ⑶ 两已知直线;一已知直线和一已知圆;或两已知圆,如果相交,可以求出交点; 以上三条,叫做作图公法.用直尺可以画出第一条公法所说的直线;用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点.一个作图题,不管多么复杂,如果能反复应用上述三条作图公法,经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题;否则,就称为尺规作图不能问题. 历史上,最著名的尺规作图不能问题是: ⑴ 三等分角问题:三等分一个任意角; ⑵ 倍立方问题:作一个立方体,使它的体积是已知立方体的体积的两倍; ⑶ 化圆为方问题:作一个正方形,使它的面积等于已知圆的面积. 这三个问题后被称为“几何作图三大问题”.直至1837年,万芝尔(Pierre Laurent Wantzel)首先证明三等分角问题和立方倍积问题属尺规作图不能问题;1882年,德国数学家林德曼(Ferdinand Lindemann)证明π是一个超越数(即π是一个不满足任何整系数代数方程的实数),由此即可推得根号π(即当圆半径1 r=时所求正方形的边长)不可能用尺规作出,从而也就证明了化圆为方问题是一个尺规作图不能问题. 若干著名的尺规作图已知是不可能的,而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此,仍有很多业余爱好者尝试这些不可能的题目,当中以化圆为方及三等分任意角最受注意.数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书. 还有另外两个著名问题: ⑴ 正多边形作法 ·只使用直尺和圆规,作正五边形. ·只使用直尺和圆规,作正六边形. ·只使用直尺和圆规,作正七边形——这个看上去非常简单的题目,曾经使许多著名数学家都束手无策,因为正七边形是不能由尺规作出的. ·只使用直尺和圆规,作正九边形,此图也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的. ·问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积,解 决了两千年来悬而未决的难题. ⑵ 四等分圆周 只准许使用圆规,将一个已知圆心的圆周4等分.这个问题传言是拿破仑·波拿巴出的,向全法国数学家的挑战. 尺规作图的相关延伸: 用生锈圆规(即半径固定的圆规)作图 1.只用直尺及生锈圆规作正五边形 2.生锈圆规作图,已知两点A、B,找出一点C使得AB BC CA ==. 3.已知两点A、B,只用半径固定的圆规,求作C使C是线段AB的中点. 4.尺规作图,是古希腊人按“尽可能简单”这个思想出发的,能更简洁的表达吗?顺着这思路就有了更简洁的 表达.10世纪时,有数学家提出用直尺和半径固定的圆规作图. 1672年,有人证明:如果把“作直线”解释
《尺规作图(思路及题练)》专题检测
2012中考数学--尺规作图(复习) 一、理解“尺规作图”的含义 1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的. 2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差. 二、熟练掌握尺规作图题的规范语言 1.用直尺作图的几何语言: ①过点×、点×作直线××;或作直线××;或作射线××; ②连结两点××;或连结××; ③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×; 2.用圆规作图的几何语言: ①在××上截取××=××; ②以点×为圆心,××的长为半径作圆(或弧); ③以点×为圆心,××的长为半径作弧,交××于点×; ④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤 尺规作图题的步骤: 1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件; 2.求作:能根据题目写出要求作出的图形及此图形应满足的条件; 3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法. 在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要. 四、基本作图 最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。 五种基本作图: 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 5、过一点作已知直线的垂线;
中考数学专题尺规作图
《尺规作图》专题训练 基本作图,要求保留作图痕迹,不要求写作法 1.作一条线段等于已知线段 已知:线段a ,求作:线段AB ,使AB=a 。 2.作一全角等于已知角 已知:∠MPN 求作:∠ABC ,使∠ABC=∠MPN 。 3.作角的平分线 已知:∠MPN 求作:∠MPN 的角平分线PO 4、作线段的垂直平分线 已知:线段AB 求作:线段AB 的垂直平分线MN 。 5、过定点作已知直线的垂线: 6、 (1)点在直线上; (2)点在直线外 6、已知三边作三角形 已知:线段a 、b 、c 求作:△ABC ,使AB=a 、BC=b 、AC=c 。 c b a
7、已知两边及其夹角作三角形 已知:线段a、b、∠α 求作:△ABC,使AB=a、BC=b、∠B=∠α。 8、已知两角及其夹边作三角形 已知:线段a、∠α、∠β求作:△ABC,使∠A=∠α、∠B=∠β、AB=a。 9、已知底边及底边上的高作等腰三角形 已知:线段a、h 求作:△ABC,使AB=AC,BC=a、BC边上的高AD=h。 10、已知底边上的高和顶角作等腰三角形 已知:线段h 、∠α 求作:△ABC,使AB=AC,∠A=∠α,高AD=h。 11、已知底边及腰长作等腰三角形 已知:线段a、b
求作:△ABC ,使AB=AC=a ,BC=b 。 12、已知一直角边及斜边作直角三角形 已知:线段a 、c 求作:Rt △ABC ,使∠C=90°、AB=c 、BC=a 作三角形的外接圆 已知:△ABC 求作:△ABC 的外接圆⊙O 作三角形的内切圆 已知:△ABC 求作:△ABC 的内切圆⊙O 如图,1O7国道OA 和320国道OB 在我市相交于O 点,在∠AOB 的内部有工厂C 和D ,现要修建一个货站P ,使P 到OA 、OB 的距离相等,且使PC =PD ,用尺规作出货站P 的位置。 16、如图,直线AB ⊥CD ,垂足为P ,∠ACP=45°, 利用尺规在图中作一段劣弧,使得它在A 、C 两 A A B C B C
尺规作图基本作图方法
初中尺规作图基本方法 1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。 2、五种基本作图: 1、作一条线段等于已知线段; 2、作一个角等于已知角; 3、作已知线段的垂直平分线; 4、作已知角的角平分线; 5、过一点作已知直线的垂线; (1)题目一:作一条线段等于已知线段。 已知:如图,线段a . 求作:线段AB,使AB = a . 作法: (1)作射线AP; (2)在射线AP上截取AB=a . 则线段AB就是所求作的图形。 (2)题目二:作已知线段的垂直平分线。 已知:如图,线段MN. 求作:点O,使MO=NO(即O是MN的中点). 作法: 1 (1)分别以M、N为圆心,大于MN 2 的相同线段为半径画弧, 两弧相交于P,Q; (2)连接PQ交MN于O. 则点PQ就是所求作的MN的垂直平分线。 (3)题目三:作已知角的角平分线。 已知:如图,∠AOB, 求作:射线OP, 使∠AOP=∠BOP(即OP平分∠AOB)。 作法: (1)以O为圆心,任意长度为半径画弧, 分别交OA,OB于M,N; 1的线段长 (2)分别以M、N为圆心,大于MN 2 为半径画弧,两弧交∠AOB内于P; (3)作射线OP。 则射线OP就是∠AOB的角平分线。 (4)题目四:作一个角等于已知角。
已知:如图,∠AOB 。 求作:∠A ’O ’B ’,使A ’O ’B ’=∠AOB 作法: (1)作射线O ’A ’; (2)以O 为圆心,任意长度为半径画弧,交OA 于M ,交OB 于N ; (3)以O ’为圆心,以OM 的长为半径画弧,交O ’A ’于M ’; (4)以M ’为圆心,以MN 的长为半径画弧,交前弧于N ’; (5)连接O ’N ’并延长到B ’。 则∠A ’O ’B ’就是所求作的角。 (5)题目五:经过直线上一点做已知直线的垂线。 已知:如图,P 是直线AB 上一点。 求作:直线CD ,是CD 经过点P ,且CD ⊥AB 。 作法: (1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ; (2)分别以M 、N 为圆心,大于MN 2 1的长为半径画弧,两弧交于点Q ; (3)过D 、Q 作直线CD 。 则直线CD 是求作的直线。 (6)题目六:经过直线外一点作已知直线的垂线 已知:如图,直线AB 及外一点P 。 求作:直线CD ,使CD 经过点P , 且CD ⊥AB 。 作法: (1)以P 为圆心,任意长为半径画弧,交AB 于M 、N ; (2)分别以M 、N 圆心,大于MN 2 1长度的一半为半径画弧,两弧交于点Q ; (3)过P 、Q 作直线CD 。 则直线CD 就是所求作的直线。 (7)题目七:已知三边作三角形。 已知:如图,线段a ,b ,c. 求作:△ABC ,使AB = c ,AC = b ,BC = a. 作法: (1) 作线段AB = c ; (2) 以A 为圆心,以b 为半径作弧, 以B 为圆心,以a 为半径作弧与 前弧相交于C ; (3) 连接AC ,BC 。 则△ABC 就是所求作的三角形。 (8)题目八:已知两边及夹角作三角形。 已知:如图,线段m ,n, ∠ .
