全错位排列递推公式的简易推导(齐麟-晋级)

公务员之路从华图起步
全错位排列递推公式的简易证明
华图教育 齐麟
错位排列作为排列组合中的一类典型题目,自身难度较高,考生往往只是知其然而不知其所以然,即只了解全错位排列的递推公式,而不能理解其含义以及灵活的运用。本文结合图示的方法,对全错位排列公式进行简易的证明。
首先,我们先来认识错位排列: 1.部分错位排列:
【例】5个人站成一排,其中甲不站第一位,乙不站第二位,共有多少种不同的站法。 用排除法:
先考虑5个人的全排列,有55A 种不同的排法,然后除去甲排第一(有44A 种)与乙排第
二(也有44A 种)
,但两种情况又有重复部分,因此多减了一部分,必须加上多减部分,这样得到共有:55A -244A +3
3A =78种。
2.全错位排列:
【例】5个人站成一排,其中A 不站第一位,B 不站第二位,C 不站第三位,D 不站第四位,E 不站第五位,共有多少种不同的站法。
【分析】仿照以上解法,我们有
51423324150
555453525150D A C A C A C A C A C A 44=-?+?-?+?-?=
故5人的全错位排列方式共有44种。
因此我们可以由容斥原理得到n 个元素的全错位排列公式: 错误!未找到引用源。=n!(1-1/1!+1/2!-1/3!+...+(-1)^n*1/n!) 错位排列的递推公式
简单计算后我们有:1D 0=;错误!未找到引用源。;3D 2=。 计算四元素全错位排列时我们可以这样考虑:
假定元素为A 、B 、C 、D ;对应的位置为a 、b 、c 、d 。对于元素A ,我们可将其
放在b 、c 、d 三个位置,容易看出,这三个位置对于元素A 来说是等价的;假定A 现在放在了b 位置。
A
B
C
D
b a
c d
公务员之路从华图起步
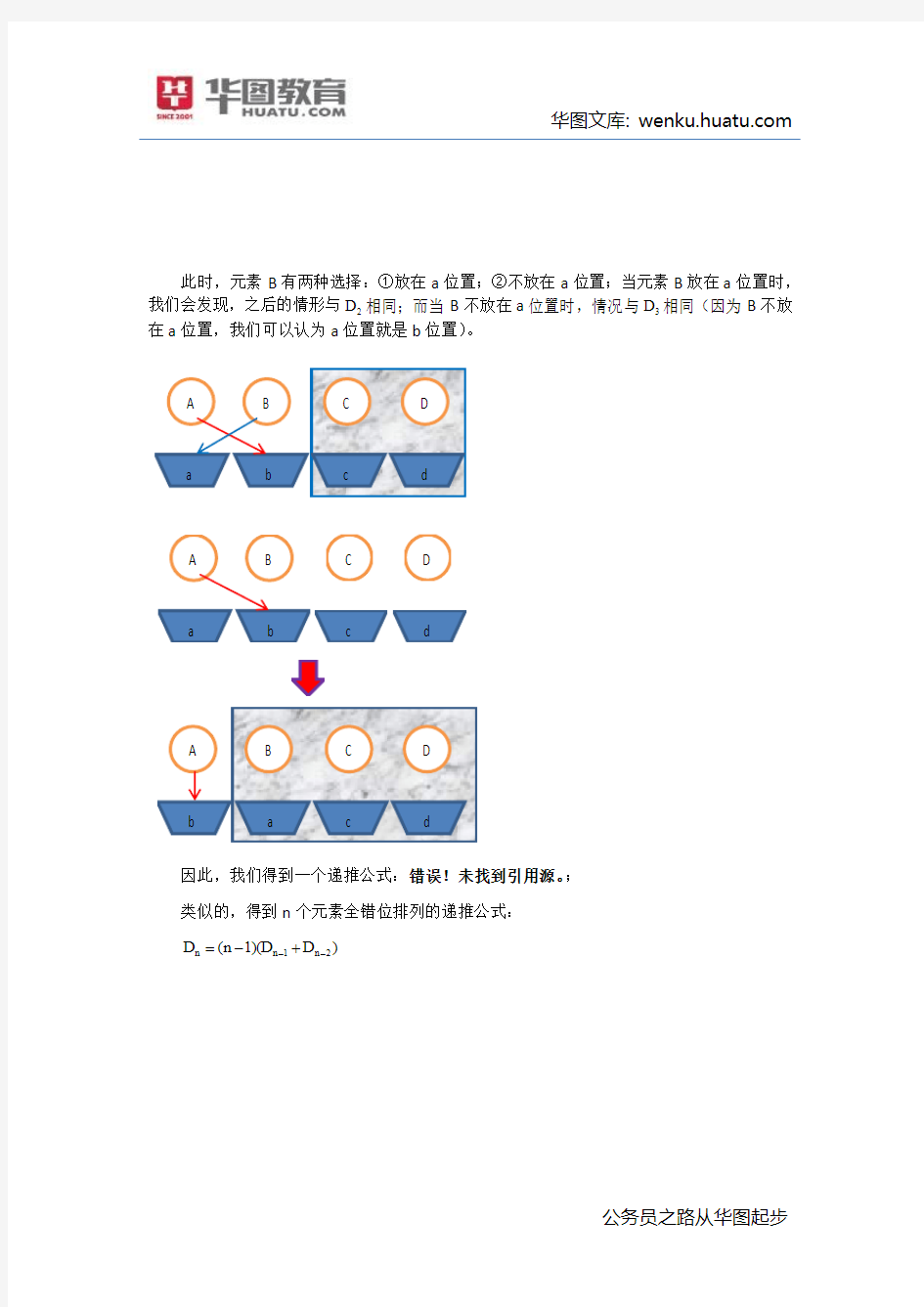
此时,元素B 有两种选择:①放在a 位置;②不放在a 位置;当元素B 放在a 位置时,我们会发现,之后的情形与2D 相同;而当B 不放在a 位置时,情况与3D 相同(因为B 不放在a 位置,我们可以认为a 位置就是b 位置)。
因此,我们得到一个递推公式:错误!未找到引用源。; 类似的,得到n 个元素全错位排列的递推公式:
n n 1n 2D (n 1)(D D )--=-+
A B C D
b a
c d
A B C D
b a
c d
A B C D
a b c d
新高二数学上期末试卷带答案
新高二数学上期末试卷带答案 一、选择题 1.将1000名学生的编号如下:0001,0002,0003,…,1000,若从中抽取50个学生,用系统抽样的方法从第一部分0001,0002,…,0020中抽取的号码为0015时,抽取的第40个号码为() A.0795B.0780C.0810D.0815 2.把五个标号为1到5的小球全部放入标号为1到4的四个盒子中,并且不许有空盒,那么任意一个小球都不能放入标有相同标号的盒子中的概率是() A.3 20 B. 7 20 C. 3 16 D. 2 5 3.七巧板是古代中国劳动人民的发明,到了明代基本定型.清陆以湉在《冷庐杂识》中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.如图,在七巧板拼成的正方形内任取一点,则该点取自图中阴影部分的概率是() A. 1 16 B. 1 8 C.3 8 D. 3 16 4.我国古代数学著作《九章算术》中,其意是:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?右图是源于其思想的一个程序框图,若输出的2 S=(单位:升),则输入k的值为 A.6 B.7 C.8 D.9 5.执行如图所示的程序框图,若输入8 x=,则输出的y值为()
A .3 B . 52 C . 12 D .34 - 6.执行如图的程序框图,如果输入72m =,输出的6n =,则输入的n 是( ) A .30 B .20 C .12 D .8 7.某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有( ) ①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人; ②用简单随机抽样的方法从新生中选出100人;
国家公务员:排列组合之错位排序
国家公务员:排列组合之错位排序 排列组合的数量题目当中,有一些技巧我们常常会用到,今天我们就一起来看一下排列组合问题中常用的方法——错位排序。 我们来讨论一个问题:这是一个很经典的数学问题:有一个人写了n封信件,对应n个信封,然而粗心的秘书却把所有信件都装错了信封,那么一共有多少种装错的装法? 这个问题可抽象为以下一个数学问题:已知一个长度为n的有序序列{a1,a2,a3,…,an},打乱其顺序,使得每一个元素都不在原位置上,则一共可以产生多少种新的排列?首先考虑几种简单的情况: 原序列长度为1 序列中只有一个元素,位置也只有一个,这个元素不可能放在别的位置上,因此原序列长度为1时该为题的解是0。 原序列长度为2 设原序列为{a,b},则全错位排列只需将两个元素对调位置{b,a},同时也只有这一种可能,因此原序列长度为2时该问题的解是1。 原序列长度为3 设原序列为{a,b,c},则其全错位排列有:{b,c,a},{c,a,b},解是2。 原序列长度为4 设原序列为{a,b,c,d},则其全错位排列有:{d,c,a,b},{b,d,a,c},{b,c,d,a},{d,a,b,c},{c,d,b,a},{c,a,d,b},{d,c,b,a},{c,d,a,b},{b,a,d,c},解是9。 在往下数,次数会更多,那我们就可以用不完全归纳得出规律:f(n)=(n-1)f(n-2)+(n-1)*f(n-1)=(n-1)[f(n-2)+f(n-1)] 。 很明显,规律不太好记。但是我们不用记,因为在公务员考试当中,题目一般情况下比较简单,我们只需要记住D1=0;D2=1;D3=2;D4=9;D5=44。即可下面我们一起来看一道例题: 【例】(2015-山东-59)某单位从下属的5个科室各抽调了一名工作人员,交流到其他科室,如每个科室只能接收一个人的话,有多少种不同的人员安排方式?()
数列求和7种方法(方法全-例子多)
数列求和 一、利用常用求和公式求和 利用下列常用求和公式求和是数列求和的最基本最重要的方法. 1、 等差数列求和公式:d n n na a a n S n n 2 )1(2)(11-+=+= 2、等比数列求和公式:?????≠--=--==)1(11)1()1(111q q q a a q q a q na S n n n 3、 )1(211+==∑=n n k S n k n 4、)12)(1(6112++==∑=n n n k S n k n 5、 213)]1(21[+==∑=n n k S n k n [例1],求???++???+++n x x x x 32的前n 项和. [例2] 设S n =1+2+3+…+n,n ∈N *,求1 )32()(++= n n S n S n f 的最大值. 题1.等比数列 的前n项和S n=2n-1,则= 题2.若12+22+…+(n -1)2=an 3+bn 2+cn ,则a = ,b = ,c = 二、错位相减法求和 { a n }、{ b n }分别是等差数列和等比数列. [例3] 求和:132)12(7531--+???++++=n n x n x x x S ………………………① [例4] 求数列??????,22,,26,24,2232n n 前n 项的和.
练习题1 已知 ,求数列{a n }的前n 项和S n . 练习题2 的前n 项和为____ 三、反序相加法求和 这是推导等差数列的前n 项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n 个)(1n a a +. [例6] 求 89sin 88sin 3sin 2sin 1sin 22222++???+++的值 题1 已知函数 (1)证明:; (2)求 的值. 练习、求值: 四、分组法求和
排列错乱的句子(一年级下)
人教版语文第二册期末复习资料(排列错乱的句子) 姓名: (一) ()没有尾巴多难看哪! ()过几天小壁虎长出一条新尾巴。 ()小壁虎的尾巴断了。 ()小壁虎向小鱼、老牛、燕子借尾巴。 (二) ()乌鸦把小石子一个一个地放进瓶子里。 ()乌鸦看见一个瓶子,瓶子里有水。 ()瓶子里的水渐渐升高,乌鸦就喝着水了。 ()可是瓶子里的水不多,瓶口又小,乌鸦喝不着水。 (三) ()然后,称一称船上的石头。 ()再把大象赶上岸,往船上装石头,装到船工下沉到画线的地方为止。()把大象赶到一艘大船上,看船身下沉多少,就沿着水面,在船舷上画一条线。 ()石头有多重,大象就有重。 (四) ()王二小把敌人带进八路军的埋伏圈。 ()有一天,敌人叫王二小带路。 ()这时候,八路军从山上冲下来,消灭了全部敌人。 ()敌人知道上了当就杀害了小英雄王二小。 (五) ()司马光兴起一块大石头,使劲砸那口缸,几下子就把缸砸破了。()有一回,他跟几个小朋友在花园里玩。 ()有个小朋友不小心掉进了大水缸。 ()缸里的水流出来了,掉进缸里的小朋友得救了。 ()古时候,有个孩子叫司马光。
(六) ()棉花姑娘请燕子、啄木鸟、青蛙帮她捉害虫。 ()棉花姑娘生病了,叶子上有许多蚜虫。 ()棉花姑娘病好,长出了碧绿碧绿的叶子,吐出了雪白雪白的棉花。()七星瓢虫给棉花姑娘治好了病。 (七) ()猴子妈妈看到一根很结实的青藤绕着大树生长,想出了办法。 ()地洞又深又滑,小猴子没办法爬上来,急得大哭。 ()她抓住青藤绕着大树转了几圈,把青藤拉直当绳子。 ()小猴子很淘气,玩时不小心,掉进了地洞。 ()小猴子拉着青藤就爬上了地面。 ()又在藤子的一头绑了一块大石头,放进洞里。 (八) ()一天,我对小明说:“咱们明天捉知了,好吗?”他愉快地答应了。()开始,我怎么也捉不到。 ()第二天,我们俩准备好了网罩,向树下跑去。 ()小明却一连捉了三、四只,我真羡慕他。 ()夏天一到,我们村口的大树上,从早到晚总能传来“知了——知了——”的叫声,我多么想亲手捉一只知了啊! ()最后,在小明的帮助下,我也套住了一只,心里别提多高兴了。 (九) ()一天,我找来一根小鞭子,赶着小鸭到村边的小溪去游泳。 ()此刻,我情不自禁地吟出一句古诗:“……白毛浮绿水,红掌拨清波。”()暑假,我到农村奶奶家度假。 ()可是,一到溪边,它们都活跃起来。“扑通!扑通!”跳进水里,游起来。()奶奶家养了一群小鸭。 ()路上小鸭晃着胖胖的身体,好像要摔倒似的。
错位重排专题
错位重排问题专项 错位重排 1-6个元素的错位重排数分别为0,1,2,9,44,265递推公式:Dm=(m-1)*[D(m-1)+D(m-2)]; 错位重排模型:把编号为1-m的小球分别放入编号为1-n的箱子错位重排(即1号球不在1号箱子、2号球不在2号箱子…m号球不在m号箱子),且每个箱子一个球,有多少种不同情况? 楚香凝证明:假设总情况数为D(m)种,如果让1号球先选,有(m-1)种选择;假设1号球选的2号箱子,接下来让2号球选箱子,进行分类讨论: ①如果2号球选的1号箱子,相当于剩下的(m-2)个球进行错位重排,有D(m-2)种; ②如果2号球选的不是1号箱子,则题目可转化为把编号为2→m的小球分别放入编号为 1、3→m的箱子错位重排(即2号球不在1号箱子、3号球不在3号箱子…m号球不在m号箱子),相当于m-1个球错位重排,有D(m-1)种; 所以可得D(m)=(m-1)*[D(m-1)+D(m-2)],得证; 例1:相邻的4个车位中停放了4辆不同的车,现将所有车开出后再重新停入这4个车位,要求所有车都不得停在原来的车位中,则一共有多少种不同的停放方式?【北京2014】 A.9 B.12 C.14 D.16 楚香凝解析: 解法一:四种元素错位重排有9种,选A 解法二:ABCD四辆车分别停放在一二三四号位置,A先选有三种情况,假设A选了二号,那么B再选、有三种选择,剩下C和D都只有一种选择,共3*3=9种,选A 例2:相邻的4个车位中停放了4辆不同的车,现将所有车开出后再重新停入这4个车位,要求有三辆车不能停在原来的车位中,则一共有多少种不同的停放方式? A.2 B.6 C.8 D.9 楚香凝解析:先选出停的正确的那辆车C(4 1)=4种,剩下三辆车错位重排有2种,共4*2=8种,选C 例3:相邻的4个车位中停放了4辆不同的车,现将所有车开出后再重新停入这4个车位,要求有两辆车不能停在原来的车位中,则一共有多少种不同的停放方式? A.2 B.6 C.8 D.9 楚香凝解析:先选出停的正确的两辆车C(4 2)=6种,剩下两辆车错位重排有1种,共6*1=6种,选B
(完整版)高中数学公式口诀大全
高中数学公式口诀大全 一、《集合与函数》 内容子交并补集,还有幂指对函数。性质奇偶与增减,观察图象最明显。复合函数式出现,性质乘法法则辨,若要详细证明它,还须将那定义抓。指数与对数函数,两者互为反函数。底数非1的正数,1两边增减变故。函数定义域好求。分母不能等于0,偶次方根须非负,零和负数无对数;正切函数角不直,余切函数角不平;其余函数实数集,多种情况求交集。两个互为反函数,单调性质都相同;图象互为轴对称,Y=X是对称轴;求解非常有规律,反解换元定义域;反函数的定义域,原来函数的值域。幂函数性质易记,指数化既约分数;函数性质看指数,奇母奇子奇函数,奇母偶子偶函数,偶母非奇偶函数;图象第一象限内,函数增减看正负。 二、《三角函数》 三角函数是函数,象限符号坐标注。函数图象单位圆,周期奇偶增减现。同角关系很重要,化简证明都需要。正六边形顶点处,从上到下弦切割;中心记上数字1,连结顶点三角形;向下三角平方和,倒数关系是对角,顶点任庖缓扔诤竺媪礁S盏脊骄褪呛茫夯蟠蠡。?nbsp; 变成税角好查表,化简证明少不了。二的一半整数倍,奇数化余偶不变,将其后者视锐角,符号原来函数判。两角和的余弦值,化为单角好求值,余弦积减正弦积,换角变形众公式。和差化积须同名,互余角度变名称。计算证明角先行,注意结构函数名,保持基本量不变,繁难向着简易变。逆反原则作指导,升幂降次和差积。条件等式的证明,方程思想指路明。万能公式不一般,化为有理式居先。公式顺用和逆用,变形运用加巧用;1加余弦想余弦,1 减余弦想正弦,幂升一次角减半,升幂降次它为范;三角函数反函数,实质就是求角度,先求三角函数值,再判角取值范围;利用直角三角形,形象直观好换名,简单三角的方程,化为最简求解集; 三、《不等式》 解不等式的途径,利用函数的性质。对指无理不等式,化为有理不等式。高次向着低次代,步步转化要等价。数形之间互转化,帮助解答作用大。证不等式的方法,实数性质威力大。求差与0比大小,作商和1争高下。直接困难分析好,思路清晰综合法。非负常用基本式,正面难则反证法。还有重要不等式,以及数学归纳法。图形函数来帮助,画图建模构造法。 四、《数列》 等差等比两数列,通项公式N项和。两个有限求极限,四则运算顺序换。数列问题多变幻,方程化归整体算。数列求和比较难,错位相消巧转换,取长补短高斯法,裂项求和公式算。归纳思想非常好,编个程序好思考:一算二看三联想,猜测证明不可少。还有数学归纳法,证明步骤程序化:首先验证再假定,从 K向着K加1,推论过程须详尽,归纳原理来肯定。 五、《复数》 虚数单位i一出,数集扩大到复数。一个复数一对数,横纵坐标实虚部。对应复平面上点,原点与它连成箭。箭杆与X轴正向,所成便是辐角度。箭杆的长即是模,常将数形来结合。代数几何三角式,相互转化试一试。代数运算的实质,有i多项式运算。i的正整数次慕,四个数值周期现。一些重要的结论,熟记巧用得结果。虚实互化本领大,复数相等来转化。利用方程思想解,注意整体代换术。几何运算图上看,加法平行四边形,减法三角法则判;乘法除法的运算,逆向顺向做旋转,伸缩全年模长短。
排列组合问题经典题型(含解析)
排列组合问题经典题型与通用方法 1.相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列. 例1.,,,, A B C D E五人并排站成一排,如果,A B必须相邻且B在A的右边,则不同的排法有() A、60种 B、48种 C、36种 D、24种 2.相离问题插空排:元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端. 例2.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是() A、1440种 B、3600种 C、4820种 D、4800种 3.定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序,可用缩小倍数的方法. 例3.A,B,C,D,E五人并排站成一排,如果B必须站在A的右边(,A B可以不相邻)那么不同的排法有()A、24种 B、60种 C、90种 D、120种 4.标号排位问题分步法:把元素排到指定位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成. 例4.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有() A、6种 B、9种 C、11种 D、23种 5.有序分配问题逐分法:有序分配问题指把元素分成若干组,可用逐步下量分组法. 例5.(1)有甲乙丙三项任务,甲需2人承担,乙丙各需一人承担,从10人中选出4人承担这三项任务,不同的选法种数是() A、1260种 B、2025种 C、2520种 D、5040种 (2)12名同学分别到三个不同的路口进行流量的调查,若每个路口4人,则不同的分配方案有() A、 444 1284 C C C 种 B、 444 1284 3C C C 种 C、 443 1283 C C A 种 D、 444 1284 3 3 C C C A种 6.全员分配问题分组法: 例6.(1)4名优秀学生全部保送到3所学校去,每所学校至少去一名,则不同的保送方案有多少种? (2)5本不同的书,全部分给4个学生,每个学生至少一本,不同的分法种数为() A、480种 B、240种 C、120种 D、96种 7.名额分配问题隔板法: 例7:10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案? 8.限制条件的分配问题分类法: 例8.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案? 9.多元问题分类法:元素多,取出的情况也多种,可按结果要求分成不相容的几类情况分别计数再相加。 例9(1)由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有()A、210种 B、300种 C、464种 D、600种 (2)从1,2,3…,100这100个数中,任取两个数,使它们的乘积能被7整除,这两个数的取法(不计顺序)共有多少种? (3)从1,2,3,…,100这100个数中任取两个数,使其和能被4整除的取法(不计顺序)有多少种?
全错位排列
全错位排列与多个特殊元素特殊位置 (C .T ) T 2=1,T 3=2,T n = (n -1) ( T n -1+T n -2) ,(n ≥3)( T n 为全错位排列数) 错位排列问题 题一 4名同学各写一张贺卡,先集中起来,然后每人从中拿出一张别人写的贺卡,则四张贺卡的不同分配方式共有 种. 题二 将编号为1,2,3,4的四个小球分别放入编号为1,2,3,4的四个盒子中,要求每个盒子放一个小球,且小球的编号与盒子的编号不能相同,则共有 种不同的放法. 这两个问题的本质都是每个元素都不在自己编号的位置上的排列问题,我们把这种限制条件的排列问题叫做全错位排列问题(所有元素均为特殊元素). 题三 五位同学坐在一排,现让五位同学重新坐,至多有两位同学坐自己原来的位置,则不 同的坐法有 种. 题三可以分类解决:第一类,所有同学都不坐自己原来的位置; 第二类,恰有一位同学坐自己原来的位置; 第三类,恰有两位同学坐自己原来的位置. 对于第一类,就是上面讲的全错位排列问题; 对于第二、第三类有部分元素还占有原来的位置,其余元素可以归结为全错位排列问题, 我们称这种排列问题为部分错位排列问题. (多个特殊元素,多个特殊位置) 部分错位排列(多个特殊元素,多个特殊位置) 例1:5个人站成一排,其中甲不站第一位,共有多少种不同的站法。 解一:(特殊元素特殊位置优先处理)第一步:安排甲这特殊元素,有14C 种; 第二步:安排其他人,其余的四个人(元素),不受限制,故有44A 种站法。由分步乘法原理 得14C 44A =96种站法。 解二:(排除法)先考虑5个人的全排列,有55A 种不同的排法,然后除去甲排第一(有44A 种) 这样得到共有:55A -44A =96种。 例2:5个人站成一排,其中甲不站第一位,乙不站第二位,共有多少种不同的站法。 解一:(特殊元素特殊位置优先处理) 分析:有两个特殊元素,分类讨论,减少限制条件。 第一类:甲站在第二位,则其他的四人(含乙),不受限制,有44A 种站法。 第二类:第一步安排特殊元素甲,甲不站在第二位,则甲也不能站在第一位,故甲的站法有 13C 种;第二步安排乙,乙不站第二位,也不能选择甲以经站的一个位置,故乙的站法有13C 种; 第三步安排其他人,其余的三个人(元素),不受限制,故有33A 种站法。由分步乘法原理得 13C 13C 33A 种站法。 由分类加法原理得44A +13C 13C 33A =78种。
数学归纳法巧记高中数学公式大全
高中数学公式大全及巧记口诀 离2012年高考只剩63天了,因为高中数学在高考中占有较大的比分,很多同学在数学上失分很多,其主要原因是同学们对数学基础知识记忆和掌握不够到位。因此我们乐恩特教育网整理了高中数学公式大全及巧计口诀,以便同学们轻松掌握数学公式,在高考数学复习上达到事半功倍的效果!以下就是整理的高中数学公式大全及巧记口诀: 一、《集合与函数》 内容子交并补集,还有幂指对函数。性质奇偶与增减,观察图象最明显。 复合函数式出现,性质乘法法则辨,若要详细证明它,还须将那定义抓。 指数与对数函数,两者互为反函数。底数非1的正数,1两边增减变故。 函数定义域好求。分母不能等于0,偶次方根须非负,零和负数无对数; 正切函数角不直,余切函数角不平;其余函数实数集,多种情况求交集。 两个互为反函数,单调性质都相同;图象互为轴对称,Y=X是对称轴; 求解非常有规律,反解换元定义域;反函数的定义域,原来函数的值域。 幂函数性质易记,指数化既约分数;函数性质看指数,奇母奇子奇函数, 奇母偶子偶函数,偶母非奇偶函数;图象第一象限内,函数增减看正负。 二、《三角函数》 三角函数是函数,象限符号坐标注。函数图象单位圆,周期奇偶增减现。 同角关系很重要,化简证明都需要。正六边形顶点处,从上到下弦切割; 中心记上数字1,连结顶点三角形;向下三角平方和,倒数关系是对角, 顶点任意一函数,等于后面两根除。诱导公式就是好,负化正后大化小, 变成税角好查表,化简证明少不了。二的一半整数倍,奇数化余偶不变, 将其后者视锐角,符号原来函数判。两角和的余弦值,化为单角好求值, 余弦积减正弦积,换角变形众公式。和差化积须同名,互余角度变名称。 计算证明角先行,注意结构函数名,保持基本量不变,繁难向着简易变。 逆反原则作指导,升幂降次和差积。条件等式的证明,方程思想指路明。
听说“9”和“44”与错位排列更配哦-全错位排列问题
听说“9”和“44”与错位排列更配哦-全错位排列问题亲,如果我说记住两个数字就能搞定数量关系中的一类难题,你信吗? 先不用忙着回答! 或许你将信将疑,但等你看完此文,你一定能找到足够的理由让自己相信。 一、问题导入 【引例1】唐僧、孙悟空、猪八戒、沙和尚4人在某公司不同岗位任职,现在需要调换岗位,要求每个人都不能在自己原来的岗位,则共有种不同的安排方法。 【引例2】有4名同学各写了一张贺卡,先全部收集起来,然后每人从中拿出一张贺卡,要求每个人都不拿自己的贺卡,则四张贺卡的不同分配方式共有种。 【引例3】将编号为1,2,3,4的四个小球分别放入编号为1,2,3,4的四个盒子中,要求每个盒子放一个小球,且小球的编号与盒子的编号不能相同(即1不放1,2不放2,3不放3,4不放4,也就是说4个全部放错),则共有种不同的放法。 不难发现,以上三个引例都是同一类问题,答案是多少呢?下面用枚举法给大家答案:假设原来顺序:A、B、C、D 枚举的时候注意按照一定规律进行,如果看成1、2、3、4号位置,那么第一步A可以放2、3、4号位置中的任意一个,第二步把B的位置确定,第三步确定C和D的位置:第1种错位排列:B、A、D、C(A在2位,B在1位,C、D位置就唯一确定了); 第2种错位排列:D、A、B、C(A在2位,B在3位,C、D位置就唯一确定了); 第3种错位排列:C、A、D、B(A在2位,B在4位,C、D位置就唯一确定了); 第4种错位排列:B、D、A、C(A在3位,B在1位,C、D位置就唯一确定了); 第5种错位排列:C、D、A、B(A在3位,B在4位,C、D位置可以是1、2); 第6种错位排列:D、C、A、B(A在3位,B在4位,C、D位置也可以是2、1); 第7种错位排列:B、C、D、A(A在4位,B在1位,C、D位置就唯一确定了); 第8种错位排列:C、D、B、A(A在4位,B在3位,C、D位置可以是1、2); 第9种错位排列:D、C、B、A(A在4位,B在3位,C、D位置也可以是2、1)。 可见,4个元素的错位排列一共有9种。即以上三道引例的答案都是9种。 那么,问题来了:图图老湿,我不想一个一个的枚举,眼睛都看花了,肿么办?而且如果下次不是4个元素了呢?答案又肿么办? 请耐心看下文。提前声明一下:接下来这一段需要一定的数学知识,如果觉得自己数学还不错的话可以详细逐字阅读;如果说NO,也没关系嗒,只需你记住最后结论即可哦! 二、理论推导
句子排序方法及习题附问题详解
句子排序方法及习题附答案 怎样排列顺序错乱的句子 把排列错乱的句子整理成一段通顺连贯的话,能训练对句子的理解能力、有条理表达能力和构段能力。这样的练习一般可按五步进行。 第一步,仔细阅读每句话或每组句子,理解它们的主要内容;第二步,综合各句的意思,想想这些话主要说的是什么内容;第三步,想想全段的内容按什么顺序排列好,即找出排列顺序的依据,如,是按事情发展顺序,还是时间顺序,或方位,还是“总分”等;第四步,按确定的排列依据排列顺序;第五步,按排好的顺序仔细读两遍,看排得对不对,如发现有的句子排得位置不对,就进行调整,直到这段话排得通顺连贯为止。把错乱的句子排列好,这是小学阶段语文练习中的一个重要形式,必须好好掌握。学会排列句子,不仅能提高我们的思维能力,还能提高我们的写作能力。那么,如何学会排列好句子呢?我们可以按下列方法进行。 一、按事情发展的顺序排列 有些错乱的句子,我们在排列时,应仔细分析句与句之间的联系。常见的错乱句子,往往叙述了一件完整的事,或者活动的具体过程。那么,我们就可以按事情发展的顺序来排列。 二、按时间先后顺序排列 对一些错乱的句子,我们可以找出表示时间概念的词语,如,早晨、上午、中午、下午等词,然后按时间先后顺序进行排列句子。 三、按先总述后分述的顺序排列 根据这段话的特点,找出这句话是个中心句,其他句子都是围绕着这句话来说的。显而易见,我们可按先总后分的顺序来排列句子。 四、按空间推移的顺序排列 所谓空间推移,就是由地点的转移,表达出不同的内容。排列时,要十分注意,不要与其他的方法相混淆。 对练习排列句子有帮助 把错乱的句子排列好,这是小学阶段语文练习中的一个重要形式,必须好好掌握。学会排列句子,不仅能提高我们的思维能力,还能提高我们的写作能力。那么,如何学会排列好句子呢?我们可以按下列方法进行。 一、按事情发展的顺序排列 有些错乱的句子,我们在排列时,应仔细分析句与句之间的联系。常见的错乱句子,往往
全装错信问题即全错位排列问题及拓展
全装错信问题即全错位排列问题及拓展 ——龙城老欧全装错信问题又称全错位排列问题,最早由瑞士数学家伯努利提出,最后由伯努利与他的学生欧拉讨论解决,这个问题就是—— 我们将编号是1、2、…、n的n封信,装入编号为1、2、…、n的n个信封,要求每封信都和信封的编号不同,即1不能装进1,2不能装进2,3不能装进3……问有多少种装法? 看到这个问题时,我们的第一反应就是退到简单处入手研究,如果只有一封信,2封信,3封信,4封信,……,然后从中再思考,之间是否有共性,是否有关联,共性用归纳,关联构成递推,或者其他。 〖解法〗 容易知道:a[1]=0,a[2]=1,a[3]=2,a[4]=6; 依我们设a[i]为i封信的全错位排列数据递归推理那么有 a[i]=(a[i-1]+a[i-2])×(i-1), (i>=3)。 为什么?为什么?为什么?大多数人看不明白。 不急,尽量先自己思考,不行的话,听我来解释: 思考1:对于插入第i个元素,只可能有两种情况: 第一种情况:插入第i个元素时,前i-1个已经错位排好,则选择其中任意一个与第i个互换一定满足要求,选择方法共i-1种,前i-1位错排f[i-1]种,记f[i-1]*(i-1),如下图: 第二种情况:插入第i个元素时,前i-1个中恰有一个元素恰好在自己的位置上,即恰好只有一个元素不满足错位排列,其他i-2个错位排好,则将i与j交换,j在i-2位中的插入共i-1种,前i-2位错排a[i-2]种,记f[i-2]*(i-1),如下图: 以上两种情况求和可得: a[i]=(a[i-1]+a[i-2])×(i-1) (i>=3) 我们还可以这样思考: 思考2:有(i-1)个人已经都坐在在自己的板凳上了,现在第i个人张三带着自己的板凳来了,下面我们来对这i个人进行全错位排排坐, 方法1:前面(i-1)个人中的某一个带着板凳出来与第i个人张三互换板凳坐(有(i-1)种方法),其它(i-2)个人进行全错位排列(有a[i-2]种方法),这样就整体上都是全错位;
7、排列组合问题之全错位排列问题(一个通项公式和两个递推关系)
排列组合问题之全错位排列问题 (一个通项公式和两个递推关系) 一、问题引入: 问题1、4名同学各写一张贺卡,先集中起来,然后每人从中拿出一张别人写的贺卡,则四张贺卡的不同分配方式共有多少种? 问题2、将编号为1,2,3,4的四个小球分别放入编号为1,2,3,4的四个盒子中,要求每个盒子放一个小球,且小球的编号与盒子的编号不能相同,则共有多少种不同的放法? 这两个问题的本质都是每个元素都不在自己编号的位置上的排列问题,我们把这种限制条件的排列问题叫做全错位排列问题。 问题3、五位同学坐在一排,现让五位同学重新坐,至多有两位同学坐自己原来的位置,则不同的坐法有多少种? 解析:可以分类解决:第一类,所有同学都不坐自己原来的位置; 第二类,恰有一位同学坐自己原来的位置; 第三类,恰有两位同学坐自己原来的位置。 对于第一类,就是全错位排列问题;对于第二、第三类有部分元素还占有原来的位置,其余元素可以归结为全错位排列问题,我们称这种排列问题为部分错位排列问题。 设n 个元素全错位排列的排列数为n T ,则对于问题3,第一类全错位排列的排列数为 5T ;第二类先确定一个排原来位置的同学有5种可能,其余四个同学全错位排列,所以第 二类的排列数为45T ;第三类先确定两个排原位的同学,有2 510C =种可能,其余三个同学 全错位排列,所以第三类的排列数为310T ,因此问题3的答案为:543510109T T T ++=。 由于生活中很多这样的问题,所以我们有必要探索一下关于全错位排列问题的解决方法。 二、全错位排列数的递推关系式之一: ()()121n n n T n T T --=-+ ()3n ≥ ①定义:一般地,设n 个编号为1、2、3、… 、i 、…、j 、…、n 的不同元素1a 、 2a 、3a 、…、i a 、…、j a 、…、n a ,排成一排,且每个元素均不排在与其编号相同的位 置,这样的全错位排列数为n T ,则 21T =;32T =;()()121n n n T n T T --=-+,()3n ≥。 ②递推关系的确立: 显然当1n =、2时,有10T =,21T =。 当3n ≥时,在n 个不同元素中任取一个元素i a 不排在与其编号相对应的i 位,必排在剩下1n -个位置之一,所以i a 有1n -种排法。 对i a 每一种排法,如i a 排在j 位,对应j 位的元素j a 的排位总有两种情况: 第一种情况:j a 恰好排在i 位上。此时,i a 排在j 位,j a 排在i 位,元素i a ,j a 排位已定。还剩2n -个元素,每个元素均有一个不能排的位置,它们的排位问题就转化为2n - 个元素全错位排列数,应有2n T -种。 第二种情况:j a 不排在i 位上。此时,i a 仍排在j 位,j a 不排在i 位,则j a 有1n -个位置可排。除i a 外,还有1n -个元素,每个元素均有一个不能排的位置,问题就转化为1n -n 个元素全错位排列数,应有1n T -种。 由乘法原理和加法原理可得:()()121n n n T n T T --=-+,()3n ≥。 利用此递推关系可以分别算出49T =,544T =。
排列组合问题的解题方法
第一课时 排列组合问题的解题方法(一) 教学目标: 掌握几类特殊的排列问题的解决技巧. 教学重点:掌握“条件排列”、“集团排列”、“间隔排列”、“部分顺序排列”问题的解题 技巧. 教学难点:如何应用“技巧”解题. 教学过程: 【例析技巧】 一.集团排列问题:部分元素必须安排在一起(相邻)的排列问题,称之为“集团排列” 问题.解决这类问题,常用“捆绑法”,其方法是先排“集团”部的元素,再把这个大“元素” 与其它元素一起排列即可. 例1 若7位同学站成一排 (1)甲、乙两同学必须相邻的排法共有多少种? (2)甲、乙和丙三个同学都相邻的排法共有多少种? (3)甲、乙两同学必须相邻,而且丙不能站在排头和排尾的排法有多少种? (4)甲、乙、丙三个同学必须站在一起,另外四个人也必须站在一起的排法有多少种? 解:(1)先将甲、乙两位同学“捆绑”在一起看成一个元素与其余的5个元素(同学) 一起进行全排列有66A 种方法;再将甲、乙两个同学“松绑”进行排列有2 2A 种方法.所以这 样的排法一共有62621440A A ?=种. (2)方法同上,一共有55A 33A =720种. (3)解法一:将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素, 因为丙不能站在排头和排尾,所以可以从其余的5个元素中选取2个元素放在排头和排尾, 有25A 种方法;将剩下的4个元素进行全排列有44A 种方法;最后将甲、乙两个同学“松绑” 进行排列有22A 种方法.所以这样的排法一共有25A 44A 2 2A =960种方法. 解法二:将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素,若丙站 在排头或排尾有255A 种方法,所以,丙不能站在排头和排尾的排法有960)2(225566=?-A A A 种方法.
关于全错位问题的结论
关于“全错位问题”的一个重要结论 一般地,我们把“1”不放在第一位,“2”不放在第二位,“3”不放在第三位……。“n ”不放在第n 位,称为“全错位问题”。在全错位问题中,如果一共有n 个元素,我们用f(n)表示全错位问题的排法种数。则可得一个重要结论: f(n)=nf(n-1)+(-1)n ,(n ≧2) * 例如:n=1时,显然f(1)=0 n=2时 共1种情况 而f(2)=2f(1)+(-1)2=1 符合*式 n=3时 或 共2种情况 而f(3)=3f(2)+(-1)3 =3×1-1=2 符合*式 n=4时,举例:用1、2、3、4这四个数字组成无重复数字的四位
数,1不在个位,2不在十位,3不在百位,4不在千位,共有多少种排法? 列举如下: 共9种排法 而f(4)=4f(3)+(-1)4=4×2+1=9符合*式 同理可验证: F(5)=5f(4)+(-1)5=44成立…… 下面给予一般性证明f(n)=nf(n-1)+(-1)n ,(n≧2) 1.当n=2时,f(3)=1,f(3)=3f(2)-1=2,等式成立, 当n=3时,f(3)=2,f(4)=4f(3)+1=9,等式成立; 2.假设n≤k (k≧3)等式成立,即k个元素a1、a2、a3……a k全错位排序的方法数的递推关系为f(k)=kf(k-1)+(-1)k, 则当n=k+1时,设全错位排序的元素为a1、a2、a3……a k、a k+1。在k个元素全错位排序的基础上,k+1个元素全错位排序后,它们全错位排序的方法分为两类,(1)a k+1与a i(i=1、2、……k)互调位置,其余元素全错位排列,方法数为kf(k-1);(2)a k+1在a i的位置上,但a i (i=1、2、……k)不在a k+1的位置上,相当于a k+1将的每一个全错位排
全错位排列公式
全错位排列 先看下面例子: 例1. 5个人站成一排,其中甲不站第一位,乙不站第二位,共有多少种不同的站法。 这个问题在高中很多参考书上都有,有几种解法,其中一种解法是用排除法: 先考虑5个全排列,有55A 种不同的排法,然后除去甲排在第一(有44A 种)与乙排第二(也有44A 种),但两种又有 重复部分,因此多减,必须加上多减部分,这样得到共有:543543278A A A -+=种。 现在考虑: 例2.5个人站成一排,其中甲不站第一位,乙不站第二位,丙不站第三位,共有多少种不同的站法。 仿上分析可得:543254323364A A A A -+-=种 这与全错位排列很相似。 全错位排列——即n 个元素全部都不在相应位置的排列。看下面的问题 例3.5个人站成一排,其中A 不站第一位,B 不站第二位,C 不站第三位,D 不站第四位,E 不站第五位,共有多少种不同的站法。 解析:上面例1,例2实际上可以看成n 个不同元素中有()m m n ≤不排在相应位置。 公式一:n 个不同元素排成一排,有m 个元素()m n ≤不排在相应位置的排列种数共有: ()1122121m n n n m n m n m n m n m n m A C A C A C A -------+++- 种 这个公式在n m =时亦成立,从而这个问题可能用上面的公式得出: 514233241505545352515044A C A C A C A C A C A -+-+-=种 (注意0000!1n C A ===) (1993年高考)同室四人各写一张贺年卡,先集中起来。然后每人从中拿一张别人送出的贺年卡。则四张贺年卡不同的分配方式有 (A)6种 (B)9种 (C)11种 (D)23种 解析:由上面公式得: 4132231404434241409A C A C A C A C A -+-+=种,∴选择B 答案 因此可得到全错位排列的公式: n 个不同元素排成一排,第一个元素不在第一位,第二个元素不在第二位,……,第n 个元素不在第n 位的排列数为: ()1122121n n n n n n n n n n n n n n n A C A C A C A -------+++- 这实际上是公式一的特殊情况。这个公式很有用,只要有特殊元素不站特殊位置的问题,都可以用这个公式很快得到解决,另一个计算公式:()111!111!2!3!!n n S n n ? ?=-+-++- ???
(完整版)高中数学完整讲义——排列与组合4.排列数组合数的计算与证明
1.基本计数原理 ⑴加法原理 分类计数原理:做一件事,完成它有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种方法,……,在第n 类办法中有n m 种不同的方法.那么完成这件事共有12n N m m m =+++L 种不同的方法.又称加法原理. ⑴乘法原理 分步计数原理:做一件事,完成它需要分成n 个子步骤,做第一个步骤有1m 种不同的方法,做第二个步骤有2m 种不同方法,……,做第n 个步骤有n m 种不同的方法.那么完成这件事共有12n N m m m =???L 种不同的方法.又称乘法原理. ⑴加法原理与乘法原理的综合运用 如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理.如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才告完成,那么计算完成这件事的方法数时,使用分步计数原理. 分类计数原理、分步计数原理是推导排列数、组合数公式的理论基础,也是求解排列、组合问题的基本思想方法,这两个原理十分重要必须认真学好,并正确地灵活加以应用. 2. 排列与组合 ⑴排列:一般地,从n 个不同的元素中任取()m m n ≤个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列.(其中被取的对象叫做元素) 排列数:从n 个不同的元素中取出()m m n ≤个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号A m n 表示. 排列数公式:A (1)(2)(1)m n n n n n m =---+L ,m n +∈N ,,并且m n ≤. 全排列:一般地,n 个不同元素全部取出的一个排列,叫做n 个不同元素的一个全排列. n 的阶乘:正整数由1到n 的连乘积,叫作n 的阶乘,用!n 表示.规定:0!1=. ⑴组合:一般地,从n 个不同元素中,任意取出m ()m n ≤个元素并成一组,叫做从n 个元素中任取知识内容 排列数组合数的计算与证明
(完整版)行测数量关系的常用公式讲解
行测常用数学公式 工作效率=工作量÷工作时间; 工作时间=工作量÷工作效率; 总工作量=各分工作量之和; 设总工作量为1或最小公倍数 (1)方阵问题: 1.实心方阵:方阵总人数=(最外层每边人数)2=(外圈人数÷4+1)2=N 2 最外层人数=(最外层每边人数-1)×4 2.空心方阵:方阵总人数=(最外层每边人数)2-(最外层每边人数-2×层数) 2 =(最外层每边人数-层数)×层数×4=中空方阵的人数。 ★无论是方阵还是长方阵:相邻两圈的人数都满足:外圈比内圈多8人。 3.N 边行每边有a 人,则一共有N(a-1)人。 4.实心长方阵:总人数=M ×N 外圈人数=2M+2N-4 5.方阵:总人数=N 2 N 排N 列外圈人数=4N-4 例:有一个3层的中空方阵,最外层有10人,问全阵有多少人? 解:(10-3)×3×4=84(人) (2)排队型:假设队伍有N 人,A 排在第M 位;则其前面有(M-1)人,后面有(N-M )人 (3)爬楼型:从地面爬到第N 层楼要爬(N-1)楼,从第N 层爬到第M 层要爬N M -层。 线型棵数=总长/间隔+1 环型棵数=总长/间隔 楼间棵数=总长/间隔-1 (1)单边线形植树:棵数=总长÷间隔+1;总长=(棵数-1)×间隔 (2)单边环形植树:棵数=总长÷间隔; 总长=棵数×间隔 (3)单边楼间植树:棵数=总长÷间隔-1;总长=(棵数+1)×间隔 (4)双边植树:相应单边植树问题所需棵数的2倍。 (5)剪绳问题:对折N 次,从中剪M 刀,则被剪成了(2N ×M +1)段 ⑴ 路程=速度×时间; 平均速度=总路程÷总时间 平均速度型:平均速度= 2 12 12v v v v + (2)相遇追及型:相遇问题:相遇距离=(大速度+小速度)×相遇时间 追及问题:追击距离=(大速度—小速度)×追及时间 背离问题:背离距离=(大速度+小速度)×背离时间 (3)流水行船型: 顺水速度=船速+水速; 逆水速度=船速-水速。 顺流行程=顺流速度×顺流时间=(船速+水速)×顺流时间 逆流行程=逆流速度×逆流时间=(船速—水速)×逆流时间 (4)火车过桥型: 列车在桥上的时间=(桥长-车长)÷列车速度 列车从开始上桥到完全下桥所用的时间=(桥长+车长)÷列车速度 列车速度=(桥长+车长)÷过桥时间 (5)环形运动型: 反向运动:环形周长=(大速度+小速度)×相遇时间 同向运动:环形周长=(大速度—小速度)×相遇时间
一年级语文下册排列错乱的句子
排列错乱的句子姓名 (一) ()没有尾巴多难看哪! ()过几天小壁虎长出一条新尾巴。 ()小壁虎的尾巴断了。 ()小壁虎向小鱼、老牛、燕子借尾巴。 (二) ()乌鸦把小石子一个一个地放进瓶子里。 ()乌鸦看见一个瓶子,瓶子里有水。 ()瓶子里的水渐渐升高,乌鸦就喝着水了。 ()可是瓶子里的水不多,瓶口又小,乌鸦喝不着水。 (三) ()然后,称一称船上的石头。 ()再把大象赶上岸,往船上装石头,装到船工下沉到画线的地方为止。 ()把大象赶到一艘大船上,看船身下沉多少,就沿着水面,在船舷上画一条线。()石头有多重,大象就有重。 (四) ()王二小把敌人带进八路军的埋伏圈。 ()有一天,敌人叫王二小带路。 ()这时候,八路军从山上冲下来,消灭了全部敌人。 ()敌人知道上了当就杀害了小英雄王二小。 (五) ()司马光兴起一块大石头,使劲砸那口缸,几下子就把缸砸破了。 ()有一回,他跟几个小朋友在花园里玩。 ()有个小朋友不小心掉进了大水缸。 ()缸里的水流出来了,掉进缸里的小朋友得救了。 ()古时候,有个孩子叫司马光。 (六) ()棉花姑娘请燕子、啄木鸟、青蛙帮她捉害虫。 ()棉花姑娘生病了,叶子上有许多蚜虫。 ()棉花姑娘病好,长出了碧绿碧绿的叶子,吐出了雪白雪白的棉花。 ()七星瓢虫给棉花姑娘治好了病。
(七) ()猴子妈妈看到一根很结实的青藤绕着大树生长,想出了办法。 ()地洞又深又滑,小猴子没办法爬上来,急得大哭。 ()她抓住青藤绕着大树转了几圈,把青藤拉直当绳子。 ()小猴子很淘气,玩时不小心,掉进了地洞。 ()小猴子拉着青藤就爬上了地面。 ()又在藤子的一头绑了一块大石头,放进洞里。 (八) ()一天,我对小明说:“咱们明天捉知了,好吗?”他愉快地答应了。 ()开始,我怎么也捉不到。 ()第二天,我们俩准备好了网罩,向树下跑去。 ()小明却一连捉了三、四只,我真羡慕他。 ()夏天一到,我们村口的大树上,从早到晚总能传来“知了——知了——”的叫声,我多么想亲手捉一只知了啊! ()最后,在小明的帮助下,我也套住了一只,心里别提多高兴了。 (九) ()一天,我找来一根小鞭子,赶着小鸭到村边的小溪去游泳。 ()此刻,我情不自禁地吟出一句古诗:“……白毛浮绿水,红掌拨清波。” ()暑假,我到农村奶奶家度假。 ()可是,一到溪边,它们都活跃起来。“扑通!扑通!”跳进水里,游起来。 ()奶奶家养了一群小鸭。 ()路上小鸭晃着胖胖的身体,好像要摔倒似的。
