(完整版)最全拉氏变换计算公式

最全拉氏变换计算公式
1
2
3
3. 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式
1110
111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++=
=----ΛΛ (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110-Λ都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根
这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n
i i
i n n i i s s c s s c s s c s s c s s c s F 122
11)(ΛΛ
式中,n s s s ,,,21Λ是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计
算:
)()(lim s F s s c i s s i i
-=→
或
i
s
s i s A s B c ='=
)()
(
式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数
[]??????-==∑=--n i i i s s c L s F L t f 11
1
)()(=t
s n i i i
e c -=∑1
②
0)(=s A 有重根
设0)(=s A 有r 重根1s ,F(s)可写为
())
()()()
(11n r r
s s s s s s s B s F ---=
+Λ =
n
n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11
111
111)()()( 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
4
其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:
)()(lim 11
s F s s c r s s r -=→
)]()([lim
111
s F s s ds
d
c r s s r -=→- M
)()(lim !11)()
(1s F s s ds
d j c r j j s s j
r -=→- (F-5) M
)()(lim )!1(11)1()
1(11s F s s ds
d r c r r r s s --=--→
原函数)(t f 为 [])()(1
s F L
t f -=
??????-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L ΛΛΛ11
111
1111)()()
( t s n
r i i t s r r r r i
e c e c t c t r c t r c ∑+=---+??
????+++-+-=112211
1
)!2()!1(Λ (F-6)
拉普拉斯变换公式总结
拉普拉斯变换、连续时间系统的S 域分析 基本要求 通过本章的学习,学生应深刻理解拉普拉斯变换的定义、收敛域的概念:熟练掌握拉普拉斯变换的性质、卷积定理的意义及它们的运用。能根据时域电路模型画出S 域等效电路模型,并求其冲激响应、零输入响应、零状态响应和全响应。能根据系统函数的零、极点分布情况分析、判断系统的时域与频域特性。理解全通网络、最小相移网络的概念以及拉普拉斯变换与傅里叶变换的关系。会判定系统的稳定性。 知识要点 1. 拉普拉斯变换的定义及定义域 (1) 定义 单边拉普拉斯变换: 正变换0[()]()()st f t F s f t dt e ζ∞ -- ==? 逆变换 1 [()]()()2j st j F s f t F s ds j e σσζπ+∞ -∞ == ? 双边拉普拉斯变换: 正变换 ()()st B s f t dt e F ∞ --∞ =? 逆变换1 ()()2j st B j f t s ds j e F σσπ+∞ -∞ = ? (2) 定义域
若0σσ>时,lim ()0t t f t e σ-→∞ =则()t f t e σ-在0σσ>的全部范围内收敛,积分0()st f t dt e +∞ -- ? 存 在,即()f t 的拉普拉斯变换存在。0σσ>就是()f t 的单边拉普拉斯变换的收敛域。0σ与函数()f t 的性质有关。 2. 拉普拉斯变换的性质 (1) 线性性 若11[()]()f t F S ζ=,22[()]()f t F S ζ=,1κ,2κ为常数时,则11221122[()()]()()f t f t F s F s ζκκκκ+=+ (2) 原函数微分 若[()]()f t F s ζ=则() [ ]()(0)df t sF s f dt ζ-=- 1 1()0 ()[]()(0)n n n n r r n r d f t s F s s f dt ζ----==-∑ 式中() (0)r f -是r 阶导数() r r d f t dt 在0-时刻的取值。 (3) 原函数积分 若[()]()f t F s ζ=,则(1)(0)()[()]t f F s f t dt s s ζ---∞ =+? 式中0(1) (0)()f f t dt ---∞=? (4) 延时性 若[()]()f t F s ζ=,则000[()()]()st f t t u t t e F s ζ---= (5) s 域平移
拉氏变换和z变换表
附录A 拉普拉斯变换及反变换 1.拉氏变换的基本性质 附表A-1 拉氏变换的基本性质 1()([n n k f t dt s s -+= +∑?个
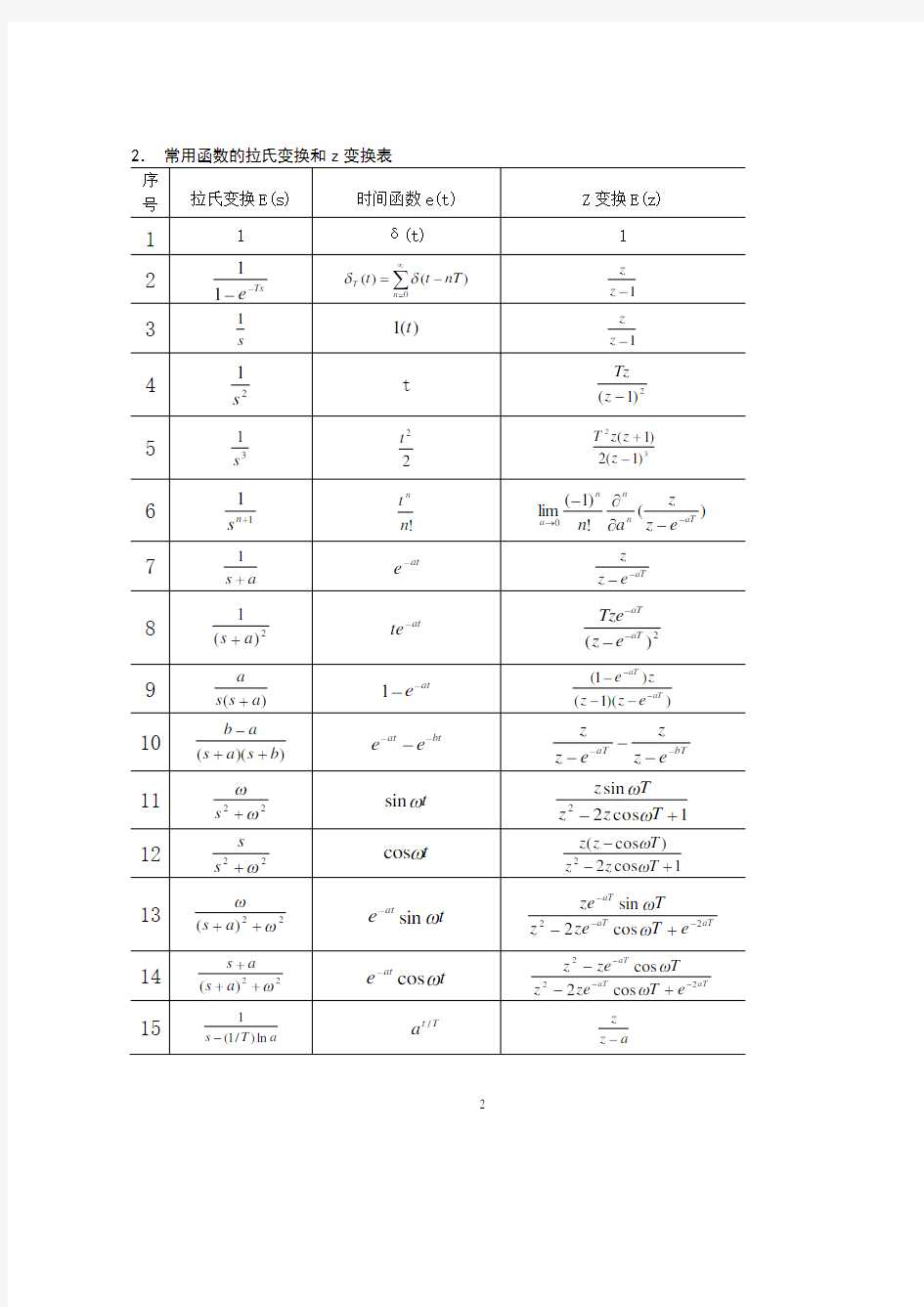
2.常用函数的拉氏变换和z变换表 附表A-2 常用函数的拉氏变换和z变换表
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式,即 11 10 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- (m n >) 式中,系数n n a a a a ,,...,,110-和011,, ,,m m b b b b -都是实常数;n m ,是正整数。按代数定理 可将)(s F 展开为部分分式。分以下两种情况讨论。 (1)0)(=s A 无重根:这时,F(s)可展开为n 个简单的部分分式之和的形式,即 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)( (F-1) 式中,n s s s ,,,21 是特征方程A(s)=0的根;i c 为待定常数,称为()F s 在i s 处的留数,可按下列两式计算:lim()()i i i s s c s s F s →=- (F-2) 或 i s s i s A s B c ='= )() ( (F-3)
式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数为 []??????-==∑=--n i i i s s c L s F L t f 11 1 )()(=1 i n s t i i c e =∑ (F-4) (2)0)(=s A 有重根:设0)(=s A 有r 重根1s ,F(s)可写为 ()) ()()() (11n r r s s s s s s s B s F ---= + = n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11 111 111)()()( 式中,1s 为F(s)的r 重根,1+r s ,…,n s 为F(s)的n r -个单根;其中,1+r c ,…,n c 仍按式(F-2)或式(F-3)计算,r c ,1-r c ,…,1c 则按下式计算: )()(lim 11 s F s s c r s s r -=→ 11lim [()()]i r r s s d c s s F s ds -→=- )()(lim !11)() (1s F s s ds d j c r j j s s j r -=→- (F-5) )()(lim )!1(11)1() 1(11s F s s ds d r c r r r s s --=--→ 原函数)(t f 为 [])()(1 s F L t f -= ??????-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 11 111 1111)()() ( t s n r i i t s r r r r i e c e c t c t r c t r c ∑+=---+?? ????+++-+-=112211 1 )!2()!1( (F-6)
拉氏变换与反变换
拉氏变换与反变换 机电控制工程所涉及的数学问题较多,经常要解算一些线性微分方程。按照一般方法解算比较麻烦,如果用拉普拉斯变换求解线性微分方程,可将经典数学中的微积分运算转化为代数运算,又能够单独地表明初始条件的影响,并有变换表可查找,因而是一种较为简便的工程数学方法。 拉普拉斯变换的定义 如果有一个以时间 t 为自变量的实变函数 ()t f ,它的定义域是 0≥t ,那么 ()t f 的拉普拉斯变换定义为 ()()()0e d st F s L f t f t t ∞ -=?????? 式中, s 是复变数, ωσj +=s (σ、ω均为实数), ?∞ -0 e st 称为拉 普拉斯积分; )(s F 是函数 )(t f 的拉普拉斯变换,它是一个复变函数,通常也称 )(s F 为 )(t f 的象函数,而称 )(t f 为 )(s F 的原函数;L 是表示进行拉普拉斯变换的符号。 式()表明:拉氏变换是这样一种变换,即在一定条件下,它能把一实数域中的实变函数变换为一个在复数域内与之等价的复变函数 )(s F 。 几种典型函数的拉氏变换
1.单位阶跃函数 )(1t 的拉氏变换 单位阶跃函数是机电控制中最常用的典型输入信号之一,常以它作为评价系统性能的标准输入,这一函数定义为 ?? ?≥s ,则 0 e lim →-∞→st t 。 所以 []s s s t L st 1)1(00e 1)(1= ??????--=∞-=-()
拉氏变换与反变换(严选内容)
2.5 拉氏变换与反变换 机电控制工程所涉及的数学问题较多,经常要解算一些线性微分方程。按照一般方法解算比较麻烦,如果用拉普拉斯变换求解线性微分方程,可将经典数学中的微积分运算转化为代数运算,又能够单独地表明初始条件的影响,并有变换表可查找,因而是一种较为简便的工程数学方法。 2.5.1 拉普拉斯变换的定义 如果有一个以时间 t 为自变量的实变函数 ()t f ,它的定义域是 0≥t ,那么 ()t f 的拉普拉斯 变换定义为 ()()()0 e d st F s L f t f t t ∞ -=??????(2.10) 式中, s 是复变数, ωσj +=s (σ、ω均为实数), ? ∞ -0 e st 称为拉普拉斯积分; )(s F 是 函数 )(t f 的拉普拉斯变换,它是一个复变函数,通常也称 )(s F 为 )(t f 的象函数,而称 )(t f 为 )(s F 的原函数;L 是表示进行拉普拉斯变换的符号。 式(2.10)表明:拉氏变换是这样一种变换,即在一定条件下,它能把一实数域中的实变函数变换为一个在复数域内与之等价的复变函数 )(s F 。 2.5.2 几种典型函数的拉氏变换 1.单位阶跃函数 )(1t 的拉氏变换 单位阶跃函数是机电控制中最常用的典型输入信号之一,常以它作为评价系统性能的标准输入,这一函数定义为 ?? ?≥s ,则 e lim →-∞ →st t 。
高强度螺栓扭矩系数、摩擦面抗滑移系数检测取样说明
何谓钢结构?钢结构有何特点? 1、由钢材轧制的型材和板材作为基本构件,采用焊接、铆接或螺栓连接等方法,按照一定的结构组成规则连接起来,能承受荷载的结构物叫钢结构。 2、钢结构的特点:(1)钢结构自重轻、强度高、塑性和韧性好、抗震性好。 (2)钢结构计算准确,安全可靠。 (3)钢结构制造简单,施工方便,具有良好的装配性。 (4)钢结构的密闭性好。便于做成密闭容器。 (5)钢结构建筑在使用中易于改造。 (6)钢结构可做成大跨度和大空间的建筑。 (7)钢结构的耐腐蚀性能差。 (8)钢结构耐热性好、耐火性差。 1、钢结构屋脊两侧的C型檩条间是否必须用撑杆(刚拉条)连接?它的作用是什么? 撑杆是必须的,主要是保障檩条避免侧向失稳。 2、Q235韧性好,Q345强度高,Q235结构钢为碳钢,Q 345为低合金钢;前者的塑性及可焊性较后者要好一些,价格前者便宜一些;强度后者好一些。 3、钢结构厂房中,以C型钢为例,檩条安装方向是开口朝向屋脊好还是檐口好? 槽型和Z型;檩条上翼缘的肢尖(或卷边)应朝向屋脊方向,以减少荷载偏心引起的扭矩…… Z或者C形檩条的安装方向为上翼缘朝向屋脊:上翼缘朝向屋脊是为了减少C、Z型檩条总存在向屋脊方向的力矩,为了克服或减少这种力矩,再加上支座处有一个檩托,可以保证檩条的侧向稳定和向屋脊倒。屋面板对其檩条起到一个很好的保护作用。并与屋面拉条一道形成支撑体系这个问题分别按照开口向上和向下计算一下就可以很容易的看出了,开口向下时最大的应力出现在卷边处,卷边没有板件支撑,容易使檩条受压屈曲。反之,开口向上,最大的应力出现在腹板边缘处处,此时腹板可以提供支撑作用,使檩条受力合理。
(推荐)拉氏变换常用公式
常用拉普拉斯变换总结 1、指数函数 00)(≥
? ? ∞ -∞ -∞ ----==0 d d ][t s e s e t t te t L st st st 2 01d 1s t e s st == ?∞- 6、正弦函数 0sin 0 )(≥
1支撑,拉条及拉条连接节点的常见错误
第!"卷第#期建筑结构$%%"年#月轻钢结构设计中几个常见错误分析 鲁莉 (交通部第三航务工程勘察设计院上海$%%%!$)梁发云(同济大学地下建筑与工程系上海$%%%&$)[提要]轻钢结构近年来在我国得以广泛应用,但部分设计人员没有接受过专门培训,由于设计不周等原因造成的事故时有发生。针对这一情况,结合具体实例,总结了轻钢结构设计中在支撑设置、拉条设置、拉条节点等几方面的常见设计错误,并加以分析,供设计人员参考。 [关键词]轻钢结构设计错误门式刚架支撑拉条 ’()*+,-()*+.+--/.+012+10-.30--4+-5.(6-/71.-8(59*(53(50-2-5+7-30.:;-231.-.<=-.+012+10-8-.() 5-0.*36-5’+>--5+03(5-8(5+*(..?-2(3/(@-8A (-/8,322(8-5+.81-+<(52<5.(8-03+-8-.()5*3??-5-8<223.(<53//7 :B -6-03/2<==<5-0C 0<0.(5+*-8-.()5032-,+-5.(<50<8,+-5.(<50<8D <(5+.30-(5+0<812-8358353/7@-8+*0<1)*-5)(5--0(5)? 032+(2-.:E +235>-0-A -008+<8-.() 5-0.(5?032+(2-:!"# $%&’(:/()*+,-()*+.+--/.+012+10-.;8-.()5-00<0.;)3>/-8A 03=-;>032-;+-5.(<50<8目前很多轻钢厂家是设计、制作、安装一体化服 务,从业人员的素质良莠不齐。因此,轻钢结构由于设 计不周等原因造成的事故时有发生[F ]。笔者通过多年 来从事轻钢结构设计的实践和体会,总结了设计工作 中常见的错误,提出来以供广大设计人员参考。 一、关于支撑的设置 正确的支撑系统应能形成完整的传力路线,否则 就不能发挥作用。设计人员对此必须有正确的认识。 (F )屋面支撑不设压杆,构造如图F (3 )所示。一般屋面支撑多采用张紧的圆钢,只能承受拉力,在不设压 杆的情况下无法形成传递水平力的桁架,支撑实际上 不起作用。正确的构造应如图F (>)所示,在承受水平 力时,其计算模型如图F (2)所示,图中虚线所示为 退 出工作的杆件。 单击来源网站https://www.360docs.net/doc/c2324108.html,/shop/view_shop.htm?nekot=0rbB6NTGMjAxMA==1294278459959&user_number_id=441536699
拉普拉斯变换公式
附录A 拉普拉斯变换及反变换
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式 1110 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++= =----ΛΛ (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110-Λ都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)(ΛΛ (F-1) 式中,n s s s ,,,21Λ是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可 按下式计算: )()(lim s F s s c i s s i i -=→ (F-2) 或 i s s i s A s B c ='= )() ( (F-3) 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数 []??????-==∑=--n i i i s s c L s F L t f 11 1 )()(=t s n i i i e c -=∑1 (F-4) ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为 ()) ()()() (11n r r s s s s s s s B s F ---= +Λ =n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11 111111)()()(
常用的拉氏变换表
精选资料,欢迎下载 常用函数的拉氏变换和z 变换表 序号 拉氏变换E(s) 时间函数e(t) Z 变换E(z) 1 1 δ(t) 1 2 Ts e --11 ∑∞ =-=0)()(n T nT t t δδ 1 -z z 3 s 1 )(1t 1 -z z 4 21s t 2 )1(-z Tz 5 3 1s 2 2t 3 2 )1(2)1(-+z z z T 6 1 1+n s !n t n )(!)1(lim 0aT n n n a e z z a n -→-??- 7 a s +1 at e - aT e z z -- 8 2 )(1a s + at te - 2 )(aT aT e z Tze --- 9 )(a s s a + at e --1 ) )(1()1(aT aT e z z z e ----- 10 ) )((b s a s a b ++- bt at e e --- bT aT e z z e z z ---- - 11 22ω ω +s t ωsin 1 cos 2sin 2+-T z z T z ωω 12 2 2ω+s s t ωcos 1 cos 2)cos (2+--T z z T z z ωω 13 22)(ω ω++a s t e at ωsin - aT aT aT e T ze z T ze 22cos 2sin ---+-ωω 14 2 2)(ω+++a s a s t e at ωcos - aT aT aT e T ze z T ze z 222cos 2cos ---+--ωω 15 a T s ln )/1(1- T t a / a z z -
拉条的设置研究
拉条的设置研究 段正光,刘堰陵 (武汉市政工程设计研究院有限责任公司武汉 430023) 摘要:结合实际设计经验,对轻钢结构设计中关于拉条的设置进行了探讨。 关键词:轻钢结构;拉条;洞口 1 概述 拉条起承受檩条侧向力、减小檩条侧向变形的作用。同时,拉条还可作为檩条的侧向支撑,减小檩条的计算长度。其作用很容易理解,但拉条力的传递却往往被忽视。 2 屋面拉条的设置 2.1 屋脊及屋面开洞时拉条设置 拉条受力一般需要传至刚架上,旧的轻钢规程CECS102:98第6.3.5条指出:“在屋脊处还应设置斜拉条和撑杆”。如图1(a)所示,拉条的力在屋脊处从斜拉条和撑杆组成的水平桁架传至檩条的端部,靠近檩条与刚架节点,相当于将拉条的力传至刚架。根据同样的原理,当屋面开孔时,在开孔的下侧也应设置斜拉条和撑杆,如图1(b)。有些设计不设这部分斜拉条和撑杆,且所有檩条也采用相同的截面,则图中檩条1以下的拉条力都传到檩条1上,可能造成檩条1强度不够。修订后的轻钢规程CECS102:2002中第6.3.5条已改为“斜拉条应与刚性檩条连接”,上述屋面开孔的情况就属于应设斜拉条的情况。
当屋面是双坡对称结构时,也可采用如图1(c)所示的拉条布置方式,即在屋脊处设拉条1,直接将屋脊檩条连起来,使两侧拉条的力互相平衡。但在这种情况下,需要注意屋脊檩条在拉条作用下受力模型如图1(d)所示,拉条会对檩条产生垂直于屋面向下的合力Ntgθ。与其它檩条相比,屋脊檩条承受的屋面荷载面积较小,但增加了拉条的垂直力Ntgθ,屋面荷载与拉条附加力的合力不一定比其它檩条所受合力小,因此,屋脊檩条需要单独计算。对于屋面不对称的情况,由于屋脊两侧拉条的力不能平衡,这种方法是不可行的。 2.2 屋檐处拉条的设置
撑杆杆件计算
支撑压弯构件计算书 〖已知参数〗 截面规格:"DD152x9" 截面类型如下图1 [图1] 材料:Q235 截面抗压削弱系数:0.95 截面抗弯削弱系数分别为:0.95,0.95 对X轴的计算长度:6.00m 对Y轴的计算长度:6.00m 长细比近似计算放大系数:1.20 轴力:-300.00kN(压力) 弯矩Mx:0.00kN.m 弯矩My:0.00kN.m 弯矩取值的正负号按下图2规定 [图2] 系数βmx:1.00 系数βtx:1.00 系数βmy:1.00 系数βty:1.00 〖强度计算〗 截面左上角应力
支撑压弯构件计算书 根据《钢结构设计规范》GB50017-2003的公式5.2.1 (公式5.2.1) 上式三项值分别为 -78.10,0.00,0.00 σ=-78.10Mpa 截面右上角应力 根据《钢结构设计规范》GB50017-2003的公式5.2.1 (公式5.2.1) 上式三项值分别为 -78.10,0.00,0.00 σ=-78.10Mpa 截面左下角应力 根据《钢结构设计规范》GB50017-2003的公式5.2.1 (公式5.2.1) 上式三项值分别为 -78.10,0.00,0.00 σ=-78.10Mpa 截面右下角应力 根据《钢结构设计规范》GB50017-2003的公式5.2.1 (公式5.2.1) 上式三项值分别为 -78.10,0.00,0.00 σ=-78.10Mpa 截面最大应力σ=78.10Mpa 应力比=0.36 〖稳定计算〗 ※计算构件长细比 根据构件的截面形状进行分类计算 构件截面属于双轴对称或极对称的实腹式,根据《钢结构设计规范》GB50017-2003的公式5.1.2-2 (公式5.1.2-2)
钢结构檩条如何计算
钢结构檩条如何计算 檁条的截面形式 实腹式檁条的截面形式 实腹式冷弯薄壁型钢截面在工程中的应用很普遍。其中,卷边槽钢(亦称C形钢)檩条适用于屋面坡度i≤1/3的情况。 直边和斜卷边z形檩条适用于屋面坡度i>1/3的情况。斜卷边Z形钢存放时可叠层堆放,占地少。做成连续梁檩条时,构造上也很简单。 檩条的荷载和荷载组合
1.2×永久荷载+1.4×max{屋面均布活荷载,雪荷载}; 1.2×永久荷载+1.4×施工检修集中荷载换算值。 当需考虑风吸力对屋面压型钢板的受力影响时,还应进行下式的荷载组合: 1.0×永久荷载+1.4×风吸力荷载。 檩条的内力分析 设置在刚架斜梁上的檩条在垂直于地面的均布荷载作用下,沿截面两个形心主轴方向都有弯矩作用,属于双向受弯构件(与一般受弯构件不同)。 在进行内力分析时,首先要把均布荷载分解为沿截面形心主轴方向的荷载分量qx 、qy。 C型檩条在荷载作用下计算简图如下:
Z型檩条在荷载作用下计算简图如下:
檩条的内力计算 檩条的截面验算—强度、整体稳定、变形 强度计算—按双向受弯构件计算 当屋面能阻止檩条的失稳和扭转时,可按下列强度公式验算截面:截面1.2.3.4点正应力计算公式如下:
整体稳定计算 当屋面不能阻止檩条的侧向失稳和扭转时(如采用扣合式屋面板时),应按稳定公式验算截面:
变形计算 实腹式檩条应验算垂直于屋面方向的挠度。 对卷边槽形截面的两端简支檩条: 对Z形截面的两端简支檩条: 容许挠度[v]按下表取值 檁条的构造要求 当檩条跨度大于4m时,应在檩条间跨中位置设置拉条。当檩条跨度大6m时,应在檩条跨度三分点处各设置一道拉条。
最全拉氏变换计算公式
1 最全拉氏变换计算公式 1. 拉氏变换的基本性质 1 线性定理 齐次性 )()]([s aF t af L = 叠加性 )()()]()([2121s F s F t f t f L ±=± 2 微分定理 一般形式 = -=][ '- -=-=----=-∑1 1 )1() 1(1 22 2) ()() 0()()(0)0()(])([)0()(]) ([ k k k k n k k n n n n dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L )( 初始条件为0时 )(])([s F s dt t f d L n n n = 3 积分定理 一般形式 ∑???????????==+-===+=+ +=+= n k t n n k n n n n t t t dt t f s s s F dt t f L s dt t f s dt t f s s F dt t f L s dt t f s s F dt t f L 10 102 2022 ]))(([1)(])()([]))(([])([)(]))(([])([)(])([个 共个 共 初始条件为0时 n n n s s F dt t f L ) (]))(([=??个 共 4 延迟定理(或称t 域平移定理) )()](1)([s F e T t T t f L Ts -=-- 5 衰减定理(或称s 域平移定理) )(])([a s F e t f L at +=- 6 终值定理 )(lim )(lim 0 s sF t f s t →∞ →= 7 初值定理 )(lim )(lim 0 s sF t f s t ∞ →→= 8 卷积定理 )()(])()([])()([210 210 21s F s F d t f t f L d f t f L t t =-=-??τττττ
拉氏变换表(包含计算公式)
1 拉氏变换及反变换公式 1. 拉氏变换的基本性质 1 线性定理 齐次性 )()]([s aF t af L = 叠加性 )()()]()([2121s F s F t f t f L ±=± 2 微分定理 一般形式 = -=][ '- -=-=----=-∑ 1 1 ) 1() 1(1 2 2 2 ) ()() 0()() (0)0()(]) ([) 0()(])([k k k k n k k n n n n dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ) ( 初始条件为0时 )(]) ([ s F s dt t f d L n n n = 3 积分定理 一般形式 ∑ ???????????==+-===+=+ + = + = n k t n n k n n n n t t t dt t f s s s F dt t f L s dt t f s dt t f s s F dt t f L s dt t f s s F dt t f L 1 1 2 2 2 2 ]))(([1)(])()([]))(([])([)(]))(([])([)(])([个 共个 共 初始条件为0时 n n n s s F dt t f L )(]))(([=??个 共 4 延迟定理(或称t 域平移定理) )()](1)([s F e T t T t f L Ts -=-- 5 衰减定理(或称s 域平移定理) )(])([a s F e t f L at +=- 6 终值定理 )(lim )(lim 0 s sF t f s t →∞ →= 7 初值定理 )(lim )(lim 0 s sF t f s t ∞ →→= 8 卷积定理 )()(])()([])()([210 210 21s F s F d t f t f L d f t f L t t =-=-??τττττ
(完整版)拉普拉斯变换及其逆变换表
拉普拉斯变换及其反变换表
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式 1 1 n 1 n n n 1 1 m 1 m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==----ΛΛ (m n >) 式中系数n 1 n 1 a ,a ,...,a ,a -,m 1 m 1 b ,b ,b ,b -Λ都是实常数;n m ,是正整数。按 代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑ =-=-++-++-+-=n 1 i i i n n i i 2 2 1 1 s s c s s c s s c s s c s s c )s (F ΛΛ 式中,Sn 2S 1S ,,,Λ是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c i s s i i -=→ 或 i s s i ) s (A ) s (B c ='= 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数 []t s n 1 i i n 1i i i 11i e c s s c L )s (F L )t (f -==--∑∑=??????-== ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为
拉氏变换常用公式
附录A 拉普拉斯变换及反变换表A-1 拉氏变换的基本性质
表A-2 常用函数的拉氏变换和z变换表
用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设 )(s F 是s 的有理真分式 11 10 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110- 都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)( (F-1) 式中,n s s s ,,,21 是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )()(lim s F s s c i s s i i -=→ (F-2) 或 i s s i s A s B c ='= )() ( (F-3) 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数 []??????-==∑=--n i i i s s c L s F L t f 1 1 1 )()(=t s n i i i e c -=∑1 (F-4) ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为 ()) ()()() (11n r r s s s s s s s B s F ---= + =n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11 111111)()()( 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
拉普拉斯变换公式
附录A拉普拉斯变换及反变换 419
420
421 3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式 1110 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++= =---- (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110- 都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)( (F-1) 式中,n s s s ,,,21 是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )()(l i m s F s s c i s s i i -=→ (F-2) 或 i s s i s A s B c ='=)() ( (F-3) 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数 []??????-==∑=--n i i i s s c L s F L t f 11 1 )()(=t s n i i i e c -=∑1 (F-4) ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为 ()) ()()() (11n r r s s s s s s s B s F ---= + = n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11 111 111)()()( 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
拉氏变换重要公式
拉氏变换重要公式 1 拉氏变换定义 ()()[]()dt e t f t f L s F st 0-∞ ?==? 2 常用公式 ()[]1t L =δ/()[]s 1t 1L = /a s 1]e [L at -= /2 at a) (s 1]e [L -= t /[]2 2 s t sin L ω ω ω+= []2 2 s s t cos L ω ω+= /[]2 s 1t L = /[]1 n n s n!t L += /[]2 2at -a)(s t sin e L ω ω ω++= /[] 2 2 at -a)(s a s t cos e L ω ω+++= 3 拉氏变换的几个重要定理 (1)线性性质: [])s (bF )s (aF )t (bf )t (af L 2121+=+ (2)微分定理: ()[]()()0f s F s t f L -?=' (3)积分定理:()[]()() ()0f s 1s F s 1dt t f L 1-+?= ? 零初始条件下有:()[]()s F s 1dt t f L ?= ? 进一步有: ()()()()()()()()0f s 10f s 10f s 1s F s 1dt t f L n 21n 1n n n n ----++++=??? ? ??????? (4)位移定理 实位移定理:()[]()s F e -t f L s ?=-ττ 虚位移定理:()[]()a -s F t f e L at =? (5)终值定理(极限确实存在时) ()()()s F s lim f t f lim 0s t ?=∞=→∞→ (6)初值定理(极限确实存在时) ()()()s F s lim 0f t f lim s 0t ?==∞ →→ 4 拉氏反变换 (1) 反变换公式:?∞ +∞ -= j j st ds e ).s (F j 21 )t (f σσ π (2) 查表法——分解部分分式(留数法,待定系数法,试凑法) 设 )m n (a s a s a s a s b s b s b s b ) s (A )s (B )s (F n 1-n 2 -n 21 -n 1n m 1-m 1 m 1m 0>+++++++++= = - 其中分母多项式可以分解因式为: )p s ()p s )(p s ()s (A n 21---= )s (A p i 为的根(特征根),分两种情形讨论:
2第二节传递函数解析
第二节控制系统的传递函数
传递函数是经典控制理论中最重要的数学模型之一。利用传递函数,在系统的分析和综合中可解决如下问题: 不必求解微分方程就可以研究初始条件为零的系统在输入信号作用下的动态过程。 可以研究系统参数变化或结构变化对系统动态过程的影响,因而使分析系统的问题大为简化。 可以把对系统性能的要求转化为对系统传递函数的要求,使综合问题易于实现。
一、传递函数的基本概念 令初始值为零,将上式求拉氏变换,得 ) ()...()()...(01110111s X b s b s b s b s Y a s a s a s a m m m m n n n n ++++=++++----当传递函数和输入已知时,Y (s )=G (s ) X (s )。通过拉氏反变换可求传递函数的定义:线性定常系统在零初始条件下输出量的拉氏变换与输入量的拉氏变换之比。 0 11 10 11 1......)()()(a s a s a s a b s b s b s b s X s Y s G n n n n m m m m ++++++++==----称为元件和系统的传递函数 )~0,~0(,m j n i b a j i ==式中:x (t ) — 输入,y (t ) — 输出 为常系数 ) ()(...)()()()(...)()(01) 1(1)(01) 1(1) (t x b t x b t x b t x b t y a t y a t y a t y a m m m m n n n n +'+++=+'+++----设系统或元件的微分方程为:
[关于传递函数的几点说明] ?传递函数的概念适用于线性定常系统,它与线性常系数微分 方程一一对应。且与系统的动态特性一一对应。 ?传递函数不能反映系统或元件的学科属性和物理性质。物理 性质和学科类别截然不同的系统可能具有完全相同的传递函数。而研究某传递函数所得结论可适用于具有这种传递函数的各种系统。 ?传递函数仅与系统的结构和参数有关,与系统的输入无关。 只反映了输入和输出之间的关系,不反映中间变量的关系。 ?传递函数的概念主要适用于单输入单输出系统。若系统有多 个输入信号,在求传递函数时,除了一个有关的输入外,其它的输入量一概视为零。 ?传递函数忽略了初始条件的影响。 ?传递函数是s的有理分式,对实际系统而言分母的阶次n大于 分子的阶次m,此时称为n阶系统。
拉条、支撑
屋面拉条;拉条;就是钢结构骨架之间的圆钢螺杆,包括系杆、上弦水平支撑、下弦水平支撑、斜十字形杆等等。主要材料一般为Q235线材生产,直径有M10、M12比较常见。拉条为檩条的平面外支承点,因此拉条所受拉力即为檩条承受的水平荷载。拉条布置应考虑风荷载影响,按实际受力计算拉条截面,并满足构造要求。 屋面撑杆;将主要构件组成一个空间构架的管状或其他形状的连接构件。 钢结构里没有撑杆这个构件名称。叫支撑、系杆 只有柱间支撑、上弦水平(剪刀)支撑、下弦水平(剪刀)支撑、屋架垂直支撑、系杆等。 屋面隅撑;隅撑就是在靠边墙角的部位、梁与柱之间、梁与檩、柱与檩之间的支撑杆。墙面上的叫墙隅撑,屋面上的叫屋面隅撑。 亦有人定义为连接钢梁和檩条的接近45度方向斜撑(在梁上的连接点靠近梁的下翼缘板).隅撑与钢架构件腹板的夹角不宜大于45度。 这些都算是辅助构件,都是为了保持主构件的稳定而设置的: 压杆、撑杆/套管,支撑构件中的受压的杆件,套管应该就是拉条加个圆管 拉条只能用于受拉,保持檩条的侧向稳定;但同时需要在局部位置为檩条设置能受压的支撑,就是拉条+套管 隅撑,在框架梁端部,往往是反弯矩,就是梁上翼缘受拉、下翼缘受压,为了保证框架梁下翼缘的受压稳定,设置隅撑。 水平支撑,为了保证平面构件形成整体、能够抵抗水平力设置的支撑体系 柱间支撑,相当于设置在柱子间的“水平”支撑。 从材料上讲 1、隅撑一般多为角钢制作 2、拉条一般多为圆钢制作 从受力上讲 1、隅撑既能受拉也能受压 2、拉条仅能受拉 使用部位 1、隅撑为斜梁受压区下缘平面外的稳定 2、拉条:1)、檩条间 2)、梁间、柱间的平面外稳定
拉氏变换表(包含计算公式)
拉氏变换及反变换公式 1
2
3 3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式 1110 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++= =----ΛΛ (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110-Λ都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)(ΛΛ 式中,n s s s ,,,21Λ是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计 算: )()(lim s F s s c i s s i i -=→ 或 i s s i s A s B c ='= )() ( 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数 []??????-==∑=--n i i i s s c L s F L t f 11 1 )()(=t s n i i i e c -=∑1 ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为 ()) ()()() (11n r r s s s s s s s B s F ---= +Λ = n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11 111 111)()()( 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
