高三数学第一轮复习 解三角形教案
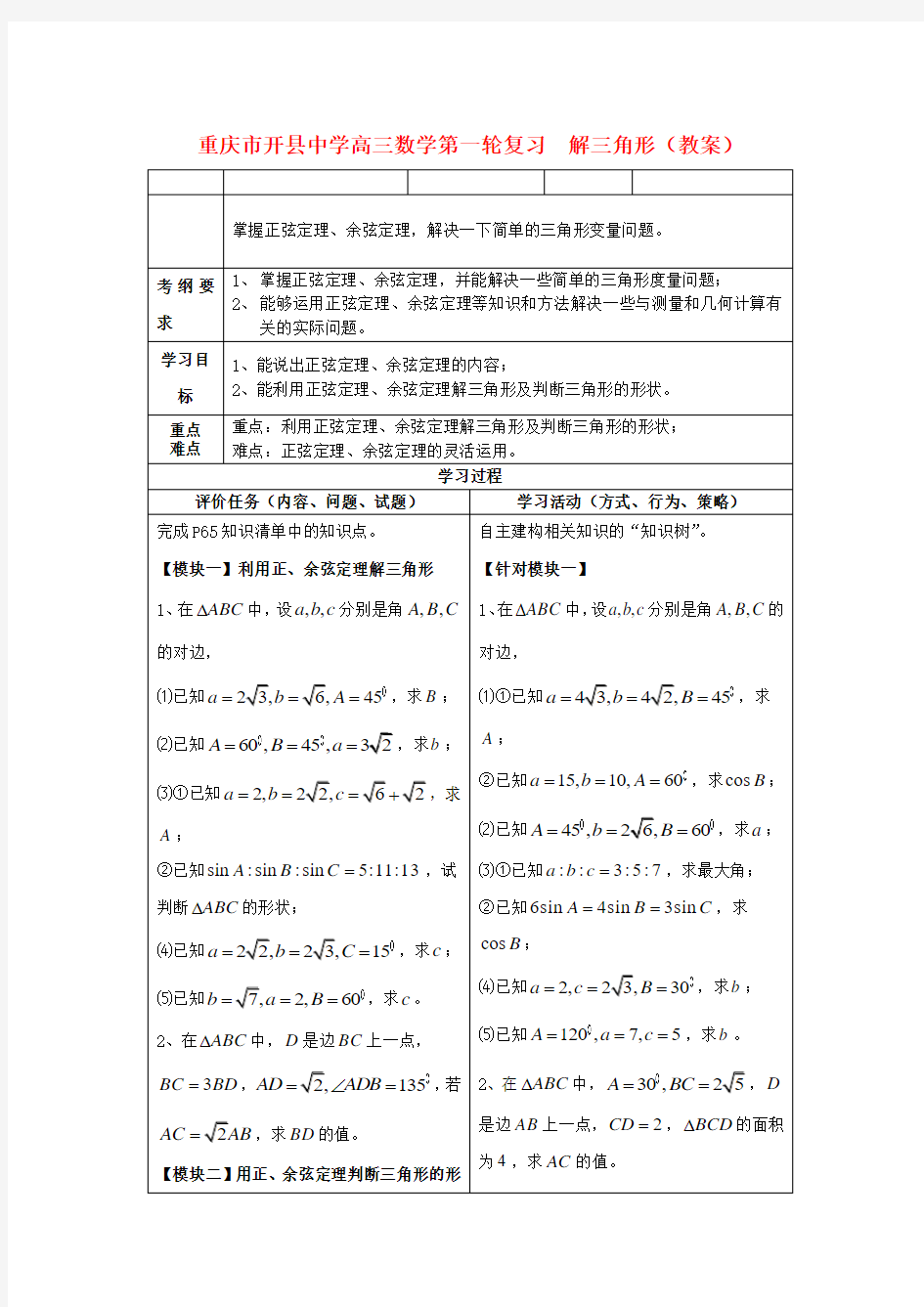

重庆市开县中学高三数学第一轮复习解三角形(教案)
32
26,
BC
?
2BCD
= b
c
处有一艘走私船,CD
快追上
高中数学-解三角形知识点汇总情况及典型例题1
实用标准
—tanC。
例 1 ? (1 )在 ABC 中,已知 A 32.00 , B 81.80 因为 00 v B v 1800,所以 B 640,或 B 1160. c as nC 空啤 30(cm). sin A s in400 ②当B 1160时, 点评:应用正弦定理时(1)应注意已知两边和其中一边的对角解三角形时,可能有两解的情形; 对于解三角形中的复杂运算可使用计算器 题型2 :三角形面积 2 , AC 2 , AB 3,求tan A 的值和 ABC 的面积。 2 (2 )在 ABC 中,已知 a 20 cm , b 28 cm , 40°,解三角形(角度精确到 10,边长精确 到 1cm ) o 解:(1 )根据三角形内角和定理, C 1800 (A B) 1800 (32.00 81.80) 66.20 ; 根据正弦定理,b asinB 42.9sin81.80 si nA 眾厂 80.1(cm); 根据正弦定理,c 聲C 丝9也彰 74.1(cm). sin 32.0 (2 )根据正弦定理, s"B 舸 A 28sin4°0 a 20 0.8999. ,a 42.9 cm ,解三角形; ①当 B 640 时, C 1800 (A B) 1800 (40° 640) 760, C 1800 (A B) 1800 (400 116。)240 , c asinC si nA 呼 13(cm). sin 40 (2) 解法一:先解三角方程,求出角 A 的值。 例2 ?在ABC 中, sin A cos A
si nA cos A j2cos(A 45 )-—, 2 1 cos(A 45 )-. 又 0 A 180 , A 45o 60o , A 105.° o o 1 \/3 L tan A tan(45 60 ) 一字 2 J3, 1 73 42 si nA sin105 sing5 60) sin4 5 co$60 cos45 si n60 ——-—. 1 1 /2 洽 n S ABC AC AB si nA 2 3 近 46)。 2 2 4 4 解法二:由sin A cos A 计算它的对偶关系式 si nA cos A 的值。 v 2 — si nA cos A —— ① 2 2 1 (si nA cos A)2 2 1 2sin Acos A — 2 Q0o A 180o , si nA 0,cos A 0. 1 另解(si n2A —) 2 2 3 (s in A cos A) 1 2 sin Acos A —, *'6 _ si nA cos A — ② 2 $2 J6 ①+②得sin A --------------- 。 4 ①-②得 cosA <6 。 4 u 而丄 A si nA J 2 J 6 4 c 匚 从而 tan A l l 2 ~3。 cosA 4 v2 v 6
第十一章三角形全章教学设计
三角形的边
检测练习一、如图,在三角形ABC中, (1)AB+BC AC AC+BC AB AB+AC BC (2)假设一只小虫从点B出发,沿三角形的边爬到点C, 有路线。路线最近,根据是:, 于是有:(得出的结 论)。 (3)下列下列长度的三条线段能否构成三角形,为什么? ①3、4、8 ②5、6、11 ③5、6、10 研读三、认真阅读课本认真看课本( P64例题,时间:5分钟) 要求:(1)、注意例题的格式和步骤,思考(2)中为什么要分情况讨论。 (2)、对这例题的解法你还有哪些不理解的? (3)、一边阅读例题一边完成检测练习三。 检测练习二 9、一个等腰三角形的周长为28cm.①已知腰长是底边长的3倍,求各边的长; ②已知其中一边的长为6cm,求其它两边的长.(要有完整的过程啊!) 解: (三)在研读的过程中,你认为有哪些不懂的问题? 四、归纳小结 (一)这节课我们学到了什么?(二)你认为应该注意什么问题? 五、强化训练 【A】组 1、下列说法正确的是 (1)等边三角形是等腰三角形 (2)三角形按边分类课分为等腰三角形、等边三角形、不等边三角形 (3)三角形的两边之差大于第三边 (4)三角形按角分类应分锐角三角形、直角三角形、钝角三角形 其中正确的是() A、1个 B、2个 C、3个 D、4个 2、一个不等边三角形有两边分别是 3、5另一边可能是() A、1 B、2 C、3 D、4 3、下列长度的各边能组成三角形的是() A、3cm、12cm、8cm B、6cm、8cm、15cm 、3cm、5cm D、6.3cm、6.3cm、12cm 【B】组 4、已知等腰三角形的一边长等于4,另一边长等于9,求这个三角形的周长。 5、已知三角形的一边长为5cm,另一边长为3cm.则第三边的长取值范围是多少? 【C】组(共小1-2题) 6、已知三角形的一边长为5cm,另一边长为3cm.则第三边的长取值范围是。 小方有两根长度分别为5cm、8cm的游戏棒,他想再找一根,使这三根游戏棒首尾相连能搭成一个三角形. (1)你能帮小方想出第三根游戏棒的长度吗?(长度为正整数) (2)想一想:如果已知两边,则构成三角形的第三边的条件是什么?
北师大版必修5高中数学第二章解三角形的实际应用举例word教案1
§3 解三角形的实际应用举例 教学目标 1、掌握正弦定理、余弦定理,并能运用它们解斜三角形。 2、能够运用正弦定理、余弦定理进行三角形边与角的互化。 3、培养和提高分析、解决问题的能力。 教学重点难点 1、正弦定理与余弦定理及其综合应用。 2、利用正弦定理、余弦定理进行三角形边与角的互化。 教学过程 一、复习引入 1、正弦定理: 2sin sin sin a b c R A B C === 2、余弦定理:,cos 22 2 2 A bc c b a -+=?bc a c b A 2cos 2 22-+= C ab b a c cos 22 2 2 -+=,?ab c b a C 2cos 2 22-+= 二、例题讲解 引例:我军有A 、B 两个小岛相距10海里,敌军在C 岛,从A 岛望C 岛和B 岛成60°的视角,从B 岛望C 岛和A 岛成75°的视角,为提高炮弹命中率,须计算B 岛和C 岛间的距离,请你算算看。 解:0 60=A 0 75=B ∴0 45=C 由正弦定理知 045 sin 10 60sin =BC 6545 sin 60sin 100 ==?BC 海里 例1.如图,自动卸货汽车采用液压机构,设 计时需要 计算油泵顶杆BC 的长度(如图).已知车厢的最大仰角为60°,油泵顶点B 与车厢支点A 之间的距离为1.95m ,AB 与水平线之间的夹角为 /02060,AC 长为1.40m ,计算BC 的长(保留三个有效数字). 分析:这个问题就是在ABC ?中,已知AB=1.95m ,AC=1.4m, 750 600 C B A
求BC 的长,由于已知的两边和它们的夹角,所以可 根据余弦定理求出BC 。 解:由余弦定理,得 答:顶杠BC 长约为1.89m. 解斜三角形理论应用于实际问题应注意: 1、认真分析题意,弄清已知元素和未知元素。 2、要明确题目中一些名词、术语的意义。如视角,仰角,俯角,方位角等等。 3、动手画出示意图,利用几何图形的性质,将已知和未知集中到一个三角形中解决。 练1.如图,一艘船以32海里/时的速度向正北航行,在A 处看灯塔S 在船的北偏东0 20, 30分钟后航行到B 处,在B 处看灯塔S 在船的北偏东0 65方向上,求灯塔S 和B 处的距离.(保留到0.1) 解:16=AB 由正弦定理知 020 sin 45sin BS AB = 7.745 sin 20 sin 100 ≈= BS 海里 答:灯塔S 和B 处的距离约为7.7海里 例2.测量高度问题 如图,要测底部不能到达的烟囱的高AB ,从与烟囱底部在同一水平直线上的C ,D 两处, 测得烟囱的仰角分别是0 45=α和0 60=β, C、D间的距离是12m.已知测角仪器高1.5m. 求烟囱的高。 图中给出了怎样的一个几何图形?已知什么,求什么? 分析:因为B A AA AB 11+=,又m AA 5.11= 所以只要求出B A 1即可 解:在11D BC ?中, 0001112060180=-=∠C BD ,00011154560=-=∠BD C D C B A 1.40m 1.95m 6020/ 600 ?S B A 1150 450 650200 A 1α β D 1C 1D C B A
解三角形(二轮专题复习)教学设计
解三角形(二轮专题复习)教学设计 教学目标: 1、知道正弦定理、余弦定理是解三角形的核心知识,会用正余弦定理进行边角转换; 2、掌握“已知一角及其对边,求相关边角的最值问题”的两种基本思路: (1)运用正弦定理化边为角,转化为三角函数最值问题; (2)运用余弦定理化角为边,利用基本不等式、判别式法等手段构造不等式进而解不等式; 3、能运用过去解三角形所积累的解题经验解决与解三角形相关的拓展问题,并获得、积累新的数学基本活动经验。 教学重点: 1、与学生一起探究例题的基本解法,并总结归纳出解这类问题的两类基本思路; 2、解决函数、不等式问题时所获得的一些数学基本活动经验在解决“已知一角及其对边,求相关边角的最值问题”时的运用、积累与升华。 教学难点: 变式2中用余弦定理寻求与错误!未找到引用源。相关的不等式、求解、验证的过程授课类型:高三第二轮专题复习课 教学过程: 一、热点分析,把握方向 近五年全国卷Ⅰ解三角形考题题号及分值统计: 通过此表,我们发现解三角形是高考的必考点,一般属于中档题,是我们的一个主要得分点,因此也是第二轮复习的重点内容. 二、小试牛刀,回顾经验 引例:(2015广东改编)设错误!未找到引用源。的内角错误!未找到引用源。的对边分别为错误!未找到引用源。,若错误!未找到引用源。,则错误!未找到引用源。. 1、给2分钟时间,让学生独立完成,请同学回答,同时板书两种方法的主要过程; 2、解法一:(余弦定理)错误!未找到引用源。,化简为错误!未找到引用源。 解法二:(正弦定理)由正弦定理得错误!未找到引用源。,
又错误!未找到引用源。,所以错误!未找到引用源。,或错误!未找到引用源。. 3、小结:通过这个题我们可以感受到正弦定理、余弦定理在解三角形中的具体应用. 4、问:如果在引例中去掉条件“错误!未找到引用源。”,这时会是什么结果呢?显然就不能求解错误!未找到引用源。的具体数值了,但能不能求 错误!未找到引用源。的范围呢?请试解如下变式。 变式:设错误!未找到引用源。的内角错误!未找到引用源。的对边分别为错误!未找到引用源。,若错误!未找到引用源。,求错误!未找到引用源。的范围. 略解: 错误!未找到引用源。 同理有错误!未找到引用源。. (有错误!未找到引用源。的范围了,我们进一步想想错误!未找到引用源。的范围为(留白,请一个同学回答说错误!未找到引用源。,(同时板书)这个范围正确吗?质疑大于0吗?(引导)学生回答两边之和大于第三边,所以错误!未找到引用源。,继续质疑,能不能等于8?我们反过来想,假设最大值为8,那么应该是错误!未找到引用源。,这时这个三角形就有四个条件了,可以选用其中三个条件来检验第四个条件.比如我们利用余弦定理求错误!未找到引用源。. 显然8不是错误!未找到引用源。的最大值,那么错误!未找到引用源。的最大值是多少?) 三、例题探究,获取经验 例 在 错误!未找到引用源。 中,错误!未找到引用源。 , 求错误!未找到引用源。的最大值. 1、请学生思考讨论后试解2分钟,再请同学回答思路,同时板书关键点; 2、解法一(正弦定理)由正弦定理得 错误!未找到引用源。 ,整理有:错误!未找到引用源。,所以错误!未找到引用源。(到这里后,问学生最大值是多少?为什么?意在引导学生注意:求函数的最值应考定义域) 因为错误!未找到引用源。,所以错误!未找到引用源。,故错误!未找到引用源。 教师评价:这位同学采用正弦定理,将边的问题转化为角的问题,进而利用和差角公式转化为三角函数求最值的问题,充分体现了函数的思想,非常不错!值得同学们注意的是函数的定义域,即角错误!未找到引用源。的取值范围. 问:请同学们想想这个题还有没有其它的思路?
高中数学解三角形和平面向量
高中数学解三角形和平面向量试题 一、选择题: 1.在△ABC 中,若a = 2 ,23b =,0 30A = , 则B 等于( B ) A .60o B .60o 或 120o C .30o D .30o 或150o 2.△ABC 的内角A,B,C 的对边分别为a,b,c ,若c =2,b =6,B =120o ,则a 等于( D ) A .6 B .2 C .3 D .2 3.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c, 且2=a ,A=45°,2=b 则sinB=( A ) A . 1 2 B .22 C . 3 2 D .1 4.ABC ?的三内角,,A B C 的对边边长分别为,,a b c ,若5 ,22 a b A B ==,则cos B =( B ) A . 53 B .54 C .55 D .5 6 5.在△ABC 中,若)())((c b b c a c a +=-+,则A ∠=( C ) A .0 90 B .0 60 C .0 120 D .0 150 6.在△ABC 中,角A,B,C 的对边分别为a,b,c ,若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为(D ) A. 6 π B. 3π C.6π或56 π D. 3π或23 π 7. 在△ABC 中, b a B A =--cos 1cos 1,则△AB C 一定是( A ) A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形 8.在ABC ?中,角A 、B 、C 所对应的边分别为a 、b 、c ,若角A 、B 、C 依次成等差数列,且a=1, ABC S b ?=则,3等于( C ) A. 2 B. 3 C. 2 3 D. 2 9.已知锐角△ABC 的面积为33,BC=4,CA=3则角C 大小为( B ) A 、75° B 、60° C 、45° D 、30° 10.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( A ) A. 3 400 米 B. 33400米 C. 2003米 D. 200米 11.已知A 、B 两地的距离为10km ,B 、C 两地的距离为20km ,现测得0 120ABC ∠=,则A,C 两地 的距离为( D )。 A. 10km B. 103km C. 105km D. 107km 12.已知M 是△ABC 的BC 边上的中点,若向量AB =a ,AC = b ,则向量AM 等于( C ) A . 21(a -b ) B .21(b -a ) C .21( a +b ) D .1 2 -(a +b ) 13.若 ,3) 1( )1, 1(B A -- ,5) (x C 共线,且 BC AB λ=则λ等于( B ) A 、1 B 、2 C 、3 D 、4 14.已知平面向量),2(),2,1(m -==,且∥,则32+=( C ) A .(-2,-4) B. (-3,-6) C. (-4,-8) D. (-5,-10) 15. 已知b a b a k b a 3),2,3(),2,1(-+-==与垂直时k 值为 ( C ) A 、17 B 、18 C 、19 D 、20 16.(2,1),(3,),(2),a b x a b b x ==-⊥r r r r r 若向量若则的值为 ( B ) A .31-或 B.13-或 C .3 D . -1 17. 若|2|= ,2||= 且(-)⊥ ,则与的夹角是 ( B ) (A ) 6π (B )4π (C )3π (D )π12 5 183 =b , a 在 b 方向上的投影是2 3 ,则 b a ?是( B ) A 、3 B 、 29 C 、2 D 、2 1 19.若||1,||2,a b c a b ===+r r r r r ,且c a ⊥r r ,则向量a r 与b r 的夹角为( C ) (A )30° (B )60° (C )120° (D )150°
解三角形全章教案(整理)
数学5 第一章 解三角形 第1课时 课题: §1.1.1 正弦定理 ●教学目标 知识与技能:通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。 过程与方法:让学生从已有的几何知识出发,共同探究在任意三角形中,边与其对角的关系,引导学生通过观察,推导,比较,由特殊到一般归纳出正弦定理,并进行定理基本应用的实践操作。 ●教学重点 正弦定理的探索和证明及其基本应用。 ●教学难点 已知两边和其中一边的对角解三角形时判断解的个数。 ●教学过程 Ⅰ.课题导入 如图1.1-1,固定?ABC 的边CB 及∠B ,使边AC 绕着顶点C 转动。 A 思考:∠C 的大小与它的对边AB 的长度之间有怎样的数量关系? 显然,边AB 的长度随着其对角∠C 的大小的增大而增大。能否 用一个等式把这种关系精确地表示出来? B C Ⅱ.讲授新课 [探索研究] (图1.1-1) 在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系。如图1.1-2,在Rt ?ABC 中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的 定 义 , 有 sin a A =, sin b B =,又s i n 1c C == , A 则sin sin sin a b c c A B C = = = b c 从而在直角三角形ABC 中, sin sin sin a b c = = C a B (图1.1-2) 思考:那么对于任意的三角形,以上关系式是否仍然成立? (由学生讨论、分析) 可分为锐角三角形和钝角三角形两种情况: 如图1.1-3,当?ABC 是锐角三角形时,设边AB 上的高是CD ,根据任意角三角函数的定义,有CD=sin sin a B b A =,则sin sin a b A B = , C 同理可得sin sin c b C B = , b a 从而 sin sin a b A B = sin c C = A c B
高三第一轮复习数学---解三角形及应用举例
高三第一轮复习数学---解三角形及应用举例 一、教学目标:1.理解并掌握正弦定理、余弦定理、面积公式; 2.能正确运用正弦定理、余弦定理及关系式A B C π++=,解决三角形中的 计算和证明问题. 二、教学重点:掌握正弦定理、余弦定理及其变形形式,利用三角公式解一些有关三角形 中的三角函数问题. 三、教学过程: (一)主要知识: 掌握三角形有关的定理: 正余弦定理:a 2 =b 2 +c 2 -2bccos θ, bc a c b 2cos 222-+=θ;R C c B b A a 2sin sin sin === 内角和定理:A+B+C=180°,sin(A+B)=sinC, cos(A+B)= -cosC, cos 2C =sin 2B A +, sin 2 C =cos 2B A + 面积公式:S=21absinC=21bcsinA=2 1 casinB S= pr =))()((c p b p a p p --- (其中p=2 c b a ++, r 为内切圆半径) 射影定理:a = b cos C + c cos B ;b = a cos C + c cos A ;c = a cos B + b cos A (二)例题分析: 例1.在ΔABC 中,已知a=3,b=2,B=45°,求A,C 及边c . 解:由正弦定理得:sinA=23 2 45sin 3sin = ?= b B a ,因为B=45°<90°且b 课题: §1.1.1正弦定理 如图1.1-1,固定?ABC 的边CB 及∠B ,使边AC 绕着顶点C 转动。 思考:∠C 的大小与它的对边AB 的长度之间有怎样的数量关系? 在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中, 角与边的等式关系。 从而在直角三角形ABC 中,sin sin sin a b c A B C == 思考:那么对于任意的三角形,以上关系式是否仍然成立? 可分为锐角三角形和钝角三角形两种情况: 如图1.1-3,当?ABC 是锐角三角形时,设边AB 上的高是CD ,根据任意角三角函数的定义,有CD=sin sin a B b A =,则 sin sin a b A B =, C 同理可得 sin sin c b C B =, b a 从而sin sin a b A B =sin c C = A c B 从上面的研探过程,可得以下定理 正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即 sin sin a b A B =sin c C = [理解定理] (1)正弦定理说明同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,即存在正数k 使sin a k A =,sin b k B =,sin c k C =; (2)sin sin a b A B =sin c C =等价于sin sin a b A B =,sin sin c b C B =,sin a A =sin c C 从而知正弦定理的基本作用为: ①已知三角形的任意两角及其一边可以求其他边,如sin sin b A a B =; ②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值,如sin sin a A B b =。 一般地,已知三角形的某些边和角,求其他的边和角的过程叫作解三角形。 例1.在?ABC 中,已知045A =,075B =,40a =cm ,解三角形。 例2.在?ABC 中,已知20=a cm ,202b =cm ,045A =,解三角形。 解斜三角形(复习)公开课教案 [教学目标] 一:巩固对正弦、余弦、面积公式的掌握,并能熟练地运用公式解决问题。 二:培养学生分析、演绎和归纳的能力。 [教学重点] 正弦、余弦、面积公式的应用。 [教学难点] 选择适当的方法解斜三角形。 [教学过程] 一:基本知识回顾: 1.1、正弦定理及其变形; 正弦定理:2sin sin sin a b c R A B C ===(R 是三角形外接圆的半径) 变式一:sin 2a A R =、sin 2b B R =、sin 2c C R = 变式二:sin :sin :sin A B C ::a b c = 1.2、余弦定理及其变形; 余弦定理:2 2 2 2cos a b c bc A =+-,变式:222 cos 2b c a A bc +-= 2 2 2 2cos b a c ac B =+-, 222 cos 2a c b B ac +-= 2 2 2 2cos c a b ab C =+-。 222 cos 2a b c C ab +-= 1.3、面积公式 二:例题分析: 1、正弦定理 (1)在△ABC 中,已知 ,则 sin B= ( ) (2)在△ABC 中,若a = 2 ,b =0 30A = , 则B 等于60?或120? 111sin sin sin 222S ab C bc A ac B ===4,303 a b A ===? 2、余弦定理 (1)在△ABC 中,满足 ,则A = 60° (2)已知△ABC 的周长为9,且4:2:3sin :sin :sin =C B A ,则cosC 的值为 A .4 1 - B .41 C .3 2 - D . 3 2 3、三角形解的个数 (1)在△ABC 中,已知 , 这个三角形解的情况是:( C ) A.一解 B.两解 C.无解 D.不能确定 (2)△ABC 中,∠A ,∠B 的对边分别为a ,b ,且∠A=60°,4,6== b a ,那么 满 足条件的△ABC ( ) A .有一个解 B .有两个解 C .无解 D .不能确定 4、判断三角形形状 (1)若c C b B a A cos cos sin = =则△ABC 为( ) A .等边三角形 B .等腰三角形 C .有一个内角为30°的直角三角形 D .有一个内角为30°的等腰三角形 (2)关于x 的方程02 cos cos cos 2 2=-??-C B A x x 有一个根为1,则△AB C 一定是 A .等腰三角形 B .直角三角形 C .锐角三角形 D .钝角三角形 5、正余弦定理的实际应用 (1)有一长为1公里的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要 伸长( ) A .1公里 B .sin10°公里 C .cos10°公里 D .cos20°公里 (2) 10105/4/o C v v B AB o 某渔船在航行中遇险发出呼救信号,我海军舰艇在A处获悉后立即测出该渔船在方向角为北偏东45,距离海里的处,渔船沿着方位角为的方向以海里小时的速度向小岛靠拢,我海军艇舰立即以海里小时的速度前去营救。设艇舰在处与渔船相遇,求方向的方位角的正弦值 18,20,150a b A ===?222a b c bc =+- 解三角形的方法 1.解三角形:一般地,把三角形的三个角和它们的对边叫做三角形的元素。已知三角形的几个元素求 其他元素的过程叫作解三角形。 以下若无特殊说明,均设ABC ?的三个内角C B A 、、的对边分别为c b a 、、,则有以下关系成立: (1)边的关系:c b a >+,b c a >+,a c b >+(或满足:两条较短的边长之和大于较长边) (2)角的关系:π=++C B A ,π< 总结:若已知三角形的两边和其中一边所对的角,解这类三角形时,要注意有两解、一解和无解的可能 如图,在ABC ?中,已知a 、b 、A (1)若A 为钝角或直角,则当b a >时,ABC ?有唯一解;否则无解。 (2)若A 为锐角,则当A b a sin <时,三角形无解; 当A b a sin =时,三角形有唯一解; 当b a A b < 解三角形(专题课)教学设计 一、教材分析 本节课是高中数学课本必修5第一章《解三角形》,而在本章中,学生应该在已有的知识基础上,通过对任意三角形的边角关系的探究,发现并掌握三角形中的边长与角度之间的关系数量关系,并认识到运用它们可以解决一些与测量和几何计算有关的实际问题。本章知识是初中解直角三角形的继续,通过本章内容的学习,学生能够系统地掌握解任意三角形的完整实施。可以从数量的角度认识三角形,使三角形成为研究几何问题的重要工具。是中学许多数学知识的交汇点,如向量、平面几何、三角函数、解析几何、立体几何等。 二、学情分析 学生已经学习并掌握了任意角及任意角的三角函数,诱导公式、三角恒等变换、正余弦定理等相关的知识。学习本节内容是对以上知识内容的综合应用,尤其是对正弦定理与余弦定理的熟练运用。通过解三角形的方法解决有关的实际问题,可以培养学生的数学应用意识,提高学生运用数学知识解决实际问题的能力,使学生逐渐形成数学的思维方式去解决问题、认识世界的意识。 三、教学目标 知识与技能:引导学生准确理解正弦定理、余弦定理、三角形面积公式,会对正余弦定理会进行简单的变形;引导学生通过观察,推导,比较等出一些结论,如射影定理,三角形边角之间的关系;会运用所学知识解三角形以及与三角形有关的实际问题。 过程与方法:引导学生通过观察,推导,比较,由特殊到一半归纳出正余弦定理以及三角形面积公式等结论。培养学生的创新意识,观察能力,总结归纳的逻辑思维能力。让学生通过学习能体会用向量作为数形结合的工具,将几何问题转化为代数问题的数学思想方法。 情感态度与价值观:面向全体学生,创造平等的教学氛围,进行高效课堂教学,激情教育,通过学生之间,师生之间的交流与讨论、合作与评价,调动学生的主动性和积极性,让学生体验学习数学的的乐趣,感受成功的喜悦,增强学生学好数学的信心,激发学生学习的兴趣。 四、教学重难点 重点:正弦定理、余弦定理的内容及基本应用。 难点:正弦定理、余弦定理的内容及基本应用;正余弦定理的变形应用;用所学知识解决解三角形问题的题型归纳总结。 五、课堂结构设计 根据教材的内容和编排的特点,为更好有效地突出重点,攻破难点,以学生的发展为本,遵照学生的认知规律,本节主要以教师为主导,学生为主体,交流讨论,互助学习为主线的指导思想,采用“6+1”高效课堂教学模式,在教师的启发引导下,学生通过独立自主思考探究、同学之间相互交流讨论合作学习为前提,以“熟练运用正余弦定理解三角形”为基本 模块一:解三角形复习 正弦定理 教学过程: 一、复习准备: 1. 讨论:在直角三角形中,边角关系有哪些(三角形内角和定理、勾股定理、锐角三角函数)如何解直角三角形那么斜三角形怎么办 2. 由已知的边和角求出未知的边和角,称为解三角形. 已学习过任意三角形的哪些边角关系(内角和、大边对大角) 是否可以把边、角关系准确量化 →引入课题:正弦定理 二、讲授新课: 1. 教学正弦定理的推导: [ ①特殊情况:直角三角形中的正弦定理:sin A = c a sin B =c b sin C =1 即 c =sin sin sin a b c A B C == . ② 能否推广到斜三角形 (先研究锐角三角形,再探究钝角三角形) 当?ABC 是锐角三角形时,设边AB 上的高是CD ,根据三角函数的定义,有 sin sin CD a B b A ==,则 sin sin a b A B = . 同理,sin sin a c A C =(思考如何作高),从而sin sin sin a b c A B C == . ③*其它证法:证明一:(等积法)在任意斜△ABC 当中S △ABC = 111 sin sin sin 222 ab C ac B bc A ==. 两边同除以 12abc 即得: sin a A =sin b B =sin c C . 证明二:(外接圆法)如图所示,∠A =∠D ,∴2sin sin a a CD R A D ===, 同理 sin b B =2R ,sin c C =2R . 证明三:(向量法)过A 作单位向量j 垂直于AC ,由AC +CB =AB 边同乘以单位向量j 得….. , ④ 正弦定理的文字语言、符号语言,及基本应用:已知三角形的任意两角及其一边可以求其他边;已知三角形的任意两边与其中一边的对角可以求其他角的正弦值. 2. 教学例题: ① 出示例1:在?ABC 中,已知045A =,060B =,42a =cm ,解三角形. 解三角形 1.解三角形:一般地,把三角形的三个角和它们的对边叫做三角形的元素。已知三角形的几个元素求 其他元素的过程叫作解三角形。 以下若无特殊说明,均设ABC ?的三个内角C B A 、、的对边分别为c b a 、、,则有以下关系成立: (1)边的关系:c b a >+,b c a >+,a c b >+(或满足:两条较短的边长之和大于较长边) (2)角的关系:π=++C B A ,π< 总结:若已知三角形的两边和其中一边所对的角,解这类三角形时,要注意有两解、一解和无解的可能如图,在ABC ?中,已知a、b、A (1)若A为钝角或直角,则当b a>时,ABC ?有唯一解;否则无解。 (2)若A为锐角,则当A b a sin <时,三角形无解; 当A b a sin =时,三角形有唯一解; 当b a A b< < sin时,三角形有两解; 当b a≥时,三角形有唯一解 实际上在解这类三角形时,我们一般根据三角形中“大角对大边”理论判定三角形是否有两解的可能。板块二:余弦定理及面积公式 1.余弦定理:在ABC ?中,角C B A、 、的对边分别为c b a、 、,则有 余弦定理: ? ? ? ? ? - + = - + = - + = C ab b a c B ac c a b A bc c b a cos 2 cos 2 cos 2 2 2 2 2 2 2 2 2 2 ,其变式为: ? ? ? ? ? ? ? ? ? - + = - + = - + = ab c b a C ac b c a B bc a c b A 2 cos 2 cos 2 cos 2 2 2 2 2 2 2 2 2 2.余弦定理及其变式可用来解决以下两类三角形问题: (1)已知三角形的两边及其夹角,先由余弦定理求出第三边,再由正弦定理求较短边所对的角(或由余弦定理求第二个角),最后根据“内角和定理”求得第三个角; (2)已知三角形的三条边,先由余弦定理求出一个角,再由正弦定理求较短边所对的角(或由余弦定理求第二个角),最后根据“内角和定理”求得第三个角; 说明:为了减少运算量,能用正弦定理就尽量用正弦定理解决 3.三角形的面积公式 (1) c b a ABC ch bh ah S 2 1 2 1 2 1 = = = ? ( a h、 b h、 c h分别表示a、b、c上的高); (2)B ac A bc C ab S ABC sin 2 1 sin 2 1 sin 2 1 = = = ? (3)= ?ABC S C B A R sin sin sin 22(R为外接圆半径) (4) R abc S ABC4 = ? ; (5)) )( )( (c p b p a p p S ABC - - - = ? 其中) ( 2 1 c b a p+ + = (6)l r S ABC ? = ?2 1 (r是内切圆的半径,l是三角形的周长) 数学5 第一章 解三角形 课题: §1.1.1 正弦定理 授课类型:新授课 ●教学目标 知识与技能:通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。 过程与方法:让学生从已有的几何知识出发,共同探究在任意三角形中,边与其对角的关系,引导学生通过观察,推导,比较,由特殊到一般归纳出正弦定理,并进行定理基本应用的实践操作。 情感态度与价值观:培养学生在方程思想指导下处理解三角形问题的运算能力;培养学生合情推理探索数学规律的数学思思想能力,通过三角形函数、正弦定理、向量的数量积等知识间的联系来体现事物之间的普遍联系与辩证统一。 ●教学重点 正弦定理的探索和证明及其基本应用。 ●教学难点 已知两边和其中一边的对角解三角形时判断解的个数。 ●教学过程 Ⅰ.课题导入 如图1.1-1,固定?ABC 的边CB 及∠B ,使边AC 绕着顶点C 转动。 A 思考:∠C 的大小与它的对边AB 的长度之间有怎样的数量关系? 显然,边AB 的长度随着其对角∠C 的大小的增大而增大。能否 用一个等式把这种关系精确地表示出来? C B Ⅱ.讲授新课 [探索研究] (图1.1-1) 在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系。如图1.1-2,在Rt ?ABC 中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的定义,有sin a A c =,sin b B c =,又sin 1c C c ==, A 则 sin sin sin a b c c A B C = = = b c 从而在直角三角形ABC 中, sin sin sin a b c A B C = = C a B (图1.1-2) 思考:那么对于任意的三角形,以上关系式是否仍然成立? (由学生讨论、分析) 可分为锐角三角形和钝角三角形两种情况: 如图1.1-3,当?ABC 是锐角三角形时,设边AB 上的高是CD ,根据任意角三角函数的定义,有CD=sin sin a B b A =,则sin sin a b A B = , C 同理可得 sin sin c b C B = , b a 高中数学必修五解三角形教案 高中数学必修五解三角形教案篇一:高中数学必修5解三角形知识总结及练习 解三角形 一、知识点: 1、正弦定理:在???C中,a、b、c分别为角?、?、C的对边,R 为???C的外接圆的半径,则有abc???2R.(两类正弦定理解三角形的问题:1、已知sin?sin?sinC 两角和任意一边,求其他的两边及一角. 2、已知两角和其中一边的对角,求其他边角.) 2、正弦定理的变形公式:①a?2Rsin?,b?2Rsin?,c?2RsinC;②sin??等式中) ③a:b:c?sin?:sin?:sinC;abc,sin??,sinC?;(正弦定理的变形经常用在有三角函数的2R2R2R a?b?cabc???.sin??sin??sinCsin?sin?sinC 1113、三角形面积公式:S???C?bcsin??absinC?acsin? 222④ ?a2?b2?c2?2bccosA?2224.余弦定理:?b?a?c?2accos(本文来自:https://www.360docs.net/doc/c39571103.html, 教师联盟网:高中数学必修五解三角形教案)B 或 ?c2?b2?a2?2bacosC??b2?c2?a2?cosA?2bc?a2?c2?b2? ?cosB?2ac?? b2?a2?c2 ?cosC?2ab? (两类余弦定理解三角形的问题:1、已知三边求三角.2、已知两边和他们的夹角,求第三边和其他两角.) 2225、设a、b、c是???C的角?、?、C的对边,则:①若a?b?c,则C?90?为 222222直角三角形;②若a?b?c,则C?90?为锐角三角形;③若a?b?c,则C?90?为 钝角三角形. 6.判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式. 7.解题中利用?ABC中A?B?C??,以及由此推得的一些基本关系式进行三角变换的运算,如:sin(A?B)?sinC,cos(A?B)??cosC,tan(A?B)??tanC, sin A?BCA?BCA?BC?cos,cos?sin,tan?cot 222222 二、知识演练 1、ΔABC中,a=1,b=3, ∠A=30°,则∠B等于() A.60°B.60°或120°C.30°或150°D.120° 2、若(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC, 那么ΔABC是()A.直角三角形B.等边三角形C.等腰三角形D.等腰直角三角形 3.己知三角形三边之比为5∶7∶8,则最大角与最小角的和为( ). 解三角形 (一)正弦定理和余弦定理 掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.(二) 应用 正弦定理、余弦定理及利用三角公式进行恒等变形的能力.以化简、求值或判断三角形的形状为主.解三角形常常作为解题工具用于立体几何中的计算或证明. 第1课时 三角形中的有关问题 变式训练1:(1)ABC ?的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c 成等比数列,且2c a =,则cos B = ( ) A . 14 B .3 4 C .4 D . 3解:B 提示:利用余弦定理 (2)在△ABC 中,由已知条件解三角形,其中有两解的是 ( )A.0 20,45,80b A C === B.0 30,28,60 a c B === C.0 14,16,45a b A === D. 0 12,15,120 a c A ===解:C 提示:在斜三角形中,用正弦定理求角时,若已知小角求大角,则有两解;若已知大角求小角,则只有一解 (3)在△ABC 中,已知5cos 13A = ,3 sin 5 B =,则cos C 的值为( )A 1665 B 5665 C 1665或 56 65 D 1665- 解:A 提示:在△ABC 中,由sin sin A B A B >?> 知角B 为锐角 (4)若钝角三角形三边长为1a +、2a +、3a +,则a 的取值范围是 . 解:02a << 提示:由222 (1)(2)3(1)(2)(3) a a a a a a +++>+?? +++<+?可得 (5)在△ABC 中,0 60,1,sin sin sin ABC a b c A b S A B C ++∠===++V 则 = . 4c =,由余弦定理可求得a =例3. 已知在△ABC 中,sinA(sinB +cosB)-sinC =0,sinB +cos2C =0,求角A 、B 、C .解:由sinA(sinB +cosB)-sinC =0,得sinAsinB +sinAcosB -sin(A +B)=0,所以sinB(sinA -cosA)=0 ∵B ∈(0, π), ∴sinB≠0, ∴cosA =sinA ,由A ∈(0, π),知A =4π从而B +C =π4 3 ,由sinB +cos2C =0得sinB +cos2(π4 3-B)=0cos =( 23π-2B)=cos[2π-(2π+2B)]=cos(2 π +2B)=-sin2B 得sinB -sin2B =0,亦即sinB -2sinBcosB =0,由此各cosB =21 ,B =3π,C =12 5π∴A = 4π B =3π C =π 12 5变式训练3:已知△ABC 中,22(sin 2A -sin 2C )=(a -b )sinB ,△ABC 外接圆半径为2.(1)求∠C ; (2)求△ABC 面积的最大值. 解:(1)由22(sin 2A -sin 2C )=(a -b )·sinB 得22( 2 24R a - 2 24R c )=(a -b ) R b 2.又∵R=2,∴a 2-c 2=ab -b 2.∴a 2+b 2-c 2=ab.∴cosC= ab c b a 2222-+=2 1 . 又∵0°<C <180°,∴C=60°.(2)S= 21absinC=21 ×2 3ab=23sinAsinB=23sinAsin (120°-A )=23sinA (sin120°cosA -cos120°sinA )=3sinAcosA+3sin 2A = 2 3 sin2A -23cos2A+23=3sin (2A -30°)+23. ∴当2A=120°,即A=60°时,S max =2 3 3.高中数学必修5第一章解三角形全章教案整理
高三数学一轮复习---解斜三角形(复习)公开课教案
高中数学解三角形方法大全
解三角形(复习课)教学设计
高中数学解三角形复习教案
(完整版)高中数学解三角形方法大全
必修5第一章《解三角形》全章教案
高中数学必修五解三角形教案
高考总复习天津101中学教学案解三角形单元(教师版全套)
