您的位置：360文档中心› 微积分知识结构

微积分知识结构

微积分知识结构
微积分知识结构

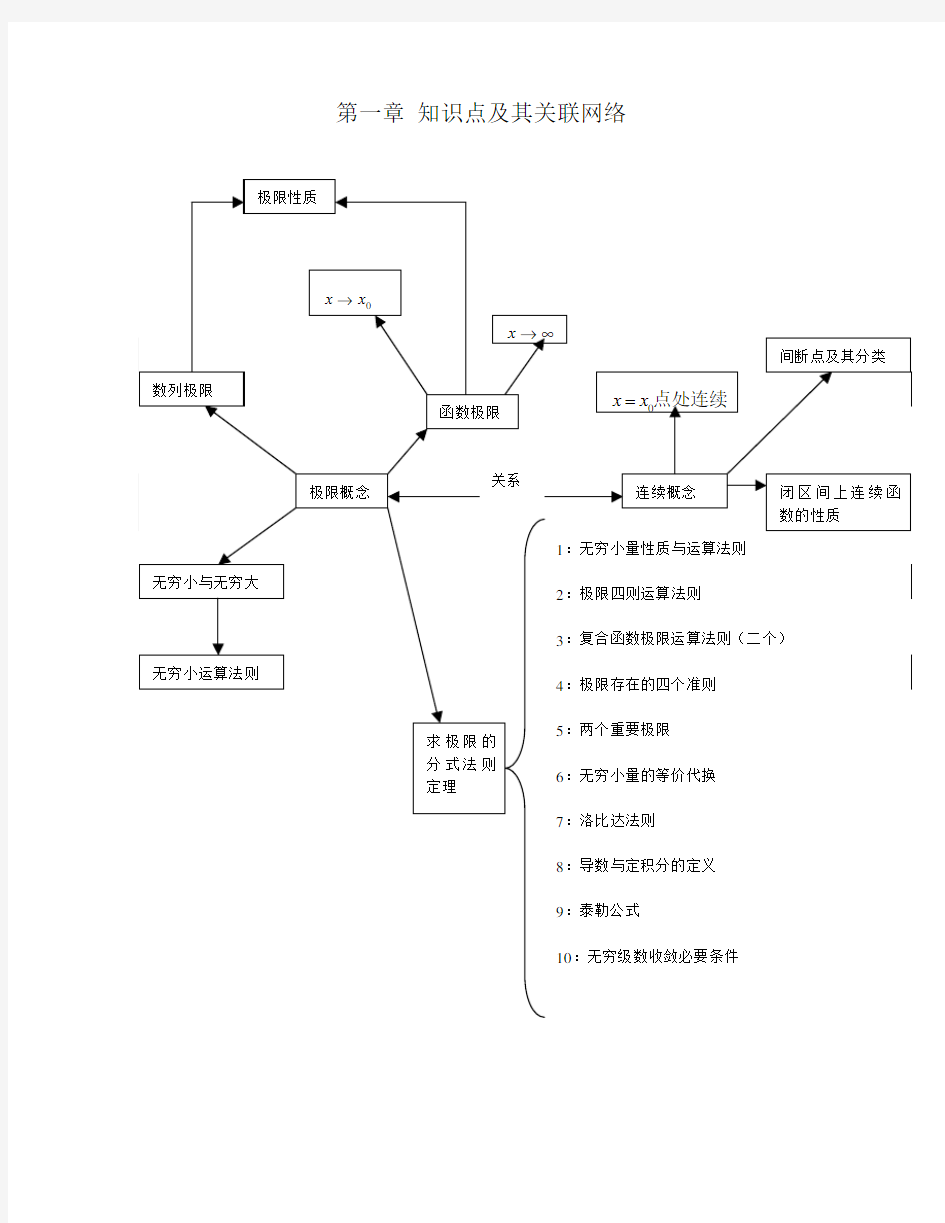
第一章知识点及其关联网络

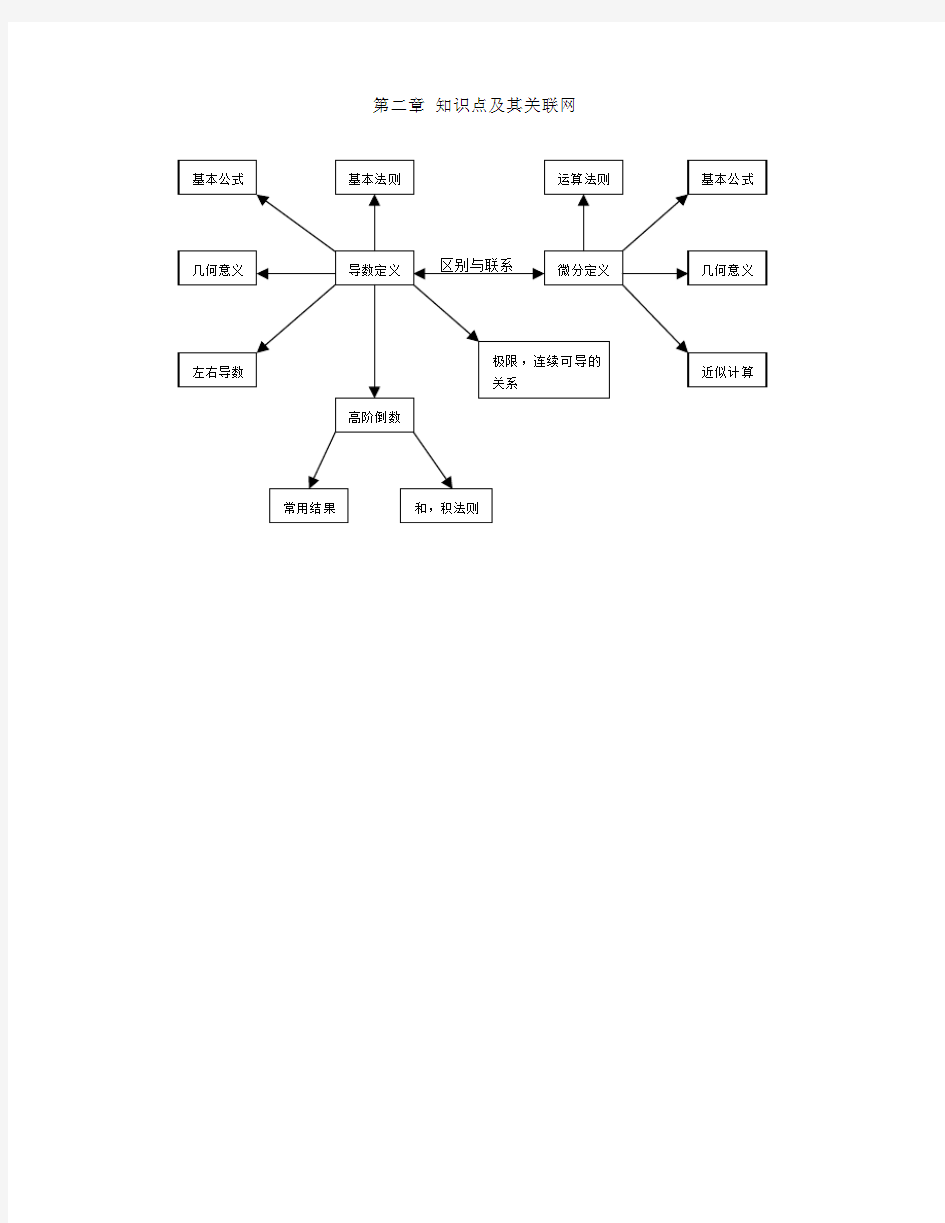
第二章知识点及其关联网

第三章知识点及其关联网络

第五章知识点及其关联网络

第八章知识点关联网络(多元函数微分法) 注：（1）公式法（2）两边求导法

第十一章知识点关联网络（幂级数傅立叶级数）

微积分知识点小结

第一章 函数 一、本章提要 基本概念 函数，定义域，单调性，奇偶性，有界性，周期性，分段函数，反函数，复合函数，基本初等函数，初等函数 第二章 极限与连续 一、本章提要 1.基本概念 函数的极限，左极限，右极限，数列的极限，无穷小量，无穷大量，等价无穷小，在一点连续，连续函数，间断点，第一类间断点（可去间断点，跳跃间断点），第二类间断点. 2.基本公式 (1) 1sin lim 0=→口 口口， (2) e )11(lim 0=+→口口口 (口代表同一变量). 3.基本方法 ⑴ 利用函数的连续性求极限； ⑵ 利用四则运算法则求极限； ⑶ 利用两个重要极限求极限； ⑷ 利用无穷小替换定理求极限； ⑸ 利用分子、分母消去共同的非零公因子求0 0形式的极限； ⑹ 利用分子，分母同除以自变量的最高次幂求 ∞∞形式的极限； ⑺ 利用连续函数的函数符号与极限符号可交换次序的特性求极限； ⑻ 利用“无穷小与有界函数之积仍为无穷小量”求极限. 4.定理 左右极限与极限的关系，单调有界原理，夹逼准则，极限的惟一性，极限的保号性，极限的四则运算法则，极限与无穷小的关系，无穷小的运算性质，无穷小的替换定理，无穷小与无穷大的关系，初等函数的连续性，闭区间上连续函数的性质. 第三章 导数与微分 一、本章提要

瞬时速度，切线，导数，变化率，加速度，高阶导数，线性主部，微分． 2.基本公式 基本导数表，求导法则，微分公式，微分法则，微分近似公式． 3.基本方法 ⑴利用导数定义求导数； ⑵利用导数公式与求导法则求导数； ⑶利用复合函数求导法则求导数； ⑷隐含数微分法； ⑸参数方程微分法； ⑹对数求导法； ⑺利用微分运算法则求微分或导数． 第四章微分学的应用 一、本章提要 1. 基本概念 未定型,极值点,驻点,尖点,可能极值点,极值,最值,曲率,上凹,下凹,拐点,渐近线,水平渐近线,铅直渐近线． 2.基本方法 ⑴用洛必达法则求未定型的极限； ⑵函数单调性的判定； ⑶单调区间的求法； ⑷可能极值点的求法与极大值（或极小值）的求法； ⑸连续函数在闭区间上的最大值及最小值的求法； ⑹求实际问题的最大（或最小）值的方法； ⑺曲线的凹向及拐点的求法； ⑻曲线的渐近线的求法； ⑼一元函数图像的描绘方法． 3. 定理 柯西中值定理,拉格朗日中值定理,罗尔中值定理, 洛必达法则,函数单调性的判定定理,极值的必要条件,极值的第一充分条件,极值的第二充分条件,曲线凹向的判别法则． 第五章不定积分 一、本章提要 1. 基本概念 原函数，不定积分．

微积分下册知识点

微积分（下）知识点 第 1 页 共 18 页 微积分下册知识点 第一章 空间解析几何与向量代数 （一） 向量及其线性运算 1、 向量，向量相等，单位向量，零向量，向量平行、共线、 共面； 2、 线性运算：加减法、数乘； 3、 空间直角坐标系：坐标轴、坐标面、卦限，向量的坐标分解式； 4、 利用坐标做向量的运算：设),,(z y x a a a a = ， ),,(z y x b b b b = ， 则 ),,(z z y y x x b a b a b a b a ±±±=± , ),,(z y x a a a a λλλλ= ； 5、 向量的模、方向角、投影： 1） 向量的模： 222z y x r ++= ； 2） 两 点 间 的 距 离公式： 212212212)()()(z z y y x x B A -+-+-= 3） 方向角：非零向量与三个坐标轴的正向的夹角γβα,, 4） 方向余弦：r z r y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα 5） 投影：?cos Pr a a j u =，其中?为向量a 与u 的夹角。 （二） 数量积，向量积 1、 数量积：θcos b a b a =? 1）2a a a =? 2）?⊥b a 0=?b a z z y y x x b a b a b a b a ++=? 2、 向量积：b a c ?=

微积分（下）知识点 第 1 页 共 18 页 大小：θsin b a ，方向：c b a ,,符合右手规则 1）0 =?a a 2）b a //?0 =?b a z y x z y x b b b a a a k j i b a =? 运算律：反交换律 b a a b ?-=? （三） 曲面及其方程 1、 曲面方程的概念：0),,(:=z y x f S 2、 旋转曲面： yoz 面上曲线0),(:=z y f C ， 绕y 轴旋转一周： 0),(2 2=+±z x y f 绕 z 轴旋转一周： 0),(22=+±z y x f 3、 柱面： ),(=y x F 表示母线平行于 z 轴，准线为 ?????==0 ),(z y x F 的柱面 4、 二次曲面（不考） 1） 椭圆锥面：2 2 222z b y a x =+ 2） 椭球面：122 222 2=++c z b y a x 旋转椭球面：122 222 2=++c z a y a x 3） 单叶双曲面：122 222 2=-+c z b y a x 4） 双叶双曲面：122 22 2 2 =--c z b y a x

高等数学基础知识点大全(94页完美打印版)

一、函数与极限 1、集合的概念 一般地我们把研究对象统称为元素，把一些元素组成的总体叫集合（简称集）。集合具有确定性（给定集合的元素必须是确定的）和互异性（给定集合中的元素是互不相同的）。比如“身材较高的人”不能构成集合，因为它的元素不是确定的。 我们通常用大字拉丁字母A、B、C、……表示集合，用小写拉丁字母a、b、c……表示集合中的元素。如果a是集合A 中的元素，就说a属于A，记作：a∈A，否则就说a不属于A，记作：a?A。 ⑴、全体非负整数组成的集合叫做非负整数集（或自然数集）。记作N ⑵、所有正整数组成的集合叫做正整数集。记作N+或N+。 ⑶、全体整数组成的集合叫做整数集。记作Z。 ⑷、全体有理数组成的集合叫做有理数集。记作Q。 ⑸、全体实数组成的集合叫做实数集。记作R。 集合的表示方法 ⑴、列举法：把集合的元素一一列举出来，并用“｛｝”括起来表示集合 ⑵、描述法：用集合所有元素的共同特征来表示集合。 集合间的基本关系 ⑴、子集：一般地，对于两个集合A、B，如果集合A中的任意一个元素都是集合B的元素，我们就说A、B有包含关系，称集合A为集合B的子集，记作A?B（或B?A）。。 ⑵相等：如何集合A是集合B的子集，且集合B是集合A的子集，此时集合A中的元素与集合B中的元素完全一样，因此集合A与集合B相等，记作A＝B。 ⑶、真子集：如何集合A是集合B的子集，但存在一个元素属于B但不属于A，我们称集合A是集合B的真子集。 ⑷、空集：我们把不含任何元素的集合叫做空集。记作?，并规定，空集是任何集合的子集。 ⑸、由上述集合之间的基本关系，可以得到下面的结论： ①、任何一个集合是它本身的子集。即A?A

1-定积分与微积分基本定理(理)含答案版

定积分与微积分基本定理(理) 基础巩固强化 1.求曲线y ＝x 2与y ＝x 所围成图形的面积，其中正确的是( ) A ．S ＝?? ?0 1(x 2－x )d x B ．S ＝?? ?0 1 (x －x 2)d x C ．S ＝?? ?0 1 (y 2－y )d y D ．S ＝??? 1 (y － y )d y [答案] B [分析] 根据定积分的几何意义，确定积分上、下限和被积函数． [解析] 两函数图象的交点坐标是(0,0)，(1,1)，故积分上限是1，下限是0，由于在[0,1]上，x ≥x 2，故函数y ＝x 2与y ＝x 所围成图 形的面积S ＝?? ?0 1 (x －x 2)d x . 2．如图，阴影部分面积等于( ) A ．2 3 B ．2－3 [答案] C [解析] 图中阴影部分面积为

S ＝??? -3 1 (3－x 2 －2x )d x ＝(3x －1 3x 3－x 2)|1 －3＝32 3. 4－x 2d x ＝( ) A ．4π B ．2π C ．π [答案] C [解析] 令y ＝4－x 2，则x 2＋y 2＝4(y ≥0)，由定积分的几何意义知所求积分为图中阴影部分的面积， ∴S ＝1 4×π×22＝π. 4.已知甲、乙两车由同一起点同时出发，并沿同一路线(假定为直线)行驶．甲车、乙车的速度曲线分别为v 甲和v 乙(如图所示)．那么对于图中给定的t 0和t 1，下列判断中一定正确的是( ) A ．在t 1时刻，甲车在乙车前面 B ．在t 1时刻，甲车在乙车后面 C ．在t 0时刻，两车的位置相同 D ．t 0时刻后，乙车在甲车前面 [答案] A [解析] 判断甲、乙两车谁在前，谁在后的问题，实际上是判断在t 0，t 1时刻，甲、乙两车行驶路程的大小问题．根据定积分的几何意义知：车在某段时间内行驶的路程就是该时间段内速度函数的定积

微积分下册主要知识点

微积分下册主要知识点

4.1不定积分 *基本积分表 *基本积分法：利用基本积分表。 4.2换元积分法 一、第一换元积分法(凑微分法) C x F C u F du u g dx x x g +=+=='??)]([)()()()]([???. 二、常用凑微分公式 三、第二换元法 x u x u x u x u x u x u a u e u x u x u b ax u x d x f dx x x f x d x f dx x x f x d x f xdx x f x d x f xdx x f x d x f xdx x f x d x f xdx x f da a f a dx a a f de e f dx e e f x d x f dx x x f x d x f dx x x f a b ax d b ax f a dx b ax f x x x x x x x x x x arcsin arctan cot tan cos sin ln ) (arcsin )(arcsin 11 )(arcsin .11) (arctan )(arctan 11 )(arctan .10cot )(cot csc )(cot .9tan )(tan sec )(tan .8cos )(cos sin )(cos .7sin )(sin cos )(sin .6)(ln 1)(.5)()(..4) (ln )(ln 1 )(ln .3) 0()()(1 )(.2)0()()(1 )(.12 2 221==========+=-=-=+-==-=?=?=?=?=?≠=≠++= +??????????????????????-μμμμμμμ 法 分 积元换 一第换元公式积分类型

微积分入门

序 中国战国时代（公元前7世纪），我国的庄周所着的《庄子》一书的“天下篇”中，记有“一尺之棰，日取其半，万世不竭”，即老庄哲学中所有的无限可分性和极限思想；公元前4世纪《墨经》中有了有穷、无穷、无限小（最小无内）、无穷大（最大无外）的定义和极限、瞬时等概念。这是朴素的、也是很典型的极限概念。而极限理论便是微分学的基础。 古希腊时期（公元前3世纪），阿基米德用内接正多边形的周长来穷尽圆周长，而求得圆周率愈来愈好的近似值，也用一连串的三角形来填充抛物线的图形，以求得其面积。这是穷尽法的古典例子之一，可以说是积分思想的起源。 17世纪，许多着名的数学家、天文学家、物理学家都为解决上述几类问题作了大量的研究工作，如法国的费马、笛卡尔、罗伯瓦、笛沙格；英国的巴罗、瓦里士；德国的开普勒；意大利的卡瓦列利等人都提出许多很有建树的理论。为微积分的创立做出了贡献。 17世纪下半叶，在前人工作的基础上，英国大科学家牛顿和德国数学家莱布尼茨分别在自己的国度里独自研究和完成了微积分的创立工作，虽然这只是十分初步的工作。 19世纪初，法国科学学院的科学家以柯西为首，对微积分的理论进行了认真研究，建立了极限理论，后来又经过德国数学家维尔斯特拉斯进一步的严格化，使极限理论成为了微积分的坚定基础。才使微积分进一步的发展开来。 1874年，德国数学家外尔斯特拉斯构造了一个没有导数的连续函数，即构造了一条没有切线的连续曲线，这与直观概念是矛盾的。它使人们认识到极限概念、连续性、可微性和收敛性对实数系的依赖比人们想象的要深奥得多。外尔斯特拉斯最终完成了对实数系更深刻的性质的理解，使得数学分析完全由实数系导出，脱离了知觉理解和几何直观。 人类对自然的认识永远不会止步，微积分这门学科在现代也一直在发展着，人类认识微积分的水平在不断深化。 ※ 微积分学(Calculus,拉丁语意为用来计数的小石头)是研究极限、微分学、积分学和无穷级数的一个数学分支，并成为了现代大学教育的重要组成部分。历史上，微积分曾经指无穷小的计算。更本质的讲，微积分学是一门研究变化的科学，正如几何学是研究空间的科学一样。 客观世界的一切事物，小至粒子，大至宇宙，始终都在运动和变化着。因此在数学中引入了变量的概念后，就有可能把运动现象用数学来加以描述了。 由于函数概念的产生和运用的加深，也由于科学技术发展的需要，一门新的数学分支就继解析几何之后产生了，这就是微积分学。微积分学这门学科在数学发展中的地位是十分重要的，可以说它是继欧氏几何后，全部数学中的最大的一个创造。 微积分学在科学、经济学和工程学领域被广泛的应用，来解决那些仅依靠代数学不能有效解决的问题。微积分学在代数学、三角学和解析几何学的基础上建立起来，并包括微分学、积分学两大分支。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。微积分学基本定理指出，微分和积分互为逆运算，这也是两种理论被统一成微积分学的原因。我们可以以两者中任意一者为起点来讨论微积分学，但是在教学中，微分学一般会先被引入。在更深的数学领域中，微积分学通常被称为分析学，并被定义为研究函数的科学。 ※ 在高二上学期的数学学习过程中，我们认识了导数和定积分，并开始了对其应用的理解和练习。其实，早在高中物理开始不久后的学习中，我们就接触到了微积分的原型——微元法。同当年的科学家一样，我们也因物理上的应用需要，开始了对微积分学的认识之旅。 借着这次研究性学习的契机，我们就了解一下微积分学的发展历史，认识数学研究对社会发展的重要意义，本着“以史为镜”的态度了解其中波折而有趣的发展历程；并由此拓展自己的知识面，

7.微积分基本定理练习题

7、微积分基本定理 一、选择题 1.??0 1(x 2 ＋2x )d x 等于( ) A.13 B.23 C ．1 D.43 2．∫2π π(sin x －cos x )d x 等于( ) A ．－3 B ．－2 C ．－1 D ．0 3．自由落体的速率v ＝gt ，则落体从t ＝0到t ＝t 0所走的路程为( ) A.13gt 20 B ．gt 2 0 C.12gt 20 D.16gt 20 4．曲线y ＝cos x ? ????0≤x ≤3π2与坐标轴所围图形的面积是( ) A ．4 B ．2 C.5 2 D ．3 5．如图，阴影部分的面积是( ) A ．2 3 B ．2－ 3 C.323 D.35 3 6.??0 3|x 2－4|d x ＝( ) A.213 B.223 C.233 D.25 3 7．??241 x d x 等于( ) A ．－2ln2 B ．2ln2 C ．－ln2 D ．ln2 8．若??1a ? ?? ??2x ＋1x d x ＝3＋ln2，则a 等于( ) A ．6 B ．4 C ．3 D ．2 9．(2010·山东理，7)由曲线y ＝x 2 ，y ＝x 3 围成的封闭图形面积为( ) A.112 B.14 C.13 D.7 12 10．设f (x )＝??? ?? x 2 0≤x <12－x 1

11．从如图所示的长方形区域内任取一个点M (x ，y )，则点M 取自阴影部分的概率为________． 12．一物体沿直线以v ＝1＋t m/s 的速度运动，该物体运动开始后10s 内所经过的路程是________． 13．求曲线y ＝sin x 与直线x ＝－π2，x ＝5 4π，y ＝0所围图形的面积为________． 14．若a ＝??02x 2 d x ，b ＝??02x 3 d x ，c ＝??0 2sin x d x ，则a 、b 、c 大小关系是________． 三、解答题 15．求下列定积分： ①??0 2(3x 2＋4x 3 )d x ； ② sin 2 x 2 d x . 17．求直线y ＝2x ＋3与抛物线y ＝x 2 所围成的图形的面积． 18．(1)已知f (a )＝??0 1(2ax 2 －a 2 x )d x ，求f (a )的最大值； (2)已知f (x )＝ax 2 ＋bx ＋c (a ≠0)，且f (－1)＝2，f ′(0)＝0，??0 1f (x )d x ＝－2，求a ，b ，c 的值． DBCDCCDDAC 11. 13 12. 23(1132－1) 13.4－2 2 [解析] 所求面积为 ＝1＋2＋? ?? ?? 1－22＝4－22. 14.[答案] c

微积分(下册)主要知识点汇总

4.1不定积分 *基本积分表 *基本积分法：利用基本积分表。 4.2换元积分法 一、第一换元积分法(凑微分法) C x F C u F du u g dx x x g +=+=='??)]([)()()()]([???. 二、常用凑微分公式 三、第二换元法 C x F C t F dt t t f dx x f +=+='=??)]([)()()]([)(ψ??, 注: 以上几例所使用的均为三角代换, 三角代换的目的是化掉根式, 其一般规律如下: 当被积函数中含有 a) ,22x a - 可令 ;sin t a x = b) ,22a x + 可令 ;tan t a x = c) ,22a x - 可令 .sec t a x = x u x u x u x u x u x u a u e u x u x u b ax u x d x f dx x x f x d x f dx x x f x d x f xdx x f x d x f xdx x f x d x f xdx x f x d x f xdx x f da a f a dx a a f de e f dx e e f x d x f dx x x f x d x f dx x x f a b ax d b ax f a dx b ax f x x x x x x x x x x arcsin arctan cot tan cos sin ln ) (arcsin )(arcsin 11 )(arcsin .11)(arctan )(arctan 11 ) (arctan .10cot )(cot csc )(cot .9tan )(tan sec )(tan .8cos )(cos sin )(cos .7sin )(sin cos )(sin .6)(ln 1)(.5)()(..4) (ln )(ln 1 )(ln .3) 0()()(1 )(.2) 0()()(1 )(.12 2221==========+=-=-=+-==-=?=?=?=?=?≠=≠++=+??????????????????????-μμμμμμμ 法 分 积元换 一第换元公式积分类型

微积分下册主要知识点

第一换元积分法(凑微分法) g[ (X)]「(x)dx = g(u)du = F(U) C = FL (x)] C J f (x)dx= J f［毋(t)］"(t)dt = F(t)+C = F［寧(X)PC , 注：以上几例所使用的均为三角代换,三角代换的目的是化掉根式，其一般规律如下当被积函数中含有 a).a2-x2,可令X =as int; b)x2a2,可令x =ata nt; C).X22 -a ,可令x =asect. 当有理分式函数中分母的阶较高时，常采用倒代换X=1 . t 四、积分表续 4.3分部积分法

UdV=UV- VdU (或微分)的逆运算.一般地，下列类型的被 n 都是正整数). n . X SInmX n X cosmx nx ? e SIn mx nx e cosmx 分部积分公式: UVdX=UV- U VdX (3.2) n mx X e n X arcsInmX X n (In x) X n arccosmx X n arcta nmx 等. 5.1定积分的概念 5.2定积分的性质 两点补充规定: 性质 性质 性质 性质 性质 推论 推论 b ⑻当 a=b 时， f(x)dx=0; (b)当 a b 时， f(x)dx - - f (x)dx . b [f (x)二g(x)]dx f (X )dx g (X )dx. a a a b b kf (x)dx =k f (x)dx, (k 为常数). a IJ a b Cb f (x)dx f(x)dx 亠 I f (x)dx . a ?a ?c 若在区间 若在区间 b dx 二b -a. a [a,b]上有 f(x)_g(x),则 f(χ)dx g(x)dx, (a ：：：b). ■a *a b [a,b]上 f(x)_0,贝 U f(x)dx_O, (a ：：b). a b I L f(X)dx 兰『I f (X)IdX (a cb). a L - 性质6 (估值定理)设M 及m 分别是函数f(x)在区间［a,b ］上的最大值及最小值，则 b m(b —a) _ f (x)dx _ M (b —a). a 性质7 (定积分中值定理)如果函数f (x)在闭区间［a,b ］上连续，则在［a,b ］上至少存在 个点，使 b f(x)dx = f( )(b-a), (a _ -b). a 5.3微积分的基本公式 一、引例 X 二、积分上限的函数及其导数 ：：?：J (X^ f(t)dt L a 定理2若函数f(x)在区间［a,b ］上连续，则函数 (3.1) 分部积分法实质上就是求两函数乘积的导数 积函数常考虑应用分部积分法 (其中m,

微积分大一基础知识经典讲解

Chapter1 Functions(函数) 1.Definition 1)A function f is a rule that assigns to each element x in a set A exactly one element, called f (x ), in a set B. 2)The set A is called the domain(定义域) of the function. 3)The range(值域) of f is the set of all possible values of f (x ) as x varies through out the domain. ? =)()(x g x f :N ote 1)(,1 1)(2 +=--= x x g x x x f Example )()(x g x f ≠? 2.Basic Elementary Functions(基本初等函数) 1) constant functions f (x )=c 2) power functions 0,)(≠=a x x f a 3) exponential functions 1,0,)(≠>=a a a x f x domain: R range: ),0(∞ 4) logarithmic functions 1,0,log )(≠>=a a x x f a domain: ),0(∞ range: R 5) trigonometric functions f (x )=sin x f (x )=cos x f (x )=tan x f (x )=cot x f (x )=sec x f (x )=csc x Given two functions f and g , the composite function(复合函数) g f is defined by )) (())((x g f x g f = Note )))((())((x h g f x h g f =

微积分(下册)主要知识点汇总

一、第一换元积分法(凑微分法) C x F C u F du u g dx x x g +=+=='??)]([)()()()]([???. 二、常用凑微分公式 三、第二换元法 C x F C t F dt t t f dx x f +=+='=??)]([)()()]([)(ψ??, 注: 以上几例所使用的均为三角代换, 三角代换的目的是化掉根式, 其一般规律如下: 当被积函数中含有 a) ,22x a - 可令 ;sin t a x = b) ,22a x + 可令 ;tan t a x = c) ,22a x - 可令 .sec t a x = 当有理分式函数中分母的阶较高时, 常采用倒代换t x 1 =. 四、积分表续 4.3分部积分法 x u x u x u x u x u x u a u e u x u x u b ax u x d x f dx x x f x d x f dx x x f x d x f xdx x f x d x f xdx x f x d x f xdx x f x d x f xdx x f da a f a dx a a f de e f dx e e f x d x f dx x x f x d x f dx x x f a b ax d b ax f a dx b ax f x x x x x x x x x x arcsin arctan cot tan cos sin ln ) (arcsin )(arcsin 11 ) (arcsin .11) (arctan )(arctan 11)(arctan .10cot )(cot csc )(cot .9tan )(tan sec )(tan .8cos )(cos sin )(cos .7sin )(sin cos )(sin .6)(ln 1)(.5)()(..4)(ln )(ln 1 )(ln .3)0()()(1)(.2) 0()()(1 )(.1法 分 积元换一第换元公式 积分类型2 2 2 2 1==========+=-=-= +-==-=?=?=?=?=?≠=≠++= +?????? ????????????????-μμ μμμμμ

知识讲解_微积分基本定理

微积分基本定理 编稿：赵雷 审稿：李霞 【学习目标】1．理解微积分基本定理的含义。 2．能够利用微积分基本定理求解定积分相关问题。 【要点梳理】 要点一、微积分基本定理的引入 我们已学过过用定积分定义计算定积分,但其计算过程比较复杂，所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法，也是比较一般的方法。 （1）导数和定积分的直观关系： 如下图：一个做变速直线运动的物体的运动规律是s=s （t ），由导数的概念可知，它在任意时刻t 的速度v （t ）=s ＇（t ）。设这个物体在时间段[a ，b]内的位移为s ，你能分别用 s （t ）、v （t ）表示s 吗？ 一方面，这段路程可以通过位置函数S （t ）在[a ，b]上的增量s （b ）－s （a ）来表达， 即 s=s （b ）－s （a ）。 另一方面，这段路程还可以通过速度函数v （t ）表示为 ()d b a v t t ? , 即 s = ()d b a v t t ? 。 所以有： ()d b a v t t =? s （b ）－s （a ） （2）导数和定积分的直观关系的推证： 上述结论可以利用定积分的方法来推证，过程如下： 如右图：用分点a=t 0＜t 1＜…＜t i －1＜t i ＜…＜t n =b ， 将区间[a ，b]等分成n 个小区间： [t 0，t 1]，[t 1，t 2]，…，[t i ―1，t i ]，…，[t n ―1，t n ]， 每个小区间的长度均为

1i i b a t t t n --?=-= 。 当Δt 很小时，在[t i ―1，t i ]上，v （t ）的变化很小，可以认为物体近似地以速度v （t i ―1）做匀速运动，物体所做的位移 111()'()'()i i i i i b a s h v t t s t t s t n ----?≈=?=?= 。 ② 从几何意义上看，设曲线s=s （t ）上与t i ―1对应的点为P ，PD 是P 点处的切线，由导数的几何意义知，切线PD 的斜率等于s ＇（t i ―1），于是 1tan '()i i i s h DPC t s t t -?≈=∠??=??。 结合图，可得物体总位移 111 1 1 1 ()'()n n n n i i i i i i i i s s h v t t s t t --=====?≈=?=?∑∑∑∑。 显然，n 越大，即Δt 越小，区间[a ，b]的分划就越细，1 11 1 ()'()n n i i i i v t t s t t --==?=?∑∑与s 的近似程度就越好。由定积分的定义有 11lim ()n i n i b a s v t n -→∞=-=∑11 lim '()n i n i b a s t n -→∞=-=∑()d '()d b b a a v t t s t t ==??。 结合①有 ()d '()d ()()b b a a s v t t s t t s b s a ===-??。 上式表明，如果做变速直线运动的物体的运动规律是s=s （t ），那么v （t ）=s ＇（t ）在 区间[a ，b]上的定积分就是物体的位移s （b ）―s （a ）。 一般地，如果()f x 是区间[a ，b]上的连续函数，并且'()()F x f x =，那么 ()d ()()b a f x x F b F a =-? 。 这个结论叫做微积分基本定理。 要点二、微积分基本定理的概念 微积分基本定理： 一般地，如果'()()F x f x =，且()f x 在[a ，b]上可积，则()d ()()b a f x x F b F a =-? 。 这个结论叫做微积分基本定理，又叫做牛顿-莱布尼兹公式。 其中，()F x 叫做()f x 的一个原函数。为了方便，我们常把()()F b F a -记作()b a F x ，即 ()d ()()()b b a a f x x F x F b F a ==-? 。

《微积分基础》作业

微积分基础形成性考核作业（一） ————函数，极限和连续 一、填空题（每小题2分，共20分） 1．函数)2ln(1 )(-= x x f 的定义域是 ． 2．函数x x f -=51)(的定义域是 ． 3．函数24) 2ln(1 )(x x x f -++= 的定义域是 ． 4．函数72)1(2+-=-x x x f ，则=)(x f ． 5．函数???>≤+=0 e 2 )(2x x x x f x ，则=)0(f ． 6．函数x x x f 2)1(2-=-，则=)(x f ． 7．函数1 3 22+--=x x x y 的间断点是 ． 8．=∞→x x x 1 sin lim ． 9．若2sin 4sin lim 0=→kx x x ，则=k ． 10．若23sin lim 0=→kx x x ，则=k ． 二、单项选择题（每小题2分，共24分） 1．设函数2 e e x x y +=-，则该函数是（ ）． A ．奇函数 B ．偶函数 C ．非奇非偶函数 D ．既奇又偶函数 2．设函数x x y sin 2=，则该函数是（ ）． A ．奇函数 B ．偶函数 C ．非奇非偶函数 D ．既奇又偶函数

3．函数2 22)(x x x x f -+=的图形是关于（ ）对称． A ．x y = B ．x 轴 C ．y 轴 D ．坐标原点 4．下列函数中为奇函数是（ ）． A ．x x sin B ．x ln C ．)1ln(2x x ++ D ．2x x + 5．函数)5ln(4 1 +++= x x y 的定义域为（ ）． A ． 5->x B ．4-≠x C ．5->x 且0≠x D ．5->x 且4-≠x 6．函数) 1ln(1 )(-= x x f 的定义域是（ ）． A ． ),1(+∞ B ．),1()1,0(+∞? C ．),2()2,0(+∞? D ．),2()2,1(+∞? 7．设1)1(2-=+x x f ，则=)(x f （ ） A ．)1(+x x B ．2x C ．)2(-x x D ．)1)(2(-+x x 8．下列各函数对中，（ ）中的两个函数相等． A ．2)()(x x f =，x x g =)( B ．2)(x x f =， x x g =)( C ．2ln )(x x f =，x x g ln 2)(= D ．3ln )(x x f =，x x g ln 3)(= 9．当0→x 时，下列变量中为无穷小量的是（ ）. A ．x 1 B ．x x sin C ．)1ln(x + D ．2x x

微积分下册知识点

微积分下册知识点 第一章 空间解析几何与向量代数 （一） 向量及其线性运算 1、 向量，向量相等，单位向量，零向量，向量平行、共线、共面； 2、 线性运算：加减法、数乘； 3、 空间直角坐标系：坐标轴、坐标面、卦限，向量的坐标分解式； 4、 利用坐标做向量的运算：设),,(z y x a a a a =ρ ，),,(z y x b b b b =ρ， 则 ),,(z z y y x x b a b a b a b a ±±±=±ρ ρ, ),,(z y x a a a a λλλλ=ρ； 5、 向量的模、方向角、投影： 1） 向量的模： 222z y x r ++=ρ； 2） 两点间的距离公式：2 12212212)()()(z z y y x x B A -+-+-= 3） 方向角：非零向量与三个坐标轴的正向的夹角γβα,, 4） 方向余弦：r z r y r x ρρρ===γβαcos ,cos ,cos 5） 投影：?cos Pr a a j u ρρρ =，其中?为向量a ρ与u ρ 的夹角。 （二） 数量积，向量积 1、 数量积：θ cos b a b a ρ ρρρ=? 1）2a a a ρρρ=? 2）?⊥b a ρρ0=?b a ρ ρ 2、 向量积：b a c ρ ρρ?=

大小：θsin b a ρρ，方向：c b a ρ ρρ,,符合右手规则 1）0ρρ=?a a 2）b a ρρ//?0ρρρ=?b a 运算律：反交换律 b a a b ρ ρρρ?-=? （三） 曲面及其方程 1、 曲面方程的概念：0),,(:=z y x f S 2、 旋转曲面： yoz 面上曲线0),(:=z y f C ， 绕y 轴旋转一周： 0),(2 2=+±z x y f 绕 z 轴旋转一周：0),(22=+±z y x f 3、 柱面： 0),(=y x F 表示母线平行于z 轴，准线为?????==0 0),(z y x F 的柱面 4、 二次曲面（不考） 1） 椭圆锥面：2 222 2z b y a x =+ 2） 椭球面：122 22 2 2 =++c z b y a x 旋转椭球面：122 222 2=++c z a y a x

定积分与微积分基本定理1

第23练 定积分与微积分基本定理 一、选择题 1．(2016·安徽示范高中联考)??1 e ? ????2x ＋1x d x 等于( ) A ．e 2 －2 B ．e －1 C ．e 2 D ．e ＋1 2．从空中自由下落的一物体，在第一秒末恰经过电视塔塔顶，在第二秒末物体落地，已知自由落体的运动速度为v ＝gt (g 为常数)，则电视塔高为( ) A.1 2g B ．g C.32 g D ．2g 3．(2016·江西师大附中期末)若? ?1 2(x －a )d x ＝∫π 40cos 2x d x ，则a 等于( ) A ．－1 B ．1 C ．2 D ．4 4.(2016·淄博一模)如图所示，曲线y ＝x 2 －1，x ＝2，x ＝0，y ＝0围成的阴影部分的面积为( ) A .??02|x 2 －1|d x B.???? ??02(x 2 －1)d x C.??0 2(x 2 －1)d x D.??01(x 2 －1)d x ＋??1 2(1－x 2 )d x

5．(2016·天津蓟县期中)由直线y ＝x 和曲线y ＝x 3 围成的封闭图形面积为( ) A.14 B.12 C ．1 D ．2 6．(2016·辽宁师大附中期中)定积分??0 1x (2－x )d x 的值为( ) A.π4 B. π2 C ．π D ．2π 7．(2016·山西四校联考)定积分??-2 2|x 2 －2x |d x 等于( ) A ．5 B ．6 C ．7 D ．8 8．若函数f (x )，g (x )满足? ?1－1f (x )g (x )d x ＝0，则称f (x )，g (x )为区间[－1,1]上的一组 正交函数．给出三组函数： ①f (x )＝sin 12x ，g (x )＝cos 12x ；②f (x )＝x ＋1，g (x )＝x －1；③f (x )＝x ，g (x )＝x 2 . 其中为区间[－1,1]上的正交函数的组数是( ) A ．0 B ．1 C ．2 D ．3 二、填空题 9．(2016·江西高安二中段考)已知? ?a －a(sin x ＋3x 2 )d x ＝16，则正实数a 的值为________． 10．(2017·德州月考)如图，已知点A ? ?? ??0，14，点P (x 0，y 0)(x 0>0)在曲线y ＝x 2 上，若阴影 部分面积与△OAP 面积相等，则x 0＝________. 11．设变力F (x )作用在质点M 上，使M 沿x 轴正向从x ＝1运动到x ＝10，已知F (x )＝x 2 ＋1且方向和x 轴正向相同，则变力F (x )对质点M 所做的功为________ J(x 的单位：m ；力的单位：N)． 12．(2016·洛阳统考)用min{a ，b }表示a ，b 两个数中的较小的数，设f (x )＝min{x 2 ，x }，那么由函数y ＝f (x )的图象、x 轴、直线x ＝1 2和直线x ＝4所围成的封闭图形的面积为 ________.

高二数学理科下学期知识点总结

高二第二学期理科数学总结 一、导数 1、导数定义：f(x)在点x 0处的导数记作x x f x x f x f y x x x ?-?+='=' →?=)()(lim )(000 00 ； 2、几何意义：切线斜率；物理意义：瞬时速度； 3、常见函数的导数公式: ①；②1')(-=n n nx x ；③x x cos )(sin '=；④x x sin )(cos '-=； ⑤a a a x x ln )('=；⑥x x e e =')(；⑦a x x a ln 1)(log ' = ；⑧x x 1)(ln ' = 。 ⑨211x x -=' ?? ? ??；⑩ ()x x 21=' 4、导数的四则运算法则：;)(;)(;)(2 v v u v u v u v u v u uv v u v u ' -'=''+'=''±'='± 5、复合函数的导数：; x u x u y y '?'=' 6、导数的应用： （1）利用导数求切线：根据导数的几何意义，求得该点的切线斜率为该处的导数（)(0x f k '=）；利用点斜式（)(00x x k y y -=-）求得切线方程。 注意ⅰ）所给点是切点吗？ⅱ）所求的是“在”还是“过”该点的切线？ （2）利用导数判断函数单调性：①)(0)(x f x f ?>'是增函数； ②)(0)(x f x f ?<'为减函数；③)(0)(x f x f ?≡'为常数； 反之，)(x f 是增函数0)(≥'x f ，)(x f 是减函数0)(≤'x f （3）利用导数求极值：ⅰ）求导数)(x f '；ⅱ）求方程0)(='x f 的根；ⅲ）列表得极值。 （4）利用导数最大值与最小值： ⅰ）求得极值；ⅱ）求区间端点值（如果有）；ⅲ得最值。 （5）求解实际优化问题： ①根据所求假设未知数和，并由题意找出两者的函数关系式，同时给出的范围；②求导，令其为0，解得值，舍去不符合要求的值； ③根据该值两侧的单调性，判断出最值情况（最大还是最小？）； ④求最值（题目需要时）；回归题意，给出结论； 7、定积分 ⑴定积分的定义： )(lim )(1 i n i b a n f n a b dx x f ξ∑ ? =∞ →-=（注意整体思想）

高等数学基础作业1(改)

高等数学基础第一次作业 第1章 函数 第2章 极限与连续 （一）单项选择题 ⒈下列各函数对中，（C ）中的两个函数相等． A. 2 )()(x x f =，x x g =)( B. 2)(x x f = ，x x g =)( C. 3 ln )(x x f =，x x g ln 3)(= D. 1)(+=x x f ，1 1)(2--=x x x g ⒉设函数)(x f 的定义域为),(+∞-∞，则函数)()(x f x f -+的图形关于（C ）对称． A. 坐标原点 B. x 轴 C. y 轴 D. x y = ⒊下列函数中为奇函数是（B ）． A. )1ln(2 x y += B. x x y cos = C. 2 x x a a y -+= D. )1ln(x y += ⒋下列函数中为基本初等函数是（C ）． A. 1+=x y B. x y -= C. 2 x y = D. ? ??≥<-=0,10 ,1x x y ⒌下列极限存计算不正确的是（D ）． A. 12lim 2 2 =+∞→x x x B. 0)1ln(lim 0 =+→x x C. 0sin lim =∞→x x x D. 01 sin lim =∞→x x x ⒍当0→x 时，变量（C ）是无穷小量． A. x x sin B. x 1 C. x x 1 sin D. 2)ln(+x ⒎若函数)(x f 在点0x 满足（A ），则)(x f 在点0x 连续。 A. )()(lim 00 x f x f x x =→ B. )(x f 在点0x 的某个邻域内有定义 C. )()(lim 00 x f x f x x =+→ D. )(lim )(lim 0 x f x f x x x x -+→→= （二）填空题 ⒈函数)1ln(3 9 )(2x x x x f ++--=的定义域是 ． ⒉已知函数x x x f +=+2 )1(，则=)(x f x 2 -x ．

相关主题
相关文档
最新文档