(完整版)近年高考理科立体几何大题汇编(可编辑修改word版)

近几年高考理科立体几何大题汇编

1.（2018 年III 卷）如图，边长为2 的正方形

ABCD所在的平面与半圆弧C D所在平面垂直，M 是

C D上异于C，

D 的点．

（1）证明：平面AMD ⊥平面BMC ；

（2）当三棱锥M ABC 体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2、[2014·新课标全国卷Ⅱ] 四棱锥P-ABCD 中，底面

ABCD 为矩形，PA⊥平面ABCD，E为PD 的中点．

(1)证明：PB∥平面AEC；

(2)设二面角D-AE-C 为60°，AP＝1，AD＝3，

求三棱锥E-ACD 的体积．

1

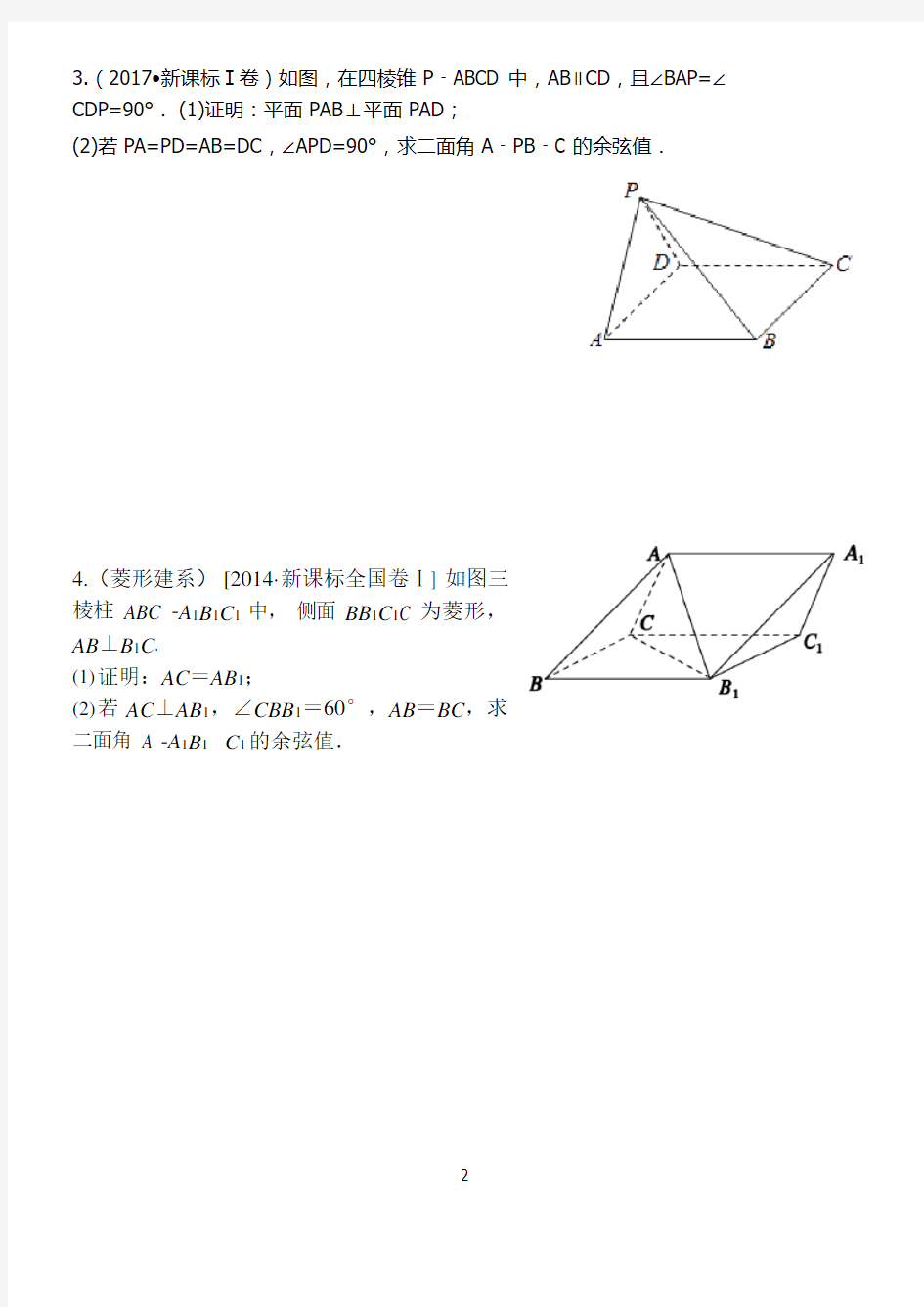
3.（2017?新课标Ⅰ卷）如图，在四棱锥P﹣ABCD 中，AB∥CD，且∠BAP=∠CDP=90°．(1)证明：平面PAB⊥平面PAD；

(2)若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C 的余弦值．

4.（菱形建系）[2014·新课标全国卷Ⅰ] 如图三

棱柱ABC -A1B1C1中，侧面BB1C1C 为菱形，

AB⊥B1C.

(1)证明：AC＝AB1；

(2)若AC⊥AB1，∠CBB1＝60°，AB＝BC，求

二面角A -A1B1-C1的余弦值．

2

5.（菱形建系）【2015 高考新课标1】如图，四边形ABCD 为菱形，∠ABC=120°，E，F 是平面ABCD 同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC. （Ⅰ）证明：平面AEC⊥平面AFC；

（Ⅱ）求直线AE 与直线CF 所成角的余弦值.

6.（翻折）(2018 年I 卷)如图，四边形ABCD 为正方形，E, F 分别为AD, BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF .

（1）证明：平面PEF ⊥平面ABFD ；

（2）求DP 与平面ABFD 所成角的正弦值.

3

10

2

P

O

B M

7.（翻折）（2016 年全国II 高考）如图，菱形ABCD 的对角线AC 与BD交于点O ，

AB = 5, AC = 6 ，点E, F 分别在AD, CD 上，AE =CF =5

，EF 交BD 于点H ．将4

?DEF 沿EF 折到?D'EF 位置，OD'=．

（Ⅰ）证明：D'H ⊥平面ABCD ；

（Ⅱ）求二面角 B -D'A -C 的正弦值．

8.（动点问题）（2018 年II 卷）如图，在三棱锥P -ABC 中，AB =BC = 2 ，

PA =PB =PC =AC = 4 ，O 为AC 的中点．

（1）证明：PO ⊥平面ABC ；

（2）若点M 在棱BC 上，且二面角M -PA -C 为30?，

求PC 与平面PAM 所成角的正弦值．

A C

4

5

DA = - = = 近几年高考理科立体几何大题汇编

1.（2018 年 III 卷）如图，边长为 2 的正方形

ABCD 所在的平面与半圆弧 C D 所在平面垂直， M 是 C

D 上异于 C ， D 的点． （1） 证明：平面 AMD ⊥ 平面 BMC ；

（2） 当三棱锥 M - ABC 体积最大时，求面 MAB 与面 MCD 所成二面角的正弦值．

1.解：（1）由题设知,平面 CMD ⊥平面 ABCD ,交线为 CD .因为 BC ⊥CD ,BC ? 平面 ABCD , 所以 BC ⊥平面 CMD ,故 BC ⊥DM .

因为 M 为 C

D 上异于 C ，D 的点,且 DC 为直径，所以 DM ⊥CM . 又 BC CM =C ,所以 DM ⊥平面 BMC .

而 DM ? 平面 AMD ,故平面 AMD ⊥平面 BMC . （2）以 D 为坐标原点,

的方向为 x 轴正方向,建立如图所示的空间直角坐标系 D ?xyz .

当三棱锥 M ?ABC 体积最大时，M 为 C

D 的中点. 由题设得 D (0, 0, 0), A (2, 0, 0), B (2, 2, 0), C (0, 2, 0), M (0,1,1) ，

AM ( 2,1,1), AB (0, 2, 0), DA (2, 0, 0)

设 n = (x , y , z ) 是平面 MAB 的法向量,则

6

5 2 5

2 5

5

DA DA

| |) ( )

= ?n ? ? AM = 0, 即?-2x + y + z = 0, ?n ? ?2 y = 0. ?? AB = 0. ?

可取 n = (1, 0, 2) .

是平面 MCD 的法向量,因此

cos n , DA n ?

=

= ， | n || DA | 5

sin

n , DA ， 5

所以面 MAB 与面 MCD 所成二面角的正弦值是

.

2、[2014·新课标全国卷Ⅱ] 如图 1-3，四棱锥 P -ABCD 中，底面 ABCD 为矩形，PA ⊥ 平面 ABCD ，E 为 PD 的中点．

(1) 证明：PB ∥平面 AEC ； (2) 设二面角 D -AE -C 为 60°，AP ＝1，AD ＝ 3，求三棱锥 E -ACD 的体积．

图 1-3

2，解：(1)证明：连接 BD 交 AC 于点 O ，连接 EO . 因为 ABCD 为矩形，所以 O 为 BD 的中点． 又 E 为 PD 的中点，所以 EO ∥PB .

因为 EO ?平面 AEC ，PB ?平面 AEC ，所以 PB ∥平面 AEC . (2)因为 PA ⊥平面 ABCD ，ABCD 为矩形， 所以 AB ，AD ，AP 两两垂直．

如图，以 A →

为坐标原点，AB ，

AD ，AP 的方向为 x 轴、y 轴、z 轴的正方向， → 为 单位长，建立空间直角坐标系 A -xyz ，则 D (0， 3，0)，E (0， 1 →

， ，AE ＝ 0， 2 2

，1 .

2 2

3 3

7

3 3 3 1 { 即

设 B (m ，0，0)(m >0)，则 C (m ，3，0) → (m ，3，0)．

，AC ＝ 设 n 1＝(x ，y ，z )为平面 ACE 的法向量，

→ n 1·AC ＝0，

则 → ) {m x ＋ 3y ＝0，

)

n 1·AE ＝0， 2 y ＋ z ＝0，

可取 n 1＝

(

2

，－1， )

.

又 n 2＝(1，0，0)为平面 DAE 的法向量，

1

由题设易知|cos 〈n 1，n 2〉|＝ ，即

2

1 3 ＝ ，解得 m ＝ .

2

2

1 1

因为 E 为 PD 的中点，所以三棱锥 E -ACD 的高为 .三棱锥 E -ACD 的体积 V ＝ ×

2 3

1 3 1 × 3× × ＝ .

2 2 2 8

3.（2017?新课标Ⅰ卷）如图，在四棱锥 P ﹣ABCD 中， AB ∥CD ，且∠BAP=∠CDP=90°．

(1) 证明：平面 PAB ⊥平面 PAD ；

(2) 若 PA=PD=AB=DC ，∠APD=90°，求二面角 A ﹣PB ﹣

C 的余弦值． 3.【答案】（ 1） 证明： ∵∠ BAP=∠ CDP=90°， ∴ PA⊥ AB ， PD⊥ C

D ， ∵ AB∥ CD ， ∴ AB⊥ PD ，

又 ∵ PA ∩PD=P ， 且

PA ? 平 面

PAD ，

PD ? 平 面 PAD ， ∴ AB⊥ 平

面 PAD ， 又

AB ? 平 面 PAB ，

∴

平

面

PAB⊥

平

面

PAD ；

（2）解：∵AB∥CD，AB=CD ，∴四边形 ABCD 为平行四边形， 由（1）知 AB⊥平面 PAD ，∴AB⊥ AD ，

则 四 边 形

ABCD 为 矩 形 ，

3

m

3 3＋4m 2

在△APD 中，由PA=PD，∠APD=90°，可得△PAD为等

腰直角三角形，

设PA=AB=2a，则AD= ．

取 AD 中点 O， BC 中点 E，连接 PO 、 OE，

以 O 为坐标原点，分别以 OA、OE、OP 所在直线为 x、y、z 轴建立空间直角坐标系，则：D（），B（）， P（0，0，），C（）．

，，．

设平面PBC 的一个法向量为，

由，得，取y=1，得．

∵AB⊥平面PAD，AD?平面PAD，∴AB⊥AD，

又PD⊥PA，PA∩AB=A，

∴ PD⊥ 平面 PAB，则为平面 PAB 的一个法向量，．

∴cos＜＞= =

．由图可知，二面角A﹣PB﹣ C

为钝角，

∴二面角A﹣PB﹣ C 的余弦值为．

4.（菱形建系）[2014·新课标全国卷Ⅰ] 如图三棱柱ABC -A1B1C1中，侧面BB1C1C 为菱形，AB⊥B1C.

(1)证明：AC＝AB1；

(2)若AC⊥AB1，∠CBB1＝60°，AB＝BC，求二面角A -A1B1-C1的余弦值．

4 解：(1)证明：连接BC1，交B1C 于点O，连接AO，因为侧面BB1C1C 为菱形，所以B1C⊥BC1，且O 为B1C 及BC1的中点．

8

又AB⊥B1C，所以B1C⊥平面ABO.

9

10

3

3 3 3 3 1

( ( )

B 1

C 1＝BC ＝ －1，－ 3

，0 . {

{

3

3 由于 AO ?平面 ABO ，故 B 1C ⊥AO . 又 B 1O ＝CO ，故 AC ＝AB 1.

(2)因为 AC ⊥AB 1，且 O 为 B 1C 的中点，所以 AO ＝CO .

又因为 AB ＝BC ，所以△BOA ≌ △BOC .故 OA ⊥OB ，从而 OA ，OB ，OB 1 两两垂直．

以 O 为坐标原点，OB 的方向为 x 轴正方向，|OB |为单位长，建立如图所示的空间直角坐标系 O - xyz .

(

3

)

因为∠CBB 1＝60°，所以△CBB 1 为等边三角形，又 AB ＝BC ，则 A 0，0， 3

，

B (1，0，0)，B (

0， 3，0)，C (0，－ 3

，0).

→ AB 1＝ 0， 3 ，－ 3) 3 → 3 ，A 1B 1＝AB ＝ 1，0，－ ，

3 3 3

→ ( )

设 n ＝(x ，y ，z )是平面 AA 1B 1 的法向量，则

n ·AB 1＝0，

3 y － z ＝0，)

→

n ·A 1B 1＝0，

)

即

所以可取 n ＝(1，3， 3)．

x － z ＝0.

{

设m 是平面A1B1C1的法向量，→

m·A1B1＝0，

则

→

m·B1C1＝0，)同理可取m＝(1，－3， 3)．

11

12

（Ⅰ）证明：平面 AEC ⊥平面 AFC ； （Ⅱ）求直线 AE 与直线 CF 所成角的余弦值.

5.，【答案】（Ⅰ）见解析（Ⅱ） 3

3

3 2 2 n ·m 1

则 cos 〈n ，m 〉＝ ＝ .

|n ||m | 7

1

所以结合图形知二面角 A -A 1B 1 - C 1 的余弦值为 .

7

5.（菱形建系）【2015 高考新课标 1】如图，四边形 ABCD 为菱形，∠ABC =120°，

E ，

F 是平面 ABCD 同一侧的两点，BE ⊥平面 ABCD ，DF ⊥平面 ABCD ，BE =2DF ， AE ⊥EC .

又∵AE ⊥EC ，∴EG = ，EG ⊥AC ， 在 Rt △EBG 中，可得 BE = ，故 DF =

2 .

2

在 Rt △FDG 中，可得 FG =

6 .

2

在直角梯形 BDFE 中，由 BD =2，BE = ，DF = 2

可 得 EF = 3 2

， 2 2 ∴ E G 2 + FG 2 = EF 2 ，∴EG ⊥FG ，

13

3 2 3

GB , G C AE , C F ?

= - ∵AC ∩FG=G ，∴EG ⊥平面 AFC ， ∵EG ? 面 AEC ，∴平面 AFC ⊥平面 AEC .

……6 分

（Ⅱ）如图，以 G 为坐标原点，分别以

的方向为 x 轴，y 轴正方向， | GB | 单位长度，建立空间直角坐标系 G-xyz ，由（Ⅰ）可得 A （0，－ ，0），E (1,0, )，

F （－1,0， ），C （0， ，0），∴ AE =（1， ， ）， CF =（-1，

2

- ， 2

）.…10 分

2

故cos < >=

AE CF 3 | AE || C F | 3 所以直线 AE 与 CF 所成的角的余弦值为

3 .

……12 分

3

6.（翻折）(2018 年 I 卷)如图，四边形 ABCD 为正方形， E , F 分别为 AD , BC 的中点，以

DF 为折痕把△DFC 折起，使点C 到达点 P 的位置，且 PF ⊥ BF .

（1） 证明：平面 PEF ⊥ 平面 ABFD ； （2） 求 DP 与平面 ABFD 所成角的正弦值.

2

3 2 3 为

.

14

3

3 3

10 HF ? ? , 0), DP (1, , ), HP

6. 解：（1）由已知可得，BF ⊥PF ，BF ⊥EF ，所以 BF ⊥平面 PEF .

又 BF ? 平面 ABFD ，所以平面 PEF ⊥平面 ABFD .

（2）作 PH ⊥EF ，垂足为 H .由（1）得，PH ⊥平面 ABFD .

以 H 为坐标原点，

的方向为 y 轴正方向， | BF | 为单位长，建立如图所示的空间直 角坐标系 H ?xyz .

由（1）可得，DE ⊥PE .又 DP =2，DE =1，所以 PE = .又 PF =1，EF =2，故 PE ⊥PF .

可得 PH =

3 , EH = 3 . 2 2

则 H (0, 0, 0), P (0, 0, 3 ), D (-1, - 3 = 3 = (0, 0, 3 ) 为平面 ABFD 的

法向量.

2 2 2 2 2

3

HP DP 4 3 设 DP 与平面 ABFD 所成角为，则sin =|

| HP | |

DP | |= =

.

4

所以 DP 与平面 ABFD 所成角的正弦值为

3 .

4

7.（翻折）（2016 年全国 II 高考）如图，菱形 ABCD 的对角线 AC 与 BD 交于点O ，

AB = 5, AC = 6 ， 点 E , F 分别在 AD , CD 上， AE = CF = 5

， EF 交 BD 于点 H ． 将

4

?DEF 沿 EF 折到 ?D 'EF 位置， OD ' = ．

（Ⅰ）证明： D 'H ⊥ 平面 ABCD ； （Ⅱ）求二面角 B - D 'A - C 的正弦值．

15

u r u u r

n 1 ? n 2 u r u u r n 1 n 2

7 5 2 95 ? ' ?

?

7. 【解析】⑴证明：∵ AE = CF = 5

，∴ AE = CF ，

4 AD CD

∴ EF ∥ AC ．∵四边形 ABCD 为菱形，∴ AC ⊥ BD ， ∴ EF ⊥ BD ，∴ EF ⊥ DH ，∴ EF ⊥ D 'H ．

∵ AC = 6 ，∴ AO = 3 ；又 AB = 5 ， AO ⊥ OB ，∴ OB = 4 ，

∴

OH = AE

? OD = 1 ， ∴ DH = D 'H = 3 ， ∴ OD ' 2 = OH 2 + D ' H 2 ， ∴ D ' H ⊥ OH

AO

．又∵ OH I EF = H ，∴ D ' H ⊥ 面 ABCD ． ⑵建立如图坐标系 H - xyz ．

B (5 ， 0 ， 0) ，

C (1， 3，

0) ， D '(0 ， 0 ， 3) ， A (1， - 3

， 0) ，

AB = (4 ， 3， 0) ， AD ' = (-1， 3， 3) ， AC = (0 ，

6 ， 0) ，

设面 ABD ' 法向量n 1 = ( x ，y ，z ) ，

? ?x = 3 由?n 1 ? AB = 0 得?4x + 3y = 0 ，取?

y = -4 ，∴ n = (3， - 4 ， 5) ． ? ??n 1 A D = 0 ?-x + 3y + 3z = 0 ? 1 ?z = 5

同理可得面 AD 'C 的法向量n 2 = (3， 0 ， 1) ，

∴ cos

= =

= ，∴ s in = ．

25 25

9 + 5

5 2 ? 10

16

2 3 8.（动点问题）（2018 年 II 卷）如图，在三棱锥 P - ABC 中， AB = BC = 2 ，

PA = PB = PC = AC = 4 ， O 为 AC 的中点．

（1） 证明： PO ⊥ 平面 ABC ；

（2） 若点 M 在棱 BC 上，且二面角 M - PA - C 为30? ，求 PC 与平面 PAM 所成角的正弦值．

解：（1）因为 AP = CP = AC = 4 ， O 为 AC 的中点，所以OP ⊥ AC ，且OP = 2 .

连结OB .因为 AB = BC =

2 AC ，所以△ABC 为等腰直角三角形，

2

且OB ⊥ AC ， OB = 1

AC = 2 .

2

由OP 2 + OB 2 = PB 2 知 PO ⊥ OB .

由OP ⊥ OB , OP ⊥ AC 知 PO ⊥ 平面 ABC .

（2）如图，以O 为坐标原点， OB 的方向为 x 轴正方向，建立空间直角坐标系O - xyz .

由已知得O (0, 0, 0), B (2, 0, 0), A (0, -2, 0), C (0, 2, 0), P (0, 0, 2 3), AP = (0, 2, 2 3), 取平面

PAC 的法向量OB = (2, 0, 0) .

17

2 3 | a - 4| 2 3(a - 4)2 + 3a 2 + a 2

3 3 ? 设 M (a , 2 - a , 0)(0 < a ≤ 2) ，则 AM = (a ,

4 - a , 0) . 设平面 PAM 的法向量为n = (x , y , z ) .

由 AP ? n = 0, AM ? n = 0 得??2 y + 2 3z = 0

??ax + (4 - a ) y = 0

，可取n = ( 3(a - 4), 3a , -a ) ，

u u u r 所以

=

2 3(a - 4)

. u u u r = 3 .

cos OB , n

2 3(a - 4)2 + 3a 2 + a 2

| cos OB , n | 2

所以

= 3 .解得a = -4 （舍去）， a = 4

.

2

所以n = (- 8 , 4 , - 4

) .又 PC = (0, 2, -2 3) ，所以

cos 3

u u u r

PC , n 3

3 3

4

所以 PC 与平面 PAM 所成角的正弦值为

3 .

4

= 3 .