线面平行垂直知识点
空间直线和平面
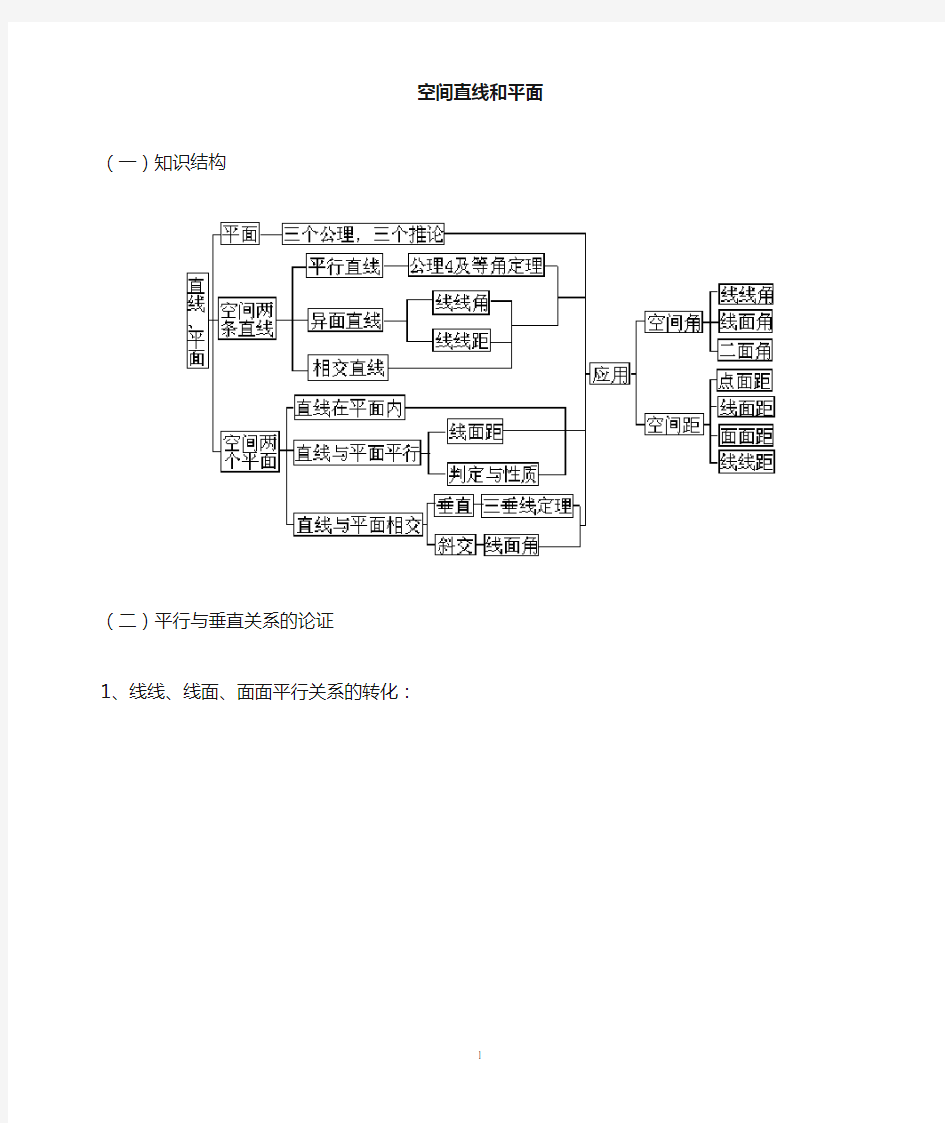
(一)知识结构
(二)平行与垂直关系的论证
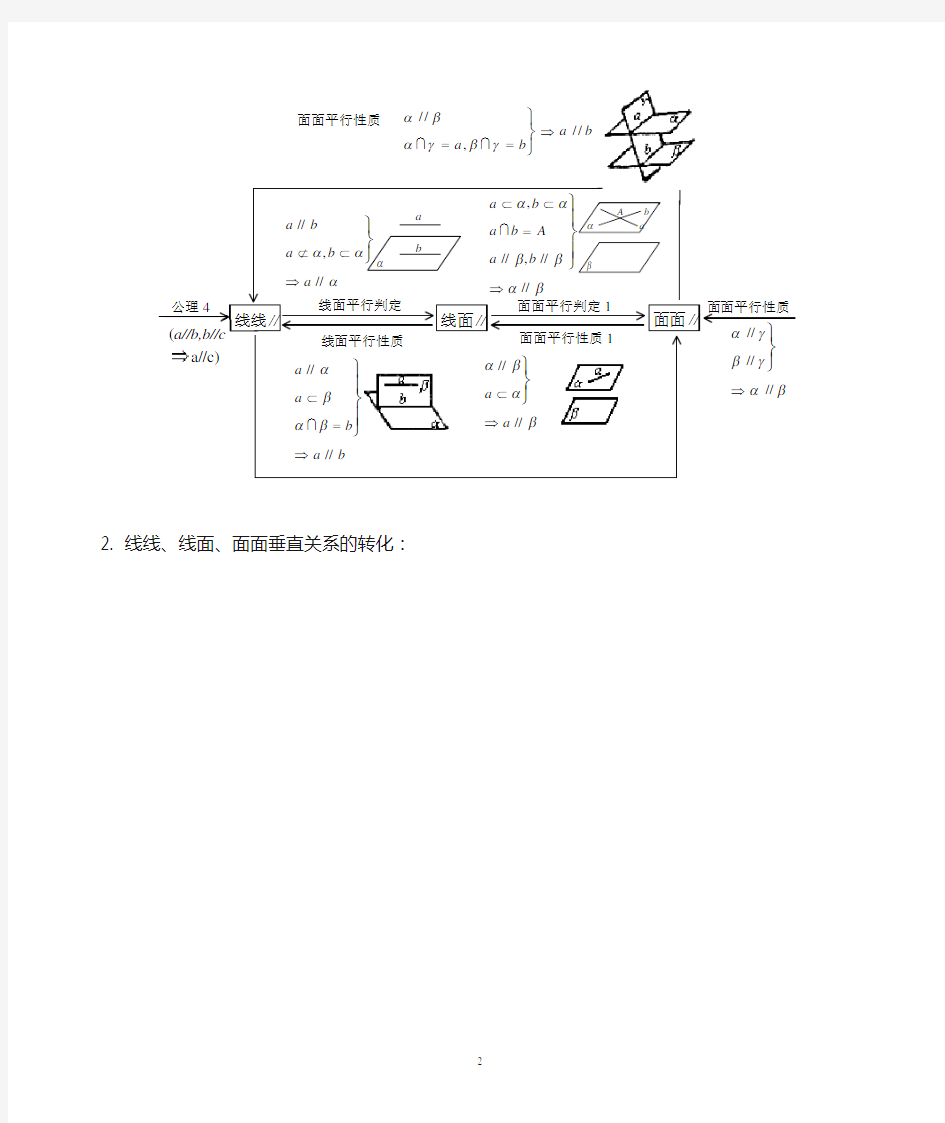
1、线线、线面、面面平行关系的转化:
线线∥
线面∥
面面∥
公理
4
(a//b,b//c a//c)
线面平行判定 αβ
αγβγ
//,// ==????
a b a b
面面平行判定1
a b a b a //,//??????ααα
面面平行性质
a b a b A a b ??=?????
?ααββ
αβ
,//,//// 线面平行性质
a a
b a b
////αβαβ?=???
?
?
? 面面平行性质1
αβαβ
////a a ???
?
?
面面平行性质
αγβγαβ
//////??
?
?
A b α a
β
a
b
α
2. 线线、线面、面面垂直关系的转化:
线线⊥ 线面⊥
面面⊥
三垂线定理、逆定理
PA AO PO
a a OA a PO a PO a AO
⊥?⊥?⊥⊥?⊥ααα
,为在内射影则
线面垂直判定1 面面垂直判定
a b
a b O l a l b l ,,?=⊥⊥?⊥??
?
?
?αα
a
a ⊥?
?⊥?
??
α
βαβ 线面垂直定义
l a l a
⊥??⊥?
??α
α
面面垂直性质,推论2
αβ
αββα⊥=?⊥?⊥???
?
? b a a b a , αγβγαβ
γ⊥⊥=?⊥?
??
?
? a a
面面垂直定义
αβαβαβ =--?⊥?
??
l l ,且二面角成直二面角
3. 平行与垂直关系的转化:
线线∥ 线面⊥
面面∥
线面垂直判定2 面面平行判定2 线面垂直性质2
面面平行性质3
a b a b //⊥?⊥???
α
α
a b a b ⊥⊥??
??
αα//
a a ⊥⊥??
??
αβαβ
//
αβα
β//a a ⊥⊥?
??
a
4. 应用以上“转化”的基本思路——“由求证想判定,由已知想性质。”
5. 唯一性结论:
(三)空间中的角与距离 1. 三类角的定义:
(1)异面直线所成的角θ:0°<θ≤90°
(2)直线与平面所成的角:0°≤θ≤90° (时,∥或)θαα=??0b b
(3)二面角:二面角的平面角θ,0°≤θ≤180°
2. 三类角的求法:转化为平面角“一找、二作、三算”
即:(1)找出或作出有关的角; (2)证明其符合定义; (3)指出所求作的角; (4)计算大小。
3. 空间距离:将空间距离转化为两点间距离——构造三角形,解三角形,求该线段的长。
4. 点到面的距离,线线间距离、线面间距离、面面间距离都可转化为点到面的距离。
常用方法:三垂线法、垂面法、体积法、向量法等。
立体几何线面平行垂直,线面角二面角的证明方法
A P B C E D 一:线面平行的证明方法: 1、用“近似平行法”先找到面上与已知直线平行的直线(一般为表示面的三角形的边界直线,或三角形某边上的中线) 看找到的这条线与已知线的长度关系,1)若相等应该构造平行四边形;2)若不相等一般利用三角形中位线的性质(将这两个不相等的线段的端点连结并延长即会出现关键三角形)。 2、若既不能构造平行四边形也不能性用中位线性质,则应再构造一个此直线所在的平面,证明此平面与已知平面平行(先证面面平行,推出线面平行) 例一:如图,已知菱形ABCD ,其边长为2, 60BAD ∠= ,ABD ?绕着BD 顺时针旋转120 得到PBD ?,M 是PC 的中点. (1)求证://PA 平面MBD ; (2)求直线AD 与平面PBD 所成角的正弦值. 例二:已知四棱锥P-ABCD ,底面ABCD 是 60=∠A 、 边 长为a 的菱形,又ABCD PD 底⊥,且PD=CD ,点M 、N 分别是 棱AD 、PC 的中点. (1)证明:DN//平面PMB ; (2)证明:平面PMB ⊥平面PAD ; (3)求点A 到平面PMB 的距离. 例三:如图,已知点P 是平行四边形ABCD 所在平面外的一点, 上的点且PE EA BF FD =∶∶,求证:EF //平面PBC . 二:线面垂直的证明方法: 通过线线垂直,证明线面垂直 1) 利用勾股定理逆定理及三角形中两个角和为90°; 2) 利用等边、等腰三角形(中线即高线),正方形、矩形邻边垂直,正方形菱形对角线垂 直等; 3) 通过线面垂直,反推线线垂直; 4) 利用面面垂直的性质,证明垂直于交线即垂直于另一个平面。 例四:如图,四边形ABCD 为矩形,CF ⊥平面ABCD ,DE ⊥平面ABCD , AB=4a ,BC= CF=2a,P 为AB 的中点. (1)求证:平面PCF ⊥平面PDE ; (2)求四面体PCEF 的体积. C
线面平行与垂直的证明题
线面平行与垂直的证明1:如图,在棱长为1的正方体ABCD-A1B1C1D1中. (1)求证:AC⊥平面B1BDD1; (2)求三棱锥B-ACB1体积. 2:如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点. 求证:(1)PA∥平面BDE;(2)平面PAC⊥平面BDE. D1 C1 B1 A1 C D B A
3:如图:在底面是直角梯形的四棱锥S —ABCD 中, ∠ABC = 90°,SA ⊥面ABCD ,SA = AB = BC = 1,2 1 AD . (Ⅰ)求四棱锥S —ABCD 的体积; (Ⅱ)证明:平面SBC ⊥平面SCD . 4:已知多面体ABCDFE 中, 四边形ABCD 为矩形,AB ∥EF ,AF ⊥BF ,平面ABEF ⊥平面ABCD , O 、M 分别为AB 、FC 的中点,且AB = 2,AD = EF = 1. (Ⅰ)求证:AF ⊥平面FBC ; (Ⅱ)求证:OM ∥平面DAF .
5:.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是P C的中点,作EF⊥PB交PB于点F. (1)证明PA//平面EDB;(2)证明PB⊥平面EFD; 6:已知正方形ABCD和正方形ABEF所在的平面相交于AB,点M,N分别在AC和BF上,且 AM=FN. C
求证:MN ‖平面BCE. 7:如图,正方体1111D C B A ABCD -中,棱长为a (1)求证:直线//1B A 平面1ACD (2)求证:平面1ACD ⊥平面D BD 1;
8:如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点, 求证:(1) FD∥平面ABC (2) AF⊥平面EDB. 9:如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点, (1)求证:平面A B1D1∥平面EFG; (2)求证:平面AA1C⊥面EFG.
线面、面面平行和垂直的八大定理
线面、面面平行和垂直的八大定理 一、线面平行。 1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平 面平行。符合表示: β ββ////a b a b a ??? ????? 2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。 符号表示: b a b a a a ////??? ?????=??βαβαα 二、面面平行。 1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。 符号表示: β α//////????? ?????==N n m M b a a m b n 2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。 符号表示: d l d l ////??? ???==γβγαβα (更加实用的性质:一个平 面内的任一直线平行另一平面) 三、线面垂直。 1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直 线垂直这个平面。 符号表示: α⊥?????? ??????=⊥⊥a M c b b a c a $:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示: PA a A oA a po oA a ⊥??? ? ????=⊥⊥??ααα 2、性质定理:垂直同一平面的两条直线互相平行。(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。) 四、面面垂直。 1、判定定理:经过一个平面的垂线的平面与该平面垂直。 βααβ⊥??⊥a a , 2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。βαβαβα⊥?⊥?=?⊥a b a a b ,,,
立体几何大题线面平行与垂直的证明题
线面平行与垂直的证明 1:如图,在棱长为1的正方体ABCD-A 1B 1C 1D 1中. (1)求证:AC ⊥平面B 1BDD 1; (2)求三棱锥B-ACB 1体积. 2:如图,ABCD 是正方形,O 是正方形的中心, PO ⊥底面ABCD ,E 是PC 的中点. 求证:(1)PA∥平面BDE ; (2)平面PAC ⊥平面BDE . 3:如图:在底面是直角梯形的四棱锥S —ABCD 中, ∠ABC = 90°,SA ⊥面ABCD ,SA = AB = BC = 1,2 1=AD . (Ⅰ)求四棱锥S —ABCD 的体积; (Ⅱ)证明:平面SBC ⊥平面SCD . 4:已知多面体ABCDFE 中, 四边形ABCD 为矩形,AB ∥EF ,AF ⊥BF ,平面ABEF ⊥平面ABCD , O 、M 分别为AB 、FC 的中点,且AB = 2,AD = EF = 1. (Ⅰ)求证:AF ⊥平面FBC ; (Ⅱ)求证:OM ∥平面DAF . 5:.如图,在四棱锥P-ABCD 中,底面ABCD 是正方形, 侧棱PD ⊥底面ABCD ,PD =DC ,E 是P C 的中点,作EF ⊥PB 交PB 于点F . (1)证明 P A //平面EDB ; (2)证明PB ⊥平面EFD ; D 1 C 1 B 1 A 1 C D B A D A B C O E P A B C D P E F
6:已知正方形ABCD 和正方形ABEF 所在的平面相交于AB ,点M ,N 分别在AC 和BF 上,且AM=FN. 求证:MN ‖平面BCE. 7:如图,正方体1111D C B A ABCD -中,棱长为a (1)求证:直线//1B A 平面1ACD (2)求证:平面1ACD ⊥平面D BD 1; 8: 如图,已知△ABC 是正三角形,EA 、CD 都垂直于平面ABC ,且EA=AB=2a,DC=a,F 是BE 的中点, 求证:(1) FD ∥平面ABC (2) AF ⊥平面EDB. 9:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 分别是CB 、CD 、CC 1的中点, (1) 求证:平面A B 1D 1∥平面EFG; (2) 求证:平面AA 1C ⊥面EFG. B C D E F N M F G E C1D1 A1 B1 D C B F E D C A M
线面平行与垂直的证明题
线面平行与垂直的证明 1:如图,在棱长为1的正方体ABCD-A 1B 1C 1D 1中. (1)求证:AC ⊥平面B 1BDD 1; (2)求三棱锥B-ACB 1体积. 2:如图,ABC D是正方形,O 是正方形的中心, PO ⊥底面ABCD ,E 是PC的中点. 求证:(1)PA∥平面BD E; (2)平面P AC ⊥平面BDE . 3:如图:在底面是直角梯形的四棱锥S —ABCD 中, ∠AB C = 90°,SA ⊥面ABCD,SA = AB = BC = 1,2 1 = AD . (Ⅰ)求四棱锥S —A BCD 的体积; (Ⅱ)证明:平面SBC ⊥平面SCD . D 1 C 1 B 1 A 1 C D B A D A B C O E P
4:已知多面体ABCDFE中, 四边形ABCD为矩形,AB ∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M 分别为AB、FC的中点,且AB= 2,AD = EF= 1. (Ⅰ)求证:AF⊥平面FBC; (Ⅱ)求证:OM∥平面DAF. 5:.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是P C的中点,作EF ⊥PB交PB于点F. (1)证明PA//平面EDB;(2)证明PB⊥平面EFD; 6:已知正方形ABCD和正方形ABEF所在的平面相交于AB,点M,N分别在AC和BF上,且AM=FN.求证:MN‖平面BCE. A B C D P E F B C D E F N M
7:如图,正方体1111D C B A ABCD -中,棱长为a (1)求证:直线//1B A 平面1ACD (2)求证:平面1ACD ⊥平面D BD 1; 8: 如图,已知△ABC 是正三角形,EA 、CD 都垂直于平面AB C,且EA=AB =2a,DC=a,F 是BE 的中点, 求证:(1) FD ∥平面ABC (2) A F⊥平面EDB . 9:如图,在正方体ABCD-A 1B1C 1D 1中,E 、F 、G 分别是CB 、CD 、CC 1的中点, (1) 求证:平面A B 1D 1∥平面EFG; (2) 求证:平面AA 1C ⊥面EFG . F E C1D1 A1 B1 D B F E D C A M
线面平行垂直知识点
线面平行垂直知识点Revised on November 25, 2020
立体几何知识点总结 一、平面 通常用一个平行四边形来表示. 平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC. 在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如: a)A∈l—点A在直线l上;A?α—点A不在平面α内; b)l?α—直线l在平面α内; c)a?α—直线a不在平面α内; d)l∩m=A—直线l与直线m相交于A点; e)α∩l=A—平面α与直线l交于A点; f)α∩β=l—平面α与平面β相交于直线l. 二、平面的基本性质 公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点,有且只有一个平面. 根据上面的公理,可得以下推论. 推论1 经过一条直线和这条直线外一点,有且只有一个平面. 推论2 经过两条相交直线,有且只有一个平面. 推论3 经过两条平行直线,有且只有一个平面. 公理4 平行于同一条直线的两条直线互相平行 三、证题方法 (1) ) 直线在平面内—有无数个公共点 (2)直线和平面直线不在平面内平行—没有公共点 (直线在平面外) 相交—有且只有一公共点 (3)平面与平面相交—有一条公共直线(无数个公共点) 平行—没有公共点 五、异面直线的判定 证明两条直线是异面直线通常采用反证法. 有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”. 六、线面平行与垂直的判定 (1)两直线平行的判定 ①定义:在同一个平面内,且没有公共点的两条直线平行. ②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a∥β ④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b(线面垂直的性质定理) ⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b(面面平行的性质公理) ⑥中位线定理、平行四边形、比例线段……,α∩β=b,则a∥b.(线面平行的判定定理) ③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.(公理4)
线线,线面平行与垂直专项练习
线面、面面平行 1、已知m、n、l1、l2表示不同直线,α、β表示不同平面.若m?α,n?α, l1?βl2?β,l1∩l2=M,则能得到结论α∥β的选项是( ) A.m∥β且l1∥αB.m∥β且n∥β C.m∥β且n∥l1 D.m∥l1且n∥l2 2、a,b是两条直线,α,β是两个平面,则能使a⊥b成立的条件是( ) A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥β C.a?α,b⊥β,α∥βD.a?α,b∥β,α⊥β 3、若有直线m、n和平面α、β,下列四个命题中,正确的是( ) A.若m∥α,n∥α,则m∥n B.若m?α,n?α,m∥β,n∥β,则α∥β C.若α⊥β,m?α,则m⊥β D.若α⊥β,m⊥β,m?α,则m∥α 4、能使平面α∥平面β成立的条件是( ) A.存在一条直线a,a∥α,a∥β B.存在一条直线a,a?α,a∥β C.存在两条平行直线a、b,a?α、b?β、a∥β、b∥α D.存在两条异面直线a、b,a?α、b?β、a∥β、b∥α 5、已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误的( ) A.若m∥β,则m∥l B.若m∥l,则m∥β C.若m⊥β,则m⊥l D.若m⊥l,则m⊥β 6、设m、n表示不同直线,α、β表示不同平面,则下列命题中正确的是( ) A.若m∥α,m∥n,则n∥α B.若m?α,n?β,m∥β,n∥α,则α∥β C.若α∥β,m∥α,m∥n,则n∥β D.若α∥β,m∥α,n∥m,n?β,则n∥β 7、设m,n为两条直线,α,β为两个平面,则下列四个命题中,正确的命题 是( ) A.若m?α,n?α,且m∥β,n∥β,则α∥β B.若m∥α,m∥n,则n∥α
线面平行与垂直关系的转化
三垂线定理 一、温故 1.线面平行的判定及性质定理 2.线面垂直的判定及性质定理 3.求线面所成角步骤 二、探究 思考1:面的垂线垂直于平面内的每一条直线;平面的斜线不能垂直于平面的每一条直线,但也不是与每一条直线都不垂直。那么平面的斜线与平面内的直线在什么情况下是垂直的呢? 例1:已知:,PA PO 分别是平面α的垂线和斜线,AO 是PO 在平面α的射影,, a α?a AO ⊥。 求证:a PO ⊥; 例2.已知P 是平面ABC 外一点,,PA ABC AC BC ⊥⊥。 求证:PC BC ⊥。 P B
例3.已知:点O 是ABC ?的垂心,PO ABC ⊥平面,垂足为O ,求证:PA BC ⊥ 例4.已知PA ⊥正方形ABCD 所在平面,O 为对角线BD 的中点。 求证:,PO BD PC BD ⊥⊥。 例5.在正方体1AC 中,求证:1111 1,AC B D AC BC ⊥⊥; 例6.已知:,PA PO 分别是平面α的垂线和斜线,AO 是PO 在平面α的射影,, a α?a PO ⊥。 求证:a AO ⊥; P B 1 A C O D A C B P
例7.在空间四边形ABCD 中,设,AB CD AC BD ⊥⊥。 求证:(1)AD BC ⊥; (2)点A 在底面BCD 上的射影是BCD ?的垂心; 线面平行与垂直关系的转化 1.对于命题:①b a a b b a ⊥?⊥,//; ②αα//,b a b a ?⊥⊥; ③ c a b a c b a ////,,,?=???βαβα;④ c b a c a b ////,,,?=?=?=?ααγγββα,其中正确的命题个数是 2.若直线a ,b 没有公共点,则下列命题:①存在与a ,b 平行的直线;②存在与a ,b 垂直的平面;③存在经过a 而与b 垂直的平面;④存在经过a 而与b 平行的平面. 其中正确的命题序号是 3.已知a ,b 和平面α,下列推理:①α⊥a 且b a a b ⊥??;②αα⊥?⊥b a b a 且//;③b a a //b //??αα且;④ααα??⊥⊥a a b a 或且//b ,其中正确的命题序号是 4.下列说法:①如果一条直线和平面内的一条直线垂直,该直线与这个平面必相交;②如果一条直线和平面的一组平行线垂直,该直线必在这个平面内;④如果一条直线和一个平面垂直,该直线垂直于平面内的任何直线,其中正确的个数是 5.空间四边形ABCD 的四条边相等,则它的对角线AD 、BC 的关系是 6.对于命题:① αα⊥????⊥a b b a //;②αα////a b b a ?????;③αα⊥?? ?? ⊥a b b a //;④ αα//b b a a ?? ?? ⊥⊥其中正确的命题是 7.在正方体ABCD-A ?B ?C ?D ?中,边对角线BD ?的一个平面交AA ?于E ,交CC ?于F , D A B C
判断或证明线面平行的或垂直常用方法
同学们早上先把下面知识点看完然后做后面的四个题。做完后再看看另一个知识点解析几何常见题型。都发布在作业里面。 线线平行的证明方法: 三线间平行的传递性,三角形中位线,平行四边形对边平行且相等,梯形的上下底平行,棱柱圆柱的侧棱平行且相等,两平行面被第三面所截交线平行,成比例(相似)证平行等等。 判断或证明线面平行的常用方法包括: (1)利用线面平行的定义,一般用反证法; (2)利用线面平行的判定定理(a?α,b?α,a∥b?a∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述; (3)利用面面平行的性质定理(α∥β,a?α?a∥β); (4)利用面面平行的性质(α∥β,a?β,a∥α?a∥β). 【垂直类证明方法总结】 证垂直的几种方法:勾股定理、等腰(边)三角形三线合一、菱形对角线、矩形(含正方形)、90度、相似三角形(与直角三角形)、圆直径对的圆周角、平行线、射影定理(三垂线定理)、线面垂直、面面垂直等 证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面).解题时,注意线线、线面与面面关系的相互转化; 1..如图,三棱柱中,侧面是菱形,其对角线的交点为,且, .
(1)求证:平面; (2)若,且,求三棱锥的体积. 2.如图,四棱锥中,平面底面,△是等边三角形,底面为梯形,且,∥,. (Ⅰ)证明:; (Ⅱ)求到平面的距离. 3.如图,在几何体中,底面四边形是边长为4的菱形,, ,,平面,且,. (1)证明:平面平面;
(2)求三棱锥的体积. 4. 已知数列的通项公式为,为其前项和,则数列的前8项和为__________.答案1.(1)∵四边形是菱形,∴,∵, ∴平面,又?平面,∴.∵,是的中点, ∴,∵,∴平面. (2)菱形的边长为,又是等边三角形,则. 由(1)知,,又是的中点,, 又是等边三角形,则.在中, , 2.(Ⅰ)由余弦定理得, ∴,∴,∴. 又平面底面,平面底面,?底面, ∴平面, 又?平面,∴. (Ⅱ)设到平面的距离为 取中点,连结,∵△是等边三角形,∴. 又平面底面,平面底面,?平面, ∴底面,且,
线面平行与垂直的证明题精选
线面平行和垂直的证明 1:如图,在棱长为1的正方体ABCD-A 1B 1C 1D 1中. (1)求证:AC ⊥平面B 1BDD 1; (2)求三棱锥B-ACB 1体积. 2:如图,ABCD 是正方形,O 是正方形的中心, PO ⊥底面ABCD ,E 是PC 的中点. 求证:(1)PA∥平面BDE ; (2)平面PAC ⊥平面BDE . 3:如图:在底面是直角梯形的四棱锥S —ABCD 中, ∠ABC = 90°,SA ⊥面ABCD ,SA = AB = BC = 1, 2 1 = AD . (Ⅰ)求四棱锥S —ABCD 的体积; (Ⅱ)证明:平面SBC ⊥平面SCD . 4:已知多面体ABCDFE 中, 四边形ABCD 为矩形,AB ∥EF ,AF ⊥BF ,平面ABEF ⊥平面ABCD , O 、M 分别为AB 、FC 的中点,且AB = 2,AD = EF = 1. (Ⅰ)求证:AF ⊥平面FBC ; (Ⅱ)求证:OM ∥平面DAF . 5:.如图,在四棱锥P-ABCD 中,底面ABCD 是正方形, 侧棱PD ⊥底面ABCD ,PD =DC ,E 是P C 的中点,作EF ⊥PB 交PB 于点F . (1)证明 P A //平面EDB ; (2)证明PB ⊥平面EFD ; 6:已知正方形ABCD 和正方形ABEF 所在的平面相 交于AB ,点M ,N 分别在AC 和BF 上,且AM=FN. 求证:MN ‖平面BCE. 7:如图,正方体1111D C B A ABCD -中,棱长为a (1)求证:直线//1B A 平面1ACD (2)求证:平面1ACD ⊥平面D BD 1; 8: 如图,已知△ABC 是正三角形,EA 、CD 都垂直于平面ABC ,且EA=AB=2a,DC=a,F 是BE 的中点, D 1 C 1 B 1 A 1 C D B A D A B C O E P A B C D P E F B C D E F N M F E D C A M
(完整版)直线、平面平行与垂直的综合问题
第六节 直线、平面平行与垂直的综合问题 考点一 立体几何中的探索性问题 [典例] (2018·全国卷Ⅲ)如图,矩形ABCD 所在平面与半圆弧?CD 所在平面垂直,M 是?CD 上异于C ,D 的点. (1)证明:平面AMD ⊥平面BMC . (2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由. [解] (1)证明:由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ?平面ABCD , 所以BC ⊥平面CMD ,所以BC ⊥DM . 因为M 为?CD 上异于C ,D 的点,且DC 为直径, 所以DM ⊥CM . 又BC ∩CM =C ,所以DM ⊥平面BMC . 因为DM ?平面AMD ,所以平面AMD ⊥平面BMC . (2)当P 为AM 的中点时,MC ∥平面PBD . 证明如下: 连接AC 交BD 于O . 因为四边形ABCD 为矩形, 所以O 为AC 的中点. 连接OP ,因为P 为AM 的中点, 所以MC ∥OP . 又MC ?平面PBD ,OP ?平面PBD , 所以MC ∥平面PBD . [题组训练] 1.如图,三棱锥P -ABC 中,P A ⊥平面ABC ,P A =1,AB =1,AC =2,∠BAC =60°. (1)求三棱锥P -ABC 的体积; (2)在线段PC 上是否存在点M ,使得AC ⊥BM ,若存在,请说明理由,并求PM MC 的值. 解:(1)由题设AB =1,AC =2,∠BAC =60°, 可得S △ABC =12·AB ·AC ·sin 60°=3 2 . 由P A ⊥平面ABC ,可知P A 是三棱锥P -ABC 的高, 又P A =1, 所以三棱锥P -ABC 的体积V =13·S △ABC ·P A =3 6 .
线面 线线面面平行垂直方法总结
线线平行 1.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。(一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.) 2.如果两个平行平面同时和第三个平面相交,那么它们的交线平行。 3.【定义】同一平面内,两直线无公共点,称两直线平行 3.【公理】平行于同一直线的两条直线互相平行.(空间平行线传递性) 4.【定理】同位角相等,或内错角相等,或同旁内角互补,两直线平行. 5.平行线分线段成比例定理的逆定理 线面平行 1.面外一条线与面内一条线平行,或两面有交线强调面外与面内(如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。) 2.面外一直线上不同两点到面的距离相等,强调面外 3.如果连条直线同时垂直于一个平面,那么这两条直线平行 4.证明线面无交点 5.反证法(线与面相交,再推翻) 6.空间向量法,证明线一平行向量与面内一向量(x1x2-y1y2=0) 7.【定义】直线与平面无公共点,称直线与平面平行 8.X7【定理】如果两个平面平行,那么其中一平面内的任一直线平行于另一平面. 面面平行 1.如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。 2.若两个平面所夹的平行线段相等,则这两个平面平行. 3.【定理】一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行. 4.【定义】两平面无公共点,称两平面平行. 5.【公理】平行于同一平面的两个平面互相平行.(空间平行面传递性) 6.【定理】一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. 线线垂直 1如果一条直线垂直于一个平面,则这个平面上的任意一条直线都与这条直线垂直。 . 2.三垂线定理:如果平面内的一条直线垂直于平面的血现在平面内的射影,则这条直线垂直于斜线。
完整版直线平面平行与垂直的综合问题
第六节直线、平面平行与垂直的综合问题 考点一立体几何中的探索性问题 [典例](2018全国卷川)如图,矩形ABCD所在平面与半圆弧C D所在平面垂直,M是 C D上异于c, D的点. ⑴证明:平面AMD丄平面BMC. ⑵在线段AM上是否存在点P,使得MC //平面PBD?说明理由. [解](1)证明:由题设知,平面CMD丄平面ABCD,交线为CD.因为BC丄CD , 平面ABCD , 所以BC丄平面CMD,所以BC丄DM . 因为M为C D上异于C, D的点,且DC为直径, 所以DM丄CM. 又BCn CM = C,所以DM丄平面BMC. 因为DM ?平面AMD,所以平面AMD丄平面BMC . ⑵当P为AM的中点时,MC //平面PBD. 证明如下: 连接AC交BD于0. 因为四边形ABCD为矩形, 所以0为AC的中点. 所以MC // 0P. 又MC?平面PBD, 0P?平面PBD , 所以MC //平面PBD. [题组训练] 1.如图,三棱锥P-ABC中,PA丄平面ABC, PA = 1 , AB = 1, AC =2, / BAC= 60°. (1)求三棱锥P-ABC的体积; (2)在线段PC上是否存在点M,使得AC丄BM,若存在,请说明理由,并求MC的值. 解:(1)由题设AB= 1 , AC = 2,/ BAC = 60° 1 可得ABC = 2 AB AC sin 60° =亍. 由PA丄平面ABC,可知PA是三棱锥P-ABC的高, 又FA= 1 , 所以三棱锥P-ABC的体积V= 3 &ABC PA晋. BC? 连接0P,因为P为AM的中点,
⑵在线段PC上存在点M,使得AC丄BM,证明如下: 如图,在平面ABC PA交PC于点M,连接 由PA丄平面ABC, 所以MN丄AC. 因为BN n MN = N, 又BM?平面MBN , 所以AC丄BM. 1 在Rt△ BAN 中,AN= AB ?os/ BAC = , 3 从而NC = AC-AN = 3, ,....,,/曰PM AN 1 由MN// PA,得MC = AC = 1. 2.如图,在四棱锥P-ABCD中,PD丄平面ABCD,底面ABCD为正方形,BC= PD = 2, E为PC的中点,CB= 3CG. ⑴求证:PC丄BC; (2)AD边上是否存在一点M,使得PA //平面MEG ?若存在,求出AM的长;若不存在,请说明理由. 解:⑴证明:因为PD丄平面ABCD, BC?平面ABCD , 所以PD丄BC. 因为四边形ABCD是正方形,所以BC丄CD. 又PD n CD = D , PD?平面PCD , CD?平面PCD , 所以BC丄平面PCD. 因为PC?平面PCD,所以PC 丄BC. ⑵连接AC, BD交于点O, 连接EO , GO ,
线面线线面面平行垂直方法总结
线面线线面面平行垂直方 法总结 -标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
线线平行 1.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。(一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.) 2.如果两个平行平面同时和第三个平面相交,那么它们的交线平行。 3.【定义】同一平面内,两直线无公共点,称两直线平行 3.【公理】平行于同一直线的两条直线互相平行.(空间平行线传递性) 4.【定理】同位角相等,或内错角相等,或同旁内角互补,两直线平行. 5.平行线分线段成比例定理的逆定理 线面平行 1.面外一条线与面内一条线平行,或两面有交线强调面外与面内(如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。) 2.面外一直线上不同两点到面的距离相等,强调面外 3.如果连条直线同时垂直于一个平面,那么这两条直线平行 4.证明线面无交点 5.反证法(线与面相交,再推翻) 6.空间向量法,证明线一平行向量与面内一向量(x1x2-y1y2=0) 7.【定义】直线与平面无公共点,称直线与平面平行 8.X7【定理】如果两个平面平行,那么其中一平面内的任一直线平行于另一平面. 面面平行 1.如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。 2.若两个平面所夹的平行线段相等,则这两个平面平行. 3.【定理】一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行. 4.【定义】两平面无公共点,称两平面平行. 5.【公理】平行于同一平面的两个平面互相平行.(空间平行面传递性) 6.【定理】一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. 线线垂直 1如果一条直线垂直于一个平面,则这个平面上的任意一条直线都与这条直线垂直。 2
线线平行垂直,线面平行垂直,面面平行垂直判定与性质
1.线线平行 判定:a用向量,方向向量平行b一条直线平行于另一个平面,则它平行于它所在平面与那个平面的交线。C若一平面与两平行平面相交,则两交线平行。D同时与一平面垂直的两直线平行。E同时平行于一条直线的两直线平行。 性质:貌似没啥性质,一般是证明线面关系的时候先证明线线关系。 2.线线垂直 判定:a向量,方向向量垂直b直线垂直于平面,则直线与平面中的任意直线都垂直c第一条直线与第二条直线平行,第一条垂直于第三条,则第二条也垂直于第三条d把两直线放在一个平面中,利用平面几何各种判定方法,如等腰三角形的底和高等。E(重点)三垂线定理:平面内的一条直线,如果和过平面的一条斜线在平面内的射影垂直,那么它就和这条斜线垂直。三垂线逆定理:在平面内的一条直线,如果和过平面的一条斜线垂直,那么它也垂直于斜线在平面内的射影。(这个比较重要,记不住的话找一下例题,多看看图就好了) 性质:貌似也没什么性质,一般也是要证明线面关系的时候用到它。注意:第一条直线垂直于第二条直线,第一条直线垂直于第三条直线,则第二条直线与第三条直线可垂直可平行也可普通相交。 3,线面平行 判定:a面外一条线与面内一条线平行。(常用)b空间向量法,证明线一平行向量与面内一向量(x1x2-y1y2=0)(常用)c面外一直线上不同两点到面的距离相等d证明线面无交点(定义)e反证法(线与面相交,再推翻) 性质:平面外一条直线与此平面平行,则过这条直线的任意平面与此平面的交线与该直线平行。 4.线面垂直 判定:a一条线和平面内两条相交直线都垂直,那么这条直线和这个平面垂直b两个平面垂直,其中一个平面内的直线垂直两平面的交线,那么这条直线和这个平面垂直c直线的方向向量与平面的法向量平行 性质:如果两条直线同时垂直一个平面,那么这两条直线平行。 5.面面平行 判定a一个平面内的两条相交直线分别与另一个平面平行,则这两个平面平行。(常用)b如果两平面同时垂直于一条直线,则两平面平行(大题一般不用) 性质:a两个平面平行,在一个平面内的任意一条直线平行于另外一个平面b两个平面平行,和一个平面垂直的直线必垂直于另外一个平面c两个平行平面,分别和第三个平面相交,交线平行d平行平面所截的线段对应成比例(这个是推论,不好描述,书上或练习册上应该有类似的题) 6.面面垂直 判定:一个面如果过另外一个面的垂线,那么这两个面相互垂直 性质:a如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。b如果两个平面垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内。C如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面。D三个两两垂直的平面的交线两两垂直。
线面垂直平行六种关系的证明方法
线面垂直平行六种关系的证明方法 一、线线平行的证明方法: 1、利用平行四边形。 2、利用三角形或梯形的中位线。(分线段成比例的直线平行) 3、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。(线面平行的性质定理) 4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。(面面平行的性质定理) 5、如果两条直线垂直于同一个平面,那么这两条直线平行。(线面垂直的性质定理) 6、平行于同一条直线的两条直线平行。(平行公理) 7、夹在两个平行平面之间的平行线段相等。(需证明) 8. 两直线的方向向量共线(平行) 二、线面平行的证明方法: 1、定义法:直线与平面没有公共点。 2、如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。(线面平行的判定定理) 3、两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面。 4、直线的方向向量与平面的法向量垂直,且线在面外。 5、直线的方向向量与平面内的两个不共线向量共面(线性表示)且线在面外。
三、面面平行的证明方法: 1、定义法:两平面没有公共点。 2、如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。(面面平行的判定定理) 3、平行于同一平面的两个平面平行。 4、经过平面外一点,有且只有一个平面和已知平面平行。 5、垂直于同一直线的两个平面平行。 6、两平面的法向量共线 四、线线垂直的证明方法: 1、勾股定理。 2、等腰三角形(三线合一)。 3、菱形对角线。 4、圆所对的圆周角是直角。 5、点在线上的射影。 6、如果一条直线和一个平面垂直,那么这条直线就和这个平面内任意的直线都垂直。 7、在平面内的一条直线,如果和这个平面一条斜线的射影垂直,那么它也和这条斜线垂直。(三垂线定理,需证明) 8、在平面内的一条直线,如果和这个平面一条斜线垂直,那么它也和这条斜线的射影垂直。(三垂线逆定理,需证明) 9、如果两条平行线中的一条垂直于一条直线,则另一条也垂直于这条直线。
线面、面面平行、垂直例题
第12讲 §2.2.1 直线与平面平行的判定 ¤学习目标:以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线 面平行的判定,掌握直线与平面平行判定定理,掌握转化思想“线线平行?线面平行”. ¤知识要点: 1. 定义:直线和平面没有公共点,则直线和平面平行. 2. 判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行. 符号表示为:,,////a b a b a ααα???. 图形如右图所示. ¤例题精讲: 【例1】已知P 是平行四边形ABCD 所在平面外一点,E 、F 分别为AB 、PD 的中点,求证:AF ∥平面PEC 【例2】在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱BC 、C 1D 1的中点. 求证:EF ∥平面BB 1D 1D. 【例3】如图,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点(1)求证:MN 4MN BC ==43PA =. 第13讲 §2.2.2 平面与平面平行的判定 ¤学习目标:以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中面面平行的判定,掌握两个平面平行的判定定理与应用及转化的思想. ¤知识要点: 面面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.用符号表示为:,,////,//a b a b P a b βββααα??=? ???I . ¤例题精讲: 【例1】如右图,在正方体ABCD —A 1B 1C 1D 1中,M 、N 、P 分别是C 1C 、B 1C 1、C 1D 1的中点,求证:平面MNP ∥平面A 1BD . . 【例2】已知四棱锥P-ABCD 中, 底面ABCD 为平行四边形. 点M 、N 、Q 分别 在PA 、BD 、PD 上, 且PM :MA =BN :ND =PQ :QD . 求证:平面MNQ ∥平面PBC . 第14讲 §2.2.3 直线与平面平行的性质 ¤学习目标:通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行的性质,掌握直线和平面平行的性质定理,灵活运用线面平行的判定定理和性质定理,掌握“线线”“线面”平行的转化. ¤知识要点: 线面平行的性质:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平 行. 即:////a a a b b αβαβ? ? ????=?I . ¤例题精讲: 【例1】经过正方体ABCD -A 1B 1C 1D 1的棱BB 1作一平面交平面AA 1D 1D 于E 1E ,求证:E 1E ∥ B 1B β a α b N M P D C Q B A
线面平行与垂直基础练习题
线面、面面平行和垂直的判定和性质 大题专练 1、在正方体1111ABCD A B C D -中,E 是11B D 的中点,F 是1BC 的中点, 求证:11//EF ABB A 平面 2、正方体中1111D C B A ABCD -中,M ,N ,E ,F 分别是棱11B A ,11D A ,11C B ,11D C 的中点。 求证:平面AMN ∥平面EFDB 。 3.如图,四棱锥P ABCD -中,底面ABCD 为平行四边 60,2,DAB AB AD PD ∠==⊥ 底面ABCD , 证明:PA BD ⊥ F E D 1 C 1 C D B 1 A 1 A
4.如图,已知四棱锥P ABCD -的底面ABCD 是菱形, PA ⊥平面ABCD , 点F 为PC 的中点. (Ⅰ)求证://PA 平面BDF ; (Ⅱ)求证:平面PAC ⊥平面BDF . 5、如图,P 为ABC ?所在平面外一点,PA ┴面BAC ,90,ABC ∠=AE ┴PB 于E ,AF ┴PC 于F ,求证:(1)BC ┴面PAB ,(2)AE ┴面PBC ,(3)PC ┴面AEF 。 6. 如图,棱长为1的正方体ABCD-A 1B 1C 1D 1中, (1)求证:AC ⊥平面B 1D 1DB; (2)求三棱锥B-ACB 1体积. A C D 1 C 1 B 1 A 1 C D B A A F P D C B
7.如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,E 是PC 的中点。 求证:(1)PA ∥平面BDE ;(2)BD ⊥平面PAC 8、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。 求证:(1)⊥AB 平面CDE; (2)平面CDE ⊥平面ABC 。 小题专练 1. 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α?,m β?( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m A E D B C
直线、平面平行与垂直的判定及其性质(证明题详解)
直线、平面平行与垂直的判定及其性质 7. 在四棱锥P-ABCD中,四边形ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD, (1)求证:PA⊥平面ABCD; (2)若平面PAB 平面PCD l =,问:直线l能否与平面ABCD平行? 请说明理由. 【解析】(1)因为∠ABC=90°,AD∥BC,所以AD⊥AB. 而平面PAB⊥平面ABCD,且平面PAB 平面ABCD=AB, 所以AD⊥平面PAB, 所以AD⊥PA. 同理可得AB⊥PA. 由于AB、AD?平面ABCD,且AB AD=A,所以PA⊥平面ABCD. (2)(方法一)不平行. 证明:假定直线l∥平面ABCD, 由于l?平面PCD,且平面PCD 平面ABCD=CD, 所以l∥CD. 同理可得l∥AB, 所以AB∥CD. 这与AB和CD是直角梯形ABCD的两腰不平行相矛盾, 故假设错误,所以直线l与平面ABCD不平行. (方法二)因为梯形ABCD中AD∥BC, 所以直线AB与直线CD相交,设AB CD=T. 由T∈CD,CD?平面PCD得T∈平面PCD. 同理T∈平面PAB. 即T为平面PCD与平面PAB的公共点,于是PT为平面PCD与平面PAB的交线. 所以直线l与平面ABCD不平行.
8. 如图,在三棱柱111ABC A B C -中,11,,AB BC BC BC AB BC ⊥⊥=,,,E F G 分别为线段1111,,AC AC BB 的中点,求证: (1)平面ABC ⊥平面1ABC ; (2)//EF 面11BCC B ; (3)GF ⊥平面11AB C 【解析】(1) BC AB ⊥ 11BC BC AB BC B ⊥= BC ∴⊥平面1ABC BC ? 平面ABC ∴平面ABC ⊥平面1ABC (2)111,AE EC A F FC == ,1//EF AA ∴ 11//BB AA 1//EF BB ∴ 11EF BCC B ? 面∴//EF 面11BCC B ; (3)连接EB ,则四边形EFGB 为平行四边形 11 111111111111 BE FG A C EB AC FG AC BC ABC B C ABC B C B C B C C ⊥∴⊥⊥∴⊥∴⊥∴⊥= 面面, GF ∴⊥平面11AB C 。 A B C A 1 B 1 C 1 E F G A B C A 1 B 1 C 1 E F G
