您的位置：360文档中心› 二分法Matlab程序

二分法Matlab程序

二分法Matlab程序
二分法Matlab程序

作业：用牛顿法或二分法求下面非线性方程组的根

()()1222,230,250

f x y x y f x y x y =+-=???=+-=?? 问题背景

牛顿迭代法（Newton's method ）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method ），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

牛顿法进行迭代的原理

对于方程：

()0f x =

设已知它的近似根，则函数()f x 在点k x 附近可用一阶：

()()()()k k k p x f x f x x x '=+-

来近似，因此方程()0f x =可以近似地表示为()0p x =，后者是一个线性方程，他的求根很容易的，本文去()0p x =的根作为()0f x =的新的近似根，记作1k x +，则有：

()()

1k k k k f x x x f x +=-' 这就是著名的牛顿公式，相应的迭代函数：

()()()

f x x x f x ?=-' 牛顿法师一种逐步迭代的线性化方法，这种方法的基本思想是将非线性方程()0f x =的根归结为计算一系线性方程()()()0k k k f x f x x x '+-=的根。

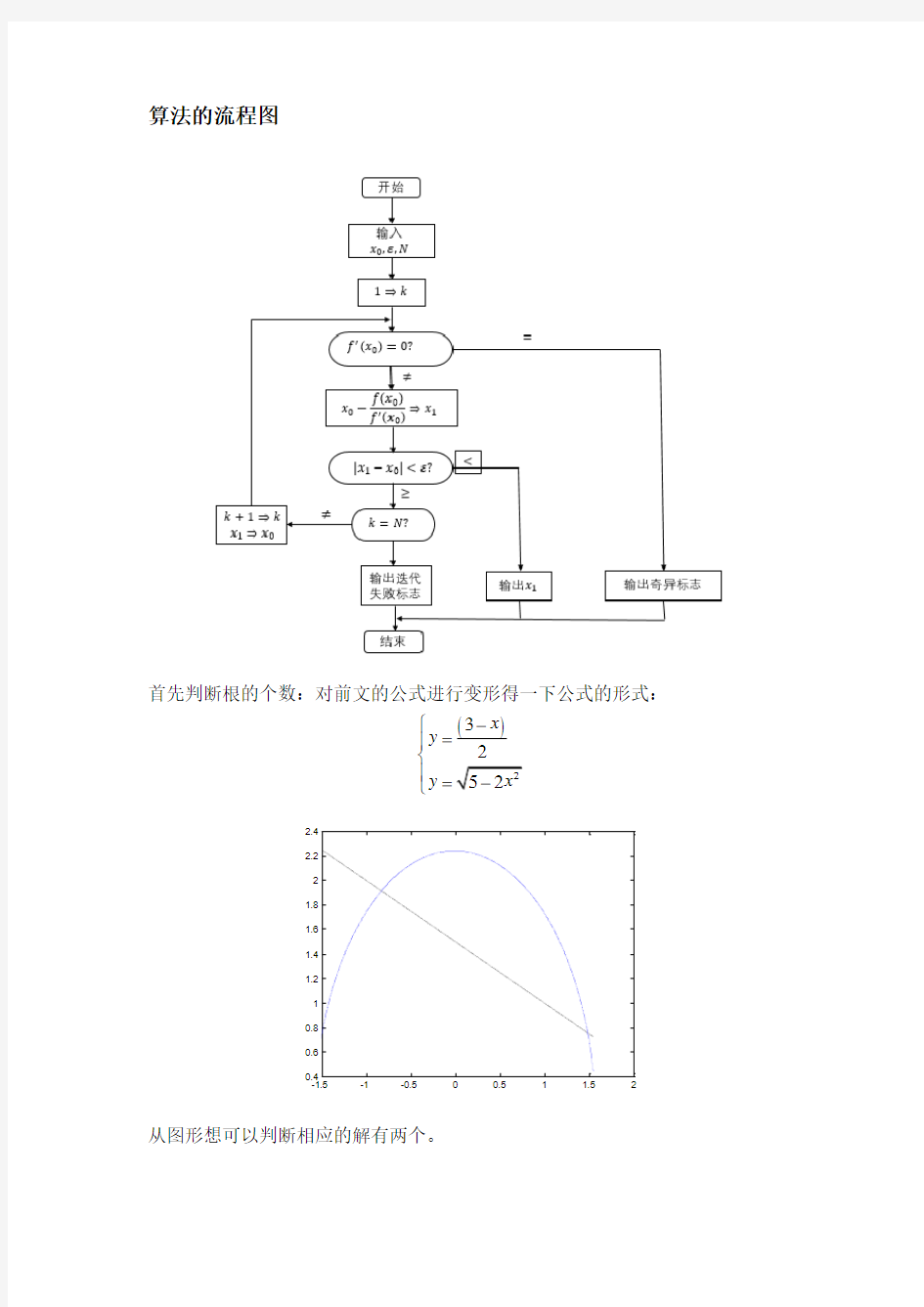
算法的流程图

首先判断根的个数：对前文的公式进行变形得一下公式的形式：

(

)32x y y ?-=???=?

从图形想可以判断相应的解有两个。

-1.5-1-0.500.51 1.52

牛顿法求解非线性方程组的基本程序如下：

计算出的相应的结果如下：

1 11.4880 0.7560

x y =

?

?

=

?

迭代次数10次

2 20.8214

1.9107

x y =

?

?

=

?

迭代次数9次算法改进：

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

用二 4224min ()f t t t t =--[,.]t ∈内的极小值点，要求准 1. function [t d]=erfenfa(a,b) k=1; %记录循环次数 while abs(a-b)>0.0005 c=(a+b)/2; C(k)=c; %存储每次循环中点c 的值 if ff(c)<0 a=c; end if ff(c)==0 t1=c; break ; end if ff(c)>0 b=c; end k=k+1; end t=(a+b)/2; %最终符合要求的值 d=f(t); %最优解 C k function y=f(t) y=t^4-2*t^2-4*t; function y=ff(t) y=4*t^3-4*t-4; 运行结果 >> [t d]=erfenfa(1,1.5) C = Columns 1 through 9 1.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252 Column 10 1.3247 k = 11

t = 1.3250 d = -5.7290 2.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3]，收敛精度0.5 function [t,f]=huangjinfenge(a,b) m=1-(sqrt(5)-1)/2; t2=a+m*(b-a) f2=g(t2); t1=a+b-t2 f1=g(t1); while abs(t1-t2)>0.5 if f1 [t,f]=huangjinfenge(0,3) t2 = 1.1459 t1 = 1.8541

二分法、简单迭代法的matlab代码实现

实验一非线性方程的数值解法(一) 信息与计算科学金融崔振威201002034031一、实验目的： 熟悉二分法和简单迭代法的算法实现。 二、实验内容： 教材P40 2.1.5 三、实验要求 1根据实验内容编写二分法和简单迭代法的算法实现 2简单比较分析两种算法的误差 3试构造不同的迭代格式，分析比较其收敛性 (一)、二分法程序： function ef=bisect(fx,xa,xb ,n, delta) % fx是由方程转化的关于x的函数，有fx=0。 % xa解区间上限 % xb解区间下限 % n最多循环步数，防止死循环。 %delta为允许误差 x=xa;fa=eval(fx); x=xb;fb=eval(fx); disp(' [ n xa xb xc fc ]'); for i=1: n xc=(xa+xb)/2;x=xc;fc=eval(fx); X=[i,xa,xb,xc,fc]; disp(X), if fc*fa<0 xb=xc; else xa=xc; end if (xb-xa)

k=0; while abs(x-xO)>eps & k> fplot('[x A5-3*x A3-2*x A2+2]',[-3,3]);grid 得下图： 由上图可得知：方程在［-3,3］区间有根。 （2 ）、二分法输出结果 >> f='xA5-3*xA3-2*xA2+2' f = X A5-3*X A3-2*X A2+2 >> bisect(f,-3,3,20,10A(-12)) 2.0000 - 3.0000 0 -1.5000 0.0313

matlab 二分法汇总

二分法的matlab主程序 function [k,x,wuca,yx]=erfen(a,b,abtol) a(1)=a; b(1)=b; ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0, disp('注意：ya*yb>0,请重新调整区间端点a和b.'), return end max1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是上取整for k=1: max1+1 a;ya=fun(a); b;yb=fun(b); x=(a+b)/2; yx=fun(x); wuca=abs(b-a)/2; k=k-1; [k,a,b,x,wuca,ya,yb,yx] if yx==0 a=x; b=x; elseif yb*yx>0 b=x;yb=yx; else a=x; ya=yx; end if b-a< abtol , return, end end k=max1; x; wuca; yx=fun(x);

区间二分法： 与对分查找法相同 1 区间二分法求出的仅仅是方程的一个单根，如果方程有重根或者多个根时，在做区间二分法时就会出现分叉，这样方程有几个根，就会产生几个实数序列，每一个实数序列的极限便是方程的一个根 2 通常用区间二分法为一些迭代法提供靠近x^*的初始选代值； 3 区间二分法的缺点是不能求方程的复数根。 format long a=5; b=6; x1=a; x2=b; f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2; step=0.000001; ii=0; while abs(x1-x2)>step ii=ii+1; x3=(x1+x2)/2; f3=4*cos(x3)+4*sin(x3)+0.5*x3-2; if f3~=0 if f1*f3<0 x2=x3; else x1=x3; end end end x3 f=[4*cos(x3)+4*sin(x3)+0.5*x3] disp(['迭代次数：',num2str(ii),'次']) 牛顿迭代法求解: 在方程f(x)=0有实数根的情况下，若能够将方程等价地转化成x=g(x)的形式，然后取一个初始值x0代入x=g(x)的右端，算得x1=g(x0)，再计算x2=g(x1)，这样依次类推 x(k+1)=g(x(k)) 可以得到一个序列xk，通常称g(x)为迭代函数，序列xk为由迭代函数产生得迭代序列，x0为迭代初始值。 同一个方程，不同等价形式的转换产生的迭代法可能收敛，也有可能发散．关于迭代法的敛散性判定有下面的定理(也称李普希兹（Lipschitz定理): 如果迭代函数g(x)在区间[a,b]上连续，且满足以下条件， 1 对于任意的x=[a,b]，有g(x)=[a,b]

matlab程序设计例题及答案

1.编写程序：计算1/3+2/5+3/7+……+10/21 法一： s=0; for i=1:10 s=s+i/(2*i+1); end s s = 4.4096 法二： sum((1:10)./(3:2:21)) ans = 4.4096 2.编写程序：计算1~100中即能被3整除，又能被7整除的所有数之和。 s=0; for i=1:100 if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end s s = 210 3.画出y=n！的图（1<=n<=10）,阶乘的函数自己编写，禁用MATLAB自带的阶乘函数。 x=1:10; for i=1:10 try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)

12345678910 0.511.522.533.54x 10 6 4.一个数恰好等于它的因子之和，这个数就称为完数。例如，6的因子为1，2,3，而6=1+2+3，因此6就是一个完数。编程找出2000以内的所有完数。 g=[]; for n=2:2000 s=0; for r=1:n-1 if mod(n,r)==0 s=s+r; end end if s==n g=[g n]; end end g g =6 28 496

5.编写一个函数，模拟numel函数的功能，函数中调用size函数。 function y=numelnumel(x) m=size(x); y=m(1)*m(2); numelnumel([1 2 3;4 5 6]) ans = 6 6. 编写一个函数，模拟length函数的功能，函数中调用size函数。 function y=lengthlength(x) m=size(x); y=max(m(1),m(2)); lengthlength([1 2 3;4 5 6]) ans = 3 7.求矩阵rand（5）的所有元素和及各行平均值，各列平均值。 s=rand(5); sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s) sum = 13.8469

二分法matlab程序

二分法基本思路 一般地，对于函数f(x),如果存在实数c,当x=c 时，若f(c)=0,那么把x=c 叫做函数f(x)的零点。 解方程即要求f(x)的所有零点。 假定f(x)在区间（x ，y ）上连续 先找到a 、b 属于区间（x ，y ），使f(a)，f(b)异号，说明在区间(a,b)内一定有零点，然后求f[(a+b)/2], 现在假设f(a)<0,f(b)>0,a=a ，从①开始继续使用 ② 中点函数值判断。 如果f[(a+b)/2]>0，则在区间(a,(a+b)/2)内有零点，(a+b)/2<=b ，从①开始继续使用 中点函数值判断。 这样就可以不断接近零点。 通过每次把f(x)的零点所在小区间收缩一半的方法，使区间的两个端点逐步迫近函数的零点，以求得零点的近似值，这种方法叫做二分法。 从以上可以看出，每次运算后，区间长度减少一半，是线形收敛。另外，二分法不能计算复根和重根。 二分法步骤 用二分法求方程()0f x =的根*x 的近似值k x 的步骤 ① 若对于a b <有()()0f a f b <，则在(,)a b 内()0f x =至少有一个根。 ② 取,a b 的中点12 a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根，停止计算， 运行后输出结果*1x x = 若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。取111,a a b x ==； 若1()()0f a f x >，则取111,a x b b ==；

二分法、简单迭代法的matlab代码实现教学文案

实验一非线性方程的数值解法（一）信息与计算科学金融崔振威201002034031 一、实验目的： 熟悉二分法和简单迭代法的算法实现。 二、实验内容： 教材P40 2.1.5 三、实验要求 1 根据实验内容编写二分法和简单迭代法的算法实现 2 简单比较分析两种算法的误差 3 试构造不同的迭代格式，分析比较其收敛性 (一)、二分法程序： function ef=bisect(fx,xa,xb,n,delta) % fx是由方程转化的关于x的函数，有fx=0。 % xa 解区间上限 % xb 解区间下限 % n 最多循环步数，防止死循环。 %delta 为允许误差 x=xa;fa=eval(fx); x=xb;fb=eval(fx); disp(' [ n xa xb xc fc ]'); for i=1:n xc=(xa+xb)/2;x=xc;fc=eval(fx); X=[i,xa,xb,xc,fc]; disp(X), if fc*fa<0 xb=xc; else xa=xc; end if (xb-xa)

k=0; while abs(x-x0)>eps & k> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图： 由上图可得知：方程在[-3,3]区间有根。 （2）、二分法输出结果 >> f='x^5-3*x^3-2*x^2+2' f = x^5-3*x^3-2*x^2+2 >> bisect(f,-3,3,20,10^(-12)) 2.0000 - 3.0000 0 -1.5000 0.0313

二分法、简单迭代法的matlab代码实现教学文案

二分法、简单迭代法的m a t l a b代码实现

实验一非线性方程的数值解法（一）信息与计算科学金融崔振威 201002034031 一、实验目的： 熟悉二分法和简单迭代法的算法实现。 二、实验内容： 教材P40 2.1.5 三、实验要求 1 根据实验内容编写二分法和简单迭代法的算法实现 2 简单比较分析两种算法的误差 3 试构造不同的迭代格式，分析比较其收敛性 (一)、二分法程序： function ef=bisect(fx,xa,xb,n,delta) % fx是由方程转化的关于x的函数，有fx=0。 % xa 解区间上限 % xb 解区间下限 % n 最多循环步数，防止死循环。 %delta 为允许误差 x=xa;fa=eval(fx); x=xb;fb=eval(fx); disp(' [ n xa xb xc fc ]'); for i=1:n xc=(xa+xb)/2;x=xc;fc=eval(fx); X=[i,xa,xb,xc,fc]; disp(X), if fc*fa<0 xb=xc; else xa=xc;

end if (xb-xa)eps & k> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图：

方程组的各种解法法的Matlab程序及运行结果

1．列主元高斯消去法 M文件 function[x]=gauss(a,b) n=length(a); x=zeros(n,1); a=[a b]; for k=1:n-1 max=k; for i=k+1:n if a(i,k)>a(max,k) max=i; end end temp=a(k,k:n+1); a(k,k:n+1)=a(max,k:n+1); a(max,k:n+1)=temp; for i=k+1:n a(i,k)=-a(i,k)/a(k,k); a(i,k+1:n+1)=a(i,k+1:n+1)+a(i,k)*a(k,k+1:n+1); end end x(n,1)=a(n,n+1)/a(n,n); for i=n-1:-1:1 sum=0; for j=i+1:n sum=sum+x(j,1)*a(i,j); end x(i,1)=(a(i,n+1)-sum)/a(i,i); end

Matlab运行结果

2．LU三角分解法 M文件 function y=LU(A,B); n=length(A); A=[A B]; for k=1:n-1; for i=k:n; if(abs(A(i,k))==max(abs(A(k:n,k)))) P(k)=i; temp=A(k,:); A(k,:)=A(i,:); A(i,:)=temp; end end for j=k+1:n; A(j,k)=A(j,k)/A(k,k); A(j,k+1:n+1)=A(j,k+1:n+1)-A(j,k)*A(k,k+1:n+1); end end P(n)=n; L(1,1)=1; L(2:n,1)=A(2:n,1); L(1,2:n)=0; U(1,1)=A(1,1); U(2:n,1)=0; U(1,2:n)=A(1,2:n); for i=2:n; L(i,1:i-1)=A(i,1:i-1); L(i,i)=1; L(i,i+1:n)=0; U(i,1:i-1)=0; U(i,i:n)=A(i,i:n); end x(n) = A(n,n+1)/U(n,n); for k = n-1:-1:1 x(k)=A(k,n+1); for p=n:-1:k+1;

二分法matlab程序

二分法 二分法基本思路 一般地，对于函数f(x),如果存在实数C,当x=c时，若f(c)=O,那么把x=c叫做函数f(x)的零点。解方程即要求f(x)的所有零点。 假定f(x)在区间(x，y)上连续 先找到a、b属于区间(x, y)，使f(a)，f(b)异号，说明在区间(a,b)内一定有零点，然后求 f[(a+b)/2], 现在假设f(a)O,a=a，从①开始继续使用 ②中点函数值判断。 如果f[(a+b)/2]>0，则在区间(a,(a+b)/2)内有零点，(a+b)/2<=b，从①开始继续使用中点函数值判断。 这样就可以不断接近零点。 通过每次把f(x)的零点所在小区间收缩一半的方法，使区间的两个端点逐步迫近函数的零 点，以求得零点的近似值，这种方法叫做二分法。 从以上可以看出，每次运算后，区间长度减少一半，是线形收敛。另外，二分法不能计算复根和重根。 二分法步骤 用二分法求方程f (x) 0的根x*的近似值x k的步骤 ①若对于a b有f(a)f(b) 0,则在(a,b)内f(x) 0至少有一个根。 a b ②取a,b的中点x i 计算f (x1) 2 ③若f(xj 0则&是f (x) 0的根，停止计算， , , * 运行后输出结果x x1 若f (a) f (x-i) 0则在(a,xj 内f(x) 0 至少有一个根。取a1a,b1 x1； 若f (a) f(x)) 0，则取a1 x1,b1 b ； 1 ④若一|b k a k ( 为预先给定的要求精度)退出计算，运行后输出结果 2 x* ak bk，反之，返回步骤1,重复步骤1,2,3 2 二分法Mtalab程序 syms x; fun=input('(输入函数形式)fx='); a=input('(输入二分法下限)a=');

matlab编的二分法求根的程序

matlab编的二分法求根的程序 2010-03-10 16:44 function varargout=erfliu(varargin) clear,clc F=inline('x^2-4*sin(x)');a=1;b=3; erff(F,a,b) function erff(F,a,b) tol=0.0000005; fprintf(' a f(a) b f(b)\n'); while((b-a)>tol) m=a+(b-a)/2; fprintf('%10.6f %10.6f %10.6f %10.6f\n',a,feval(F,a),b,feval(F,b)'); if feval(F,a)*feval(F,m)>=0 a=m; else b=m; end end 结果 a f(a) b f(b) 1.000000 - 2.365884 3.000000 8.435520 1.000000 - 2.365884 2.000000 0.362810 1.500000 -1.739980 2.000000 0.362810 1.750000 -0.873444 2.000000 0.362810 1.875000 -0.300718 2.000000 0.362810 1.875000 -0.300718 1.937500 0.019849 1.906250 -0.143255 1.937500 0.019849 1.921875 -0.062406 1.937500 0.019849 1.929688 -0.021454 1.937500 0.019849 1.933594 -0.000846 1.937500 0.019849 1.933594 -0.000846 1.935547 0.009491 1.933594 -0.000846 1.934570 0.004320 1.933594 -0.000846 1.934082 0.001736 1.933594 -0.000846 1.933838 0.000445 1.933716 -0.000201 1.933838 0.000445 1.933716 -0.000201 1.933777 0.000122 1.933746 -0.000039 1.933777 0.000122 1.933746 -0.000039 1.933762 0.000041 1.933746 -0.000039 1.933754 0.000001 1.933750 -0.000019 1.933754 0.000001 1.933752 -0.000009 1.933754 0.000001 1.933753 -0.000004 1.933754 0.000001

(完整word版)同济大学数值分析matlab编程题汇编

MATLAB 编程题库 1.下面的数据表近似地满足函数2 1cx b ax y ++=，请适当变换成为线性最小二乘问题，编程求最好的系数c b a ,,，并在同一个图上画出所有数据和函数图像. 625 .0718.0801.0823.0802 .0687 .0606 .0356 .0995.0628.0544.0008.0213.0362.0586.0931.0i i y x ---- 解： x=[-0.931 -0.586 -0.362 -0.213 0.008 0.544 0.628 0.995]'; y=[0.356 0.606 0.687 0.802 0.823 0.801 0.718 0.625]'; A=[x ones(8,1) -x.^2.*y]; z=A\y; a=z(1); b=z(2); c=z(3); xh=-1:0.1:1; yh=(a.*xh+b)./(1+c.*xh.^2); plot(x,y,'r+',xh,yh,'b*')

2.若在Matlab工作目录下已经有如下两个函数文件，写一个割线法程序，求出这两个函数 10 的近似根，并写出调用方式： 精度为10 解： >> edit gexianfa.m function [x iter]=gexianfa(f,x0,x1,tol) iter=0; while(norm(x1-x0)>tol) iter=iter+1; x=x1-feval(f,x1).*(x1-x0)./(feval(f,x1)-feval(f,x0)); x0=x1;x1=x; end >> edit f.m function v=f(x) v=x.*log(x)-1; >> edit g.m function z=g(y) z=y.^5+y-1; >> [x1 iter1]=gexianfa('f',1,3,1e-10) x1 = 1.7632 iter1 = 6 >> [x2 iter2]=gexianfa('g',0,1,1e-10) x2 = 0.7549 iter2 = 8

数值计算方法matlab程序

function [x0,k]=bisect1(fun1,a,b,ep) if nargin<4 ep=1e-5; end fa=feval(fun1,a); fb=feval(fun1,b); if fa*fb>0 x0=[fa,fb]; k=0; return; end k=1; while abs(b-a)/2>ep x=(a+b)/2; fx=feval(fun1,x); if fx*fa<0 b=x; fb=fx; else a=x; fa=fx; k=k+1; end end x0=(a+b)/2; >> fun1=inline('x^3-x-1'); >> [x0,k]=bisect1(fun1,1.3,1.4,1e-4) x0 = 1.3247 k = 7 >> 简单迭代法 function [x0,k]=iterate1(fun1,x0,ep,N) if nargin<4 N=500; end if nargin<3 ep=1e-5; end x=x0; x0=x+2*ep;

while abs(x-x0)>ep & k> fun1=inline('(x+1)^(1/3)'); >> [x0,k]=iterate1(fun1,1.5) x0 = 1.3247 k = 7 >> fun1=inline('x^3-1'); >> [x0,k]=iterate1(fun1,1.5) x0 = Inf k = 9 >> Steffesen加速迭代（简单迭代法的加速）function [x0,k]=steffesen1(fun1,x0,ep,N) if nargin<4 N=500; end if nargin<3 ep=1e-5; end x=x0; x0=x+2*ep; k=0; while abs(x-x0)>ep & k

MATLAB计算方法迭代法牛顿法二分法实验报告要点

姓名实验报告成绩 评语： 指导教师（签名） 年月日

说明：指导教师评分后，实验报告交院（系）办公室保存。 实验一 方程求根 一、 实验目的 用各种方法求任意实函数方程0)(=x f 在自变量区间[a ，b]上，或某一点附近的实根。并比较方法的优劣。 二、 实验原理 (1)、二分法 对方程0)(=x f 在[a ，b]内求根。将所给区间二分，在分点2a b x -= 判 断是否0)(=x f ；若是，则有根 2a b x -= 。否则，继续判断是否0)()(

（1）11x =0.09033 （2）5x =0.09052 （3）2x =0,09052 五、 实验内容 （1）、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根，要求误差不 超过 3 105.0-?。 （2）、取初值00=x ，用迭代公式=+1k x -0x )(') (k k x f x f ，求方程0210=-+x e x 的 近似根。要求误差不超过 3 105.0-?。 （3）、取初值00=x ，用牛顿迭代法求方程0210=-+x e x 的近似根。要求误 差不超过 3 105.0-?。 六、 实验步骤与实验程序 （1） 二分法 第一步：在MATLAB 7.0软件，建立一个实现二分法的MATLAB 函数文件agui_bisect.m 如下： function x=agui_bisect(fname,a,b,e) %fname 为函数名，a,b 为区间端点，e 为精度 fa=feval(fname,a); %把a 端点代入函数，求fa fb=feval(fname,b); %把b 端点代入函数，求fb if fa*fb>0 error('两端函数值为同号'); end %如果fa*fb>0，则输出两端函数值为同号 k=0 x=(a+b)/2 while(b-a)>(2*e) %循环条件的限制

3 MatLab练习题-程序设计

MatLab 练习题（3）-程序设计 班级：1班 学号：201410430124姓名：李远 注意:1、请按要求作题（即写出程序代码+结果）. 2、整理好格式，排版好，不留过多的空格。 3、讲程序设计时，暂时先完成1、5、6、9、11. 4、另外8题作为思考题，若做出，可以加分。 *1, 编辑函数文件hanshu.m,该函数是32()33f x x x x =--+，并用它来计算(0.34)f 、(3)f 、(6.87)f 、2(3)(2)(4)f f f -- 答案：(填写程序语句和结果) 函数文件: hanshu.m function f=hanshu(x) f=x^3-3*x^2-x+3; （1）程序： hanshu(0.34) hanshu(3) hanshu(6.87) hanshu(3)-hanshu(2)*[hanshu(-4)]^2 （2）结果： ans = 2.3525 ans = ans = 178.7820 ans = 33075 2，编程求一个四位数abca ，使2(51)abca c =+。 答案：(填写程序语句和结果) 程序： for a=1:9 for b=0:9 for c=0:9

if a*1000+b*100+c*10+a==(5*c+1)^2 x=a*1000+b*100+c*10+a end end end end x 结果： x = 1681 3利用二分法编程求方程 03323=+--x x x 在[0,3]内的根. 答案： (填写程序语句和结果) 程序： a=0; b=3; x=a:b; f =@(x)x^3-3*x^2-x+3; c=(a+b)./2; while abs(b-a)>1e-6 if f(c)*f(b)<0 a=c; else b=c; end c=(a+b)./2; x=c; end x 结果： x = 1.0000 *4, 利用二分法编程求方程 tan(x)-x-0.5=0 在[0,1.5]内的根. 答案：(填写程序语句和结果) a=0; b=1.5; x=a:b; f =@(x)tan(x)-x-0.5; c=(a+b)./2; while abs(b-a)>1e-6 if f(c)*f(b)<0 a=c; else

二分法Matlab程序

作业：用牛顿法或二分法求下面非线性方程组的根 ()()1222,230,250 f x y x y f x y x y =+-=???=+-=?? 问题背景 牛顿迭代法（Newton's method ）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method ），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。 牛顿法进行迭代的原理 对于方程： ()0f x = 设已知它的近似根，则函数()f x 在点k x 附近可用一阶： ()()()()k k k p x f x f x x x '=+- 来近似，因此方程()0f x =可以近似地表示为()0p x =，后者是一个线性方程，他的求根很容易的，本文去()0p x =的根作为()0f x =的新的近似根，记作1k x +，则有： ()() 1k k k k f x x x f x +=-' 这就是著名的牛顿公式，相应的迭代函数： ()()() f x x x f x ?=-' 牛顿法师一种逐步迭代的线性化方法，这种方法的基本思想是将非线性方程()0f x =的根归结为计算一系线性方程()()()0k k k f x f x x x '+-=的根。

0.618法和二分法的MATLAB程序及实验比较 最优化

最优化实验报告一 学号：1186320…姓名： 一、实验目的 1.能够对具体的问题用适合的最优化方法进行求解。 2.对同一个问题用不同的进行求解并比较优劣。 二、实验方法 利用MATLAB软件，用0.618法和二分法求解问题。 三、实验题目 书本p27 1.求解minf(x)=x^2-x-1. 初始区间为[-1,1]，区间精度为0.05. 2.求minf(x)=x^3-2x+1的近似解，初始搜索区间为[0,3],区间精度为0.15. 3.minf(x)=x^3-3*x+1,初始区间为[0,1],区间精度为0.10 4.minf(x)=x^4+2*x+4;初始区间为[0,2]，区间精度为0.05 5.minf(x)=3*x^4-4*x^3+12*x^2,初始区间为[-1,2],区间精度为0.02 四、解答 此外程序的运行时间与电脑的负载有一定的联系。在进行比较复杂的运算时，电脑空闲空间大，就能更快的输出结果。 五、实验程序 1. ①用0.618程序 function [s,phis,k,G,E]=golds(phi,a,b,delta,epsilon) t=(sqrt(5)-1)/2; h=b-a; phia=feval(phi,a); phib=feval(phi,b); p=a+(1-t)*h; q=a+t*h; phip=feval(phi,p); phiq=feval(phi,q); k=1; G(k,:)=[a, p, q, b]; while(abs(phib-phia)>epsilon)|(h>delta) if(phip

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

用二分法求解 4224min ()f t t t t =--115[,.]t ∈内的极小值点，要求准 1. function [t d]=erfenfa(a,b) k=1; %记录循环次数 while abs(a-b)>0.0005 c=(a+b)/2; C(k)=c; %存储每次循环中点c 的值 if ff(c)<0 a=c; end if ff(c)==0 t1=c; break ; end if ff(c)>0 b=c; end k=k+1; end t=(a+b)/2; %最终符合要求的值 d=f(t); %最优解 C k function y=f(t) y=t^4-2*t^2-4*t; function y=ff(t) y=4*t^3-4*t-4; 运行结果 >> [t d]=erfenfa(1,1.5) C = Columns 1 through 9 1.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252 Column 10 1.3247 k = 11

t = 1.3250 d = -5.7290 2.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3]，收敛精度0.5 function [t,f]=huangjinfenge(a,b) m=1-(sqrt(5)-1)/2; t2=a+m*(b-a) f2=g(t2); t1=a+b-t2 f1=g(t1); while abs(t1-t2)>0.5 if f1 [t,f]=huangjinfenge(0,3) t2 = 1.1459 t1 = 1.8541

【精品】浅析二分法及其Matlab和C程序实现

浅析二分法及其Matlab和C程序实现 第一部分：二分法浅析 用二分法求方程的近似解是紧跟在“函数的零点"之后的教学内容。从联系的角度看,前面一节，学生已经学习了方程的根与函数的零点之间存在着对立统一的关系，这一节则是介绍一种具体的方法来运用这一关系解决问题。 从整个教材来分析,这一部分的内容是在“函数的应用”这一大章节之下。新课程标准中强调函数的应用性，这里包括两个方面：一方面是函数在生活实践中的应用，函数建模等内容属于这个范畴;另一方面则是函数在数学自身范围内的应用，“二分法”即是其中的代表。 基于以上的分析,笔者给出了以下的一些教学建议,与读者朋友们分享。 一、为什么要用二分法 就通过试验缩小搜索区间来讲，试验点不一定取中点，取其他的点也可以，那么为什么取中点呢？ 下面以搜索区间为[0，1]的情况作讨论。 一种对所有搜索区间为[0，1］的方程f(x)=0都适用的方法，即对集合G={f（x)=0,f （x)连续,且f（0)·f（1)〈0｝中的所有方程都适用的方法.一个合理的假设是：G中

所有方程f（x）=0的根在[0，1]上均匀分布。设试验点是c，那么c将［0,1]分成[0，c]和[c,1]两部分,它们的长度分别是c和1—c.由假设，通过试验保留的搜索区间是[0，c］（即方程f（x)=0的根在[0，c]中）的概率是c,通过试验保留的搜索区间是［c，1]的概率是1-c.因此，通过一次试验保留的搜索区间的期望长度为c2+(1-c)2=2c2—2c+1=2（c—)2+,容易看出，当c=的时候，通过一次试验保留的搜索区间的期望长度最小。这就是取中点作为试验点的原因. 二、引入方法 方法1：已知商店里一件商品的利润y与它的价格x之间满足函数关系y=x2-4x+3，请画出这个函数的图像，并思考当价格为多少元的时候商店不盈也不亏。 方法2：创设问题情景：蹦极运动.设下落的时间t秒。人离开参照点“礁石尖端”的位移为S（S=0表示人在礁石点处，向下取负,向上取正），开始下落时，时间t=0，在t∈［4，6]时的变化如下表:

二分法matlab程序

二分法m a t l a b程序Prepared on 21 November 2021

二分法 二分法基本思路 一般地，对于函数f(x),如果存在实数c,当x=c 时，若f(c)=0,那么把x=c 叫做函数f(x)的零点。 解方程即要求f(x)的所有零点。 假定f(x)在区间（x ，y ）上连续 先找到a 、b 属于区间（x ，y ），使f(a)，f(b)异号，说明在区间(a,b)内一定有零点，然后求f[(a+b)/2], 现在假设f(a)<0,f(b)>0,a=a ，从①开始继续使用 ② 中点函数值判断。 如果f[(a+b)/2]>0，则在区间(a,(a+b)/2)内有零点，(a+b)/2<=b ，从①开始继续使用 中点函数值判断。 这样就可以不断接近零点。 通过每次把f(x)的零点所在小区间收缩一半的方法，使区间的两个端点逐步迫近函数的零点，以求得零点的近似值，这种方法叫做二分法。 从以上可以看出，每次运算后，区间长度减少一半，是线形收敛。另外，二分法不能计算复根和重根。 二分法步骤 用二分法求方程()0f x =的根*x 的近似值k x 的步骤 ① 若对于a b <有()()0f a f b <，则在(,)a b 内()0f x =至少有一个根。 ② 取,a b 的中点12 a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根，停止计算， 运行后输出结果*1x x = 若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。取111,a a b x ==； 若1()()0f a f x >，则取111,a x b b ==； ④ 若 12 k k b a ε-≤（ε为预先给定的要求精度）退出计算，运行后输出结果*2 k k a b x +≈，反之，返回步骤1，重复步骤1,2,3 二分法Mtalab 程序 syms x; fun=input('(输入函数形式)fx='); a=input('（输入二分法下限）a='); b=input('（输入二分法上限）b='); d=input('输入误差限 d=')%二分法求根

二分法matlab程序

分法 二分法基本思路 一般地，对于函数f(x),如果存在实数C,当x=c时，若f(c)=O那么把x=c叫做函数f(x)的零点。xx即要求f(x)的所有零点。 假定f(x)在区间(X, y)上连续 先找到a、b属于区间(x，y)，使f(a)，f(b)异号，说明在区间(a,b)内一定有零点，然后求f[(a+b)/2], 现在假设f(a)vO,f(b)>O,avb 如果f[(a+b)/2]=0，该点就是零点, 如果f[(a+b)/2]<0,则在区间((a+b)/2，b)内有零点, 续 (a+b)/2>=a,从①开始继使用 中点函数值判断。 如果f[(a+b)/2]>0，则在区间(a,(a+b)/2)内有零点, 续 (a+b)/2<=b,从①开始继使用中点函数值判断。 这样就可以不断接近零点。 通过每次把f(x)的零点所在小区间收缩一半的方法， 使区间的两个端点逐步迫近函数的零点，以求得零点的近似值，这种方法叫做二分法。 从以上可以看出，每次运算后，区间XX减少一半，是线形收敛。另外，二分法不能计算复根和重根。 二分法步骤 用二分法求方程的根的近似值的步骤 若对于有，则在内至少有一个根。 取的中点计算

若则是的根，停止计算, 运行后输出结果 若则在内至少有一个根。取; 若，则取; ④ 若（为预先给定的要求精度）退出计算，运行后输出结果，反之，返回步骤1,重复步骤1,2,3 二分法Mtalab程序 syms X； fun=input('(输入函数形式)fx='); a=input（'（输入二分法下限）a='）; b=input（'（输入二分法上限）b='）; d=input（'输入误差限d='）%二分法求根 %f=i nii ne(x八2-4*x+4); %修改需要求解的inline函数的函数体 f=inline（fun）;%修改需要求解的inline函数的函数体 e=b-a; k=0 ; while e>d c=(a+b)/2; if f(a)*f(c)<0 b=c;

相关主题