2007-2008春季高数A试题(A卷)解答
高数A2(A卷)

……………………………… 密 ……………………………… 封 ………………………………… 线 ………………………………安 徽 工 业 大 学 工 商 学 院 试 题 纸(一)2007 ~ 2008学年第二学期期末考试《 高等数学A2》试卷(A 卷)一、选择题(共4分×6)(将结果填入下表中: ) 1、函数),(y x f z =在),(y x 点有偏导数是它在该点连续的( ).(A)充分而非必要条件; (B )必要而非充分条件;(C)充分必要条件; (D )既非充分又非必要条件.2、设),2ln(),(xy x y x f += 则=)0,1(y f ( ).(A) 21-; (B)21; (C) 0; (D) 1.3、函数3121x cx y -=(c 为任意常数)是微分方程222x dxy d -=的( ).(A)解,但既非通解又非特解; (B)通解;(C)特解; (D)不是解.4、函数y x xy y x z 84222-+++-=的驻点是( ). (A )(-1,3); (B )(3,-1); (C )(3, 1); (D )(-1,-3).5、二阶线性非齐次方程xe x y y y )1(2-=+'-''的特解形式是( ).(A)x e b ax )(+; (B )xe bx ax )(2+; (C)xe bx ax )(23+; (D )xe bx ax )(3+.6、设级数∑∞=1)1(!3n nn nn 与级数∑∞=1)2(!2n nnnn , 则成立( ).(A)级数(1)、(2)均收敛; (B)级数(1)、(2)均发散.; (C)级数(1)收敛, 级数(2)发散; (D)级数(1)发散, 级数(2)收敛二、填空题(共4分×6)1、设),(v u f 有连续偏导数,且),(yxe ef z =, 则=dz __________________.2、级数∑∞=+1623n nnn 的和是__________.3、)(x f 在某区域内有连续导数, 若积分⎰+Ly dy x f xdx e ])([2与路径无关, 则.____________________)(=x f4、设一个二阶常系数线性齐次微分方程的特征方程有两个特征根,为-2和3,则此微分方程是________________________, 其通解为___________________________.5、设Ω是由光滑闭曲面∑围成的空间区域,其体积是V , 则沿∑内侧的曲面积分⎰⎰∑=-+-+-.______________)2()3()(dxdy y z dzdx x y dydz z x6、设平面上力j xy i y F 32+-=, 在力F 的作用下, 质点沿曲线L 运动, 则力F 所做的功用曲线积分表示为__________________________.三、解答题(共47分) 1、[5分]求曲面1232=+z xy 在点(1,-2,2)处的切平面与法线方程.2、[5分]计算积分: ⎰⎰ππydx xx dy sin 0.3、[5分]求微分方程满足初始条件的特解: ⎪⎩⎪⎨⎧==+1)0(y ey dx dy x .高数试卷A2(A 卷)(第1页)……………………………… 密……………………………… 封 ………………………………… 线 ………………………………安 徽 工 业 大 学 工 商 学 院 试 题 纸(二)4、[5分]用重积分算出半球体0,2222≥≤++z a z y x 的体积V .(用其它方法不给分)5、[5分]),(v u f 可微, 且32),(x x x f =, 422),(x x x x f u -=,求 ),(2x x f v .6、 [5分]设L 是圆周x y x 222=+的正向曲线,计算第二类曲线积分dy y xydx y x x I L⎰-+-=)()(3223. (注:163cossin204204πππ⎰⎰==xdx xdx )7、[6分]求幂级数∑∞=-1)3(n nnx 的收敛域(含端点讨论).8、[6分]求幂级数∑∞=-11n n nx 在(-1,1)上的和函数.9、[5分]设222),,(z y x z y x f ++= ,求函数在点M (1,1,0)沿方向)1,2,1(=l的方向导数lf ∂∂.四、[5分]计算二重积分:,)1ln(2dxdy y y x I D⎰⎰++=其中D 由x y 3-=,24x y -=,x = 1 所围成的闭区域.五、附加题 [6分]设微分分方程0)4(32='++''y ey y(1)若把x 看成未知函数,y 看成自变量,则方程化成什么形式; (2)求此方程的通解.高数试卷A2(A 卷)(第2页)。
2007-2008(2)高等数学试题(A卷)(90)

学院领导 审批并签名A 卷广州大学 2007-2008 学年第二学期考试卷课 程:高等数学(A 卷)(90 学时) 考 试 形 式: 闭卷 考试 题 次 一 二 三 四 五 六 七八总 分 分 数 301616121610100得 分 评卷人一.填空题(每空 2分,本大题满分 30分) 1.设 y z x = ,则 zx ¶ = ¶ ____________, z y ¶ = ¶ ____________.2.已知 (,) z f u v = 具有二阶连续偏导数,且 ,23 u xy v x y ==+ ,则zx ¶ = ¶ __________________, (,) uf u v y¶ ¢ = ¶ __________________. 3.曲线 23,, x t y t z t === 在点(1,1,1)处的切向量T = u r______________,切线方程为__________________________________.4.点M 的直角坐标(,,) x y z 与球面坐标(,,) r j q 的关系为x =_____________, sin sin y r j q = , cos z r j = . 在球面坐标下,体积元素dv =________________________.5.设L 为曲线弧 2 (01) y x x =££ ,则ds dx = ,14 Ly ds += ò________.学院 专业 班 级姓 名学号6.在区间(1,1) - 内,写出下列幂级数的和函数:(1) 22 1(1) n n x x -++-+= L L __________;(2) 3 21(1) 321nn x x x n + - -+++= + L L __________.7.已知级数 1n n a ¥= å 条件收敛,则幂级数 1nnn a x ¥= å 的收敛区间为_________. 8.微分方程 560 y y y ¢¢¢ -+= 的通解为y =________________________, 微分方程 562 x y y y e ¢¢¢ -+= 的通解为y =_________________________.二.解答下列各题(每小题 8 分,本大题满分 16 分) 1.写出函数 2 ln() z x y =- 的定义域,并求函数的全微分.2.已知 ) , ( y x f z = 是由方程 2sin z z x y += 确定的隐函数,求 x z ¶ ¶ 和 2 2 xz ¶ ¶ .三.解答下列各题(每小题 8分,本大题满分16 分)1.计算 (32) Dx y d s + òò ,其中D 是由两坐标轴及直线 2 x y += 所围成的闭区域.2.设L 为正向圆周 x y x 2 2 2 = + ,计算 ò + - Ldy xy dx yx x 2 2 ) ( .装订 线 内 不 要答题四.解答下列各题(每小题 6分,本大题满分12 分)1.判别级数å ¥=1223 cosnnnnp的收敛性.2.求幂级数1 (2) nn x n¥ = -å 的收敛域.五.解答下列各题(每小题 8分,本大题满分16 分) 1.求微分方程 ln dy yxy dx x= 的通解. 2.设可导函数 () f x 满足 0()cos 2()sin 1 xf x x f t tdt x +=+ ò ,求 () f x .装订 线 内 不 要答题六.(本大题满分 10分)设 (,) z f x y = 满足条件: 2 2 z y x x ¶ =-- ¶ , z y x y ¶ =- ¶ ,且 (0,0)1 f = .求 (,) f x y 的极值.。
2007-2008上学期高数I试A卷答案

暨 南 大 学 考 试 试 卷一、填空题(共5小题,每小题3分,共15分)1. 设)(x y y =是由方程0sin 21=+-y y x 所确定,则=dy dx ycos 22-. 2. 数列的极限⎪⎪⎭⎫⎝⎛++++++∞→n n n n n 12111lim = __1____________________. 3. 函数xxe y =的带有佩亚诺余项的三阶麦克劳林公式为).(21332x o x x x +++4. 函数xe x y ++=4)1(的凹区间为),(+∞-∞.5. 抛物线22y x x y ==和围成的面积为____1/3________________________.二、选择题(共5小题,每小题3分,共15分)1. 当时, 不为等价无穷小量的是 (D) (A) 22sin x x 和; (B)nx x n和11-+;(C) x x 和)1ln(+; (D) 2cos 1x x 和-.2.设]1,0[上0)(">x f ,则)1()0()0()1(),1('),0('f f f f f f --或几个数的大小顺序为(B)(A) );0()1()0(')1('f f f f ->> (B) );0(')0()1()1('f f f f >-> (C) );0(')1(')0()1(•f f f f >>- (D) ).0(')1()0()1('f f f f >-> 3. 以下函数有可去间断点的是 (B )(A) ⎩⎨⎧>-≤-=;0,3,0,1)(x x x x x f (B) ;39)(2--=x x x f(C) ⎪⎩⎪⎨⎧=≠=;0,0,0,1sin )(x x xx f (D) .|sin |)(x x x f = 4. 摆线⎩⎨⎧-=-=)cos 1(),sin (θθθa y a x 的一摆)20(πθ≤≤的长度为 (D)(A) a 2; (B) a 4; (C) a 6; (D) a 8.5. 函数],[)(b a x f 在区间上连续是],[)(b a x f 在可积的 (A) (A) 充分条件; (B) 必要条件;(D) 即不是充分条件也不是必要条件.三、计算题(共7小题,每小题7分,共49分)1. 求定积分⎰210arcsin xdx ;解: 原式⎰--=21022101|arcsin dx xx x x ----------------------------------4⎰--+=21022)1(112112x d x π----------------------------------5 2102112x -+=π--------------------------------------------6.12312-+=π----------------------------------------------7 2. 求极限3sin 1tan 1limx xx x +-+→;解: 原式)sin 1tan 1()sin 1(tan 1lim3x x x x x x ++++-+=→-------------------------------------------------230sin tan lim21x xx x -=→ )21~cos 1,~sin ,0(cos )cos 1(sin lim 21230x x x x x xx x x x -→-=→时当 --------5.4121lim 21320=⋅=→x x x x -----------------------------------------------------------------73. 设)(x y y =由参数方程⎪⎩⎪⎨⎧==te y t e x ttsin ,cos 所确定,求22dx y d ; 解:)sin (cos t t e dt dx t -=, )cos (sin t t e dtdyt +=,-------------------------------------2,s in c o s c o s s in t t t t dtdx dt dy dx dy -+==-------------------------------------------------------4dx dtt t t t dt d dx dy dx d dx y d ⋅-+==)sin cos cos sin ()(22------------------------------------------------6 )sin (cos 1)sin (cos )cos (sin )cos (sin 222t t e t t t t t t t -⋅-++-=.)s i n (c o s 23t t e t -=--------------------------------------------------------------------74. 求不定积分⎰+x x xdxcos sin cos ;解: 原式⎰+-++=dx x x x x x x cos sin )sin (cos )sin (cos 21-------------- -- ----------------------3⎰⎰+++=x x x x d dx cos sin )cos (sin 2121----------------------------------------------------5C x x x +++=|cos sin |ln 2121.---------------------------------------------------75. 求极限2020222)1(limxdte t x x tx ⎰-→+;解: 原式22222)1(limxdt e t ex t x x ⎰+=-→------------- ---------------------------------------222022)1(limx dt e t x t x ⎰+=→-----------------------------------------------------------4xxe x x x 22)1(lim 440⋅+=→------------------------------------------------------------61)1(lim 440=+=→x x e x .-------------------------------------------------------------76. 求过点)0,23(与曲线21xy =相切的直线方程; 解: 设切点为)1,(20x x , 32'xy -=, 所以切线方程为-----------------------------1 )(21032x x x x y --=-.-----------------------4因)0,23(过切线, 所以)23(210032x x x --=-.-----------------------6 解得.10=x 因此切线方程为 .032=-+x y --------------------------------------7 7. 讨论瑕积分⎰10q x dx(q >0)的收敛性,如果收敛则计算其值.解: 对任意)1,0(∈ε,⎪⎪⎩⎪⎪⎨⎧≠--=-=-==--⎰.1),1(1111,1,ln |ln 11111q q x q q x x dx q q q εεεεε------------------------------------------3因此⎪⎩⎪⎨⎧≥∞+<-=⎰+→.1,,1,11lim10q q q x dx qεε--------------------------------------------------------------------6即1≥q 发散,当1<q 时收敛,其值为q-11.----------------------------------------------------------7四、应用题(共2小题,每小题8分,共16分)h m, 底面半径为r m , 桶内盛满了某种液体. 试问要把桶内的液体全部吸出需要作多少功? 已知这种液体的密度为ρ.解: 建立如图所示的坐标. 在任一小区间 上的一薄液体的 O的重力为dx r g 2ρπ(KN)----------------------------------3这薄层液体吸出桶外所做的功(功元素)为 xdx r g dW 2ρπ=----------------------------5所求的功为 hh x r g xdx r g W 02202|21ρπρπ==⎰2221h r g ρπ=(KN).---------------------8 2. 要做一个容积为V 的圆柱形罐头筒, 怎样设计才能使所用的材料最省? 解: 设底面半径为r , 则高为2r Vπ,表面积为 .0,2222222>+=⋅+=r r Vr rV r r S ππππ------------------------------------3令022'2=-=rV r S π得3πV r =,--------------------------------------------------------------------------5 又0|)42(|'333>+===πππV r Vr r V S , 因此当3πV r =时S 取最--------------------------------------7 即当底面半径为3πV,高为3πV时所用的材料最少.--------------------------------------------------8五、证明题(共1小题,每小题5分,共5分)1. 设)(x f 在区间],[b a 上连续,且0)(>x f ,⎰⎰∈+=x bx ab a x t f dtdt t f x F ],[,)()()(. 证明: (1) 2)('≥x F ; (2) 方程0)(=x F 在),(b a 内有且仅有一个根.证明: (1) .2)(1)(2)(1)()('=⋅≥+=x f x f x f x f x F ---------------------------------------------2 (2) )(x F 在],[b a 上连续, 且]d ,[x x x +0)()()()()()()(<-===⋅⎰⎰⎰⎰b a b a baa bdt t f t f dt •dt t f t f dt x F b F a F ,因此由介值定理)(x F 在),(b a 至少有一根, ----------------------------------------------------------4 又0)('>x F , 所以)(x F 在],[b a 上单调增, 因此)(x F 在),(b a 是只有一根.----------------5。
2007年上海市春季高考数学试卷及解析

2007年上海市春季高考数学试卷一、填空题(本大题满分44分)本大题共有11题,只要求直接填写结果,每题填对得4分,否则一律得零分.1.(4分)计算=.2.(4分)若关于x的一元二次实系数方程x2+px+q=0有一个根为1+i(i是虚数单位),则q=.3.(4分)若关于x的不等式的解集为(﹣∞,﹣1)∪(4,+∞),则实数a=.4.(4分)函数y=(sinx+cosx)2的最小正周期是.5.(4分)设函数y=f(x)是奇函数.若f(﹣2)+f(﹣1)﹣3=f(1)+f(2)+3,则f(1)+f(2)=.6.(4分)在平面直角坐标系xoy中,若抛物线y2=4x上的点P到该抛物线的焦点的距离为6,则点P的横坐标x=.7.(4分)在平面直角坐标系xOy中,若曲线与直线x=m有且只有一个公共点,则实数m=.8.(4分)若向量,满足||=,||=1,•(+)=1,则向量,的夹角的大小为.9.(4分)若x1、x2为方程2x=的两个实数解,则x1+x2=.10.(4分)在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目.若选到男教师的概率为,则参加联欢会的教师共有人.11.(4分)函数的反函数是.二、选择题(本大题满分16分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分.12.(4分)若集合A={1,m2},B={2,4},则“m=2”是“A∩B={4}”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件13.(4分)如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若,且点P落在第Ⅲ部分,则实数a、b满足()A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<014.(4分)下列四个函数中,图象如图所示的只能是()A.y=x+lgx B.y=x﹣lgx C.y=﹣x+lgx D.y=﹣x﹣lgx15.(4分)设a、b是正实数,以下不等式:①>;②a>|a﹣b|﹣b;③a2+b2>4ab﹣3b2;④ab+>2恒成立的序号为()A.①③B.①④C.②③D.②④三、解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.16.(12分)如图,在棱长为2的正方体ABCD﹣A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小(结果用反三角函数值表示).17.(14分)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为,求侧棱长”;也可以是“若正四棱锥的体积为,求所有侧面面积之和的最小值”.试给出问题“在平面直角坐标系xoy中,求点P(2,1)到直线3x+4y=0的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.18.(14分)在直角坐标系中,设椭圆C:+=1(a>b>0)的左、右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(,1).(1)求椭圆C的方程;(2)设椭圆C的一个顶点为B(0,﹣b),直线BF2交椭圆C于另一点N,求△F1BN的面积.19.(14分)某人定制了一批地砖.每块地砖(如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.(1)求证:四边形EFGH是正方形;(2)E,F在什么位置时,定制这批地砖所需的材料费用最省?20.(18分)通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.(1)如图所示,在以O为圆心,半径为2的⊙O中,BC和BA是⊙O的弦,其中BC=2,∠ABC=45°,求弦AB的长;(2)在△ABC中,若∠C是钝角,求证:a2+b2<4R2;(3)给定三个正实数a、b、R,其中b≤a,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的△ABC不存在,存在一个或两个(全等的三角形算作同一个)?在△ABC存在的情况下,用a、b、R表示c.21.(18分)我们在下面的表格内填写数值:先将第1行的所有空格填上1;再把一个首项为1,公比为q的数列{a n}依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其它空格.第1列第2列第3列…第n列第1行111 (1)第2行q第3行q2……第n行q n﹣1(1)设第2行的数依次为B1,B2,…,B n,试用n,q表示B1+B2+…+B n的值;(2)设第3列的数依次为c1,c2,c3,…,c n,求证:对于任意非零实数q,c1+c3>2c2;(3)请在以下两个问题中选择一个进行研究(只能选择一个问题,如果都选,被认为选择了第一问).①能否找到q的值,使得(2)中的数列c1,c2,c3,…,c n的前m项c1,c2,…,c m(m≥3)成为等比数列?若能找到,m的值有多少个?若不能找到,说明理由.②能否找到q的值,使得填完表格后,除第1列外,还有不同的两列数的前三项各自依次成等比数列?并说明理由.2007年上海市春季高考数学试卷参考答案与试题解析一、填空题(本大题满分44分)本大题共有11题,只要求直接填写结果,每题填对得4分,否则一律得零分.1.(4分)(2007•上海)计算=.【分析】变形为,然后取极限即可得到结果.【解答】解:==,故答案为:.2.(4分)(2007•上海)若关于x的一元二次实系数方程x2+px+q=0有一个根为1+i(i是虚数单位),则q=2.【分析】根据实系数一元二次方程得虚根成对原理可知:1﹣i也是方程x2+px+q=0的一个根,再根据根与系数的关系即可得出.【解答】解:根据实系数一元二次方程得虚根成对原理可知:1﹣i也是方程x2+px+q=0的一个根,根据根与系数的关系可得(1+i)(1﹣i)=q,∴q=2.故答案为:2.3.(4分)(2007•上海)若关于x的不等式的解集为(﹣∞,﹣1)∪(4,+∞),则实数a=4.【分析】a不等式即(x+1)(x﹣a)>0,再再由它的解集为(﹣∞,﹣1)∪(4,+∞),可得﹣1和4是(x+1)(x﹣a)=0的两个实数根,由此可得a的值.【解答】解:关于x的不等式即(x+1)(x﹣a)>0.再由它的解集为(﹣∞,﹣1)∪(4,+∞),可得﹣1和4是(x+1)(x﹣a)=0的两个实数根,故a=4,故答案为4.4.(4分)(2007•上海)函数y=(sinx+cosx)2的最小正周期是π.【分析】利用同角三角函数的基本关系,二倍角公式可得函数y=1+sin2x,根据最小正周期等于求出结果.【解答】解:函数y=(sinx+cosx)2=1+2sinxcosx=1+sin2x,故它的最小正周期等于=π,故答案为:π.5.(4分)(2007•上海)设函数y=f(x)是奇函数.若f(﹣2)+f(﹣1)﹣3=f (1)+f(2)+3,则f(1)+f(2)=﹣3.【分析】先由函数y=f(x)是奇函数,求得f(﹣2)=﹣f(2),f(﹣1)=﹣f(1)代入f(﹣2)+f(﹣1)﹣3=f(1)+f(2)+3求解.【解答】解:∵函数y=f(x)是奇函数∴f(﹣2)=﹣f(2),f(﹣1)=﹣f(1)∴f(﹣2)+f(﹣1)﹣3=f(1)+f(2)+3可解得f(1)+f(2)=﹣3故答案为:﹣3.6.(4分)(2007•上海)在平面直角坐标系xoy中,若抛物线y2=4x上的点P到该抛物线的焦点的距离为6,则点P的横坐标x=5.【分析】由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,已知|PF|=6,则P到准线的距离也为6,即x+=6,将p的值代入,进而求出x.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+=6,∴x=5,故答案为:5.7.(4分)(2007•上海)在平面直角坐标系xOy中,若曲线与直线x=m 有且只有一个公共点,则实数m=2.【分析】由曲线方程可知:曲线为以原点O(0,0)为圆心,2为半径的半圆(y轴右侧),从而根据曲线与直线x=m有且只有一个公共点,可求实数m的值.【解答】解:由题意,曲线为以原点O(0,0)为圆心,2为半径的半圆(y轴右侧)与直线L:x=m(L∥y轴)有且只有一个公共点∴m=2故答案为28.(4分)(2007•上海)若向量,满足||=,||=1,•(+)=1,则向量,的夹角的大小为.【分析】先由已知条件求出•=﹣1,代入两个向量的夹角公式求出cosθ的值,结合θ的范围求出θ值.【解答】解:设,的夹角为θ.∵•(+)=1,∴+•=1,又∵||=,∴•=﹣1.∴cosθ===﹣.又∵0≤θ≤π,∴θ=.故答案为.9.(4分)(2007•上海)若x1、x2为方程2x=的两个实数解,则x1+x2=﹣1.【分析】先将方程两边化成同底的指数函数,根据函数的单调性建立等式关系,最后利用根与系数的关系求出两根的和.【解答】解:2x==根据指数函数的单调性可知x=设x1、x2为x=的两个根即x2+x﹣1=0的两个根x1、x2,根据根与系数的关系可知x1+x2=﹣1故答案为﹣110.(4分)(2007•上海)在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目.若选到男教师的概率为,则参加联欢会的教师共有120人.【分析】设出女教师的人数,用女教师人数表示出到会的总人数,根据从这些人中随机挑选一人表演节目,若选到女教师的概率为,列出方程,解出女教师人数,从而得到总人数.【解答】解:设男教师有x人,由题得=,∴x=54,∴2x+12=108+12=120.故答案为:120.11.(4分)(2007•上海)函数的反函数是.【分析】由原函数的分段解析式分别解出自变量x的解析式,再把x 和y交换位置,注明反函数的定义域(即原函数的值域),最后再写成分段函数的形式即可.【解答】解:∵y=x2+1(x≥0),∴x=,y≥1,故y=x2+1(x≥0)的反函数为y=(x≥1),同样地,y=(x<0)的反函数为y=(x<0),∴函数的反函数是.故答案为:.二、选择题(本大题满分16分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分.12.(4分)(2007•上海)若集合A={1,m2},B={2,4},则“m=2”是“A∩B={4}”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】当m=2时,可直接求A∩B;反之A∩B={4}时,可求m,再根据必要条件、充分条件与充要条件的定义进行判断即可.【解答】解:若m=2,则A={1,4},B={2,4},A∩B={4},“m=2”是“A∩B={4}”的充分条件;若A∩B={4},则m2=4,m=±2,所以“m=2”不是“A∩B={4}”的必要条件.则“m=2”是“A∩B={4}”的充分不必要条件.故选A.13.(4分)(2007•上海)如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若,且点P落在第Ⅲ部分,则实数a、b满足()A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0【分析】根据所给的图形知,点P落在第Ⅲ部分,则根据实数与向量的积的定义及平行四边形法则知a与方向相同,b与方向相反,得到a与b 的符号.【解答】解:∵=a+b,由于点P落在第Ⅲ部分,则根据实数与向量的积的定义及平行四边形法则知a与方向相同,b与方向相反,∴a>0,b<0.故选:B.14.(4分)(2007•上海)下列四个函数中,图象如图所示的只能是()A.y=x+lgx B.y=x﹣lgx C.y=﹣x+lgx D.y=﹣x﹣lgx【分析】先求出所给函数的导数,再结合导数的符号,判断函数的单调性,然后利用函数的单调性进行判定,可得正确选项.【解答】解:在y=x+lgx中,>0,∴y=x+lgx是(0,+∞)上单调递增函数,∴A不成立;在y=x﹣lgx中,,当0<x<lge时,<0,当x>lge 时,>0.∴y=x﹣lgx的增区间是(lge,+∞),减区间是(0,lge),∴B成立;在y=﹣x+lgx中,.当0<x<lge时,>0,当x >lge时,<0.∴y=﹣x+lgx的减区间是(lge,+∞),增区间是(0,lge),∴C不成立;在y=﹣x﹣lgx中,<0,∴y=﹣x﹣lgx是(0,+∞)上单调递减函数,∴D不成立.故选B.15.(4分)(2007•上海)设a、b是正实数,以下不等式:①>;②a>|a﹣b|﹣b;③a2+b2>4ab﹣3b2;④ab+>2恒成立的序号为()A.①③B.①④C.②③D.②④【分析】由a,b为正实数,对于①①利用基本不等式变形分析取值特点即可;对于②利用含绝对值不等式的性质即可加以判断;对于③取出反例数值即可;对于④利用均值不等式进行条件下的等价变形即可.【解答】解:∵a、b是正实数,∴①a+b≥2⇒1≥⇒≥.当且仅当a=b时取等号,∴①不恒成立;②a+b>|a﹣b|⇒a>|a﹣b|﹣b恒成立;③a2+b2﹣4ab+3b2=(a﹣2b)2≥0,当a=2b时,取等号,例如:a=2,b=1时,左边=5,右边=4×1×2﹣3×22=﹣4∴③不恒成立;④ab+≥2=2>2恒成立.答案:D三、解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.16.(12分)(2007•上海)如图,在棱长为2的正方体ABCD﹣A'B'C'D'中,E,F 分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小(结果用反三角函数值表示).【分析】(法一)如图建立空间直角坐标系,把要求的角转化为向量的夹角,用坐标运算求解;(法二):连接EB,可证A'FBE是平行四边形,可得异面直线A'F与CE所成的角就是CE与EB所成的角,在Rt△CEB中,可得,由反正切可得所求的角.【解答】解:(法一)如图建立空间直角坐标系.…(2分)由题意可知A′(2,0,2),C(0,2,0),E(2,1,2),F(2,1,0).∴.…(6分)设直线A′F与CE所成角为θ,则.…(10分)∴,即异面直线A'F与CE所成角的大小为.…(12分)(法二):连接EB,…(2分)∵A'E∥BF,且A'E=BF,∴A'FBE是平行四边形,则A'F∥EB,∴异面直线A'F与CE所成的角就是CE与EB所成的角.…(6分)由CB⊥平面ABB'A',得CB⊥BE.在Rt△CEB中,,则,…(10分)∴.∴异面直线A'F与CE所成角的大小为.…(12分)17.(14分)(2007•上海)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为,求侧棱长”;也可以是“若正四棱锥的体积为,求所有侧面面积之和的最小值”.试给出问题“在平面直角坐标系xoy中,求点P(2,1)到直线3x+4y=0的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.【分析】利用逆向”问题的意义可以是:(1)求到直线3x+4y=0的距离为2的点的轨迹方程.或者(2)若点P(2,1)到直线l:ax+by=0的距离为2,求直线l的方程.利用点到直线的距离公式即可得出.【解答】解:点(2,1)到直线3x+4y=0的距离为.“逆向”问题可以是:(1)求到直线3x+4y=0的距离为2的点的轨迹方程.设所求轨迹上任意一点为P(x,y),则,所求轨迹为3x+4y﹣10=0或3x+4y+10=0.(2)若点P(2,1)到直线l:ax+by=0的距离为2,求直线l的方程.由,化简得4ab﹣3b2=0,b=0或4a=3b,所以,直线l的方程为x=0或3x+4y=0.18.(14分)(2007•上海)在直角坐标系中,设椭圆C:+=1(a>b>0)的左、右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(,1).(1)求椭圆C的方程;(2)设椭圆C的一个顶点为B(0,﹣b),直线BF2交椭圆C于另一点N,求△F1BN的面积.【分析】(1)由已知易得c值与线段MF2的长度,在直角三角形MF1F2中勾股定理求出a即可写出椭圆C的标准方程.(2)此题可转化为求以线段为底边的两个三角形的和问题,一个三角形的高为b,另一个为|y n|.故只须求y n即可.【解答】解:(1)由椭圆定义可知|MF1|+|MF2|=2a.由题意|MF2|=1,∴|MF1|=2a﹣1.又由Rt△MF1F2可知,a>0,∴a=2,又a2﹣b2=2,得b2=2.∴椭圆C的方程为.(2)直线BF2的方程为.由得点N的纵坐标为.又,∴.19.(14分)(2007•上海)某人定制了一批地砖.每块地砖(如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.(1)求证:四边形EFGH是正方形;(2)E,F在什么位置时,定制这批地砖所需的材料费用最省?【分析】(1)图2是由四块图1所示地砖组成,由图1依次逆时针旋转90°,180°,270°后得到,由此能够证明四边形EFGH是正方形.(2)设CE=x,则BE=0.4﹣x,每块地砖的费用为W,求出W的表达式,借助二次函数的性质能求出E,F在什么位置时,做这批地砖所需的材料费用最省.【解答】解:(1)证明:图2是由四块图1所示地砖组成,由图1依次逆时针旋转90°,180°,270°后得到,∴EF=FG=GH=HE.又CE=CF,∴△CEF为等腰直角三角形.∴四边形EFGH是正方形.(2)设CE=x,则BE=0.4﹣x,每块地砖的费用为W,制成△CEF、△ABE和四边形AEFD三种材料的每平方米价格依次为3a,2a,a(元),则=a(x2﹣0.2x+0.24)=a[(x﹣0.1)2+0.23](0<x<0.4)由a>0,当x=0.1时,W有最小值,即总费用最省.当CE=CF=0.1米时最省.20.(18分)(2007•上海)通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.(1)如图所示,在以O为圆心,半径为2的⊙O中,BC和BA是⊙O的弦,其中BC=2,∠ABC=45°,求弦AB的长;(2)在△ABC中,若∠C是钝角,求证:a2+b2<4R2;(3)给定三个正实数a、b、R,其中b≤a,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的△ABC不存在,存在一个或两个(全等的三角形算作同一个)?在△ABC存在的情况下,用a、b、R表示c.【分析】(1)由正弦定理知===2R,根据题目中所给的条件,不难得出弦AB的长;(2)若∠C是钝角,故其余弦值小于0,由余弦定理得到a2+b2<c2<(2R)2,即可证得结果;(3)根据图形进行分类讨论判断三角形的形状与两边a,b的关系,以及与直径的大小的比较,分成三类讨论即可.【解答】解:(1)在△ABC中,BC=2,∠ABC=45°===2R⇒b=2 sinA=∵A为锐角∴A=30°,B=45°∴C=105°∴AB=2Rsin75°=4sin105°=;(2)∠C为钝角,∴cosC<0,且cosC≠1cosC=<0∴a2+b2<c2<(2R)2即a2+b2<4R2(8分)(3)a>2R或a=b=2R时,△ABC不存在当时,A=90,△ABC存在且只有一个∴c=当时,∠A=∠B且都是锐角sinA=sinB=时,△ABC存在且只有一个∴c=2RsinC=2Rsin2AC=当时,∠B总是锐角,∠A可以是钝角,可是锐角∴△ABC存在两个∠A<90°时,c=∠A>90°时,c=21.(18分)(2007•上海)我们在下面的表格内填写数值:先将第1行的所有空格填上1;再把一个首项为1,公比为q的数列{a n}依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其它空格.第1列第2列第3列…第n列第1行111 (1)第2行q第3行q2……第n行q n﹣1(1)设第2行的数依次为B1,B2,…,B n,试用n,q表示B1+B2+…+B n的值;(2)设第3列的数依次为c1,c2,c3,…,c n,求证:对于任意非零实数q,c1+c3>2c2;(3)请在以下两个问题中选择一个进行研究(只能选择一个问题,如果都选,被认为选择了第一问).①能否找到q的值,使得(2)中的数列c1,c2,c3,…,c n的前m项c1,c2,…,c m(m≥3)成为等比数列?若能找到,m的值有多少个?若不能找到,说明理由.②能否找到q的值,使得填完表格后,除第1列外,还有不同的两列数的前三项各自依次成等比数列?并说明理由.【分析】(1)根据题意分别求出B1、B2,利用归纳法求出B n,再由分组求和法求出和式的值;(2)根据题意分别求出c1,c2,c3,再进行作差:c1+c3﹣2c2,化简后判断出符号,即得证;(3)①先设c1,c2,c3成等比数列求出公比q,再去检验是否为q,求出m和q;②设x1,x2,x3和y1,y2,y3分别为第k+1列和第m+1列的前三项,有条件分别求出各项,再求出对应的公比,再由k≠m进行判断.【解答】解:(1)由题意得,B1=q,B2=1+q,B3=1+(1+q)=2+q,…,B n=(n﹣1)+q,∴B1+B2+…+B n=1+2+…+(n﹣1)+nq=.(2)由题意得,c1=1,c2=1+(1+q)=2+q,,由,即c1+c3>2c2.(3)①先设c1,c2,c3成等比数列,由得,3+2q+q2=(2+q)2,.此时c1=1,,∴c1,c2,c3是一个公比为的等比数列.如果m≥4,c1,c2,…,c m为等比数列,那么c1,c2,c3一定是等比数列.由上所述,此时,,,由于,因此,对于任意m≥4,c1,c2,…,c m一定不是等比数列.综上所述,当且仅当m=3且时,数列c1,c2,…,c m是等比数列.②设x1,x2,x3和y1,y2,y3分别为第k+1列和第m+1列的前三项,1≤k<m≤n ﹣1,则,若第k+1列的前三项x1,x2,x3是等比数列,则由,得,,,同理,若第m+1列的前三项y1,y2,y3是等比数列,则.当k≠m时,.所以,无论怎样的q,都不能同时找到两列数(除第1列外),使它们的前三项都成等比数列.。
0708高等数学A(一)答案

高等数学(一)、(二)(上)试题(A )评分标准与分工一、 填空题(每小题4分, 共24分)1.e . 2. =a -1. 3.)4ln 2,2(+ .4.0 . 5. x e x C C y )(21+=). 6.21=ξ注:该题评分原则是 非对即错二、选择题 (每小题4分, 共20分) D C BB C 三、(5分)解: 30sin tan sin limx x x x -→30tan sin lim xxx x -=→ x x x x x sin cos 1cos lim 30-=→22021lim xx x -=→21-= -------------------------------- 5分注:该题评分原则 体现方法3分、结果正确2分;主要有以下几种方法 1)洛必达法则、2)等价无穷小替换、3)其他 四、(8分)解: 212)111(22tt t tdtdxdt dy dx dt dt dy dx dy =++-==⋅=; ------------- 4分t t dt dx t dt d dx dy dx d dx y d 412222+=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=……. ------------- 4分 五、(8分)1)⎰-+x x e e dx ⎰+=xxede 21-------------------------------- 4分 C e x+=arctan -------------------------------- 4分2). 解: ⎰⎰⎰⎰+=+=ππππ002200222]2cos [2122cos 1cos xdx x dx x dx x x xdx x ………2分 (第一个积分1分;第二个积分3分)⎰⎰⎰-==ππππ22122122122sin 0|2sin 2sin 2cos xdx x x x d x xdx x ………3分=⎰⎰=-=ππππ0022121212cos 0|2cos 2cos xdx x x x xd4361ππ+=∴原式 ……………………………………3分 注:本题主要考察学生对分部积分的内容的掌握情况。
07-08高等数学试题(A)解答

广州大学2007-2008学年第一学期考试卷高等数学A 卷(90学时)参考解答一.填空题(每小题3分,本大题满分15分)1.设{1,01()1,12x f x x ≤≤=-<≤, 则(3)f x +的定义域为]1,3[--.2.设1s i n ,0(),01s i n ,x x x f x a x x b x x ⎧<⎪⎪==⎨⎪⎪+>⎩, 当a =1, b =1时, ()f x 在0x =处连续.3.曲线22sin y x x =+上横坐标为0x =处的法线方程为12y x=-.4.设()f x 可导, 2()y f x =, 则y '=)(22x f x '.5.曲线xy xe -=在区间)2,(-∞内是凸的, 拐点为)2,2(2e.二.选择题 (每小题3分, 本大题满分15分)1. 函数lnsin y x =在区间5[,]66ππ上满足罗尔定理的ξ=( C ).A. 0;B. 6π;C. 2π; D. 56π.2. 当0x →时, 123(1)1ax +-与cos 1x -是等价无穷小, 则a =( C ). A. 1; B.23; C. 32-; D. 0.3. 若()f x 在x a =处可导, 则0()()lim x f a x f a x x→+--=( B ).A. ()f a ';B. 2()f a ';C. 0;D. (2)f a '.4. 曲线1siny x x=有一条( A ). A. 水平渐近线1y =; B. 水平渐近线0y =; C. 铅直渐近线1x =; D. 铅直渐近线0x =. 5. 若2()f x dx x C =+⎰,则2()xf x dx -=⎰ ( B ).A. 412x C +;B. 412x C -+; C. 4x C +; D. 4x C -+.三.解答下列各题(每小题6分,本大题满分12分) 1.设22tan (12)y x =+,求d y . 解 ])1[t a n ()1t a n (222'+⋅+='x x y 。
华东交大历年高数上册期末试题及答案07-08高数上试卷及答案
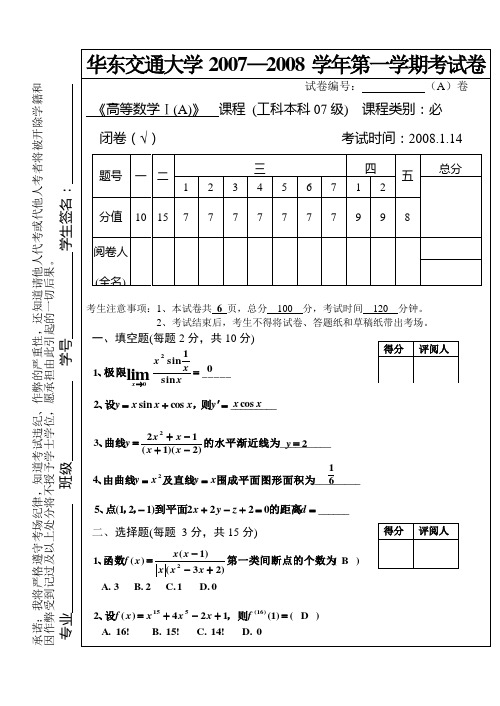
3x y x 3y
2
2
dy y dx
3x y x 3y
2
2
2
dx
2பைடு நூலகம்
或两边取微分得: 3 x dx ydx xdy 3 y dy 0
dy 3x y x 3y
2 2
dx
4、 求曲线 y x ln x的凹凸区间及拐点
2
得分
评阅人
1 y 2 x ln x x 2 2 x ln x x x y 2 ln x 2 x
( x 1) ln( x 1) 1 ( x 2 1)d ln( x 1) 2 2
2
( x 1) ln( x 1) 1 ( x 1)dx 2 2
2
( x 1) ln( x 1) x 2 x C 2 4 2
2
6、 求定积分
2 2 0
令y 0得: xe
3 2
1 1 2 ln x 3 x
3 2
3
当0 x e 时y 0, 当x e 2 时y 0 故凹区间为 [ e 2, ) 凸区间为 (0, e
3
3
3 2
]
3 )
拐点为 (e 2,
2e 3
5、 求 不 定 积 分 x ln( x 1)dx
2 xe
x2
2 xe 6x
x2
x2
lim
x 0
e
x2
e 3
2 3
2、 当x 0时 , 无 穷 小 1 x 1 x与x是 否 为 等价无穷小 ? 说明理由 .
山东省春季高考数学试题2008年真题(附答案)

学校______________班级______________专业______________考试号______________姓名______________山东省春季高考数学试题2008年真题第Ⅰ卷1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮.、选择题.已知全集U={a,b,c,d},集合M={a,c},则UM等于(A) {a,b}(B) {a,d}(C) {b,d}(D) {b,c}.设a,b ∈R,则“a>0且b>0”是“a b>0”的(A) 充分条件(B) 必要条件(C) 充要条件(D) 既不充分也不必要条件.函数f (x)=12-| x |的定义域是(A) (-2,2) (B) (-∞,-2)∪ (2,+∞)(C) [-2,2] (D) (-∞,-2]∪ [2,+∞).设x>1,a=log0.5(x2+1),b=log0.5(x+1),c=log0.5(2 x),则下列关系正确的是(A) 3a>3b>3c(B) 3b>3c>3a(C) 3c>3a>3b(D) 3a>c>3b.在等差数列{a n}中,若a2+a5=19,a7=20,则该数列前9项的和是(A) 26 (B) 100 (C) 126 (D) 155.已知平行四边形ABCD(如图),若→AC=→a,→BD=→b,则→CD 可以表示为(A) →a-→b→→(C)12→a-12→b.下列平面直角坐标系中给出的四个图形,可作为函数y=f (x) 图象的图形共有(A) 1个(B) 2个(C) 3个 (D) 4个8.若直线l 经过两条直线2 x+y+1=0和3 x-y+4=0的交点,且与直线2 x-y+1=0垂直,则直线l 的方程是(A) x+2 y+1=0 (B) x+2 y-1=0 (C) 2 x+y-3=0 (D) 2 x+y+3=09.用0,1,2,3可以组成没有重复数字的三位数的个数是(A) 9 (B) 12 (C) 18 (D) 2410.设M,N 表示集合,x 表示元素.下列命题错误的是(A) 若x ∈M ∩ N,则x ∈M 且x ∈N(B) 若x ∈M∪N,则x ∈M 或x ∈N(C) 若M ⊆N,则M ∩ N=M 且M ∪N=N(D) 若M ∩ N=∅,则M=∅或N=∅11.在△ABC 中,若a=3,b=4,且a2+b2=c2+a b,则△ABC 的面积是(B) 6 3 (C) 3 (D) 612.若圆x2+y2+a x-2=0的圆心是(1,0),则该圆的半径是(A) 2 (C)22(D)3213.某中等职业学校现有学生会干部9名,其中男生5名,女生4名.学校要从这9名同学中任选42名的概率是(A)521(C)563(D)106314.二项式(x2-12 x)9的展开式中第3项是(A) -212x9(B) 212x9 (C) -9 x12 (D) 9 x1215.函数y=A sin(ω x+ϕ)(其中(A) y=2sin(x4+π4)(B) y=2sin(x4-π4)(D) y=2sin(π4x-π4)16.曲线y=x2+1在点P(2,5)处的切线的斜率是(A) 2 (B) 4(C) 8 (D) 16学校______________班级______________专业______________考试号______________姓名______________.某工厂为了节约水资源,不断进行技术创新,从而使得用水量逐月减少.如果该工厂今年4 000 m 3,计划从二月份起,每个月的用水量比上个月都减少12%,则预计(A ) 1 439 m 3(B ) 1 635 m 3(C ) 1 971 m 3(D ) 2 134 m 3.某射击运动员射击1次,击中目标的概率是0.6.若他连续射击2次,且各次射击是否击中 (A ) 0.06 (B ) 0.14(C ) 0.24 (D ) 0.48.若 α,β 表示平面,m ,n 表示直线,P 表示点,则下列命题错误的是 (A ) α ∩ β=n ,m ⊂ β,m // α ⇒ m // n(B ) m ⊂ β,n ⊂ β,m ∩ n =P ,m // α,n // α ⇒ β // α (C ) m ⊥ α,m ⊂ β ⇒ β ⊥ α (D ) m ⊥ α,m ⊥ n ⇒ n // α.M 是抛物线 y 2=a x 上的任一点,若点 M 到焦点和到 y 轴的距离之差是1,则 a 的值 (A ) 2 (B ) ±2(C ) 4 (D ) ±4第Ⅱ卷1.答卷前将密封线内的项目填写清楚.2.用钢笔或圆珠笔直接答在试卷上,解答题和应用题应写出推理、演算步骤. 3.本试题允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.(本大题共4小题,每题3分,共12分.请将答案填在答题卡相应题号的横线上).若 sin α=-35,且 α 是第三象限角,则 cos (α+π3 ).已知三点 A (1,-2),B (-1,m ),C (4,1)在同一条直线上,则实数 m .函数 y =2 x 3-6 x 2+3在区间 [-2,4] .已知椭圆 x 2a 2+y 2b 2=1(a >b >0)的两个焦点分别是 F 1(-3,0),F 2(3,0),过点 F 2 且垂x 轴的直线与椭圆交于 P ,Q 两点,∠PF 1Q =60︒三、解答题(本大题共4小题,共28分.请在答题卡相应的题号处写出解答过程)25.已知一元二次函数 f (x )=a x 2+b x +c 的图象在 y 轴上的截距是1,对任意实数 x ,都有 f (x )=f (2-x )成立,且 f (2)=f (-2)+8.求函数 f (x ) 的解析式.(6分)解:因为函数的图象在 y 轴上的截距是1,所以 c =1. ①因为 f (x )=f (2-x ),所以函数 f (x ) 的对称轴为 x =1,即 -b2 a =1. ②因为 f (2)=f (-2)+8,所以 4 a +2 b +c =4 a -2 b +c +8. ③ 由②,③解得 a =-1, b =2,所以函数 f (x ) 的解析式为 f (x )=-x 2+2 x +1.26.已知 f (x )=→a ·→b ,其中→a =(1+sin 2x ,cos 2x ),→b =(m ,-1),x ∈ R ,且函数 y =f (x ) 的图象经过点( π4,2).(1) 求实数 m 的值;(2) 求函数 y =f (x ) 的最大值及此时 x 的取值集合.(7分)解:(1) f (x )=→a ·→b =(1+sin 2x ,cos 2x )·(m ,-1) =m (1+sin 2x )-cos 2x =m +m sin 2x -cos 2x .因为函数 y =f (x )的图象经过点( π4,2),即 f ( π4 )=2,所以 m +m sin π2-cos π2=2,解得 m =1.(2) 因为 m =1,所以 f (x )=1+sin 2x -cos 2x =1+2sin (2 x -π4),所以当 sin (2 x -π4)=1时,函数 y =f (x ) 取得最大值,因此,函数 y =f (x ) 的最大值是1+2.因为 sin (2 x -π4)=1,所以 2 x -π4=π2+2 k π,k ∈ Z ,解得 x =3 π8+k π,k ∈ Z .因此,使函数 y =f (x ) 取最大值时 x 的取值集合是{ x | x =3π8+k π,k ∈ Z }.学校______________班级______________专业______________考试号______________姓名______________.如图,四边形 ABCD 是矩形,SA ⊥ 平面 ABCD , =1,SA =AD =2,E ,F 分别是 SB ,SD 的中点. 求证:EF ∥ 平面 ABCD ;求直线 EF 和直线 SC 的夹角的余弦值.(7分)(1) 证明:连结 BD .在△SBD 中,因为 E ,F分别是 SB ,SD 的中点,所以 EF // BD , 又因为 EF ⊄ 平面 ABCD ,BD ⊂ 平面 ABCD , 所以 EF ∥平面 ABCD .(2) 解:以顶点 A 为坐标原点,建立如图所示的空间直角坐标系 O -x y z . 则E (12 ,0,1),F (0,1,1),S (0,0,2),C (1,2,0),于是 →EF =(0,1,1)-(12,0,1)=(-12,1,0),→SC =(1,2,0)-(0,0,2)=(1,2,-2),所以 →EF ·→SC =(-12,1,0)·(1,2,-2)=-12+2=32 ,|→EF |=52,| →SC |=3,所以 cos<→EF ,→SC >=→EF ·→SC | →EF |·| →SC | =325 2 ×3=55 .因此直线 EF 和直线 SC 的夹角的余弦值是55. 28.如图,双曲线 x 2a 2-y 2b 2=1(a >0,b >0),两个焦点分别是 F 1,F 2,离心率 e =3,且焦点到渐近线的距离是2. (1) 求实数 a ,b 的值;(2) 若平行于向量 →v =(1,2)的直线 l 与 该双曲线相交于 A ,B 两点,且 OA ⊥ OB (O 是坐标原点). 求直线 l 的方程.(8分)解:(1) 设 F 1(-c ,0),F 2(c ,0),其中 c >0.因为 e =3,所以 ca =3. ①双曲线的渐近线方程为 y =±ba x ,即 b x ±a y =0.因为双曲线的焦点到每条渐近线的距离都相等, 所以 F 2(c ,0)到渐近线 b x -a y =0的距离是2, 即b cb 2+(-a )2=2. ②又知 a 2+b 2=c 2. ③解由联立①,②,③所组成的方程组, 得到 a =1,b =2.(2) 因为 a =1,b =2,所以双曲线的方程是 x 2-y 22=1.因为直线 l 的方向向量 →v =(1,2),所以直线 l 的斜率 k =2,因此可设直线 l 的方程为 y =2 x +n .设直线 l 与双曲线的两个交点分别为 A (x 1,y 1),B (x 2,y 2), 则 →OA =(x 1,y 1),→OB =(x 2,y 2).学校______________班级______________专业______________考试号______________姓名______________联立直线 l 与双曲线的方程得 ⎪⎩⎪⎨⎧+==-n x y y x 21222 , 消去 y ,并整理得到 2 x 2+4 n x +n 2+2=0. 则 x 1+x 2=-2 n ,x 1·x 2=n 2+22,因为直线 l 与双曲线有两个交点,所以 (4 n )2-4×2×(n 2+2)>0,解得 n 的取值范围是 { n | n <- 2 或 n > 2 }.因为 OA ⊥ OB ,所以 →OA ·→OB =0,从而 (x 1,y 1)·(x 2,y 2)=0, 即 x 1 x 2+y 1 y 2=0,亦即 x 1 x 2+(2 x 1+n ) (2 x 2+n )=0, 整理得 5 x 1 x 2+2 n ( x 1+x 2)+n 2=0. 将 x 1+x 2=-2 n ,x 1·x 2=n 2+22 代入上式,得到 5×n 2+22+2 n ×(-2 n )=0,解得 n =10 或 n =-10 ,又因为 10 ∈{ n | n <- 2 或 n > 2 },-10 ∈{ n | n <- 2 或 n > 2 }, 所以直线 l 的方程是 y =2 x +10 或 y =2 x -10 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 证明
∑
n =1
∞
n = 1. ( n + 1)!
解: (1) 设 s ( x ) =
d ⎛ ex −1 ⎞ ⎜ ⎟ ,由于 dx ⎝ x ⎠
xn ∑ − 1 ∞ x n−1 e x − 1 n=0 n ! = =∑ x x n =1 n !
∞
( − ∞ < x < +∞ )
因此,
d ⎛ e x − 1 ⎞ d ⎡ ∞ x n −1 ⎤ s ( x) = ⎜ ⎟ = ⎢∑ ⎥ dx ⎝ x ⎠ dx ⎣ n =1 n ! ⎦
=∑ n − 1 n−2 ∞ n x =∑ x n −1 n=2 n ! n =1 ( n + 1) !
∞
(2)
又
s ( x) =
d ⎛ ex −1 ⎞ x ex − ex + 1 ⎜ ⎟= dx ⎝ x ⎠ x2
所以, 当 x = 1 时,
x ex − ex + 1 ∞ n =∑ x n −1 2 x n =1 ( n + 1) !
要使切平面与三个坐标面所围体积最小,只需 最小,其中 x0 , y0 , z0 满足 z0 = 4 − x0 2 − y0 2 . 构造拉格朗日函数 F ( x, y, z , λ ) =
1 3 (8 − z ) + λ ( x2 + y 2 + z − 4) xy
求解方程组
1 3 ⎧ ′ ⎪ Fx = − x 2 y ( 8 − z ) + 2λ x = 0 ⎪ 1 3 ⎪ ′ F = − 8 − z ) + 2λ y = 0 y 2 ( ⎪ xy ⎨ ⎪ 3 2 ⎪ Fz′ = − ( 8 − z ) + λ = 0 xy ⎪ ⎪ 2 2 ⎩ Fλ ′ = x + y + z − 4 = 0
∫ (1 + xe )dx + (x
2y L
2
e 2 y − 1 dy =
)
∫ (1 + x )dx
4
0
= −12
七、(11 分)求解线性微分方程 y′′ − y = sin 2 x 的通解. 解: 特征方程为: r 2 − 1 = 0 ,有根 r1 = −1, r2 = 1 ,
故对应齐次方程的通解为 Y = C1 e x + C2 e − x . 因为 f ( x ) = sin x =
∂x ∂y ∂z ⋅ ⋅ = ∂y ∂z ∂x
【
A
】.
A. -1;
B. 1;
C. 2;
D. -2.
2.设曲面 Σ 是介于两平面 z
= 0 与 z = 1 之间的圆柱面 x 2 + y 2 = 1 ,则曲面积分
】.
∫∫ x
Σ
2
dS 的值是【 D + y2 + z2
A.
π
2
∞
;
B.
2π ;
C.
2;
D.
π2
得 x = y = 1, z = 2
因驻点唯一,实际问题存在最小值,因此点 (1, 1, 2 ) 为所求的点。最小值为
V=
1 1 3 ⋅ (8 − 2 ) = 9 . 24 1 ⋅1
九 、 (5 分 ) 证 明
∫∫∫ f ( z ) dxdydz =π ∫
Ω
1 −1
f ( u ) (1 − u 2 ) du , 其 中 f ( x ) 为 连 续 函 数 , Ω 为
1 0
1
1
ρ2
f ( ρ cos θ , ρ sin θ , z ) ρ dz ;
C.
1 0
dx ∫
1− x 2 0
dy ∫
x2 + y 2 0
f ( x, y, z ) dz ;
D.
∫
dx ∫
1− x 2 0
dy ∫
1 x2 + y 2
f ( x, y, z ) dz .
二、填空题(满分 15 分,每小题 3 分,共 5 道小题),请将答案填在横线上. 1. 设二元函数 z = e
∂2 z . ∂x∂y
解
∂z ∂2 z ∂ y y ′′ − 2 f 22 ′′ = f 21 ′′ − 2 f 22 ′′ = f 2′ , = ( f 2′) = f12 ∂y ∂x∂y ∂x x x
x dydz + y dzdx + z dxdy (x + y + z )
2 2 2 3
四、(11 分) 计算曲面积分 I = w ∫∫
2
(
)
(
)
L
象限沿逆时针方向的半圆弧.
解:
P( x, y ) = 1 + xe 2 y , Q( x, y ) = x 2e 2 y − 1
3
由
∂Q ∂P = 2 xe 2 y = 可知该曲线积分与路径无关. ∂x ∂y
因此我们可取直线 y = 0 上从 x = 4 到 x = 0 这一段直线段,得
( − ∞ < x < +∞ )
s (1) = 1 = ∑
n , n =1 ( n + 1) !
∞
所以,
∑ ( n + 1)! = 1
n =1
∞
n
六、(11 分) 计算曲线积分 1 dy ,其中 L 为 ( x − 2 ) + y 2 = 4 在第一
2
1 − cos 2 x 2
故令 y * = A + B cos 2 x + C sin 2 x
代入原方程比较系数得, A = −
1 1 , B= , C=0 2 10
于是
y* = −
1 1 + cos 2 x 2 10
故原方程得通解为
1 1 y = Y + y * = C1 e x + C2 e − x − + cos 2 x 2 10
B
】.
5. 设区域 Ω 是 z = x 2 + y 2 与 z = 1 所围区域在第一卦限的部分, 则三重积分 ∫∫∫ f ( x, y, z )dv 不
Ω
等于【
C
】.
1
A.
∫ ∫
1 0
dz ∫
z 0
dx ∫
z − x2 0
f ( x , y , z ) dy ;
B.
∫
π
2 0
dθ ∫ dρ ∫
0
2
.
3. 若级数
∑u
n =1 ∞ n =1
n
收敛,则下列级数发散的是【
∞
B
】.
∞ ∞
A.
∑ 2u
n
;
B.
∑ (u
n =1
n
+ 2) ;
C.
2 + ∑ un ;
n =1
D.
∑u
n=k
n
.
4. 设微分方程 y = xy ′ + f ( y ′) ,则函数 y = cx + f (c ) (其中 c 为任意常数)是【 A. C. 该方程的特解; 无法确定; B. D. 该方程的通解; 该方程的解.
∞
5. 设幂级数 ∑ an x n 的收敛半径为 3,则幂级数 ∑ nan ( x − 1)
n =0
n =1
n +1
的收敛区间为
( − 2, 4 ) .
∂z y , 三、(10 分) 设 z = x f ( x, ) 且 f 具有二阶连续偏导数,求 ∂x x
y ∂z = f + x f1′− f 2′ ∂x x
−2 x0 ( x − x0 ) − 2 y0 ( y − y0 ) − ( z − z0 ) = 0 ⇒ 2 x0 x + 2 y0 y + z = 8 − z0
4
切平面在三个坐标轴上的截距分别为
8 − z0 8 − z0 , , 8 − z0 2 x0 2 y0 1 1 3 V= ⋅ ⋅ ( 8 − z0 ) 6 4 x0 y0
中国农业大学 2007 ~2008 学年春季学期 高等数学A课程考试试题(A卷) 2008/06/27 解答及评分标准
一、单项选择题(满分 15 分,每小题 3 分,共 5 道小题), 请将合适选项填在括号内. 1. 1.设二元函数 x = x( y, z ), y = y ( x, z ), z = z ( x, y ) 是由方程 F ( x, y, z ) = 0 所定义的隐函数,则
x2 + y 2 + z 2 ≤ 1 .
证 在 Ω 中有 −1 ≤ z ≤ 1 ,用截面法
1 −1
∫∫∫ f ( z ) dxdydz =∫
Ω
dz ∫∫ f ( z )dxdy = ∫
Dz
1 −1
f ( z ) π (1 − z 2 ) dz
=π∫
1 −1
f ( u ) (1 − u 2 ) du
5
Σ
,其中曲面∑为球面 x 2 + y 2 + z 2 = 4
的外侧. 解 I=
1 x dydz + y dzdx + z dxdy ∫∫ 8w Σ
2
由高斯公式有 I =
1 3 dv (其中 Ω 是由∑围成的立体) 8 ∫∫∫ Ω
= 4π .
五、(11 分) (1) 把
d ⎛ ex −1 ⎞ ⎟ 展开为 x 的幂级数; ⎜ dx ⎝ x ⎠
{1, 0, 3} .
x 3. 若某个三阶常系数线性齐次微分方程的通解为 y = C1 + C 2 x + C 3e ,其中 C1 , C 2 , C3 为
