2020年九年级数学上册期末测试卷及答案人教版

合集下载

人教版九年级数学上册期末测试题及答案【2020精】

第一学期九年级期末考试数学试题一、选择题（每小题3分，共42分）1．计算a7•（1a）2的结果是（）A．a B．a5 C．a6 D．a82．要使分式15--x有意义，则x的取值范围是（）A、x≠1B、x＞1C、x＜1D、x≠1-3．下列手机屏幕解锁图案中不是轴对称图形的是（）A． B． C． D．4.根据下列已知条件，能唯一画出△ABC的是( )A．AB=2，BC=4，AC=7 B．AB=5，BC=3，∠A=30°C．∠A=60°，∠B=45°，AC=4 D．∠C=90°，AB=65．下列各式2ba-，xx3+，πy+5，baba-+，)(1yxm-中，是分式的共有（）A.1个B.2个C.3个D.4个6．若（x+3）（x-4）=x2+px+q，那么p、q的值是（）A．p=1，q=－12 B．p=－1，q=－12C．p=7，q=12 D．p=7，q=－127．下列能判定△ABC为等腰三角形的是（）A．AB=AC=3，BC=6 B．∠A=40º、∠B=70ºC．AB=3、BC=8，周长为16 D．∠A=40º、∠B=50º8．若一个多边形的每一个外角都是45°，则这个多边形是（）A．六边形 B．八边形 C．九边形 D．十边形9．如图，AB∥CD，BC∥AD，AB=CD，BE=DF，图中全等的三角形的对数是A．1B.2C.3D.410．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠2=55°，则∠1的度数为（）A．65° B．25° C．35° D．45°11．已知2y10y m++是完全平方式，则m的值是（）A．25± B．25 C．5 D．5±12．如图，若∠A=27°，∠B=50°，∠C=38°，则∠BFE等于（）A．65° B．115° C．105° D．75°AB CDE F13．若分式方程22x x +=+x m 无解，则m 的值为（） A ．2 B ．0 C ．1 D ．—2 14．若1002=m ，753=n 则n m , 的大小关系为（）A ．n m >B ．n m <C ．n m =D ．无法确定二、填空题（本大题满16分，每小题4分）15．计算：111x x x -=-- . 16．一个矩形的面积为222)46(cm b a ab +，一边长为2ab cm ，则它的周长为 cm .17．等腰三角形一个顶角和一个底角之和是︒100，则顶角等于 .18.下列图形中对称轴最多的是 .三、解答题（本大题满分62分）19.计算：（每题5分，共10分）（1）()()()ab b a ab 53322-⋅-⋅ （2）[])2()()(22xy y x y x ÷--+20 把下列多项式分解因式：（每题5分，共10分）（1）4x 2y 2－4 （2）221218pm pm p -+．21.（10分）如图，已知△ABC 的三个顶点的坐标分别为A （﹣2，3）、B （﹣6，0）、C （﹣1，0）．（1）将△ABC 沿y 轴翻折，，画出翻折后的△A 1B 1C 1，点A 的对应点A 1的坐标是．(2) △ABC 关于x 轴对称的图形△A 2B 2C 2，直接写出点A 2的坐标．（3）若△DBC 与△ABC 全等（点D 与点A 重合除外），请直接写出满足条件点D 的坐标．22.（10分）如图，△ABC 中，AB =AC ，AD ⊥BC ，CE ⊥AB ，AE =CE ．线段圆长方形正方形求证：（1）△AEF≌△CEB；（2）AF=2CD．23 （10分）．有两块面积相同的试验田，分别收获蔬菜900kg和1500kg，已知第一块试验田每亩收获蔬菜比第二块少300kg，求第一块试验田每亩收获蔬菜多少千克？24．（12分）（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为．（2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？（3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，则根据（2）的结论E、F之间的距离是多少？并说明理由．选择题BADCC BDBCC AADB15 -116 3b+2a17 20°18 圆19、计算：（每题5分，共10分）（1）解：原式=)5()(3942ab b a b a -⋅-⋅（3分）=8125b a （3分）（2）解：原式=xy xy 24÷ （3分）=2 （3分）20（1） 4（xy+1）（xy-1）（2） ()223p m -21、（1）∵AD ⊥BC ，CE ⊥AB ∴∠AEF=∠CEB=90° 即∠AFE+∠EAF=∠CFD+∠ECB=90° 又∵∠AEF=∠CFD ∴∠EAF=∠ECB在△AEF 和△CEB 中，∠AEF=∠CEB ，AE=CE ，∠EAF=∠ECB∴△AEF ≌△CEB （6分）（2）由△AEF ≌△CEB 得：AF=BC 在△ABC 中，AB=AC ，AD ⊥BC∴CD=BD ，BC=2CD∴AF=2CD. （4分）22 （1）画图 3分 A1（2,3）（2分）（2）（-2，-3）（2分）（3）（-5,3）（-5，-3）（-2，-3）（3分）23 解：设第一块试验田每亩收获蔬菜x 千克，由题意得：（1分） 9001500300x x =+，（4分）解得：x=450，（2分）经检验：x=450是原分式方程的解，（2分）答：第一块试验田每亩收获蔬菜450千克．（1分）24 （1）EF=BE+DF ；（2分）（2）EF=BE+DF 仍然成立．（1分）证明：如图2，延长FD 到G ，使DG=BE ，连接AG ， ∵∠B+∠ADC=180°，∠ADC+∠ADG=180°， ∴∠B=∠ADG ，在△ABE 和△ADG 中，， ∴△ABE ≌△ADG （SAS ），（2分） ∴AE=AG ，∠BAE=∠DAG ，∵∠EAF=∠BAD ， ∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD ﹣∠EAF=∠EAF ， ∴∠EAF=∠GAF ，在△AEF 和△GAF 中，， ∴△AEF ≌△GAF （SAS ），（2分）∴EF=FG ， ∵FG=DG+DF=BE+DF ，∴EF=BE+DF ；（1分）（3）E 、F 之间的距离是583米。

2020 年新人教版九年级上期末考试数学试题含答案解析

2020-2021学年北京市朝阳区九年级(上)期末数学试卷一、选择题(本题共30分，每小题3分)第1-10题均有四个选项，符合题意的选项只有一个.1．二次函数y=(x﹣1)2﹣3的最小值是()A．2 B．1 C．﹣2 D．﹣32．下列事件中，是必然事件的是()A．明天太阳从东方升起B．射击运动员射击一次，命中靶心C．随意翻到一本书的某页，这页的页码是奇数D．经过有交通信号灯的路口，遇到红灯3．一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是()A．B．C．D．4．如图，在△ABC中，DE∥BC，DE分别交AB，AC于点D，E，若AD:DB=1:2，则△ADE与△ABC的面积之比是()A．1:3 B．1:4 C．1:9 D．1:165．已知点A(1，a)与点B(3，b)都在反比例函数y=﹣的图象上，则a与b之间的关系是()A．a＞b B．a＜b C．a≥b D．a=b6．已知圆锥的底面半径为2cm，母线长为3cm，则它的侧面展开图的面积为() A．18πcm2B．12πcm2C．6πcm2D．3πcm27．已知蓄电池的电压为定值，使用蓄电池时，电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为()A．B．C．D．8．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为5，AC=8．则cosB的值是()A．B．C．D．9．《九章算术》是我国古代内容极为丰富的数学名著，书中有这样一个问题:“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是:“如图，今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形能容纳的圆形(内切圆)直径是多少？”此问题中，该内切圆的直径是()A．5步 B．6步 C．8步 D．10步10．已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示，下面有四个推断:①二次函数y1有最大值②二次函数y1的图象关于直线x=﹣1对称③当x=﹣2时，二次函数y1的值大于0④过动点P(m，0)且垂直于x轴的直线与y1，y2的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜﹣3或m＞﹣1．其中正确的是()A．①③B．①④C．②③D．②④二、填空题(本题共18分，每小题3分)11．将二次函数y=x2﹣2x﹣5化为y=a(x﹣h)2+k的形式为y=．12．抛物线y=x2﹣2x+m与x轴有两个公共点，请写出一个符合条件的表达式为．13．如图，若点P在反比例函数y=﹣(x＜0)的图象上，过点P作PM⊥x轴于点M，PN⊥y轴于点N，则矩形PMON的面积为．14．某农科所在相同条件下做某种作物种子发芽率的试验，结果如表所示:种子个数n10001500250040008000150002020030000发芽种子个数m8991365224536447272136801816027300发芽种子频率0.8990.9100.8980.9110.9090.9120.9080.910则该作物种子发芽的概率约为．15．如图，△ABC中，D、E分别是AB、AC边上一点，连接DE．请你添加一个条件，使△ADE∽△ABC，则你添加的这一个条件可以是(写出一个即可)．16．阅读下面材料:①作线段AB的垂直平分线m；②作线段BC的垂直平分线n，与直线m交于点O；③以点O为圆心，OA为半径作△ABC的外接圆；④在弧ACB上取一点P，连结AP，BP．所以∠APB=∠ACB．老师说:“小明的作法正确．”请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是；(2)∠APB=∠ACB的依据是．三、解答题(本题共72分，第17-26题每小题5分，第27题7分，第28题7分，第29题8分)17．(5分)计算:2sin45°+tan60°+2cos30°﹣．18．(5分)如图，△ABC中，点D在边AB上，满足∠ACD=∠ABC，若AC=，AD=1，求DB的长．19．(5分)已知二次函数y=ax2+bx+c(a≠0)中，函数y与自变量x的部分对应值如表:x…﹣2﹣102…y…﹣3﹣4﹣35…(1)求二次函数的表达式，并写出这个二次函数图象的顶点坐标；(2)求出该函数图象与x轴的交点坐标．20205分)如图，在平面直角坐标系xOy中，△ABC的三个顶点分别为A(2，6)，B(4，2)，C(6，2)．(1)以原点O为位似中心，将△ABC缩小为原来的，得到△DEF．请在第一象限内，画出△DEF．(2)在(1)的条件下，点A的对应点D的坐标为，点B的对应点E的坐标为．21．(5分)如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分．如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，CD=10，EM=25．求⊙O的半径．22．(5分)如图，在Rt△ABC中，∠C=90°，点D是BC边的中点，CD=2，tanB=．(1)求AD和AB的长；(2)求sin∠BAD的值．23．(5分)已知一次函数y=﹣2x+1的图象与y轴交于点A，点B(﹣1，n)是该函数图象与反比例函数y=(k≠0)图象在第二象限内的交点．(1)求点B的坐标及k的值；(2)试在x轴上确定点C，使AC=AB，直接写出点C的坐标．24．(5分)如图，用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD，墙长28m．设AB长为x m，矩形的面积为y m2．(1)写出y与x的函数关系式；(2)当AB长为多少米时，所围成的花圃面积最大？最大值是多少？(3)当花圃的面积为150m2时，AB长为多少米？25．(5分)如图，AB是⊙O的直径，C，D是⊙O上两点，且=，过点C的直线CF⊥AD于点F，交AB的延长线于点E，连接AC．(1)求证:EF是⊙O的切线；(2)连接FO，若sinE=，⊙O的半径为r，请写出求线段FO长的思路．26．(5分)某“数学兴趣小组”根据学习函数的经验，对函数y=﹣x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整:(1)自变量x的取值范围是全体实数，x与y的几组对应数值如表:x…﹣3﹣﹣2﹣10123…y…﹣2﹣m2121﹣﹣2…其中m=；(2)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(3)根据函数图象，写出:①该函数的一条性质；②直线y=kx+b经过点(﹣1，2)，若关于x的方程﹣x2+2|x|+1=kx+b有4个互不相等的实数根，则b的取值范围是．27．(7分)在平面直角坐标系xOy中，直线y=﹣x+n经过点A(﹣4，2)，分别与x，y轴交于点B，C，抛物线y=x2﹣2mx+m2﹣n的顶点为D．(1)求点B，C的坐标；(2)①直接写出抛物线顶点D的坐标(用含m的式子表示)；②若抛物线y=x2﹣2mx+m2﹣n与线段BC有公共点，求m的取值范围．28．(7分)在Rt△ABC中，∠ACB=90°，O为AB边上的一点，且tanB=，点D为AC边上的动点(不与点A，C重合)，将线段OD绕点O顺时针旋转90°，交BC于点E．(1)如图1，若O为AB边中点，D为AC边中点，则的值为；(2)若O为AB边中点，D不是AC边的中点，①请根据题意将图2补全；②小军通过观察、实验，提出猜想:点D在AC边上运动的过程中，(1)中的值不变．小军把这个猜想与同学们进行交流，通过讨论，形成了求的值的几种想法:想法1:过点O作OF⊥AB交BC于点F，要求的值，需证明△OEF∽△ODA．想法2:分别取AC，BC的中点H，G，连接OH，OG，要求的值，需证明△OGE ∽△OHD．想法3:连接OC，DE，要求的值，需证C，D，O，E四点共圆．…请你参考上面的想法，帮助小军写出求的值的过程(一种方法即可)；(3)若=(n≥2且n为正整数)，则的值为(用含n的式子表示)．29．(8分)在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，P是圆内与圆心C 不重合的点，⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A，B，满足|PA ﹣PB|=2，则称点P为⊙C的“完美点”，如图为⊙C及其“完美点”P的示意图．(1)当⊙O的半径为2时，①在点M(，0)，N(0，1)，T(﹣，﹣)中，⊙O的“完美点”是；②若⊙O的“完美点”P在直线y=x上，求PO的长及点P的坐标；(2)⊙C的圆心在直线y=x+1上，半径为2，若y轴上存在⊙C的“完美点”，求圆心C的纵坐标t的取值范围．2020-2021学年北京市朝阳区九年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共30分，每小题3分)第1-10题均有四个选项，符合题意的选项只有一个.1．二次函数y=(x﹣1)2﹣3的最小值是()A．2 B．1 C．﹣2 D．﹣3【考点】二次函数的最值．【分析】由顶点式可知当x=1时，y取得最小值﹣3．【解答】解:∵y=(x﹣1)2﹣3，∴当x=1时，y取得最小值﹣3，故选:D．【点评】本题主要考查二次函数的最值，熟练掌握二次函数的性质是解题的关键．2．下列事件中，是必然事件的是()A．明天太阳从东方升起B．射击运动员射击一次，命中靶心C．随意翻到一本书的某页，这页的页码是奇数D．经过有交通信号灯的路口，遇到红灯【考点】随机事件．【分析】根据必然事件、不可能事件、随机事件的概念，可得答案．【解答】解:A、明天太阳从东方升起是必然事件，故A正确；B、射击运动员射击一次，命中靶心是随机事件，故B错误；C、随意翻到一本书的某页，这页的页码是奇数是随机事件，故C错误；D、经过有交通信号灯的路口，遇到红灯是随机事件，故D错误；故选:A．【点评】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．3．一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是()A．B．C．D．【考点】概率公式．【分析】直接利用概率公式求解．【解答】解:从该盒子中任意摸出一个球，摸到黄球的概率==．故选A．【点评】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数．4．如图，在△ABC中，DE∥BC，DE分别交AB，AC于点D，E，若AD:DB=1:2，则△ADE与△ABC的面积之比是()A．1:3 B．1:4 C．1:9 D．1:16【考点】相似三角形的判定与性质．【分析】根据DE∥BC，即可证得△ADE∽△ABC，然后根据相似三角形的面积的比等于相似比的平方，即可求解．【解答】解:∵AD:DB=1:2，∴AD:AB=1:3，∵DE∥BC，∴△ADE∽△ABC，∴=()2=．故选:C．【点评】本题考查了三角形的判定和性质:熟练掌握相似三角形的面积比是相似比的平方是解题的关键．5．已知点A(1，a)与点B(3，b)都在反比例函数y=﹣的图象上，则a与b之间的关系是()A．a＞b B．a＜b C．a≥b D．a=b【考点】反比例函数图象上点的坐标特征．【分析】把所给点的横纵坐标代入反比例函数的解析式，求出a与b的值，比较大小即可．【解答】解:点A(1，a)在反比例函数y=﹣的图象上，a=﹣12，点(3，b)在反比例函数y=﹣的图象上，b=﹣4，∴a＜b．故选:B．【点评】本题主要考查反比例函数图象上点的坐标特征，所有在反比例函数上的点的横纵坐标的积等于比例系数．6．已知圆锥的底面半径为2cm，母线长为3cm，则它的侧面展开图的面积为() A．18πcm2B．12πcm2C．6πcm2D．3πcm2【考点】圆锥的计算．【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算．【解答】解:它的侧面展开图的面积=•2π•2•3=6π(cm2)．故选C．【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．7．已知蓄电池的电压为定值，使用蓄电池时，电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为()A．B．C．D．【考点】反比例函数的应用；根据实际问题列反比例函数关系式．【分析】根据函数图象可用电阻R表示电流I的函数解析式为I=，再把(2，3)代入可得k的值，进而可得函数解析式．【解答】解:设用电阻R表示电流I的函数解析式为I=，∵过(2，3)，∴k=3×2=6，∴I=，故选:D．【点评】此题主要考查了待定系数法求反比例函数解析式，关键是掌握凡是函数图象经过的点必能满足解析式．8．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为5，AC=8．则cosB的值是()A．B．C．D．【考点】三角形的外接圆与外心；解直角三角形．【分析】连接CD，则可得∠ACD=90°，且∠B=∠D，在Rt△ADC中可求得CD，则可求得cosD，即可求得答案．【解答】解:如图，连接CD，∵AD⊙O的直径，∴∠ACD=90°，且∠B=∠D，在Rt△ACD中，AD=5×2=10，AC=8，∴CD=6，∴cosD===，∴cosB=cosD=，故选B．【点评】本题主要考查圆周角定理及三角函数的定义，构造直角三角形是解题的关键．9．《九章算术》是我国古代内容极为丰富的数学名著，书中有这样一个问题:“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是:“如图，今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形能容纳的圆形(内切圆)直径是多少？”此问题中，该内切圆的直径是()A．5步 B．6步 C．8步 D．10步【考点】三角形的内切圆与内心．【分析】由勾股定理可求得斜边长，分别连接圆心和三个切点，设内切圆的半径为r，利用面积相等可得到关于r的方程，可求得内切圆的半径，则可求得内切圆的直径．【解答】解:如图，在Rt△ABC中，AC=8，BC=15，∠C=90°，∴AB==17，=AC•BC=×8×15=60，∴S△ABC设内切圆的圆心为O，分别连接圆心和三个切点，及OA、OB、OC，设内切圆的半径为r，=S△AOB+S△BOC+S△AOC=×r(AB+BC+AC)=2020∴S△ABC∴202060，解得r=3，∴内切圆的直径为6步，故选B．【点评】本题主要考查三角形的内切圆，连接圆心和切点，把三角形的面积分成三个三个角形的面积得到关于r的方程是解题的关键．10．已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示，下面有四个推断:①二次函数y1有最大值②二次函数y1的图象关于直线x=﹣1对称③当x=﹣2时，二次函数y1的值大于0④过动点P(m，0)且垂直于x轴的直线与y1，y2的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜﹣3或m＞﹣1．其中正确的是()A．①③B．①④C．②③D．②④【考点】二次函数图象上点的坐标特征；一次函数图象与系数的关系；二次函数的最值．【分析】根据函数的图象即可得到结论．【解答】解:∵二次函数y1=ax2+bx+c(a≠0)的图象的开口向上，∴二次函数y1有最小值，故①错误；观察函数图象可知二次函数y1的图象关于直线x=﹣1对称，故②正确；当x=﹣2时，二次函数y1的值小于0，故③错误；当x＜﹣3或x＞﹣1时，抛物线在直线的上方，∴m的取值范围为:m＜﹣3或m＞﹣1，故④正确．故选D．【点评】本题考查了二次函数图象上点的坐标特征以及函数图象，熟练运用二次函数图象上点的坐标特征求出二次函数解析式是解题的关键．二、填空题(本题共18分，每小题3分)11．将二次函数y=x2﹣2x﹣5化为y=a(x﹣h)2+k的形式为y=(x﹣1)2﹣6．【考点】二次函数的三种形式．【分析】利用配方法整理即可得解；【解答】解:(1)y=x2﹣2x﹣5=x2﹣2x+1﹣6=(x﹣1)2﹣6，故答案为:(x﹣1)2﹣6．【点评】本题考查了二次函数的三种形式的转化，二次函数的性质，熟练掌握配方法是解题的关键．12．抛物线y=x2﹣2x+m与x轴有两个公共点，请写出一个符合条件的表达式为y=x2﹣2x．【考点】抛物线与x轴的交点．【分析】根据判别式的意义得到△=(﹣2)2﹣4m＞0，然后解不等式组求出m的范围，再在此范围内写出一个m的值即可．【解答】解:根据题意得到△=(﹣2)2﹣4m＞0，解得m＜1，若m取0，抛物线解析式为y=x2﹣2x．故答案为y=x2﹣2x．【点评】本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a，b，c是常数，a≠0)，△=b2﹣4ac决定抛物线与x轴的交点个数:△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．13．如图，若点P在反比例函数y=﹣(x＜0)的图象上，过点P作PM⊥x轴于点M，PN⊥y轴于点N，则矩形PMON的面积为3．【考点】反比例函数系数k的几何意义．【分析】设PN=a，PM=b，根据P点在第二象限得P(﹣a，b)，根据矩形的面积公式即可得到结论．【解答】解:设PN=a，PM=b，∵P点在第二象限，∴P(﹣a，b)，代入y=中，得k=﹣ab=﹣3，∴矩形PMON的面积=PN•PM=ab=3，故答案为:3．【点评】本题考查了反比例函数系数k的几何意义．过反比例函数图象上一点作x轴、y轴的垂线，所得矩形的面积为反比例函数系数k的绝对值．14．某农科所在相同条件下做某种作物种子发芽率的试验，结果如表所示:种子个数n10001500250040008000150002020030000发芽种子个数m8991365224536447272136801816027300发芽种子频率0.8990.9100.8980.9110.9090.9120.9080.910则该作物种子发芽的概率约为0.910．【考点】模拟实验．【分析】选一个表格中发芽种子频率比较按近的数，如0.900、0.910等都可以．【解答】解:答案不唯一，如:0.910．故答案为:0.910．【点评】本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．15．如图，△ABC中，D、E分别是AB、AC边上一点，连接DE．请你添加一个条件，使△ADE∽△ABC，则你添加的这一个条件可以是∠ADE=∠B(写出一个即可)．【考点】相似三角形的判定．【分析】利用有两组角对应相等的两个三角形相似添加条件．【解答】解:∵∠DAE=∠BAC，∴当∠ADE=∠B时，△ADE∽△ABC．故答案为∠ADE=∠B．【点评】本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．16．阅读下面材料:①作线段AB的垂直平分线m；②作线段BC的垂直平分线n，与直线m交于点O；③以点O为圆心，OA为半径作△ABC的外接圆；④在弧ACB上取一点P，连结AP，BP．所以∠APB=∠ACB．老师说:“小明的作法正确．”请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是①线段垂直平分线上的点与这条线段两个端点的距离相等；②等量代换；(2)∠APB=∠ACB的依据是同弧所对的圆周角相等．【考点】作图—复杂作图；线段垂直平分线的性质；三角形的外接圆与外心．【分析】(1)根据线段的垂直平分线的性质定理以及等量代换即可得出结论．(2)根据同弧所对的圆周角相等即可得出结论．【解答】解:(1)如图2中，∵MN垂直平分AB，EF垂直平分BC，∴OA=OB，OB=OC(线段垂直平分线上的点与这条线段两个端点的距离相等)，∴OA=OB=OC(等量代换)故答案为①线段垂直平分线上的点与这条线段两个端点的距离相等；②等量代换．(2)∵=，∴∠APB=∠ACB(同弧所对的圆周角相等)．故答案为同弧所对的圆周角相等．【点评】本题考查作图﹣复杂作图、线段的垂直平分线的性质、三角形的外心等知识，解题的关键是熟练掌握三角形外心的性质，属于中考常考题型．三、解答题(本题共72分，第17-26题每小题5分，第27题7分，第28题7分，第29题8分)17．计算:2sin45°+tan60°+2cos30°﹣．【考点】实数的运算；特殊角的三角函数值．【分析】直接利用特殊角的三角函数值代入求出答案．【解答】解:原式=2×++2×﹣2=．【点评】此题主要考查了实数运算以及特殊角的三角函数值，正确记忆相关数据是解题关键．18．如图，△ABC中，点D在边AB上，满足∠ACD=∠ABC，若AC=，AD=1，求DB的长．【考点】相似三角形的判定与性质．【分析】由∠ACD=∠ABC与∠A是公共角，根据有两角对应相等的三角形相似，即可证得△ADC∽△ACB，又由相似三角形的对应边成比例，即可求得AB，进而得到DB的长．【解答】解:∵∠ACD=∠ABC，∠A=∠A，∴△ACD∽△ABC．∴，∴．∴AB=3，∴DB=AB﹣AD=2．【点评】此题考查了相似三角形的判定与性质．此题难度不大，解题的关键是注意方程思想与数形结合思想的应用．19．已知二次函数y=ax2+bx+c(a≠0)中，函数y与自变量x的部分对应值如表: x…﹣2﹣102…y…﹣3﹣4﹣35…(1)求二次函数的表达式，并写出这个二次函数图象的顶点坐标；(2)求出该函数图象与x轴的交点坐标．【考点】抛物线与x轴的交点；待定系数法求二次函数解析式．【分析】(1)由待定系数法即可得出答案；(2)求出y=0时x的值，即可得出答案．【解答】解:(1)由题意，得c=﹣3．将点(2，5)，(﹣1，﹣4)代入，得解得∴y=x2+2x﹣3．顶点坐标为(﹣1，﹣4)．(2)当y=0时，x2+2x﹣3，解得:x=﹣3或x=1，∴函数图象与x轴的交点坐标为(﹣3，0)，(1，0)．【点评】本题考查了待定系数法求二次函数的解析式、抛物线与x轴的交点；求出二次函数的解析式是解决问题的关键．2020图，在平面直角坐标系xOy中，△ABC的三个顶点分别为A(2，6)，B(4，2)，C(6，2)．(1)以原点O为位似中心，将△ABC缩小为原来的，得到△DEF．请在第一象限内，画出△DEF．(2)在(1)的条件下，点A的对应点D的坐标为(1，3)，点B的对应点E的坐标为(2，1)．【考点】作图-位似变换．【分析】(1)分别连接OA、OB、OC，然后分别取它们的中点得到D、E、F；(2)利用线段中点坐标公式可得到D点和E点坐标．【解答】解:(1)如图，△DEF为所作；(2)D(1，3)，E(2，1)．故答案为(1，3)，(2，1)．【点评】本题考查了作图﹣位似变换:先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；接着根据位似比，确定能代表所作的位似图形的关键点；然后顺次连接上述各点，得到放大或缩小的图形．21．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分．如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，CD=10，EM=25．求⊙O的半径．【考点】垂径定理的应用．【分析】根据垂径定理得出EM⊥CD，则CM=DM=2，在Rt△COM中，有OC2=CM2+OM2，进而可求得半径OC．【解答】解:如图，连接OC，∵M是弦CD的中点，EM过圆心O，∴EM⊥CD．∴CM=MD．∵CD=10，∴CM=5．设OC=x，则OM=25﹣x，在Rt△COM中，根据勾股定理，得52+(25﹣x)2=x2．解得x=13．∴⊙O的半径为13．【点评】此题主要考查了垂径定理的应用，解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形．22．如图，在Rt△ABC中，∠C=90°，点D是BC边的中点，CD=2，tanB=．(1)求AD和AB的长；(2)求sin∠BAD的值．【考点】解直角三角形．【分析】(1)由中点定义求BC=4，根据tanB=得:AC=3，由勾股定理得:AB=5，AD=；(2)作高线DE，证明△DEB∽△ACB，求DE的长，再利用三角函数定义求结果．【解答】解:(1)∵D是BC的中点，CD=2，∴BD=DC=2，BC=4，在Rt△ACB中，由tanB=，∴，∴AC=3，由勾股定理得:AD===，AB===5；(2)过点D作DE⊥AB于E，∴∠C=∠DEB=90°，又∠B=∠B，∴△DEB∽△ACB，∴，∴，∴，∴sin∠BAD===．【点评】本题考查了解直角三角形，熟练掌握直角三角形的边角关系是解题的关键．23．已知一次函数y=﹣2x+1的图象与y轴交于点A，点B(﹣1，n)是该函数图象与反比例函数y=(k≠0)图象在第二象限内的交点．(1)求点B的坐标及k的值；(2)试在x轴上确定点C，使AC=AB，直接写出点C的坐标．【考点】反比例函数与一次函数的交点问题．【分析】(1)由点B的横坐标利用一次函数图象上点的坐标特征即可求出点B的坐标，根据点B的坐标利用反比例函数图象上点的坐标特征即可求出k值；(2)令x=0利用一次函数图象上点的坐标特征可求出点A的坐标，设点C的坐标为(m，0)，根据两点间的距离公式结合AC=AB即可得出关于m无理方程，解之即可得出m的值，进而得出点C的坐标．【解答】解:(1)∵点B(﹣1，n)在直线y=﹣2x+1上，∴n=2+1=3．∴点B的坐标为(﹣1，3)．∵点B(﹣1，3)在反比例函数的图象上，∴k=﹣3．(2)当x=0时，y=﹣2x+1=1，∴点A的坐标为(0，1)．设点C的坐标为(m，0)，∵AC=AB，∴==，解得:m=±2．∴点C的坐标为(2，0)或(﹣2，0)．【点评】本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征，根据一次函数图象上点的坐标特征找出点A、B的坐标是解题的关键．24．如图，用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD，墙长28m．设AB长为x m，矩形的面积为y m2．(1)写出y与x的函数关系式；(2)当AB长为多少米时，所围成的花圃面积最大？最大值是多少？(3)当花圃的面积为150m2时，AB长为多少米？【考点】二次函数的应用；一元二次方程的应用．【分析】(1)根据题意可以得到y与x的函数关系式；(2)根据(1)中的函数关系式化为顶点式，注意x的取值范围；(3)根据(1)和(2)中的关系可以求得AB的长．【解答】解:(1)y=x(40﹣2x)=﹣2x2+40x，即y与x的函数关系式是y=﹣2x2+40x；(2)由题意，得，解得，6≤x＜2020由题意，得y=﹣2x2+40x=﹣2(x﹣10)2+2020∴当x=10时，y有最大值，y的最大值为2020即当AB长为10m时，花圃面积最大，最大面积为20202；(3)令y=150，则﹣2x2+40x=150．解得，x1=5，x2=15，∵6≤x＜2020∴x=15，即当AB长为15m时，面积为150m2．【点评】本题考查二次函数的应用、一元二次方程的应用，解题的关键是明确题意，找出所求问题需要的条件．25．如图，AB是⊙O的直径，C，D是⊙O上两点，且=，过点C的直线CF ⊥AD于点F，交AB的延长线于点E，连接AC．(1)求证:EF是⊙O的切线；(2)连接FO，若sinE=，⊙O的半径为r，请写出求线段FO长的思路．【考点】切线的判定；圆心角、弧、弦的关系；解直角三角形．【分析】(1)连接OC，根据等腰三角形的性质得到∠1=∠2，根据圆周角定理得到∠1=∠3，推出OC∥AF，根据切线的判定定理即可得到结论；(2)由sinE=，推出△AEF，△OEC都为含30°的直角三角形；推出△ACF为含30°的直角三角形；由勾股定理可求OF的长．【解答】(1)证明:如图，连接OC，∵OC=OA，∴∠1=∠2，∵=，∴∠1=∠3，∴∠2=∠3，∴OC∥AF，∵CF⊥AD，∴∠CFA=90°，∴∠OCF=90°，∴OC⊥EF，∵OC为⊙O的半径，∴EF是⊙O的切线；(2)解:求解思路如下:①在Rt△AEF和Rt△OEC中，由sinE=，可得△AEF，△OEC都为含30°的直角三角形；②由∠1=∠3，可知△ACF为含30°的直角三角形；③由⊙O的半径为r，可求OE，AE的长，从而可求CF的长；④在Rt△COF中，由勾股定理可求OF的长．【点评】本题考查了切线的判定，直角三角形的性质，圆周角定理，平行线的判定和性质，正确的作出辅助线是解题的关键．26．某“数学兴趣小组”根据学习函数的经验，对函数y=﹣x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整:(1)自变量x的取值范围是全体实数，x与y的几组对应数值如表:x…﹣3﹣﹣2﹣10123…y…﹣2﹣m2121﹣﹣2…其中m=1；(2)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(3)根据函数图象，写出:①该函数的一条性质函数图象关于y轴对称；②直线y=kx+b经过点(﹣1，2)，若关于x的方程﹣x2+2|x|+1=kx+b有4个互不相等的实数根，则b的取值范围是1＜b＜2．【考点】抛物线与x轴的交点；一次函数的图象；一次函数与一元一次方程；二次函数的图象．【分析】(1)把x=﹣2代入函数解释式即可得m的值；(2)描点、连线即可得到函数的图象；(3)①根据函数图象得到函数y=x2﹣2|x|+1的图象关于y轴对称；当x＞1时，y 随x的增大而减少；②根据函数的图象即可得到b的取值范围是1＜b＜2．【解答】解:(1)当x=﹣2时，m=﹣(﹣2)2+2×|﹣2|+1=﹣4+4+1=1．(2)如图所示:(3)①答案不唯一．如:函数图象关于y轴对称．②由函数图象知:∵关于x的方程﹣x2+2|x|+1=kx+b有4个互不相等的实数根，∴b的取值范围是1＜b＜2．故答案为:1；函数图象关于y轴对称；1＜b＜2．【点评】本题考查了抛物线与x轴的交点，二次函数的图象和性质，正确的识别图象是解题的关键．27．在平面直角坐标系xOy中，直线y=﹣x+n经过点A(﹣4，2)，分别与x，y轴交于点B，C，抛物线y=x2﹣2mx+m2﹣n的顶点为D．(1)求点B，C的坐标；(2)①直接写出抛物线顶点D的坐标(用含m的式子表示)；②若抛物线y=x2﹣2mx+m2﹣n与线段BC有公共点，求m的取值范围．【考点】二次函数的性质；一次函数的性质；一次函数图象上点的坐标特征．【分析】(1)把A点坐标代入直线解析式，可求得n的值，可得直线解析式，即可求得B、C的坐标；(2)①把抛物线解析式化为顶点式，结合(1)中所求n的值，可求得D点坐标；②把B、C两点的坐标分别代入抛物线解析式，可求得m的值，从而可求得其取值范围．【解答】解:(1)把A(﹣4，2)代入y=x+n中，得n=1，∴直线解析式为y=x+1，令y=0可求得x=4，令x=0可得y=1，∴B(4，0)，C(0，1)；(2)①∵y=x2﹣2mx+m2﹣n=(x﹣m)2﹣1，∴D(m，﹣1)；②将点(0，1)代入y=x2﹣2mx+m2﹣1中，得1=m2﹣1，解得m=或m=﹣，将点(4，0)代入y=x2﹣2mx+m2﹣1中，得0=16﹣8m+m2﹣1，解得m=5或m=3，∴．。

人教版2020---2021学年度上学期九年级数学期末考试卷及答案含3套

密学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：120分时间：120分钟）一、选择题（本大题共10小题，每小题4分，满分40分） 1．在﹣2，0，2，﹣3这四个数中，最小的数是（） A ．2 B ．0 C ．﹣2 D ．﹣32．如果我们都能改掉餐桌上的陋习，珍惜每一粒粮食，合肥市每年就能避免浪费30.1亿元，将30.1亿用科学记数法表示为（）A ．30.1×108B ．3.01×108C ．3.01×109D ．0.301×10103．一元二次方程（x+6）2=16可转化为两个一元一次方程，其中一个一元一次方程是x+6=4，则另一个一元一次方程是（） A ．x ﹣6=﹣4 B ．x ﹣6=4 C ．x+6=4 D ．x+6=﹣44．设a=2﹣1，a 在两个相邻整数之间，则这两个整数是（） A ．1和2 B ．2和3 C ．3和4 D ．4和55．直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与∠1互余的角有几个（）A ．2个B ．3个C ．4个D ．6个6．某选手在青歌赛中的得分如下（单位：分）：99.60，99.45，99.60，99.70，98.80，99.60，99.83，则这位选手得分的众数和中位数分别是（）A ．99.60，99.70B ．99.60，99.60C ．99.60，98.80D ．99.70，99.607．如图为抛物线y=ax 2+bx+c 的图象，A 、B 、C 为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（）A ．ac ＜0B ．a ﹣b=1C ．a+b=﹣1D ．b ＞2a8．如图，过▱ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ，那么图中的▱AEMG 的面积S 1与▱HCFM 的面积S 2的大小关系是（）A ．S 1＞S 2B ．S 1＜S 2C ．S 1=S 2D ．2S 1=S 2密封线内9．如果三角形的两条边分别为4和6，那么连结该三角形三边中点所得的周长可能是下列数据中的（）A．6 B．8 C．10 D．1210．附加题：如图，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是（）A． B． C．D．二、填空题（本大题共4小题，每小题5分，满分20分．11．的平方根是．12．因式分解：a2b+2ab+b= ．13．如图，在直角三角形ABC中，∠ACB=90°，AC=1，BC=2，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为．14．如图，等腰直角△ABC腰长为a，现分别按图1，图2在△ABC内内接一个正方形ADFE和正方形PMNQ．设△ABC积为S，正方形ADFE的面积为S1，正方形PMNQ的面积为S2AD：AB=1：2；②AP：AB=1：3；③S1+S2＞S；④设在△ABC意截取一个正方形的面积为S3，则S3≤S1是．三、（本大题共2小题，每小题8分，满分16分）15为分母）构造一个分式，并化简该分式．a2﹣1，a2﹣1，a2﹣然后请你自选一个合理的数代入求值．16．如图，在平面直角坐标系中，△ABC上，点A的坐标为（2，4），请解答下列问题：（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2出点A2的坐标．密线学校班级姓名学号密封线内不得答题四、（本大题共2小题，每小题8分，满分16分） 17．2014年3月8日凌晨，马来西亚航空公司一架航班号为MH370的波音777客机于凌晨零点左右从吉隆坡飞往北京，计划6：30抵达北京首都国际机场，却在凌晨1：30分失去联系．已知该飞机起飞时油箱内存有15000升油，起飞后一直保持速度为400km/h 匀速直线运动，且每千米的耗油量为5升，请用不等式的知识求出该飞机在失去联系后能最多航行多少千米？18．如图，矩形ABCD 中，AB=6，第1次平移将矩形ABCD 沿AB 的方向向右平移5个单位，得到矩形A 1B 1C 1D 1，第2次平移将矩形A 1B 1C 1D 1沿A 1B 1的方向向右平移5个单位，得到矩形A 2B 2C 2D 2…，第n 次平移将矩形A n ﹣1B n ﹣1C n ﹣1D n ﹣1沿A n ﹣1B n ﹣1的方向平移5个单位，得到矩形A n B n C n D n （n ＞2）．（1）求AB 1和AB 2的长．（2）若AB n 的长为56，求n ．五、（本大题共2小题，每小题10分，满分20分） 19．一透明的敞口正方体容器ABCD ﹣A ′B ′C ′D ′装有一些液体，棱AB 始终在水平桌面上，容器底部的倾斜角为α （∠CBE=α，如图所示）．探究如图1，液面刚好过棱CD ，并与棱BB ′交于点Q ，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．解决问题：（1）CQ 与BE 的位置关系是，BQ 的长是 dm ；（2）求液体的体积；（参考算法：直棱柱体积V 液=底面积S △BCQ ×高AB ）；（3）求液面到桌面的高度和倾斜角α的度数．（注：sin37°=，tan37°=）．20．面对即将到来的五一小长假，胡老师一家计划用两天时间参观岱山湖、紫蓬山森林公园、滨湖湿地公园、三国遗址公园四个景区中的两个；第一天从4个景区中随机选择一个，第二天从余下3个景区中再随机选择一个，如果每个景区被选中的机会均等．（1）请画树状图或表格的方法表示出所有可能出现的结果；（2）求滨湖湿地公园被选中的概率．六、（本题满分12分）21．已知：如图，在△ABC 中，AB=AC ，AE 是角平分线，BM 平分∠ABC 交AE 于点M ，经过B ，M 两点的⊙O 交BC 于点G ，交AB 于点F ，FB 恰为⊙O 的直径．（1）求证：AE 与⊙O 相切；（2）当BC=4，cosC=时，求⊙O 的半径．七、（本题满分12分）22．自2010年6月1消费者在购买政策限定的新家电时，部分由政府提供，其中三种家电的补贴方式如下表：补贴额度新家电销售价格的10%说明：电视补贴的金额最多不超过400元/台；洗衣机补贴的金额最多不超过250元/台；冰箱补贴的金额最多不超过300元/台．为此，某商场家电部准备购进电视、洗衣机、冰箱共100这批家电的进价和售价如下表：家电名进价（元/台）售价（元/台）密学校班级姓名学号密封线内不得答题称电视39004300 洗衣机 1500 1800 冰箱20002400设购进的电视机和洗衣机数量均为x 台，这100台家电政府需要补贴y 元，商场所获利润w 元（利润=售价﹣进价）（1）请分别求出y 与x 和w 与x 的函数表达式；（2）若商场决定购进每种家电不少于30台，则有几种进货方案？若商场想获得最大利润，应该怎样安排进货？若这100台家电全部售出，政府需要补贴多少元钱？八、（本题满分14分）23．如图1，在正方形ABCD 中，点M 、N 分别在AD 、CD 上．（1）若∠MBN=45°且∠ABM=∠CBN ，则易证．（选择正确答案填空）①AM+CN ＞MN ；②（AM+CN ）=MN ；③MN=AM+CN ．（2）若∠MBN=∠ABC ，在（1）中线段MN 、AM 、CN 之间的数量关系是否仍然成立？若成立给予证明，若不成立探究出它们之间关系．【拓展】如图2，在四边形ABCD 中，AB=BC ，∠ABC 与∠ADC互补．点M 、N 分别在DA 、CD 的延长线上，若∠MBN=∠ABC ，试探究线段MN 、AM 、CN 又有怎样的数量关系？请写出猜想并证明．参考答案一、选择题（本大题共10小题，每小题4分，满分40分） 1．D ． 2. C ．3.D ．4.B ．5.B ．6. B ．7.D ．8.C ． 9.B ．10.C ．二、填空题（本大题共4小题，每小题5分，满分20分． 11．的平方根是 ± ．12．因式分解：a 2b+2ab+b= b （a+1）2．13．如图，在直角三角形ABC 中，∠ACB=90°，AC=1，BC=2，以点C 为圆心，CA 为半径的圆与AB 交于点D ，则AD 的长为．线内不得答题14．如图，等腰直角△ABC腰长为a，现分别按图1，图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ．设△ABC的面积为S，正方形ADFE的面积为S1，正方形PMNQ的面积为S2．①AD：AB=1：2；②AP：AB=1：3；③S1+S2＞S；④设在△ABC内任意截取一个正方形的面积为S3，则S3≤S1．上述结论中正确的是①②④．三、（本大题共2小题，每小题8分，满分16分）15．请从下列三个代数式中任选两个（一个作为分子，一个作为分母）构造一个分式，并化简该分式．a2﹣1，a2﹣1，a2﹣2a+1，然后请你自选一个合理的数代入求值．解： ==，当a=2时，原式==3．或=，当a=2时，原式==．16．如图，在平面直角坐标系中，△ABC上，点A的坐标为（2，4），请解答下列问题：（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2出点A2的坐标．解：（1）如图所示：点A1的坐标（2，﹣4）；（2）如图所示，点A2的坐标（﹣2，4）．密线学校班级姓名学号密封线内不得答题四、（本大题共2小题，每小题8分，满分16分）17. 解：设该飞机在失去联系后能航行x 千米， 1：30﹣0：00=1.5（小时），由题意得：1.5×400×5+5x ≤15000 解得：x ≤2400．答：该飞机在失去联系后最多能航行2400千米．18.解：（1）∵AB=6，第1次平移将矩形ABCD 沿AB 的方向向右平移5个单位，得到矩形A 1B 1C 1D 1，第2次平移将矩形A 1B 1C 1D 1沿A 1B 1的方向向右平移5个单位，得到矩形A 2B 2C 2D 2…，∴AA 1=5，A 1A 2=5，A 2B 1=A 1B 1﹣A 1A 2=6﹣5=1， ∴AB 1=AA 1+A 1A 2+A 2B 1=5+5+1=11， ∴AB 2的长为：5+5+6=16；（2）∵AB 1=2×5+1=11，AB 2=3×5+1=16， ∴AB n =（n+1）×5+1=56，解得：n=10．五、（本大题共2小题，每小题10分，满分20分）19．(1)解：（1）CQ ∥BE ，BQ==3dm ；故答案为：平行，3；（2）V 液=×3×4×4=24（dm 3）；（3）过点B 作BF ⊥CQ ，垂足为F ， ∵×3×4=×5×BF ， ∴BF=，∴液面到桌面的高度； ∵在Rt △BCQ 中，tan ∠BCQ=， ∴α=∠BCQ=37°．内不得题20.解：（1）用A、B、C、D分别表示岱山湖、紫蓬山森林公园、滨湖湿地公园、三国遗址公园四个景区，画树状图为：共有12种等可能的结果数；（2）滨湖湿地公园被选中的结果数为6，所以滨湖湿地公园被选中的概率==．六、（本题满分12分）21．解（1）证明：连接OM，则OM=OB∴∠1=∠2∵BM平分∠ABC∴∠1=∠3∴∠2=∠3∴OM∥BC∴∠AMO=∠AEB在△ABC中，AB=AC，AE是角平分线∴AE⊥BC∴∠AEB=90°∴∠AMO=90°∴OM⊥AE∵点M在圆O上，∴AE与⊙O相切；（2）解：在△ABC中，AB=AC，AE是角平分线∴BE=BC，∠ABC=∠C∵BC=4，cosC=∴BE=2，cos∠ABC=在△ABE中，∠AEB=90°∴AB==6设⊙O的半径为r，则AO=6﹣r∵OM∥BC∴△AOM∽△ABE∴∴解得密线学校班级姓名学号密封线内不得答题∴⊙O 的半径为．七、（本题满分12分）22．解：（1）y=400x+1800×10%x+2400×10%（100﹣2x ）=100x+24000商场所获利润：W=400x+300x+400（100﹣2x ） =﹣100x+40000．（2）根据题意得，解得30≤x ≤35，因为x 为整数，所以x=30，31，32，33，34，35，因此共有6种进货方案．对于W=﹣100x+40000， ∵k=﹣100＜0，30≤x ≤35， ∴当x=30时，W 有最大值，所以当购进30台电视，30台洗衣机，40台电冰箱时商场将获得最大的利润．因此政府的补贴为y=100×30+24000=27000元．八、（本题满分14分）23．解：（1）解：设BD 于MN 交于点H ，如图1（1）， ∵BD 为正方形ABCD 的正方形， ∴∠ABH=∠CBH=45°，BA=BC ， ∵∠MBN=45°，∠ABM=∠CBN ， ∴∠ABM=∠HBM=∠HBN=∠CBN ，在△ABM 和△CBN 中，∴△ABM ≌△CBN ， ∴BM=BN ，AM=CN ，而∠HBM=∠HBN ， ∴BH ⊥MN ， ∴MA=MH ，NH=NC ， ∴AM=MH=HN=NC ， ∴MN=AM+CN ；故答案为③；封线内题（2）解：在（1）中线段MN 、AM 、CN 之间的数量关系仍然成立．理由如下：把△BAM 绕点B 顺时针旋转90°得到△BCP ，如图1（2）， ∴BM=BP ，AM=CP ，∠MBP=90°，∠BCP=∠A=90°， ∵∠BCP+∠BCN=180°， ∴点P 在DC 的延长线上， ∴NC+CP=NP ，∵∠MBN=∠ABC=45°， ∴∠NBP=45°，在△BNM 和△BNP 中，∴△BNM ≌△BNP ， ∴MN=NP ，∴MN=CP+CN=AM+CN ；【拓展】解：如图2，∵∠ABC+∠ADC=180°， ∴∠BAD+∠BCD=180°，而∠BAD+∠BAM=180°， ∴∠BAM=∠BCD ， ∵AB=BC ，∴把△BAM 绕点B 顺时针旋转90°得到△BCQ ，∴∠BAM=∠BCQ ，BM=BQ ，∠MBQ=∠ABC ， ∴∠BCQ=∠BCD ， ∴点Q 在CN 上， ∴CN=CQ+MQ=AM+NQ ， ∵∠MBN=∠ABC ， ∴∠MBN=MBQ ，∴∠MBN=∠QBN ，在△BMN 和△BQN 中，∴△BMN ≌△BQN ， ∴MN=QN ， ∴CN=AM+MN ，即MN=CN ﹣AM ．第37页,共40页第38页,共40页密封线学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：120分时间：120分钟）一、选择题（本大题每小题3分，满分42分）1．2-的相反数是（）A.21 B.21- C.2- D.22．在实数2、0、1-、2-中，最小的实数是（） A ．2 B ．0 C ．1- D ．2- 3．海南的富铁矿是国内少有的富铁矿之一，储量居全国第六位，其储量约为237 000 000吨，用科学记数法表示应为（）A. 237×106吨 B. 2.37×107吨 C. 2.37×108吨 D. 0.237×109吨 4.下列运算，正确的是（）A.523a a a =⋅B.ab b a 532=+C.326a a a =÷D.523a a a =+ 5. 下列各图中，是中心对称图形的是（）6. 方程042=-x 的根是（）A. 2,221-==x xB. 4=xC. 2=xD. 2-=x7. 不等式组⎩⎨⎧-><-12x x 的解集是（） A. 1->x B. 2-<x C. 2<x D. 21<<-x 8．函数1-=x y 中，自变量x 的取值范围是（）A. 1≥xB. 1->xC. 0>xD. 1≠x 9．下列各点中，在函数xy 2=图象上的点是（）A ．(2,4)B ．(-1,2)C ．(-2,-1)D ．(21-,1-)10.一次函数2+=x y 的图象不经过．．．（） A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限11. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：跳高成绩(m) 1.501.551.601.651.70 1.75跳高人数1 323 5 1这些运动员跳高成绩的中位数和众数分别是（） A ．1.65，1.70 B ．1.70，1.65 C ．1.70，1.70 D ．3，5 12．某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验，得到两个品种每公顷产量的两组数据，其方题号一二三总分得分ABCD第11页,共40页第12页,共40页差分别为s 甲2＝0.002、s 乙2＝0.03，则（） A ．甲比乙的产量稳定 B ．乙比甲的产量稳定 C ．甲、乙的产量一样稳定D ．无法确定哪一品种的产量更稳定13. 如图1，AB 、CD 相交于点O ，∠1=80°，如果DE ∥AB ，那么∠D 的度数为（）A. 80°B. 90°C. 100°D. 110°14．如图2，正方形ABCD 的边长为2cm ，以B 点为圆心、AB长为半径作⋂AC ，则图中阴影部分的面积为（） A.2)4(cm π- B. 2)8(cm π- C. 2)42(cm -π D. 2)2(cm -π二、填空题（本大题满分12分，每小题3分） 15. 计算：=-283.16.在一个不透明的布袋中装有2个白球，n 个黄球，它们除颜色不同外，其余均相同.若从中随机摸出一个球，它是黄球的概率是54，则n = .17.如图3，在等腰梯形ABCD 中，AD ∥BC ，AE ∥DC ，AB =6cm ，则AE = cm .18. 如图4，∠ABC=90°，O 为射线BC 上一点，以点O 21BO长为半径作⊙O ，当射线BA 绕点B 度时与⊙0相切.三、解答题(本大题满分56分) 19．计算(满分8分，每小题4分)（12314(2)2-⨯+-（2）化简：(a +1)(a -1)-a (a20．（满分8分）某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和一枚徽章的价格各是多少元？A BC图3E DA B CO E1D图1A第38页,共40页密封线学校班级姓名学号密封线内不得答题图1021.（8分）某中学学生会为考察该校学生参加课外体育活动的情况，采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好（每人只能选其中一项），并将调查结果绘制成如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：（1）在这次考察中一共调查了多少名学生？（2）在扇形统计图中，“乒乓球”部分所对应的圆心角是多少度？（3）补全条形统计图；（4）若全校有1800名学生，试估计该校喜欢篮球的学生约有多少人？22．（本题满分8分）如图的方格纸中，ABC∆的顶点坐标分别为()5,2-A、()1,4-B和()3,1-C（1）作出ABC∆关于x轴对称的111CBA∆，并写出点A、B、C的对称点1A、1B、1C的坐标；（2）作出ABC∆关于原点O对称的222CBA∆，并写出点A、B、C的对称点2A、2B、2C的坐标；（3）试判断：111CBA∆与222CBA∆是否关于y轴对称（只需写出判断结果）.23．（本大题满分11分）如图，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F.yAOxBC共计145元共计280元第21题图第37页,共40页第11页,共40页第12页,共40页（1）在图中找出一对全等三角形，并加以证明；（2）求证：AE=FC+EF.24．（13分）如图，已知二次函数图象的顶点坐标为C(1,0)，直线m x y +=与该二次函数的图象交于A 、B 两点，其中A 点的坐标为(3,4)，B 点在轴y 上. （1）求m 的值及这个二次函数的关系式；（2）P 为线段AB 上的一个动点（点P 与A 、B 不重合），过P 作x 轴的垂线与这个二次函数的图象交于点E 点，设线段PE 的长为h ，点P 的横坐标为x①求h 与x 之间的函数关系式，并写出自变量x 的取值范围；②线段PE 的长h 最大值及此时的xABCDEFG第37页,共40页第38页,共40页密线学校班级姓名学号密封线内不得答题参考答案一、选择题（本大题每小题3分，满分42分）二、填空题（本大题满分12分，每小题3分）15．25 16． 8 17． 6 18． 60°或120 ° 三、解答题（本大题满分56分） 19．(本题满分8分,每小题4分)（1）原式=3 - 2 +（-8）（2）原式=a 2-1-a 2+a= -7 =a -120．(满分8分)解：设一盒“福娃”玩具和一枚徽章的价格分别为x 元和y 元.依题意，得 ⎩⎨⎧=+=+280321452y x y x 解这个方程组，得 ⎩⎨⎧==10125y x 答：一盒“福娃”玩具和一枚徽章的价格分别为125元和10元.21、（本题满分8分）解：（1）∵，∴这次考察中一共调查了60名学生.（2）∵∴∴在扇形统计图中，“乒乓球”部分所对应的圆心角为90°（3），∴补全统计图如下图（4）∵∴可以估计该校学生喜欢篮球活动的约有450人22．满分（8分）解：（1）111C B A ∆如图，)5,2(1--A 、)1,4(1--B 、)3,1(1--C（2）222C B A ∆如图，)5,2(2-A 、)1,4(2-B 、)3,1(2-C（3）111C B A ∆与222C B A ∆关于y 轴对称60%106=%25%20%20%10%251=----︒=⨯︒90%2536012%2060=⨯450%251800=⨯题号 1 2 3 4 5 6 7 选择项 D D C A B A D 题号 8 9 10 11 12 13 14 选择项ACDAACAB 2yCAB C 1B 1A 1C 2A 2Ox第21题答案图第11页,共40页第12页,共40页23. (满分11分) (1) ΔAED ≌ΔDFC.∵ 四边形ABCD 是正方形,∴ AD=DC ，∠ADC=90º.又∵ AE ⊥DG ，CF ∥AE ， ∴ ∠AED=∠DFC=90º,… ∴ ∠EAD+∠ADE=∠FDC+∠ADE=90º， ∴ ∠EAD=∠FDC.∴ ΔAED ≌ΔDFC （AAS ）. (2) ∵ ΔAED ≌ΔDFC ，∴ AE=DF ，ED=FC. … ∵ DF=DE+EF ， ∴ AE=FC+EF. ）24. (1) ∵ 点A(3,4)在直线y=x+m 上，∴ 4=3+m. ∴ m=1.设所求二次函数的关系式为y=a(x-1)2. ∵ 点A(3,4)在二次函数y=a(x-1)2的图象上， ∴ 4=a(3-1)2, ∴ a=1.∴ 所求二次函数的关系式为y=(x-1)2. 即y=x 2-2x+1.(2) 设P 、E 两点的纵坐标分别为y P 和y E .∴ PE=h=y P -y E=(x+1)-(x 2-2x+1)=-x 2+3x.… 即h=-x 2+3x (0＜x ＜3). （3）略ABCDE F图6G图7第37页,共40页第38页,共40页密线学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：100分时间：100分钟）一、选择题（本大题共15小题，每小题4分，共60分） 1. 用配方法解一元二次方程01062=--x x 时，下列变形正确的是（） A ．1)3(2=+x B ．1)3(2=-x C ．19)3(2=+x D ．19)3(2=-x2. 一元二次方程0412=++x x 的根的情况是（）A ．有两个不相等的实数根B ．有两个相等的实数根C ．无实数根D ．无法确定根的情况 3. 若抛物线c x xy +-=22与y 轴的交点为（0，﹣3），则下列说法中，不正确的是（） A 抛物线开口向上B ．抛物线的对称轴是x =1C 当x =1时，y 有最大值为﹣4D. 抛物线与x 轴的交点坐标为（﹣1，0），（3，0）4. 二次函数y =x 2﹣4x +5的最小值是（） A ．﹣1 B ．1 C ．3 D ．55.下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（）A ．B ．C ．D ．6. 如图，在△ABC 中，∠CAB=65°，将△ABC 在平面内绕点A 旋转到△AB ′C ′的位置，使CC ′∥AB ，则旋转角的度数为（）A ．35°B ．40°C ．50°D ．65°7. 如图为二次函数y =ax 2+bx +c （a ≠0）的图象，与x 轴交点坐标为)0,1(-和)0,3(，对称轴是x =1，则下列说法：①a ＞0；②2a +b =0； ③a +b +c ＞0； ④当﹣1＜x ＜3时，y ＞0 其中正确的个数为（）A ．1B ．2C ．3D ．4题号一二三总分得分第6题第8题x =1第7题第11页,共40页第12页,共40页密封线内不得答题8. 如图，⊙O 的直径AB 垂直于弦CD ，垂足为E ，∠OAC=22.5°，OC=4，则CD 的长为（）A ．2B ．4C ．4D ．89.如图，A ，B ，C 是⊙O 上三点，∠ACB=25°，则∠BAO 的度数是（）A ．55°B ．60°C ．65°D ．70°10. 如图，AB 是⊙O 的弦，AC 是⊙O 切线，A 为切点，BC 经过圆心．若∠B=20°，则∠C=（）A ．20°B ．25°C ．40°D ．50° 11.如图，正比例函数x y =与反比例函数xy 1=的图象相交于A 、B 两点，BC ⊥x 轴于点C ，则△ABC 的面积为（） A .1B .2C ． 23D.2512. 如图，AB 是⊙O 的直径，弦CD ⊥AB ，∠CDB=30°，CD=，则阴影部分图形的面积为（）A ．4πB ．2πC ．πD ．13. 如图，在方格纸中，△ABC 经过变换得到△DEF ，则正确的变换是（）A ．把△ABC 绕点C 逆时针方向旋转90°，再向下平移2格B ．把△ABC 绕点C 顺时针方向旋转90°，再向下平移5格 C ．把△ABC 向下平移4格，再绕点C 逆时针方向旋转180°D ．把△ABC 向下平移5格，再绕点C 顺时针方向旋转180° 14. 在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为（）A ．B ．C ．D ．15. 若点（x 1，y 1），（x 2，y 2），（x 3，y 3）都是反比例函数xy 1-=图象上的点，并且y 1＜0＜y 2＜y 3，则下列各式中正确的是（）A.x 1＜x 2＜x 3 B ．x 1＜x 3＜x 2第11题第9题第10题第12题第13题第37页,共40页第38页,共40页密线学校班级姓名学号密封线内不得答题C ．x 2＜x 1＜x 3D ．x 2＜x 3＜x 1二、填空题（本大题共4小题，每小题7分，共28分）． 16. 某种型号的电脑，原售价为7200元/台，经连续两次降价后，现售价为4608元/台，则平均每次降价的百分率为．17. 在平面直角坐标系中，以原点为中心，把点A （4，5）逆时针旋转90°，得到的点A ′的坐标为___________． 18. 如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，连接AC ．若∠CAB=22.5°，CD=8cm ，则⊙O 的半径为 cm ．19. 如图，直线2+=x y 与抛物线y =ax 2+bx +6（a ≠0）相交于A （，）和B （4，m ），点P 是线段AB 上异于A 、B 的动点，过点P 作PC ⊥x 轴于点D ，交抛物线于点C ．当△PAC 为直角三角形时, 点P 的坐标____________________．三、解答题(共12分)20. (满分12分) 某市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y （千克）是销售单价x （元）的一次函数，且当x =60时，y =80；x =50时，y =100．在销售过程中，每天还要支付其它费用450元．（1）求y 与x 的函数关系式，并写出自变量x 的取值范围．（2）求该公司销售该原料日获利润w （元）与销售单价x （元）之间的函数关系式．（3）当销售单价为多少元时，该公司日获利润最大？最大利润是多少元？第18题第19题第11页,共40页第12页,共40页参考答案一、选择题（本大题共15小题，每小题4分，共60分）16. 20% 17. （﹣5，4） 18. 24 19. （3，5）或（，）三、解答题(共12分)20. 解：（1）设y=kx+b ，根据题意得，⎩⎨⎧５０ｋ＋ｂ＝１００ｋ＋ｂ＝８０60解得：k=﹣2，b=200，y=﹣2x+200 ------------ 3分自变量x 的取值范围是： 30≤x ≤60 --------4分（2）W=（x ﹣30）（﹣2x+200）﹣450=﹣2x 2+260x ﹣6450 ----------------8分（3）W=﹣2x 2+260x ﹣6450=﹣2（x ﹣65）2+2000； --------------------10分∵30≤x ≤60，∴x=60时，w 有最大值为1950元，∴当销售单价为60元时，该公司日获利最大，为1950元． -------------------12分。

2020年新人教版九年级数学上册期末测试卷及答案【必备】

期末检测题(二)时间：120分钟满分：120分一、选择题(每小题3分，共30分)1．(2016·沈阳)一元二次方程x 2－4x ＝12的根是( )A ．x 1＝2，x 2＝－6B ．x 1＝－2，x 2＝6C ．x 1＝－2，x 2＝－6D ．x 1＝2，x 2＝62．(2016·宁德)已知袋中有若干个球，其中只有2个红球，它们除颜色外其它都相同．若随机从中摸出一个，摸到红球的概率是14，则袋中球的总个数是( )A ．2B ．4C ．6D ．83．(2016·玉林)如图，CD 是⊙O 的直径，已知∠1＝30°，则∠2＝( )A ．30°B ．45°C ．60°D ．70°4．(2016·泸州)若关于x 的一元二次方程x 2＋2(k －1)x ＋k 2－1＝0有实数根，则k 的取值范围是( )A ．k ≥1B ．k ＞1C ．k ＜1D ．k ≤15．(2016·孝感)将含有30°角的直角三角板OAB 如图放置在平面直角坐标系中，OB 在x 轴上，若OA ＝2，将三角板绕原点O 顺时针旋转75°，则点A 的对应点A′的坐标为( )A ．(3，－1)B ．(1，－3)C ．(2，－2)D ．(－2，2)第3题图第5题图第6题图6．(2016·新疆)已知二次函数y ＝ax 2＋bx ＋c(a≠0)的图象如图所示，则下列结论中正确的是( )A ．a ＞0B ．c ＜0C ．3是方程ax 2＋bx ＋c ＝0的一个根D ．当x ＜1时，y 随x 的增大而减小7．如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为( )A ．①②B ．②③C ．①③D ．①②③8．已知点A(a －2b ，2－4ab)在抛物线y ＝x 2＋4x ＋10上，则点A 关于抛物线对称轴的对称点坐标为( )A ．(－3，7)B ．(－1，7)C ．(－4，10)D ．(0，10)第7题图第9题图第10题图9．如图，菱形ABCD 的边长为2，∠A ＝60°，以点B 为圆心的圆与AD ，DC 相切，与AB ，CB 的延长线分别相交于点E ，F ，则图中阴影部分的面积为( )A .3＋π2B .3＋πC .3－π2D ．23＋π210．如图，二次函数y ＝ax 2＋bx ＋c(a≠0)的图象与x 轴交于A ，B 两点，与y 轴交于点C ，且OA ＝OC.则下列结论：①abc＜0；②b 2－4ac 4a ＞0；③ac－b ＋1＝0；④OA·OB＝－ca .其中正确结论的个数是( )A ．4B ．3C ．2D ．1二、填空题(每小题3分，共24分)11．(2016·达州)设m ，n 分别为一元二次方程x 2＋2x －2 018＝0的两个实数根，则m 2＋3m ＋n ＝______．12．如图，AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F.若∠ACF＝65°，则∠E＝________．第12题图第14题图13．(2016·长沙)若同时抛掷两枚质地均匀的骰子，则事件“两枚骰子朝上的点数互不相同”的概率是________．14．(2016·南通)如图，BD 为正方形ABCD 的对角线，BE 平分∠DBC，交DC 与点E ，将△BCE 绕点C 顺时针旋转90°得到△DCF，若CE ＝1 cm ，则BF ＝__________cm .15．(2016·眉山)一个圆锥的侧面展开图是半径为8 cm 、圆心角为120°的扇形，则此圆锥底面圆的半径为________．16．(2016·荆州)若函数y ＝(a －1)x 2－4x ＋2a 的图象与x 轴有且只有一个交点，则a 的值为________．17．(2016·梧州)如图，点B 、C 把AD ︵分成三等分，ED 是⊙O 的切线，过点B 、C 分别作半径的垂线段，已知∠E ＝45°，半径OD ＝1，则图中阴影部分的面积是________．第17题图第18题图18．(2016·茂名)如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A1BO1的位置，使点A的对应点A1落在直线y＝33x上，再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y＝33x上，依次进行下去…，若点A的坐标是(0，1)，点B的坐标是(3，1)，则点A8的横坐标是________．三、解答题(共66分)19．(6分)解方程：(1)(2016·淄博)x2＋4x－1＝0；(2)(x－2)2－3x(x－2)＝0.20．(7分)(2016·青岛)小明和小亮用下面两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形．转动两个转盘各一次，若两次数字之积大于2，则小明胜，否则小亮胜．这个游戏对双方公平吗？请说明理由．21．(7分)(2016·宁夏)已知△ABC，以AB为直径的⊙O分别交AC于点D，BC于点E，连接ED，若ED＝EC.(1)求证：AB＝AC；(2)若AB＝4，BC＝23，求CD的长．22．(7分)如图，将矩形ABCD绕点A顺时针旋转，得到矩形AB′C′D′，点C的对应点C′恰好落在CB的延长线上，边AB交边C′D′于点E.(1)求证：BC＝BC′；(2)若AB＝2，BC＝1，求AE的长．23．(8分)(2016·贵港)为了经济发展的需要，某市2014年投入科研经费500万元，2016年投入科研经费720万元．(1)求2014至2016年该市投入科研经费的年平均增长率；(2)根据目前经济发展的实际情况，该市计划2017年投入的科研经费比2016年有所增加，但年增长率不超过15%，假定该市计划2017年投入的科研经费为a万元，请求出a的取值范围．24．(9分)如图，点A在x轴的正半轴上，以OA为直径作⊙P，C是⊙P上一点，过点C的直线y＝33x＋23与x轴，y轴分别相交于点D，点E，连接AC并延长与y轴相交于点B，点B的坐标为(0，43)．(1)求证：OE＝CE；(2)请判断直线CD与⊙P位置关系，证明你的结论，并求出⊙P半径的值．25．(10分)(2016·葫芦岛)某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．(1)请直接写出y与x的函数解析式；(2)当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？(3)设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？26．(12分)(2016·衡阳)如图，抛物线y ＝ax 2＋bx ＋c 经过△ABC 的三个顶点，与y 轴相交于(0，94)，点A 坐标为(－1，2)，点B 是点A 关于y 轴的对称点，点C 在x 轴的正半轴上．(1)求该抛物线的函数解析式；(2)点F 为线段AC 上一动点，过点F 作FE⊥x 轴，FG ⊥y 轴，垂足分别为点E ，G ，当四边形OEFG 为正方形时，求出点F 的坐标；(3)将(2)中的正方形OEFG 沿OC 向右平移，记平移中的正方形OEFG 为正方形DEFG ，当点E 和点C 重合时停止运动，设平移的距离为t ，正方形的边EF 与AC 交于点M ，DG 所在的直线与AC 交于点N ，连接DM ，是否存在这样的t ，使△DMN 是等腰三角形？若存在，求t 的值；若不存在，请说明理由．参考答案1．B 2.D 3.C 4.D 5.C 6.C 7.A 8.D 9.A10．B 11.2 016 12.50° 13.5614.2＋ 215.83 cm 16.－1或2或1 17.π818.63＋6 19．(1)x 1＝－2＋5，x 2＝－2－ 5.(2)x 1＝2，x 2＝－1. 20.这个游戏对双方是公平的．列表得：∴一共有6种情况，积大于2的有3种，∴P(积大于2)＝36＝12，∴这个游戏对双方是公平的． 21.(1)证明：∵ED＝EC ，∴∠EDC＝∠C，∵∠EDC＝∠B ，∴∠B＝∠C，∴AB＝AC.(2)如图所示，连接BD ，∵AB 为直径，∴BD⊥AC，设CD ＝a ，由(1)知AC ＝AB ＝4，则AD ＝4－a ，在Rt △ABD 中，由勾股定理可得BD 2＝AB 2－AD 2＝42－(4－a)2.在Rt △CBD 中，由勾股定理可得BD 2＝BC 2－CD 2＝(23)2－a 2.∴42－(4－a)2＝(23)2－a 2，整理得a ＝32，即CD ＝32.22.(1)证明：如图所示，连接AC ，AC′，∵四边形ABCD 为矩形，∴∠ABC＝90°，即AB⊥CC′，∵将矩形ABCD 绕点A 顺时针旋转，得到矩形AB′C′D′，∴AC＝AC′，∴BC＝BC′.(2)∵四边形ABCD 为矩形，∴AD＝BC ，∠D＝∠ABC′＝90°，将矩形ABCD 绕点A 顺时针旋转，得到矩形AB′C′D′，∴AD ＝AD′，∵BC ＝BC′，∴BC′＝AD′，在△AD′E 与△C′BE 中，⎩⎪⎨⎪⎧∠D′＝∠ABC′，∠AED′＝∠BEC′，AD′＝BC′，∴△AD′E≌△C′BE，∴BE＝D′E，设AE ＝x ，则D ′E＝2－x ，在Rt △AD′E 中，∠D′＝90°，由勾股定理，得x 2－(2－x)2＝1，解得x ＝54，∴AE＝54. 23.(1)设2014至2016年该市投入科研经费的年平均增长率为x ，根据题意，得500(1＋x)2＝720，解得x 1＝0.2＝20%，x 2＝－2.2(舍)，答：2014至2016年该市投入科研经费的年平均增长率为20%.(2)根据题意，得a －720720×100%≤15%，解得a≤828，又∵该市计划2017年投入的科研经费比2016年有所增加，故a 的取值范围为720＜a≤828.24.(1)证明：如图所示，连接OC ，∵直线y ＝33x ＋23与y 轴相交于点E ，∴点E 的坐标为(0，23)，即OE ＝2 3.又∵点B 的坐标为(0，43)，∴OB＝43，∴BE＝OE ＝23，又∵OA 是⊙P 的直径，∴∠ACO＝90°，即OC⊥AB，∴OE＝CE.(2)直线CD 是⊙P 的切线．证明：连接PC ，PE ，由(1)可知OE ＝CE.在△POE 和△PCE 中，⎩⎪⎨⎪⎧PO ＝PC ，PE ＝PE ，OE ＝CE ，∴△POE≌△PCE，∴∠POE＝∠PCE.又∵x 轴⊥y轴，∴∠POE＝∠PCE＝90°，∴PC⊥CE，即PC⊥CD.又∵直线CD 经过半径PC 的外端点C ，∴直线CD 是⊙P 的切线．∵对y ＝33x ＋23，当y ＝0时，x ＝－6，即OD ＝6，在Rt △DOE 中，DE ＝OD 2＋OE2＝62＋（23）2＝43，∴CD＝DE ＋EC ＝DE ＋OE ＝43＋23＝6 3.设⊙P 的半径为r ，则在Rt △PCD 中，由勾股定理知PC 2＋CD 2＝PD 2，即 r 2＋(63)2＝(6＋r)2，解得r ＝6，即⊙P 半径的值为6. 25.y ＝－2x ＋80(20≤x≤28)．(2)设当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是x 元，根据题意，得(x －20)y ＝150，则(x －20)(－2x ＋80)＝150，整理，得x 2－60x ＋875＝0，(x －25)(x －35)＝0，解得x 1＝25，x 2＝35(不合题意舍去)，答：每本纪念册的销售单价是25元．(3)由题意可得w ＝(x －20)(－2x ＋80)＝－2x 2＋120x －1600＝－2(x －30)2＋200，此时当x ＝30时，w 最大，又∵售价不低于20元且不高于28元，x ＜30时，y 随x 的增大而增大，∴当x ＝28时，w 最大＝－2(28－30)2＋200＝192(元)，答：该纪念册销售单价定为28元时，才能使文具店销售该纪念册所获利润最大，最大利润是192元． 26.(1)∵点B 是点A 关于y 轴的对称点，∴抛物线的对称轴为y 轴，∴抛物线的顶点为(0，94)，故抛物线的解析式可设为y ＝ax2＋94. ∵A(－1，2)在抛物线y ＝ax 2＋94上，∴a＋94＝2，解得a ＝－14，∴抛物线的函数解析式为y ＝－14x 2＋94.(2)①当点F 在第一象限时，如图1，令y ＝0得，－14x 2＋94＝0，解得x 1＝3，x 2＝－3，∴点C的坐标为(3，0)．设直线AC 的解析式为y ＝mx ＋n ，则有⎩⎪⎨⎪⎧－m ＋n ＝2，3m ＋n ＝0，解得⎩⎪⎨⎪⎧m ＝－12，n ＝32，∴直线AC 的解析式为y ＝－12x ＋32.设正方形OEFG 的边长为p ，则F(p ，p)．∵点F(p ，p)在直线y ＝－12x ＋32上，∴－12p ＋32＝p ，解得p ＝1，∴点F 的坐标为(1，1)．②当点F 在第二象限时，同理可得，点F 的坐标为(－3，3)，此时点F 不在线段AC 上，故舍去．综上所述，点F 的坐标为(1，1)．(3)过点M 作MH⊥DN 于点H ，如图2，则OD ＝t ，OE ＝t ＋1.∵点E 和点C 重合时停止运动，∴0≤t≤2.当x ＝t 时，y ＝－12t ＋32，则N(t ，－12t ＋32)，DN ＝－12t ＋32.当x ＝t ＋1时，y ＝－12(t＋1)＋32＝－12t ＋1，则M(t ＋1，－12t ＋1)，ME ＝－12t ＋1.在Rt △DEM 中，DM 2＝12＋(－12t ＋1)2＝14t2－t ＋2.在Rt △NHM 中，MH ＝1，NH ＝(－12t ＋32)－(－12t ＋1)＝12，∴MN 2＝12＋(12)2＝54.①当DN ＝DM时，(－12t ＋32)2＝14t 2－t ＋2，解得t ＝12；②当ND ＝NM 时，－12t ＋32＝54＝52，解得t ＝3－5；③当MN ＝MD 时，54＝14t 2－t ＋2，解得t 1＝1，t 2＝3.∵0≤t≤2，∴t＝1.综上所述，存在这样的t ，使△DMN 是等腰三角形，t 的值为12，3－5或1.。

【人教版】2020届九年级数学上学期期末考试试题(含解析) 新人教版

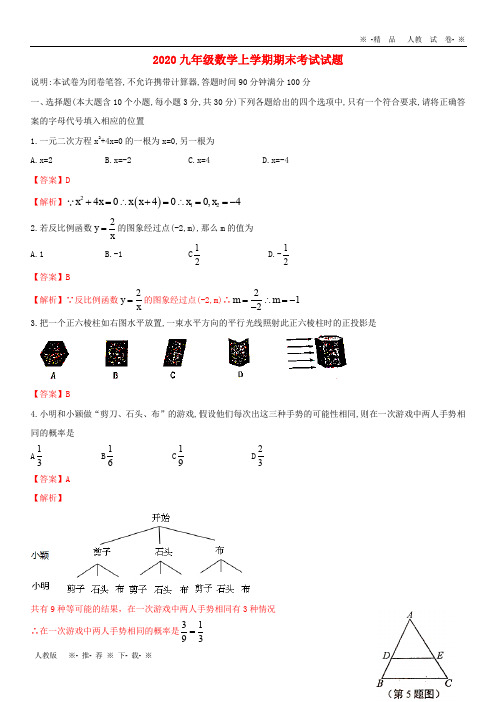
2020九年级数学上学期期末考试试题说明:本试卷为闭卷笔答,不允许携带计算器,答题时间90分钟满分100分一、选择题(本大题含10个小题,每小题3分,共30分)下列各题给出的四个选项中,只有一个符合要求,请将正确答案的字母代号填入相应的位置1.一元二次方程x 2+4x=0的一根为x=0,另一根为A.x=2B.x=-2C.x=4D.x=-4 【答案】D 【解析】()21240400,4x x x x x x +=∴+=∴==-2.若反比例函数2y x=的图象经过点(-2,m),那么m 的值为 A.1 B.-1 C 12 D.-12【答案】B【解析】∵反比例函数2y x =的图象经过点(-2,m)∴212m m =∴=-- 3.把一个正六棱柱如右图水平放置,一束水平方向的平行光线照射此正六棱柱时的正投影是【答案】B4.小明和小颖做“剪刀、石头、布”的游戏,假设他们每次出这三种手势的可能性相同,则在一次游戏中两人手势相同的概率是 A13 B 16 C 19 D 23【答案】A 【解析】共有9种等可能的结果，在一次游戏中两人手势相同有3种情况∴在一次游戏中两人手势相同的概率是3193=5.如图,△ABC中,点D,E分别在AB,AC边上,DE//BC,若AD=2DB,则△ADE与△ABC的面积比为A 23B49C25D35【答案】B【解析】∵DE∥BC，∴△ADE∽△ABC，∴=（）2=（23）2=496.下列四个表格表示的变量关系中,变量y是x的反比例函数的是【答案】C【解析】根据反比例函数的自变量与相应函数值的乘积是常数，可得答案7.在平面直角坐标系中,将四边形OABC四个顶点的横坐标、纵坐标分别乘-2,依次连接得到的四个点,可得到一个新四边形,关于所得四边形,下列说法正确的是A与原四边形关于x轴对称 B.与原四边形关于原点位似,相似比为1:2C.与原四边形关于原点中心对称D.与原四边形关于原点位似,相似比为2:1【答案】D【解析】在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.8,股市规定:股每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停:当跌了原价的10%后,便不能再跌,叫做跌停,现有一支股票某天涨停,之后两天时间又跌回到涨停之前的价格.若这两天此股票股价的平均下跌率为x,则x满足的方程是A.(1+10%)(1-x)2=1B.(1-10%)(1+x)2=1C.(1-10%)(1+2x)=1D.(1+10%)(1-2x)=1【答案】A【解析】(1+10%)(1-x)2=1；9.如图是一个几何体的三视图,则该几何体可能是下列的【答案】A【注意】左视图左内右外10.书画经装后更便于收藏,如图,画心ABCD 为长90cm 、宽30cm 的矩形,装裱后整幅画为矩形A B C D '''',两矩形的对应边互相平行,且AB 与A'B 的距离、CD 与C D ''的距离都等于4cm.当AD 与A D ''的距离、BC 与B'C'距离都等于acm,且矩形ABCD ∽矩形A B C D ''''时,整幅书画最美观,此时,a 的值为A.4B.6C.12D.24 【答案】C【解析】∵矩形ABCD ∽矩形A B C D ''''∴9030129023024AB BC a A B B C a =∴=∴=''''++⨯ 二、填空题(本大题含5个小题,每小题2分,共10分)把结果直接填在横线上 11.反比例函数3-y x=的图象位于坐标系的第_________________象限【答案】二、四【解析】当k>0时，两支曲线分别位于第一、三象限内，在图象所在的每一象限内，Y 随X 的增大而减小；当k<0时，两支曲线分别位于第二、四象限内，在图象所在的每一象限内，Y 随X 的增大而增大；两个分支无限接近x 和y 轴，但永远不会与x 轴和y 轴相交.12.如图,两张宽均为3cm 的矩形纸条交又重叠在一起,重叠的部分为四边形 ABCD.若测得AB=5cm,则四边形ABCD 的周长为___________cm.【答案】20 (第12题图) 【解析】过点A 作AE ⊥BC 于E ，AF ⊥CD 于F ，∵两条纸条宽度相同，∴AE=AF ．∵AB ∥CD ，AD ∥BC ，∴四边形ABCD 是平行四边形．∵S ▱ABCD =BC•AE=CD•AF．AE=AF ．∴BC=CD ，∴四边形ABCD 是菱形． ∵菱形四边相等∴四边形ABCD 的周长为4AB=2013.如图,正五边形ABCDE 的各条对角线的交点为M,N,P,Q,R,它们分别是各条对角线的黄金分割点,若AB=2,则MN 的长为_________【答案】3【解析】∵M 为线段AD 的黄金分割点，AM ＞DM∴12AM AD =即32DM DA =同理可得DN DB =MDN ＝∠ADB ∴MND ADB ∆∆ ∴MN DM AB DA =即2MN =∴3MN =14新年期间,某游乐场准备推出幸运玩家抽奖活动,其规则是:在一个不透明的袋子里装有若干个红球和白球(每个球除颜色外都完全相同),参加抽奖的人随机摸一个球,若摸到红球,则可获赠游乐场通票一张.游乐场预估有300人参加抽奖活动,计划发放游乐场通票60张,则袋中红、白两种颜色小球的数量比应为______________ 【答案】1:4【解析】设红球m 个，白球y 个，根据大量反复试验下频率稳定值即概率可得60300mm n=+ 化简得4m n =∴袋中红、白两种颜色小球的数量比应为m:n=1:4 15.如图,点A,C 分别在反比例函数4-y x= (x<0)与9y x = (x>0)的图象上,若四边形OABC 是矩形,且点B 恰好在y 轴上,则点B 的坐标为______________ 【答案】B(0,6) 【解析】如图，作AD ⊥x 轴，垂足为D ，CE ⊥x 轴，垂足为E. 约定49,,,A m C n m n ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭（m<0,n>0）由k 字形结论可得AD OD OE CE=即49m m n n--=化简得mn=-6 再根据平行四边形坐标特点相邻之和减相对可得00490B B x m n y m n =+-=⎧⎪⎨=-+-⎪⎩∴6B m n y ==== ∴) DE三、解答题(本大题含8个小题,共60分)解答时应写出必要的文字说明、演算步骤或推理过程 16.解下列方程:(每题4分,共8分) (1)x 2-8x+1=0; 解：移项得：x 2-8x=-1 配方得：x 2-8x+42=-1+42即（x-4）2=15直接开平方得4x -=∴原方程的根为1244x x ==(2)x(x-2)+x-2=0解：提取公因式（x-2）得（x-2）（x+1）=0 ∴原方程的根为122,1x x ==-17.(本题6分)已知矩形ABCD,AE 平分∠DAB 交DC 的延长线于点E,过点E 作EF ⊥AB,垂足F 在边AB 的延长线上,求证:四边形ADEF 是正方形.【解析】∵矩形ABCD ∴∠D=∠DAB=90°，∵EF ⊥AB ∴∠F=90° ∴四边形ADEF 是矩形 ∵∠D=90°∴ED ⊥DA∵AE 平分∠DAB ，EF ⊥AB ∴ED=EF ∴四边形ADEF 是正方形 18.(本题9分)花园的护栏由木杆组成,小明以其中三根等高的木杆为观测对象,研究它们影子的规律图1,图2中的点A,B,C 均为这三根木杆的俯视图(点A,B,C 在同一直线上) (1)图1中线段AD 是点A 处的木杆在阳光下的影子,请在图1中画出表示另外两根木杆同一时刻阳光下的影子的线段;(2)图2中线段AD,BE 分别是点A,B 处的木杆在路灯照射下的影子,其中DE ∥AB,点O 是路灯的俯视图,请在图2中画出表示点C 处木杆在同一灯光下影子的线段;(3)在(2)中,若O,A 的距离为2m,AD=2.4m,OB=1.5m,则点B 处木杆的影子线段BE 的长为___________m 【解析】(1)如图1,线段BE,CF 即为所求（太阳光是平行光，考查平行投影）(2)如图2,线段CG 即为所求;（考查点投影） ⑶1.8 ∵DE//AB ∴OA OB OD OE =即2 1.51.822.4 1.5OA OB BE m OA OD OB BE BE=∴=∴=++++19.(本题6分)王叔叔计划购买一套商品房,首付30万元后,剩余部分用贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,每月所还贷款本金数相同,设王叔叔每月偿还贷款本金y 万元,x 个月还清,且y 是x 的反比例函数,其图象如图所示(1)求y 与x 的函数关系式;(2)王叔叔购买的商品房的总价是__________万元;(3)若王叔叔计划每月偿还贷款本金不超过2000元,则至少需要多少个月还清?【解析】(1)设y 与x 之间的函数关系式为ky x= (k ≠0). 根据题意,得点(120,0.5)在k y x =的图象上,∴0.5120k=解得k=60∴y 与x 之间的函数关系式为60y x= (x>0)(2)90;∵王叔叔每月偿还贷款本金y 万元,x 个月还清∴贷款金额xy=60万元 ∴王叔叔购买的商品房的总价为首付与贷款金额的和即30+60=90（万元） (3)2000元=0.2万元根据题意,得y=0.2,x=300由图，y ≤2000的图像位于Ⅱ区域即x ≥300 ∴至少需要300个月还清.20.(本题6分)新年联欢会,班里组织同学们进行才艺展示,如图所示的转盘被等分成四个扇形,每个扇形区域代表一项才艺：1-唱歌；2-舞蹈；3-朗诵；4-演奏.每名同学要随机转动转盘两次,转盘停止后,根据指针指向的区域确定要展示的两项内容(若两次转到同一区域或分割线上,则重新转动,直至得出不同结果).求小明恰好展示“唱歌”和“演奏”两项才艺的概率.【解析】转动转盘两次所有可能出现的结果列表如下:由列表可知共有12种结果,每种结果出现的可能性相同小明恰好展示“唱歌”和“演奏”才艺的结果有2种:(1, 4),(4,1) 所以小明恰好展示“唱歌”和“演奏”才艺的概率是21126. 21.(本题6分)为了弘扬山西地方文化,我省举办了“第三届山西文化博览会”,博览会上一种文化商品的进价为30元/件,售价为40元/件,平均每天能售出600件.调查发现,售价在40元至60元范围内,这种商品的售价每上涨1元,其每天的销售量就减少10件,为使这种商品平均每天的销售利润为10000元,这种商品的售价应定为多少元? 解:设这种商品的涨价x 元，根据题意,得（40-30+x ）（600-10x ）=10000Ⅱ0.2即（10+x ）（60-x ）=1000 ()()106070(205070,20501000)x x ++-=+=⨯= 解得x 1=10,x 2=40∴售价为40+10=50或40+40=80∵售价在40元至60元范围内∴售价应定为50元答:售价应定为50元. 22.(本题12分)综合与实践: 问题情境:如图1,矩形ABCD 中,BD 为对角线,ADk AB= ,且k>1.将△ABD 以B 为旋转中心,按顺时针方向旋转,得到△FBE(点D 的对应点为点E,点A 的对应点为点F),直线EF 交直线AD 于点G(1)在图1中连接AF,DE,可以发现在旋转过程中存在一个三角形始终与△ABF 相似,这个三角形是_______,它与△ABF 的相似比为______(用含k 的式子表示);【答案】(1)△【解析】本题考查子母牵手模型由旋转性质可得△ABD ≌△FBE ∴BA=BF,BD=BE ，∠ABD=∠FBE ∴,AB BFABF DBE BD BE=∠=∠ ∴△ABF ∽△DBE ∵AD k AB =∴△DBE 与△ABF相似比为BD AB =数学思考:(2)如图2,当点E 落在DC 边的延长线上时,点F 恰好落在矩形ABCD 的对角线BD 上,此时k 的值为______【解析】由旋转性质可得△ABD ≌△FBE∴BD=BE ，AD=FE ∵ 矩形ABCD ∴AD=BC ∴EF=BC∵BD FE DE BC =(等面积转换) ∴BD=DE ∴等边三角形BDE∴tan 603ADAB==实践探究A B※ -精品人教试卷- ※(3)如图3,当点E 恰好落在BC 边的延长线上时,求证:CE=FG; 【解析】(首推方法2) 方法1：常规法设EF 与BD 交于点O由旋转性质可得△ABD ≌△FBE ∴∠ADB=∠FEB,BD=BE,AD=FE, ∵四边形ABCD 是矩形,AD//BC,AD=BC ∴∠ADB=∠DBC,∠FEB=∠EGD ∠ADB=∠EGD,∠FEB=∠DBC OD= OG, OE=OB OD+OB=OG+OE,即BD=GE ∵BD=BE ∴BE= EG∵CE= BE- BC, GF= GE- EF, E 且BC= AD=FF ∴CE= GE 方法2面积法由旋转性质可得△ABD ≌△FBE ∴∠BAD=∠BFE,BA=BF,AD=FE, ∵四边形ABCD 是矩形,AD//BC,AB=DC ∴BDE BGE S S BE DC GE BF ∆∆=∴= ∵BA=BF, AB=DC ∴DC=BF ∴BE=GE∵CE= BE- BC, GF= GE- EF, E 且BC= AD=FF ∴CE= GE (4)当k=43时,在△ABD 绕点B 旋转的过程中,利用图4探究下面的问题请从A,B 两题中任选一题作答,我选择 A:当AB 的对应边FB 与AB 垂直时,直接写出DGAB的值. 【答案】1733或【解析】如图B:当AB 的对应边FB 在直线BD 上时,4m3m3mBG3mA※ -精品人教试卷- ※【答案】51063或【解析】如图情况1：425cos 5255236AD FD m ADB GD m BD GD GD mDG AB m ∠==∴=∴=∴==情况2：48cos 105101033AD FD mADB GD m BD GD GDDG m AB m ∠==∴=∴=∴==23.(本题12分)如图1,平面直角坐标系中,△OAB 的顶点A,B 的坐标分别为(-2,4)、(-5,0).将△OAB 沿OA 翻折,点B 的对应点C 恰好落在反比例函数ky x=(k ≠0)的图象上(1)判断四边形OBAC 的形状,并证明. 【解析】(1)四边形OBAC 是菱形证明:过点A 作AE ⊥x 轴于点E∵A(-2,4)∴ OE=2, AE=4 ∵B(-5,0)∴BE= OB- OE= 3 在Rt △ABE 中,由勾股定理得∴ AB= BO∵△AOB 沿AO 折叠,点B 的对应点是点C ∴AB= AC, OB= OC ∴AB= OB= AC = OC.4mCG∴四边形OBAC 是菱形(2)直接写出反比例函数k y x =(k ≠0)的表达式. 【答案】12y x= 【解析】20(5)3,4004C A O B C A O B x x x x y y y y =+-=-+--==+-=+-=∴C （3,4）∵C 恰好落在反比例函数k y x =的图象上∴4123k k =∴=∴12y x = (3)如图2,将△OAB 沿y 轴向下平移得到△OA'B',设平移的距离为m(0<m<4),平移过程中△O'A'B'与△OAB 重叠部分的面积为S.探究下列问题请从A,B 两题中任选一题作答,我选择___________A:若点B 的对应点B’恰好落在反比例函数k y x =(k ≠0)的图象上,求m 的值,并直接写出此时S 的值【解析】连接BB’△OAB 沿y 轴向下平移得到△OA’B',BB’∥y 轴,BB’=m∵B(-5,0)∴点B'的横坐标为-5将x=-5代入12y x =.得y=-2.4 B'(-5,-2,4),BB’=2.4,即m=2.4B:若S=12OAB S ∆,求m 的值; 【解析】连接AA ′并延长AA’交x 轴于点H,设A'B',A’O′交OB于点M,N 则AA ′=m,由平移可知∠MAN=∠BAO,AH ⊥OB,A’M∥AB,∴△A’MN∽△ABO212A MN ABO S A H A H SAH AH '''⎛⎫==∴= ⎪⎝⎭∵AH=4, ∴A H '=∴AA’=AH -A’H=4- ,即m=4-(4)如图3,连接BC,交AO 于点D,点P 是反比例函数k y x=(k ≠0)的图象上的一点, 请从A,B两题中任选一题作答,我选择____________A:在x 轴上是否存在点Q,使得以点O,D,P,Q 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的平行四边形的顶点P,Q 的坐标;若不存在,说明理由;【答案】存在,点P 与Q 的坐标如下:P 1(6,2)与Q 1(7,0); P 2(6,-2)与Q 2(-7,0); P 3(-6,-2)与Q 3(-7,0);【解析】由题意D 为AO 中点∵A(-2,4) ∴D （-1,2）设Q （t ，0），P （12,m m） OP 为对角线：()016127002Q O P D Q O P D x x x x t m m t y y y y m ⎧=+-∴=+--=⎧⎪⇒⎨⎨==+-∴=+-⎩⎪⎩∴P 1(6,2)与Q 1(7,0) OD 为对角线：0(1)161270202P O D Q P O D Q x x x x m t t m t y y y y m =+-∴=+--=--⎧=⎧⎪⇒⎨⎨=-=+-∴=+-=⎩⎪⎩∴P 2(6,-2)与Q 2(-7,0); PD 为对角线：(1)06127020Q P D O Q P D O x x x x t m m t y y y y m =+-∴=+--⎧=-⎧⎪⇒⎨⎨=-=+-∴=+-⎩⎪⎩∴P 3(-6,-2)与Q 3(-7,0) B:在坐标平面内是否存在点Q,使得以点A,O,P,Q 为顶点的四边形是矩形?若存在,直接写出所有满足条件的点Q 的坐标;若不存在,说明理由【答案】存在,点Q 的坐标如下()()()12344,24,10,5,(2,4)Q Q Q Q ---【解析】先求P 点坐标，分别过O 、A 作直线交12y x=于 P 1，P 2，P 3，P 4 设P 2P 4所在直线为y=kx ，P 2（m ，n ）∴n=mk由A(-2,4)易得tan ∠1=tan ∠2=12 则12n k m == 直线12y x =与12y x =联立解得x x y y ⎧⎧==-⎪⎪⎨⎨==⎪⎪⎩⎩∴((24,P P -22202Q A P O x x x x =+-=-+=,22404Q A P O y y y y =+-==∴()24Q同理4(2,4)Q -设P 1P 3所在直线为12y x =+b 将A(-2,4)代入可得b=5 152y x =+与12y x =联立解得122,16x x y y =-=⎧⎧⎨⎨=-=⎩⎩∴()()132,6,12,1P P -- ()112024Q P O A x x x x =+-=+--= 116042Q P O A y y y y =+-=+-= ∴()14,2Q同理()310,5Q --。

2020人教版九年级(上)期末数学试卷含解析答案(五套)

人教版九年级（上）期末数学试卷（一）一．选择题（共10小题）1．已知m，n是一元二次方程x2＝x的两个实数根，则下列结论错误的是（）A．m+n＝0 B．m•n＝0 C．m2＝m D．n2＝n2．在平面直角坐标系中，抛物线y＝x（x+2）经过平移变换后得到抛物线y＝（x﹣1）2，其变换是（）A．右移2个单位，下移1个单位B．右移2个单位，上移1个单位C．左移2个单位，上移1个单位D．左移2个单位，下移1个单位3．在平面直角坐标系中，等腰直角三角形的两个锐角顶点坐标为（2，3），（0，﹣1），则它的直角顶点坐标为（）A．（3，0）B．（﹣1，2）C．（1，1）D．（3，0），（﹣1，2）4．如图，AB是⊙O的弦，AC是⊙O的直径，将沿着AB弦翻折，恰好经过圆心O．若⊙O 的半径为6，则图中阴影部分的面积等于（）A．6πB．9C．9πD．65．已知事件：①掷一次骰子，向上一面的点数是偶数；②在13位同学中至少有2人生肖相同；③若彩票中奖率10%，那么买10张彩票一定中奖；④任意画一个三角形，其内角和为360°，其中随机事件是（）A．①②B．①③C．②④D．③④6．如图，点P在函数y＝（x＞0）的图象上，过点P分别作x轴，y轴的平行线，交函数y＝﹣的图象于点A，B，则△PAB的面积等于（）A．B．C．D．7．已知A（0，﹣1），B（1，﹣3），先将线段AB向左平移3个单位，再以原点O为位似中心，在第一象限内，将其扩大为原来3倍，则点A的对应点坐标为（）A．（3，9）B．（6，3）C．（6，9）D．（9，3）8．如图，过菱形ABCD的顶点C的直线与AB的延长线交于点E，与AD的延长线交于点F，若菱形的边长为x，BE＝a，DF＝b，则a，b，x满足的关系是（）A．2x＝a+b B．x2＝a•b C．x（a+b）＝a•b D．2x2＝a2+b29．直线y＝kx+4与函数y＝的图象有且只有一个公共点，则k的值为（）A．2 B．﹣2 C．﹣1 D．±210．如图，在△ABC中，∠ACB＝90°，点D是AB边上的动点，设AD＝x，CD＝y，y关于x 的函数关系图象如图所示，其中M为曲线部分的最低点，则BC的长为（）A．10 B．15 C．20 D．25二．填空题（共5小题）11．配方4a（ax2+bx+c）＝（2ax+b）2+m，则m＝．12．已知抛物线y＝﹣x2+bx+c经过（﹣1，a）和（3，a）两点，则a﹣c＝．13．直线y＝ax（a≠0）与函数y＝（k≠0）的图象交于点A（1，2），若＞ax，则x的取值范围是．14．某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为．15．如图，在矩形ABCD中，已知AB＝2，点E是BC边的中点，连接AE，△AB′E和△ABE 关于AE所在直线对称，若△B′CD是直角三角形，则BC边的长为．三．解答题（共8小题）16．关于x的方程（m+2）x2﹣4x+1＝0有两个不相等实数根．（1）求m的取值范围；（2）当m为正整数时，求方程的根．17．某公司推出一款新产品，该产品的成本单价是80元，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系y＝﹣5x+600．（注：日销售利润＝日销售量×（销售单价﹣成本单价））（1）销售单价x＝元时，日销售利润w最大，最大值是元；（2）要实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？18．在甲、乙两个不透明的盒子中，分别装有除颜色外其它完全相同的小球，其中，甲盒子装有2个白球，1个红球；乙盒子装有2个红球，1个白球．（1）将甲盒子摇匀后，随机取出一个小球，求小球是白色的概率；（2）小华和同桌商定：将两个盒子摇匀后，各随机摸出一个小球．若颜色相同，则小华获胜；若颜色不同，则同桌获胜，请用列表法或画出树状图的方法说明谁赢的可能性大．19．如图，是一座横跨沙颖河的斜拉桥，拉索两端分别固定在主梁l和索塔h上，索塔h 垂直于主梁l，垂足为D．拉索AE，BF，CG的仰角分别是α，45°，β，且α+β＝90°（α＜β），AB＝15m，BC＝5m，CD＝4m，EF＝3FG，求拉索AE的长．（精确到1m，参考数据：≈2.24，≈1.41）20．如图，直线y＝x+b与y轴交于点A（0，4），与函数y＝（k＞0，x＜0）的图象交于点C，以AC为对角线作矩形ABCD，使顶点B，D落在x轴上（点D在点B的右边），BD 与AC交于点E．（1）求b和k的值；（2）求顶点B，D的坐标．21．如图，点P在∠MAN内，PA平分∠MAN，PB⊥AM于点B，PC⊥AN于点C，点D是射线AM 上点B右侧的一个定点．（1）作经过A，P，D三点的圆；（保留作图痕进，不写作法）（2）设圆与AN交于点E，∠MAN＝60°，PA＝4，求AE+AD的值．22．在△ABC中，CA＝CB，∠ACB＝α（0°＜α＜180°）．点P是平面内不与A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，CP．点M 是AB的中点，点N是AD的中点．（1）问题发现如图1，当α＝60°时，的值是，直线MN与直线PC相交所成的较小角的度数是．（2）类比探究如图2，当α＝120°时，请写出的值及直线MN与直线PC相交所成的较小角的度数，并就图2的情形说明理由．（3）解决问题如图3，当α＝90°时，若点E是CB的中点，点P在直线ME上，请直接写出点B，P，D在同一条直线上时的值．23．如图，抛物线y＝ax2+x+c交x轴于A，B两点，交y轴于点C．直线y＝﹣+2经过点A，C．（1）求抛物线的解析式；（2）点P在抛物线在第一象限内的图象上，过点P作x轴的垂线，垂足为D，交直线AC 于点E，连接PC，设点P的横坐标为m．①当△PCE是等腰三角形时，求m的值；②过点C作直线PD的垂线，垂足为F．点F关于直线PC的对称点为F′，当点F′落在坐标轴上时，请直接写出点P的坐标．参考答案与试题解析一．选择题（共10小题）1．已知m，n是一元二次方程x2＝x的两个实数根，则下列结论错误的是（）A．m+n＝0 B．m•n＝0 C．m2＝m D．n2＝n【分析】可以根据根与系数的关系判断选项A、B；求出方程的解，即可判断选项C、D．【解答】解：x2＝x，x2﹣x＝0，由根与系数的关系得：m+n＝1，m•n＝0，解方程x2﹣x＝0得：x＝0或1，∵m，n是一元二次方程x2＝x的两个实数根，∴设m＝0，n＝1，∴m2＝m，n2＝n，即只有选项A符合题意，选项B、C、D都不符合题意；故选：A．2．在平面直角坐标系中，抛物线y＝x（x+2）经过平移变换后得到抛物线y＝（x﹣1）2，其变换是（）A．右移2个单位，下移1个单位B．右移2个单位，上移1个单位C．左移2个单位，上移1个单位D．左移2个单位，下移1个单位【分析】根据变换前后的两抛物线的顶点坐标找变换规律．【解答】解：y＝x（x+2）＝（x+1）2﹣1，顶点坐标是（﹣1，﹣1）．y＝（x﹣1）2，顶点坐标是（1，0）．所以将抛物线y＝x（x+2）右移2个单位，上移1个单位得到抛物线y＝（x﹣1）2，故选：B．3．在平面直角坐标系中，等腰直角三角形的两个锐角顶点坐标为（2，3），（0，﹣1），则它的直角顶点坐标为（）A．（3，0）B．（﹣1，2）C．（1，1）D．（3，0），（﹣1，2）【分析】画出相应的图形，借助网格作出AB的中垂线，直角顶点一定在AB的中垂线上，借助可求出四边形ACBD的边长，进而得出ACBD是正方形，得到点C、D符合题意．【解答】解：将A（2，3），B（0，﹣1）描述在坐标系中，如图所示：借助网格，可以作出AB的中垂线CD，此时由勾股定理可求出：AD＝BD＝BC＝AC＝＝，可得ACBD是正方形，从而△ACB，△DAB是等腰直角三角形，∴C（﹣1，2），D（3，0）符合题意，故选：D．4．如图，AB是⊙O的弦，AC是⊙O的直径，将沿着AB弦翻折，恰好经过圆心O．若⊙O 的半径为6，则图中阴影部分的面积等于（）A．6πB．9C．9πD．6【分析】由题意△OBC是等边三角形，弓形OnB的面积＝弓形BmC的面积，根据S阴＝S计算即可．△OBC【解答】解：如图，连接OB，BC．由题意△OBC是等边三角形，弓形OnB的面积＝弓形BmC的面积，∴S阴＝S△OBC＝×62＝9，故选：B．5．已知事件：①掷一次骰子，向上一面的点数是偶数；②在13位同学中至少有2人生肖相同；③若彩票中奖率10%，那么买10张彩票一定中奖；④任意画一个三角形，其内角和为360°，其中随机事件是（）A．①②B．①③C．②④D．③④【分析】根据随机事件、必然事件以及不可能事件的定义即可作出判断．【解答】解：随机事件：①③；必然事件：②；不可能事件：④．故选：B．6．如图，点P在函数y＝（x＞0）的图象上，过点P分别作x轴，y轴的平行线，交函数y＝﹣的图象于点A，B，则△PAB的面积等于（）A．B．C．D．【分析】根据题意设P点坐标为P（x，），再利用反比例函数解析式y＝﹣分别表示点A、点B的坐标，然后根据三角形面积公式计算．【解答】解：∵点P在函数y＝（x＞0）的图象上，PA∥x轴，PB∥y轴，∴设P（x，），∴点B的坐标为（x，﹣），A点坐标为（﹣x，），∴△PAB的面积＝（x+）（+）＝．故选：D．7．已知A（0，﹣1），B（1，﹣3），先将线段AB向左平移3个单位，再以原点O为位似中心，在第一象限内，将其扩大为原来3倍，则点A的对应点坐标为（）A．（3，9）B．（6，3）C．（6，9）D．（9，3）【分析】先利用点平移的坐标特征写出平移后A点的对应点的坐标，然后把平移后的点的横纵坐标都乘以﹣3得到位似后点A的对应点坐标．【解答】解：线段AB向左平移3个单位得到A点的对应点的坐标为（﹣3，﹣1），以原点O为位似中心，在第一象限内，将其扩大为原来3倍，所以点A的对应点坐标为（9，3）．故选：D．8．如图，过菱形ABCD的顶点C的直线与AB的延长线交于点E，与AD的延长线交于点F，若菱形的边长为x，BE＝a，DF＝b，则a，b，x满足的关系是（）A．2x＝a+b B．x2＝a•b C．x（a+b）＝a•b D．2x2＝a2+b2【分析】利用相似三角形的性质构建关系式即可解决问题．【解答】解：∵四边形ABCD是菱形，∴CD∥AE，∴△FDC∽△FAE，∴＝，∴＝，整理得：x2＝ab，故选：B．9．直线y＝kx+4与函数y＝的图象有且只有一个公共点，则k的值为（）A．2 B．﹣2 C．﹣1 D．±2【分析】解方程组得到kx2+4x﹣2＝0，由反比例函数的图象与直线y＝kx+4（k≠0）只有一个公共点，得到△＝16+8k＝0，求得k＝﹣2．【解答】解：解得kx2+4x﹣2＝0，∵线y＝kx+4与函数y＝的图象有且只有一个公共点，∴△＝16+8k＝0，∴k＝﹣2，故选：B．10．如图，在△ABC中，∠ACB＝90°，点D是AB边上的动点，设AD＝x，CD＝y，y关于x 的函数关系图象如图所示，其中M为曲线部分的最低点，则BC的长为（）A．10 B．15 C．20 D．25【分析】由图象可得当CD⊥AB时，CD的长最小，可得此时AD＝9，CD＝12，由勾股定理可求AC，由锐角三角函数可求BC的长．【解答】解：由题意可得当CD⊥AB时，CD的长最小，∴此时AD＝9，CD＝12，∴AC＝＝＝15，∵tan∠A＝，∴∴BC＝20，故选：C．二．填空题（共5小题）11．配方4a（ax2+bx+c）＝（2ax+b）2+m，则m＝4ac﹣b2．【分析】根据完全平方公式配方，即可得m．【解答】解：4a（ax2+bx+c）＝4a2x2+4abx+b2﹣b2+4ac＝（2ax+b）2+﹣b2+4ac＝（2ax+b）2+m，则m＝4ac﹣b2．故答案是：4ac﹣b2．12．已知抛物线y＝﹣x2+bx+c经过（﹣1，a）和（3，a）两点，则a﹣c＝﹣3 ．【分析】根据已知抛物线y＝﹣x2+bx+c经过（﹣1，a）和（3，a）两点求出抛物线的对称轴，求出b的值，再把点（﹣1，a）代入，即可求出答案．【解答】解：∵抛物线y＝﹣x2+bx+c经过（﹣1，a）和（3，a）两点，∴抛物线的对称轴是直线x＝＝1，即﹣＝1，解得：b＝2，即y＝﹣x2+bx+c＝﹣x2+2x+c，把（﹣1，a）代入得：a＝﹣1﹣2+c，即a﹣c＝﹣3，故答案为：﹣3．13．直线y＝ax（a≠0）与函数y＝（k≠0）的图象交于点A（1，2），若＞ax，则x的取值范围是0＜x＜1或x＜﹣1 ．【分析】根据对称性即可得到点B的坐标，然后根据A、B点的坐标即可求得x的取值范围．【解答】解：∵直线y＝ax（a≠0）与函数y＝（k≠0）的图象交于点A（1，2），∴直线y＝ax（a≠0）与函数y＝（k≠0）的图象交于另一个点B的坐标是（﹣1，﹣2），如图，若＞ax，则x的取值范围是0＜x＜1或x＜﹣1，故答案为0＜x＜1或x＜﹣1．14．某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为．【分析】随机事件A的概率P（A）＝事件A可能出现的结果数÷所有可能出现的结果数，据此用绿灯亮的时间除以三种灯亮的总时间，求出抬头看信号灯时，是绿灯的概率为多少即可．【解答】解：抬头看信号灯时，是绿灯的概率为．故答案为：．15．如图，在矩形ABCD中，已知AB＝2，点E是BC边的中点，连接AE，△AB′E和△ABE 关于AE所在直线对称，若△B′CD是直角三角形，则BC边的长为4或2．【分析】连接BB′，根据直角三角形的判定定理得到∠BB′C＝90°，求得∠B′CD＜90°，（1）如图1，∠B′DC＝90°，（2）如图2，∠CB′D＝90°，则B，B′D三点共线，设AE，BB′交于F，根据相似三角形的性质即可得到结论．【解答】解：连接BB′，∵BE＝B′E＝EC，∴∠BB′C＝90°，∴∠B′CD＜90°，（1）如图1，∠B′DC＝90°，则四边形ABEB′和ECDB′是正方形，∴BC＝2AB＝4，（2）如图2，∠CB′D＝90°，则B，B′D三点共线，设AE，BB′交于F，则F，B′是对角线BD的三等分点，∵△BCB′∽△CDB′，∴＝＝，∴＝，∴BC＝CD＝2，故答案为：4或2．三．解答题（共8小题）16．关于x的方程（m+2）x2﹣4x+1＝0有两个不相等实数根．（1）求m的取值范围；（2）当m为正整数时，求方程的根．【分析】（1）根据当△＞0时，方程有两个不相等的两个实数根、一元二次方程的定义列式计算即可；（2）根据题意求出m，利用因式分解法解出方程．【解答】解：（1）由题意得，m+2≠0，（﹣4）2﹣4×（m+2）＞0，解得，m＜2且m≠﹣2；（2）∵m＜2，m为正整数，∴m＝1，则原方程可化为3x2﹣4x+1＝0，（3x﹣1）（x﹣1）＝0，解得，x1＝，x2＝1．17．某公司推出一款新产品，该产品的成本单价是80元，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系y＝﹣5x+600．（注：日销售利润＝日销售量×（销售单价﹣成本单价））（1）销售单价x＝100 元时，日销售利润w最大，最大值是2000 元；（2）要实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？【分析】（1）根据题意列出有关利润w与销售单价x之间的二次函数，配方后即可确定最值；（2）根据销售利润不低于3750元列出不等式即可确定正确的答案．【解答】解：（1）w＝（﹣5x+600）（x﹣80）＝﹣5x2+1000x﹣48000＝﹣5（x﹣100）2+2000，∵﹣5＜0，∴当x＝100时，w取得最大值，最大值是2000；故答案为：100，2000；（2）设成本单价为a圆，当x＝100时，w＝（﹣5×90+600）（90﹣a）≥3750，解得，a≤65，答：该产品的成本单价应不超过65元．18．在甲、乙两个不透明的盒子中，分别装有除颜色外其它完全相同的小球，其中，甲盒子装有2个白球，1个红球；乙盒子装有2个红球，1个白球．（1）将甲盒子摇匀后，随机取出一个小球，求小球是白色的概率；（2）小华和同桌商定：将两个盒子摇匀后，各随机摸出一个小球．若颜色相同，则小华获胜；若颜色不同，则同桌获胜，请用列表法或画出树状图的方法说明谁赢的可能性大．【分析】（1）由概率公式即可得出答案；（2）由列表可知，共有9种等可能结果，其中颜色不相同的结果有4种，颜色相同的结果有5种，P（颜色不相同）＝，P（颜色相同）＝，即可得出答案．【解答】解：（1）共有3种等可能结果，而摸出白球的结果有2种∴P（摸出白球）＝；（2）根据题意，列表如下：由上表可知，共有9种等可能结果，其中颜色不相同的结果有5种，颜色相同的结果有4种，∴P（颜色不相同）＝，P（颜色相同）＝，∵＜，∴同桌获胜获胜的可能性大．19．如图，是一座横跨沙颖河的斜拉桥，拉索两端分别固定在主梁l和索塔h上，索塔h 垂直于主梁l，垂足为D．拉索AE，BF，CG的仰角分别是α，45°，β，且α+β＝90°（α＜β），AB＝15m，BC＝5m，CD＝4m，EF＝3FG，求拉索AE的长．（精确到1m，参考数据：≈2.24，≈1.41）【分析】证出△BDF是等腰直角三角形，得出FD＝BD＝BC+CD＝9m，证明△ADE∽△GDC，得出＝，则AD•CD＝GD•ED，设EF＝3FG＝3x，则24×4＝（9﹣x）（9+3x），解得EF＝3，得出DE＝EF+FD＝12m，由勾股定理求出AE即可．【解答】解：在Rt△BDF中，∵∠DBF＝45°，∠BDF＝90°，∴△BDF是等腰直角三角形，∴FD＝BD＝BC+CD＝9m，∵α+β＝90°，∠ADE＝∠GDC＝90°，∴△ADE∽△GDC，∴＝，∴AD•CD＝GD•ED，设EF＝3FG＝3x，则24×4＝（9﹣x）（9+3x），解得：x＝1，或x＝5（舍去），∴EF＝3，∴DE＝EF+FD＝12m，∵AD＝AB+BD＝24m，∴AE＝＝＝12≈27（m），答：拉索AE的长约为27m．20．如图，直线y＝x+b与y轴交于点A（0，4），与函数y＝（k＞0，x＜0）的图象交于点C，以AC为对角线作矩形ABCD，使顶点B，D落在x轴上（点D在点B的右边），BD 与AC交于点E．（1）求b和k的值；（2）求顶点B，D的坐标．【分析】（1）根据点A坐标可以确定b的值，得出直线的解析式，令y＝0，求得E的坐标，由E（﹣3，0）是AC的中点，推出点C（﹣6，﹣4），然后根据待定系数法即可求得k；（2）根据勾股定理求得AE，利用矩形的性质EA＝EB＝ED，即可解决问题；【解答】解：（1）∵直线y＝x+b与y轴交于点A（0，4），∴b＝4，∴直线为y＝x+4，令y＝0，解得x＝﹣3，∴E（﹣3，0），∵四边形ABCD是矩形，∴E（﹣3，0）是AC的中点，∴C（﹣6，﹣4），∵点C在函数y＝的图象上，∴k＝﹣6×（﹣4）＝24；（2）∵AE2＝AO2+EO2，∴AE＝＝5，∵四边形ABCD是矩形，∴ED＝EB＝EA＝5，∴B（﹣8，0），D（2，0）．21．如图，点P在∠MAN内，PA平分∠MAN，PB⊥AM于点B，PC⊥AN于点C，点D是射线AM 上点B右侧的一个定点．（1）作经过A，P，D三点的圆；（保留作图痕进，不写作法）（2）设圆与AN交于点E，∠MAN＝60°，PA＝4，求AE+AD的值．【分析】（1）作AP和AD的垂直平分线，两条直线的交点即为过A、P、D三点的圆心；（2）连接PE、PD证明△PCE与△PBD全等即可求解．【解答】解：（1）如图所示：作AP和AD的垂直平分线，两条线相交于点O，以点为圆心，OA为半径的圆即为所求作的图形；（2）连接PE、PD，∵PA平分∠MAN，PB⊥AD于点B，PC⊥AN于点C，∴PB＝PC，在圆中，∵∠EAP＝∠DAP，∴PE＝PD，在△PCE和△PBD中，∵∠PCE＝∠PBD＝90°，PB＝PC，PE＝PD．∴Rt△PCE≌Rt△PBD（HL）．∴CE＝BD．∵∠MAN＝60°，PA平分∠MAN，∴∠PAB＝30°，PA＝4，∴AB＝2，∴AE+AD＝2AB＝4．22．在△ABC中，CA＝CB，∠ACB＝α（0°＜α＜180°）．点P是平面内不与A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，CP．点M 是AB的中点，点N是AD的中点．（1）问题发现如图1，当α＝60°时，的值是，直线MN与直线PC相交所成的较小角的度数是60°．（2）类比探究如图2，当α＝120°时，请写出的值及直线MN与直线PC相交所成的较小角的度数，并就图2的情形说明理由．（3）解决问题如图3，当α＝90°时，若点E是CB的中点，点P在直线ME上，请直接写出点B，P，D在同一条直线上时的值．【分析】（1）如图1中，连接PC，BD，延长BD交PC于K，交AC于G．证明△PAC≌△DAB（SAS），利用全等三角形的性质以及三角形的中位线定理即可解决问题．（2）如图设MN交AC于F，延长MN交PC于E．证明△ACP∽△AMN，推出∠ACP＝∠AMN，＝＝可得结论．（3）分两种情形分别画出图形，利用三角形中位线定理即可解决问题．【解答】解：（1）如图1中，连接PC，BD，延长BD交PC于K，交AC于G．∵CA＝CB，∠ACB＝60°，∴△ABC是等边三角形，∴∠CAB＝∠PAD＝60°，AC＝AB，∴∠PAC＝∠DAB，∵AP＝AD，∴△PAC≌△DAB（SAS），∴PC＝BD，∠ACP＝∠ABD，∵AN＝ND，AM＝BM，∴BD＝2MN，∴＝．∵∠CGK＝∠BGA，∠GCK＝∠GBA，∴∠CKG＝∠BAG＝60°，∴BK与PC的较小的夹角为60°，∵MN∥BK，∴MN与PC较小的夹角为60°．故答案为，60°．（2）如图设MN交AC于F，延长MN交PC于E．∵CA＝CB，PA＝PD，∠APD＝∠ACB＝120°，∴△PAD∽△CAB，∴＝，∵AM＝MB，AN＝ND，∴＝，∴△ACP∽△AMN，∴∠ACP＝∠AMN，＝＝，∵∠CFE＝∠AFM，∴∠FEC＝∠FAM＝30°．（3）设MN＝a，∵＝＝，∴PC＝a，∵ME是△ABC的中位线，∠ACB＝90°，∴ME是线段BC的中垂线，∴PB＝PC＝a，∵MN是△ADB的中位线，∴DB＝2MN＝2a，如图3﹣1中，当点P在线段BD上时，PD＝DB﹣PB＝（2﹣）a，∴＝2﹣．如图3﹣2中，PD＝DB+PB＝（2+）a，∴＝2+．23．如图，抛物线y＝ax2+x+c交x轴于A，B两点，交y轴于点C．直线y＝﹣+2经过点A，C．（1）求抛物线的解析式；（2）点P在抛物线在第一象限内的图象上，过点P作x轴的垂线，垂足为D，交直线AC 于点E，连接PC，设点P的横坐标为m．①当△PCE是等腰三角形时，求m的值；②过点C作直线PD的垂线，垂足为F．点F关于直线PC的对称点为F′，当点F′落在坐标轴上时，请直接写出点P的坐标．【分析】（1）先由直线y＝﹣x+2求出A，C的坐标，再将其代入抛物线y＝ax2+x+c 中，即可求出抛物线解析式；（2）①用含m的代数表示出P，E的坐标，再求出含m的代数式的PE的长度，将等腰三角形分三种情况进行讨论，即可分别求出m的值；②当点F'落在坐标轴上时，存在两种情形，一种是点F'落在y轴上，一种是点F′落在x轴上，分情况即可求出点P的坐标．【解答】解：（1）∵直线y＝﹣x+2经过A，C，∴A（4，0），C（0，2），∵抛物线y＝ax2+x+c交x轴于点B，交y轴于点C，∴，∴a＝﹣，c＝2，∴抛物线的解析式为y＝﹣x2+x+2；（2）∵点P在抛物线在第一象限内的图象上，点P的横坐标为m，∴0＜m＜4，P（m，﹣m2+m+2），①∵PD⊥x轴，交直线y＝﹣x+2于点E，∴E（m，﹣m+2），∴PE＝（﹣m2+m+2）﹣（﹣m+2）＝﹣m2+2m，∵PD∥CO，∴＝，∴CE＝＝m，当PE＝CE时，﹣m2+2m＝m，解得，m1＝4﹣，m2＝0（舍去）；当PC＝CE时，PD+ED＝2CO，即（﹣m2+m+2）+（﹣m+2）＝2×2，∴﹣m2+m＝0，解得，m1＝2，m2＝0（舍去）；当PC＝PE时，取CE中点G，则G（m，﹣m+2），PG⊥AC，∴∠GEP＝∠OCA，∴Rt△PGE∽Rt△AOC，∴＝＝2，∴（﹣m2+m+2）﹣（﹣m+2）＝2（m﹣m），﹣m2+m＝0，解得，m1＝，m2＝0（舍去），综上，当△PCE是等腰三角形时，m的值为m＝4﹣，2，；②P（1，3），P（，），理由如下，当点F'落在坐标轴上时，存在两种情形：如图2﹣1，当点F'落在y轴上时，点P（m，﹣m2+m+2）在直线y＝x +2上，∴﹣m2+m+2＝m+2，解得，m1＝1，m2＝0（舍去），∴P（1，3）；如图2﹣2，当点F'落在x轴上时，△COF'∽△F'DP，∴＝＝，∴＝，∵PF＝2﹣（﹣m2+m+2）＝m（m﹣3），∴F'D＝＝m﹣3，∴OF'＝OD﹣FD＝m﹣（m﹣3）＝3，在△CBF'中，CF'＝＝，∴m＝，P（，），综上所述，当点F′落在坐标轴上时，点P的坐标为（1，3）或（，）．人教版九年级（上）期末数学试卷（二）一．选择题（共10小题）1．若一元二次方程x2+2x+a＝0有一根为1，则a的值为（）A．1 B．﹣1 C．3 D．﹣32．下列语句描述的事件中，是随机事件的为（）A．心想事成B．只手遮天C．瓜熟蒂落D．水能载舟亦能覆舟3．把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（）A．30°B．90°C．120°D．180°4．根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）A．B．C．D．5．某农产品市场经销一种销售成本为40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克：销售单价每涨1元，月销售量就减少10千克，设销售单价为每干克x元，月销售利润可以表示为（）A．（x﹣40）[500﹣10（x﹣50）]元B．（x﹣40）（10x﹣500）元C．（x﹣40）（500﹣10x）元D．（x﹣40）[500﹣10（50﹣x）]元6．下列四个图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．7．如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM和的长分别为（）A．2，B．2，πC．，D．2，8．小明乘坐摩天轮转一圈，他距离地面的高度y（米）与旋转时间x（分）之间的关系可以近似地用二次函数来刻画．经侧试得部分数据如下表：x/分… 2.66 3.23 3.46 …y/米…69.16 69.62 68.46 …下列选项中，最接近摩天轮转一圈的时间的是（）A．7分B．6.5分C．6分D．5.5分9．如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果下面有三个推断：①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．其中合理的是（）A．①B．②C．①②D．①③10．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x1，0）、（x2，0），其中0＜x1＜1，有下列结论：①c＞0；②﹣3＜x2＜﹣2；③a+b+c ＜0；④b2﹣4ac＞0；⑤已知图象上点A（4，y1），B（1，y2），则y1＞y2．其中，正确结论的个数有（）A．5 B．4 C．3 D．2二．填空题（共8小题）11．已知二次函数y＝ax2的图象开口向上，则a．12．如果关于x的一元二次方程ax2+x+1＝0没有实数根，则a的取值范围是．13．如图，小艾同学坐在秋千上，秋千旋转了80°，小艾同学的位置也从A点运动到了A'点，则∠OAA'的度数为．14．将抛物线y＝3x2先向左平移一个单位，再向上平移两个单位，两次平移后得到的抛物线解析式为．15．如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为．16．电影《中国机长》首映当日票房已经达到1.92亿元，2天后当日票房达到2.61亿元，设平均每天票房的增长率为x，则可列方程为．17．欧阳修在《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆其扣，徐以杓酌油沥之，自钱孔入，而钱不湿，因曰：我亦无他，唯手熟尔．”可见技能通过反复苦练而达到熟能生巧．若铜钱是直径为4cm的圆，中间有边长为1cm的正方形孔，你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率为．（结果保留π）18．如图，在单位长度为1米的平面直角坐标系中，曲线是由半径为2米，圆心角为120°圆弧多次复制并首尾连接而成，现有一点P从A（A为坐标原点），以每秒米的速度沿曲线向右运动，则在第2020秒时点P的纵坐标为．三．解答题（共8小题）19．先化简，再求值：（﹣）÷，其中a是一元二次方程对a2+3a﹣2＝0的根．20．对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境．为了检查垃圾分类的落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的A，B，C，D四个小区进行检查，并且每个小区不重复检查．（1）甲组抽到A小区的概率是；（2）请用列表或画树状图的方法求甲组抽到A小区，同时乙组抽到C小区的概率．21．在如图所示8×7的正方形网格中，A（2，0），B（3，2），C（4，2），请按要求解答下列问题：（1）将△ABO向右平移4个单位长度得到△A1B1O1，请画出△A1B1O1并写出点A1的坐标；（2）将△ABO绕点C（4，2）顺时针旋转90°得到△A2B2O2，请画出△A2B2O2并写出点A2的坐标；（3）将△A1B1O1绕点Q旋转90°可以和△A2B2O2完全重合，请直接写出点Q的坐标．22．（北师大版）连接着汉口集家咀的江汉三桥（晴川桥），是一座下承式钢管混凝土系杆拱桥．它犹如一道美丽的彩虹跨越汉江，是江城武汉的一道靓丽景观．桥的拱肋ACB视为抛物线的一部分，桥面（视为水平的）与拱肋用垂直于桥面的系杆连接，相邻系杆之间的间距均为5米（不考虑系杆的粗细），拱肋的跨度AB为280米，距离拱肋的右端70米处的系杆EF的长度为42米．以AB所在直线为x轴，抛物线的对称轴为y轴建立如图②所示的平面直角坐标系．（1）求抛物线的解析式；（2）正中间系杆OC的长度是多少米？是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．23．如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．（1）试判断直线DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，∠B＝50°，AC＝6，求图中阴影部分的面积．24．每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送花，感恩母亲，祝福母亲．今年节日前夕，某花店采购了一批康乃馨，经分析上一年的销售情况，发现这种康乃馨每天的销售量y（支）是销售单价x（元）的一次函数，已知销售单价为7元/支时，销售量为16支；销售单价为8元/支时，销售量为14支．（1）求这种康乃馨每天的销售量y（支）关于销售单价x（元/支）的一次函数解析式；（2）若按去年方式销售，已知今年这种康乃馨的进价是每支5元，商家若想每天获得42元的利润，销售单价要定为多少元？（3）在（2）的条件下，当销售单价x为何值时，花店销售这种康乃馨每天获得的利润最大？并求出获得的最大利润．25．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN ＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．26．如图1，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴分别交于A（﹣3，0），B两点，与y轴交于点C，抛物线的顶点E（﹣1，4），对称轴交x轴于点F．（1）请直接写出这条抛物线和直线AE、直线AC的解析式；（2）连接AC、AE、CE，判断△ACE的形状，并说明理由；（3）如图2，点D是抛物线上一动点，它的横坐标为m，且﹣3＜m＜﹣1，过点D作DK ⊥x轴于点K，DK分别交线段AE、AC于点G、H．在点D的运动过程中，①DG、GH、HK这三条线段能否相等？若相等，请求出点D的坐标；若不相等，请说明理由；②在①的条件下，判断CG与AE的数量关系，并直接写出结论．参考答案与试题解析一．选择题（共10小题）1．若一元二次方程x2+2x+a＝0有一根为1，则a的值为（）A．1 B．﹣1 C．3 D．﹣3【分析】将x＝1代入方程即可求出a的值．【解答】解：将x＝1代入方程可得：1+2+a＝0，∴a＝﹣3，故选：D．2．下列语句描述的事件中，是随机事件的为（）A．心想事成B．只手遮天C．瓜熟蒂落D．水能载舟亦能覆舟【分析】直接利用随机事件以及必然事件、不可能事件的定义分别分析得出答案．【解答】解：A、心想事成是随机事件，故此选项正确．B、只手遮天是不可能事件，故此选项错误；C、瓜熟蒂落是必然事件，故此选项错误；D、水能载舟，亦能覆舟是必然事件，故此选项错误；故选：A．3．把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（）A．30°B．90°C．120°D．180°【分析】根据图形的对称性，用360°除以3计算即可得解．【解答】解：∵360°÷3＝120°，∴旋转的角度是120°的整数倍，∴旋转的角度至少是120°．故选：C．。

2020年九年级数学上册期末测试卷(附答案)人教版新版

九年级（上）期末数学试卷一、选择题（每题3分，共30分）1．下列函数中，不是反比例函数的是（）A．y= B．y=﹣（m不等于0）C．y=D．y=2．下列方程是一元二次方程的是（）A．3x2+=0 B．2x﹣3y+1=0 C．（x﹣3）（x﹣2）=x2D．（3x﹣1）（3x+1）=33．三角形两边的长分别是8和6，第三边的长是一元二次方程x2﹣16x+60=0的一个实数根，则该三角形的面积是（）A．24 B．24或8C．48或16D．84．若，则等于（）A．8 B．9 C．10 D．115．如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（）A．∠B=∠C B．∠ADC=∠AEB C．BE=CD，AB=AC D．AD：AC=AE：AB6．下列等式成立的是（）A．sin 45°+cos45°=1 B．2tan30°=tan60°C．2sin60°=tan45° D．sin230°=cos60°7．在Rt△ABC中，∠C=90°，sinA=，则tanB的值为（）A．B．C．D．8．把中考体检调查学生的身高作为样本，样本数据落在1.6～2.0（单位：米）之间的频率为0.28，于是可估计2 000名体检中学生中，身高在1.6～2.0米之间的学生有（）A．56 B．560 C．80 D．1509．为了解自己家的用电情况，李明在6月初连续几天同一时刻观察电表显示的情况记录如下：日期1号2号3号4号5号6号7号8号电表显示（千瓦时）117 120 124 129 135 138 142 145按照这种用法，李明家6月份的用电量约为（）A．105千瓦时B．115千瓦时C．120千瓦时D．95千瓦时10．已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是（）A． B． C．D．二、填空题（毎题3分，共24分）11．点P（2m﹣3，1）在反比例函数的图象上，则m=______．12．已知一个函数的图象与y=的图象关于y轴成轴对称，则该函数的解析式为______．13．若关于x的一元二次方程x2﹣3x+c=0有一个根是2，则另一根是______．14．如果方程x2+2x+m=0有两个同号的实数根，m的取值范围是______．15．已知线段a=3cm，b=6cm，c=5cm，且a，b，d，c成比例线段，则d=______cm．16．如图，把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中的阴影部分）的面积是△ABC的面积的一半，若AB=，则此三角形移动的距离AA′=______．17．学校校园内有一块如图所示的三角形空地，计划将这块空地建成一个花园，以美化校园环境．预计花园每平方米造价为30元，学校建这个花园需要投资______元．（精确到1元）18．如图，条形统计图是从曙光中学800名学生中帮助失学儿童捐款金额的部分抽样调查数据，扇形图统计图是该校各年级人数比例分布图．那么该校七年级同学捐款的总数大约为______元．三、解答题（每题8分，共24分）19．用适当的方法解下列方程：（1）4（x﹣3）2﹣25=0（2）2x2+7x﹣4=0．20．已知反比例函数y=（k为常数，k≠1）．（1）若点A（1，2）在这个函数的图象上，求k的值；（2）若在这个函数图象的每一分支上，y随x的增大而减小，求k的取值范围．21．计算下列各题：（1）tan45°﹣sin60°•cos30°；（2）sin230°+sin45°•tan30°．四、应用题（每题8分，共24分）22．关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根．（1）求k的取值范围；（2）请选择一个k的负整数值，并求出方程的根．23．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．24．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？五、综合题（共18分）25．马航MH370失联后，我国政府积极参与搜救．某日，我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息，可疑漂浮物P在救助船A的北偏东53.50°方向上，在救助船B的西北方向上，船B在船A正东方向140海里处．（参考数据：sin36.5°≈0.6，cos36.5°≈0.8，tan36.5°≈0.75）．（1）求可疑漂浮物P到A、B两船所在直线的距离；（2）若救助船A、救助船B分别以40海里/时，30海里/时的速度同时出发，匀速直线前往搜救，试通过计算判断哪艘船先到达P处．26．如图，已知反比例函数y=（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．（1）写出反比例函数解析式；（2）求证：△ACB∽△NOM；（3）若△ACB与△NOM的相似比为2，求出B点的坐标及AB所在直线的解析式．参考答案与试题解析一、选择题（每题3分，共30分）1．下列函数中，不是反比例函数的是（）A．y= B．y=﹣（m不等于0）C．y=D．y=【考点】反比例函数的定义．【分析】根据反比例函数的定义，反比例函数的一般式是（k≠0），即可判定各函数的类型是否符合题意．【解答】解：A、符合反比例函数的定义，y是x的反比例函数，错误；B、符合反比例函数的定义，y是x的反比例函数，错误；C、y与x﹣1成正比例，y不是x的反比例函数，正确；D、符合反比例函数的定义，y是x的反比例函数，错误．故选C．2．下列方程是一元二次方程的是（）A．3x2+=0 B．2x﹣3y+1=0 C．（x﹣3）（x﹣2）=x2D．（3x﹣1）（3x+1）=3【考点】一元二次方程的定义．【分析】只含有一个未知数，且未知数的最高次数是2的整式方程叫做一元二次方程．一元二次方程有三个特点：（1）只含有一个未知数；（2）未知数的最高次数是2；（3）是整式方程．【解答】解：A、3x2+=0是分式方程，故此选项错误；B、2x﹣3y+1=0为二元一次方程，故此选项错误；C、（x﹣3）（x﹣2）=x2是一元一次方程，故此选项错误；D、（3x﹣1）（3x+1）=3是一元二次方程，故此选项正确．故选D．3．三角形两边的长分别是8和6，第三边的长是一元二次方程x2﹣16x+60=0的一个实数根，则该三角形的面积是（）A．24 B．24或8C．48或16D．8【考点】解一元二次方程-因式分解法；勾股定理；勾股定理的逆定理．【分析】由x2﹣16x+60=0，可利用因式分解法求得x的值，然后分别从x=6时，是等腰三角形；与x=10时，是直角三角形去分析求解即可求得答案．【解答】解：∵x2﹣16x+60=0，∴（x﹣6）（x﹣10）=0，解得：x1=6，x2=10，当x=6时，则三角形是等腰三角形，如图①，AB=AC=6，BC=8，AD是高，∴BD=4，AD==2，=BC•AD=×8×2=8；∴S△ABC当x=10时，如图②，AC=6，BC=8，AB=10，∵AC2+BC2=AB2，∴△ABC是直角三角形，∠C=90°，=BC•AC=×8×6=24．S△ABC∴该三角形的面积是：24或8．故选：B．4．若，则等于（）A．8 B．9 C．10 D．11【考点】比例的性质．【分析】设=k，得出a=2k，b=3k，c=4k，代入求出即可．【解答】解：设=k，则a=2k，b=3k，c=4k，即===10，故选C．5．如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（）A．∠B=∠C B．∠ADC=∠AEB C．BE=CD，AB=AC D．AD：AC=AE：AB【考点】相似三角形的判定．【分析】根据已知及相似三角形的判定方法进行分析，从而得到答案．【解答】解：∵∠A=∠A∴当∠B=∠C或∠ADC=∠AEB或AD：AC=AE：AB时，△ABE和△ACD相似．故选C．6．下列等式成立的是（）A．sin 45°+cos45°=1 B．2tan30°=tan60°C．2sin60°=tan45° D．sin230°=cos60°【考点】特殊角的三角函数值．【分析】根据特殊角的三角函数值，分别计算即可判断．【解答】解：A、因为sin45°+cos45°=+=．故错误．B、因为2tan30°=，tan60°=，所以2tan30°≠tan60°，故错误．C、因为2sin60°=，tan45°=1，所以2sin60°≠tan45°故错误，D、因为sin230°=，cos60°=，所以sin230°=cos60°，故正确．故选D．7．在Rt△ABC中，∠C=90°，sinA=，则tanB的值为（）A．B．C．D．【考点】互余两角三角函数的关系．【分析】根据题意作出直角△ABC，然后根据sinA=，设一条直角边BC为5x，斜边AB为13x，根据勾股定理求出另一条直角边AC的长度，然后根据三角函数的定义可求出tan∠B．【解答】解：∵sinA=，∴设BC=5x，AB=13x，则AC==12x，故tan∠B==．故选：D．8．把中考体检调查学生的身高作为样本，样本数据落在1.6～2.0（单位：米）之间的频率为0.28，于是可估计2 000名体检中学生中，身高在1.6～2.0米之间的学生有（）A．56 B．560 C．80 D．150【考点】用样本估计总体；频数与频率．【分析】根据频率的意义，每组的频率=该组的频数：样本容量，即频数=频率×样本容量．数据落在1.6～2.0（单位：米）之间的频率为0.28，于是2 000名体检中学生中，身高在1.6～2.0米之间的学生数即可求解．【解答】解：0.28×2000=560．故选B．9．为了解自己家的用电情况，李明在6月初连续几天同一时刻观察电表显示的情况记录如下：日期1号2号3号4号5号6号7号8号电表显示（千瓦时）117 120 124 129 135 138 142 145按照这种用法，李明家6月份的用电量约为（）A．105千瓦时B．115千瓦时C．120千瓦时D．95千瓦时【考点】用样本估计总体．【分析】根据样本估计总体的统计思想：可先求出7天中用电量的平均数，作为6月份用电量的平均数，则一个月的用电总量即可求得．【解答】解：30×=120（千瓦时）．故选C．10．已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是（）A． B． C．D．【考点】反比例函数的图象；一次函数的图象；一次函数图象与系数的关系．【分析】根据一次函数图象可以确定k、b的符号，根据k、b的符号来判定正比例函数y=kx和反比例函数y=图象所在的象限．【解答】解：如图所示，∵一次函数y=kx+b的图象经过第一、三、四象限，∴k＞0，b＜0．∴正比例函数y=kx的图象经过第一、三象限，反比例函数y=的图象经过第二、四象限．综上所述，符合条件的图象是C选项．故选：C．二、填空题（毎题3分，共24分）11．点P（2m﹣3，1）在反比例函数的图象上，则m=2．【考点】反比例函数图象上点的坐标特征．【分析】此题可以直接将P（2m﹣3，1）代入反比例函数解析式即可求得m的值．【解答】解：∵点P（2m﹣3，1）在反比例函数的图象上，∴（2m﹣3）×1=1，解得m=2．故答案为：2．12．已知一个函数的图象与y=的图象关于y轴成轴对称，则该函数的解析式为y=﹣．【考点】反比例函数的性质．【分析】根据图象关于y轴对称，可得出所求的函数解析式．【解答】解：关于y轴对称，横坐标互为相反数，纵坐标相等，即y=，∴y=﹣故答案为：y=﹣．13．若关于x的一元二次方程x2﹣3x+c=0有一个根是2，则另一根是1．【考点】根与系数的关系．【分析】首先设另一个根为α，由关于x的一元二次方程x2﹣3x+c=0有一个根是2，根据根与系数的关系可得α+2=3，继而求得答案．【解答】解：设另一个根为α，∵关于x的一元二次方程x2﹣3x+c=0有一个根是2，∴α+2=3，∴α=1，即另一个根为1．故答案为1．14．如果方程x2+2x+m=0有两个同号的实数根，m的取值范围是0＜m≤1．【考点】根的判别式；根与系数的关系．【分析】根据题意得出△≥0，m＞0，代入求出m的范围即可．【解答】解：∵方程x2+2x+m=0有两个同号的实数根，∴△≥0，m＞0，△=22﹣4×1×m=4﹣4m≥0，解得：m≤1，即m的取值范围是0＜m≤1，故答案为：0＜m≤1．15．已知线段a=3cm，b=6cm，c=5cm，且a，b，d，c成比例线段，则d= 2.5cm．【考点】比例线段．【分析】根据线段成比例，则可以列出方程a：b=d：c，代入数值求解即可．【解答】解：∵线段a，b，c，d成比例，∴a：b=d：c，由题中a=3cm，b=6cm，c=5cm，∴代入方程可得d=2.5．16．如图，把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中的阴影部分）的面积是△ABC的面积的一半，若AB=，则此三角形移动的距离AA′=．【考点】相似三角形的判定与性质；平移的性质．【分析】利用相似三角形面积的比等于相似比的平方先求出A′B，再求AA′就可以了．【解答】解：设BC与A′C′交于点E，由平移的性质知，AC∥A′C′，∴△BEA′∽△BCA，∴S△BEA′：S△BCA=A′B2：AB2=1：2，∵AB=，∴A′B=1，∴AA′=AB﹣A′B=，故答案为：．17．学校校园内有一块如图所示的三角形空地，计划将这块空地建成一个花园，以美化校园环境．预计花园每平方米造价为30元，学校建这个花园需要投资7794元．（精确到1元）【考点】解直角三角形的应用．【分析】延长BC，过A作AD⊥BC的延长线于点D，再根据补角的定义求出∠ACD的度数，由锐角三角函数的定义接可求出AD的长，再根据三角形的面积公式求出此三角形的面积，再根据每平方米造价为30元计算出所需投资即可．【解答】解：延长BC，过A作AD⊥BC的延长线于点D，∵∠ACB=120°，∴∠ACD=180°﹣120°=60°，∵AC=20米，∴AD=AC•sin60°=20×=10（米），∴S△ABC=BC•AD=×30×10=150（平方米），∴所需投资=150×30≈7794（元）．故答案为：7794．18．如图，条形统计图是从曙光中学800名学生中帮助失学儿童捐款金额的部分抽样调查数据，扇形图统计图是该校各年级人数比例分布图．那么该校七年级同学捐款的总数大约为5010元．【考点】条形统计图；扇形统计图．【分析】首先根据扇形统计图和已知条件求出七年级同学的人数，然后求出样本平均数，再利用样本估计总体的思想即可求出该校七年级同学捐款的总数．【解答】解：∵曙光中学有800名学生，∴七年级同学的人数为：800×36%=288人，而抽样调查数据平均数为：=≈17.4元，∴17.4×288≈5010元，∴该校七年级同学捐款的总数为5010元，故答案为：5010．三、解答题（每题8分，共24分）19．用适当的方法解下列方程：（1）4（x﹣3）2﹣25=0（2）2x2+7x﹣4=0．【考点】解一元二次方程-因式分解法；解一元二次方程-直接开平方法．【分析】（1）先移项得到4（x﹣3）2=25，然后利用直接开平方法解方程；（2）利用因式分解法解方程．【解答】解：（1）4（x﹣3）2=25，2（x﹣3）=±5，所以x1=，x2=；（2）（2x﹣1）（x+4）=0，2x﹣1=0或x+4=0，所以x1=，x2=﹣4．20．已知反比例函数y=（k为常数，k≠1）．（1）若点A（1，2）在这个函数的图象上，求k的值；（2）若在这个函数图象的每一分支上，y随x的增大而减小，求k的取值范围．【考点】反比例函数图象上点的坐标特征；反比例函数的性质．【分析】（1）根据反比例函数图象上点的坐标特征得到k﹣1=1×2，然后解方程即可；（2）根据反比例函数的性质得k﹣1＞0，然后解不等式即可．【解答】解：（1）根据题意得k﹣1=1×2，解得k=3；（2）因为反比例函数y=，在这个函数图象的每一分支上，y随x的增大而减小，所以k﹣1＞0，解得k＞1．21．计算下列各题：（1）tan45°﹣sin60°•cos30°；（2）sin230°+sin45°•tan30°．【考点】实数的运算；特殊角的三角函数值．【分析】（1）原式利用特殊角的三角函数值计算即可得到结果；（2）原式利用特殊角的三角函数值计算即可得到结果．【解答】解：（1）原式=1﹣×=1﹣=；（2）原式=×+×=．四、应用题（每题8分，共24分）22．关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根．（1）求k的取值范围；（2）请选择一个k的负整数值，并求出方程的根．【考点】根的判别式；解一元二次方程-公式法．【分析】（1）因为方程有两个不相等的实数根，△＞0，由此可求k的取值范围；（2）在k的取值范围内，取负整数，代入方程，解方程即可．【解答】解：（1）∵方程有两个不相等的实数根，∴（﹣3）2﹣4（﹣k）＞0，即4k＞﹣9，解得；（2）若k是负整数，k只能为﹣1或﹣2；如果k=﹣1，原方程为x2﹣3x+1=0，解得，，．（如果k=﹣2，原方程为x2﹣3x+2=0，解得，x1=1，x2=2）23．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．【考点】相似三角形的判定；平行线的性质．【分析】根据平行线的性质可知∠AED=∠C，∠A=∠FEC，根据相似三角形的判定定理可知△ADE ∽△EFC．【解答】证明：∵DE∥BC，∴∠AED=∠C．又∵EF∥AB，∴∠A=∠FEC．∴△ADE∽△EFC．24．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？【考点】相似三角形的应用．【分析】如图，由于AC∥BD∥OP，故有△MAC∽△MOP，△NBD∽△NOP即可由相似三角形的性质求解．【解答】解：∵∠MAC=∠MOP=90°，∠AMC=∠OMP，∴△MAC∽△MOP．∴，即，解得，MA=5米；同理，由△NBD∽△NOP，可求得NB=1.5米，∴小明的身影变短了5﹣1.5=3.5米．五、综合题（共18分）25．马航MH370失联后，我国政府积极参与搜救．某日，我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息，可疑漂浮物P在救助船A的北偏东53.50°方向上，在救助船B的西北方向上，船B在船A正东方向140海里处．（参考数据：sin36.5°≈0.6，cos36.5°≈0.8，tan36.5°≈0.75）．（1）求可疑漂浮物P到A、B两船所在直线的距离；（2）若救助船A、救助船B分别以40海里/时，30海里/时的速度同时出发，匀速直线前往搜救，试通过计算判断哪艘船先到达P处．【考点】解直角三角形的应用-方向角问题．【分析】（1）过点P作PE⊥AB于点E，在Rt△APE中解出PE即可；（2）分别求出PA、PB的长，根据两船航行速度，计算出两艘船到达P点时各自所需要的时间，即可作出判断．【解答】解：（1）过点P作PE⊥AB于点E，由题意得，∠PAE=36.5°，∠PBA=45°，设PE为x海里，则BE=PE=x海里，∵AB=140海里，∴AE=海里，在Rt△PAE中，，即：解得：x=60，∴可疑漂浮物P到A、B两船所在直线的距离约为60海里；（2）在Rt△PBE中，PE=60海里，∠PBE=45°，则BP=PE=60≈84.8海里，B船需要的时间为：84.8÷30≈2.83小时，在Rt△PAE中，=sin∠PAE，∴AP=PE÷sin∠PAE=60÷0.6=100海里，∴A船需要的时间为：100÷40=2.5小时，∵2.83＞2.5，∴A船先到达．26．如图，已知反比例函数y=（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．（1）写出反比例函数解析式；（2）求证：△ACB∽△NOM；（3）若△ACB与△NOM的相似比为2，求出B点的坐标及AB所在直线的解析式．【考点】反比例函数综合题．【分析】（1）把A点坐标代入y=可得k的值，进而得到函数解析式；（2）根据A、B两点坐标可得AC=4﹣n，BC=m﹣1，ON=n，OM=1，则=，再根据反比例函数解析式可得=n，则=m﹣1，而=，可得=，再由∠ACB=∠NOM=90°，可得△ACB∽△NOM；（3）根据△ACB与△NOM的相似比为2可得m﹣1=2，进而得到m的值，然后可得B点坐标，再利用待定系数法求出AB的解析式即可．【解答】解：（1）∵y=（x＞0，k是常数）的图象经过点A（1，4），∴k=4，∴反比例函数解析式为y=；（2）∵点A（1，4），点B（m，n），∴AC=4﹣n，BC=m﹣1，ON=n，OM=1，∴==﹣1，∵B（m，n）在y=上，∴=n，∴=m﹣1，而=，∴=，∵∠ACB=∠NOM=90°，∴△ACB∽△NOM；（3）∵△ACB与△NOM的相似比为2，∴m﹣1=2，m=3，∴B（3，），设AB所在直线解析式为y=kx+b，∴，解得，∴解析式为y=﹣x+．。

人教版2020---2021学年度上学期九年级数学期末考试卷及答案含4套

密学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：120分时间：120分钟）一、选择题（共8小题，每小题3分，满分24分） 1．已知四条线段满足，将它改写成为比例式，下面正确的是（） A ．B ．C ．D ．2．二次函数y=﹣2（x ﹣1）2+3的图象的顶点坐标是（） A ．（1，3） B ．（﹣1，3） C ．（1，﹣3） D ．（﹣1，﹣3） 3．下列事件中，必然事件是（） A ．抛出一枚硬币，落地后正面向上 B ．打开电视，正在播放广告C ．篮球队员在罚球线投篮一次，未投中D ．实心铁球投入水中会沉入水底4．如图，点A ，B ，C ，D 都在⊙O 上，AC ，BD 相交于点E ，则∠ABD=（）A ．∠ACDB ．∠ADBC ．∠AED D ．∠ACB5．用配方法解一元二次方程x 2﹣4x=5时，此方程可变形为（）A ．（x+2）2=1B ．（x ﹣2）2=1C ．（x+2）2=9D ．（x ﹣2）2=96．若△ABC ∽△A ′B ′C ′，相似比为1：2，则△ABC 与△A ′B ′C ′的面积的比为（） A ．1：2 B ．2：1 C ．1：4 D ．4：17．已知函数y=x 2+2x ﹣3，当x=m 时，y ＜0，则m 的值可能是（）A ．﹣4B ．0C ．2D ．38．一个圆锥的高为4cm ，底面圆的半径为3cm ，则这个圆锥的侧面积为（）A ．12πcm 2B ．15πcm 2C ．20πcm 2D ．30πcm 2二、填空题（本大题共有10小题，每小题3分，共30分） 9．方程x 2﹣4x+c=0有两个不相等的实数根，则c 的取值范围是．密封线内不得答题10．在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为m．11．如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB= °．12．抽屉里放着黑白两种颜色的袜子各1双（除颜色外其余都相同），在看不见的情况下随机摸出两只袜子，它们恰好同色的概率是．13．一元二次方程x2+px﹣2=0的一个根为2，则p的值．14．如图，在⊙O中，已知半径为5，弦AB的长为8，那么圆心O到AB的距离为．15．如图，要使△ABC与△DBA相似，则只需添加一个适当的条件是（填一个即可）16．二次函数y=ax2+bx+c的图象如图所示，其对称轴与x轴交于点（﹣1，0），图象上有三个点分别为（2，y1），（﹣3，y2），（0，y3），则y1、y2、y3的大小关系是（用“＞”“＜”或“=”连接）．三、解答题（本大题共有4小题，共39分）17．解方程：（1）x2﹣4x+1=0；（2）x（x﹣2）+x﹣2=0．18．如图，△ABC的三个顶点都在格点上，每个小方格边长均为1个单位长度．（1）请你作出△ABC关于点O成中心对称的△A1B1C1（其中A的对称点是A1，B的对称点是B1，C的对称点是C1）；（2）直接写出点B1、C1的坐标．密线学校班级姓名学号密封线内不得答题19．如图，四边形ABCD 内接于⊙O ，E 为AB 延长线上一点，若∠AOC=140°．求∠EBC 的度数．20．一只不透明的箱子里共有3个球，把它们的分别编号为1，2，3，这些球除编号不同外其余都相同，从箱子中随机摸出一个球，记录下编号后将它放回箱子，搅匀后再摸出一个球并记录下编号．（1）用树状图或列表法举出所有可能出现的结果；（2）求两次摸出的球都是编号为3的球的概率．四、解答题（本大题共有4小题，共39分）21．如图，Rt △ABC 中，∠C=90°，AB=10，AC=8，E 是AC 上一点，AE=5，ED ⊥AB 于D ．（1）求证：△ACB ∽△ADE ；（2）求AD 的长度．22．如图，进行绿地的长、宽各增加xm ．（1）写出扩充后的绿地的面积y （m 2）与x （m ）之间的函数关系式；（2）若扩充后的绿地面积y 是原矩形面积的2倍，求x 的值．23．如图，AB 是⊙O 的直径，点C 、D 在⊙O 上，且AC 平分∠BAD ，点E 为AB 的延长线上一点，且∠ECB=∠CAD ．（1）①填空：∠ACB= ，理由是； ②求证：CE 与⊙O 相切；（2）若AB=6，CE=4，求AD 的长．密封线内不得五、解答题（本大题共有3小题，共35分）24．如图1，在△ABC 中，∠A=120°，AB=AC ，点P 、Q 同时从点B 出发，以相同的速度分别沿折线B →A →C 、射线BC 运动，连接PQ ．当点P 到达点C 时，点P 、Q 同时停止运动．设BQ=x ，△BPQ 与△ABC 重叠部分的面积为S ．如图2是S 关于x 的函数图象（其中0≤x ≤8，8＜x ≤m ，m ＜x ≤16时，函数的解析式不同）．（1）填空：m 的值为；（2）求S 关于x 的函数关系式，并写出x 的取值范围；（3）请直接写出△PCQ 为等腰三角形时x 的值．25．如图（1），将线段AB 绕点A 逆时针旋转2α（0°＜α＜90°）至AC ，P 是过A ，B ，C 的三点圆上任意一点．（1）当α=30°时，如图（1），求证：PC=PA+PB ；（2）当α=45°时，如图（2），PA ，PB ，PC 它们的数量关系．26．如图，抛物线y=a （x ﹣m ）2﹣m （其中m ＞1）与其对称轴l 相交于点P ，与y 轴相交于点A （0，m ）．点A 关于直线l 的对称点为B ，作BC ⊥x 轴于点C ，连接PC 、PB ，与抛物线、x 轴分别相交于点D 、E ，连接DE ．将△PBC 沿直线PB 翻折，得到△PBC ′．（1）该抛物线的解析式为（用含m 的式子表示）；（2）探究线段DE 、BC 的关系，并证明你的结论；（3）直接写出C ′点的坐标（用含m 的式子表示）．密学校班级姓名学号密封线内不得答题参考答案一、选择题（共8小题，每小题3分，满分24分） 1．C 2．A ．3．D ．4．A ．5．D ．6．C ．7．B ．8.B ．二、填空题（本大题共有10小题，每小题3分，共30分）9．方程x 2﹣4x+c=0有两个不相等的实数根，则c 的取值范围是 c ＜4 ．10．在某一时刻，测得一根高为1.8m 的竹竿的影长为3m ，同时测得一根旗杆的影长为25m ，那么这根旗杆的高度为 15 m ． 11．如图，在直角△OAB 中，∠AOB=30°，将△OAB 绕点O 逆时针旋转100°得到△OA 1B 1，则∠A 1OB= 70 °．12．抽屉里放着黑白两种颜色的袜子各1双（除颜色外其余都相同），在看不见的情况下随机摸出两只袜子，它们恰好同色的概率是．13．一元二次方程x 2+px ﹣2=0的一个根为2，则p 的值 ﹣1 ．14．如图，在⊙O 中，已知半径为5，弦AB 的长为8，那么圆心O 到AB 的距离为 3 ．15．如图，要使△ABC 与△DBA 相似，则只需添加一个适当的条件是 ∠C=∠BAD （填一个即可）16．二次函数y=ax 2+bx+c 的图象如图所示，其对称轴与x 轴交于点（﹣1，0），图象上有三个点分别为（2，y 1），（﹣3，y 2），（0，y 3），则y 1、y 2、y 3的大小关系是 y 3＜y 2＜y 1 （用“＞”“＜”或“=”连接）．三、解答题（本大题共有4小题，共39分）17．解方程：解：（1）方程变形得：x 2﹣4x=﹣1，配方得：x 2﹣4x+4=3，即（x ﹣2）2=3，开方得：x ﹣2=±，得答题则x 1=2+，x 2=2﹣；（2）（x+1）（x ﹣2）=0，（x+1）（x ﹣2）=0，解得x 1=﹣1，x 2=2． 18.解：（1）如图所示：．（2）根据上图可知，B 1（2，2），C 1（5，﹣1）．19．解：由圆周角定理得，∠D=∠AOC=70°，由圆内接四边形的性质得，∠EBC=∠D=70°． 20．解：（1）画树状图如下：由树状图可知所有可能出现的结果共9种；（2）由（1）中考共有9种等可能的结果，两次摸出的球都是编号为3的球的情况数是1种，所以其概率为．四、解答题（本大题共有4小题，共39分） 21．（1）证明：∵DE ⊥AB ，∠C=90°，∴∠EDA=∠C=90°， ∵∠A=∠A ，∴△ACB ∽△ADE ；（2）解：∵△ACB ∽△ADE ，∴=， ∴=，∴AD=4．22．如图，进行绿地的长、宽各增加xm ．（1）写出扩充后的绿地的面积y （m 2）与x （m 系式；（2）若扩充后的绿地面积y 是原矩形面积的2倍，求x密线学校班级姓名学号密封线内不得答题解：（1）由图可得，扩充后的绿地的面积y （m 2）与x （m ）之间的函数关系式是：y=（30xm+m ）（20xm+m ）=600x 2m 2+50xm 2+m 2，即扩充后的绿地的面积y （m 2）与x （m ）之间的函数关系式是：y=600x 2m 2+50xm 2+m 2；（2）∵扩充后的绿地面积y 是原矩形面积的2倍， ∴600x 2m 2+50xm 2+m 2=2×30xm ×20xm ，解得（舍去），即扩充后的绿地面积y 是原矩形面积的2倍，x 的值是．23.解：(1)①∵AB 为⊙O 的直径， ∴∠ACB=90°，故答案为90°，直径所对的圆周角是直角； ②连接OC ，则∠CAO=∠ACO ， ∵AC 平分∠BAB ， ∴∠BAC=∠CAD ， ∵∠ECB=∠CAD ． ∴∠BAC=∠ECB ．∴∠ECB=∠ACO ，∵∠ACO+∠OCB=90°，∴∠ECB+∠OCB=90°，即CE ⊥OC ．∴CE 与⊙O 相切；（2）∵CE 与⊙O 相切， ∴CE 2=BE •AE ， ∵AB=6，CE=4， ∴42=BE （BE+6）， ∴BE=2， ∴AE=6+2=8， ∵△ACE ∽△CBE ，∴=，即=，∴AC=4， ∴AC=CE=4， ∴∠CAB=∠E ， ∴∠ECB=∠E ，∴∠ABC=2∠ECB=2∠BAC ，BC=BE=2， ∴∠DAB=∠ABC ， ∴AD=BC=2．五、解答题（本大题共有3小题，共35分）24.解:(1)如图1中，作AM ⊥BC ，PN ⊥BC ，垂足分别为M ，N ．密封线内不得答题由题意AB=AC=8，∠A=120°， ∴∠BAM=∠CAM=60°，∠B=∠C=30°， ∴AM=AB=4，BM=CM=4， ∴BC=8， ∴m=BC=8，故答案为8．（2）①当0≤m ≤8时，如图1中，在RT △PBN 中，∵∠PNB=90°，∠B=30°，PB=x ， ∴PN=x ． s=•BQ •PN=•x ••x=x 2．②当8＜x ≤16，如图2中，在RT △PBN 中，∵PC=16﹣x ，∠PNC=90°，∠C=30°， ∴PN=PC=8﹣x ，∴s=•BQ •PN=•x •（8﹣x ）=﹣x 2+4x ． ③当8＜x ≤16时，s=•8•（8﹣•x ）=﹣2x+32．（3）①当点P 在AB 上，点Q 在BC 上时，△PQC 不可能是等腰三角形．②当点P 在AC 上，点Q 在BC 上时，PQ=QC ， ∵PC=QC ，∴16﹣x=（8﹣x ）， ∴x=4+4．③当点P 在AC 上，点Q 在BC 的延长线时，PC=CQ ，即16﹣x=x ﹣8， ∴x=8+4．∴△PCQ 为等腰三角形时x 的值为4+4或8+4．25.证明：（1）如图（1），在PA 上截取PD=PA ， ∵AB=AC ，∠CAB=60°， ∴△ABC 为等边三角形， ∴∠APC=∠CPB=60°， ∴△APD 为等边三角形， ∴AP=AD=PD ，∴∠ADC=∠APB=120°，在△ACD 和△ABP 中，，∴△ACD ≌△ABP （AAS ），密线学校班级姓名学号密封线内不得答题∴CD=PB ，∵PC=PD+DC ， ∴PC=PA+PB ；（2）PC=PA+PB ，如图（2），作AD ⊥AP 与PC 交于一点D ， ∵∠BAC=90°，∴∠CAD=∠BAP ，在△ACD 和△ABP 中，，∴△ACD ≌△ABP ，∴CD=PB ，AD=AP ，根据勾股定理PD=PA ， ∴PC=PD+CD=PA+PB ．26.解：（1）把点A （0，m ）代入y=，得：2am 2﹣m=m ， am ﹣1=0， ∵am ＞1，∴a=， ∴y=，故答案为：y=；（2）DE=BC ．理由：又抛物线y=，可得抛物线的顶点坐标P （m ，﹣m ），由l ：x=m ，可得：点B （2m ，m ）， ∴点C （2m ，0）．设直线BP 的解析式为y=kx+b ，点P （m ，﹣m ）和点B （2m ，m ）在这条直线上，得：，解得：，∴直线BP 的解析式为：y=x ﹣3m ，令y=0， x ﹣3m=0，解得：x=，∴点D （，0）；设直线CP 的解析式为y=k 1x+b 1，点P （m ，﹣m ）和点C （2m ，0）在这条直线上，得：，解得：， ∴直线CP 的解析式为：y=x ﹣2m ；密封线内不得答题抛物线与直线CP 相交于点E ，可得：，解得：，（舍去）， ∴点E （，﹣）；∵x D =x E ， ∴DE ⊥x 轴，∴DE=y D ﹣y E =，BC=y B ﹣y C =m=2DE ，即DE=BC ；（3）C ′（，）．连接CC ′，交直线BP 于点F ， ∵BC ′=BC ，∠C ′BF=∠CBF ， ∴CC ′⊥BP ，CF=C ′F ，设直线BP 的解析式为y=kx+b ，点B （2m ，m ），P （m ，﹣m ）在直线上， ∴，解得：，∴直线BP 的解析式为：y=x ﹣3m ， ∵CC ′⊥BP ，∴设直线CC ′的解析式为：y=x+b 1，∴，解得：b 1=2m ，联立①②，得：，解得：，∴点F （，），∴CF==，设点C ′的坐标为（a ，）， ∴C ′F==，解得：a=，∴， ∴C ′（，）．密学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：120分时间：120分钟）一、选择题：每小题3分，共36分． 1．方程x 2=4x 的解是（）A ．x=4B ．x=2C ．x=4或x=0D ．x=0 2．在下列事件中，是必然事件的是（） A ．购买一张彩票中奖一百万元B ．抛掷两枚硬币，两枚硬币全部正面朝上C ．在地球上，上抛出去的篮球会下落D ．打开电视机，任选一个频道，正在播新闻3．一件商品的原价是100元，经过两次提价后的价格为121元，如果每次提价的百分率都是x ，根据题意，下面列出的方程正确的是（）A ．100（1+x ）=121B ．100（1﹣x ）=121C ．100（1+x ）2=121 D ．100（1﹣x ）2=1214．关于x 的一元二次方程（m ﹣1）x 2+5x+m 2﹣3m+2=0的常数项为0，则m 等于（）A ．1B ．2C ．1或2D ．05．对于抛物线y=﹣（x ﹣5）2+3，下列说法正确的是（）A ．开口向下，顶点坐标（5，3）B ．开口向上，顶点坐标（5，3）C ．开口向下，顶点坐标（﹣5，3）D ．开口向上，顶点坐标（﹣5，3）6．二次函数y=kx 2﹣6x+3的图象与x 轴有交点，则k 的取值范围是（）A ．k ＜3 B ．k ＜3且k ≠0 C ．k ≤3 D ．k ≤3且k ≠0 7．二次函数y=ax 2+bx+c 的图象如图所示，则下列关系式中错误的是（）A ．a ＜0B ．c ＞0C ．b 2﹣4ac ＞0 D ．a+b+c ＞0 8．一个布袋里装有6个只有颜色不同的球，其中2个红球，4个白球．从布袋里任意摸出1个球，则摸出的球是白球的概率为（）封线内不A． B． C． D．9．两圆的半径分别为3和7，圆心距为7，则两圆的位置关系是（）A．内切 B．相交 C．外切 D．外离10．在Rt△ABC中，∠C=90°，AC=12，BC=5，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是（）A．25π B．65πC．90π D．130π11．如图，四个边长为2的小正方形拼成一个大正方形，A、B、O是小正方形顶点，⊙O的半径为2，P是⊙O上的点，且位于右上方的小正方形内，则∠APB等于（）A．30° B．45° C．60° D．90°12．如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（）A．矩形 B．菱形 C．正方形 D．梯形二、填空题：每小题3分，共18分．13．已知关于x的方程x2﹣3x+k=0有一个根为1，个根为．14．抛物线y=3x2向右平移1个单位，再向下平移2所得到的抛物线是．15．如图，⊙O的直径AB=12，弦CD⊥AB于M，且M是半径的中点，则CD的长是（结果保留根号）．16．一元二次方程x2﹣3x+1=0的两根为x1、x2，则x1+x2﹣•x2= ．17．如图，已知以直角梯形ABCD的腰CD为直径的半圆O形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是．密线学校班级姓名学号密封线内不得答题18．如图，△ABC 绕点A 顺时针旋转45°得到△AB ′C ′，若∠BAC=90°，AB=AC=2，则图中阴影部分的面积等于．三、解答题：本大题共7小题，19题10分，其余每题6分，共46分． 19．解方程：（1）3x 2﹣2x=4x 2﹣3x ﹣6 （2）3x 2﹣6x ﹣2=0．20．某商场服装部销售一种名牌衬衫，平均每天可售出40件，每件盈利50元．为了扩大销售，减少库存，商场决定降价销售，经调查，每件降价1元时，平均每天可多卖出2件．（1）若商场要求该服装部每天盈利2400元，尽量减少库存，每件衬衫应降价多少元？（2）试说明每件衬衫降价多少元时，商场服装部每天盈利最多．21．如图，甲转盘被分成3个面积相等的扇形，乙转盘被分成2个半圆，每一个扇形或半圆都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为x ，乙转盘中指针所指区域内的数字为y （当指针指在边界线上时，重转一次，直到指针指向一个区域为止）．（1）请你用画树状图或列表格的方法，列出所有等可能情况，并求出点（x ，y ）落在坐标轴上的概率；（2）直接写出点（x ，y ）落在以坐标原点为圆心，2为半径的圆内的概率．密封线内22．如图，AB是⊙O的直径，CB是弦，OD⊥CB于E，交劣弧CB于D，连接AC．（1）请写出两个不同的正确结论；（2）若CB=8，ED=2，求⊙O的半径．23．在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=∠ABC．（1）如图1，以点B为旋转中心，将△EBC得到△E′BA（点C与点A重合，点E到点E′处），连接DE证：DE′=DE；（2）如图2，若∠ABC=90°，AD=4，EC=2，求DE的长．24．如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45∥AD，CD∥AB．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为1，求图中阴影部分的面积密学校班级姓名学号密封线内不得答题25．如图，对称轴为直线x=2的抛物线经过点A （﹣1，0），C （0，5）两点，与x 轴另一交点为B ，已知M （0，1），E （a ，0），F （a+1，0），点P 是第一象限内的抛物线上的动点．（1）求此抛物线的解析式；（2）当a=1时，求四边形MEFP 面积的最大值，并求此时点P 的坐标．参考答案一、选择题：每小题3分，共36分．1．C ．2.C ． 3．C ．4．B ．5.A ．6.D ．7．D ．8．D ．9．B ． 10．B ．11．B ．12．A ．二、填空题：每小题3分，共18分．13．已知关于x 的方程x 2﹣3x+k=0有一个根为1，则它的另一个根为 2 ．14．抛物线y=3x 2向右平移1个单位，再向下平移2个单位，所得到的抛物线是 y=3（x ﹣1）2﹣2 ．15．如图，⊙O 的直径AB=12，弦CD ⊥AB 于M ，且M 是半径OB 的中点，则CD 的长是 6 （结果保留根号）．密封线内不得答题16．一元二次方程x2﹣3x+1=0的两根为x1、x2，则x1+x2﹣x1•x2= 2 ．17．如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是14 ．18．如图，△ABC绕点A顺时针旋转45°得到△AB′C′，若∠BAC=90°，AB=AC=2，则图中阴影部分的面积等于4﹣4 ．三、解答题：本大题共7小题，19题10分，其余每题6分，共46分．19．解方程：解：（1）x2﹣x﹣6=0，（x﹣3）（x+2）=0，x﹣3=0或x+2=0，所以x1=3，x2=﹣2；（2）△=（﹣6）2﹣4×3×（﹣2）=60，x==，所以x1=，x2=．20.解：（1）设每件衬衫应降价x元，由题意得：（50﹣x）（40+2x）=2400，解得：x1=10，x2=20，因为尽量减少库存，x1=10舍去．答：每件衬衫应降价20元．（2）设每天盈利为W元，则W=（50﹣x）（40+2x）=﹣2（x﹣15）2+2450，当x=15时，W最大为2450．答：每件衬衫降价15元时，商场服装部每天盈利最多．21．密线学校班级姓名学号密封线内不得答题解：（1）树状图得： ∴一共有6种等可能的情况点（x ，y ）落在坐标轴上的有4种， ∴P （点（x ，y ）在坐标轴上）=；（2）∵点（x ，y ）落在以坐标原点为圆心，2为半径的圆内的有（0，0），（（0，﹣1）， ∴P （点（x ，y ）在圆内）=．22．解：（1）∵AB 是⊙O 的直径， ∴∠C=90°，∵OD ⊥CB ，∴CE=BE ， =，则三个不同类型的正确结论：∠C=90°；CE=BE ； =；（2）∵OD ⊥CB ，∴CE=BE=BC=4，又DE=2， ∴OE 2=OB 2﹣BE 2，设⊙O 的半径为R ，则OE=R ﹣2， ∴R 2=（R ﹣2）2+42，解得R=5．答：⊙O 的半径为5．23.（1）证明：∵以点B 为旋转中心，将△EBC 按顺时针方向旋转，得到△E ′BA （点C 与点A 重合，点E 到点E ′处）， ∴BE ′=BE ，∠E ′BA=∠EBC ， ∴∠E ′BE=∠ABC ，∵∠DBE=∠ABC ，∴∠DBE=∠E ′BE ，即∠DBE ′=∠DBE ，在△BDE ′和△BDE 中，，∴△BDE ′≌△BDE （SAS ）， ∴DE ′=DE ；密封线内不得答题（2）解：以点B为旋转中心，将△EBC按顺时针方向旋转90°得到△E′BA（点C与点A重合，点E到点E′处），如图2，∵∠ABC=90°，BA=BC，∴∠BCE=∠BAD=45°，∵△EBC按顺时针方向旋转90°得到△E′BA，∴∠BAE′=∠BCE=45°，AE′=CE=2，∴∠DAE′=∠BAD+∠BAE′=90°，在Rt△DAE′中，∵DE′2=AD2+AE′2=42+22=20，∴DE′=2，由（1）的结论得DE=DE′=2．23.解：（1）直线CD与⊙O相切．理由如下：如图，连接OD∵OA=OD，∠DAB=45°，∴∠ODA=45°∴∠AOD=90°∵CD∥AB∴∠ODC=∠AOD=90°，即OD⊥CD又∵点D在⊙O上，∴直线CD与⊙O相切；（2）∵⊙O的半径为1，AB是⊙O的直径，∴AB=2，∵BC∥AD，CD∥AB∴四边形ABCD是平行四边形∴CD=AB=2∴S梯形OBCD===；∴图中阴影部分的面积等于S梯形OBCD﹣S扇形OBD=﹣×π×12=﹣．25.解：（1）∵对称轴为直线x=2，∴设抛物线解析式为y=a（x﹣2）2+k．将A（﹣1，0），C（0，5）代入得：，解得，∴y=﹣（x﹣2）2+9=﹣x2+4x+5．（2）当a=1时，E（1，0），F（2，0），OE=1，OF=2．设P（x，﹣x2+4x+5），密学校班级姓名学号密封线内不得答题人教版2020---2021学年度上学期九年级数学期末考试卷及答案（满分：120分时间：120分钟）一、选择题（共12小题，每小题3分，满分36分） 1．一元二次方程x 2﹣2x=0的根是（） A ．x 1=0，x 2=﹣2 B ．x 1=1，x 2=2 C ．x 1=1，x 2=﹣2 D ．x 1=0，x 2=22．在一个不透明的布袋中，红色、黑色、白色的乒乓球共有20个，除颜色外，形状、大小、质地等完全相同．小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%，则口袋中白色球的个数很可能是（） A ．3个 B ．4个 C ．10个 D ．16个 3．下列说法错误的是（）A ．二次函数y=3x 2中，当x ＞0时，y 随x 的增大而增大B ．二次函数y=﹣6x 2中，当x=0时，y 有最大值0C ．抛物线y=ax 2（a ≠0）中，a 越大图象开口越小，a 越小图象开口越大D ．不论a 是正数还是负数，抛物线y=ax 2（a ≠0）的顶点一定是坐标原点4．下列命题中，是真命题的为（） A ．锐角三角形都相似 B ．直角三角形都相似 C ．等腰三角形都相似 D ．等边三角形都相似5．某公司10月份的利润为320万元，要使12月份的利润达到500万元，则平均每月增长的百分率是（） A ．30% B ．25% C ．20% D ．15%6．在一个不透明的袋子中装有4个除颜色外完全相同的小球，其中白球1个，黄球1个，红球2个，摸出一个球不放回，再摸出一个球，两次都摸到红球的概率是（） A ． B ． C ． D ．7．圆锥的地面半径为10cm ．它的展开图扇形半径为30cm ，则这个扇形圆心角的度数是（）A ．60°B ．90°C ．120° D ．150°8．在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（）A．与x轴相离，与y轴相切B．与x轴，y轴都相离C．与x轴相切，与y轴相离D．与x轴，y轴都相切9．若二次函数y=x2+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解为（）A．x1=0，x2=4 B．x1=1，x2=5C．x1=1，x2=﹣5 D．x1=﹣1，x2=510．如图，AC是矩形ABCD的对角线，E是边BC延长线上一点，AE与CD相交于F，则图中的相似三角形共有（）A．2对 B．3对 C．4对D．5对11．将△ACE绕点C旋转一定的角度后使点A落在点B处，点E在落在点D处，且B、C、E在同一直线上，AC、BD交于点F，CD、AE交于点G，AE、BD交于点H，连接AB、DE．则下列结论错误的是（）A．∠DHE=∠ACB B．△ABH∽△GDHC．DHG∽△ECG D．△ABC∽△DEC12．抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）经过点1，0）和（m，0），且1＜m＜2，当x＜﹣1时，y随着x大而减小．下列结论①a+b＞0；②若点A（﹣3，y1），点B3，y2）都在抛物线上，则y1＜y2；③a（m﹣1）+b=0；④若≤﹣1，则b2﹣4ac≤4a．其中正确结论的个数是（）A．1 B．2 C．3 D．4二、填空题（共6小题，每小题3分，满分18分）13．二次函数y=x2+1的最小值是．14．已知正六边形的半径是2，则这个正六边形的边长是．15．如图，点D是等边△ABC内的一点，如果△ABD绕点A时针旋转后能与△ACE重合，那么旋转了度．密学校班级姓名学号密封线内不得答题16．有两把不同的锁和三把钥匙，其中两把钥匙分别能打开其中一把锁，第三把钥匙不能打开这两把锁，任意取出一把钥匙去开任意的一把锁，一次打开锁的概率为．17．如图，点M 、N 分别是等边三角形ABC 中AB ，AC 边上的点，点A 关于MN 的对称点落在BC 边上的点D 处．若=，则的值．18．定义：长宽比为：1（n 为正整数）的矩形称为矩形．下面，我们通过折叠的方式折出一个矩形，如图①所示操作1：将正方形ABCD 沿过点B 的直线折叠，使折叠后的点C 落在对角线BD 上的点G 处，折痕为BH ．操作2：将AD 沿过点G 的直线折叠，使点A ，点D 分别落在边AB ，CD 上，折痕为EF ．可以证明四边形BCEF 为矩形．（Ⅰ）在图①中，的值为；（Ⅱ）已知四边形BCEF 为矩形，仿照上述操作，得到四边形BCMN ，如图②，可以证明四边形BCMN 为矩形，则n 的值是．三、解答题（共7小题，满分66分）19．已知y 是x 的反比例函数，并且当x=2时，y=6（1）求y 关于x 的解析式；（2）当x=4时，y 的值为该函数的图象位于第象限在图象的每一支上，y 随x 的增大而． 20．（1）解方程：x 2﹣2x+1=25（2）利用判别式判断方程3x 2+10=2x 2+8x 的根的情况． 21．已知，AG 是⊙O 的切线，切点为A ，AB 是⊙O 的弦，过点B 作BC ∥AG 交⊙O 于点C ，连接AO 并延长交BC 于点M（Ⅰ）如图1，若BC=10，求BM 的长；题（Ⅱ）如图2，连接AC，过点C作CD∥AB∠AG于点D，AM的延长线交过点C的直线于点P，且∠BCP=∠ACD．求证：PC是⊙O的切线．22．如图，AB是⊙O的直径，点D是⊙O上一点，点C是弧AD的中点，连接AC、BD、AD、BC交于点Q．（1）若∠DAB=40°，求∠CAD的大小；（2）若CA=10，CB=16，求CQ的长．23．如图所示，一拱桥的截面呈抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，拱桥与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m景观灯．（1）求抛物线的解析式；（2）求两盏景观灯之间的水平距离．24．已知，△ABC中，AB=AC，点E是边AC上一点，过点EEF∥BC交AB于点F（1）如图①，求证：AE=AF；（2）如图②，将△AEF绕点A逆时针旋转α（0°＜α＜144得到△AE′F′．连接CE′BF′．①若BF′=6，求CE′的长；②若∠EBC=∠BAC=36°，在图②的旋转过程中，当CE时，直接写出旋转角α的大小．25．已知抛物线y=x2+x﹣2（1）求抛物线与x轴的交点坐标；密线学校班级姓名学号密封线内不得答题（2）将抛物线y=x 2+x ﹣2沿y 轴向上平移，平移后与直线y=x+2的一个交点为点P ，与y 轴相交于点Q ，当PQ ∥x 轴时，求抛物线平移了几个单位；（3）将抛物线y=x 2+x ﹣2在x 轴下方的部分沿x 轴翻折到x 轴上方，图象的起步部分保持不变，翻折后的图象与原图象在x 轴上方的部分组成一个“W ”形状的新图象，若直线y=x+b与该新图象恰好有三个公共点，求b 的值．参考答案一、选择题（共12小题，每小题3分，满分36分） 1．D ；2．D ；3．C ；4．D ；5．B ；6．C ；7．C ；8．A ；9．D ；10．C ；11．B ；12．B ；二、填空题（共6小题，每小题3分，满分18分） 13．1；14．2；15．60；16．；17．；18．；3；三、解答题（共7小题，满分66分） 19．一；减小；20.（1）（x-1）2=25 ；开平方x-1=±5；x=6或x=-4。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。