江苏省盐城市时杨中学高考数学 第2讲 数形结合思想练习
高考数学第 2 讲 数形结合思想26页文档

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自形结合思想
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
专题1 数形结合思想【高考文科数学】数学思想方法 含答案

第二讲数形结合思想1.数形结合思想,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.数形结合思想的应用包括以下两个方面:(1)“以形助数”,把某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,揭示数学问题的本质;(2)“以数定形”,把直观图形数量化,使形更加精确.2.数形结合思想的实质、关键及运用时应注意的问题:其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化,在运用数形结合思想分析和解决问题时,要注意三点:第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二是恰当设参,合理用参,建立关系,由数思形,以形思数,做好数形转化;第三是正确确定参数的取值范围.3.实现数形结合,常与以下内容有关:(1)实数与数轴上的点的对应关系;(2)函数与图象的对应关系;(3)以几何元素和几何条件为背景,建立起来的概念,如复数、三角函数等;(4)所给的等式或代数式的结构含有明显的几何意义.如等式(x-2)2+(y-1)2=4,表示坐标平面内以(2,1)为圆心,以2为半径的圆.1.(2013·重庆)已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( ) A.52-4 B.17-1C.6-2 2 D.17答案 A解析设P(x,0),设C1(2,3)关于x轴的对称点为C1′(2,-3),那么|PC1|+|PC2|=|PC1′|+|PC2|≥|C1′C2|=2-32+-3-42=5 2.而|PM|=|PC1|-1,|PN|=|PC2|-3,∴|PM|+|PN|=|PC1|+|PC2|-4≥52-4.2. (2011·大纲全国)已知a、b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b -c)=0,则|c|的最大值是( )A.1 B.2 C. 2 D.2 2答案 C解析 如图,设OA →=a ,OB →=b ,OC →=c ,则CA →=a -c ,CB →=b -c .由题意知CA →⊥CB →,∴O 、A 、C 、B 四点共圆.∴当OC 为圆的直径时,|c |最大,此时,|OC →|= 2.3. (2013·山东)在平面直角坐标系xOy 中,M 为不等式组⎩⎪⎨⎪⎧2x -y -2≥0,x +2y -1≥0,3x +y -8≤0所表示的区域上一动点,则直线OM 斜率的最小值为( )A .2B .1C .-13D .-12答案 C解析 如图,由⎩⎪⎨⎪⎧x +2y -1=0,3x +y -8=0得A (3,-1).此时直线OM 的斜率最小,且为-13.4. (2013·课标全国Ⅰ)已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x , x ≤0,ln x +1, x >0.若|f (x )|≥ax ,则a的取值范围是( )A .(-∞,0]B .(-∞,1]C .[-2,1]D .[-2,0]答案 D解析 函数y =|f (x )|的图象如图. ①当a =0时,|f (x )|≥ax 显然成立. ②当a >0时,只需在x >0时, ln(x +1)≥ax 成立.比较对数函数与一次函数y =ax 的增长速度. 显然不存在a >0使ln(x +1)≥ax 在x >0上恒成立. ③当a <0时,只需在x <0时,x 2-2x ≥ax 成立. 即a ≥x -2成立,∴a ≥-2.综上所述:-2≤a ≤0.故选D.5. (2012·天津)已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是________.答案 (0,1)∪(1,4)解析 根据绝对值的意义,y =|x 2-1|x -1=⎩⎪⎨⎪⎧x +1x >1或x <-1,-x -1-1≤x <1.在直角坐标系中作出该函数的图象,如图中实线所示. 根据图象可知,当0<k <1或1<k <4时有两个交点.题型一 数形结合解决方程的根的个数问题 例1 (2012·福建)对于实数a和b ,定义运算“*”:a *b =⎩⎪⎨⎪⎧a 2-ab ,a ≤b ,b 2-ab ,a >b .设f (x )=(2x -1)*(x -1),且关于x 的方程f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是________.审题破题 本题以新定义为背景,要先写出f (x )的解析式,然后将方程f (x )=m 根的个数转化为函数y =f (x )的图象和直线y =m 的交点个数.答案 ⎝ ⎛⎭⎪⎫1-316,0解析 由定义可知,f (x )=⎩⎪⎨⎪⎧2x -1x ,x ≤0,-x -1x ,x >0.作出函数f (x )的图象,如图所示.由图可知,当0<m <14时,f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3. 不妨设x 1<x 2<x 3, 易知x 2>0,且x 2+x 3=2×12=1,∴x 2x 3<14.令⎩⎪⎨⎪⎧2x -1x =14,x <0,解得x =1-34.1-34<x1<0,∴1-316<x1x2x3<0.∴反思归纳 研究方程的根的个数、根的范围等问题时,经常采用数形结合的方法.一般 地,方程f (x )=0的根,就是函数f (x )的零点,方程f (x )=g (x )的根,就是函数f (x )和g (x )的图象的交点的横坐标.变式训练1 已知:函数f (x )满足下面关系:①f (x +1)=f (x -1);②当x ∈[-1,1]时,f (x )=x 2,则方程f (x )=lg x 解的个数是( )A .5B .7C .9D .10答案 C解析 由题意可知,f (x )是以2为周期,值域为[0,1]的函数.又f (x )=lg x ,则x ∈(0,10],画出两函数图象,则交点个数即为解的个数.由图象可知共9个交点.题型二 数形结合解不等式问题例2 设有函数f (x )=a +-x 2-4x 和g (x )=43x +1,已知x ∈[-4,0]时恒有f (x )≤g (x ),求实数a 的取值范围.审题破题 x ∈[-4,0]时恒有f (x )≤g (x ),可以转化为x ∈[-4,0]时,函数f (x )的图象都在函数g (x )的图象下方或者两图象有交点. 解 f (x )≤g (x ),即a +-x 2-4x ≤43x +1,变形得-x 2-4x ≤43x +1-a ,令y =-x 2-4x , ① y =43x +1-a .②①变形得(x +2)2+y 2=4(y ≥0),即表示以(-2,0)为圆心,2为半径的圆的上半圆;②表示斜率为43,纵截距为1-a 的平行直线系.设与圆相切的直线为AT ,AT 的直线方程为: y =43x +b (b >0), 则圆心(-2,0)到AT 的距离为d =|-8+3b |5,由|-8+3b |5=2得,b =6或-23(舍去).∴当1-a ≥6即a ≤-5时,f (x )≤g (x ).反思归纳 解决含参数的不等式和不等式恒成立问题,可以将题目中的某些条件用图象表现出来,利用图象间的关系以形助数,求方程的解集或其中参数的范围.变式训练2 已知不等式x 2+ax -2a 2<0的解集为P ,不等式|x +1|<3的解集为Q ,若P ⊆Q ,求实数a 的取值范围.解 x 2+ax -2a 2=(x +2a )(x -a )<0. |x +1|<3⇒Q ={x |-4<x <2}.当-2a <a ,即a >0时,P ={x |-2a <x <a }.∵P ⊆Q ,∴⎩⎪⎨⎪⎧-2a ≥-4,a ≤2,a >0.解得0<a ≤2.当-2a =a ,即a =0时,P =∅,P ⊆Q . 当-2a >a ,即a <0时,P ={x |a <x <-2a },∵P ⊆Q ,∴⎩⎪⎨⎪⎧a ≥-4,-2a ≤2,a <0,解得-1≤a <0,综上可得-1≤a ≤2.题型三 数形结合解决有明显几何意义的式子(概念)问题例3 已知函数f (x )=ax 2+bx -1(a ,b ∈R 且a >0)有两个零点,其中一个零点在区间(1,2)内,则ba +1的取值范围为( )A .(-∞,1)B .(-∞,1]C .(-2,1]D .(-2,1)审题破题 先根据图象确定a ,b 满足的条件,然后利用ba +1的几何意义——两点(a ,b ),(-1,0)连线斜率求范围.答案 D解析 因为a >0,所以二次函数f (x )的图象开口向上.又f (0)=-1,所以要使函数f (x )的一个零点在区间(1,2)内,则有⎩⎪⎨⎪⎧a >0,f 1<0,f 2>0,即⎩⎪⎨⎪⎧a >0,a +b -1<0,4a +2b -1>0.如图所示的阴影部分是上述不等式组所确定的平面区域,式 子ba +1表示平面区域内的点 P (a ,b )与点Q (-1,0)连线的斜率.而直线QA 的斜率k =1-00--1=1,直线4a +2b -1=0的斜率为-2,显然不等式组所表示的平面区域不包括边界,所以P ,Q 连线的斜率的取值范围为(-2,1).故选D. 反思归纳 如果等式、代数式的结构蕴含着明显的几何特征,就要考虑用数形结合的思想方法来解题,即所谓的几何法求解,比较常见的对应有: (1)b -n a -m ↔(a ,b )、(m ,n )连线的斜率; (2)a -m2+b -n2↔(a ,b )、(m ,n )之间的距离;(3)a 2+b 2=c 2↔a 、b 、c 为直角三角形的三边; (4)f (a -x )=f (b +x )↔f (x )图象的对称轴为x =a +b2.只要具有一定的观察能力,再掌握常见的数与形的对应类型,就一定能得心应手地运用数形结合的思想方法.变式训练3 已知点P (x ,y )的坐标x ,y 满足⎩⎪⎨⎪⎧x -2y +1≥0,|x |-y -1≤0,则x 2+y 2-6x +9的取值范围是( )A .[2,4]B .[2,16]C .[4,10]D .[4,16]答案 B解析 画出可行域如图,所求的x 2+y 2-6x +9=(x -3)2+y 2是点Q (3,0)到可行域上的点的距离的平方,由图形知最小值为Q 到射线x -y -1=0(x ≥0)的距离d 的平方,最大值为|QA |2=16.∵d 2=⎝⎛⎭⎪⎫|3-0-1|12+-122=(2)2=2. ∴取值范围是[2,16]. 题型四 数形结合解几何问题例4 已知点P 在抛物线y 2=4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( )A .(14,-1)B .(14,1)C .(1,2)D .(1,-2)审题破题 本题可以结合图形将抛物线上的点P 到焦点的距离转化为到准线的距离,再探求最值. 答案 A解析 定点Q (2,-1)在抛物线内部,由抛物线的定义知,动点P到抛物线焦点的距离等于它到准线的距离,问题转化为当点P 到点Q 的距离和点P 到抛物线的准线距离之和最小时,求点P 的坐标,显然点P 是直线y =-1和抛物线y 2=4x的交点时,两距离之和取最小值,解得这个点的坐标是(14,-1).反思归纳 在几何中的一些最值问题中,可以根据图形的性质结合图形上点的条件进行转换,快速求得最值.变式训练4 已知P 是直线l :3x +4y +8=0上的动点,PA 、PB 是圆x 2+y 2-2x -2y +1=0的两条切线,A 、B 是切点,C 是圆心,求四边形PACB 面积的最小值. 解 从运动的观点看问题,当动点P 沿直线3x +4y +8=0向左上方或右下方无穷远处运动时,直角三角形PAC 的面积S Rt △PAC=12|PA |·|AC |=12|PA |越来越大,从而S 四边形PACB 也越来越大;当点P 从左上、右下两个方向向中间运动时,S四边形PACB变小,显然,当点P 到达一个最特殊的位置,即CP 垂直直线l 时,S四边形PACB应有唯一的最小值,此时|PC |=|3×1+4×1+8|32+42=3, 从而|PA |=|PC |2-|AC |2=2 2.∴(S 四边形PACB )min =2×12×|PA |×|AC |=2 2.典例 (12分)已知函数f (x )=x 3-3ax -1,a ≠0.(1)求f (x )的单调区间;(2)若f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图象有三个不同的交点,求m 的取值范围.规范解答解 (1)f ′(x )=3x 2-3a =3(x 2-a ), 当a <0时,对x ∈R ,有f ′(x )>0,∴当a <0时,f (x )的单调增区间为(-∞,+∞); 当a >0时,由f ′(x )>0,解得x <-a 或x >a , 由f ′(x )<0,解得-a <x <a ,∴当a >0时,f (x )的单调增区间为(-∞,-a ),(a ,+∞); 单调减区间为(-a ,a ). [4分](2)∵f (x )在x =-1处取得极值, ∴f ′(-1)=3×(-1)2-3a =0,∴a =1. [6分]∴f (x )=x 3-3x -1,f ′(x )=3x 2-3,由f ′(x )=0, 解得x 1=-1,x 2=1.由(1)中f (x )的单调性可知,f (x )在x =-1处取得极大值f (-1)=1,在x =1处取得极小值f (1)=-3.因为直线y =m 与函数y =f (x )的图象有三个不同的交点, 结合如图所示f (x )的图象可知:m 的取值范围是(-3,1).[12分]评分细则 (1)求出f ′(x )给1分,不写出单调区间扣1分;(2)只画图象没有说明极值扣2分;(3)没有结论扣1分,结论中范围写成不等式形式不扣分.阅卷老师提醒 (1)解答本题的关键是数形结合,根据函数的性质勾画函数的大致图象; (2)解答中一定要将函数图象的特点交待清楚,单调性和极值是勾画函数的前提,然后结合图象找出实数m 的取值范围.1. 设函数f (x )定义在实数集上,f (2-x )=f (x ),且当x ≥1时,f (x )=ln x ,则有( )A .f (13)<f (2)<f (12)B .f (12)<f (2)<f (13)C .f (12)<f (13)<f (2)D .f (2)<f (12)<f (13)答案 C解析 由f (2-x )=f (x )知f (x )的图象关于直线x =2-x +x2=1对称,又当x ≥1时,f (x )=ln x ,所以离对称轴x =1距离大的x 的函数值大,∵|2-1|>|13-1|>|12-1|,∴f (12)<f (13)<f (2).2. 设函数f (x )=⎩⎪⎨⎪⎧x 2+bx +c , x ≤0,2, x >0.若f (-4)=f (0),f (-2)=-2,则函数y =g (x )=f (x )-x 的零点个数为( )A .1B .2C .3D .4答案 C解析 由f (-4)=f (0) 得16-4b +c =c .由f (-2)=-2,得4-2b +c =-2. 联立两方程解得:b =4,c =2.于是,f (x )=⎩⎪⎨⎪⎧x 2+4x +2, x ≤0,2, x >0.在同一直角坐标系内,作出函数y =f (x )与函数y =x 的图象,知它们有3个交点,进而函数亦有3个零点.3. 若方程x +k =1-x 2有且只有一个解,则k 的取值范围是( )A .[-1,1)B .k =± 2C .[-1,1]D .k =2或k ∈[-1,1)答案 D解析 令y =x +k ,令y =1-x 2,则x 2+y 2=1(y ≥0). 作出图象如图:而y =x +k 中,k 是直线的纵截距,由图知:方程有一个解⇔直线与 上述半圆只有一个公共点⇔k =2或-1≤k <1.4. 设a ,b ,c 是单位向量,且a ·b =0,则(a -c )·(b -c )的最小值为( ) A .-2 B.2-2 C .-1D .1- 2答案 D解析 由于(a -c )·(b -c )=-(a +b )·c +1,因此等价于求(a +b )·c 的最大值,这个最大值只有当向量a +b 与向量c 同向共线时取得.由于a ·b =0,故a ⊥b ,如图所示,|a +b |=2,|c |=1,当θ=0时,(a +b )·c 取最大值2,故所求的最小值为1- 2. 5. 当0<x ≤12时,4x<log a x ,则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,22 B.⎝⎛⎭⎪⎫22,1 C .(1,2)D .(2,2)答案 B解析 由0<x ≤12,且log a x >4x>0,可得0<a <1,12由4 =log a 12可得a =22.令f (x )=4x,g (x )=log a x , 若4x<log a x ,则说明当0<x ≤12时,f (x )的图象恒在g (x )图象的下方(如图所示),此时需a >22. 综上可得a 的取值范围是⎝⎛⎭⎪⎫22,1. 6. 已知P 为抛物线y =14x 2上的动点,点P 在x 轴上的射影为M ,点A 的坐标是(2,0),则|PA |+|PM |的最小值是________. 答案5-1解析 如图,抛物线y =14x 2,即x 2=4y 的焦点F (0,1),记点P 在抛物线的准线l :y =-1上的射影为P ′,根据抛物线的定义知, |PP ′|=|PF |,则|PP ′|+|PA |=|PF |+|PA |≥|AF |=22+12=5.所以(|PA |+|PM |)min =(|PA |+|PP ′|-1)min =5-1.专题限时规范训练一、选择题1. 已知f (x )是定义在(-3,3)上的奇函数,当0<x <3时,f (x )的图象如图所示,那么不等式f (x )·cos x <0的解集是( )A.⎝ ⎛⎭⎪⎫-3,-π2∪(0,1)∪⎝ ⎛⎭⎪⎫π2,3B.⎝ ⎛⎭⎪⎫-π2,-1∪(0,1)∪⎝ ⎛⎭⎪⎫π2,3 C .(-3,-1)∪(0,1)∪(1,3)D.⎝ ⎛⎭⎪⎫-3,-π2∪(0,1)∪(1,3) 答案 B解析 根据对称性画出f (x )在(-3,0)上的图象如图,结合y =cos x 在(-3,0),(0,3)上函数值的正负,易知不等式f (x )cos x <0的解集是⎝ ⎛⎭⎪⎫-π2,-1∪(0,1)∪⎝ ⎛⎭⎪⎫π2,3.2. 已知函数f (x )=⎩⎪⎨⎪⎧|lg x |,0<x ≤10,-12x +6,x >10,若a 、b 、c 互不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是( )A .(1,10)B .(5,6)C .(10,12)D .(20,24)答案 C解析 a ,b ,c 互不相等,不妨设a <b <c , ∵f (a )=f (b )=f (c ),由图象可知,0<a <1,1<b <10,10<c <12. ∵f (a )=f (b ),∴|lg a |=|lg b |,即lg a =lg 1b ,a =1b.则ab =1,所以abc =c ∈(10,12).3. 用min{a ,b ,c }表示a ,b ,c 三个数中的最小值.设f (x )=min{2x,x +2,10-x } (x≥0),则f (x )的最大值为( )A .4B .5C .6D .7答案 C解析 画出y =2x,y =x +2,y =10-x 的图象,如图所示,观察图象,可知当0≤x ≤2,f (x )=2x,当2<x ≤4时,f (x )=x +2,当x >4时,f (x )=10-x ,f (x )的最大值在x =4时取得,为6.4. 函数f (x )=(12)x-sin x 在区间[0,2π]上的零点个数为( ) A .1 B .2 C .3D .4答案 B解析 函数f (x )=(12)x-sin x 在区间[0,2π]上的零点个数即为方程(12)x -sin x =0在区间[0,2π]上解的个数.因此可以转化为两函数y =(12)x 与y=sin x 交点的个数.根据图象可得交点个数为2,即零点个数为2.5. 已知双曲线x 2a 2-y 2b2=1 (a >0,b >0)的右焦点为F ,若过点F 且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )A .(1,2]B .(1,2)C .[2,+∞)D .(2,+∞)答案 C解析 ∵渐近线y =bax 与过焦点F 的直线l 平行,或渐近线从该位置绕原点按逆时针旋转时,直线l 与双曲线的右支有一个交点,∴b a≥3,即c 2=a 2+b 2≥4a 2,∴e ≥2.6. 设a =sin 5π7,b =cos 2π7,c =tan 2π7,则( ) A .a <b <c B .a <c <b C .b <c <aD .b <a <c答案 D解析 a =sin 5π7=sin ⎝⎛⎭⎪⎫π-2π7=sin 2π7,又π4<2π7<π2,可通过单位圆中的三角函数线进行比较:如图所示,cos 2π7=OA ,sin 2π7=AB ,tan 2π7=MN ,∴cos 2π7<sin 2π7<tan 2π7,即b <a <c .7. 不等式x 2-log a x <0在x ∈(0,12)时恒成立,则a 的取值范围是( )A .0<a <1 B.116≤a <1C .a >1D .0<a ≤116答案 B解析 不等式x 2-log a x <0转化为x 2<log a x , 由图形知0<a <1且 (12)2≤log a 12, ∴a ≥116,故a 的取值范围为⎣⎢⎡⎭⎪⎫116,1.8. 函数y =11-x的图象与函数y =2sin πx (-2≤x ≤4)的图象所有交点的横坐标之和等于( )A .2B .4C .6D .8 答案 D解析 令1-x =t ,则x =1-t .由-2≤x ≤4,知-2≤1-t ≤4,所以-3≤t ≤3. 又y =2sin πx =2sin π(1-t )=2sin πt .在同一坐标系下作出y =1t和y =2sin πt 的图象.由图可知两函数图象在[-3,3]上共有8个交点,且这8个交点两两关于原点对称.因此这8个交点的横坐标的和为0,即t 1+t 2+…+t 8=0.也就是1-x 1+1-x 2+…+1-x 8=0, 因此x 1+x 2+…+x 8=8. 二、填空题9. 若实数x 、y 满足⎩⎪⎨⎪⎧x -y +1≤0,x >0,y ≤2,则yx的最小值是________.答案 2解析 可行域如图所示.又y x的几何意义是可行域内的点与坐标原点连线的斜率k . 由图知,过点A 的直线OA 的斜率最小.联立⎩⎪⎨⎪⎧x -y +1=0,y =2,得A (1,2),∴k OA =2-01-0=2.∴y x的最小值为2.10.设A ={(x ,y )|x 2+(y -1)2=1},B ={(x ,y )|x +y +m ≥0},则使A ⊆B 成立的实数m的取值范围是__________. 答案 m ≥2-1解析 集合A 是一个圆x 2+(y -1)2=1上的点的集合,集合B 是一个不等式x +y +m ≥0表示的平面区域内的点的集合,要使A ⊆B ,则应使圆被平面区域所包含(如图),即直线x +y +m =0应与圆相切或相离(在圆的下方),而当直线与圆相切时有|m +1|2=1,又m >0,∴m =2-1,故m 的取值范围是m ≥2-1.11.若函数f (x )=a x-x -a (a >0且a ≠1)有两个零点,则实数a 的取值范围是________.答案 a >1解析 设函数y =a x(a >0且a ≠1)和函数y =x +a .则函数f (x )=a x-x -a (a >0且a ≠1)有两个零点,就是函数y =a x(a >0且a ≠1)的图象与函数y =x +a 的图象有两个交点.由图象可知,当0<a <1时,两函数只有一个交点,不符合;当a >1时,因为函数y =a x(a >1)的图象过点(0,1),而直线y =x +a 的图象与y 轴的交点一定在点(0,1)的上方,所以一定有两个交点.所以实数a 的取值范围是a >1.12.已知函数f (x )=⎩⎪⎨⎪⎧e x,x ≥0-2x ,x <0,则关于x 的方程f [f (x )]+k =0,给出下列四个命题:①存在实数k ,使得方程恰有1个实根; ②存在实数k ,使得方程恰有2个不相等的实根; ③存在实数k ,使得方程恰有3个不相等的实根; ④存在实数k ,使得方程恰有4个不相等的实根.其中正确命题的序号是________.(把所有满足要求的命题序号都填上) 答案 ①②解析 依题意知函数f (x )>0,又f [f (x )]=依据y =f [f (x )]的大致图象(如图)知,存在实数k ,使得方程f [f (x )]+k =0恰有1个实根;存在实数k ,使得方程f [f (x )]+k=0恰有2个不相等的实根;不存在实数k ,使得方程恰有3个不相等的实根;不存在实数k ,使得方程恰有4个不相等的实根.综上所述,其中正确命题的序号是①②. 三、解答题13.已知函数f (x )=x 3+ax 2+bx .(1)若函数y =f (x )在x =2处有极值-6,求y =f (x )的单调递减区间; (2)若y =f (x )的导数f ′(x )对x ∈[-1,1]都有f ′(x )≤2,求ba -1的范围.解 (1)f ′(x )=3x 2+2ax +b ,依题意有⎩⎪⎨⎪⎧ f ′2=0,f 2=-6.即⎩⎪⎨⎪⎧12+4a +b =0,8+4a +2b =-6,解得⎩⎪⎨⎪⎧a =-52,b =-2.∴f ′(x )=3x 2-5x -2.由f ′(x )<0,得-13<x <2.∴y =f (x )的单调递减区间是⎝ ⎛⎭⎪⎫-13,2. (2)由⎩⎪⎨⎪⎧f ′-1=3-2a +b ≤2,f ′1=3+2a +b ≤2,得⎩⎪⎨⎪⎧2a -b -1≥0,2a +b +1≤0.不等式组确定的平面区域如图阴影部分所示:由⎩⎪⎨⎪⎧ 2a -b -1=0,2a +b +1=0,得⎩⎪⎨⎪⎧a =0,b =-1. ∴Q 点的坐标为(0,-1). 设z =ba -1,则z 表示平面区域内的点(a ,b )与点P (1,0)连线的斜率.∵k PQ =1,由图可知z ≥1或z <-2, 即ba -1∈(-∞,-2)∪[1,+∞).14.设关于θ的方程3cos θ+sin θ+a =0在区间(0,2π)内有相异的两个实根α、β.(1)求实数a 的取值范围; (2)求α+β的值.解 方法一(1)设x =cos θ,y =sin θ,则由题设知,直线l :3x +y +a =0与圆x 2+y 2=1有两个不同的交点A (cos α,sin α)和B (cos β,sin β).所以原点O 到直线l 的距离小于半径1,即 d =||0+0+a 32+12=|a |2<1,∴-2<a <2. 又∵α、β∈(0,2π),且α≠β. ∴直线l 不过点(1,0),即3+a ≠0.∴a ≠-3,即a ∈(-2,-3)∪(-3,2).(2)如图,不妨设∠xOA =α,∠xOB =-β,作OH ⊥AB ,垂足为H ,则∠BOH =α-β2.∵OH ⊥AB ,∴kAB ·k OH =-1.∴tan α+β2=33.又∵α+β2∈(0,2π),∴α+β=π3或α+β=7π3.方法二 (1)原方程可化为sin (θ+π3)=-a 2,作出函数y =sin (x +π3)(x ∈(0,2π))的图象.由图知,方程在(0,2π)内有相异实根α,β的充要条件是⎩⎪⎨⎪⎧-1<-a2<1-a 2≠32,即-2<a <-3或-3<a <2.(2)由图知:当-3<a <2,即-a 2∈⎝ ⎛⎭⎪⎫-1,32时,直线y =-a 2与三角函数y =sin(x+π3)的图象交于C 、D 两点,它们中点的横坐标为7π6,∴α+β2=7π6,∴α+β=7π3. 当-2<a <-3,即-a 2∈⎝ ⎛⎭⎪⎫32,1时,直线y =-a 2与三角函数y =sin(x +π3)的图象有两交点A 、B ,由对称性知,α+β2=π6,∴α+β=π3,综上所述,α+β=π3或α+β=7π3.。
高考数学运用数形结合的思想方法解题专项练习(含答案解析)

高考数学运用数形结合的思想方法解题专项练习(含答案解析)一、单选题1.(2023春·江苏盐城·高三盐城中学校考)若直线():40l x m y +−=与曲线x =有两个交点,则实数m 的取值范围是( )A .0m <<B .0m ≤<C .0m <≤D .0m ≤【答案】B【解析】x =()0,0,半径为2的圆在y 轴以及右侧的部分,如图所示:直线():40l x m y +−=必过定点()0,4, 当直线l 与圆相切时,直线和圆恰有一个交点,2=,结合直线与半圆的相切可得m =当直l 的斜率不存在时,即0m =时,直线和曲线恰有两个交点, 所以要使直线和曲线有两个交点,则0m ≤故选:B.2.(2023春·湖北随州·高三随州市曾都区第一中学校考阶段练习)已知x ,y 是实数,且22410x y x +−+=,则21y x ++的最大值是( )A B .116C .336D 【答案】D【解析】方程可化为()223x y −+=,表示以()2,021y x ++的几何意义是圆上一点与点A ()1,2−−连线的斜率,设21k y x =++,即()21y k x +=+,当此直线与圆相切时,斜率最大或最小,当切线位于切线AB 时斜率最大.=k =,所以21y x ++故选:D .3.(2023春·陕西渭南·高一统考)已知函数()f x 是定义在R 上的偶函数,当[)0,x ∈+∞时,()24f x x x =−.若函数()()()R g x f x m m =+∈,则函数()g x 的零点个数不可能是( )A .1B .2C .3D .4【答案】A【解析】函数()f x 是定义在R 上的偶函数,当[)0,x ∈+∞时,()224(2)4f x x x x =−=−−,作出()f x 的图像如图:,故当0m =时,()()g x f x =有3个零点;当0m <或4m =时,()()g x f x m =+的图像与x 轴有两个交点,则函数有2个零点; 当04m <<时,()()g x f x m =+的图像与x 轴有4个交点,则函数有4个零点;由于()()g x f x m =+也为偶函数,结合()f x 图像可知,()()g x f x m =+不可能有1个零点, 故选:A4.(2023春·陕西西安·高三统考期末)已知函数()e ,03,0x x f x x x ⎧≥=⎨−<⎩, 若函数()()()g x f x f x =−−,则函数()g x 的零点个数为( ) A .1 B .3 C .4 D .5【答案】D【解析】当0x >时,0x −<,()3f x x −=当0x <时,0x −>,()e xf x −−=()()()3e ,00,0e 3,0x x x x g x f x f x x x x −⎧−>⎪∴=−−==⎨⎪+<⎩,()()()()g x f x f x g x −=−−=−,且定义域为R ,关于原点对称,故()g x 为奇函数,所以我们求出0x >时零点个数即可,(0,)3e x g x x x =−>,()3e 0x g x '=−>,令()3e 0x g x '=−>,解得0ln3x <<,故()g x 在()0,ln 3上单调递增,在(ln3,)+∞单调递减,且(ln3)3ln330g =−>,而()226e 0g =−<,故()g x 在(ln 3,2)有1零点,1311e 03g ⎛⎫=−< ⎪⎝⎭,故()g x 在1(,ln 3)3上有1零点,图像大致如图所示:故()g x 在()0,∞+上有2个零点,又因为其为奇函数,则其在(),0∞−上也有2个零点,且()00g =,故()g x 共5个零点, 故选:D.5.(2023春·黑龙江哈尔滨·高一哈尔滨三中校考阶段练习)若函数()f x 的定义域为(),1f x −R 为偶函数,当1x ≥−时,()31xf x −=−,则函数()()12g x f x =−的零点个数为( )A .0B .1C .2D .4【答案】D【解析】令310x −−≥解得0x ≤,令310x −−<解得0x >, 所以当1x ≥−时,()11,1033111,03xxxx f x x −⎧⎛⎫−−≤≤⎪ ⎪⎪⎝⎭=−=⎨⎛⎫⎪−+> ⎪⎪⎝⎭⎩, ()1f x −为偶函数,所以()1f x −的图像关于y 轴对称,所以()f x 的图像关于直线=1x −轴对称, 故作出()f x 的图像如下,令()()102g x f x =−=,即()12f x =, 由图像可知,()f x 的图像与12y =的图像共有四个交点, 所以函数()()12g x f x =−的零点个数为4个.故选:D.6.(2023·山东潍坊·统考模拟预测)已知函数()f x 是定义域为R 的偶函数,且(1)f x −是奇函数,当01x 剟时,有()f x =()(2021)y f x k x =−−的零点个数为5,则实数k 取值范围是( ) A .15<2<1kB .16<3<1kC k k =D .k <k 【答案】C【解析】∵偶函数()f x ,()()f x f x ∴−=,(1)f x −是奇函数,得(1)(1)f x f x −=−−−,即 ()(2)f x f x =−−−,(2)()f x f x −−−=−,得4T =,()(2021)0f x k x −−=,即()y f x =与(2021)y k x =−的图像交点的个数,因为4T =,即为()y f x =与(1)y k x =−的图像交点的个数,因为()f x =k 应该在1k 与2k 之间或为3k ,213k k k ==k k =故选:C.7.(2023·全国·高三专题练习)已知函数()()ln2,01ln 2ln 2,12xx f x x x ⎧<<⎪=⎨−+≤<⎪⎩,若存在02a b c <<<<使得()()()f a f b f c ==,则111ab bc ca++的取值范围是( ) A .20,93⎛⎫⎪⎝⎭B .20,3⎛⎫+∞ ⎪⎝⎭C .∞⎫+⎪⎪⎣⎭ D .⎫⎪⎪⎣⎭【答案】A【解析】∵()()ln 2ln2ln 22x x ⎡⎤−+=−⎣⎦,∴ln 2y x =与()ln 2ln2y x =−+的图像关于直线1x =对称,作出()f x 的大致图像如图所示,易知2b c +=,由ln2ln2a b =,即ln 2ln 2a b −=,ln 40ab =,得14ab =, ∵112b <<,∴11124a<<,得1142a <<,∴()()421621112181244a a a a b c a c ab bc ca abc a a+++++++====−−. 设81t a =−, 则()1,3t ∈,111117184t ab bc ca t ⎛⎫++=++ ⎪⎝⎭. 17t t+≥=t 故当()1,3t ∈时,令()1718h t t t +=+,()h t 单减,()()80136,33h h ==, 故1172018,943t t ⎛⎫⎛⎫++∈ ⎪ ⎪⎝⎭⎝⎭. 故选:A 二、多选题8.(2023·全国·高三专题练习)已知1F ,2F 是双曲线()2222:10,0x yE a b a b−=>>的左、右焦点,过1F 作倾斜角为30的直线分别交y 轴与双曲线右支于点,M P ,1PM MF =,下列判断正确的是( )A .2160PF F ∠=,B .2112MF PF =C .ED .E的渐近线方程为y =【答案】BCD【解析】如下图所示,因为1PM MF =,即M 为1PF 中点,O 为12F F 中点,所以2//OM PF ,因为12OM F F ⊥,所以212PF F F ⊥,所以212PF F π∠=,2112MF PF =,A 错误,B 正确; 由212PF F F ⊥知:22b PF a=,又122F F c =,1230PF F ∠=,2c =)222c a ac −=220e −,解得:e =C 正确;所以==c e a 223c a =,所以22222b c a a =−=,所以ba= 所以E 的渐近线方程为y =,D 正确.故选:BCD .9.(2023·全国·高三专题练习)已知直线l 过抛物线2:8C y x =的焦点F l 与抛物线交于,P Q 两点(P 在第一象限),以,PF QF 为直径的圆分别与y 轴相切于,A B 两点,则下列结论正确的是( ) A .32||3PQ =B .AB =C .若M 为抛物线C 上的动点,(2,1)N ,则min (||||)4MF MN +=D .若0(,M x 为抛物线C 上的点,则9MF = 【答案】ABC【解析】设直线PQ 的方程为:y x ﹣2),与28y x =联立整理可得:3x 2﹣20x +12=0,解得:x 23=或6,则P (6,,Q (23,;所以|PQ |=623++4323=,选项A 正确;因为F (2,0),所以PF ,QF 的中点分别为:(4,,(43,,所以A (0,,B (0,,所以|AB =, 选项B 正确;如图M 在抛物线上,ME 垂直于准线交于E ,可得|MF |=|ME |, 所以|MF |+|MN |=|ME |+|MN |≥NE =2+2=4,当N ,M ,E 三点共线时, |MF |+|MN |最小,且最小值为4,选项C 正确;对于选项D ,若0(M x 为抛物线C 上的点,则05x =,又4p =, 所以072pMF x =+=,选项D 错误. 故选:ABC.10.(2023春·河南·高三校联考)在三棱锥A BCD −中,平面ABD ⊥平面BCD ,BD CD ⊥,2BD CD ==,ABD △为等边三角形,E 是棱AC 的中点,F 是棱AD 上一点,若异面直线DE与BF AF 的值可能为( ) A .23B .1C .43D .53【答案】AC【解析】由ABD △为等边三角形,取BD 的中点O ,连接AO ,则AO BD ⊥ 又平面ABD ⊥平面BCD ,且平面ABD ⋂平面BCD BD = 所以AO ⊥平面BCD ,由BD CD ⊥过O 作与CD 平行的直线为y 轴,分别以,OB OA 为,x z 轴建立如图所示的空间直角坐标系,因为2BD CD ==,则()1,0,0B ,()()(1,0,0,1,2,0,D C A −−,所以12E ⎛− ⎝⎭.设()F a ,则12DE ⎛= ⎝⎭,()BF a =−,则28=13a =−或23a =−, 故1233AF AD ==或2433AF AD ==.故选:AC11.(2023秋·福建三明·高一福建省宁化第一中学校考阶段练习)已知G 为ABC 的重心,60BAC ∠=︒,2AB AC ⋅=,则||AG uuu r的可能取值为( )A .23B .1CD .32【答案】CD【解析】如图,G 是ABC 的重心,记,,AB c AC b AB a ===, 则2211()()3323AG AD AB AC AB AC ==⨯+=+, 222222111()(2)(4)999AG AB AC AB AB AC AC b c =+=+⋅+=++,又1cos6022AB AC bc bc ⋅=︒==,即4bc =,所以2228b c bc +≥=,当且仅当2b c ==时等号成立,所以214(84)93AG ≥⨯+=.即233AG ≥CD 满足. 故选:CD .12.(2023春·湖北黄冈·高三校考开学考试)已知ABC 的重心为G ,过G 点的直线与边AB ,AC 的交点分别为M ,N ,若AM MB λ=,且AMN 与ABC 的面积之比为920,则λ的可能取值为( )A .43B .32C .53D .3【答案】BD【解析】如图,()AM MB AB AM λλ==−,1AM AB λλ∴=+,即1AB AM λλ+=,设AC t AN =,则11()333tAG AB AC AM AN λλ+=+=+, M G N 、、三点共线,1=133t λλ+∴+,12t λ∴=−, 所以12AC AN λ⎛⎫=− ⎪⎝⎭,AMN ∴与ABC 的面积之比为920,191sin sin 2202AM AN A AB AC A ∴=⨯⨯, 即112029λλλ+⎛⎫⎛⎫−=⎪⎪⎝⎭⎝⎭,化简得22990λλ−+=,解得32λ=或3. 故选:BD13.(2023春·湖南长沙·高三长沙一中校联考)在三维空间中,定义向量的外积:a b ⨯叫做向量a 与b 的外积,它是一个向量,满足下列两个条件:①()a a b ⊥⨯,()b a b ⊥⨯,且a ,b 和a b ⨯构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示);②a b ⨯的模sin ,a b a b a b ⨯=,(,a b 表示向量a ,b 的夹角). 在正方体1111ABCD A B C D −中,有以下四个结论,正确的有( )A .11AB AC AD DB ⨯=⨯ B .111AC A D ⨯与1BD 共线C .AB AD AD AB ⨯=⨯ D .6BC AC ⨯与正方体表面积的数值相等【答案】ABD【解析】对于A ,设正方体的棱长为1,在正方体中1,60AB AC =︒,则111sin ,2AB AC AB AC AB AC ⨯===, 因为11//BD B D ,且1160AD B ∠=︒,所以1,120AD DB =︒,所以111sin ,2AD DB AD DB AD DB ⨯=== 所以11AB AC AD DB ⨯=⨯,所以A 正确;对于B ,1111AC B D ⊥,111AC BB ⊥,1111B B B D B ⋂=,111,B B B D ⊂平面11BB D D ,11AC ⊥平面11BB D D ,因为1BD ⊂平面11BB D D ,所以111BD AC ⊥,同理可证11BD A D ⊥, 再由右手系知,111AC A D ⨯与1BD 同向,所以B 正确;对于C ,由a ,b 和a b ⨯构成右手系知,a b ⨯与b a ⨯方向相反, 又由a b ⨯模的定义知,sin ,sin ,a b a b a b b a a b b a ⨯===⨯, 所以a b ba ⨯=−⨯,则AB AD AD AB ⨯=−⨯,所以C 错误; 对于D ,正方体棱长为a ,266sin 456BC AC BC AC a a ⨯=⋅︒=⨯, 正方体表面积为26a ,所以D 对. 故选:ABD .三、填空题14.(2023·全国·高三专题练习)已知函数243,0()41,01x x x f x x x ⎧++≤⎪=⎨−>⎪+⎩.若关于x 的方程()()()2[]2110f x m f x m +−−+=有6个不同的实数根,则m 的取值范围___________.【答案】7,5⎛− ⎝⎭【解析】因为243,0()41,01x x x f x x x ⎧++≤⎪=⎨−>⎪+⎩,所以当0x ≤时,()243f x x x =++开口向上,对称轴为2x =−,()()min 21f x f =−=−,两零点为1,3x x =−=−;当0x >时,()411f x x =−+,则()f x 在()0,∞+上单调递减,零点为3x =,且()1f x >−; 由此作出()f x 的图像如图,.令()t f x =,则当13t −<<时,()t f x =有三个实数根,因为()()()2[]2110f x m f x m +−−+=有6个不同的实数根,所以()22110t m t m +−−+=必须有两个不等实根12,t t ,且()21,1,3t t ∈−,令()()2211g t t m t m =+−−+,则()()103021132Δ0g g m ⎧−>⎪>⎪⎪⎨−−<−<⎪⎪>⎪⎩,即()()()()212110932110621221410m m m m m m m ⎧−−−+>⎪+−−+>⎪⎨−<−<⎪⎪−−−+>⎩,解得75m −<<7,5m ⎛∈− ⎝⎭.故答案为:7,5⎛− ⎝⎭. 15.(2023春·全国·高一期末)已知函数241,1()log 3,1xx f x x x ⎧−⎪=⎨+>⎪⎩…集合21()2()02M x f x t f x t ⎧⎫⎛⎫=−++=⎨⎬ ⎪⎝⎭⎩⎭∣,若集合M 中有3个元素,则实数t 的取值范围为________.【答案】{|0t t =或1}2t ≥【解析】令()f x m =,记21()(2)2g m m t m t =−++的零点为12,m m ,因为集合M 中有3个元素,所以()f x 的图像与直线12,y m y m ==共有三个交点,则,12001m m =⎧⎨<<⎩或12101m m =⎧⎨<<⎩或12001m m >⎧⎨<<⎩当10m =时,得0=t ,212m =,满足题意; 当11m =时,得12t =,212m =,满足题意;当12001m m >⎧⎨<<⎩时,(0)01(1)1202g t g t t =>⎧⎪⎨=−−+<⎪⎩,解得12t >. 综上,t 的取值范围为{|0t t =或1}2t ≥.故答案为:{|0t t =或1}2t ≥16.(2023秋·黑龙江绥化·高一校考期末)ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知30,12=︒=A b ,若ABC 有两解,写出a 的一个可能的值为__________.【答案】7(满足(612)a ∈,均可,答案不唯一) 【解析】由于满足条件的ABC 有两个,则sin b A a b <<,即612a <<.故答案为:7(满足(612)a ∈,均可,答案不唯一).17.(2023·海南·统考模拟预测)已知函数()314f x x m π⎛⎫=++− ⎪⎝⎭在3,04π⎡⎤−⎢⎥⎣⎦上有3个零点1x ,2x ,3x ,其中123x x x <<,则1232x x x ++=______. 【答案】53π−【解析】令()0f x =314x m π⎛⎫++= ⎪⎝⎭,故()314f x x m π⎛⎫++− ⎪⎝⎭的零点为函数()314g x x π⎛⎫++ ⎪⎝⎭与函数y =m 交点的横坐标,作出函数g (x )在3,04π⎡⎤−⎢⎥⎣⎦上的大致图像:令3()42x k k πππ+=+∈Z ,解得()123k x k ππ=+∈Z , 令1k =−,得4x π=−,则由图知2322=4x x ππ⎛⎫+=⨯−− ⎪⎝⎭,令2k =−,得712x π=−,则由图知12772=126x x ππ⎛⎫+=⨯−− ⎪⎝⎭, 故123752263x x x πππ++=−−=−. 故答案为:53π−﹒18.(2023春·辽宁沈阳·高三沈阳市第一二〇中学校考阶段练习)已知双曲线22:14x y C m −=与直线2y x =无交点,则m 的取值范围是_____. 【答案】(]0,16【解析】依题意,由22:14x y C m −=可得0m >,双曲线C 的渐近线方程为y =,因为双曲线C 与直线2y x =无交点,所以直线2y x =应在两条渐近线上下两部分之间,2≤,解得016m <≤,即(]0,16m ∈. 故答案为:(]0,16..。
高三数学第二轮数形结合思想
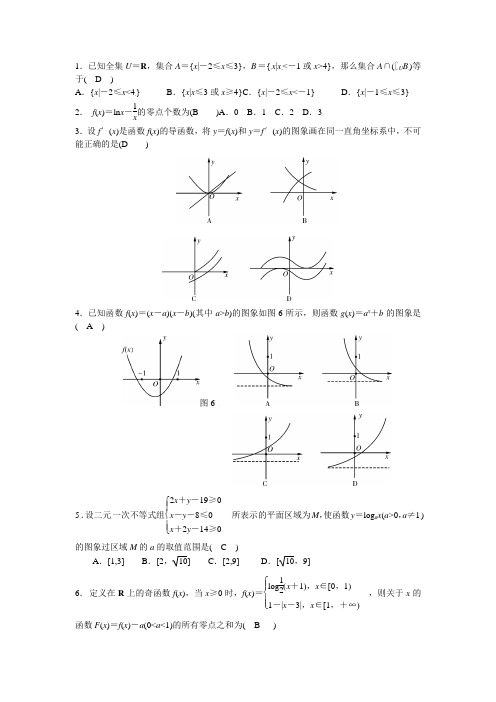
1.已知全集U =R ,集合A ={x |-2≤x ≤3},B ={x |x <-1或x >4},那么集合A ∩(∁U B )等于( D )A .{x |-2≤x <4}B .{x |x ≤3或x ≥4}C .{x |-2≤x <-1}D .{x |-1≤x ≤3} 2. f (x )=ln x -1x的零点个数为(B )A .0 B .1 C .2 D .33.设f ′(x )是函数f (x )的导函数,将y =f (x )和y =f ′(x )的图象画在同一直角坐标系中,不可能正确的是(D )4.已知函数f (x )=(x -a )(x -b )(其中a >b )的图象如图6所示,则函数g (x )=a x +b 的图象是( A )图65.设二元一次不等式组⎩⎪⎨⎪⎧2x +y -19≥0x -y -8≤0x +2y -14≥0所表示的平面区域为M ,使函数y =log a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是( C )A .[1,3]B .[2,10]C .[2,9]D .[10,9]6.定义在R 上的奇函数f (x ),当x ≥0时,f (x )=⎩⎪⎨⎪⎧log 12(x +1),x ∈[0,1)1-|x -3|,x ∈[1,+∞),则关于x 的函数F (x )=f (x )-a (0<a <1)的所有零点之和为( B )A . 2a -1B .2-a -1 C .1-2-a D .1-2a7.如果关于x 的方程213ax x+=正实数解有且仅有一个,那么实数a 的取值范围为(B )A .{|0}a a ≤B .{|02}a a a ≤=或C .{|0}a a ≥D .{|02}a a a ≥=-或8 已知函数)0()0()1(12)(>≤⎩⎨⎧--=-x x x f x f x ,若方程a x x f +=)(有且只有两个不相等的实数根,则实数a 的取值范围是AA.(-∞,1)B.(0,1)C.(-∞,1]D.[0,+∞) 9.设定义域为R 的函数⎩⎨⎧-=12lg )(x x f )2()2(=≠x x ,若关于x 的方程0)()(2=++c x bf x f 恰有5个不同的实数解54321,,,,x x x x x ,则)(54321x x x x x f ++++的值等于( C )A. 0B. 2lg 2C. 2lg 3D. 110.下列命题中的真命题是 ( B )A .x ∃∈R ,使得 sin cos 1.5x x += B. (0,),1xx e x ∀∈+∞>+ C .(,0),23x x x ∃∈-∞< D .(0,),sin cos x x x π∀∈> 12、定义在R 上的偶函数f(x)在[0,+∞)上是增函数,且0)31(=f ,则不等式0)(log 81>x f 的解集是( D )A 、)0,21(B 、),2(+∞C 、),2()21,0(+∞ D 、),2()1,21(+∞13、已知2221x y +=,则2x y +的最大值是CA 、2B 、2C 、3D 、314.若点O 和点F 分别为椭圆x 2/4 +y 2/3 =1的中心和左焦点,点P 为椭圆上点的任意一点,则的最大值为C A.2 B.3 C.6 D.815.若直线y x b =+与曲线234y x x =--有公共点,则b 的取值范围是A A.[122-,122+] B.[12-,3] C.[-1,122+]D.[122-,3]16.已知椭圆22:12x c y +=的两焦点为12,F F ,点00(,)P x y 满足2200012x y <+<,则|1PF |+2PF |的取值范围为__)2,22⎡⎣_____,直线0012x xy y +=与椭圆C 的公共点个数_0____。
江苏高二文科复习学案练习函数作图问题(数形结合思想)

2. 卜图中,有一个是函数 f(x) 1x 3 3 2 ax (a 2 1)x 1 (a€ R, a 卡眄导函数f (x)的图 象,则f ( 1)=f (x)的图象过原点且它的导函数g f (x)的图象是如图所示的一条直线,则y f (x)图象 的顶点在第4.函数f(x)的定义域为开区间(a,b),导函数开区间(a,b)内极小值点有 个.5 .求函数f (x) x 4 2x 2 3的最值27.数形结合在导数中的应用-、课前准备: 【自主梳理】数形结合思想,其实质是将抽象的数学语言与直观的图象结合起来,也就是对题目中的条 件和结论既分析其代数含义又挖掘其几何背景,在代数与几何的结合上寻找解题思路。
最常用 的是以形助数的解题方法,其实质就是对图形性质的研究,使要解决的数的问题转化为形的讨 论,实现“由一种代数形式转化为几何形式”的数学化归。
【自我检测】y x 8 ,则 f(5)=函数y f (x)的图像在点p的切线方程是2 .x x 上两点A , B 的横坐标分别是-1,1在抛物线的弧 AB 上求一点C ,使ABC 得面积最大。
变式:曲线y ln (2x1)上的点到直线2x y 3 0的最短距离是x【例2】已知函数f(x) (x k)2e k ,求f(x)的单调区间。
、课堂活动:【例1】已知抛物线y【例3】已知a 0,函数.f (x) (x2 2ax)e x,设f (x)在[—1, 1]上是单调函数,求a的取值范围。
【例4】设a R,试分别确定关于的x的三次方程x3 3x2 a 0有一根、有两根、有三根时a的取值范围。
课堂小结1、数形结合,利用导数几何意义解题。
2、利用数形结合思想求函数的单调区间3、利用数形结合思想研究恒成立问题4、利用数形结合思想研究函数图像交点问题三、课后作业1.已知函数f(x) -X 3 -X 2 2bx c,当X (0,1)时取得极大值,当x (1,2)时取 3 2 得极小值,求点(a,b )对应的区域的面积以及 J 的取值范围. a 1x a 2a4.已知函数 f (x) In , g(x) -(a 0),是否存在实数 m ,使得函数y g( ——)m 1x x 1 2的图像与y f (1 x )的图像恰好有四个不同的交点?若存在,求出m 的取值范围;若不存在,说明理由。
江苏省盐城市时杨中学高三数学二轮复习-立体几何(有详细答案)

盐城市时杨中学二轮复习——立体几何2009年3月1.用一些棱长为1cm 的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图则这个几何体的体积最大是 7 cm 3.图1(俯视图) 图2(主视图)2.一个多面体的直观图及三视图如图所示,则多面体A CDEF -的体积为 ▲ .383.如下左图所示是三棱锥D-ABC 的三视图,其中△DAC 、△DAB 、△BAC 都是直角三角形,点O 在三个视图中都是所在边的中点,则在三棱锥D-ABC 中DO 的长度为 ★ ; 34.右图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体共有▲ 个.5 5.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是2420+ 2cm 。
DA DABCOO BACO1 22主视图侧(左)视图俯视图主视图俯视图左视图2俯视图左视图2126.矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体积为π61257.一个几何体的三视图中,正视图和侧视图都是矩形,俯视图是等腰直角三角形(如图),根据图中标注的长度,可以计算出该几何体的表面积是 12+42 . 8.已知:正方体1111ABCD-A B C D ,1AA =2,E 为棱1CC 的中点.⑴求证:11B D AE ⊥;⑵求证://AC 平面1B DE ;⑶求三棱锥1B ADE -的体积证明:连结BD ,则BD //11B D , ∵ABCD 是正方形,∴AC BD ⊥.∵CE ⊥面ABCD ,∴CE BD ⊥. 又C =AC CE ,∴BD ⊥面ACE .∵AE ⊂面ACE ,∴BD AE ⊥, ∴11B D AE ⊥.⑵证明:作1BB 的中点F ,连结AF CF EF 、、. ∵E F 、是1BB 1CC 、的中点,∴CE1B F ,∴四边形1B FCE 是平行四边形,∴ 1CF// B E . ∵,E F 是1BB 1CC 、的中点,∴//EF BC , 又//BC AD ,∴//EF AD .∴四边形ADEF 是平行四边形,AF ∴//ED , ∵AF CF C =,1B E ED E =, ∴平面//ACF 面1B DE . 又AC ⊂平面ACF ,∴//AC 面1B DE9.如图,在三棱柱111ABC A B C -中,四边形11A ABB 为菱形,160A AB ∠=︒,四边形11BCC B 为矩形,若AB BC ⊥且4AB =,3BC =⑴求证:平面1A CB ⊥平面1ACB ; ⑵求三棱柱111ABC A B C -的体积. ⑴略;⑵111123ABC A B C V -=10.一个多面体的直观图及三视图如图所示:(其中M 、N 分别是AF 、BC 的中点).C 1B 1A 1CBA(I )求证:MN ∥平面CDEF ;(II )求多面体A —CDEF 的体积.解:由三视图可知,该多面体是底面为直 角三角形的直三棱住ADE —BCF , 且AB=BC=BF=2,DE=CF=2.2∴∠CBF=.2π(1) 取BF 中点G ,连MG 、NG ,由M 、N 分别为AF 、BC 的中点可得,NG ∥CF ,MG ∥EF ,∴平面MNG ∥平面CDEF.∴MN ∥平面CDEF. (2)取DE 的中点H.∵AD=AE ,∴AH ⊥DE ,在直三棱柱ADE —BCF 中,平面ADE ⊥平面CDEF ,面ADE ∩面CDEF=DE.∴AH ⊥平面CDEF.∴多面体A —CDEF 是以AH 为高,以矩形CDEF 为底面的棱锥, 在△ADE 中,AH=24,2=⋅=EF DE S CDEF 矩形, ∴棱锥A—CDEF的体积为.382243131=⨯⨯=⋅⋅=AH S V CDEF 矩形11. 多面体ABCDE 中,1====AE AC BC AB ,2=CD ,ABC AE 面⊥,CD AE //。
江苏省盐城市时杨中学高三数学综合练习(二)(无答案)

高三数学综合练习(二)1.已知集合{}1A x x =≥,{}1,0,1,4B =−,则A B =________.2.设复数z a bi =+(a ,b R ∈,i 是虚数单位),且22z i =,则a b +=______.3.若一组样本数据21,19,x ,20,18的平均数为20,则该组样本数据的方差为________.4.椭圆222125x y b +=(0b >)与双曲线2218x y −=有公共的焦点,则b =______. 5.执行如图所示的伪代码,则输出的结果为 .6.把分别标有“诚”“信”“考”“试”的四张卡片随意的排成一排,则能使卡片从左到右可以念成“诚信考试”和“考试诚信”的概率是_____.7.已知圆柱的高为2,它的两个底面的圆周在半径为2的同一个球的球面上.则球的体积与圆柱的体积的比值为__________.8.已知数列{}n a 的前n 项和为n S ,且满足()*123n n n S a n N =−∈,2020S =_______________. 9.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin sin sin sin B A c B C a b−=−+则sin 6A π⎛⎫−= ⎪⎝⎭________. 10.如图,在平面四边形ABCD 中,90CBA CAD ∠=∠=︒,30ACD ∠=︒,AB BC =,点E 在线段BC 上,且3BC BE =,若(,)AC AD AE R λμλμ=+∈,则μλ的值为_______.11.过直线l :2y x =−上任意一点P 作圆C :221x y +=的一条切线,切点为A ,若存在定()00,B x y ,使得PA PB =恒成立,则00x y −=______.12.设0021a ,b ,a -b >>=,则22(4)(1)a b ab++的最小值为________.15.在ABC 中,角,,A B C 的对边分别为,,a b c ,且22cos a c b C −=.(1)求B ;(2)若3b =,ABC 的面积为32,求ABC 的周长.16.如图,在三棱锥A -BCD 中,点M ,N 分别在棱AC ,CD 上,且N 为CD 的中点. (1)当M 为AC 的中点时,求证:AD //平面BMN ;(2)若平面ABD ⊥平面BCD ,AB ⊥BC ,求证:BC ⊥AD .17.如图所示,一座小岛A 距离海岸线上最近的点P 的距离是2km ,从点P 沿海岸正东12km 处有一城镇B .一年青人从小岛A 出发,先驾驶小船到海岸线上的某点C 处,再沿海岸线步行到城镇B .若PAC θ∠=,假设该年青人驾驶小船的平均速度为2/km h ,步行速度为4/km h .(1)试将该年青人从小岛A 到城镇B 的时间t 表示成角θ的函数;(2)该年青人欲使从小岛A 到城镇B 的时间t 最小,请你告诉他角θ的值.。
高中数学数形结合思想经典例题(含解析)

高中数学数形结合思想经典例题一、选择题1.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0)D .(0,1)3.函数f (x )=ln|x +cos x |的图象为( )4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-2,0)∩(2,+∞)B .(-∞,-2)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-2,0)∪(0,2)5.实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )A.2155B .21C .20D .256.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根, 则实数k 的取值范围是( ) A .(0,12)B .(12,1)C .(1,2)D .(2,+∞)7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +yx +y 的最小值为( )A.53 B .2 C.35D.128.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1D .0<x 1x 2<19.已知函数y =f (x )在(0,1)内的一段图象是如图所示的一段曲线,若0<x 1<x 2<1,则( )A.f (x 1)x 1<f (x 2)x 2B.f (x 1)x 1=f (x 2)x 2C.f (x 1)x 1>f (x 2)x 2D .不能确定10.设关于x ,y 的不等式组⎩⎪⎨⎪⎧2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2,求m 的取值范围是( ) A .(-∞,43)B .(-∞,13)C .(-∞,-23)D .(-∞,-53)11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF →=( ) A.89 B.109 C.259D.26912.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤45成立,则实数a的值为( )A.15B.25C.12D .113.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( ) A.72 B.52 C .3D .214.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于34,抛物线E :y 2=2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:x =-1的距离之和的最小值为( ) A .1 B .2 C .3 D .4二、填空题15.已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是__________.16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________.17.已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值为________.18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,C ,D 四点,则|AB |+|CD |=________.19.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x≤0,ln (x +1),x>0.若|f (x )|≥ax ,则a 的取值范围是______.20.已知函数f (x )=⎩⎪⎨⎪⎧|x|,x≤m ,x 2-2mx +4m ,x>m ,其中m >0.若存在实数b ,使得关于x 的方程f (x )=b有三个不同的根,则m 的取值范围是________.高中数学数形结合思想经典例题解析一、选择题1.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数【答案】 B【解析】 作出函数f (x )的图象,如图所示,可知A ,C ,D 均错.f (f (14))=3log 214=3-2=19,故B 正确.2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0) D .(0,1)【答案】 C【解析】 ∵f (x )=ax 2-(a +2)x +1,Δ=(a +2)2-4a =a 2+4>0, ∴函数f (x )=ax 2-(a +2)x +1必有两个不同的零点. 又∵f (x )在(-2,-1)上有一个零点,则f (-2)f (-1)<0, ∴(6a +5)(2a +3)<0,解得-32<a <-56.又∵a ∈Z ,∴a =-1.不等式f (x )>1,即-x 2-x >0.解得-1<x <0. 3.函数f (x )=ln|x +cos x |的图象为( )【答案】 A【解析】 因为f (0)=ln|cos0|=0,故排除C ,D ;又f (1)=ln|1+cos1|>ln 1=0,故排 除B ,选A.4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-2,0)∩(2,+∞)B .(-∞,-2)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-2,0)∪(0,2)【答案】 D【解析】 由已知条件可以画出函数f (x )的草图,如图所示.由函数f (x )为奇函数可化简不等式f (x )-f (-x )x <0为2f (x )x <0.若x >0,则需有f (x )<0,结合图象可知0<x <2;若x <0,则需有f (x )>0,结合图象可知-2<x <0.综上可知,不等式的解集为(-2,0)∪(0,2).5.实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )A.2155B .21C .20D .25【答案】 B【解析】 作出不等式组表示的平面区域,如下图中阴影部分所示.z =|x +2y -4|=|x +2y -4|5·5,即其几何含义为阴影区域内的点到直线x +2y -4=0的距离的5倍.由⎩⎪⎨⎪⎧x -y +2=0,2x -y -5=0,得B 点坐标为(7,9),显然点B 到直线x +2y -4=0的距离最大,此时z max=21.6.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根, 则实数k 的取值范围是( ) A .(0,12)B .(12,1)C .(1,2)D .(2,+∞)【答案】 B【解析】 在同一坐标系中分别画出函数f (x ),g (x )的图象如图所示,方程f (x )=g (x )有两个不相等的实根等价于两个函数的图象有两个不同的交点,结合图象可知,当直线y =kx 的斜率大于坐标原点与点(2,1)连线的斜率且小于直线y =x -1的斜率时符合题意,故12<k <1.7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +yx +y 的最小值为( )A.53 B .2 C.35D.12【答案】 A【解析】 依题意,得实数x ,y 满足⎩⎪⎨⎪⎧x +y -3≥0,x -y -3≤0,0≤y≤1,画出可行域如图阴影部分所示,其中A (3,0),C (2,1),z =2+yx 1+y x =1+11+y x ∈[53,2],故选A.8.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1 D .0<x 1x 2<1【答案】 D【解析】 本题考查函数的性质.在同一坐标系下,画出函数y =10x 与y =|lg(-x )|的图象,结合图象不难看出,它们的两个交点中,其中一个交点横坐标属于(-∞,-1),另一个交点横坐标属于(-1,0),即在x 1,x 2中,其中一个属于(-∞,-1),另一个属于(-1,0),不妨设x 1∈(-∞,-1),x 2∈(-1,0),则有10x 1=|lg(-x 1)|=lg(-x 1),10x 2=|lg(-x 2)|=-lg(-x 2),10x 1-10x 2=lg(-x 1)+lg(-x 2)=lg(x 1x 2)<0,0<x 1x 2<1,故选D. 9.已知函数y =f (x )在(0,1)内的一段图象是如图所示的一段曲线,若0<x 1<x 2<1,则( )A.f (x 1)x 1<f (x 2)x 2B.f (x 1)x 1=f (x 2)x 2C.f (x 1)x 1>f (x 2)x 2D .不能确定【答案】 C【解析】 如图,设曲线上两点P 1(x 1,f (x 1)),P 2(x 2,f (x 2)),kOP 1=f (x 1)-0x 1-0=f (x 1)x 1,kOP 2=f (x 2)-0x 2-0=f (x 2)x 2,由于0<x 1<x 2<1,根据斜率与倾斜角之间的关系,显然有kOP 1>kOP 2,即f (x 1)x 1>f (x 2)x 2,故选C. 10.设关于x ,y 的不等式组⎩⎪⎨⎪⎧2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2,求m 的取值范围是( ) A .(-∞,43)B .(-∞,13)C .(-∞,-23)D .(-∞,-53)【答案】 C【解析】 作出不等式组所表示的平面区域,根据题设条件分析求解. 当m ≥0时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P (x 0,y 0)满足x 0-2y 0=2,因此m <0. 如图所示的阴影部分为不等式组表示的平面区域.要使可行域内包含y =12x -1上的点,只需可行域边界点(-m ,m )在直线y =12x -1的下方即可,即m <-12m -1,解得m <-23. 11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF→=( ) A.89 B.109 C.259 D.269【答案】 B【解析】 由|AB →+AC →|=|AB →-AC →|,化简得AB →·AC →=0,又因为AB 和AC 为三角形的两条边,不可能为0,所以AB →与AC →垂直,所以△ABC 为直角三角形.以AC 为x 轴,以AB 为y 轴建立平面直角坐标系,如图所示,则A (0,0),B (0,2),C (1,0),由E ,F 为BC 的三等分点知E (23,23),F (13,43),所以AE →=(23,23),AF →=(13,43),所以AE →·AF →=23×13+23×43=109. 12.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤45成立,则实数a的值为( ) A.15 B.25 C.12D .1 【答案】 A【解析】 (x -a )2+(ln x 2-2a )2表示点P (x ,ln x 2)与点Q (a ,2a )距离的平方. 而点P 在曲线g (x )=2ln x 上,点Q (a ,2a )在直线y =2x 上.因为g ′(x )=2x ,且y =2x 表示斜率为2的直线,所以由2x=2,解得x =1.从而曲线g (x )=2ln x 在x =1处的切线方程为y =2(x -1),又直线y =2(x -1)与直线y =2x 平行,且它们间的距离为222+(-1)2=255,如图所示.故|PQ |的最小值为255,即f (x )=(x -a )2+(ln x 2-2a )2的最小值为(255)2=45,当|PQ |最小时,P 点的坐标为(1,0),所以2a -0a -1×2=-1,解得a =15.13.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( ) A.72 B.52 C .3 D .2【答案】 C【解析】 利用FP →=4FQ →转化长度关系,再利用抛物线定义求解. ∵FP →=4FQ →, ∴|FP →|=4|FQ →|. ∴|PQ||PF|=34.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4. ∴|PQ||PF|=|QQ′||AF|=34.∴|QQ ′|=3. 根据抛物线定义可知|QQ ′|=|QF |=3,故选C.14.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于34,抛物线E :y 2=2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:x =-1的距离之和的最小值为( ) A .1 B .2 C .3 D .4【答案】 B【解析】 x 2a 2-4y 2=1的右顶点坐标为(a ,0),一条渐近线为x -2ay =0.由点到直线的距离公式得d =|a|12+4a 2=34,解得a =32或a =-32(舍去),故双曲线的方程为4x 23-4y 2=1.因为c =34+14=1,故双曲线的右焦点为(1,0),即抛物线的焦点为(1,0),所以p =2,x =-1是抛物线的准线,如图,作MA ⊥l 1于点A ,MB ⊥l 2于点B ,设抛物线的焦点为F ,连接MF ,则由抛物线的定义知|MB |=|MF |,当M ,A ,F 三点共线时,距离之和最小,其最小值是点F 到l 1的距离,由点到直线的距离公式可得d 1=|4+6|(-3)2+42=105=2,即距离之和的最小值为2,选B.二、填空题15.已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是__________.【答案】 (0,1)∪(1,4) 【解析】 根据绝对值的意义,y =|x 2-1|x -1=⎩⎪⎨⎪⎧x +1,x>1或x<-1,-x -1,-1≤x<1.在直角坐标系中作出该函数的图象,如下图中实线所示.根据图象可知,当0<k <1或1<k <4时有两个交点.16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________. 【答案】 (-7,3)【解析】 当x ≥0时,f (x )=x 2-4x <5的解集为[0,5),又f (x )为偶函数,所以f (x )<5的解集为(-5,5).所以f (x +2)<5的解集为(-7,3).17.已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值为________. 【答案】 -2【解析】 F (x ,y )=log 2(y +1)+log 12(x +1)=log 2(y +1)-log 2(x +1)=log 2y +1x +1,令k =y +1x +1=y -(-1)x -(-1),则k 表示可行域内(如图所示)的点与P (-1,-1)所在直线的斜率.18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省盐城市时杨中学高考数学:第2讲数形结合思想
思想方法概述
1.数形结合的数学思想:包含“以形助数”和“以数辅形”
两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.
2.运用数形结合思想分析解决问题时,要遵循三个原则:
(1)等价性原则.在数形结合时,代数性质和几何性质的转换必须是等价的,否则解题将会出现漏洞.有时,由于图形的局限性,不能完整的表现数的一般性,这时图形的性质只能是一种直观而浅显的说明,要注意其带来的负面效应.
(2)双方性原则.既要进行几何直观分析,又要进行相应的代数抽象探求,仅对代数问题进行几何分析容易出错.
(3)简单性原则.不要为了“数形结合”而数形结合.具体运用时,一要考虑是否可行和是否有利;二要选择好突破口,恰当设参、用参、建立关系、做好转化;三要挖掘隐含条件,准确界定参变量的取值范围,特别是运用函数图象时应设法选择动直线与定二次曲线.
3.数形结合思想解决的问题常有以下几种:
(1)构建函数模型并结合其图象求参数的取值范围;
(2)构建函数模型并结合其图象研究方程根的范围;
(3)构建函数模型并结合其图象研究量与量之间的大小关系;
(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式;
(5)构建立体几何模型研究代数问题;
(6)构建解析几何中的斜率、截距、距离等模型研究最值问题;
(7)构建方程模型,求根的个数;
(8)研究图形的形状、位置关系、性质等.
4.数形结合思想是解答高考数学试题的一种常用方法与技巧,
特别是在解填空题时发挥着奇特功效,这就要求我们在平时学习中加强这方面的训练,以提高解题能力和速度.具体操作时,应注意以下几点:
(1)准确画出函数图象,注意函数的定义域;
(2)用图象法讨论方程(特别是含参数的方程)的解的个数是一种行之有效的方法,值得注意的是首先要把方程两边的代数式看作是两个函数的表达式(有时可能先作适当调整,以便于作图),然后作出两个函数的图象,由图求解.
题型一数形结合思想在解决方程的根、不等式解集问题中的应用
例1 (1)设函数f(x)=
2,0
2,0
x bx c x
x
⎧++≤
⎨
>
⎩
若f(-4)=f(0),f(-2)=-2,则函数y=g(x)=f(x)-x
的零点个数为_____.
(2)使log2(-x)<x+1成立的x的取值范围是________.
变式训练1 已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m (m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
题型二 数形结合思想在求参数、代数式取值范围问题中的应用
例2 已知函数f (x )=221,02,0
x x x x x ⎧->⎪⎨--≤⎪⎩若函数g (x )=f (x )-m 有3个零点,则实数m 的取值范围为__________.
变式训练 2 若不等式log a x >sin 2x (a >0,a ≠1)对任意x ∈⎝
⎛⎭⎪⎫0,π4都成立,则a 的取值范围为____________.
题型三 数形结合思想在求几何量中最值问题中的应用
例3 已知P 是直线3x +4y +8=0上的动点,PA 、PB 是圆x 2+y 2-2x -2y +1=0的两条切线,A 、B 是切
点,C 是圆心,求四边形PACB 面积的最小值.
规律方法总结
1.利用数形结合解题,只需把图象大致形状画出即可,不需要精确图象.
2.数形结合思想是解决高考数学试题的一种常用方法与技巧,特别在解填空题时更方便,可以提高解题速度.
3.数形结合思想常用模型:一次、二次函数图象;斜率公式;两点间的距离公式(或向量的模、复数的模);点到直线的距离公式等.
名师押题我来做
1.函数f (x )=(12
)x -sin x 在区间[0,2π]上的零点个数为_____. 2.已知函数f (x )=21,0(1),0
x x f x x -⎧-+≤⎨->⎩若方程f (x )=log a (x +2) (0<a <1)有且只有两个不同的实根,则实
数a 的取值范围是________.
第2讲 数形结合思想
(推荐时间:60分钟)
一、填空题
1.若实数x ,y 满足等式(x -2)2+y 2=3,那么y x 的最大值为________. 2.设函数f (x )=1221,0,0x x x
x -⎧-≤⎪⎨⎪>⎩若f (x 0)>1,则x 0的取值范围是____________.
3.若直线y =k (x -2)+4与曲线y =1+4-x 2有两个不同的交点,则实数k 的取值范围是________.
4.函数f (θ)=sin θ2+cos θ
的最大值为________.
5.设x ,y 满足约束条件00134x y x y a a
≥⎧⎪⎪⎪≥⎨⎪⎪+≤⎪⎩若z =x +2y +3x +1的最小值为32,则a 的值为________.
6.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之
和的最小值是________.
7.已知y =f (x )是以2为周期的偶函数,当x ∈[0,1]时,f (x )=x ,那么在区间[-1,3]内,关于x 的方程f (x )=kx +k +1 (k ∈R ,k ≠1)有4个根,则k 的取值范围为__________.
8. 设函数y =f (x )是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图
所示的线段AB ,则在区间[1,2]上f (x )=________.
9.若方程x 3-3x -a =0有三个不相等的实根,则实数a 的取值范围是________.
10.函数f (x )=x 2+9+x -32+1的最小值为________.
11.若不等式9-x 2≤k (x +2)-2的解集为区间[a ,b ],且b -a =2,则k =________.
12.y =f (x )=36,263,2
x x x x +≥-⎧⎨--<-⎩,若不等式f (x )≥2x -m 恒成立,则实数m 的取值范围是________.
二、解答题
13.不等式x 2+|2x -4|≥p 对所有x 都成立,求实数p 的最大值.
14.设有函数f (x )=a +-x 2-4x 和g (x )=43
x +1,已知x ∈[-4,0]时恒有f (x )≤g (x ),求实数a 的取值范围.
15.已知a >0,函数f (x )=x |x -a |+1 (x ∈R ).
(1)当a =1时,求所有使f (x )=x 成立的x 的值;
(2)当a ∈(0,3)时,求函数y =f (x )在闭区间[1,2]上的最小值;
(3)试讨论函数y =f (x )的图象与直线y =a 的交点个数.。
