ROBUST TIMEKEEPING IN CIRCADIAN NETWORKS FROM GENES TO CELLS
黄土高原北部日本弓背蚁巢穴结构特征及其影响因素

黄土高原北部日本弓背蚁巢穴结构特征及其影响因素杨析;邵明安;李同川;贾玉华;贾小旭;黄来明【摘要】黄土高原大量的植被恢复为地栖性土壤动物提供了合适的栖息地和充足的食物,土壤动物的筑巢活动可提高土壤大孔隙的数量.以黄土高原北部神木县六道沟小流域的日本弓背蚁为研究对象,通过石膏浇筑法研究了日本弓背蚁巢穴结构特征,对比了日本弓背蚁(Camponotus japonicus)和针毛收获蚁(Messor aciculatus)成熟巢穴结构的异同,分析了土壤质地、土壤含水量和土壤容重对日本弓背蚁巢穴结构的影响.结果表明:日本弓背蚁的巢穴结构由通道和巢室组合而成,通道为圆柱形,其直径大小为4.1~ 6.6 mm,巢室的形状为倒置漏斗形或立体椭圆形,巢室横截面面积为606~2 117mm2;日本弓背蚁和针毛收获蚁巢穴在通道直径、巢室形状和横截面积、巢穴深度等方面有较大的差异;巢穴体积随着蚂蚁群落规模的增加而增加;日本弓背蚁群落在壤土和壤砂土中均有广泛分布,适宜其生存和繁殖的土壤含水量在60~200 g kg-1之间,在土壤颗粒较大的干燥砂土中并不常见;土壤容重越大,蚂蚁巢穴的结构越简单,其通道的长度、分支、节点和巢穴总体积较小.但是,通道直径主要与蚂蚁的体型相关,不受土壤质地、含水量和容重的影响.本研究从小尺度分析了黄土高原植被恢复通过土柄性蚂蚁对土壤结构产生的间接影响,拓宽了黄土高原北部土壤大孔隙的研究范围.【期刊名称】《土壤学报》【年(卷),期】2018(055)004【总页数】11页(P868-878)【关键词】蚂蚁;土壤含水量;土壤质地;土壤容重;巢穴结构【作者】杨析;邵明安;李同川;贾玉华;贾小旭;黄来明【作者单位】西北农林科技大学资源环境学院,陕西杨凌712100;西北农林科技大学资源环境学院,陕西杨凌712100;中国科学院水利部水土保持研究所,陕西杨凌712100;中国科学院地理科学与资源研究所,北京 100101;中国科学院大学资源与环境学院,北京 100190;中国科学院地理科学与资源研究所,北京 100101;沈阳农业大学水利学院,沈阳 110866;中国科学院地理科学与资源研究所,北京 100101;中国科学院地理科学与资源研究所,北京 100101【正文语种】中文【中图分类】S152自1999年国家实施退耕还林还草措施以来,黄土高原植被覆盖度由20世纪70年代的6.5%上升至2010年的50%左右[1],生态环境有了较大改善。
基因沉默番木瓜环斑病毒复制酶基因(PRSV-Nib)获得抗病毒病番木瓜的研究

热带作物学报2024, 45(4): 837 846Chinese Journal of Tropical Crops基因沉默番木瓜环斑病毒复制酶基因(PRSV-Nib)获得抗病毒病番木瓜的研究吴清铧1,2,贾瑞宗2*,郭静远2,杨牧之2,胡玉娟2,郝志刚2,赵辉2**,郭安平2** 1. 海南大学热带作物学院,海南海口 570228;2. 海南省南繁生物安全与分子育种重点实验室/中国热带农业科学院三亚研究院/中国热带农业科学院热带生物技术研究所,海南三亚 572024摘要:番木瓜是重要的热带经济水果。
番木瓜环斑病毒(Papaya ringspot virus, PRSV)是番木瓜的重要病毒病,经常导致严重的产量损失和质量恶化。
自从1998年第一例转基因番木瓜问世以来,使得基于“致病菌衍生的抗病性(pathogen-derived resistance, PDR)”的抗病育种策略获得成功广泛应用。
然而依赖于序列同源性的抗病性与病毒突变导致多样性增加之间的矛盾成为番木瓜育种科学家的新挑战。
本研究拟采用RNAi策略针对复制酶(nuclear inclusion b. Nib)获得广谱抗PRSV番木瓜新种质。
通过团队已建立的胚性愈伤诱导-农杆菌介导转化-再生苗诱导的番木瓜遗传转化体系,共获得经过抗性筛选的再生苗52株,通过特异性PCR进行筛选共计获得24株转基因阳性植株。
通过对T0代田间自然发病试验中,转基因番木瓜株系抗病性明显高于非转基因对照,其中NibB5-2田间抗病性最优。
通过hi TAIL-PCR方法确定NibB5-2插入位点位于第2号染色体supercontig_30的1976766的位置。
T1代接种试验中,无病毒积累且无发病症状,初步确认具有良好的病毒抗性,为番木瓜抗病育种提供新思路。
关键词:番木瓜;番木瓜环斑病毒;Nib基因;RNA介导的病毒抗性中图分类号:S436.67 文献标志码:AGene Silencing of Papaya ringspot virus Replicase Gene (PRSV-Nib) to Obtain Virus Resistant PapayaWU Qinghua1,2, JIA Ruizong2*, GUO Jingyuan2, YANG Muzhi2, HU Yujuan2, HAO Zhigang2, ZHAO Hui2**, GUO Anping2**1. College of Tropical Crops, Hainan University, Haikou, Hainan 570228, China;2. Hainan Key Laboratory for Biosafety Monitor-ing and Molecular Breeding in Off-Season Reproduction Regions / Sanya Research Institutey, Chinese Academy of Tropical Agri-cultural Sciences / Institute of Tropical Bioscience and Biotechnology, Chinese Academy of Tropical Agricultural Sciences, Sanya, Hainan 572024, ChinaAbstract: Papaya is an economically important tropical fruit. Papaya ringspot virus (PRSV) is an important virus dis-ease of papaya, often causing significant yield losses and quality deterioration. Since the introduction of the first trans-genic papaya in 1998, PDR-based breeding strategies for disease resistance have been successfully applied. The contra-diction between disease resistance based on sequence homology and increased virus genetic diversity became a new challenge for papaya breeding. In this study, we propose to use RNAi strategies aim at nuclear inclusion b gene (Nib) to obtain broad-spectrum resistance to PRSV papaya. With optimized embryo callus generation-Agrobatium meidated transformation-shoot regeneration, 52 shoots were obtained after resistance screening and a total of 24 transgenic posi-tive shoots were obtained by specific PCR screening for the T0 generation. In the T0 generation field natural disease test, 收稿日期 2022-12-16;修回日期 2023-02-15基金项目 海南省重大科技计划项目(No. ZDKJ202002);海南省重点研发计划项目(No. ZDYF2022XDNY257);崖州湾科技城菁英人才项目(No. SCKJ-JYRC-2022-67)。
智能控制理论和方法(第二版)李人厚1-5章 (4)

优;xid∈[-xmaxd, xmaxd], 根据实际问题将解空间限制在一定 的范围;vid∈[-vmaxd, vmaxd], 根据实际问题将粒子的飞行速 度设定在一定的范围。
第9章 粒子群算法及其在智能控制中的应用 图9.2 基本粒子群算法流程
第9章 粒子群算法及其在智能控制中的应用 9.2 基本粒子群算法
9.2.1 基本粒子群算法的原理 设想有这样一个场景: 一群鸟在某一个区域里随机搜寻食
物。在这个区域里,只存在一处食物源,而所有的鸟都不知道 食物的具体位置,但是每只鸟知道自己当前的位置离食物源有 多远,也知道哪一只鸟距离食物源最近。在这样的情况下,鸟 群找到食物的最优策略是什么呢? 最简单有效的方法就是搜寻 目前离食物源最近的那只鸟的周围区域。PSO就是从这种搜寻食 物的场景中得到启示,并用于解决优化问题。PSO的形象图示见 图9.1。
第9章 粒子群算法及其在智能控制中的应用 在PSO算法中,每个优化问题的潜在解都类似搜索空间中的 一只鸟,称其为“粒子”。粒子们追随当前群体中的最优粒子, 在解空间中不断进行搜索以寻找最优解。PSO算法首先初始化一 群随机粒子(随机解集),通过不断迭代,且在每一次迭代中, 粒子通过跟踪两个极值来更新自己;第一个极值是粒子本身截 至目前所找到的最优解,这个解称为个体极值pb(pbest);另一 个极值是整个粒子群迄今为止所找到的最优解,称为全局极值 gb(gbest),最终找到图9.1 PSO的形象图示
第9章 粒子群算法及其在智能控制中的应用
9.2.2 基本粒子群算法 在基本PSO算法中,首先初始化一群粒子。设有N个粒子,
每个粒子定义为D维空间中的一个点,第i个粒子pi在D维空间 中的位置记为Xi=(xi1, xi2, …, xiD), i=1, 2, …, N,粒子 pi的飞翔速度记为Vi,Vi=(vi1, vi2, …, viD), i=1, 2, …, N。粒子pi从诞生到目前为止(第k次迭代后),搜索到最好位置 称其为粒子pi的个体极值,表示为pbki=(pbki1, pbki2, …, pbkiD)。在整个粒子群中,某粒子是迄今为止(第k次迭代后)所 有粒子搜索到的最好位置,称其为全局极值,表示为gbk=(gbk1, gbk2, …, gbkD),则PSO算法进行优化迭代中,第i个粒子pi按 照下面公式来更新自己的速度和位置:
Collective dynamics of 'small-world' networks

Nature © Macmillan Publishers Ltd 19988typically slower than ϳ1km s −1)might differ significantly from what is assumed by current modelling efforts 27.The expected equation-of-state differences among small bodies (ice versus rock,for instance)presents another dimension of study;having recently adapted our code for massively parallel architectures (K.M.Olson and E.A,manuscript in preparation),we are now ready to perform a more comprehensive analysis.The exploratory simulations presented here suggest that when a young,non-porous asteroid (if such exist)suffers extensive impact damage,the resulting fracture pattern largely defines the asteroid’s response to future impacts.The stochastic nature of collisions implies that small asteroid interiors may be as diverse as their shapes and spin states.Detailed numerical simulations of impacts,using accurate shape models and rheologies,could shed light on how asteroid collisional response depends on internal configuration and shape,and hence on how planetesimals evolve.Detailed simulations are also required before one can predict the quantitative effects of nuclear explosions on Earth-crossing comets and asteroids,either for hazard mitigation 28through disruption and deflection,or for resource exploitation 29.Such predictions would require detailed reconnaissance concerning the composition andinternal structure of the targeted object.ⅪReceived 4February;accepted 18March 1998.1.Asphaug,E.&Melosh,H.J.The Stickney impact of Phobos:A dynamical model.Icarus 101,144–164(1993).2.Asphaug,E.et al .Mechanical and geological effects of impact cratering on Ida.Icarus 120,158–184(1996).3.Nolan,M.C.,Asphaug,E.,Melosh,H.J.&Greenberg,R.Impact craters on asteroids:Does strength orgravity control their size?Icarus 124,359–371(1996).4.Love,S.J.&Ahrens,T.J.Catastrophic impacts on gravity dominated asteroids.Icarus 124,141–155(1996).5.Melosh,H.J.&Ryan,E.V.Asteroids:Shattered but not dispersed.Icarus 129,562–564(1997).6.Housen,K.R.,Schmidt,R.M.&Holsapple,K.A.Crater ejecta scaling laws:Fundamental forms basedon dimensional analysis.J.Geophys.Res.88,2485–2499(1983).7.Holsapple,K.A.&Schmidt,R.M.Point source solutions and coupling parameters in crateringmechanics.J.Geophys.Res.92,6350–6376(1987).8.Housen,K.R.&Holsapple,K.A.On the fragmentation of asteroids and planetary satellites.Icarus 84,226–253(1990).9.Benz,W.&Asphaug,E.Simulations of brittle solids using smooth particle put.mun.87,253–265(1995).10.Asphaug,E.et al .Mechanical and geological effects of impact cratering on Ida.Icarus 120,158–184(1996).11.Hudson,R.S.&Ostro,S.J.Shape of asteroid 4769Castalia (1989PB)from inversion of radar images.Science 263,940–943(1994).12.Ostro,S.J.et al .Asteroid radar astrometry.Astron.J.102,1490–1502(1991).13.Ahrens,T.J.&O’Keefe,J.D.in Impact and Explosion Cratering (eds Roddy,D.J.,Pepin,R.O.&Merrill,R.B.)639–656(Pergamon,New York,1977).14.Tillotson,J.H.Metallic equations of state for hypervelocity impact.(General Atomic Report GA-3216,San Diego,1962).15.Nakamura,A.&Fujiwara,A.Velocity distribution of fragments formed in a simulated collisionaldisruption.Icarus 92,132–146(1991).16.Benz,W.&Asphaug,E.Simulations of brittle solids using smooth particle put.mun.87,253–265(1995).17.Bottke,W.F.,Nolan,M.C.,Greenberg,R.&Kolvoord,R.A.Velocity distributions among collidingasteroids.Icarus 107,255–268(1994).18.Belton,M.J.S.et al .Galileo encounter with 951Gaspra—First pictures of an asteroid.Science 257,1647–1652(1992).19.Belton,M.J.S.et al .Galileo’s encounter with 243Ida:An overview of the imaging experiment.Icarus120,1–19(1996).20.Asphaug,E.&Melosh,H.J.The Stickney impact of Phobos:A dynamical model.Icarus 101,144–164(1993).21.Asphaug,E.et al .Mechanical and geological effects of impact cratering on Ida.Icarus 120,158–184(1996).22.Housen,K.R.,Schmidt,R.M.&Holsapple,K.A.Crater ejecta scaling laws:Fundamental forms basedon dimensional analysis.J.Geophys.Res.88,2485–2499(1983).23.Veverka,J.et al .NEAR’s flyby of 253Mathilde:Images of a C asteroid.Science 278,2109–2112(1997).24.Asphaug,E.et al .Impact evolution of icy regoliths.Lunar Planet.Sci.Conf.(Abstr.)XXVIII,63–64(1997).25.Love,S.G.,Ho¨rz,F.&Brownlee,D.E.Target porosity effects in impact cratering and collisional disruption.Icarus 105,216–224(1993).26.Fujiwara,A.,Cerroni,P .,Davis,D.R.,Ryan,E.V.&DiMartino,M.in Asteroids II (eds Binzel,R.P .,Gehrels,T.&Matthews,A.S.)240–265(Univ.Arizona Press,Tucson,1989).27.Davis,D.R.&Farinella,P.Collisional evolution of Edgeworth-Kuiper Belt objects.Icarus 125,50–60(1997).28.Ahrens,T.J.&Harris,A.W.Deflection and fragmentation of near-Earth asteroids.Nature 360,429–433(1992).29.Resources of Near-Earth Space (eds Lewis,J.S.,Matthews,M.S.&Guerrieri,M.L.)(Univ.ArizonaPress,Tucson,1993).Acknowledgements.This work was supported by NASA’s Planetary Geology and Geophysics Program.Correspondence and requests for materials should be addressed to E.A.(e-mail:asphaug@).letters to nature440NATURE |VOL 393|4JUNE 1998Collective dynamics of ‘small-world’networksDuncan J.Watts *&Steven H.StrogatzDepartment of Theoretical and Applied Mechanics,Kimball Hall,Cornell University,Ithaca,New York 14853,USA.........................................................................................................................Networks of coupled dynamical systems have been used to model biological oscillators 1–4,Josephson junction arrays 5,6,excitable media 7,neural networks 8–10,spatial games 11,genetic control networks 12and many other self-organizing systems.Ordinarily,the connection topology is assumed to be either completely regular or completely random.But many biological,technological and social networks lie somewhere between these two extremes.Here we explore simple models of networks that can be tuned through this middle ground:regular networks ‘rewired’to intro-duce increasing amounts of disorder.We find that these systems can be highly clustered,like regular lattices,yet have small characteristic path lengths,like random graphs.We call them ‘small-world’networks,by analogy with the small-world phenomenon 13,14(popularly known as six degrees of separation 15).The neural network of the worm Caenorhabditis elegans ,the power grid of the western United States,and the collaboration graph of film actors are shown to be small-world networks.Models of dynamical systems with small-world coupling display enhanced signal-propagation speed,computational power,and synchronizability.In particular,infectious diseases spread more easily in small-world networks than in regular lattices.To interpolate between regular and random networks,we con-sider the following random rewiring procedure (Fig.1).Starting from a ring lattice with n vertices and k edges per vertex,we rewire each edge at random with probability p .This construction allows us to ‘tune’the graph between regularity (p ¼0)and disorder (p ¼1),and thereby to probe the intermediate region 0Ͻp Ͻ1,about which little is known.We quantify the structural properties of these graphs by their characteristic path length L (p )and clustering coefficient C (p ),as defined in Fig.2legend.Here L (p )measures the typical separation between two vertices in the graph (a global property),whereas C (p )measures the cliquishness of a typical neighbourhood (a local property).The networks of interest to us have many vertices with sparse connections,but not so sparse that the graph is in danger of becoming disconnected.Specifically,we require n q k q ln ðn Þq 1,where k q ln ðn Þguarantees that a random graph will be connected 16.In this regime,we find that L ϳn =2k q 1and C ϳ3=4as p →0,while L ϷL random ϳln ðn Þ=ln ðk Þand C ϷC random ϳk =n p 1as p →1.Thus the regular lattice at p ¼0is a highly clustered,large world where L grows linearly with n ,whereas the random network at p ¼1is a poorly clustered,small world where L grows only logarithmically with n .These limiting cases might lead one to suspect that large C is always associated with large L ,and small C with small L .On the contrary,Fig.2reveals that there is a broad interval of p over which L (p )is almost as small as L random yet C ðp Þq C random .These small-world networks result from the immediate drop in L (p )caused by the introduction of a few long-range edges.Such ‘short cuts’connect vertices that would otherwise be much farther apart than L random .For small p ,each short cut has a highly nonlinear effect on L ,contracting the distance not just between the pair of vertices that it connects,but between their immediate neighbourhoods,neighbourhoods of neighbourhoods and so on.By contrast,an edge*Present address:Paul zarsfeld Center for the Social Sciences,Columbia University,812SIPA Building,420W118St,New York,New York 10027,USA.Nature © Macmillan Publishers Ltd 19988letters to natureNATURE |VOL 393|4JUNE 1998441removed from a clustered neighbourhood to make a short cut has,at most,a linear effect on C ;hence C (p )remains practically unchanged for small p even though L (p )drops rapidly.The important implica-tion here is that at the local level (as reflected by C (p )),the transition to a small world is almost undetectable.To check the robustness of these results,we have tested many different types of initial regular graphs,as well as different algorithms for random rewiring,and all give qualitatively similar results.The only requirement is that the rewired edges must typically connect vertices that would otherwise be much farther apart than L random .The idealized construction above reveals the key role of short cuts.It suggests that the small-world phenomenon might be common in sparse networks with many vertices,as even a tiny fraction of short cuts would suffice.To test this idea,we have computed L and C for the collaboration graph of actors in feature films (generated from data available at ),the electrical power grid of the western United States,and the neural network of the nematode worm C.elegans 17.All three graphs are of scientific interest.The graph of film actors is a surrogate for a social network 18,with the advantage of being much more easily specified.It is also akin to the graph of mathematical collaborations centred,traditionally,on P.Erdo¨s (partial data available at /ϳgrossman/erdoshp.html).The graph of the power grid is relevant to the efficiency and robustness of power networks 19.And C.elegans is the sole example of a completely mapped neural network.Table 1shows that all three graphs are small-world networks.These examples were not hand-picked;they were chosen because of their inherent interest and because complete wiring diagrams were available.Thus the small-world phenomenon is not merely a curiosity of social networks 13,14nor an artefact of an idealizedmodel—it is probably generic for many large,sparse networks found in nature.We now investigate the functional significance of small-world connectivity for dynamical systems.Our test case is a deliberately simplified model for the spread of an infectious disease.The population structure is modelled by the family of graphs described in Fig.1.At time t ¼0,a single infective individual is introduced into an otherwise healthy population.Infective individuals are removed permanently (by immunity or death)after a period of sickness that lasts one unit of dimensionless time.During this time,each infective individual can infect each of its healthy neighbours with probability r .On subsequent time steps,the disease spreads along the edges of the graph until it either infects the entire population,or it dies out,having infected some fraction of the population in theprocess.p = 0p = 1Regular Small-worldRandomFigure 1Random rewiring procedure for interpolating between a regular ring lattice and a random network,without altering the number of vertices or edges in the graph.We start with a ring of n vertices,each connected to its k nearest neighbours by undirected edges.(For clarity,n ¼20and k ¼4in the schematic examples shown here,but much larger n and k are used in the rest of this Letter.)We choose a vertex and the edge that connects it to its nearest neighbour in a clockwise sense.With probability p ,we reconnect this edge to a vertex chosen uniformly at random over the entire ring,with duplicate edges forbidden;other-wise we leave the edge in place.We repeat this process by moving clockwise around the ring,considering each vertex in turn until one lap is completed.Next,we consider the edges that connect vertices to their second-nearest neighbours clockwise.As before,we randomly rewire each of these edges with probability p ,and continue this process,circulating around the ring and proceeding outward to more distant neighbours after each lap,until each edge in the original lattice has been considered once.(As there are nk /2edges in the entire graph,the rewiring process stops after k /2laps.)Three realizations of this process are shown,for different values of p .For p ¼0,the original ring is unchanged;as p increases,the graph becomes increasingly disordered until for p ¼1,all edges are rewired randomly.One of our main results is that for intermediate values of p ,the graph is a small-world network:highly clustered like a regular graph,yet with small characteristic path length,like a random graph.(See Fig.2.)T able 1Empirical examples of small-world networksL actual L random C actual C random.............................................................................................................................................................................Film actors 3.65 2.990.790.00027Power grid 18.712.40.0800.005C.elegans 2.65 2.250.280.05.............................................................................................................................................................................Characteristic path length L and clustering coefficient C for three real networks,compared to random graphs with the same number of vertices (n )and average number of edges per vertex (k ).(Actors:n ¼225;226,k ¼61.Power grid:n ¼4;941,k ¼2:67.C.elegans :n ¼282,k ¼14.)The graphs are defined as follows.Two actors are joined by an edge if they have acted in a film together.We restrict attention to the giant connected component 16of this graph,which includes ϳ90%of all actors listed in the Internet Movie Database (available at ),as of April 1997.For the power grid,vertices represent generators,transformers and substations,and edges represent high-voltage transmission lines between them.For C.elegans ,an edge joins two neurons if they are connected by either a synapse or a gap junction.We treat all edges as undirected and unweighted,and all vertices as identical,recognizing that these are crude approximations.All three networks show the small-world phenomenon:L ՌL random but C q C random.00.20.40.60.810.00010.0010.010.11pFigure 2Characteristic path length L (p )and clustering coefficient C (p )for the family of randomly rewired graphs described in Fig.1.Here L is defined as the number of edges in the shortest path between two vertices,averaged over all pairs of vertices.The clustering coefficient C (p )is defined as follows.Suppose that a vertex v has k v neighbours;then at most k v ðk v Ϫ1Þ=2edges can exist between them (this occurs when every neighbour of v is connected to every other neighbour of v ).Let C v denote the fraction of these allowable edges that actually exist.Define C as the average of C v over all v .For friendship networks,these statistics have intuitive meanings:L is the average number of friendships in the shortest chain connecting two people;C v reflects the extent to which friends of v are also friends of each other;and thus C measures the cliquishness of a typical friendship circle.The data shown in the figure are averages over 20random realizations of the rewiring process described in Fig.1,and have been normalized by the values L (0),C (0)for a regular lattice.All the graphs have n ¼1;000vertices and an average degree of k ¼10edges per vertex.We note that a logarithmic horizontal scale has been used to resolve the rapid drop in L (p ),corresponding to the onset of the small-world phenomenon.During this drop,C (p )remains almost constant at its value for the regular lattice,indicating that the transition to a small world is almost undetectable at the local level.Nature © Macmillan Publishers Ltd 19988letters to nature442NATURE |VOL 393|4JUNE 1998Two results emerge.First,the critical infectiousness r half ,at which the disease infects half the population,decreases rapidly for small p (Fig.3a).Second,for a disease that is sufficiently infectious to infect the entire population regardless of its structure,the time T (p )required for global infection resembles the L (p )curve (Fig.3b).Thus,infectious diseases are predicted to spread much more easily and quickly in a small world;the alarming and less obvious point is how few short cuts are needed to make the world small.Our model differs in some significant ways from other network models of disease spreading 20–24.All the models indicate that net-work structure influences the speed and extent of disease transmis-sion,but our model illuminates the dynamics as an explicit function of structure (Fig.3),rather than for a few particular topologies,such as random graphs,stars and chains 20–23.In the work closest to ours,Kretschmar and Morris 24have shown that increases in the number of concurrent partnerships can significantly accelerate the propaga-tion of a sexually-transmitted disease that spreads along the edges of a graph.All their graphs are disconnected because they fix the average number of partners per person at k ¼1.An increase in the number of concurrent partnerships causes faster spreading by increasing the number of vertices in the graph’s largest connected component.In contrast,all our graphs are connected;hence the predicted changes in the spreading dynamics are due to more subtle structural features than changes in connectedness.Moreover,changes in the number of concurrent partners are obvious to an individual,whereas transitions leading to a smaller world are not.We have also examined the effect of small-world connectivity on three other dynamical systems.In each case,the elements were coupled according to the family of graphs described in Fig.1.(1)For cellular automata charged with the computational task of density classification 25,we find that a simple ‘majority-rule’running on a small-world graph can outperform all known human and genetic algorithm-generated rules running on a ring lattice.(2)For the iterated,multi-player ‘Prisoner’s dilemma’11played on a graph,we find that as the fraction of short cuts increases,cooperation is less likely to emerge in a population of players using a generalized ‘tit-for-tat’26strategy.The likelihood of cooperative strategies evolving out of an initial cooperative/non-cooperative mix also decreases with increasing p .(3)Small-world networks of coupled phase oscillators synchronize almost as readily as in the mean-field model 2,despite having orders of magnitude fewer edges.This result may be relevant to the observed synchronization of widely separated neurons in the visual cortex 27if,as seems plausible,the brain has a small-world architecture.We hope that our work will stimulate further studies of small-world networks.Their distinctive combination of high clustering with short characteristic path length cannot be captured by traditional approximations such as those based on regular lattices or random graphs.Although small-world architecture has not received much attention,we suggest that it will probably turn out to be widespread in biological,social and man-made systems,oftenwith important dynamical consequences.ⅪReceived 27November 1997;accepted 6April 1998.1.Winfree,A.T.The Geometry of Biological Time (Springer,New Y ork,1980).2.Kuramoto,Y.Chemical Oscillations,Waves,and Turbulence (Springer,Berlin,1984).3.Strogatz,S.H.&Stewart,I.Coupled oscillators and biological synchronization.Sci.Am.269(6),102–109(1993).4.Bressloff,P .C.,Coombes,S.&De Souza,B.Dynamics of a ring of pulse-coupled oscillators:a group theoretic approach.Phys.Rev.Lett.79,2791–2794(1997).5.Braiman,Y.,Lindner,J.F.&Ditto,W.L.Taming spatiotemporal chaos with disorder.Nature 378,465–467(1995).6.Wiesenfeld,K.New results on frequency-locking dynamics of disordered Josephson arrays.Physica B 222,315–319(1996).7.Gerhardt,M.,Schuster,H.&Tyson,J.J.A cellular automaton model of excitable media including curvature and dispersion.Science 247,1563–1566(1990).8.Collins,J.J.,Chow,C.C.&Imhoff,T.T.Stochastic resonance without tuning.Nature 376,236–238(1995).9.Hopfield,J.J.&Herz,A.V.M.Rapid local synchronization of action potentials:Toward computation with coupled integrate-and-fire neurons.Proc.Natl A 92,6655–6662(1995).10.Abbott,L.F.&van Vreeswijk,C.Asynchronous states in neural networks of pulse-coupled oscillators.Phys.Rev.E 48(2),1483–1490(1993).11.Nowak,M.A.&May,R.M.Evolutionary games and spatial chaos.Nature 359,826–829(1992).12.Kauffman,S.A.Metabolic stability and epigenesis in randomly constructed genetic nets.J.Theor.Biol.22,437–467(1969).gram,S.The small world problem.Psychol.Today 2,60–67(1967).14.Kochen,M.(ed.)The Small World (Ablex,Norwood,NJ,1989).15.Guare,J.Six Degrees of Separation:A Play (Vintage Books,New Y ork,1990).16.Bollaba´s,B.Random Graphs (Academic,London,1985).17.Achacoso,T.B.&Yamamoto,W.S.AY’s Neuroanatomy of C.elegans for Computation (CRC Press,BocaRaton,FL,1992).18.Wasserman,S.&Faust,K.Social Network Analysis:Methods and Applications (Cambridge Univ.Press,1994).19.Phadke,A.G.&Thorp,puter Relaying for Power Systems (Wiley,New Y ork,1988).20.Sattenspiel,L.&Simon,C.P .The spread and persistence of infectious diseases in structured populations.Math.Biosci.90,341–366(1988).21.Longini,I.M.Jr A mathematical model for predicting the geographic spread of new infectious agents.Math.Biosci.90,367–383(1988).22.Hess,G.Disease in metapopulation models:implications for conservation.Ecology 77,1617–1632(1996).23.Blythe,S.P .,Castillo-Chavez,C.&Palmer,J.S.T oward a unified theory of sexual mixing and pair formation.Math.Biosci.107,379–405(1991).24.Kretschmar,M.&Morris,M.Measures of concurrency in networks and the spread of infectious disease.Math.Biosci.133,165–195(1996).25.Das,R.,Mitchell,M.&Crutchfield,J.P .in Parallel Problem Solving from Nature (eds Davido,Y.,Schwefel,H.-P.&Ma¨nner,R.)344–353(Lecture Notes in Computer Science 866,Springer,Berlin,1994).26.Axelrod,R.The Evolution of Cooperation (Basic Books,New Y ork,1984).27.Gray,C.M.,Ko¨nig,P .,Engel,A.K.&Singer,W.Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties.Nature 338,334–337(1989).Acknowledgements.We thank B.Tjaden for providing the film actor data,and J.Thorp and K.Bae for the Western States Power Grid data.This work was supported by the US National Science Foundation (Division of Mathematical Sciences).Correspondence and requests for materials should be addressed to D.J.W.(e-mail:djw24@).0.150.20.250.30.350.00010.0010.010.11rhalfpaFigure 3Simulation results for a simple model of disease spreading.The community structure is given by one realization of the family of randomly rewired graphs used in Fig.1.a ,Critical infectiousness r half ,at which the disease infects half the population,decreases with p .b ,The time T (p )required for a maximally infectious disease (r ¼1)to spread throughout the entire population has essen-tially the same functional form as the characteristic path length L (p ).Even if only a few per cent of the edges in the original lattice are randomly rewired,the time to global infection is nearly as short as for a random graph.0.20.40.60.810.00010.0010.010.11pb。
2023年甘肃省定西市大学英语6级大学英语六级预测试题(含答案)
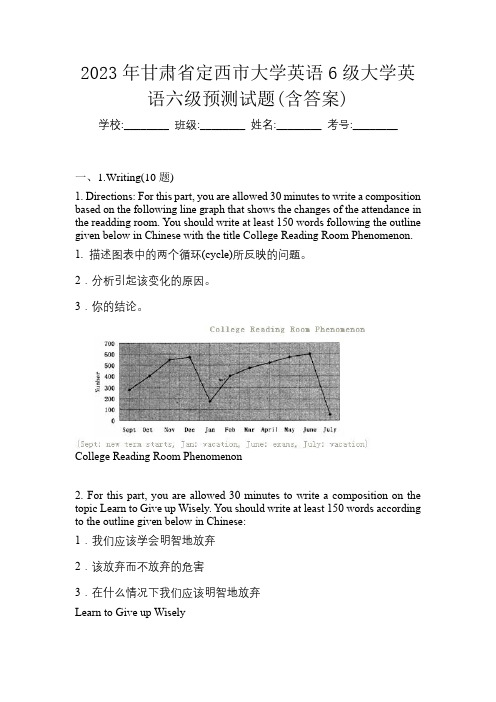
2023年甘肃省定西市大学英语6级大学英语六级预测试题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、1.Writing(10题)1. Directions: For this part, you are allowed 30 minutes to write a composition based on the following line graph that shows the changes of the attendance in the readding room. You should write at least 150 words following the outline given below in Chinese with the title College Reading Room Phenomenon.1. 描述图表中的两个循环(cycle)所反映的问题。
2.分析引起该变化的原因。
3.你的结论。
College Reading Room Phenomenon2. For this part, you are allowed 30 minutes to write a composition on the topic Learn to Give up Wisely. You should write at least 150 words according to the outline given below in Chinese:1.我们应该学会明智地放弃2.该放弃而不放弃的危害3.在什么情况下我们应该明智地放弃Learn to Give up Wisely3. Directions: For this part, you are allowed 30 minutes to write a short essay entitled Social Practice. You should write at least 150 words following the outline given below:1. 为什么要参加社会实践?2. 参加社会实践可能会产生的问题。
诺奖得主对话浙大学子:年龄不仅仅是时间概念

诺奖得主对话浙大学子:年龄不仅仅是时间概念佚名【期刊名称】《浙江大学学报(医学版)》【年(卷),期】2011(040)004【总页数】1页(P426)【正文语种】中文今年4月28日晚,近千位浙江大学师生的目光聚集在诺贝尔物理学奖获得者、扫描隧道显微镜发明者之一海因里希·罗勒(Heinrich Rohrer)博士身上,聆听他《从爱因斯坦到纳米技术!》的演讲。
中科院院士、浙大材料系教授张泽主持了“对话大师”环节,在整整1个小时的互动中,罗勒博士充满睿智与妙趣横生的回答让浙大学子为之折服,深受启发。
海因里希·罗勒1933年出生于瑞士,大学毕业后加入新成立的IBM苏黎世实验室,主要从事Kondo问题和反铁磁等方面的研究工作,后来转向扫描隧道显微镜的研制工作。
1981年,与他的同事研制出了一种新型的科学仪器——扫描隧道显微镜(Scanning Tunneling Microscope,简称STM)。
利用STM,他们在硅单晶表面直接观察到周期性排列的硅原子阵列,这是人类有史以来首次直接看到个别的原子。
在STM的基础上,人类陆续发明了原子力显微镜、磁力显微镜等近20种相关的科学仪器。
所有这些发明为科学家们探索纳米世界提供了另一种强有力的现代工具,促进了国际纳米科学研究时代的到来。
由于STM的开创性影响,罗勒与他的同事被授予1986年诺贝尔物理学奖。
海因里希·罗勒说,年龄并不是一个单纯的时间概念,对于科学工作者来说,年龄是你思考问题处于激发状态的时间,和知识的积累。
“但知识有时候也会有麻烦,当你的导师和你说‘这不行’的时候,倒有可能真的是一个研究的机会。
在你证明一个事情不可能之前,一切都是有可能的。
”他说,科学探索并没有一个固定的方法可以参照,而是当你遇到问题的时候,你用尽所有的办法去解决,就可能有新发现。
他希望大家在科研的过程中,“思考要像一个理论家,动手要像一个工程师。
”。
沙棘果渣还田对水稻土性质、温室气体排放和微生物数量的影响

浙江大学学报(农业与生命科学版)48(4):483~492,2022Journal of Zhejiang University (Agric.&Life Sci.)http :///agr E -mail :zdxbnsb @沙棘果渣还田对水稻土性质、温室气体排放和微生物数量的影响万清1,杨小渔1,吴丹2,张奇春1*(1.浙江大学环境与资源学院,污染环境修复与生态健康教育部重点实验室,杭州310058;2.浙江大学生物系统工程与食品科学学院,杭州310058)摘要采用28d 的土壤培养试验,选用沙棘果渣(R )、生物质炭(B )和生物陶粒(T )3组材料,以自然培养组作为对照(CK ),探讨沙棘果渣对土壤理化性质、温室气体(CO 2、CH 4和N 2O )排放和微生物数量等方面的影响。
结果表明:沙棘果渣能够显著提升土壤中全碳、全氮、速效钾等养分的含量,平均提升率分别为16.31%、14.99%、46.15%;对土壤pH 也存在一定的提升效果,提升范围为0.25~0.69。
沙棘果渣还田后土壤微生物丰度显著升高,其中前14d 微生物数量较对照平均增长335.6%。
对不同材料还田后的温室气体排放和全球增温潜势分析表明,与生物质炭和生物陶粒相比,沙棘果渣还田的CO 2排放量和全球增温潜势显著较高,但其CH 4排放量较小且可以显著降低N 2O 的排放量。
总体来看,沙棘果渣具有较高的还田价值,但需要考虑对温室气体排放的风险,本研究可为沙棘果渣的农业还田利用提供一定参考。
关键词沙棘果渣;生物质炭;生物陶粒;微生物数量;温室气体;土壤理化性质中图分类号X 172文献标志码A引用格式万清,杨小渔,吴丹,等.沙棘果渣还田对水稻土性质、温室气体排放和微生物数量的影响[J].浙江大学学报(农业与生命科学版),2022,48(4):483-492.DOI:10.3785/j.issn.1008-9209.2021.06.291WAN Qing,YANG Xiaoyu,WU Dan,et al.Effects of returning seabuckthorn fruit residue into field on paddy soil properties,greenhouse gas emissions and microbial numbers[J].Journal of Zhejiang University (Agriculture &Life Sciences),2022,48(4):483-492.Effects of returning seabuckthorn fruit residue into field on paddy soilproperties,greenhouse gas emissions and microbial numbersWAN Qing 1,YANG Xiaoyu 1,WU Dan 2,ZHANG Qichun 1*(1.Ministry of Education Key Laboratory of Environmental Remediation and Ecological Health,College of Environmental and Resource Sciences,Zhejiang University,Hangzhou 310058,China;2.College of Biosystems Engineering and Food Science,Zhejiang University,Hangzhou 310058,China )AbstractTo explore the effects of seabuckthorn fruit residue on soil physicochemical properties,greenhousegas (CO 2,CH 4,N 2O)emissions,and the microbial numbers,a 28-day soil pot experiment was conducted.Three groups of materials were used,including seabuckthorn fruit residue (R),biochar (B),and biological ceramsite (T)in the experiment,and a natural culture was used as the control group (CK).The results showed that the seabuckthorn fruit residue significantly promoted the contents of soil nutrients such as total carbon,total nitrogen,and available potassium,and the average increase rates were 16.31%,14.99%,and 46.15%,respectively.Besides,the soil pHDOI :10.3785/j.issn.1008-9209.2021.06.291基金项目:国家重点研发计划课题(2021YFD1700803);浙江省重点研发计划项目(2021C04032)。
阿尔兹海默症最新研究进展一览

阿尔兹海默症最新研究进展一览本期为大家带来的是阿尔兹海默症领域的最新研究进展,希望读者朋友们能够喜欢。
1. Nat Commun:人工智能促进阿尔兹海默症的研究DOI: 10.1038/s41467-019-10212-1加州大学戴维斯分校和加州大学旧金山分校的研究人员已经找到了一种方法来训练计算机精确检测人类大脑组织中阿尔茨海默病的生物标志物。
淀粉样斑块是阿尔茨海默病患者大脑中蛋白质碎片的团块,可破坏神经细胞的连接。
加州大学科学家团队开发的机器学习工具可以“看到”脑组织样本是否有一种类型的淀粉样蛋白斑块,并且很快就能完成。
该研究结果于5月15日发表在Nature Communications上,表明机器学习可以增强专家神经病理学家的专业知识和分析。
该工具允许他们分析数千倍的数据,并提出即使是训练有素的人类专家的有限数据处理能力也无法实现的新问题。
“我们仍然需要病理学家,”加州大学戴维斯分校加州大学戴维斯分校病理学和检验医学系助理教授,该研究的主要作者布列塔尼N. Dugger博士说。
“这是一个工具,就像键盘一样用于写作。
由于键盘有助于编写工作流程,数字病理学与机器学习相结合可以帮助进行神经病理学工作流程。
”在这项研究中,她与加州大学旧金山分校神经退行性疾病研究所和药物化学系助理教授Michael J. Keizer博士合作,确定他们是否可以教一台计算机来自动识别和分析微小淀粉样蛋白斑块的繁琐过程。
各种类型的大片尸检人脑组织。
对于这项工作,Keiser和他的团队设计了一个“卷积神经网络”(CNN),这是一个计算机程序,旨在识别基于数千个人类标记示例的模式。
为了创建足够的训练样例来教授CNN算法Dugger如何分析脑组织,UCSF团队与她合作设计了一种方法,允许她快速注释或标记来自50万个特写图像的数万张图像。
来自43个健康和患病大脑样本的组织。
UCSF团队使用这个数以万计的标记示例图像数据库来训练他们的CNN机器学习算法,以识别阿尔茨海默病中所见的不同类型的大脑变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ROBUST TIMEKEEPING IN CIRCADIANNETWORKS:FROM GENES TO CELLSNeda Bagheri∗,1Stephanie R.Taylor∗∗,1Kirsten Meeker∗∗Linda R.Petzold∗∗Francis J.Doyle III∗∗∗,2∗Dept.of Electrical and Computer Engineering,Universityof California Santa Barbara93106-9560,U.S.A.∗∗Dept.of Computer Science,University of CaliforniaSanta Barbara93106-5070,U.S.A.∗∗∗Dept.of Chemical Engineering,University of CaliforniaSanta Barbara93106-5080,U.S.A.Abstract:Systems theoretic tools,including mathematical modeling,control theoretic analysis,and feedback design,advance the understanding of the circadian clock:a set of noisy oscillators that communicate to ensure its function as a reliable pacemaker.The clock’s internal time,or phase,is a key performance measure used to investigate dynamics of a single deterministic oscillator for the purpose of generating insight into the behavior of coupled stochastic oscillators.The analysis of a single oscillator identifies appropriate coupling mechanisms for an ensemble of stochastic oscillators.Phase also serves as a critical control objective for a model predictive control algorithm that aims to correct mismatch between the biological clock and its environment.Keywords:Phase dynamics,circadian rhythms,analysis,control,performance.1.INTRODUCTIONBiological systems are characterized by com-plex dynamics.Undergirding a system’s function are networks of interacting components(Sontag, 2004).To elucidate the mechanisms employed by these networks,biological experimentation and intuition are by themselves insufficient(Kitano, 2002).In thefield of systems biology,investi-gators formalize the dynamical interactions as 1N.B.and S.R.T.contributed equally to this work.We thank H.Mirsky and P.Chang for insightful comments. 2Corresponding author:frank.doyle@.This project was supported in part by The Institute for Collaborative Biotechnologies,DAAD19-03-D-0004; NIH,GM078993;IGERT NSF,DGE02-21715;The Re-search Participation Program between the US DOE and AFRL/HEP.mathematical models and subject these models to systems theoretical analyses,with the goal of guiding further experimentation and increased un-derstanding(Fall et al.,2005).A perfect example of biological complexity is the circadian clock, which coordinates daily physiological behaviors of organisms across the kingdoms of life.The mammalian circadian master clock resides in the suprachiasmatic nucleus(SCN),located in the hypothalamus(Reppert and Weaver,2002).It is a network of multiple autonomous noisy oscillators, which communicate via neuropeptides to synchro-nize and form a coherent oscillator(Herzog et al.,2004;Liu et al.,2007).This coherent oscillator then coordinates the timing of daily behaviors, such as the sleep/wake cycle.Left in constant conditions,the clock will free-run with a periodof only approximately24hours and its internal time,or phase,will drift away from that of its environment.Thus,vital to a circadian clock is its ability to entrain to external time through en-vironmental factors(Boulos et al.,2002;Dunlap et al.,2004;Daan and Pittendrigh,1976a).To study the timekeeping abilities of the circadian clock,we employ a systems biology approach.Mathematical models are used in two complementary investiga-tions,one involving the network of coupled oscil-lators,and the other involving the single coherent oscillator.In both cases we investigate the phase response behavior.Proper phase response behavior is critical for syn-chronization both to environmental factors such as light,temperature,nutrition intake,and so-cial interaction(Boulos et al.,2002;Dunlap et al.,2004;Daan and Pittendrigh,1976a),and to other oscillators via intercellular signals such as vasoactive intestinal polypeptide(VIP)(Herzog et al.,2004;To et al.,2007).To study this behavior, phase response curves(PRCs)are collected.By mapping the arrival time of a stimulus to its resulting phase shift(advance or delay),the PRC characterizes the clock’s time-dependent sensitiv-ity to the given stimulus.In experimental settings, the best-studied factor is light(Daan and Pitten-drigh,1976b;Johnson,1999;Winfree,2001).Light PRCs have been used extensively to predict and better understand how biological oscillators are entrained by light input(Johnson,1999;Johnson et al.,2003;Comas et al.,2006).A similar analysis is extended to mathematical models. Commonly,circadian clocks are modeled with or-dinary differential equations(ODEs)as single, deterministic limit cycle oscillators(Leloup and Goldbeter,2003;Forger and Peskin,2003).These models are used to reverse-engineer both the inter-nal composition(transcriptional feedback loops) of the clock and the process of entrainment by light/dark cycles(Johnson et al.,2003;Geier et al.,2005).To capture the variability observed in biological data,additional models introduce stochasticity,via multiplicative noise in stochastic differential equations(SDEs)(Ueda et al.,2002) or via a transformation from the differential equa-tion setting to a discrete stochastic setting(Forger and Peskin,2005;Gonze and Goldbeter,2006).To capture the network behavior,spontaneous syn-chronization of coupled oscillators is modeled for the mammal andfly in(Ueda et al.,2002;Gonze et al.,2005;To et al.,2007).Synchronization and entrainment are critical phe-nomena of the circadian network that dictate an organism’s level of performance.To further our understanding of such processes,we use ODEs, SDEs,and a discrete stochastic model in both the network and single-cell setting.In Section2we analyze synchronization of neurons in an SDE model by studying the phase response behavior of a single,deterministic cell.In Section3we define a population of neurons through a discrete stochastic model where the challenges associated with achieving synchronization are addressed via the study of a single oscillator.Section4describes a strategy for correcting the phase mismatch that arises when there is a difference between internal and external time.2.ANALYSIS OF AND PREDICTIONS FORCOUPLED OSCILLATORSWe analyze the phase behavior of an SDE model of100coupled neurons in the Drosophila melanogaster circadian pacemaker(Ueda et al., 2002).In an investigation of potential coupling mechanisms,Ueda et al.have developed a frame-work in which there are960potential coupling mechanisms.Each coupling mechanism is con-structed such that each cell contains a compo-nent that sends a signal which is received by its neighbor cells.The signal then modulates a given target parameter.The authors show that a subset of the target/signal pairs produce spontaneous (in phase)synchronization among the cells.They discuss this phenomenon in terms of“day”and “night”systems,in which the mutual entrainment occurs in a manner similar to light(or dark)pulse entrainment.We expand upon their analyses by modeling all 960signal/target pairs.Of the960,there are84 that produce(in phase)synchrony.However,not all synchronizing mechanisms produce the same behavior.Notably,the period of oscillation is different for each target/signal pair,with values ranging from20hours to37hours.Because we are interested in rhythms that are circadian,we consider only those pairs that produce periods in the range of20to28hours.We examine the relationship between the signal/target pair and the resultant period of the synchronized system using a combination of numerical experimentation and mathematical analysis with an infinitesimal analog to the PRC.This is a step in pursuit of the fundamental question:What causes these cou-pling mechanisms to bring about synchronization while the others fail?Understanding the transi-tion from asynchrony to synchrony is a signifi-cantly more complicated endeavor;thus,we focus on a synchronized system.2.1MethodsWe simulate the SDE system for the82sig-nal/target pairs that cause synchrony with a “circadian”period.The data describe what willhappen,but leave unanswered questions such as: Why are some signal/target pairs speeding up the oscillations and some slowing them down? How would an adjustment of the relative timing between the signal and the cell’s phase change the timing?There is a rich literature concern-ing the mathematical analysis of coupled oscilla-tors(Kuramoto,1984;Hoppensteadt and Izhike-vich,1997;Winfree,2001;Brown et al.,2004). The most heavily studied systems,such as the Kuramoto model,assume either that interactions among oscillators are sinusoidal(Kuramoto,1984; Strogatz,2000)or that they perturb state veloc-ities directly(Brown et al.,2004).In circadian clock models,a signal sent to an oscillator ulti-mately manifests as the manipulation of a single parameter.Thus,to study the effects of signaling on the phase behavior,we must examine the ef-fects of parametric manipulation on phase behav-ior.This motivated us to develop the parametric impulse phase response curve(pIPRC)in(Taylor et al.,2007),which predicts the oscillator’s veloc-ity change in response to parametric perturbation. In the present work,we demonstrate its utility as a complement to numerical experimentation.To utilize the pIPRC,we are compelled to inves-tigate a deterministic model.Thus,we study a single neuron,modeled as a set of ODEs with a stable attracting limit cycle,e.g.˙x(t)=f(x(t),p). The solution along the limit cycle is periodic with periodτ,and we describe its progress along the cycle by its internal time,or phase,φ.When the clock is unperturbed,the phase progresses at the same rate as time,i.e.,dφ(x(t,p))/dt≡1.When the clock is perturbed the velocity response is predicted by the pIPRC,i.e.pIPRC(φ)=ddt∂φ∂p(t).Consider a signal∆p j(t,φ)which is a function either of time or phase.This signal will change the oscillator’s velocity according to∆φ/∆t≈pIPRC j(φ)∆p j(t,φ).Another interpretation is that for a pulse of duration∆t,a phase shift is in-curred according to∆φ≈pIPRC j(φ)∆p j(t,φ)∆t. Using this interpretation,the pIPRC is a predictor for the PRC–the pIPRC characterizes the timing behavior of an oscillator alone while the PRC describes the response to a particular signal.To understand the period of the synchronized cells of the Drosophila clock,we study the relationship between the signal and the pIPRC for the target. We must acquire the signal.To begin,we capital-ize on the stable synchrony–in a synchronized system,each neuron sends the same signal at the same time.Thus,we mimic the intercellular sig-naling simply by assuming that all signals match that of a single neuron.The trace of the signal is acquired by simulating one cell as it sends the signal(without allowing the signal to feed back onto the cell).Two example signals along with the pIPRCs corresponding to their targets are shown in Fig.2.Before we begin our analysis,we evaluate the predictive power of the single cell model and of the pIPRC for each signal/target pair.First,we predict the period of the synchronized SDE pop-ulation by simulating the ODE model,allowing it to signal itself.After several cycles it converges to a new limit cycle with a new period–the period of the synchronized system.In Fig.1we plot our prediction for the new period against the observed period of the SDE model of the full population. The square of the Pearson correlation coefficient, R2,is0.91and the data is located within an hour of the observed values.Second,we use the pIPRC directly to make similar predictions.By treating φas the independent variable(instead of time), we predict the change in period by assessing the effect of the signal on the oscillator over a single cycle.Integrating over the cycle,∆τ≈−τpIPRC j(φ)∆p j(φ)dφ,wefind that the predictions are qualitatively ac-curate.Fig.1shows the predicted period change of the synchronized system versus the observed period change of the synchronized system.The R2 value between observed and predicted periods is 0.65.The data are more scattered than those from the full-cell simulation,though the majority are within1hour of perfect prediction.We conclude that although neither of these methods are perfect predictors,their qualitative correctness supports our approach.2.2AnalysisFig.2contains the traces of two signal/target pairs.Fig.2(a)shows the relationship for a pair that causes the system to slow down.In this case, the target reaction rate is the maximal rate of degradation for clock component tim mRNA.The signal arrives at the tail end of the advance zone, and is active during the deadzone and thefirst half of the delay zone,leading to a cycle that is slower than nominal.Fig.2(b)shows a pair for which the target reaction rate is the maximal rate of clk mRNA degradation.Here,the pIPRC shows nearly negligible delay regions.It follows that,regardless of the phase relationship between the signal and target,the oscillator will respond by speeding up.In both of these cases,and in all cases that produce synchrony,the relationship between the222426282122232425262728Predicted τ [hr]O b s e r v e d τ [h r ]R 2= 0.65 (o)R 2 = 0.91 (+)Fig.1.Observed vs.Predicted Periods.For eachsignal/target pair that produces synchrony there is a black circle and a gray plus.The x-axis position indicates the period predicted using the pIPRC (circles)or using a single cell,signaling itself (pluses).For both data,the y-axis position indicates the period ob-served once collection of noisy cells becomes (and remains)synchronized.Perfect predic-tions fall on the dotted line.The dashed and solid lines represent the best fit by linear regression analysis,with R 2=0.65for the pIPRC-predicted data and R 2=0.91for the single-cell data.signal and target meets the criteria for stable entrainment (data not shown).If the signal arrives early (because the phase of the system is a little behind),the system is sped up more (or slowed down less)than usual,and vice versa.The study of the pIPRC and signal is consistent with the ob-served behavior –the mutual entrainment is stable and the system remains synchronized.However,meeting the conditions for mutual entrainment is only a necessary factor;pairs arise that meet the requirements for stable entrainment but do not yield a transition to synchrony (data not shown).Figure 2(a)makes clear that a leftward signal shift of several hours produces a greater overlap of the advance region,meets the conditions for stable en-trainment,and shortens the synchronized period.Thus,an understanding of the phase response behavior is key to unraveling the mechanisms in vivo .3.STOCHASTIC MODEL OF COUPLED MAMMALIAN CIRCADIAN NEURONS Phase response analysis is an important tool used to predict the coupling mechanism used by the mammalian clock.Evidence suggests that neurons in the SCN are synchronized via the neuropeptide VIP (Herzog et al.,2004).VIP levels are high012243648−22Observed τ = 25.2119Time [hr]R e l a t i v e p I P R C−101S i g n a l (a)Signal/Target Pair Producing Slow Oscillations012243648−22Observed τ = 22.6764Time [hr]R e l a t i v e p I P R C−101S i g n a l(b)Signal/Target Pair Producing Fast OscillationsFig.2.Shown are the pIPRC (black dotted line)and signal trace (gray solid line)pairs that cause the coupled SDE system to synchronize with (a)long and (b)short periods.All curves are relative to the target parameter’s nominal value;i.e.,each signal represents fractional changes in the target parameter’s value and each pIPRC predicts the velocity response to fractional changes.during the subjective day,and preliminary results show that VIP signals cause light-like phase shifts.Thus,the VIP signal is similar to the light signal,and the VIP target is similar to the light tar-get.Data show that both VIP and light induce Per transcription (Piggins et al.,1995),and it is predicted that the target of VIP signaling is Per ing this evidence,the authors of (Hao et al.,2006;To et al.,2007)model postulated mechanisms in which VIP signals are received by a cell through signal cascades culminating in the modulation of the parameter associated with Per ing an ODE model,To et al.incorporate this coupling mechanism into a population of non-identical cells,each of which is based on the gene regulatory network model of (Leloup and Goldbeter,2003).They simulate sce-narios in which (1)no coupling is present (and the cells drift out phase)and (2)coupling is present (and the cells form a coherent oscillator),thus demonstrating that their mechanism is capable of creating the spontaneous synchronization seen in the data.Biological experiments show that uncoupled neu-rons are either damped or sloppy oscillators (Aton et al.,2005).The periods of isolated neurons show both a broad distribution of periods and temporal (cycle-to-cycle)variability (Herzog et al.,2004).The model presented in (To et al.,2007)shows a broad distribution of periods across cells,butnone of the cycle-to-cycle variability.To introduce that variability,we develop a stochastic model that builds on these efforts,adding the intrin-sic noise due to the discrete nature of reactionsin the SCN neuron.The present model employsa2-dimensional grid of9SCN neurons and is the discrete stochastic version of the model in (Leloup and Goldbeter,2003)with the coupling mechanism from(To et al.,2007).Preliminary results,synchronizing a small number of coupled cells,support the validity of the mechanism in the presence of noise.For a more detailed descriptionof the signaling mechanism,see Equations1-7 and Table1in the model supplement of(To et al.,2007).3.1Discrete Stochastic SimulationThe stochastic simulation algorithm(SSA)(Gillespie, 1976;Gillespie,1977)generates exact trajectoriesof the populations of chemical species,given a description of the reaction system consisting of the stoichiometric matrix,νij,and the propen-sity functions a j.The probability density func-tion P(x,t|x0,t0)is defined as the probability the system will be in state x at time t,given that it was in state x0at time t0.The time evolution ofP(x,t|x0,t0)is described by the chemical master equation,∂P(x,t|x0,t0)∂t =Mj=1[a j(x−νj)P(x−νj,t|x0,t0)−a j(x)P(x,t|x0,t0)].(1)The stoichiometric matrixνij describes how the populations of species change with each reaction and has dimensions of number of species i= 1,···,N by number of reactions j=1,···,M. The propensity function a j predicts the probabil-ity of each reaction occurring during the next in-finitesimal time interval,given the current species populations.We use StochKit(StochKit,2007) package,a stochastic simulation tool developed at University of California,Santa Barbara,to simu-late the two dimensional grid of neurons using the SSA.3.2Oscillatory Range of Per Transcription Rate The introduction of noise alters the behavior of the single cells such that additional tuning is required to achieve synchrony.In particular,be-cause VIP signaling ultimately manifests as mod-ulation of the rate of Per transcription,special attention must be paid to the levels of Per mRNA and its rate of transcription,νsP(t).The basal rate,νsP0,characterizes the behavior of an iso-lated cell.Per mRNA for severalνsP0are shown in Fig.3.The depletion or accumulation of per mRNA that occurs whenνsP0is below 1.2or above1.8indicates that we have upset the balance between(1)the transcription rate and(2)the combination of the transport(from nucleus to cytoplasm)and degradation.The current model normalizes the coupling for the size of the grid, but does not maintain the median ofνsP(t)as coupling is added.For the coupled population to exhibit synchrony,we have observed that the median value ofνsP(t)must stay within the range that produces oscillations in an individual cell. Thus,to achieve synchrony,the basal transcrip-tion rateνsP0is decreased to1.0for the coupling weight used in the present work.This produces a median per mRNA population comparable to the uncoupled case withνsP0=1.5.At this basal transcription rate,all isolated cells are damped oscillators.To better match the biological obser-vation that many isolated cells show sustained oscillations,it is necessary either to weaken the coupling or to adjust the transport or degradation rate to re-balance the per mRNA level.050100150200Time [hr]PermRNAConcentration[nM]Fig.3.Per mRNA concentration as a function of basal transcription rateνsP0in uncoupled cells.ForνsP0below1.2per mRNA concen-trations exhibit damped oscillations for the ten day period simulated.ForνsP0above1.8 per mRNA concentrations begin to grow in amplitude with minima greater than zero.3.3Discrete Stochastic SimulationThe results of a single simulation trajectory of a 3x3grid of coupled cells are shown in Fig.4(a)andFig.4(b).The radius r (t )of the complex order parameterri Ψ=1N Nj =1iθj (2)measures the phase coherence of the collective rhythm of N coupled oscillators (Strogatz,2000).If the oscillators are in phase,then r ≈ 1.θj are the phase of each oscillator and Ψ(t )is the average phase.The increase in r (t )from 0.6to 0.8in one cycle is comparable to the results from (To et al.,2007),where a deterministic model with normal distribution of some of the parameters was used to create a grid of coupled heterogeneous cells.The difference in peak amplitudes in Fig.4(a)is due to the small grid and the effect of its bound-aries.The discrete stochastic simulation of larger grids is a goal of this research and will require im-provements in code performance.Reproducing the period and cycle-to-cycle variability of uncoupled single neurons will require increasing the effective noise level by lowering the volume.This study,done at a high volume,demonstrates a method for balancing the coupling strength that will produce phase coherence with a basal Per transcription rate that will sustain oscillations.50100150200012345Time [hr]P e r m R N A C o n c e n t r a t i o n [n M ](a)Per mRNA in Coupled 3x3Grid24680.60.81Cycler (t )(b)Complex Order Parameter Radius for 3x3Coupled GridFig.4.For a single SSA simulation of a 3x3gridof coupled cells (with Ω=2000),we show (a)the trajectory of Per mRNA concentra-tion over time,and (b)its degree of phase coherence.4.PHASE AS A CONTROL OBJECTIVE As signaling among a network of cells serves to synchronize the phase of the individuals,signaling from the environment serves to entrain the phase of the emergent coherent oscillator.Thus,the light signal received by an organism induces phase shifts that calibrate its internal phase to external time.In this section the clock is regarded as a single deterministic oscillator and we apply a model predictive control (MPC)algorithm as a tool to minimize the phase difference between the organism and the environment.In the early 1970’s,Daan and Pittendrigh inves-tigated light-induced phase shifts in free-running organisms through the development of phase re-sponse curves.Watanabe et al.(2001)build upon Daan and Pittendrigh’s investigation of light-induced phase shifts in free-running organisms by proving that the basis for phase entrainment in mammals involves both advance and delay components of the phase response curve .Boulos et al.(2002)extend the investigation/application of phase response curves by establishing bright light treatment as a means to accelerate circa-dian re-synchronization rates.In a previous study,a closed-loop model predictive control algorithm that relies on an evolutionary strategy to deter-mine an optimal sequence of light pulses is used to reset the organisms’phase (Bagheri et al.,2007).In this study the optimal sequence of light inputs is determined as a function of MPC tuning pa-rameters as well as the attributes of the driving force (light).4.1A Mammalian ModelA detailed model that describes circadian dy-namics of a single mammalian cell through 61ODEs serves as the example system (Forger and Peskin,2003;Mirsky et al.,2007).It may be generally defined as a set of nonlinear ordinary differential equations where t is continuous in time,x (t )defines the n -length state vector,L (t )defines the environmental light input,u (t )defines the controlled light input,and f (x (t ),L (t ),u (t ))defines the n -length system dynamics:˙x (t )=f (x (t ),L (t ),u (t )),(3)x (t 0)=x (0),where x (t )∈ n ×1,L (t ),and u (t )∈ 1×1.Oncethe asymptotically stable nonlinear oscillator con-verges to a limit cycle,it exhibits a period τ:x (t +τ)=x (t ).In this paper,the nominal model (a version of the model that has converged to the natural light/dark environment where u (t )=0and L(t)oscillates as a square wave between val-ues3.39E-2and0)is used to define the reference trajectory,r(t).A circadian time of0reflects dawn while a circadian time of12reflects dusk, assuming regular24hour day:night cycles.4.2MPC of Light PulsesA model predictive control strategy(Henson and Seborg,1997;Morari and Lee,1999)is used to in-crease the re-synchronization rate of circadian os-cillators through the systematic addition of light. The control algorithm steps through state trajec-tories at t s-hour intervals,where k serves as the discrete time index reflecting the current simula-tion time t evaluated at t s intervals.In this work, the time step and duration of the manipulated control variable,light,are equivalent.The manipulated light profile,u(t),optimizes an open-loop performance objective on a time in-terval extending from the current time to the current time plus a prediction horizon,P=54hr, allowing the algorithm to take control action at the current time in response to a forecasted error. The move horizon limits the number of controlled light pulses within the prediction horizon;M= 3hr.Beyond M hours of simulation,the predicted model defaults to u(t)=0.Future behaviors for a variety of control inputs are computed according to a model of the plant.The algorithm chooses a series of control inputs by minimizing a performance criterion over a future horizon.Once the mostfit control sequence, u∗∈ M/t s×1,only thefirst control,u∗(1),is implemented.Feedback is incorporated by using the next measurement to update the optimization problem for the next time step.Assuming u min(t)=-3.39E-2,u max(t)=3.39E-2, and L(k)+u(k)≥0,the performance function penalizes the normalized predicted error between the reference and controlled trajectories,e(k), and its corresponding control sequence,u(k).To avoid penalizing transient effects,the state error is weighted uniformly over the move horizon and with increasing weight of slope2over the predic-tion horizon(via Q).The cost of applying a light input is always weighted uniformly(via R).The cost of implementing an M-length control input u(·)beginning at time k that minimizes the error over P hours is defined asJ=minu(·)(eQ)T(eQ)+(¯u R)T(¯u R).(4)Once the controlled state trajectories converge to within15%of the corresponding nominal(or ref-erence)state trajectories,the system is considered to be in phase:T r=min k[|e(k)|∞≤0.15].For further details concerning the MPC algorithm, please refer to(Bagheri et al.,2007).4.3MPC Tuning ParametersThe optimum control sequence,u∗,is determined by enumerating the solutions over a grid in the solution space(light magnitude as a function of time).The algorithm approaches a globally optimal solution as the total possible quantization steps of the control input and computational expense increase.The efficacy of the algorithm is tested with respect to a quantization step of 2,4,8,and16steps(Fig.5(a)).Results suggest that the decrease in phase recovery time may not outweigh the increase in computation time.The phase resetting dynamics of a control input with 2and8possible steps are investigated below. Similarly,the efficacy of the algorithm is tested with respect to a control input of duration1,2, and3hours(reflecting a move horizon of3,6,and 9-hours,respectively)(Fig.5(b)).Results suggest that although shorter light pulses offer a more dynamic manipulated variable profile,it shortens the move horizon and may reduce the utility of model predictive control.Conversely,while longer light pulses offer a longer move horizon,it may reduce the possible control profiles since longer light pulses eventually lead to arrhythmic behav-ior(Ohta et al.,2005).In the remainder of this study,the duration of control is set to2hours.4.4ResultsThe nonlinear properties of biological oscillators often cause different phase-resetting dynamics with respect to the initial condition,IC,and initial phase difference,IP.The initial condition describes the time at which the organism settles into the new environment and begins entrainment; the initial phase difference describes the number of time zones bypassed upon arrival.Hence,phase recovery times are described as a function of both the IC and IP.We generate phase recovery dynamics for three different simulation schemes:(1)The open-loop algorithm where environmental light/dark cycles entrain the system,(2)the closed-loop MPC al-gorithm where the manipulated control variable (light)has two possible values,and(3)where the manipulated control variable has eight possible values.Phase recovery times may be consolidated into a3-dimensional diagram(Fig.6)where the recovery times are plotted with respect to both initial phase differences and initial conditions. As such,we may better visualize the nonlinear dynamic behavior of phase resetting.Although。
