Chosen-ciphertext security without redundancy
cca安全证明方法

cca安全证明方法CCA安全证明方法随着互联网的发展,网络安全问题越来越受到人们的关注。
在这个信息化时代,保护个人隐私和企业机密已经成为了一项重要的任务。
而在网络安全领域,CCA安全证明方法是一种非常有效的保护手段。
一、什么是CCA安全证明方法CCA安全证明方法是一种密码学中的概念,全称为“Chosen Ciphertext Attack Security”。
它是一种用于衡量加密算法安全性的标准,也是一种用于评估加密算法强度的方法。
简单来说,CCA安全证明方法是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全。
二、CCA安全证明方法的分类根据加密算法的不同,CCA安全证明方法可以分为对称加密算法和非对称加密算法两种。
1. 对称加密算法对称加密算法是指加密和解密使用同一个密钥的加密算法。
在对称加密算法中,CCA安全证明方法主要有两种:IND-CCA1和IND-CCA2。
IND-CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
IND-CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
2. 非对称加密算法非对称加密算法是指加密和解密使用不同密钥的加密算法。
在非对称加密算法中,CCA安全证明方法主要有两种:CCA1和CCA2。
CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
三、CCA安全证明方法的应用CCA安全证明方法在实际应用中非常广泛。
在电子商务、在线支付、电子邮件等领域,都需要使用加密算法来保护数据的安全性。
而CCA 安全证明方法可以帮助我们评估加密算法的安全性,从而选择更加安全的加密算法来保护数据。
此外,CCA安全证明方法还可以用于评估数字签名算法的安全性。
Chosen ciphertext attacks

C r y p t o g r a p h y
C o u r s e
Authenticated Encryption
Chosen ciphertext attacks
Dan Boneh
Example chosen ciphertext attacks
Adversary has ciphertext c that it wants to decrypt
≈p
⊥
Adv.
≈p
Adv.
Chal. CPA query: mi,0 , mi,1
kK ci=E(k,mi,1)
Chal. CPA query: mi,0 , mi,1
CCA query: ci
D(k,ci)
≈p
kK
ci=E(k,mi,1)
CCA query: ci
⊥
Dan Boneh
So what?
Dan Boneh
Proof by pictures
Chal. CPA query: mi,0 , mi,1 kK Adv. Chal. CPA query: mi,0 , mi,1 Adv.
ci=E(k,mi,0)
CCA query: ci
D(k,ci)
≈p
kK
ci=E(k,mi,0)
CCA query: ci
TCP/IP packet ACK if valid checksum
Dan Boneh
Chosen ciphertext security
Adversary’s power: both CPA and CCA • Can obtain the encryption of arbitrary messages of his choice • Can decrypt any ciphertext of his choice, other than challenge (conservative modeling of real life) Adversary’s goal: Break sematic security
信息系统安全工程_密码学基础和古典加密_软件

密码分析的攻击条件
根据密码分析者对明文、密文等信息掌握的多 少,可将密码分析分为以下四种情形(强度依 次递增 ):
1、唯密文攻击(Ciphertext Only Attack):破译 者仅有待破译的密文。 2、已知明文攻击(Known Plaintext Attack):破 译者拥有一定数量的密文和对应的明文。 3、选择明文攻击(Chosen Plaintext Attack): 破译者可以选定一些明文,并获得对应的密文。 4、选择密文攻击(Chosen Ciphertext Attack): 破译者可以选定一些密文,并获得对应的明文。
密钥空间:26
对移位密码的强行攻击
由于移位密码的可能密钥只有 26 个,因此可以对密 钥进行穷举尝试,将每一个密钥带入解密规则,直到 获得一个“有意义”的明文串 例如对于前面凯撒密码的例子进行强行攻击如下(唯 密文攻击):
Key P H H W P H D I W H U W K H W R J D S D U W B 1 2 3 o g g v o g c h v g t v j g v q i c r c t v a n f f u n f b g u f s u i f u p h b q b s u z m e e t m e a f t e r t h e t o g a p a r t y
2、可证明安全性
3、无条件安全性
2、密码体制分类
按通信双方使用的密钥,分为单钥密码体制 和公钥密码体制 按对明文数据的处理方式,分为分组密码体 制和流密码体制
单钥体制和公钥体制
单钥体制
也叫对称加密体制或常规加密体制 同一次加解密中发送者和接收者使用相同的密 钥(或虽然不同,但容易从一个密钥推出另一 个密钥)
素数无限证明及对RSA攻击描述

1、证明素数为无限的用反证法证明。
假设素数只有有限的n个,从小到大依次排列为p1,p2,...,pn,则x = (p1·p2·...·pn)+1 显然是不能被p1,p2,...,pn中的任何一个素数整除的,因此x也是一个素数,这和只有n个素数矛盾,所以素数是无限多的。
2、针对RSA的攻击潜在攻击的分类:(1)因数分解攻击(Factorization Attack)RSA的安全性基于这么一种想法,那就是模要足够大以至于在适当的时间内把它分解是不可能的。
乙选择p和q,并且计算出n = p×q。
虽然n是公开的,但p和q是保密的。
如果甲能分解n并获得p和q,她就可以计算出。
然后,因为e是公开的,甲还可以计算出。
私密指数d是甲可以用来对任何加密信息进行解密的暗门。
有许多种因数分解算法,但是没有一种可以分解带有多项式时间复杂度的大整数。
为了安全,目前的RSA要求n必须大于300个十进制数位,这就是说模必须最小是1024比特。
即使运用现在最大最快的计算机,分解这么大的整数所要花费的时间也是不可想象的。
这就表明只要还没有发现更有效的因数分解算法,RSA就是安全的。
(2)选择密文攻击(chosen-Ciphertext attack)针对RSA的潜在攻击都基于RSA的乘法特性,我们假定丙创建了密文C = Pe mod n并且把C发送给乙。
我们也假定乙要对甲的任意密文解密,而不是只解密C。
甲拦截C并运用下列步骤求出P:(1) 甲选择中的一个随机整数X。
(2) 甲计算出。
(3) 为了解密甲把Y发送给乙并得到;这个步骤就是选择密文攻击的一个例子。
(4) 甲能够很容易地得到P,因为甲运用扩展的欧几里得算法求X的乘法逆,并最终求得。
(3)对加密指数的攻击为了缩短加密时间,使用小的加密指数e是非常诱人的。
普通的e值是e = 3(第二个素数)。
不过有几种针对低加密指数的潜在攻击,在这里我们只作简单的讨论。
Ciphertext-Policy Attribute-Based Encryption

∗ Supported by NSF CNS-0524252, CNS-0716199, CNS-0749931; the US Army Research Office under the CyberTA Grant No. W911NF-06-1-0316; and the U.S. Department of Homeland Securit06CS-001-000001.
1
Introduction
Public-Key encryption is a powerful mechanism for protecting the confidentiality of stored and transmitted information. Traditionally, encryption is viewed as a method for a user to share data to a targeted user or device. While this is useful for applications where the data provider knows specifically which user he wants to share with, in many applications the provider will want to share data according to some policy based on the receiving user’s credentials. Sahai and Waters [34] presented a new vision for encryption where the data provider can express how he wants to share data in the encryption algorithm itself. The data provider will provide a predicate f (·) describing how he wants to share the data and a user will be ascribed a secret key associated with their credentials X ; the user with credentials X can decrypt a ciphertext encrypted with predicate f if f (X ) = 1. Sahai and Waters [34] presented a particular formulation of this problem that they called Attribute-Based Encryption (ABE), in which a user’s credentials is represented by a set of string called “attributes” and the predicate is represented by a formula over these attributes. Several techniques used by SW were inspired by prior work on Identity-Based Encryption [35, 13, 24, 18, 10]. One drawback of the Sahai-Waters approach is that their initial construction was limited to handling formulas consisting of one threshold gate. In subsequent work, Goyal, Pandey, Sahai, and Waters [28] further clarified the concept of Attribute-Based Encryption. In particular, they proposed two complementary forms of ABE. In the first, Key-Policy ABE, attributes are used to annotate the ciphertexts and formulas over these attributes are ascribed to users’ secret keys. The second type, Ciphertext-Policy ABE, is complementary in that attributes are used to describe the user’s credentials and the formulas over these credentials are attached to the ciphertext by the encrypting party. In addition, Goyal et al. [28] provided a construction for Key-Policy ABE that was very expressive in that it allowed keys to be expressed by any monotonic formula over encrypted data. The system was proved selectively secure under the Bilinear Diffie-Hellman assumption. However, they left creating expressive Ciphertext Policy ABE schemes as an open problem. The first work to explicitly address the problem of Ciphertext-Policy Attribute-Based Encryption was by Bethencourt, Sahai, and Waters [7]. They described an efficient system that was expressive in that it allowed an encryptor to express an access predicate f in terms of any monotonic formula over attributes. Their system achieved analogous expressiveness and efficiency to the Goyal et al. construction, but in the Ciphertext-Policy ABE setting. While the BSW construction is very expressive, the proof model used was less than ideal — the authors only showed the scheme secure in the generic group model, an artificial model which assumes the attacker needs to access an oracle in order to perform any group operations.1 Recently, ABE has been applied in building a variety of secure systems [33, 39, 9, 8]. These systems motivate the need for ABE constructions that are both foundationally sound and practical. Ciphertext Policy ABE in the Standard Model The lack of satisfaction with generic group model proofs has motivated the problem of finding an expressive CP-ABE system under a more solid model. There have been multiple approaches in this direction. First, we can view the Sahai-Waters[34] construction most “naturally” as Key-Policy ABE for a threshold gate. In their work, Sahai and Waters describe how to realize Ciphertext-Policy ABE
第1章 古典密码

1.2.3 代换密码
定义1.2.2 代换密码体制
K 令 M = C = Z 26 , 是 Z 26 上所有可能置换构成的集合。 y 对任意的置换 π ∈ K ,x ∈ M , ∈ C,定义
eπ ( x) = π ( x)
d π ( y ) = π −1 ( y )
这里π 和 π 互为逆置换。
−1
注:由于所有可能的置换有26!,故代换密码的密钥空间大小为 26!。
基本目的:面对攻击者Oscar,在Alice和Bob的 通信双方之间应用不安全信道通信时,设法保 证通信安全。 发送方:Alice 接收方:Bob 明文(Plaintext):待发送的信息或消息。 密钥(Key):用于加密明文的变换法则的参数。 密文(Ciphertext):明文加密后的结果。
保密通信的一般机制
本章小结
密码学的基本概念 典型的古典密码体制(加、解密算法,密 钥空间,安全性) 古典密码体制的两个基本思想:代换和 置换 常用的密码分析攻击技术及其分类
密码体制定义(续)
关于密码体制需要做以下几点说明: 1. 密码体制的基本条件:对任意的 key ∈ K ,存在一个加密规则 ekey ∈ E 和相应的解密规则 d key ∈ D ,使得对任意的明文 x ∈ M ,e key ( x ) ∈ C且 d key (e key ( x )) = x。 2. 在以上密码体制的定义中,最关键的条件是加密过程 ekey 的可 逆性,即密码体制不仅能够对明文 x 应用 ekey进行加密,而且应 该可以使用相应的 d key 对得到的密文进行解密,从而恢复出明文。 3. 密码体制中的机密函数 ekey 必须是一个一一映射。要避免出现 多个明文对应同一密文的情况,否则在解密过程将无法准确确定 明文。
信息安全工程师教程内1.5节专业英语翻译

Cryptography is the practice and study of hiding information. In modern times, cryptography is considered a branch of both mathematics and computer science, and is affiliated closely with information theory,computer security, and engineering. Cryptography is used in applications present in technologically advanced societies; examples include the security of ATM cards, computer passwords,and electronic commerce, which all depend on cryptography.密码学是信息隐藏的实践与研究。
现代密码学被认为是数学和计算机科学的一个分支,它与信息论、计算机安全和工程密切相关。
密码技术被应用于技术先进的社会中,例如A TM卡、计算机密码和电子商务的安全,这些都依赖于密码学。
(1 )TerminologyUntil modem times, cryptography referred almost exclusively to encryption, the process of converting ordinary information (plaintext) into unintelligible gibberish (i.e., ciphertext). Decryption is the reverse, moving from unintelligible ciphertext to plaintext. A cipher (or cypher) is a pair of algorithms which creates the encryption and the reversing decryption. The detailed operation of a cipher is controlled both by the algorithm and, in each instance, by a key. This is a secret parameter (ideal以known only to the communicants) for a specific message exchange context. Keys are important, as ciphers without variable keys are trivially breakable and therefore less than useful for most purposes. Historically, ciphers were often used directly for encryption or decryption, without additional procedures such as authentication or integrity checks.直到近代,加密提到几乎完全加密,普通的转换过程的信息(明文)到不知所云胡言乱语(即密文)。
网络信息安全-密码学基本概念
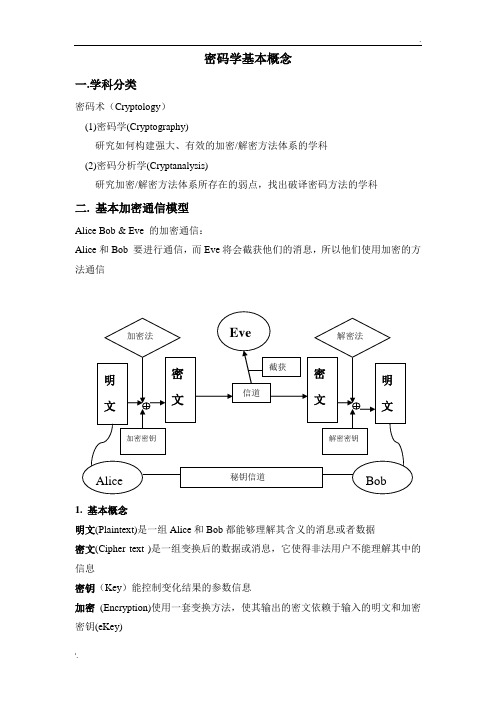
密码学基本概念一.学科分类密码术(Cryptology)(1)密码学(Cryptography)研究如何构建强大、有效的加密/解密方法体系的学科(2)密码分析学(Cryptanalysis)研究加密/解密方法体系所存在的弱点,找出破译密码方法的学科二. 基本加密通信模型Alice Bob & Eve 的加密通信:Alice和Bob 要进行通信,而Eve将会截获他们的消息,所以他们使用加密的方法通信1. 基本概念明文(Plaintext)是一组Alice和Bob都能够理解其含义的消息或者数据密文(Cipher text )是一组变换后的数据或消息,它使得非法用户不能理解其中的信息密钥(Key)能控制变化结果的参数信息加密(Encryption)使用一套变换方法,使其输出的密文依赖于输入的明文和加密密钥(eKey)解密(Decryption)使用一套变换方法,使其输出的明文依赖于输入的密文和解密密钥(dKey)用符号表示加密:Cipher text = Encryption (Plaintext, eKey)解密:Plaintext = Decryption (Cipher text, dKey)2. 体系划分以加密密钥和解密密钥的关系来划分为体系:1。
如果加密密钥(eKey)和解密密钥(dKey)相同,或者实质上相同,这样的加密体系称为单钥或对称密钥体系2。
如果加密密钥(eKey)和解密密钥(dKey)不相同,或者很难从其中一个密钥推导出另一个密钥,这样的加密体系称为双钥或非对称密钥体系三. 实例1 对称密钥在经典加密方法中使用两种类型进行变换:(1)换位法(Permutation cipher / Transposition cipher):明文中的每个字母或符号没有改变,但它们在密文中的位置进行了重新排列。
经典换位加密法(2)替换法(Substitution cipher):将明文中每个字母、数字、符号按一定规则替换成另外一个符号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chosen-Ciphertext Securitywithout RedundancyDuong Hieu Phan and David Pointcheval´Ecole normale sup´e rieure–D´e pt d’informatique45rue d’Ulm,75230Paris Cedex05,France{duong.hieu.phan,david.pointcheval}@ens.frAbstract.We propose asymmetric encryption schemes for which all ci-phertexts are valid(which means here“reachable”:the encryption func-tion is not only a probabilistic injection,but also a surjection).We thusintroduce the Full-Domain Permutation encryption scheme which usesa random permutation.This is thefirst IND-CCA cryptosystem basedon any trapdoor one-way permutation without redundancy,and moreinterestingly,the bandwidth is optimal:the ciphertext is over k morebits only than the plaintext,where2−k is the expected security level.Thereafter,we apply it into the random oracle model by instantiatingthe random permutation with a Feistel network construction,and thususing OAEP.Unfortunately,the usual2-round OAEP does not seem tobe provably secure,but a3-round can be proved IND-CCA even withoutthe usual redundancy m 0k1,under the partial-domain one-wayness ofany trapdoor permutation.Although the bandwidth is not as good as inthe random permutation model,absence of redundancy is quite new andinteresting:many implementation risks are ruled out.1IntroductionBy now,the widely admitted appropriate security level for asymmetric encryp-tion is the so-called chosen-ciphertext security(IND-CCA):that is actually the semantic security[16]against adaptive chosen-ciphertext attacks[21].For achiev-ing semantic security,even in the basic chosen-plaintext scenario,the encryption algorithm must be probabilistic,which means that a given plaintext(with afixed public key)should be possibly encrypted in many different ways(at least2k dif-ferent ciphertexts if2−k is the expected security level).This naturally implies an expansion:the ciphertext is at least over k more bits than the plaintext.OAEP achieves the optimal bound if one considers IND-CPA only,but fails when con-sidering IND-CCA[5,15].The general idea for designing cryptosystems which are secure in the sense of chosen-ciphertext security is indeed to make the decryption oracle useless by making the creation of new“valid”ciphertexts(which are not produced by actually encrypting some known plaintexts)impossible.The general approach is thus to add some redundancy either to the plaintext before encrypting[5]or in a tag appended to the ciphertext[4,18].The former method can be named ih(Ed.):ASIACRYPT2003,LNCS2894,pp.1–18,2003.c International Association for Cryptologic Research20032Duong Hieu Phan and David Pointcheval“encode-then-encrypt”,with a randomized bijective encoding(padding),and a trapdoor injective one-way function as encryption[5,23,8].The latter is more like a key-encapsulation technique combined with a MAC of the plaintext,the ciphertext and/or the ephemeral key[10,1,18].For symmetric encryption schemes,Desai[11]avoids the overhead due to the MAC or redundancy by using variable-length input PRF,variable-length output PRF(unbalanced Feistel paradigm)or variable-length input super-PRF(encode-then-encipher).The proposed schemes are chosen-ciphertext secure,without re-dundancy and the ciphertext expansion is smaller than for any other provably secure scheme.In the present paper,inspired by this idea(encode-then-encipher),we con-sider the case of asymmetric encryption,by using a public random permutation which is clearly a bijective encoding,and this leads to thefirst IND-CCA scheme without any redundancy.More interestingly,the bandwidth of this scheme is optimal.On the other hand,the security proof holds in the strong and ideal“random permutation model”.Such a scheme in a weaker model(the random oracle model or the standard model)would be better.The second part of this paper is devoted to this goal.We use the construction of OAEP but with3rounds,instead of 2,and we can prove that such a scheme is IND-CCA and all the ciphertexts are reachable by the encryption algorithm,and are thus valid(or almost all in the most general case).The rest of the paper is organized as follows:Wefirst briefly recall the security notions for asymmetric encryption;then we present the FDH encryption and we prove that it is IND-CCA secure with any trapdoor one-way permutation. Finally we consider the random oracle model,in which we propose a3-round OAEP for which(almost)any ciphertext is valid(i.e.,reachable)and we show that it achieves IND-CCA under the partial-domain one-wayness of any trapdoor permutation[15].2Public Key EncryptionThe aim of a public-key encryption scheme is to allow anybody who knows the public key of Alice to send her a message that she will be the only one able to recover,thanks to her private key.2.1DefinitionsA public-key encryption schemeπis defined by the three following algorithms:–The key generation algorithm G.On input1k,where k is the security param-eter,the algorithm G produces a pair(pk,sk)of matching public and private keys.–The encryption algorithm E.Given a message m and a public key pk,E pk(m) produces a ciphertext c of m.This algorithm may be probabilistic(involving random coins r∈R,and then denoted E pk(m;r).)–The decryption algorithm D.Given a ciphertext c and the secret key sk,D sk(c)gives back the plaintext m.Chosen-Ciphertext Security without Redundancy3 2.2Security NotionsThe widely admitted security notion for encryption schemes is the so-called semantic security[16](a.k.a.polynomial security/indistinguishability of encryp-tions):if the attacker has some a priori information about the plaintext,the view of the ciphertext should not increase this information.This security notion requires the computational impossibility to distinguish between two messages, chosen by the adversary itself,which one has been encrypted,with a probabil-ity significantly better than one half:its advantage Adv indπ(A),as defined below where the adversary A is seen as a2-stage Turing machine(A1,A2),should be negligible.Adv indπ(A)=2×Prb,r(pk,sk)←G(1k);(m0,m1,s)←A1(pk)c=E pk(m b;r):A2(m0,m1,s,c)=b−1.Another notion has been thereafter defined,the so-called non-malleability[12], but this notion is equivalent to the above one in some specific scenarios[7]. Moreover,it is equivalent to the semantic security[3]in the most interesting scenarios,described below.Indeed,an attacker can play many kinds of attacks:it may just have access to public data,and then encrypt any plaintext of its choice(chosen-plaintext attacks),or have access to extra information,modeled by various oracles.In this model,the strongest oracle is definitely the decryption algorithm,which can be queried on any ciphertext,except the challenge ciphertext(adaptive/non-adaptive chosen-ciphertext attacks[17,21]).A general study of these security notions and attacks has been driven in[3], we therefore refer the reader to this paper for more details.Actually,one conclu-sion is that the strongest security level is the so-called chosen-ciphertext security, which is the semantic security(IND)under adaptive chosen-ciphertext attacks (CCA),hence the notation IND-CCA,also known as IND-CCA2,to be compared to IND-CCA1,which captures lunchtime attacks[17]only.2.3Secure DesignsThe expected security level is thus IND-CCA,which is now required to be prov-ably achieved before any practical use.The last ten years have seen several practical proposals which provide this strong security level.Thefirst,and most famous one,is definitely OAEP[5],a generic conversion proposed by Bellare and Rogaway,which applies to any trapdoor partial-domain one-way permutation, such as RSA,in the random oracle model[15].Some variants have been recently proposed,which either apply to particular cases(SAEP,SAEP+[8])or more general ones(OAEP+[23]).But they all add some redundancy in the plaintext before encrypting it:a ciphertext that is not properly generated,without know-ing the plaintext,is valid with negligible probability only.The latter property had been formally defined by the plaintext-awareness notion[5,3].Granted it, a decryption oracle does not provide any information.4Duong Hieu Phan and David PointchevalSome other paddings have also been proposed to apply to more general fami-lies of functions,which are not necessarily one-to-one:Fujisaki and Okamoto[13, 14],Pointcheval[20]and Okamoto and Pointcheval[18].Once again,chosen-ciphertext security is achieved granted redundancy,but in the ciphertext:only properly generated ciphertexts(with some known plaintexts)have a chance to be valid:plaintext-awareness.3FDP:Full-Domain Permutation EncryptionIn the same vein as the Full-Domain Hash signature[6,9],we suggest the Full-Domain Permutation encryption,in which one applies a random permutation to the message(and the random coins)before encrypting it with the trapdoor one-way permutation.We therefore obtain thefirst cryptosystem which achieves chosen-ciphertext security,without redundancy:any ciphertext is valid,and the bandwidth is optimal.3.1DescriptionThe FDP-encryption is quite simple,since it uses a random permutation P (which is a bijective random oracle,or an ideal-cipher with a particular key, say0.See also[22]).The key generation algorithm selects a trapdoor one-way permutationϕpk(and its inverseψsk,granted the trapdoor sk)over{0,1}k+ ,and a random permutation P over the same space—{0,1} ×{0,1}k is identified to {0,1} +k.The public key pk thus defines the permutationϕpk,while the privatekey sk defines the inverseψsk ofϕpk.Then,E pk(m;r)=ϕpk(P(m,r))D sk(c)=m,where(m,r)=P−1(ψsk(c)). The space of the plaintexts is{0,1} ,while the space of the random coins r is {0,1}k.Note that both P and P−1are public permutations.Note that usual trapdoor one-way permutations are not on a binary set,as it will be discussed in a more extensive way in the following.Anyway,just doubling the computational cost,on average,one easily gets such a particular case from any permutation over an interval:[2]suggested an iterated version.3.2Security ResultAs already said,thefirst advantage of this scheme is that any ciphertext is valid: any ciphertext can be decrypted into a plaintext,furthermore any ciphertext can also be reached by the encryption algorithm.The second important advantage comes from the security result given below:it provides chosen-ciphertext secu-rity under the intractability of invertingϕ,with a security level in2k,with an overhead of k bits(the random coins).This means that the bandwidth is opti-mal:contrary to OAEP or OAEP+which need an overhead of at least2k bits (the random coins and the redundancy),for a similar security level.Of course, this remark only applies to the most general case where ≥k(e.g.,k=80and k+ =1024.)Chosen-Ciphertext Security without Redundancy5 Theorem1.Let A be any chosen-ciphertext adversary againstϕ-FDP,within timeτ.After q p and q d queries to the permutation oracles and the decryption oracle respectively,Adv ind-ccaπ(A)≤2×Succ owϕ(τ+2q p×Tϕ)+2×(q p+q d+1)22k++q p2k+(q d+1)22where Tϕis the time complexity for evaluatingϕ. Let us briefly recall that for any algorithm A,Succ owϕ(A)=Prpk,x∈{0,1}k+ [A(ϕpk(x))=x],and Succ owϕ(τ)=max|A|≤τSucc owϕ(A).3.3Sketch of the ProofThe goal of the proof is to simulate the oracles P,P−1,and D sk in such a way that the adversary can not distinguish the simulations from the real oracles.In the simulation,the decryption answer for a ciphertext that has not been obtained before is a new random value(and independent with others).We then have to keep the simulation of the random permutation consistent.On the other hand, the challenge is made independent with the plaintexts m0and m1:the adversary has no advantage.The proof follows by successively modifying the rules involved in the(perfect) simulation where the oracles P and P−1arefirst simulated by using a perfectly random permutation P and its inverse P−1.The last game provides a simulation of D sk,without invertingϕpk.Anyway,the simulation remains almost perfect unless the adversary asks the pre-image viaϕpk of the challenge ciphertext to the random permutation P−1: it thus helps to invertϕ.The complete proof can be found in the full version of this paper[19].4The Random Oracle Model and OAEPThe above result is not so surprising,but the optimal bandwidth is a very good news.However the proof requires a full-domain random permutation,which is hard tofind:practical block-ciphers have smaller block sizes.In this section,we present an instantiation of this random permutation,in the random oracle model only.The counter-part will be the need of a stronger assumption about the trap-door one-way permutation:with a3-round OAEP,a trapdoor partial-domain one-way permutation leads to an IND-CCA cryptosystem,without redundancy.4.1The2-Round OAEP CaseBefore studying the3-round OAEP,let usfirst consider the more classical2-round OAEP which can be described as follows:we use two hash functions G and6Duong Hieu Phan and David PointchevalH before encrypting with a trapdoor one-way permutationϕpk.More precisely, for encrypting a message m,one randomly chooses r,and computes s and t:s=m⊕G(r)t=r⊕H(s).Then,the ciphertext is c=ϕpk(s,t).For decryption,one computes(s,t)=ψsk(c)r=t⊕H(s)m=s⊕G(r).The usual way to prove the security of a scheme is to exploit an adversary to break the assumption(for instance,the partial-domain one-wayness of the permutationϕpk).For that,we must simulate all the resources that the attacker can access,namely,the oracles G,H but also the decryption oracle D sk.For the above2-round OAEP,the decryption oracle does not seem simulatable.The following attack game uses the same arguments as the counter-example shown by Shoup against the original OAEP security result[23].Let us consider an attacker who chooses s,s and calls for H to get respectively h=H(s)and h =H(s ). Then it chooses t and computes c=ϕpk(s,t).If it asks c to D sk,it gets the corresponding plaintext m.Then,it computes t =t⊕h⊕h and c =ϕpk(s ,t ). If it asks c to D sk,it gets the corresponding plaintext m .One can easily see that,since r =r,the relation m⊕m=s⊕s should hold.But if the simulator can not detect that r =r,it can not output a consistent value for m .Unfortunately,we did notfind any easy way to make a consistent simulation for the2-round OAEP.But a3-round is more promising.4.2Description of the3-Round OAEPThe public key is any trapdoor(partial-domain)one-way bijectionϕpk from a set E to a set F,while the private key is the inverseψsk.For the sake of generality, we do not stick to binary sets(of the form{0,1}k):we just assume that there is an integerκsuch that:{0}κ×{0,1}k+ ⊆E⊆{0,1}κ+k+ (identified to{0,1}κ×{0,1}k×{0,1} ). However,note that in the case that E=0κ {0,1}k+ we won’t get(as an-nounced)a surjective encryption.But contrary to all the previous IND-CCA schemes,the proportion of valid ciphertexts(i.e.,which are reachable)is greater than1/2κ,which is not negligible:for efficient applications with RSA,it can be equal to1/2,or even1(by loosing a factor2in efficiency,one can getκ=0, with the iterated-RSA[2]).The encryption and decryption algorithms use three hash functions:F,G,H (assumed to behave like random oracles in the security analysis):F:{0,1}k→{0,1} G:{0,1} →{0,1}k H:{0,1}k+κ→{0,1} .Encryption Algorithm:The space of the plaintexts is M={0,1} ,the en-cryption algorithm uses random coins in R={0,1}k,and outputs a ciphertext c into F:on a plaintext m∈M,and a random r∈R,one computess=m⊕F(r)t=r⊕G(s)u=s⊕H(0κ t)c=ϕpk(0κ,t,u).Chosen-Ciphertext Security without Redundancy7 Decryption Algorithm:On a ciphertext c,onefirst computes(B,t,u)=ϕsk(c),where B∈{0,1}κ,t∈{0,1}k,u∈{0,1} and thens=u⊕H(B t)r=t⊕G(s)m=s⊕F(r).4.3Security ResultAbout the3-round OAEP,one can claim the following security result,which states that the IND-CCA security level is achieved under the(set)partial-domain one-wayness of the trapdoor permutationϕ[15].Theorem2.Let A be any chosen-ciphertext adversary against the3-round OAEP construction with the trapdoor permutation familyϕ,within timeτ.After q f,q g,q h and q d queries to the random oracles F,G and H,and the decryption oracle respectively,Adv ind-ccaπ(τ)≤2κ×Succ s-pd-owϕ(τ+q g·q h×Tϕ+q d·T lu,q h) q f+q g+2κ×q d(2q g+q d)+q d(3q f+2q d)where Tϕis the time complexity for evaluatingϕ,and T lu is the time complexity for a look up in a list.Let us recall the definition of the(set)partial-domain one-wayness in our partic-ular case,where A is any algorithm which outputs a subset of{0,1}k of size q:Succ s-pd-owϕ(A,q)=Prpk,(B,t,u)∈E[t∈A(ϕpk(B,t,u))]and Succ owϕ(τ,q)=max|A|≤τSucc s-pd-owϕ(A,q),is small for any reasonable time boundτ.4.4Sketch of the ProofThe goal of the proof is again to simulate the oracles.For simulating the random oracles,we use lists as usual to store the known answers.We simulate the de-cryption oracle as follows:when we receive a query y,either the corresponding s and t have both been asked to G and H,we can extract m,or one of them has not been asked,we can safely answer a random plaintext.However,such a plaintext-ciphertext relation implicitly defines several relations about the ran-dom oracles F,G and H.We show that it is still possible to answer consistently. The challenge ciphertext also implicitly defines relations.We show that possible inconsistencies with the latter relations can not be detected by the adversary unless it has partially inverted the functionϕpk on the challenge ciphertext.The proof is provided by a sequence of games,but for clarity reasons,we briefly explain only the distances between two consecutive games.The formal and full proofs are provided in the Appendix A.8Duong Hieu Phan and David PointchevalGame G0:The adversary is fed with the public key pk,and outputs apair of messages(m0,m1).Next a challenge ciphertext is produced byflipping a coin b and producing a ciphertext c of m =m b.This ciphertext comes froma random r ←{0,1}k and c =E(m b,r )=ϕpk(0κ,t,u).On input c ,A2 outputs bitb in the time t.We denote by S0the event b =b and use the samenotation S n in any game G n below.Note that the adversary is given access tothe decryption oracle D sk during both steps of the attack.The adversary canalso ask the random oracles F,G,and H.Game G1:The simulation in this game is presented on the Figure1.Wesimulate the way that the challenge c is generated as the challenger would do,and we simulate the random oracles F,G,and H,as well as the decryptionoracle D sk,by maintaining lists F-List,G-List,H-List and D-List to deal withidentical queries,since they all are deterministic.Since the simulation is perfect,we directly derive thatPr[S1]=Pr[S0].(1) Game G2:We manufacture the challenge c independently of anything else. Rule Chal(2)Choose randomly ahead of time c+R←F and set c =c+.Lemma3.Let us note(B+,t+,u+)the pre-image of the challenge c+.We de-note by AskH2the event that B+ t+has been asked to H.Then,Pr[S1]≤12+q f2k+q g2+2κ×Pr[AskH2].(2)Proof(Full proof in the Appendix A.1).The main idea in simulating this game is that we make the components of the challenge c (namely r ,f ,s ,g ,t , h ,u and c )independent to m .We can do this by choosing ahead of time random values for r ,s ,and t ,and we can see that a difference occurs when one of these values is asked to the corresponding oracle.On the other hand, when the challenge is independent to m ,the attacker has only the chance of one half to guess the bit b. Game G3:In this game,we modify the simulation of the decryption oracle, by outputting a random message when the ciphertext has not been“correctly”encrypted.We thereafter define in a consistent way the values of the random oracles:Rule Decrypt-TnoS(3)Choose m R←{0,1} and g R←{0,1}k,then define r=t⊕g and f=m⊕s.Add(r,f)in F-List,and(s,g)in G-List.Rule Decrypt-noT(3)Choose m R←{0,1} ,h R←{0,1} and g R←{0,1}k,then define s=u⊕h,r=t⊕g and f=m⊕s.Add(r,f)in F-List,(s,g)in G-List,and(B,t,h)in H-List.Chosen-Ciphertext Security without Redundancy9F ,G a n d H O r a c l e sQuery F (r ):if a record (r,f )appears in F -List ,the answer is f .Otherwise the answer f is chosen randomly:f ∈{0,1}k and the record (r,f )is added in F -List .Query G (s ):if a record (s,g )appears in G -List ,the answer is g .Otherwise the answer g is chosen randomly:g ∈{0,1} and the record (s,g )is added in G -List .Rule EvalGAdd (1)Do nothingQuery H (B t ):if a record (B,t,h )appears in H -List ,the answer is h .Otherwise the answer h is chosen randomly:h ∈{0,1}k and the record (B,t,h )is added in H -List .D O r a c l e Query D sk (c ):if a record (m,c )appears in D -List ,the answer is m .Otherwise the answer m is defined according to the following rules: Rule Decrypt -Init (1)Compute (B,t,u )=ψsk (c );Look up for (B,t,h )∈H -List :–if the record is found,compute s =u ⊕h .Look up for (s,g )∈G -List :•if the record is found Rule Decrypt -TS (1)h =H (B t ),s =u ⊕h,g =G (s ),r =t ⊕g,f =F (r ),m =s ⊕f .•otherwise Rule Decrypt -TnoS (1)same as rule Decrypt -TS (1).–otherwiseRule Decrypt -noT (1)same as rule Decrypt -TS (1).Answer m and add (m,c )to D -List .C h a l l e n g e rFor two messages (m 0,m 1),flip a coin b and set m =m b ,choose randomly r ,then answer c ,whereRule Chal (1)f =F (r ),s =m ⊕f ,g =G (s ),t =r ⊕g ,h =H (0κ t ),u =s ⊕h .Compute c =ϕpk (0κ,t ,u ).Fig.1.Formal Simulation of the IND-CCA Game against 3-OAEP.10Duong Hieu Phan and David Pointcheval Lemma4.|Pr[AskH3]−Pr[AskH2]|≤q d(q g+q d)2+2q d(q f+q d)2k.(3)Proof(Full proof in the Appendix A.2).In the proof,one successively modifies the simulation of the decryption oracle,just changing the order of elements to be randomly chosen,so that the decryption of a ciphertext which has not been correctly encrypted is a truly random plaintext. Game G4:In this game,we delay the explicit definitions of some oracle answers implicitly defined by some plaintext-ciphertext relations:we do not in-troduce them during the simulation of the decryption oracle,but when s is asked to G.Some problems may appear if the implicitly defined answers are asked be-fore G(s)is queried.Rule Decrypt-TnoS(4)Choose m R←{0,1} .Rule Decrypt-noT(4)Choose m R←{0,1} .Rule EvalGAdd(4)Look up for(B,t,h)∈H-List and(m,c)∈D-List such thatc=ϕpk(B,t,h⊕s).If the record is found,we compute r=t⊕g and f=m⊕s,andfinally add(r,f)in F-List.Lemma5.|Pr[AskH4]−Pr[AskH3]|≤q d·q f2k+q d·q g2.(4)Proof(Full proof in the Appendix A.3).Since we don’t store anymore(r,f), (s,g),(B,t,h),inconsistencies could occur when B t,s or r are asked.For solving this problem,we modify the rule EvalGAdd by defining in a consistent way F(r)at the moment that s is asked to G.But there is still a problem if r is asked before G(s)is queried,or if s is asked before H(B t)is queried. Game G5:We now complete the simulation of the oracle D sk.We don’t ask any query toψsk.Intuitively,if both B t and s have been asked,we can easily find them,and then m.Otherwise,we give a random answer as in the game G4.Rule Decrypt-Init(5)Look up for(B,t,h)∈H-List and(s,g)∈G-List such thatϕpk(B,t,s⊕h)=c.–if the record is found,we furthermore define u=s⊕h.–otherwise,we take B=⊥,t=⊥,u=⊥.Rule Decrypt-TS(5)r=t⊕g,f=F(r),m=s⊕f.The two games G5and G4are perfectly indistinguishable.In fact,in thefirst case,nothing is modified and in the second case,by making B=⊥,t=⊥,u=⊥, the answer of the decryption oracle for the question c will be a random m as in the game G4:Pr[AskH5]=Pr[AskH4].(5) Simply outputting the list of queries to H during this game,one gets:Pr[AskH5]≤Succ s-pd-owϕ(τ ,q h),(6) whereτ is the running time of the simulation in this game:τ ≤q g·q h×Tϕ+q d×T lu.We can indeed perform the simulation granted an additional list GH-List which contains all the tuples(B,t,h,s,g,y)where(B,t,h)∈H-List, (s,g)∈G-List and y=ϕpk(B,t,s⊕h).This concludes the proof of the Theorem.4.5Special CasesIn the particular but classical case whereκ=0and k≤ ,one can claim Theorem6.Let A be any chosen-ciphertext adversary against the3-round OAEP construction with the trapdoor permutation familyϕ,within timeτ.After q o and q d queries to the random oracles and the decryption oracle respectively,Adv ind-ccaπ(τ)≤Succ s-pd-owϕ(τ+q2o×Tϕ+q d×T lu,q o)+2q o+q d(5q o+2q d)2kwhere Tϕis the time complexity for evaluatingϕ,and T lu is the time complexity for a look up in a list.5ConclusionWe have described the Full-Domain Permutation encryption which is IND-CCA without redundancy and provides an optimal bandwidth.In the random oracle model,we have shown that the absence redundancy can be obtained by consid-ering the3-round OAEP construction.However,the bandwidth is not optimal, and the security relies on the strong partial-domain one-wayness assumption. AcknowledgmentsWe thank Anand Desai for fruitful discussions.References1.M.Abdalla,M.Bellare,and P.Rogaway.The Oracle Diffie-Hellman Assumptionsand an Analysis of DHIES.In CT–RSA’01,LNCS2020,pages143–158.Springer-Verlag,Berlin,2001.2.M.Bellare,A.Boldyreva,A.Desai,and D.Pointcheval.Key-Privacy in Public-Key Encryption.In Asiacrypt’01,LNCS2248,pages566–582.Springer-Verlag, Berlin,2001.3.M.Bellare,A.Desai,D.Pointcheval,and P.Rogaway.Relations among Notionsof Security for Public-Key Encryption Schemes.In Crypto’98,LNCS1462,pages 26–45.Springer-Verlag,Berlin,1998.4.M.Bellare and P.Rogaway.Random Oracles Are Practical:a Paradigm for De-signing Efficient Protocols.In Proc.of the1st CCS,pages62–73.ACM Press,New York,1993.5.M.Bellare and P.Rogaway.Optimal Asymmetric Encryption–How to Encryptwith RSA.In Eurocrypt’94,LNCS950,pages92–111.Springer-Verlag,Berlin, 1995.6.M.Bellare and P.Rogaway.The Exact Security of Digital Signatures–How toSign with RSA and Rabin.In Eurocrypt’96,LNCS1070,pages399–416.Springer-Verlag,Berlin,1996.7.M.Bellare and A.Sahai.Non-Malleable Encryption:Equivalence between TwoNotions,and an Indistinguishability-Based Characterization.In Crypto’99,LNCS 1666,pages519–536.Springer-Verlag,Berlin,1999.8. D.Boneh.Simplified OAEP for the RSA and Rabin Functions.In Crypto’01,LNCS2139,pages275–291.Springer-Verlag,Berlin,2001.9.J.-S.Coron.On the Exact Security of Full-Domain-Hash.In Crypto’00,LNCS1880,pages229–235.Springer-Verlag,Berlin,2000.10.R.Cramer and V.Shoup.A Practical Public Key Cryptosystem Provably Secureagainst Adaptive Chosen Ciphertext Attack.In Crypto’98,LNCS1462,pages 13–25.Springer-Verlag,Berlin,1998.11. A.Desai.New Paradigms for Constructing Symmetric Encryption Schemes SecureAgainst Chosen-Ciphertext Attack.In Crypto’00,LNCS1880,pages394–412.Springer-Verlag,Berlin,2000.12. D.Dolev,C.Dwork,and M.Naor.Non-Malleable Cryptography.In Proc.of the23rd STOC.ACM Press,New York,1991.13. E.Fujisaki and T.Okamoto.How to Enhance the Security of Public-Key Encryp-tion at Minimum Cost.In PKC’99,LNCS1560,pages53–68.Springer-Verlag, Berlin,1999.14. E.Fujisaki and T.Okamoto.Secure Integration of Asymmetric and SymmetricEncryption Schemes.In Crypto’99,LNCS1666,pages537–554.Springer-Verlag, Berlin,1999.15. E.Fujisaki,T.Okamoto,D.Pointcheval,and J.Stern.RSA–OAEP is Secure underthe RSA Assumption.Journal of Cryptology,2003.To appear.16.S.Goldwasser and S.Micali.Probabilistic Encryption.Journal of Computer andSystem Sciences,28:270–299,1984.17.M.Naor and M.Yung.Public-Key Cryptosystems Provably Secure against ChosenCiphertext Attacks.In Proc.of the22nd STOC,pages427–437.ACM Press,New York,1990.18.T.Okamoto and D.Pointcheval.REACT:Rapid Enhanced-security AsymmetricCryptosystem Transform.In CT–RSA’01,LNCS2020,pages159–175.Springer-Verlag,Berlin,2001.。
