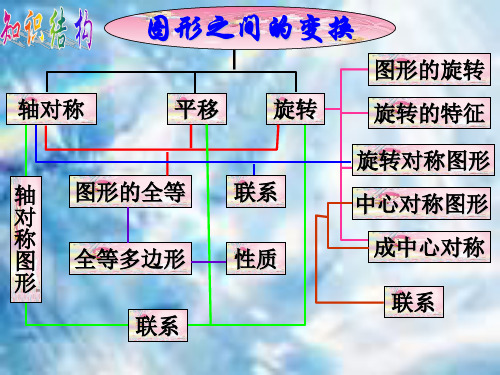
《图形的平移与旋转》复习课
图形的平移与旋转复习课导学案

第三章《图形的平移与旋转》复习课学案学习目标1、掌握平移的定义及性质;会利用平移的性质作图;2、掌握旋转的定义及性质,会利用旋转的性质作图;3、知道一个基本图案通过变换得到一个图形;学习重点:简单图形的平移与旋转作图学习难点:图形的平移与旋转与几何做题自主探学:1、平移的定义:在平面内,将__________沿__________移动___________,这样的_________称为平移,平移不改变图形的____和______,只改变图形的________。
2、平移的性质:①____________________________;②_________________________;③____________________________。
3、平移作图的条件:__________________; _____________。
4、旋转的定义:在平面内,将__________绕_________沿__________转动___________,这样的_________称为旋转,旋转不改变图形的____和______,只改变图形的________。
5、旋转的性质:①___________________________;②__________________________;③___________________________________。
6、旋转作图的条件:__________________; _____________;_______________。
合作研学:例1、如图3所示,等边三角形ABC中,边长为4cm,BD AC⊥于D,将△ABC沿射线BD方向平移,得到△EDF,那么平移的距离是()A.4cm B.23cm C.43cm D.3cm例2、如图10所示,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A逆时针旋转到△ACD'的位置,则ADD'∠的度数是()A.25°B.30°C.35°D.45°例3、如图19所示,将图形向下平移4个方格,再向左平移3个方格.例4、画图,先将△ABC绕点C按逆时针旋转900,得到△EFC,再将△EFC向右平移7个单位,得到△E1F1C1。
第二章《图形的运动》第三课:平移与旋转 期末学业考复习 三年级数学下册(解析版)北师大版
北师大版三年级下册重难点题型同步训练第二章《图形的运动》第三课:平移与旋转一、单选题1.(2020模拟三上·武城期末)图形平移后得到的图形是()。
A. B. C. D.【答案】 C【解析】【解答】图形平移后得到的图形是。
故答案分为:C。
【分析】注意平移不改变图形的形状和大小,平移后的图形与原图形上对应点连接的线段平行(或在同一条直线上)且相等。
2.(2020模拟三上·宁津期中)下面图案中,()是通过下图平移得到的。
A. B. C.【答案】 A【解析】【解答】解:平移不改变图形的形状和方向,所以A的图案是通过已知图形平移得到的。
故答案为:A。
【分析】平移不改变图形的形状和方向。
3.下图中,甲、乙两图的周长相比,结果是()。
A. 甲长B. 乙长C. 一样长【答案】 C【解析】【解答】根据图形可以看出,甲乙两图的周长一样长。
故答案为:C。
【分析】利用平移法,把甲图的线段向上,向右平移,刚好是一个长方形,和乙图一样。
4.(2020模拟三下·龙华期末)地球自转的运动现象是()。
A. 旋转B. 平移C. 对称【答案】 A【解析】【解答】解:地球自转的运动现象是旋转。
故答案为:A。
【分析】旋转是物体绕着一个中心点做圆周运动;平移是物体沿着一条直线运动。
5.下面是做平移运动的是()。
A. B. C.【答案】 C【解析】【解答】拉抽屉做的是平移运动,风车和轮子是旋转运动。
故答案为:C。
【分析】旋转就是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
旋转改变的是图形的方向,不改变图形的形状和大小;平移就是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动。
平移不改变图形的形状和大小,改变的是图形的位置,平移可以不是水平的。
6.(2020模拟三下·龙华期中)轴对称、旋转、平移这三种图形变换的共同点是()。
A. 都是沿一定方向移动了一定的距离B. 都不改变图形的形状和大小C. 对应线段互相平行【答案】 B【解析】【解答】解:轴对称、旋转、平移这三种图形变换的共同点是都不改变图形的形状和大小。
平移与旋转的概念复习
1 1 ·
1 1
·
中心对称图形是旋转对称图形的一种特殊形式. 中心对称图形是旋转对称图形的一种特殊形式.
把一个图形绕着某一 点旋转180 点旋转1800,如果它 能够和另一个图形重 合,我们就说这两个 成中心对称 图形成中心对称。这 个点叫做对称中心。 这两个图形中的对应 点叫做关于中心的对
B C A O C´ ´ B´ ´ A´ ´
C´ ´
O C
轴对称、 轴对称、平移与旋转三种图形 变换的异同
相同点 轴对称 平 旋 移 转
1.对应线段 1.对应线段 相等, 相等,对应角 相等, 相等,图形的 形状与大小 都没有发生 变化. 变化.
不同点 对折重合
直线方向、 直线方向、 对应线段平行 或在一条直线 按一定的角度、 按一定的角度、 2.移动的都 对应点到对应 2.移动的都 是线段和角. 是线段和角. 中心距离相等
对应点的连线也可能在一条直线上。 对应点的连线也可能在一条直线上。
C B´ ´
(如图中的BB′与CC′) 如图中的 B 与 C ) C´ ´ 当在一条直线上时,就不存在平行了。 当在一条直线上时,就不存在平行了。
点 在平面内,将一个图形绕一个定点 旋转一定的角度, 旋转一定的角度,这样的图形运动称为 一定的角度
称点。 称点。
1.对称点的连线都经过对称中心。(即,在一条 1.对称点的连线都经过对称中心。(即 对称点的连线都经过对称中心。( 直线上。) 直线上。) 2.对称点的连线被对称中心平分。 2.对称点的连线被对称中心平分 对称点的连线被对称中心平分。 B 3.反过来,如果两个 3.反过来 反过来, 图形的所有对应点的 C 连线都经过某一点, 连线都经过某一点, 并且都被该点平分, 并且都被该点平分, A A´ ´ O 那么这两个图形一定 C´ ´ 关于这一点成中心对 称。
中考数学总复习专项课件图形的对称平移与旋转

40
14.(2023·吉林)如图,在Rt△ABC中,∠C=90°,BC<AC.点D,E分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,CE=3,则BC的长为 9 .
9
15.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度,再向右平移1个单位长度,得到△A1B1C1,请画出△A1B1C1;
(2)请画出△ABC关于y轴对称的△A2B2C2.
16.如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
A
B
C
D
A
4.(2023·贵阳模拟)某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x轴、y轴的平面直角坐标系内,若点A的坐标为(-6,2),则点B的坐标为( A )
A.(6,2)
B.(-6,-2)
C.(2,6)
11.如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A逆时针旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的度数是 75° .
12.在平面直角坐标系中,点(4,5)绕原点O逆时针旋转90°,得到的点的坐标是 (-5,4) .
75°
第四章 图形的平移与旋转小结与复习

考点4中心对称图形
例6下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
A B C D
分析:利用中心对称图形的概念逐一对照筛选.
解:根据概念可判断选项A、B、C中的图形是轴对称图形,也是中心对称图形,选项D中的图形是轴对称图形,但不是中心对称图形.故选D.
正解:选B.
二、混淆旋转、轴对称
例2如图2所示,在正方形网格中,△OAB绕点O旋转后,顶点B的对应点为点
B′,试画出旋转后的三角形.
错解:如图3所示,△OA′B′即为所求.
剖析:此题错因是没按要求画图,画成了轴对称图形.在画旋转图形时,应注意关键点旋转后的位置.根据题意可知,旋转方向是顺时针方向,旋转角度是90°,那么点A也要同样沿顺时针方向旋转90°.
解:答案不唯一.各给出一种,如图8和图9.
说明:求解本题时要注意正确理解题目,要求仅限用七巧板中标号①,②,③的三块板.
误区点拨
一、平移概念理解有误
例1如图1,△FDE是由△ABC经过平移后得到的,则平移的距离是()
A.BC的长 B.BD的长
C.BE的长 D.CD的长
错解: 选D.
剖析:平移的距离是指对应点间线段的长度,所以平移的距离可以是BD、CE或AF.
8.
9.答案不唯一,以下提供三种图案.
一边上的中线平分其面积求解.
解:依题意,得(1)将△ABC向右平移3个单位长度得△A1B1C1,如图6所示.
(2)将△ABC的三个顶点A,B,C绕点O旋转180°后得A2,B2,C2,连接得到
△A2B2C2,如图6所示.
(3)因为点O是AA2的中点,而三角形一边上的中线平分三角形的面积,于是Байду номын сангаас过点
苏教版四年级下册数学《图形的旋转》平移旋转和轴对称培优说课教学复习课件

课件
学习目标
1.认识绕点顺时针或逆时针旋转90°的含义, 能在方格纸上画出把简单图形旋转90°后的图形。
2.认识对图形变化的兴趣,并进一步感受旋 转在生活中的应用。
讲授新课
与时针旋转方向相同的是顺时针旋转,相反的是逆时针旋转。
顺时针旋转
逆时针旋转
1、使学生通过观察、操作等活动,认识图形的旋转,能在方格纸上将简单 的图形旋转90°。 2、使学生经历从旋转的角度欣赏和设计图案的过程,体验旋转的应用价值, 发展初步的推理能力和空间观念。 3、使学生在认识旋转的过程中,感受与他人合作的乐趣,获得学习成功的 愉悦体验,增强对图形变换的兴趣。
与时针旋转方向相同的是顺时针, 与时针旋转方向相反的是逆时针。
栏杆的打开和关闭是怎样旋转的? 它们的运动有什么相同点和不同点?
逆时针方向
顺时针方向
O
O
课堂探究
探究一: 转杆的打开和关闭,分别是绕哪个点按什么方向旋转的?旋转了多少度?
转杆的打开是绕o顺时针旋转90°。 ②转杆的打开是绕o逆时针旋转90°
了。
(×)
7.一个图形顺时针旋转( 360 )°后,又回到原来的位置。
课后习题
1.与时针旋转方向相同的是(顺时)针旋转,方向相反的是(逆时) 针旋转。 2.高层电梯的运动是(平移),方向盘的运动是(旋转)。 3.从6时到12时,时针旋转了(180)度,分针走( 15 )分针旋 转90°。 4.在自然数中最小的奇数( 1 ),最小的偶数是( 2 ),最小 的合示,将小旗图围绕A点顺时针旋转90°。
【解析】以A点为中心,先将小旗的旗杆顺时针旋转90°,并画出旗杆,然后根据旗杆就直 接可以画出其他部分。
课堂练习
1. 如图所示:指针从“12”绕点O顺时针旋转(90度)到 “3”;指针从“3”绕点O顺时针旋转180°到(“9”);指针 从“5”绕点O顺时针旋转90° 到 (“8”)。
第三章 图形的平移与旋转小结与复习

第三章图形的平移与旋转小结与复习基础盘点1.图形的________简称平移,图形的平移是由_______和_______决定的.2.由平移特征可知,一个图形平移前后图形的_______和_______不变,•对应线段_______且________,对应角相等,对应点连成的线段相等.3.要作出平移后的图形,须知平移的________和_________.4.旋转:在平面内,将一个图形绕着一个沿着转动一个角度,这样的图形运动称为旋转.这个定点为,转动的角度为.图形的旋转有三个基本要素:、和.图形的旋转是由旋转中心和旋转角所决定的.5.旋转的性质:(1)旋转变化前后对应线段、对应角分别,图形的大小、形状.(2)旋转过程中,图形上每一点都绕旋转中心沿相同的方向旋转相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离都.考点呈现考点1 图形的平移例1 如图1,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为___.分析:由平移可知AC∥BE,所以∠CBE=∠C,再由条件,结合三角形的内角和即可求解.解:由平移,得AC∥BE,所以∠CBE=∠C.又因为∠CAB=50°,∠ABC=100°,所以∠C=180°-∠CAB-∠ABC=30°.即∠CBE的度数为30°. 图1说明:本题意在考查平移的知识,求解时要能结合平行线的性质与三角形的内角和知识.另外,本题也可以直接利用平角知识求得,即∠CBE=180°-∠ABC-∠EBD.例2 作图题:如图2,在方格纸中,将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.分析:根据平移的性质确定三角形平移后三个顶点的对应点,连接即可.解:依题意,可作出如图中所示的△A1B1C1.说明:依据条件准确地确定对应点是正确作图的关键.求解时要注意运用“以部分确定整体”的作图方法.考点2 图形的旋转例3分析图3-①,3-②,3-④中阴影部分的分布规律,按此规律在图3-③中画出其中的阴影部分.图3分析:由图3-①,3-②来看,图3-②是由图3-①绕着中心顺时针旋转90o得到的,图3-④是图3-②顺时针旋转180o得到的,由于本题按图3-①到图3-②的规律分布,因此图3-③是由图3-②顺时针旋转90o得到的.解:旋转后如图3-⑤.图4说明:注意细心观察图形的变化规律.DCBAEDCBAOC1B1A1CBA例4 如图4,点A ,B ,C ,D ,O 都在方格纸的格点上,若△COD 是由△AOB 绕点O 按逆时针方向旋转而得,则旋转的角度为( )A.30°B.45°C.90°D.135°分析:由于对应点与旋转中心的连线的夹角就是旋转角,所以∠BOD 和∠AOC 都是旋转角,由此,结合图形即可求解.解:由图可知,OB 、OD 是对应边,∠BOD 是旋转角,所以旋转角∠BOD =90°.故应选C. 说明:求解本题的关键是要根据题意,确定旋转中心、旋转方向和旋转角. 考点3 旋转作图例5 如图5,每个小方格都是边长为1个单位长度的小 正方形. (1)将△ABC 向右平移3个单位长度,画出平移后的△A 1B 1C 1. (2)将△ABC 绕点O 旋转180°,画出旋转后的△A 2B 2C 2. (3)画出一条直线将△AC 1A 2的面积分成相等的两部分. 分析:对于(1)和(2)可依据图形的平移、旋转等步骤进行作图.(3)可利用三角形 一边上的中线平分其面积求解. 解:依题意,得(1)将△ABC 向右平移3个单位长度得△A 1B 1C 1,如图6所示.(2)将△ABC 的三个顶点A ,B ,C 绕点O 旋转180°后得A 2,B 2,C 2,连接得到 △A 2B 2C 2,如图6所示.(3)因为点O 是AA 2的中点,而三角形一边上的中线平分三角形的面积,于是可过点O ,C 1作直线OC 1,如图6所示.说明:本题考查了图形的平移、旋转和等分三角形的面积,求解时要根据已知正确地确定对应点和理解中线的特征.考点4 中心对称图形例6 下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )A B C D分析:利用中心对称图形的概念逐一对照筛选.解:根据概念可判断选项A 、B 、C 中的图形是轴对称图形,也是中心对称图形,选项D 中的图形是轴对称图形,但不是中心对称图形.故选D.考点5 图案设计例7 七巧板是我们祖先的一项卓越创造,用它可以拼出多种图形,请你用七巧板中标号①,②,③的三块板(如图7)经过平移、旋转拼成图形.(1)拼成矩形,在图8中画出示意图;(2)拼成等腰直角三角形,在图9中画出示意图.注意:相邻两块板之间无空隙,无重叠;示意图的顶点画在小方格顶点上.分析:考虑到①,②,③的三块板分别是等腰直角三角形、正方形和等腰直角三角形,而且等腰直角三角形的腰与正方形的边长相等,所以可直接对相关图形进行平移或旋转即得矩形或等腰直角三角形.图7③② ① 图9图8 CBAO 图6 A B A 1B 1C 1 A 2C 2 B 2 O C解:答案不唯一.各给出一种,如图8和图9.说明:求解本题时要注意正确理解题目,要求仅限用七巧板中标号①,②,③的三块板.误区点拨一、平移概念理解有误例1 如图1,△FDE 是由△ABC 经过平移后得到的,则平移的距离是( ) A.BC 的长 B.BD 的长 C.BE 的长 D.CD 的长 错解: 选D.剖析:平移的距离是指对应点间线段的长度,所以平移的距离可以是BD 、CE 或AF. 正解:选B.二、混淆旋转、轴对称例2 如图2所示,在正方形网格中,△OAB 绕点O 旋转后,顶点B 的对应点为点 B′,试画出旋转后的三角形.错解:如图3所示,△OA′B′即为所求.剖析:此题错因是没按要求画图,画成了轴对称图形.在画旋转图形时,应注意关键点旋转后的位置.根据题意可知,旋转方向是顺时针方向,旋转角度是90°,那么点A 也要同样沿顺时针方向旋转90°.正解:如图4所示,△OA′B′即为所求.跟踪训练1.如图1所示,4根火柴棒形成象形汉字“口”,平移火柴棒后,原图形能变成的象形汉字是( )图12.如图2,将左边的图案变成右边的图案,经过的操作是( ) A.平移 B.旋转 C.轴对称 D.以上三种方法都可以图2图2 图3图 4AE DF B C 图3图4(D)(C)(B)(A)3. 如图3,四边形ABCD 是正方形,ΔADF 绕着点A 旋转90°后到达ΔABE 的位置,连接EF ,则ΔAEF 的形状是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形4. 如图4,在直角△ABC 中,∠C =90°,∠A =35°,以直角顶点C 为旋转中心,将△ABC 旋转到△A ′B ′C 的位置,其中A ′、B ′ 分别是A 、B 的对应点,且点B 在斜边A ′B ′上,直角边CA ′ 交AB 于点D ,则∠BDC 的度数是( )A.70°B.90°C.100°D.105°5.如图5,将左边的长方形绕点B 旋转一定角度后,变成右边的长方形,则∠ABC=___ ___ .6. 如图6,△A′B′C′是由△ABC 沿BC 方向平移2个单位得到的,则点A 与点A′的距离等于 个单位.7. 如图7,当半径为30 cm 的转动轮转过120 角时,传送带上的物体A 平移的距离为 cm8. 如图8,在10 ×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC 向右平移4个单位,得到△A ′B ′C ′, 再把△A′B′C′绕点 A′逆时针旋转 90○得到△A″B″C″请你画出△A′B′C′,和△A″B″C″.(不要求写画法)图89.如图9,已知每个网格中小正方形的边长都是1,图(1)中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.请你在图2中以图1为基本图案,借助轴对称、平移或旋转设计一个完整的花边图案(要求至少含有两次图形变换).图9图5ABCA ′B ′C ′图6图7图(2)图(1)参考答案:基础盘点:略.跟踪训练1.B2.B3.C4.D5.90°6.27. 20π8.9.答案不唯一,以下提供三种图案.。
11章图形的平移与旋转复习课

第11章《图形的平移与旋转》复习学案主备人:学习目标:1.能判断实例中的平移和旋转。
2.能根据平移、旋转的基本性质解决实际问题。
3.能作出简单的平面图形平移、旋转后的图形。
4.能够运用平移、旋转、轴对称及其组合进行图案设计。
【知识整理】1. 平移的定义:在平面内将一个图形沿某个方向移动一定的距离,这种图形变换称为平移.平移变换的两个要素:________________、________________.2. 平移变换的性质:(1)平移前、后的图形_____,即:平移只改变图形的_____,不改变图形的_____________;(2)对应点所连的线段 .3. 旋转的定义:在平面内,将一个图形绕一个定点沿某个方向(逆时针或顺时针)转动一定的角度,这样的图形变换叫做旋转.这个定点叫做_________,转动的角称为_________.旋转变换的三个要素:_________,_________,_________.4. 旋转变换的性质:(1)旋转前、后的图形_____;(2)对应点到旋转中心的距离_____。
(3)对应点与旋转中心所连线段的夹角等于_________.5.把一个图形绕着某一点旋转,如果它能够与重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称。
这个点叫,两个图形中的对应点叫。
6.成中心对称的两个图形,对称点的连线都,并且被。
7.把一个图形绕着某一点旋转,如果旋转后的图形能重合,那么称这个图形叫中心对称图形。
这个点叫。
例题解析例1、下列各组图形,可经过平移变换由一个图形得到另一个图形的是( )A. B. C. D.例2、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度α到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度α等于( )A.120° B.90° C.60° D.30°例题3、在上题中,若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为( )A. 10πcmB. 103πcmC. 303cmD. 20πcm例题4、如图,在平面直角坐标系内有一个△ABC.(1) 在平面直角坐标系内画出△ABC向下平移4个单位得到的△A1B1C1;(2) 在平面直角坐标系内画出△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;(3) 分别写出△A1B1C1与△A2B2C2各顶点的坐标.例5、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当a=150°时,试判断△AOD的形状,并说明理由;课下作业:1.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是______.2. 如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为______cm2.3. 如图,阴影部分为2m宽的道路,则余下的部分面积为______m2.4. 如图,△ACE,△ABF均为等腰直角三角形,∠BAF=∠EAC=90°,那么△AFC以点A为旋转中心逆时针旋转90°之后与________重合,其中点F与点____对应,点C与点____对应.5. 如图,在直角坐标系中,AO=AB,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上,点O′、B′在x轴上. 则点B′的坐标是_______.6. 如图,将正方形ABCD中的△ABP绕点B顺时针旋转90°,使得AB与CB重合,若BP=4,则点P所走过的路径长为_____.7、如图5,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为()A、100B、150C、200D、250(5)F EDCBA8. 在下列现象中,是平移现象的是( )①方向盘的转动②电梯的上下移动③保持一定姿势滑行④钟摆的运动A. ①②B. ②③C. ③④D. ①④9. 下列命题不正确的是()A.任何一个成中心对称的四边形是平行四边形B.平行四边形既是轴对称图形又是中心对称图形C.线段、平行四边形、矩形、菱形、正方形都是中心对称图形D.等边三角形、矩形、菱形、圆都是轴对称图形10. △ABC在平面直角坐标系中的位置如图所示.(1) 将△ABC向右平移6个单位得到△A1B1C1,请画出△A1B1C1,并写出点C1的坐标;(2) 将△ABC绕点C顺时针旋转90°得到△A2B2C,请画出△A2B2C,并写出点A2的坐标.11. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),这时AB与CD1相交于点O,与D1E1相交于点F.(1) 求∠OFE1的度数;(2) 求线段AD 1的长;第2题第3题第4题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变式练习2ຫໍສະໝຸດ △ ABC是等腰直角三角形,把△ ABC绕点C顺时针任意 旋转一个角度得到△ A′B′C,则分别连接AA ′、BB ′,点M、 N分别是线段AA ′、BB ′的中点。 (1)求证:△BCB ′≌△ACA′ (2)求证:△NCM是等腰直角三角形
问题探究
问题探究二
如图,四边形ABCD是正方形,E、F分别是边DC 和CB延长线上的点,且DE=BF,连接AE、AF、EF。 (1)求证:△ADE≌△ABF 点A 、按 (2)△ ADE可以由△ ABF绕旋转中心_______ 90° 逆时针方向旋转_________ 得到。 (3)若BC=8,DE=6,求△AEF的面积。
小组讨论
变式练习 问题探究 变式练习1
如图, △ABC是等边三角形, △ABP旋转后与△CBP′重合, 点 B ∠ABC、∠PBP ′ , 那么旋转中心点是 ______. 旋转角是_________________ 等边 连结PP′后, △BPP′是_______ 三角形。你能说明理由吗?
问题探究
对 质:成中心对称的两个图形中,对应点所连线段经过____
平分 . 称中心 ,而且被对称中心所_________ _________ 全等 律:成中心对称的两个图形_________.
规
课前小测
2.(2016· 贵州安顺)如图,将△PQR向右平移2个单 位长度,再向下平移3个单位长度,则顶点P平移后的 坐标是( A ) A.(﹣2,﹣4)
知 识 梳 理
图形的平移与旋转是两种_________ 全等 变换
平 移
平行(或在同一条直线上)且相等 对应点所连的线段____________________________; 平行 对应线段相等且________;
平移方向 和___________ 平移距离 决定的. 主要是由__________ 对应点到旋转中心的距离______; 相等 相等 旋转角________;
旋 转
旋转中心 旋转方向 、 主 要 是 由 ___________ 和 __________ 旋转角 决定的。 ___________
问题探究 问题探究一 问题探究1
如图,△ABC,△ADE均是顶角为42°的等腰 三角形,BC、DE分别是底边,图中哪两个三角形可 以通过怎样的旋转而相互得到?(课本P89页第12题) 结论:将△ABD绕点A逆时针旋转 42°得到△ACE。 或者:将△ ACE绕点A顺时针旋转 42°得到△ ABD 。
4 A′ 3 P 2 B′ 1 C′ A O -3 -2 -1 1 2 3 4 -1 -2 B -3 C -4
x
问题探究
4.(2016四川达州)如图,P是等边三角形ABC内一 点,将线段AP绕点A顺时针旋转60°得到线段AQ, 连接BQ.若PA=6,PB=8,PC=10,则四边形 APBQ的周长为 30 .
问题探究
变式练习3
点 P是正方形内一点,将△ ABP绕点B顺时针方向 旋转至与△CBP′重合,若PB=3,求PP′的长。
A D P
解:由旋转的性质可知
BP=BP′,
∠ PBP=∠ABC=90° ∴ PP ′=
B
P′
C
∴ △ PBP ′是等腰直角三 角形。
BP BP 3 3 3 2
2 '2 2 2
中心对称 这个点对称或___________ . 180 ° 把一个图形绕着某个点旋转_____ ,如果旋转后的图
重合 形能与原来的图形____ ,那么这个图形叫做_______,
中心对称图形 这个点叫做_________。对称中心
对 称 点:这两个图形中的对应点叫做关于中心的__________ 对称点 . 2.中心对称的性质 性
C B A
(A) (B )
(C) (D)
2.(2016年济宁)如图,将△ABE向右平移 2cm得到△DCF,如果△ABE的周长是16cm, 20cm 那么四边形ABFD的周长是_____
课 堂 检 测
3.平面直角坐标系中,△ABC的顶点坐标为A (-1,0),B(-3,-2),C(0,-2).将 △ABC先向上平移3个单位,再向右平移3个 单位,得到△A′B′C′,则A点对应点A′ ( 2 , 3) 的坐标是________; 若将△ABC绕点A顺时针 (-3,2) 旋转90°后,点B的对应点 P 的坐标是 ______. y
小
结
通过这节课的学习,你学到了哪些知识和方法?
1、知识技能方面
变换.
图形的平移与旋转是两种全等
2、思想方法方面
在题设条件与结论间不易沟通 或条件分散不易集中利用的情形下,常常平移或旋转 部分图形,使题设中隐蔽着的关系明朗起来,从而找 到解题途径.
驶向胜利的 彼岸
当 堂 检 测
1、在下图右侧的四个三角形中,不能由 △ABC经过旋转或平移得到的是( D )
B.(﹣2,4)
C.(2,﹣3)
D.(﹣1,﹣3)
知 识 梳 理
1、一个图形沿x轴方向平移a(a>0)个单位长度:
(x , y)
向右平移a个单位 向左平移a个单位
(x+a , y)
(x-a , y) (x , y+a)
(x , y-a)
2、一个图形沿y轴方向平移a(a>0)个单位长度:
(x , y)
向上平移a个单位
向下平移a个单位
课前小测
3.(2016· 广东广州)如图 ,△ABC 中, AB=AC ,BC=12cm,点 D在 AC上,DC=4cm ,将线 段DC 沿CB 方向平移7cm 得到线段EF ,点 E、F分 别落在边 AB、BC上,则 △BEF的周长是 13 cm.
课前小测
4. (2016年温州市)如图,将△ABC绕点C按顺时针方 向旋转至△A′B′C,使点A′落在BC的延长线上.已知 46 ∠A=27°,∠B=40°,则∠ACB′= 度.
《图形的平移与旋转》复习课
课前小测
1.(2015年深圳)下列图形中既是中心对称又是轴对 称图形的是( D )
2.下列交通标志中,是中心对称图形的是( D)
知 识 梳 理
1.中心对称的概念 定 180 °,如果 义:把一个图形绕着平面内某一点旋转_______
它能够与另一个图形重合,那么就说这两个图形关于
