高三寒假作业 数学(二)Word版含答案
高三寒假作业数学(二)Word版含答案

【原创】高三数学寒假作业(二)一、选择题,每题只有一项为哪一项正确的。
1.设会合Ax x 12, B x log2x 2,则 A B =A.1,3B.1,4C.0,3D.,42.已知函数f ( x)sin x,x0,2)的值为f ( x1),x那么 f (0,31B.3C.13A.22D.223.已知函数 f (x)x26x7,x0,则 f (0)+f (1) =()=x0,10x,(A) 9(B)71(C) 3(D)11 10104.已知函数f (x)2x 2 ,则函数 y|f ( x) |的图像可能是..()5.若互不相等的实数a, b, c 成等差数列,c, a, b 成等比数列,且 a 3b c10 ,则a ()A.4B.2C.-2D.-46.以下各式中值为的是()A. sin45 ° cos15 °+cos45 °sin15 °B. sin45 ° cos15 °﹣ cos45 ° sin15 °C. cos75 ° cos30 °+sin75 °sin30 °D.4x y 10 07. 设实数 x , y 知足条件x 2 y 8 0 , 若目标函数 z = ax + by(a > 0, b > 0) 的最大值为12,x0, y则23 的最小值为 ( )a b8.已知函数 f ( x) 知足 f ( x)f (1) , 当 x 1, 3 时 , f ( x) ln x , 若在区间 1 内, 曲线 , 3x3 g(x) f ( x) ax 与 x 轴有三个不一样的交点 , 则实数 a 的取值范围是( )1B.1C.ln 3 1D.ln 31A. 0,0,3 ,,2ee2ee39. 圆心在直线 y =x 上,经过原点,且在 x 轴上截得弦长为 2 的圆的方程为 ()A .(x -1) 2+(y -1) 2=2B .(x -1) 2+(y +1) 2=2C .(x -1) 2+(y -1) 2=2 或 (x +1) 2+(y +1) 2=2D .(x -1) 2+(y +1) 2=或 (x +1) 2+(y -1) 2 =2二、填空题10.已知会合 A x | x1 , Bx | xa,且 AB R ,则实数 a 的取值范围是__________ .11.理:已知会合My y2x, x 0, Nx ylg( 2xx 2 ) ,则MN.12.已知等差数列a n的前n 项和为 S n ,且a 1a 53a 3 , a 1014 ,则 S 12 =13.抛物线y1 x2 上的动点M到两定点(0, -1)、( 1, -3)的距离之和的最小值为4三、计算题14.(本小题满分 13 分)已知函数f ( x)log1 ( ax 2) x 12(a 为常数 ).(1) 若常数a 2 且 a 0,求f ( x)的定义域;(2)若 f ( x) 在区间(2,4)上是减函数,求 a 的取值范围.15.(本小题满分 12 分)已知直三棱柱 ABC A1B1C1中,△ABC为等腰直角三角形,∠BAC =90°,且 AB =1,D、E、F分别为1A 、 C1C 、 BC 的中点.AA B(1)求证:DE∥平面ABC;(2)求证:B1F⊥平面AEF;(3)求二面角B1AE F的余弦值.16.(本小题满分12 分)x2y23已知椭圆 C :22 1 a b 0 的离心率为,短轴端点到焦点的距离为2。
数学寒假作业2023年2月1日-2日(综合试题)

……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前数学寒假作业2023年2月1日-2日(综合试题)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I 卷(选择题)一、选择题(本大题共10小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1. 下列图形中,不具有稳定性的是( ) A. 等腰三角形B. 平行四边形C. 锐角三角形D. 等边三角形2. 下面的轴对称图形中,对称轴数量最多的是( ) A.B.C.D.3. 下面的计算正确的是( ) A. (ab)2=ab 2B. (ab)2=2abC. a 3⋅a 4=a 12D. (a 3)4=a 124. 当x =−2时,下列分式没有意义的是( ) A. x−2x+2B. xx−2C.x+22xD. x−2−2x5. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )A. 115°B. 65°C. 40°D. 25°6. 计算(2x −1)(x +2)的结果是( )……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※……○…………内…………○…………装…………○…………订…………○…………线…………○…………A. 2x 2+x −2B. 2x 2−2C. 2x 2−3x −2D. 2x 2+3x −27. 设等腰三角形的一边长为5,另一边长为10,则其周长为( ) A. 15 B. 20 C. 25 D. 20或258. 如图,Rt △ABC 中,∠C =90°,AD 平分∠BAC ,交BC 于点D ,CD =6,AB =12,则△ABD 的面积是( )A. 18B. 24C. 36D. 729. 如图,将△ABC 沿着DE 减去一个角后得到四边形BCED ,若∠BDE 和∠DEC 的平分线交于点F ,∠DFE =α,则∠A 的度数是( )A. 180°−αB. 180°−2αC. 360°−αD. 360°−2α10. 若正整数m 使关于x 的分式方程m(x+2)(x−1)=xx+2−x−2x−1的解为正数,则符合条件的m 的个数是( )……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………A. 2B. 3C. 4D. 5第II 卷(非选择题)二、填空题(本大题共6小题,共18.0分)11. 红细胞也称红血球,是血液中数量最多的一种血细胞,也是我们体内通过血液运送氧气的最主要的媒介,同时还具有免疫功能.红细胞的直径单位一般用微米(μm),1μm =0.000001m ,人类的红细胞直径通常是6μm ~8μm.6μm 用科学记数法可以表示为 m.12. 在一场足球比赛中,运动员甲、乙两人与足球的距离分别是8m ,17m ,那么甲、乙两人的距离d 的范围是 .13. 化简:3y 2x−2y +2xyx 2−xy 的计算结果是 .14. 把多项式x 2−6x +m 分解因式得(x +3)(x −n),则m +n 的值是 .15. 如图,在四边形中ABCD 中,BD 平分∠ABC ,∠DAB +∠DCB =180°,DE ⊥AB 于点E ,AB =8,BC =4,则BE 的长度是 .16. 若|2x −4|+(y +3)2=0,点A(x,y)关于x 轴对称的点为B ,点B 关于y 轴对称的点为C ,则点C 的坐标是 . 三、计算题(本大题共1小题,共4.0分)……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※……○…………内…………○…………装…………○…………订…………○…………线…………○…………17. 计算:(结果用幂的形式表示)3x 2·x 4−(−x 3)2.四、解答题(本大题共8小题,共68.0分。
20210307高三寒假测试二数学答案
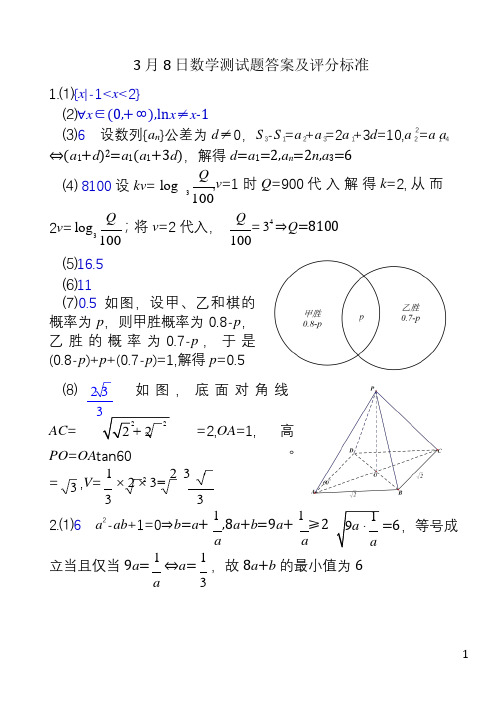
3 3 1 2 3 1 2 14 23 月 8 日数学测试题答案及评分标准1.⑴{x |-1<x <2}⑵∀x ∈(0,+∞),ln x ≠x -1⑶6 设数列{a n }公差为 d ≠0,S -S =a +a =2a +3d =10,a 2=a a ⇔(a 1+d )2=a 1(a 1+3d ),解得 d =a 1=2,a n =2n ,a 3=6⑷ 8100 设 kv = log Q,v =1 时 Q =900 代 入 解 得 k =2, 从 而3 1002v = log Q ;将 v =2 代入,3 100 Q = 34⇒Q =8100 100 ⑸16.5 ⑹11⑺0.5 如图,设甲、乙和棋的概率为 p ,则甲胜概率为 0.8-p , 乙 胜 的 概 率 为 0.7-p , 于 是(0.8-p )+p +(0.7-p )=1,解得 p =0.5⑻ AC = 如 图 , 底 面 对 角 线=2,OA =1, 高 PO =OA tan60°= ,V = 1 ⨯ 2 ⨯ 3= 2 33 32.⑴6 a 2-ab +1=0⇒b =a + 1 ,8a +b =9a + 1 ≥2=6,等号成a a 立当且仅当 9a = 1 ⇔a = 1,故 8a +b 的最小值为 6a 32 3 3 2 + 2 2 29a ⋅ 1a2 2 (x - r )2 + y 20 02(r 2 - rx ) 03 2 ⎨ 6 3 00 0⑵ (x - 2)2 + ( y - 2)2 = 2 如图,设 l 1 、l 2 与圆 M 分别相切于点 A 、B,l 1 ⊥l 2⇒∠AOB 为直角⇒∠AOM =45°⇒⎧x 0> 0, y 0 > 0 ⎪ x 2 y 2 OM = MA =2,于是, ⎪0 + 0 = 1⎪ ⎪⎩x 0 2 + y 0 2 = 4解得 x 0 = y 0 = ,从而得圆 M 的方程⑶(-2,-1) f (x )=f (1) - f (0)⇔1 - 04x - 2 ⨯ 2x -m =1⇔m = (2x )2 - 2 ⨯ 2x -1 在 0<x <1 上有解,设 2x =t, 则 m =t 2-2t -1 在 1<t <2 上有解,后者在 1<t <2 上单调增,从而 m 的取值范围是(-2,-1)⑷ MP ⋅ NP =0⇒MP ⊥NP ,M 、N 、P 都是圆 O 上的点⇒MN 是圆的直径,不放设 P (r ,0),M (0,r ),N (0,-r ),Q(x 0,y 0),则 x 2+ y 2 = r 2 , (PM + PN ) ⋅ PQ =2 PO ⋅ PQPO = (-r , 0), PQ = (x - r , y ) 2(r 2 - x r )=2⇒ r 2- x r =1, | PQ | == = =⑸ - A 、B 在单位圆 x 2 + y 2 = 1上,从而直线 l :y = 3x + 与圆2x - 2rx + r 222 0 0+ y 0 23 O x 2 + y 2 = 1 相较于 A 、B 两点 设 AB 的中点为 C ,如图:射线 OA 、OB 分别与角α、β的终边重合,OC ⊥l ,直线 l 的倾斜角∠ BDx =60°⇒直线OC 的倾斜角∠ xOC =90°+60°=150°;又射线OC α+β 与 的 终 边 重 合 , 故2 α+ β=150°+k 360°,k ∈Z ⇒α+β 2=300°+2k 360°⇒tan(α+β)=tan300°=- ⑹ - 25,2 2 = λ2 22 | λAB + 3(1 - λ) AC | 16AB + 6λ(1 - λ) AB ⋅ AC + 9(1 - λ) AC=9[2(1-cos A ) λ2-2(1-cos A )λ+1],因 0<A <π,故 1-cos A >0,故当1 |2 λ= 时, λAB + 3(1 - λ) AC | 取 2得最小值= 9 (1+cos A )= 27⇒2 4 cos A = 1 ,又 A ∈(0,π)⇒A = π,2 3如图建立平面直角坐标系B (3,0),C( 1 , 32 2 ) , 设 P (x ,0),0 ≤ x ≤3, =(3-x ,0),1x , ),PB PC =( -2 231 PB ⋅ PC =(3-x )(2 -x )=x 2- 72 x +3 2 ,当 x = 74 时,取得最小值- 2516 3.⑴tan α=2= sin α⇒sin α=2cos α, 又 sin 2α+cos 2α=1 故 cos 2 αcos α= 1,…………………………………………………………………….(2 分) 5cos2α=2cos 2α-1= 25-1= - 3 5 …………………………………(4 分)⑵ tan α =2>1, α ∈ (0, π )⇒ π < α < π ⇒ π<2 α < π , 由⑴ cos2 α4 2 23 =- ,sin2α= 5 1- cos 22α= 4 …………………………………..(6 分) 5β∈(0,π),cos β=- 7 2 <0⇒β∈( π,π),sin β= 1- cos 2 β= 2 .(8 分)10 2 102 -π πα β∈(- , )…………………………………………………….(10 分)2 2sin(2α-β)=sin2αcos β-cos2αsin β= 4 ×(- 7 2 )-(- 3 )× 25 10 5 10=- 2……………………………………………………………………(12 分 )2 2α-β=- π……………………………………………………………….(14 分)44. ⑴证明:设 M 为 PD 的中点,连接 AM ……………(说明及图各 1 分,共 2 分)MF ∥= 1 DC ⎫ 2 ⎪⇒ MF ∥ AE ⇒AEFM 为AE ∥= ⎬ =1 DC ⎪2⎬ ⎭ ⎪ ⎭ 平行四边形……………………………(4 分)⇒ EF ∥AM ⎫EF ⊄ 平面PAD ⎪⇒EF ∥平面 PAD ……………………………….(6 分)AM ⊂ 平面PAD ⎪⑵证明:在矩形 ABCD 中, DE ⋅ AC = ( AE - AD ) ⋅ ( AB + AD )= 1= 121 2 = 1 ⨯2 2 -0-1=0 ( AB - AD ) ⋅ ( AB + A D ) 2⇒ DE ⊥ AC ........(8分)⎫ AB - AB ⋅ AD - AD222DE ⊥ PA ⎪⇒ DE ⊥ 平面PAC ...(12分)⎫⎪ PA ⋂ AC = A ⎬ PA , AC ⊂ 平面PAC ⎪⎭DE ⊂ 平面PDE ⎬⇒平面 PAC ⊥平面 PDE ………………………………………………(14 分)5.⑴南北方向每 min 流过的水量为 3 设东西方向水流速度为 v (m 3/min),则×2×5=30 m 3…(2 分)2v ×3×1=30 ,v =5 ………………………………………………….(4 分)答:东西向水渠内水的流速为 5 ⑵设竹竿过点 B 时,与东西向 πm 3/min …………………..(6 分) 的夹角为θ,θ∈(0,), 如图,2能否通过取决于 PQ >12 是否恒成立,………………….....(8 分) 3 3 3 3 33 ( 3 + 1)ca 2 - 1 3 PQ =PB +BQ = 1sin θ + 3 3 cos θ ,设其为 f (θ), θ∈(0, π)……..(10 分)2f '(θ) = - cos θ sin 2 θ + 3 3 sin θ cos 2θ =3 3 sin 3 θ- cos 3 θ sin 2 θcos 2 θ - 3=0⇔ tan 3 θ= 3 2⇔t an θ= 33 ⇔θ= π,当 0<θ< 6 π时, 6 f '(θ) >0,f (θ)单调递减;当π<6θ< π时, f '(θ) <0,f (θ)单调递增 2故 f (θ)最小值=f ( π)=8<12…………………………………………(12 分)6 即 PQ>12 不恒成立答:不能通过………………………………………………………………(14 分) 6.⑴连接 PF 1,|OP |=|OF 2|,∠POF 2= π⇒△POF 2 是等边三角形,3|PF 2|=c ,又|OP |=|OF 2|=|OF 1|⇒∠OF 1P =∠OPF 1= ∠POF 2 = π;2 6从而∠F 2PF 1=90°,在△POF 1 中|PF 1|= c…………………(2 分)离心率 e= 2c = 2a 2c | PF 1 | + | PF 2 | = 2c = 3-1…………….(4 分 )x 2 ⑵ ① 设 椭 圆 方程 为+ y 2a2c=1 ,c= , 1 + 1 = e ⇔ 1 + 1 =a , 联立解得| OF 2 | | OA | | F 2 A | c a 3(a - c )c = ,a =2,故椭圆方程为∆ 4 4k 2- 3 k 2 + 1 7 (1 - 22 x+ y 2 = 1……………………………………………………………….(6 分) 4x 2②将 y =kx -2 代入椭圆 4+ y 2 =1,并整理得到(1 + 4k 2 )x 2 -16kx + 12 = 0 …………………………………………….(8 分)此方程有两个不等的实数解,△=16(4k 2-3)>0………….(10 分)|PQ |= ⋅ 1 + 4k 2 ⋅ 1 + 4k 2………………..(12 分)点 O 到直线 y =kx -2 的距离 d =1 | k 0 - 0 -2 |2 ,△POQ 的面 k 2 + 1 积为 | PQ | d 2 解得 k = ± …………..(14 分) 2经检验满足,故 k = ± 37……………………………………….(16 分)2x 2 37.⑴a = 4 λ时, f (x ) =λ+ x - λln x ,x >0 4f '(x ) = 2x (λ+ x ) - 3 λ1 第一项分子分母同除以x 2(λ+ x )24 x 2(λ+ 1) -1x - 3 λ λ2t + 1 -3(2t + 1)4 - 3t (t + 1)2设 = t(λ+ 1)24 x xx(t + 1)2 t 通分44(t + 1)2(t -1)(3t 2 + 9t + 4) =- 4(t + 1)2= λλ )[3( ) x x λ + 9 λ+ 4]x =04( + 1)2x⇒x =λ………………………………………………………………………….(2 分)1 + k2 1 + k 2 4 4k 2 -3 =当 x >λ时, f '(x ) >0,f(x )单调递增;当 0<x <λ时, f '(x ) <0,f (x )单调递减;故 f (x ) 的极小值=f (λ)=λ( 1 - 3ln λ)=0,λ>02 42解得λ= e 3 …………………………………………………………………….(4 分)' 2x (λ+ x ) - x 2 ax (2λ+ x ) a ⑵证明: f (x ) = - = (λ+ x )2x (λ+ x )2 - …………(6 分 ) xf (x )在(t ,f (t ))处切线方程为 y = [t (2λ+ t ) - a] (x -t )+f (t )…..(8 分)设 f (x )-{ [t (2λ+ t ) (λ+ t )2 (λ+ t )2 t - a ] (x -t )+f (t )}=g(x )tg '(x ) = f '(x ) - [t (2λ+ t ) - a ] = x (2λ+ x ) - t (2λ+ t ) +a (x - t )(λ+ t )2 t (λ+ x )2 (λ+ t )2 tx x (2λ+ x ) x 2 + 2λx λ2(λ+ x )2 = x 2 + 2λx + λ2 =1- x 2 + 2λx + λ2在 x >0 上单调递增, 故当 x >t 时, g '(x ) >0,g(x )单调递增,g(x )>g(t )=0f (x )> [t (2λ+ t ) - a ] (x -t )+f (t )……………………………….(10 分)(λ+ t )2 t [t (2λ+ t ) - a ] (x -t )+f (t )≥0 时,f (x )>0……………….(12 分) (λ+ t )2 t t (2λ+ t ) a(λ+ t )2在 t >0 的单调增函数, t 在 t >0 上单调减,故存在t 0 >0使得 t 0 (2λ+ t 0 ) - a >0,[ t 0 (2λ+ t 0 ) - a ](x -t )+f (t )是 x 的单调减函(λ+ t )2 t (λ+ t )2t0 0 0 0数,[ t 0 (2λ+ t 0 ) - a ](x -t )+f (t )>0 有解 x >s …………….(14 分)(λ+ t )2t0 0∃x 0=max{t 0,s },当 x >x 0 时,f (x )>0…………………………(16 分)8.⑴S1=1+t,S2=3+t,S3=6+t⇒a1=1+t,a2=S2-S1=2,a3=S3-S2=3又 a 1,a 2,a 3 称等差数列⇔2a 2=a 1+a 3⇔4=4+t ⇔t =0……..(2 分) 于是 a n =n …………………………………………………………………..(4 分) 3(1 - 3n ) 3n +1 - 3 3n + 2 - 3 3(2T + 3) - 3 ⑵ T = = ⇒ T = = n =3 T +3n 1 - 3 2 n +12 2 n c = (-1)n +1 4T n +3 = (-1)n +1 T n + T n +1 = (-1)n +1 ( 1 + 1 ) ……(6 分)T n T n +1 T n T n +1 T n T n +1 n 为偶 数 时 , c + c + c + ... + c = 1 + 1 -( 1 + 1)+( 1 + 1 )-……-( 1 + 1 ) 1 2 3 T 1 T 2 T 2 T 3 T 3 T 4T n T n +1 = 1 - 1 = 1 - 2 < 1 T T 3 3n + 2 - 3 3 1 n +1同理 n 为奇数时, c + c + c + ... + c = 1 + 2 ≤ 1 + 2 = 51 2 3 n 3 3n + 2 - 3 3 33 -3 12总之 c + c + c + ... + c = 1 + 2 ≤ 5 ………………….(8 分 )1 2 3 n 3 3n + 2 - 3 125 -m + 41 ⇔12 12>m -3⇔1≤m <5 m 的取值范围是[1,5)……………………………………………………(10 分) ⑶ e = n ⇒ e = 1 , e = 2 , e = 1 ⇒ e , e , e 称等差数列……(12 分)n 3n 1 3 2 9 3 9 1 2 3检验其他, e - e =1-2n <0⇒数列{ e }单调递减, n +1 n 3n +1n 当 1<m <p <n 时⇒m ≤p -1,n ≥p +1,p >2e m + e n - 2e p≥ e + e - 2e = p - 1 + p + 1 - 2 p = 4 p - 8 >0⇒ e , e , e 不可能成 p -1 p +1 p 3p -1 3p +1 3p 3p +1m p n 等差数列……………………………………………(14 分)n n总之,仅存在e1,e2,e3 成等差数列…………………………………(16 分)。
首发吉林省高三寒假作业 数学2含答案

高三数学寒假作业(函数与导数)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分,考试时间120分钟,考生作答时将答案答在答题卡上,在本试卷上答题无效。
第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求。
) 1.)()()(0000limx f xx f x x f x '=∆-∆+→∆,其中x ∆( )(A )恒取正值或恒取负值 (B )有时可以取0(C )恒取正值 (D )可以取正值和负值,但不能取02.设函数()y f x =在(0,+∞)内有定义,对于给定的正数K ,定义函数(),()(),()K f x f x K f x K f x K≤⎧=⎨>⎩,取函数ln 1()xx f x e +=,恒有()()K f x f x =,则 A .K 的最大值为1e B .K 的最小值为1eC .K 的最大值为2D .K 的最小值为23.双曲线221y x m-=的离心率大于2的充分必要条件是 ( )A .12m > B .1m ≥ C .1m > D .2m >4.函数32()f x x bx cx d =+++的大致图象如图所示,则2212x x +等于( )(A )89(B )109(C )169(D )2895.“使lg 1m <”成立的一个充分不必要条件是( )A. 0m >B. {}1,2m ∈C. 010m <<D. 1m <6.已知a ,b ,c ,d 为实数,且c>d ,则“a>b ”是“a+c>b +d”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件7.已知复数z =,则“3πθ=”是“z 是纯虚数”的( )A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件8.对12,(0,)2x x π∀∈,若21x x >,且1111sin x y x +=,2221sin x y x +=,则( ) (A )y 1=y 2 (B )y 1>y 2(C )y 1<y 2 (D )y 1,y 2的大小关系不能确定9.已知复数i i z 1)3(tan --=θ,则“3πθ=”是“z 是纯虚数”的( )A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件10.设函数()f x 为偶函数,且当0x ≥时,()14xf x ⎛⎫= ⎪⎝⎭,又函数()sin g x x x π=,则函数()()()h x f x g x =-在1,22⎡⎤-⎢⎥⎣⎦上的零点的个数为( )个。
高三数学寒假作业(完整答案)

高三数学寒假作业—数列答案一、选择题:1.在等差数列{a n }中,a 1=2,a 3+a 5=10,则a 7=()A .5B .8C .10D .14解析 解法一:设等差数列的公差为d ,则a 3+a 5=2a 1+6d =4+6d =10,所以d =1,a 7=a 1+6d =2+6=8.解法二:由等差数列的性质可得a 1+a 7=a 3+a 5=10,又a 1=2,所以a 7=8. 答案 B2.设等比数列{a n }的前n 项和为S n ,若S 2=3,S 4=15,则S 6=( ) A .31 B .32 C .63 D .64解析 在等比数列{a n }中,S 2,S 4-S 2,S 6-S 4也成等比数列,故(S 4-S 2)2=S 2(S 6-S 4),则(15-3)2=3(S 6-15),解得S 6=63. 答案 C3.设S n 为等差数列{a n }的前n 项和,若a 1=1,a 3=5,S k +2-S k =36,则k 的值为( ) A .8 B .7 C .6 D .5解析 设等差数列的公差为d ,由等差数列的性质可得2d =a 3-a 1=4,得d =2,所以a n =1+2(n -1)=2n -1.S k +2-S k =a k +2+a k +1=2(k +2)-1+2(k +1)-1=4k +4=36,解得k =8.4.已知等比数列{a n }的前n 项和为S n ,若S 2n =4(a 1+a 3+a 5+…+a 2n -1),a 1a 2a 3=27,则a 6=( )A .27B .81C .243D .729 解析 设数列{a n }的公比为q ,∵S 2n =4×a 1-q 2n1-q2=a 1-q 2n1-q,∴q =3,又a 1a 2a 3=27,∴a 32=27,∴a 2=3,∴a 6=a 2q 4=35=243,故选C. 答案 C5.已知数列{a n }满足a 1=1,a 2=3,a n +1·a n -1=a n (n ≥2),则a 2 013的值等于( ) A .3 B .1 C.13 D .32 013解析 由已知得a n +1=a n a n -1,a n +3=a n +2a n +1=a n +1a n ×1a n +1=1a n ,故a n +6=1a n +3=a n , 于是,该数列是周期为6的数列,a 2 013=a 3=a 2a 1=3. 答案 A6.已知数列{a n }中a 1=1,a 2=2,当整数n >1时,S n +1+S n -1=2(S n +S 1)都成立,则S 15等于( )A .201B .210C .211D .212解析 由S n +1+S n -1=2(S n +S 1),得(S n +1-S n )-(S n -S n -1)=2S 1=2,即a n +1-a n =2(n ≥2),数列{a n }从第二项起构成等差数列,S 15=1+2+4+6+8+…+28=211. 答案 C7.在等比数列{a n }中,a 1+a n =34,a 2a n -1=64,且前n 项和S n =62,则项数n 等于( ) A .4 B .5 C .6 D .7解析 在等比数列中,a 2a n -1=a 1a n =64,又a 1+a n =34,解得a 1=2,a n =32或a 1=32,a n =2.当a 1=2,a n =32时,S n =a 1-qn1-q=a 1-qa n 1-q =2-32q 1-q=62,解得q =2,又a n =a 1q n -1,所以2×2n -1=2n=32,解得n =5.同理当a 1=32,a n =2时,由S n =62解得q =12,由a n=a 1qn -1=32×⎝ ⎛⎭⎪⎫12n -1=2,得⎝ ⎛⎭⎪⎫12n -1=116=⎝ ⎛⎭⎪⎫124,即n -1=4,n =5,综上项数n 等于5,选B.答案 B8.设等差数列{a n }的前n 项和为S n ,且a 1>0,a 3+a 10>0,a 6a 7<0,则满足S n >0的最大自然数n 的值为( )A .6B .7C .12D .13解析 ∵a 1>0,a 6a 7<0,∴a 6>0,a 7<0,等差数列的公差小于零,又a 3+a 10=a 1+a 12>0,a 1+a 13=2a 7<0,∴S 12>0,S 13<0,∴满足S n >0的最大自然数n 的值为12. 答案 C9.设等差数列{a n }的前n 项和是S n ,若-a m <a 1<-a m +1(m ∈N *,且m ≥2),则必定有( ) A .S m >0,且S m +1<0 B .S m <0,且S m +1>0 C .S m >0,且S m +1>0 D .S m <0,且S m +1<0解析 由题意,得:-a m <a 1<-a m +1⇔⎩⎪⎨⎪⎧a 1+a m >0,a 1+a m +1<0.显然,易得S m =a 1+a m2·m >0,S m +1=a 1+a m +12·(m +1)<0.答案 A10.已知数列{a n }满足a n +1=a n -a n -1(n ≥2),a 1=1,a 2=3,记S n =a 1+a 2+…+a n ,则下列结论正确的是( ) A .a 2 014=-1,S 2 014=2 B .a 2 014=-3,S 2 014=5 C .a 2 014=-3,S 2 014=2D .a 2 014=-1,S 2 014=5解析 由已知数列{a n }满足a n +1=a n -a n -1(n ≥2),知a n +2=a n +1-a n ,a n +2=-a n -1(n ≥2),a n +3=-a n ,a n +6=a n ,又a 1=1,a 2=3,a 3=2,a 4=-1,a 5=-3,a 6=-2,所以当k ∈N时,a k +1+a k +2+a k +3+a k +4+a k +5+a k +6=a 1+a 2+a 3+a 4+a 5+a 6=0,a 2 014=a 4=-1,S 2 014=a 1+a 2+a 3+a 4=1+3+2+(-1)=5.答案 D10(理)已知定义在R 上的函数f(x)和g(x)满足g(x)≠0,f'(x)·g(x)<f(x)·g'(x),f(x)=a x ·g(x),+=.令a n =,则使数列{a n }的前n 项和S n 超过的最小自然数n 的值为二、填空题:13.(2014·江西卷)在等差数列{a n }中,a 1=7,公差为d ,前n 项和为S n ,当且仅当n =8时S n 取最大值,则d 的取值范围________.解析 当且仅当n =8时,S n 取得最大值,说明⎩⎪⎨⎪⎧a 8>0,a 9<0.∴⎩⎪⎨⎪⎧7+7d >0,7+8d <0.∴-1<d <-78.答案 ⎝⎛⎭⎪⎫-1,-78 12.已知函数f (x )=x +sin x ,项数为19的等差数列{a n }满足a n ∈⎝ ⎛⎭⎪⎫-π2,π2,且公差d ≠0.若f (a 1)+f (a 2)+…+f (a 18)+f (a 19)=0,则当k =________时,f (a k )=0.解析 因为函数f (x )=x +sin x 是奇函数,所以图象关于原点对称,图象过原点.而(1)(1)f g (-1)(-1)f g 52()()f n g n 1516等差数列{a n }有19项,a n ∈⎝ ⎛⎭⎪⎫-π2,π2,若f (a 1)+f (a 2)+…+f (a 18)+f (a 19)=0,则必有f (a 10)=0,所以k =10. 答案 1011.(2013·湖南)设S n 为数列{a n }的前n 项和,S n =(-1)n a n -12n ,n ∈N *,则:(1)a 3=________;(2)S 1+S 2+…+S 100=________. 解析 ∵a n =S n -S n -1=(-1)n a n -12n -(-1)n -1a n -1+12n -1(n ≥2),∴a n =(-1)na n -(-1)n -1a n -1+12n (n ≥2).当n 为偶数时,a n -1=-12n (n ≥2),当n 为奇数时,2a n +a n -1=12n (n ≥2),∴当n =4时,a 3=-124=-116.根据以上{a n }的关系式及递推式可求.a 1=-122,a 3=-124,a 5=-126,a 7=-128,…, a 2=12,a 4=12,a 6=12,a 8=12,….∴a 2-a 1=12,a 4-a 3=123,a 6-a 5=125,…,∴S 1+S 2+…+S 100=(a 2-a 1)+(a 4-a 3)+…+(a 100-a 99)-⎝ ⎛⎭⎪⎫12+122+123+…+12100=⎝ ⎛⎭⎪⎫12+123+…+1299-⎝ ⎛⎭⎪⎫12+122+…+12100=13⎝ ⎛⎭⎪⎫12100-1.答案 (1)-116 (2)13⎝ ⎛⎭⎪⎫12100-114.已知对于任意的自然数n ,抛物线y =(n 2+n )x 2-(2n +1)x +1与x 轴相交于A n ,B n 两点,则|A 1B 1|+|A 2B 2|+…+|A 2 014B 2 014|=________.解析 令(n 2+n )x 2-(2n +1)x +1=0,则x 1+x 2=2n +1n 2+n ,x 1x 2=1n 2+n ,由题意得|A n B n |=|x 2-x 1|,所以|A n B n |=x 1+x 22-4x 1x 2=⎝ ⎛⎭⎪⎫2n+1n 2+n 2-4·1n 2+n =1n 2+n =1n -1n +1,因此|A 1B 1|+|A 2B 2|+…+|A 2 014B 2 014|=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫12 014-12 015=1-12 015=2 0142 015. 答案2 0142 01515.(文) 设S n 为数列{a n }的前n 项和,若S 2n S n(n ∈N *)是非零常数,则称该数列为“和等比数列”;若数列{c n }是首项为2,公差为d (d ≠0)的等差数列,且数列{c n }是“和等比数列”,则d =________.解析 由题意可知,数列{c n }的前n 项和为S n =n c 1+c n2,前2n 项和为S 2n =2nc 1+c 2n2,所以S 2nS n =2nc 1+c 2n2n c 1+c n2=2+2nd 4+nd -d =2+21+4-d nd.因为数列{c n }是“和等比数列”,即S 2nS n为非零常数,所以d =4. 答案 415.(理)在正项等比数列{a n }中,a 5=12,a 6+a 7=3,则满足a 1+a 2+…+a n >a 1a 2…a n 的最大正整数n 的值为________.解析 设正项等比数列{a n }的首项为a 1,公比为q (q >0),则由a 5=12得a 6+a 7=a 5q +a 5q 2=12(q +q 2)=3,即q +q 2=6,解得q =2,代入a 5=a 1q 4=a 124=12⇒a 1=125,式子a 1+a 2+…+a n >a 1a 2…a n 变为a 1-qn1-q>答案 12三、解答题:.16.(2014·北京卷)已知{a n }是等差数列,满足a 1=3,a 4=12,数列{b n }满足b 1=4,b 4=20且{b n -a n }是等比数列. (1)求数列{a n }和{b n }的通项公式; (2)求数列{b n }的前n 项和.解 (1)设等差数列{a n }的公差为d ,由题意得d =a 4-a 13=12-33=3.所以a n =a 1+(n -1)d =3n (n =1,2,…). 设等比数列{b n -a n }的公比为q , 由题意得q 3=b 4-a 4b 1-a 1=20-124-3=8,解得q =2. 所以b n -a n =(b 1-a 1)q n -1=2n -1,从而b n =3n +2n -1(n =1,2,…).(2)由(1)知b n =3n +2n -1(n =1,2,…).数列{3n }的前n 项和为32n (n +1),数列{2n -1}的前n 项和为1×1-2n1-2=2n-1.所以,数列{b n }的前n 项和为32n (n +1)+2n-1.17.(2014·安徽卷)数列{a n }满足a 1=1,na n +1=(n +1)a n +n (n +1),n ∈N *. (1)证明:数列⎩⎨⎧⎭⎬⎫a n n 是等差数列;(2)设b n =3n·a n ,求数列{b n }的前n 项和S n . 解 (1)证明:由已知可得a n +1n +1=a n n +1,即a n +1n +1-a nn=1,所以⎩⎨⎧⎭⎬⎫a n n 是以a 11=1为首项,1为公差的等差数列.(2)由(1)得a n n=1+(n -1)·1=n , 所以a n =n 2,从而b n =n ·3nS n =1×31+2×32+3×33+…+n ·3n ①3S n =1×32+2×33+3×34+…+(n -1)·3n +n ·3n +1②①-②得:-2S n =31+32+33+…+3n -n ·3n +1=-3n1-3-n ·3n +1=-2nn +1-32所以S n =n -n +1+3418.已知单调递增的等比数列{a n }满足:a 2+a 3+a 4=28,且a 3+2是a 2和a 4的等差中项. (1)求数列{a n }的通项公式a n ;(2)令b n =a n log 12 a n ,S n =b 1+b 2+…+b n ,求使S n +n ·2n +1>50成立的最小的正整数n .解 (1)设{a n }的公比为q ,由已知, 得⎩⎪⎨⎪⎧a 2+a 3+a 4=28,a 3+=a 2+a 4,∴⎩⎪⎨⎪⎧a 3=8,a 2+a 4=20,即⎩⎪⎨⎪⎧a 1q 2=8,a 1q +a 1q 3=20,解得⎩⎪⎨⎪⎧a 1=2q =2或⎩⎪⎨⎪⎧a 1=32q =12(舍去)∴a n =a 1qn -1=2n.(2)b n =2nlog 122n=-n ·2n , 设T n =1×2+2×22+3×23+…+n ×2n,① 则2T n =1×22+2×23+…+(n -1)×2n +n ×2n +1,②①-②得-T n =(2+22+…+2n )-n ×2n +1=-(n -1)·2n +1-2,∴S n =-T n =-(n -1)×2n +1-2.由S n +n ·2n +1>50,得-(n -1)·2n +1-2+n ·2n +1>50,则2n>26,故满足不等式的最小的正整数n =5.19.(2014·山东)已知等差数列{a n }的公差为2,前n 项和为S n ,且S 1,S 2,S 4成等比数列. (1)求数列{a n }的通项公式;(2)令b n =(-1)n-14na n a n +1,求数列{b n }的前n 项和T n . 解 (1)因为S 1=a 1,S 2=2a 1+2×12×2=2a 1+2,S 4=4a 1+4×32×2=4a 1+12,由题意,得(2a 1+2)2=a 1(4a 1+12),解得a 1=1, 所以a n =2n -1. (2)b n =(-1)n-14n a n a n +1=(-1)n -14n (2n -1)(2n +1)=(-1)n -1(12n -1+12n +1).当n 为偶数时,T n =(1+13)-(13+15)+…+(12n -3+12n -1)-(12n -1+12n +1)=1-12n +1=2n2n +1.当n 为奇数时,T n =(1+13)-(13+15)+…-(12n -3+12n -1)+(12n -1+12n +1)=1+12n +1=2n +22n +1.所以T n=⎩⎪⎨⎪⎧2n +22n +1,n 为奇数,2n2n +1,n 为偶数.(或T n =2n +1+(-1)n -12n +1)20.已知数列{a n }满足a 1=1,a 1+a 2+…+a n -1-a n =-1(n ≥2且n ∈N *). (1)求数列{a n }的通项公式a n ; (2)令d n =1+log aa 2n +1+a 2n +25(a >0,a ≠1),记数列{d n }的前n 项和为S n ,若S 2nS n恒为一个与n 无关的常数λ,试求常数a 和λ.解 (1)由题知a 1+a 2+…+a n -1-a n =-1(n ∈N *),① 所以a 1+a 2+…+a n -a n +1=-1,② 由①-②得:a n +1-2a n =0,即a n +1a n=2(n ≥2). 当n =2时,a 1-a 2=-1, 因为a 1=1,所以a 2=2,a 2a 1=2,所以,数列{a n }是首项为1,公比为2的等比数列. 故a n =2n -1(n ∈N *).(2)因为a n =2n -1,所以d n =1+log aa 2n +1+a 2n +25=1+2n log a 2.因为d n +1-d n =2log a 2,所以{d n }是以d 1=1+2log a 2为首项,以2log a 2为公差的等差数列,所以S 2nS n=2n +2log a +2n n -2×2log a 2n+2log a+nn -2×2log a 2=2+n +a21+n +a 2=λ ⇒(λ-4)n log a 2+(λ-2)(1+log a 2)=0, 因为S 2nS n恒为一个与n 无关的常数λ, 所以⎩⎪⎨⎪⎧λ-a2=0,λ-+log a=0,解得λ=4,a =12.21.(文)数列{a n }的前n 项和为S n ,a 1=1,且对任意正整数n ,点(a n +1,S n )在直线2x +y -2=0上.(1)求数列{a n }的通项公式;(2)是否存在实数λ,使得数列⎩⎨⎧⎭⎬⎫S n +λn +λ2n 为等差数列?若存在,求出λ的值;若不存在,请说明理由.解(1)由题意,可得2a n +1+S n -2=0.① 当n ≥2时,2a n +S n -1-2=0.② ①-②,得2a n +1-2a n +a n =0,所以a n +1a n =12(n ≥2). 因为a 1=1,2a 2+a 1=2,所以a 2=12.所以{a n }是首项为1,公比为12的等比数列.所以数列{a n }的通项公式为a n =⎝ ⎛⎭⎪⎫12n -1.(2)由(1)知,S n =1-12n1-12=2-12.若⎩⎨⎧⎭⎬⎫S n +λn +λ2n 为等差数列,则S 1+λ+λ2,S 2+2λ+λ22,S 3+3λ+λ23成等差数列,则2⎝ ⎛⎭⎪⎫S 2+9λ4=S 1+3λ2+S 3+25λ8,即2⎝ ⎛⎭⎪⎫32+9λ4=1+3λ2+74+25λ8,解得λ=2.又λ=2时,S n +2n +22n =2n +2,显然{2n +2}成等差数列,故存在实数λ=2, 使得数列{S n +λn +λ2n }成等差数列.21.(理)(2014·江苏卷)设数列{a n }的前n 项和为S n .若对任意的正整数n ,总存在正整数m ,使得S n =a m ,则称{a n }是“H 数列”.(1)若数列{a n }的前n 项和S n =2n (n ∈N *),证明:{a n }是“H 数列”;(2)设{a n }是等差数列,其首项a 1=1,公差d <0.若{a n }是“H 数列”,求d 的值; (3)证明:对任意的等差数列{a n },总存在两个“H 数列”{b n }和{c n },使得a n =b n +c n (n ∈N *)成立.解 (1)证明:由已知,当n ≥1时,a n +1=S n +1-S n =2n +1-2n =2n.于是对任意的正整数n ,总存在正整数m =n +1,使得S n =2n=a m .所以{a n }是“H 数列”. (2)由已知,得S 2=2a 1+d =2+d . 因为{a n }是“H 数列”, 所以存在正整数m ,使得S 2=a m , 即2+d =1+(m -1)d ,于是(m -2)d =1. 因为d <0,所以m -2<0,故m =1.从而d =-1. 当d =-1时,a n =2-n ,S n =n-n 2是小于2的整数,n ∈N *.于是对任意的正整数n ,总存在正整数m =2-S n =2-n-n2,使得S n =2-m =a m , 所以{a n }是“H 数列”.因此d 的值为-1. (3)证明:设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d =na 1+(n -1)(d -a 1)(n ∈N *). 令b n =na 1,c n =(n -1)(d -a 1), 则a n =b n +c n (n ∈N *). 下证{b n }是“H 数列”. 设{b n }的前n 项和为T n ,则T n =n n +2a 1(n ∈N *).于是对任意的正整数n ,总存在正整数m =n n +2,使得T n =b m ,所以{b n }是“H 数列”. 同理可证{c n }也是“H 数列”. 所以,对任意的等差数列{a n },总存在两个“H 数列”{ b n }和{c n },使得a n =b n +c n (n ∈N *)成立.。
高三数学附加卷作业寒假作业参考答案

2019高三数学附加卷作业寒假作业参考答案寒假马上就要到了,同学们不要忘了在放松的时候还有寒假作业在等着我们去完成,下面是2019高三数学附加卷作业寒假作业参考答案,供学生参考。
一、A.(选修41:几何证明选讲)自圆O外一点引切线与圆切于点,为中点,过引割线交圆于,两点.求证: .证明:∵与圆相切于,,∵为中点,,B. 解由题知,四边形ABCD是直角梯形,其的面积为S1=3。
hellip,高中语文;3分A,B,C,D四点经矩阵M对应的变换后依次为7分因为A1D1与B1C1平行且距离为2,且四边形A1B1C1D1也是直角梯形,所以四边形A1B1C1D1的面积为综上所述,四边形ABCD与四边形A1B1C1D1的面积相等。
10分C.解:两圆的普通方程为:所以的最大值为:.D..证:由柯西不等式得,记为的面积,则ks5u ,故不等式成立.22. 解:(1)不能被4整除的数分为两类:①4个数均为奇数,概率为;②有3个为奇数,1个为2,其概率为所以不能被4整除的概率为.(2)X01234P(X)因为,所以23. 解:(1)设点的坐标为,由,得点是线段的中点,则,,又,w.w.w.k.s.5.u.c.o.m由,得,???????????①由,得t=y ????②由①②消去,得即为所求点的轨迹的方程(2)证明:设直线的斜率依次为,并记,,语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。
如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。
现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。
结果教师费劲,学生头疼。
分析完之后,学生收效甚微,没过几天便忘的一干二净。
造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。
常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。
首发天津市高三寒假作业2数学 含答案

【KS5U 首发】天津市2013-2014学年高三寒假作业(2)数学 Word 版含答案.doc第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人 得分一、选择题(题型注释)1.已知幂函数y=f (x )的图象过(4,2)点,则=( )A .B .C .D .2.已知向量(1,)a x =,(8,4)b =,且a b ⊥,则x =( ) A. 12B.2C. 2-D. 2± 3.B4.执行右图程序框图,如果输入的N 是6,那么输出的p 是( )A.120B.720C.1440D.50405.如右图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用x 代替,则这位运动员这8场比赛的得分平均数不小于得分中位数的概率为( )A .102B . 103C .106D .1076.已知抛物线x y M 4:2=,圆222)1(:r y x N =+-(其中r 为常数,r >0)过点)0,1(的直线l 交圆N 于D C ,两点,交抛物线M 于B A ,两点,且满足BD AC =的直线l 只有三条的必要条件是 ( )A .(0,1]r ∈ B. (1,2]r ∈ C. 3(,4)2r ∈ D. 3[,)2r ∈+∞7.若集合12{|,01}A y y x x ==<≤,1{|2,01}B y y x x==-<≤,则A B 等于( ) (A)(],1-∞ (B)(]0,1 (C)φ (D){1}8.函数)(x f y =为定义在R 上的减函数,函数)1(-=x f y 的图像关于点(1,0)对称, ,x y 满足不等式0)2()2(22≤-+-y y f x x f ,(1,2),(,)M N x y ,O 为坐标原点,则当41≤≤x 时,OM ON ⋅的取值范围为 ( ) A .[)+∞,12 B .[]3,0C .[]12,3D .[]12,00 1 2 7 8 0 7 x 9 3 1运动员第II 卷(非选择题)二、填空题(题型注释)9.命题“存在x ∈R,使得x2+2x+5=0”的否定是__________.10.函数)1lg()(-=x x f 的定义域是______________.11.在△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若2=a ,32=c ,3π=C ,则=b .12.在nx )3(-的展开式中,若第3项的系数为27,则=n .13.若圆1)1(22=-+y x 的圆心到直线:n l 0=+ny x (*N n ∈)的距离为n d ,则=∞→n n d lim .14.设1e 、2e 是平面内两个不平行的向量,若21e e +=与21e e m -=平行,则实数=m .三、解答题(题型注释)15.(本小题满分12分) 某市对该市小微企业资金短缺情况统计如下表:(I)试估计该市小微企业资金缺额的平均值;(II)某银行为更好的支持小微企业健康发展,从其第一批注资的A 行业3家小微企业和B 行业的2家小微企业中随机选取3家小微企业,进行跟踪调研.求选取的3家小微企业中A 行业的小微企业至少有2家的概率.16.(本小题满分12分)如图,在直三棱柱111ABC A B C -中,12=2AA AC AB ==,且11BC A C ⊥. (Ⅰ)求证:平面1ABC ⊥平面11A ACC ;(Ⅱ)设D 是11A C 的中点,判断并证明在线段1BB 上是否存在点E ,使DE ‖平面1ABC ;若存在,求三棱锥1E ABC -的体积.17.(本小题满分10分)已知关于x 的不等式2|21||1|log x x a +--≤(其中0a >)。
2019-2020寒假高三数学寒假作业二.doc

高三数学寒假作业二1. 设全集是(){}(){},2|,,,|,+==∈=x y y x A R y x y x U (),124|,⎭⎬⎫⎩⎨⎧=--=x y y x B 则=B C A U IA. φB. (2,4)C. BD. (){}4,22. 函数()2)1(22+-+=x a x x f 在区间(4,∞-)上是减函数,那么实数a 的取值范围是A. )[+∞,3B. (]3,-∞-C. {}3-D. (5,∞-)3. 已知不等式012≥--bx ax 的解集是⎥⎦⎤⎢⎣⎡--31,21,则不等式02<--a bx x 的解集是A. (2,3)B. ()(),32,+∞∞-YC. (21,31) D. () ⎝⎛∞+⎪⎭⎫∞-,2131,Y4. 关于函数),(33)(R x x f xx ∈-=-下列三个结论正确的是 ( )(1) )(x f 的值域为R; (2) )(x f 是R 上的增函数; (3) 0)()(,=+-∈∀x f x f R x 成立.A. (1)(2)(3)B. (1)(3)C. (1)(2)D. (2)(3)5. 若数列{}n a 满足),0(*N n q q a n n ∈>=,以下命题正确的是 ( )(1) {}n a 2是等比数列; (2) ⎭⎬⎫⎩⎨⎧n a 1是等比数列; (3) {}n a lg 是等差数列; (4) {}2lg n a 是等差数列;A. (1)(3)B. (3)(4)C. (1)(2)(3)(4)D.(2)(3)(4)6. 已知=+++=)2007()2()1(,3sin)(f f f n n f Λπ( ) A. 3 B. 23 C. 0 D. --237. 设βα,为钝角,=+-==βαβα,10103cos ,55sin ( ) A . π43 B. π45 C. π47 D. π45或π478. 已知函数)0)(3sin()(>+=ωπωx x f 的最小正周期为π,则该函数图象( )A. 关于点)0,3(π对称; B. 关于直线4π=x 对称; C. 关于点)0,4(π对称; D. 关于直线3π=x 对称;9. 已知向量b a ,夹角为︒60,=-⊥+==m b a m b a b a ),()53(,2,3 ( )A.2332B. 4229C. 4223D. 294210.编辑一个运算程序:1&1=2,m &n =k ,m &(n +1)=k +3(m 、n 、k *N ∈),1&2004的输出结果为( )A.2004B.2006C.4008D.601111. 已知点A(2,3),B(--3,--2).若直线l 过点P(1,1)且与线段AB 相交,则直线l 的斜率k 的取值范围是A. 43≥k B.243≤≤k C. 2≥k 或43≤k D. 2≤k 12. 设21,F F 分别是双曲线1922=-y x 的左右焦点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【原创】高三数学寒假作业(二)
一、
选择题,每小题只有一项是正确的。
1.设集合{}
{}212,log 2A x x B x x =-≤=<,则A B ⋃= A. []1,3-
B. [)1,4-
C. (]0,3
D. (),4-∞
2.已知函数sin ,0,()(1),0,
x x f x f x x π≤⎧=⎨->⎩那么)32
(f 的值为
A. 21-
B. 23-
C. 2
1
D. 23
3.已知函数f (x)=2
67,0,
100,,x x x x x ++<≥⎧⎪⎨⎪⎩
则 f (0)+f (-1)= ( )
(A) 9 (B)
7110
(C) 3 (D)
1110
4.已知函数()22x f x =-,则函数|()|y f x =的图像可能是………………………………..( )
5.若互不相等的实数c b a ,,成等差数列,b a c ,,成等比数列,且103=++c b a ,则
=a ( )
A. 4
B. 2
C. -2
D. -4 6.下列各式中值为
的是( )
A.sin45°cos15°+cos45°sin15°B.sin45°cos15°﹣cos45°sin15°C.c os75°cos30°+sin75°sin30°D.
7.设实数x,y满足条件
⎪
⎩
⎪
⎨
⎧
≥
≥
≥
+
-
≤
-
-
,0
8
2
10
4
y
x
y
x
y
x
,若目标函数z=ax+by(a>0,b>0)的
最大值为12,则23
a b
+的最小值为( )
8.已知函数()
f x满足1
()()
f x f
x
=, 当[]
1,3
x∈时,()ln
f x x
=,若在区间
1
,3
3
⎡⎤
⎢⎥
⎣⎦
内,曲线
()()
g x f x ax
=-与x轴有三个不同的交点,则实数a的取值范围是( )
A.10,
e
⎛⎫
⎪
⎝⎭
B.1
0,
2e
⎛⎫
⎪
⎝⎭
C.ln31,
3e
⎡⎫
⎪
⎢⎣⎭
D.ln31,
32e
⎡⎫
⎪
⎢⎣⎭
9.圆心在直线y=x上,经过原点,且在x轴上截得弦长为2的圆的方程为( )
A.(x-1)2+(y-1)2=2
B.(x-1)2+(y+1)2=2
C.(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2
D.(x-1)2+(y+1)2=或(x+1)2+(y-1)2=2
二、填空题
10.已知集合{}
|1
A x x
=≤,{}
|
B x x a
=≥,且A B R
⋃=,则实数a的取值范围是__________ .
11.理:已知集合{}0
,2>
=
=x
x
y y
M,{})
2
lg(2x
x
y
x
N-
=
=,则=
N
M I .
12.已知等差数列{}n a 的前n 项和为n S ,且1533a a a +=,1014a =,则12S =
13.抛物线24
1
x y -=上的动点M 到两定点(0,-1)、(1,-3)的距离之和的最小
值为 三、计算题
14.(本小题满分13分) 已知函数)1
2
(
log )(2
1--=x ax x f (a 为常数). (1)若常数2a <且0a ≠,求()f x 的定义域;
(2)若()f x 在区间(2,4)上是减函数,求a 的取值范围. 15.(本小题满分12分)
已知直三棱柱111C B A ABC -中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =1AA ,D 、E 、F 分别为A B 1、C C 1、BC 的中点. (1)求证:DE ∥平面ABC ; (2)求证:F B 1⊥平面AEF ; (3)求二面角F AE B --1的余弦值.。
