2023年高三数学寒假作业16(Word含答案解析)

合集下载

高二数学寒假作业：(四)(Word版含答案)

高二数学寒假作业（四）一、选择题，每小题只有一项是正确的。

1.公比为2的等比数列{an)的各项都是正数，且=16，则a6等于A ．1B ．2C ．4D ．82.等比数列{a n }的前n 项和为S n ，已知S 3＝a 2＋10a 1，a 5＝9，则a 1＝( )3.一个有11项的等差数列，奇数项之和为30，则它的中间项为( ) A ．8 B ．7 C ．6D ．54.在ABC △中，已知4,6a b ==，60B =，则sin A 的值为A.26 B. 23 C. 36D. 335.在060,20,40===∆C c b ABC 中，已知，则此三角形的解为（） A.有一解 B.有两解 C.无解 D.有解但解的个数不确定6.若n ＝(1，－2,2)是平面α的一个法向量，则下列向量能作为平面α法向量的是 A ．(1，－2,0) B ．(0，－2,2) C ．(2，－4,4) D ．(2,4, 4)7.已知点(3,1,4)A --，(3,5,10)B -则线段AB 的中点M 的坐标为（） A. ()0,4,6-B. ()0,2,3-C. ()0,2,3D. ()0,2,6-8.已知椭圆12222=+b x a y ( a > b > 0) 的离心率为1e ，准线为1l 、2l ；双曲线132222=-b y a x 离心率为2e ，准线为3l 、4l ；；若1l 、2l 、3l 、4l 正好围成一个正方形，则21e e 等于（）A.33 B .36 C.22D. 2 9.下列命题是真命题的为 ( ) A ．若11x y=,则x y = B ．若21x =,则1x =C ．若x y =,D ．若x y <,则 22x y <二、填空题10.已知条件p ：1≤x ，条件q ：11<x，则p ⌝是q 的_____________________条件. 11.已知x 、y 满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ，则y x z 42+=的最小值为 .12.设椭圆22162x y +=和双曲线2213x y -=的公共焦点为1F ,2F ,P 是两曲线的一个交点，12cos PF F ∠的值是。

上海市2014届高三寒假作业数学1Word版含答案

高三数学寒假作业满分150分，考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分，共56分)： 1、已知i 2321+-=ω，则行列式=111222ωωωωωω2、函数2()43(3)f x x x x =-++≥的反函数是1()f x -，则1(9)f --的值是_______3、已知等差数列{}n a 的前n 项和为n S ，且111634a a a +=-，则11S = 。

4、已知向量a,b 夹角为60,2,1a b ==，则b a -=_________. 5、若集合|,3A x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭，{}|22B x x =-≤≤，则B A =________ 6、如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><的图象，则其解析式是___.7、在集合{|,1,2,,10}6n M x x n π=== 中任取一个元素，所取元素恰好满足方程1cos 2x = 的概率是_________8、若行列式,021421=-x 则=x ▲． 9、阅读右面的程序框图，则输出的S = .10、设AB 是椭圆Γ的长轴，点C 在Γ上，且4CBA π∠=，若AB=4，BC =，则Γ的两个焦点之间的距离为________11、已知关于x 的不等式x 2-ax ＋2a ＞0在R 上恒成立，则实数a 的取值范围是_________. 12、设函数()f x 在(0,)+∞内可导,且()x x f e x e =+,则(1)x f =______________ 13、在xOy 平面上，将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y =和1y =-围成的封闭图形记为D ，如图中阴影部分．记D 绕y 轴旋转一周而成的几何体为Ω，过(0,)(||1)y y ≤作Ω的水平截面，所得截面面积为48π，试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为__________ 14、关于函数()(sin cos )cos f x x x x =+⋅，给出下列命题： ①()f x 的最小正周期为2π； ②()f x 在区间(0,)8π上为增函数；③直线38x π=-是函数()f x 图像的一条对称轴； ④对任意x R ∈，恒有()()14f x f x π-+-=。

山东省重点高中高三数学寒假作业10Word版含答案

新课标高三数学寒假作业10一、选择题.1.已知命题p ：?x ∈R ，sinx ≤１，则￢p 为() A ．?x ∈R ，sinx ≥１B ．?x ∈R ，sinx ≥１C ．?x ∈R ，sinx ＞1D ．?x ∈R ，sinx ＞1 2.已知函数)(x f 是R 上的增函数，(0,2)A ，(3,2)B 是其图象上的两点，那么2|)1(|x f 的解集是（）A ．（1，4）B ．（-1，2）C ．),4[)1,(D ．),2[)1,(3.若{a n }为等差数列，S n 是其前n 项和，且，则tana 6的值为() A ．B ．C ．D ．4.log 2sin +log 2sin +log 2sin π=( )A ．﹣3B ．﹣1C ．1D ．35.已知向量=（2，2），=（4，1），点P 在x 轴上，则?取最小值时P 点坐标是( )A ．（﹣3，0）B ．（1，0）C ．（2，0）D ．（3，0）6.若实数经，x ，y 满足，则z=y ﹣x 的最小值为（）A ． 0B ． 1C ． 2D ． 37.某几何体的三视图如图，则该几何体的表面积为( )A ．3+3B ．8+3C ．6+6D ．8+68.（5分）执行如图所示的程序框图，则输出S 的值等于（）A ．B ．C ．D ．9.（5分）已知O 为坐标原点，A 、B 为曲线y=上的两个不同点，若?=6，则直线AB 与圆x 2+y 2=的位置关系是（） A ．相交 B ．相离 C ．相交或相切 D ．相切或相离10.双曲线221x ym 的离心率3e ，则以双曲线的两条渐近线与抛物线2y mx 的交点为顶点的三角形的面积为A ．42B ．122C ．82D ．162二．填空题.11.在数列n a 中，已知111,(1)cos(1)n n n a a a n ，记n S 为数列n a 的前n 项和，则2015S . 12.已知ABC 中，设三个内角C B A ,,所对的边长分别为c b a ,,，且6,3,1A b a , 则c =．13.点M(x ，y)是不等式组表示的平面区域Ω内的一动点，使z ＝y －2x 的值取得最小的点为A(x 0，y 0)，则(O 为坐标原点)的取值范围是________．14.（5分）设变量x，y满足，则z=|x﹣3y|的最大值为．三、解答题.15.（13分）函数．（1）若f（x）在点（1，f（1））处的切线斜率为，求实数a的值；（2）若f（x）在x=1取得极值，求函数f（x）的单调区间．16.已知椭圆C：+=1（a＞b＞0）的左，右焦点分别为F1，F2，上顶点为B．Q为抛物线y2=12x 的焦点，且?=0，2+=0．（Ⅰ）求椭圆C的标准方程；（Ⅱ）过定点P（0，2）的直线l与椭圆C交于M，N两点（M在P，N之间），设直线l的斜率为k （k＞0），在x轴上是否存在点A（m，0），使得以AM，AN为邻边的平行四边形为菱形？若存在，求出实数m的取值范围；若不存在，请说明理由．17.（14分）（2007?天津）设函数f（x）=﹣x（x﹣a）2（x∈R），其中a∈R．（Ⅰ）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；（Ⅱ）当a≠０时，求函数f（x）的极大值和极小值；（Ⅲ）当a＞3时，证明存在k∈，使得不等式f（k﹣cosx）≥ｆ（k2﹣cos2x）对任意的x∈R恒成立．。

高三数学寒假作业十五(含答案)

高三数学寒假作业十五一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程） 1．已知集合A ＝{}220x x x -≤，B ＝{﹣1，1，2}，则AB ＝．2．设复数21iz =+（其中i 为虚数单位），则z ＝． 3．右图是一个算法的伪代码，则输出的结果是．4．顶点在原点且以双曲线221124x y -=的右焦点为焦点的抛物线方程是．第3题 5．已知在平面直角坐标系xOy 中，直线l 1：20x my m -+-=，l 2：(2)10mx m y +--=，若直线l 1∥l 2，则m ＝．6．从“1，2，3，4，5”这组数据中随机去掉两个不同的数，则剩余三个数能构成等差数列的概率是．7．若实数x ，y 满足条件1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩，则32z x y =+的最大值为．8．将函数()cos 2f x x =的图象向左平移6π个单位长度后，再将图象上各点的纵坐标变为原来的2倍，得到函数()y g x =的图象，则()4g π＝．9．已知正方体ABCD —A 1B 1C 1D 1棱长为1，点E 是棱AD 上的任意一点，点F 是棱B 1C 1上的任意一点，则三棱锥B —ECF 的体积为．10．等比数列{}n a 的前三项和342S =，若1a ，23a +，3a 成等差数列，则公比q ＝．11．记集合A ＝[a ，b ]，当θ∈[6π-，4π]时，函数2()23sin cos 2cos f θθθθ=+的值域为B ，若“A x ∈”是“B x ∈”的必要条件，则b ﹣a 的最小值是．12．已知函数331()0()220x x x x f x x x ⎧-+<⎪=⎨⎪--≥⎩，，，若对任意的x ∈[m ，m ＋1]，不等式(1)f x -≤()f x m +恒成立，则实数m 的取值范围是．13．过直线l ：2y x =-上任意一点P 作圆C ：221x y +=的一条切线，切点为A ，若存在定点B(0x ，0y )，使得PA ＝PB 恒成立，则0x ﹣0y ＝．14．在平面直角坐标系xOy 中，已知三个点A(2，1)，B(1，﹣2)，C(3，﹣1)，点P(x ，y )满足(OP OA)(OP OB)1⋅⨯⋅=-，则2OP OC OP⋅的最大值为．二、解答题（本大题共6小题，共计90分．解答应写出文字说明，证明过程或演算步骤．） 15．（本题满分14分）在四棱锥P —ABCD 中，底面ABCD 是平行四边形，E 是AP 的中点，AB ⊥BD, PB ⊥PD ，平面PBD ⊥底面ABCD ．（1）求证：PC ∥平面BDE ；（2）求证：PD ⊥平面PAB ．16．（本题满分14分）如图，在△ABC 中，点D 是边BC 上一点，AB ＝14，BD ＝6，BA BD 66⋅=．（1）若C ＞B ，且cos(C ﹣B)＝1314，求角C ；（2）若△ACD 的面积为S ，且1CA CD 2S =⋅，求AC 的长度．17．（本题满分14分）在平面直角坐标系xOy中，椭圆E：22221x ya b+=(a＞b＞0)的长轴长为4，左准线l的方程为x＝﹣4．（1）求椭圆的标准方程；（2）直线l1过椭圆E的左焦点F1，且与椭圆E交于A，B两点．①若AB＝247，求直线l1的方程；②过A作左准线l的垂线，垂足为A1，点G(52-，0)，求证：A1，B，G三点共线．18．（本题满分16分）某游乐场过山车轨道在同一竖直钢架平面内，如图所示，矩形PQRS的长PS为130米，宽RS为120米，圆弧形轨道所在圆的圆心为O，圆O与PS，SR，QR分别相切于点A，D，C，T为PQ的中点．现欲设计过山车轨道，轨道由五段连接而成．出发点N在线段PT 上（不含端点，游客从点Q处乘升降电梯至点N），轨道第一段NM与圆O相切于点M，再沿着圆弧轨道MA到达最高点A，然后在点A处沿垂直轨道急速下降至点O处，接着沿直线轨道OG滑行至地面点G处（设计要求M，O，G三点共线），最后通过制动装置减速沿水平轨道GR滑行到达终点R．记∠MOT为α，轨道总长度为l米．lα，并写出α的取值范围；（1）试将l表示为α的函数()（2）求l最小时cosα的值．19．（本题满分16分）已知函数2()ln ()f x x a x x =+-(a ∈R)．（1）当a ＝0，证明：()1f x x <-；（2）如果函数()f x 有两个极值点1x ，2x (1x ＜2x )，且12()()f x f x k +<恒成立，求实数k 的取值范围；（3）当a ＜0时，求函数()f x 的零点个数．20．（本题满分16分）已知N n *∈，数列{}n a 的前n 项和为n S ，且11n n S a a +=-；数列{}n b 的前n 项和为n T ，且满足1(1)2n n n T b n n b +=++，且12a b =．（1）求数列{}n a 的通项公式；（2）求数列{}n b 的通项公式；（3）设n n na cb =，问：数列{}n c 中是否存在不同两项i c ，j c （1≤i ＜j ，i ，j N *∈），使i c ＋j c 仍是数列{}n c 中的项?，j ；若不存在，请说明理由．高三数学寒假作业十五参考答案11．3 12．13．14．15．16．17．18．19．20．高三数学寒假作业十五(含答案)11。

高一寒假作业数学试题第十六天 Word版含答案

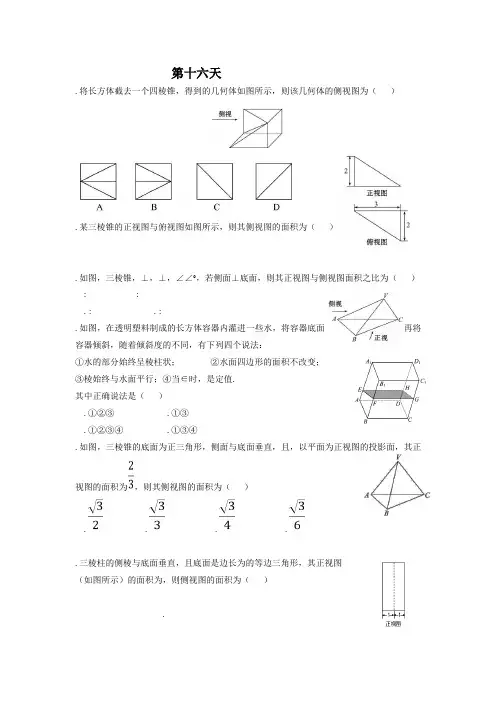
第十六天.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为（）.某三棱锥的正视图与俯视图如图所示，则其侧视图的面积为（）.如图，三棱锥，⊥，⊥，∠∠°，若侧面⊥底面，则其正视图与侧视图面积之比为（）::.: .:.如图，在透明塑料制成的长方体容器内灌进一些水，将容器底面一边固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：①水的部分始终呈棱柱状；②水面四边形的面积不改变；③棱始终与水面平行；④当∈时，是定值.其中正确说法是（）.①②③ .①③.①②③④ .①③④.如图，三棱锥的底面为正三角形，侧面与底面垂直，且，以平面为正视图的投影面，其正视图的面积为，则其侧视图的面积为（）.....三棱柱的侧棱与底面垂直，且底面是边长为的等边三角形，其正视图（如图所示）的面积为，则侧视图的面积为（）..多面体的底面为矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则的长为（）. . ..一个几何体的三视图如图所示，其中正视图和侧视图是腰长为的两个全等的等腰直角三角形. 用多少个这样的几何体可以拼成一个棱长为的正方体（）个个个.个.如图，网格纸上正方形小格的边长为（表示），图中粗线画出的是某零件的三视图，该零件由一个底面半径为，高为的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）.....某空间几何体的三视图如图所示，则这个空间几何体的表面积是（）ππππ.一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的（填入所有可能的几何体的编号）.①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱.。

上海市2014届高三寒假作业数学2Word版含答案

高三数学寒假作业满分150分，考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分，共56分)： 1、若0)231(=-∞→nn x lin ，则实数x 的取值范围是____________; 2、函数)1(log )(2-=x x f )21(≤<x 的反函数=-)(1x f.3、数列{}n a 是公差不为0的等差数列，且862a a a =+，则=55a S ． 4、已知向量2)(,6||,1||=-⋅==，则向量与向量的夹角是__________. 5、已知集合A ＝{x ||x －1|<2}，B ＝{x | 02x bx -<+}，若A ∩B ≠φ，则实数b 的取值范围是________．6、在ABC ∆中，内角,,A B C 的对边分别为,,c a b ，若22,sin a b C B -==，则A =__________.7、如右图，该程序运行后输出的结果为．8、设非零常数d 是等差数列12319,,,,x x x x 的公差，随机变量ξ等可能地取值12319,,,,x x x x ，则方差_______D ξ=9、已知直线1)13()2(--=-x a y a ，为使这条直线不经过第二象限，则实数a 的范围是 10、已知实数x 、y 满足方程()()22111x a y -++-=，当0y b ≤≤（b R ∈）时，由此方程可以确定一个偶函数()y f x =，则抛物线212y x =-的焦点F 到点(,)a b 的轨迹上点的距离最大值为____________.11、四棱锥P —ABCD ABCD 是边长为2的正方形，则CD 与PA 所成角的余弦值为 .12、设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则)122sin(π+a 的值为 ▲ ．13、函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为__________.14、下列五个命题中，正确的命题的序号是_____________. ①函数2tanxy =的图象的对称中心是Z k k ∈),0,(π； ②)(x f 在()b a ,上连续，()()0)()(0,,00<=∈b f a f x f b a x 则且； ③函数)32sin(3π+=x y 的图象可由函数x y 2sin 3=的图象向右平移3π个单位得到； ④)(x f 在R 上的导数)1(2)2(,0)()(),(f f x f x f x x f <<-''则且； ⑤函数)2cos 21ln(x y +=的递减区间是⎪⎭⎫⎢⎣⎡+4,πππk k ()Z k ∈. 二、选择题（每题5分，共20分）： 15、已知函数1()ln 2(0),f x x x x=-+>则函数)(x f 的零点个数是（） A.0 B.1 C.2 D.316、连掷两次骰子得到的点数分别为m 和n ,若记向量()m n，a =与向量(12)=- ，b 的夹角为θ,则θ为锐角的概率是 .17、已知1l 、2l 、3l 是空间三条不同的直线，下列命题中正确的是（）.A 如果21l l ⊥ ，32//l l ．则31l l ⊥． .B 如果21//l l ，32//l l ．则1l 、2l 、3l 共面． .C 如果21l l ⊥ ，32l l ⊥．则31l l ⊥． .D 如果1l 、2l 、3l 共点．则1l 、2l 、3l 共面．18、已知点F 1、F 2分别是椭圆22221x y a b+=的左、右焦点，过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点，若△ABF 2为正三角形，则该椭圆的离心率e 为（）（A ）12 （B ）（C ）13（D三、解答题（本大题满分74分）：19、（本题满分12分）已知真命题:“函数()y f x =的图像关于点( )P a b 、成中心对称图形”的充要条件为“函数()y f x a b =+- 是奇函数”.(1)将函数32()3g x x x =-的图像向左平移1个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数()g x 图像对称中心的坐标; (2)求函数22()log 4xh x x=- 图像对称中心的坐标; (3)已知命题:“函数 ()y f x =的图像关于某直线成轴对称图像”的充要条件为“存在实数a 和b,使得函数()y f x a b =+- 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).20、（本题满分14分）已知数列{}n a 的首项14a =，前n 项和为n S ，且+n+1n -3S -2n-4=0(n N )S ∈ （1）求数列{}n a 的通项公式；（2）设函数23121()n n n n f x a x a x a x a x --=++++ ，/()f x 是函数()f x 的导函数，令/(1)n b f =，求数列{}n b 的通项公式，并研究其单调性。

上海市2014届高三寒假作业数学4Word版含答案

高三数学寒假作业满分150分，考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分，共56分)：1、复数5i2i =+ ． 2、已知,a b 均为单位向量，且它们的夹角为60°，当||()a b R λλ-∈取最小值时，λ=___________．3、已知集合⎭⎬⎫⎩⎨⎧∈==R x y y A x ,21|，{}R x x y y B ∈-==),1(log |2，则=⋂B A ▲ ．4、求值：002cos10sin 20cos 20-= ．5、在锐角ABC ∆中，1,2,BC B A ==则AC 的取值范围为 ______6、盒子中装有编号为1，2，3，4，5，6，7的七个球，从中任意取出两个，则这两个球的编号之积为偶数的概率是（结果用最简分数表示）.7、执行右面的程序框图，若输出的3132S =，则输入的整数p 的值为__________．8、设m 为常数，若点(0,5)F 是双曲线2219y x m -=的一个焦点，则m = 。

9、不等式的解集是___________。

10、曲线y =x (3ln x +1)在点)1,1(处的切线方程为________11、给定区域D :4440x y x y x +≥⎧⎪+≤⎨⎪≥⎩,令点集()()000000{,|,,,T x y D x y Z x y =∈∈,是z x y =+在D 上取得最大值或最小值的点},则T 中的点共确定______条不同的直线.12、若22221231111,,,x S x dx S dx S e dx x ===⎰⎰⎰则123S S S 的大小关系为________________.13、已知函数()y f x =的图像是折线段ABC ，其中(0,0)A 、1(,1)2B 、(1,0)C ，函数()y xf x =（01x ≤≤）的图像与x 轴围成的图形的面积为14、已知数列，圆，圆，若圆C 2平分圆C 1的周长，则的所有项的和为 .二、选择题（每题5分，共20分）：15、当210≤<x 时x a x log 4<，则a 的取值范围是（）A )22,0( B )1,22( C )2,1( D )2,2( 16、下列判断正确的是（）A ．棱柱中只能有两个面可以互相平行B ．底面是正方形的直四棱柱是正四棱柱C ．底面是正六边形的棱台是正六棱台D ．底面是正方形的四棱锥是正四棱锥17、双曲线22221124x y m m-=+-的焦距为（）Ａ．４Ｂ．Ｃ．８Ｄ．与m 无关18、棱长为1的正三棱柱111C B A ABC -中，异面直线1AB 与BC 所成角的大小为三、解答题（本大题满分74分）： 19、（本题满分12分）在△ABC 中，内角,,A B C 所对的边分别为,,a b c ，已知s i n (t a n t a n )t a n t aB AC A C +=. (Ⅰ)求证：,,a b c 成等比数列； (Ⅱ)若1,2a c ==，求△ABC 的面积S .20、（本题满分14分）设函数22()(1)f x ax a x =-+,其中0a >,区间|()>0I x f x =(Ⅰ)求的长度(注:区间(,)αβ的长度定义为βα-); (Ⅱ)给定常数(0,1)k ∈,当时,求l 长度的最小值.21、（本题满分14分）如图,在三棱锥ABC S -中,平面⊥S A B 平面S B C ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.22、（本题满分16分）正项数列{}n a 的前n 项和n S 满足:222(1)()0n n S n n S n n -+--+=． (1)求数列{}n a 的通项公式n a ; (2)令221(2)n nn b n a +=+,数列{}n b 的前n 项和为n T ，证明:对于任意的*n N ∈,都有564n T <． 23、（本题满分18分）已知函数a ax x a x x f ---+=232131)(，x 其中a>0.（I ）求函数)(x f 的单调区间；（II ）若函数)(x f 在区间（-2，0）内恰有两个零点，求a 的取值范围；（III ）当a=1时，设函数)(x f 在区间]3,[+t t 上的最大值为M （t ），最小值为m （t ）,记g(t)=M(t)-m(t),求函数g(t)在区间]1,3[--上的最小值。

上海市2014届高三寒假作业数学6Word版含答案

高三数学寒假作业满分150分，考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分，共56分)：1、若2()(1)1f x x a x =+-+是定义在R 上的偶函数，则实数a=________. 2、设1111()1232f n n n n n=+++++++ ，则 2lim [(1)()]n n f n f n →∞+-=___________.3、设O 是ABC ∆的三边中垂线的交点，,,a b c 分别为角,,A B C对应的边，已知4、满足条件｛0，1｝∪A={0,1}的所有集合A 的个数是个5、已知函数f(x)＝R x x x ∈--+,12cos 3)4(sin 22π，若函数)()(a x f x h +=的图象关于点)0,3(π-对称，且),,0(π∈a 则a 的值为________．6、把4个不同的球任意投入4个不同的盒子内（每盒装球数不限），则无空盒的概率为________.7x b =+有实根，则实数b 的取值范围是 .8、如图，过抛物线22(0)y px p =>的焦点F 的直线l 依次交抛物线及其准线于点A 、B 、C ，若|BC|=2|BF|，且|AF|=3，则抛物线的方程是。

9、在△ABC 中，若222sin sin sin A B C +<，则△ABC 的形状是__________________.10、设y kx z +=,其中实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥-+04204202y x y x y x ,若z 的最大值为12,则实数=k ________.11、直线l 过抛物线C : x 2=4y 的焦点且与y 轴垂直,则l 与C 所围成的图形的面积等于__________. 12、设()g x 是定义在R 上，以1为周期的函数，若函数()()f x x g x =+在区间[0,1]上的值域为[2,5]-，则()f x 在区间[0,3]上的值域为____________________. 13、已知函数()y =f x 满足(+1)=(-1)f x f x ，且[1,1]x ∈-时，2()=f x x ,则函数()y =f x 与3log y =|x |的图象的交点的个数是 .14、函数()f x 的定义域为A ，若12,x x A ∈且12()()f x f x =时总有12x x =，则称()f x 为单函数．例如，函数()f x =2x+1(x ∈R )是单函数．下列命题：①函数2()f x x =（x ∈R ）是单函数；②若()f x 为单函数，12,x x A ∈且12x x ≠，则12()()f x f x ≠； ③若f ：A→B 为单函数，则对于任意b B ∈，它至多有一个原象； ④函数()f x 在某区间上具有单调性，则()f x 一定是单函数．其中的真命题是_________．（写出所有真命题的编号）二、选择题（每题5分，共20分）：15、用数学归纳法证明4221232n n n ++++⋅⋅⋅+=，则当1n k =+时左端应在n=k 的基础上加上 A.21k + B.()21k +C.()()42112k k +++D.()()()()22221231k k k k ++++++⋅⋅⋅++16、设0a >且1a ≠，则“函数()x f x a =”在R 上是增函数”是“函数()ag x x =”“在(0,)+∞上是增函数”的(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 17、已知m ，n 是两条不同的直线，α为平面，则下列命题正确的是 (A) //,////m n m n αα若则 (B),,m n m n αα⊥⊥⊥若则 (C),//,m n m n αα⊥⊥若则(D)若m 与α相交，n 与α相交，则m,n 一定不相交18、已知圆()()221:231C x y -+-=,圆()()222:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN +的最小值为（）A．4B1C．6-D三、解答题（本大题满分74分）：19、（本题满分12分）()sin()f x A x ωϕ=+（其中0,0,A ωπϕπ>>-<< ）在6x π=处取得最大值2，其图象与轴的相邻两个交点的距离为2π（I ）求()f x 的解析式；（II ）求函数426cos sin 1()()6x x g x f x π--=+的值域。

湖南省长沙市2023-2024学年高二上学期寒假作业检测数学试卷含答案

2023年高二寒假作业检测试卷数学（答案在最后）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共8页.时量120分钟.满分150分.第I 卷一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知数列{}n a 为等比数列，则“5a ，7a 是方程2202210x x ++=的两实根”是”61a =，或61a=-”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据等比数列的性质，利用充分条件和必要条件的定义进行判断即可．【详解】解：在等比数列中，若5a ，7a 是方程2202210x x ++=的两实根，571a a ∴=，5720220a a +=-<，则50a <，70a <，则57661a a a a ==，则61a =或61a =-，即充分性成立，当61a =，或61a =-时，能推出57661a a a a ==，但无法推出572022a a +=-，即必要性不成立，即“5a ，7a 是方程2202210x x ++=的两实根”是“61a =，或61a =-”的充分不必要条件，故选：A ．2.某中学高三（1）班有50名学生，在一次高三模拟考试中，经统计得：数学成绩(110,100)X N ~，则估计该班数学得分大于120分的学生人数为（）（参考数据：()0.68,(2)0.95P X P X μσμσ-<≈-<≈）A.16B.10C.8D.2【答案】C 【解析】【分析】根据正态分布的性质，结合题中所给的公式进行求解即可.【详解】因为数学成绩(110,100)X N ~，所以110,10μσ==，因此由1(11010)0.68(100120)0.68(110120)0.680.34,2P X P X P X -<≈⇒<<≈⇒<<≈⨯=所以有11(120)(110120)]0.340.1622P X P X ≥=-<<=-=，估计该班数学得分大于120分的学生人数为0.16508⨯=，故选：C 3.若21π2cos cos 23αα⎛⎫-=+ ⎪⎝⎭，则tan 2α的值为（）A.3-B.3C. D.【答案】D 【解析】【分析】利用两角差的余弦公式和二倍角的正弦公式化简题给条件，得到三角函数齐次式，进而求得tan 2α的值【详解】2221112cos 2cos sin sin 21cos 2sin 23222π222ααααααα⎛⎫⎛⎫-=+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭由11cos 2sin 21cos 222ααα-=+，可得32cos 222αα=又cos 20α≠，则tan 2α=故选：D4.按从小到大顺序排列的9个数据：10，16，25，33，39，43，m ，65，70，若这组数据的第一四分位数与第三四分位数的和是73，则m 等于（）A.40B.48C.50D.57【答案】B 【解析】【分析】利用百分位数的求法，分别求出第一四分位数与第三四分位数，进而求出m 的值.【详解】对于已知9个数据：1016253339,43,,6570m ,,,,,， 925% 2.25⨯=，∴第一四分位数为25，975% 6.75⨯= ，∴第三四分位数为m ，2573m ∴+=，解得48m =.故选：B.5.若函数()sin 6f x x πω⎛⎫=+ ⎪⎝⎭（0ω>）在,44ππ⎛⎫- ⎪⎝⎭有最大值无最小值，则ω的取值范围是（）A.48,33⎛⎫⎪⎝⎭B.48,33⎛⎤⎥⎝⎦C.416,33⎛⎫⎪⎝⎭D.416,33⎛⎤⎥⎝⎦【答案】B 【解析】【分析】求出,64646x ππωππωπω⎛⎫+∈-++ ⎪⎝⎭，根据题意结合正弦函数图象可得答案.【详解】∵,44x ππ⎛⎫∈-⎪⎝⎭，∴,64646x ππωππωπω⎛⎫+∈-++ ⎪⎝⎭，根据题意结合正弦函数图象可得46232462πωππππωππ⎧-+≥-⎪⎪⎨⎪<+≤⎪⎩，解得4833ω<≤.故选：B.6.椭圆C ：()222210y x a b a b+=>>的上顶点为A ，点P ，Q 均在C 上，且关于x 轴对称，若直线AP ，AQ的斜率之积为43，则C 的离心率为（）A.2B.2C.12D.13【答案】C 【解析】【分析】设P 点坐标，Q 点与P 点关于x 轴对称，坐标可用P 点坐标表示，代入斜率之积的关系式，再结合椭圆方程，化简可得a 与b 的关系，即可求出离心率.【详解】()0,A a ，设()11,P x y ，则()11,Q x y -，则11AP y a k x -=，11AQ y ak x --=，22111211143AP AQy a y a a y k k x x x ----⋅=⋅==，又2211221y x a b +=，则()2221212b a y x a -=，所以()222122221243a y a b b a y a -==-，即2234b a =，所以椭圆C的离心率12c e a ===，故选：C.7.在平面内，定点A ，B ，C ，D 满足DA =DB =DC ,DA ⋅ DB =DB ⋅ DC =DC ⋅ DA=–2，动点P ，M满足AP =1，PM =MC，则2BM 的最大值是A.434B.494C.37634+ D.372334+【答案】B 【解析】【详解】试题分析：由已知易得120,2ADC ADB BDC DA DB DC ∠=∠=∠=︒===.以D 为原点，直线DA 为x 轴建立平面直角坐标系，如图所示，则()((2,0,1,,.A B C ---设(),,P x y 由已知1AP = ，得()2221x y -+=，又13133,,,,,2222x y x y PM MC M BM ⎛⎫⎛⎫-+++=∴∴= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ()(222+14x y BM ++∴=，它表示圆()2221x y -+=上的点()x y ，与点(1,--的距离的平方的14，()22max149144BM⎫∴==⎪⎭，故选B.【考点】平面向量的数量积运算，向量的夹角，解析几何中与圆有关的最值问题【名师点睛】本题考查平面向量的夹角与向量的模，由于结论是要求向量模的平方的最大值，因此我们要把它用一个参数表示出来，解题时首先对条件进行化简变形，本题中得出120ADC ADB BDC ∠=∠=∠=︒，且2DA DB DC ===，因此我们采用解析法，即建立直角坐标系，写出点,,,A B C D 的坐标，同时动点P 的轨迹是圆，则()(22214x y BM +++=，因此可用圆的性质得出最值．因此本题又考查了数形结合的数学思想．8.甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球（球除颜色外，大小质地均相同）.先从甲罐中随机取出一球放入乙罐，分别以1A ，2A 和3A 表示由甲罐中取出的球是红球，白球和黑球的事件；再从乙罐中随机取出一球，以B 表示由乙罐中取出的球是红球的事件.下列结论正确的个数是（）①事件1A 与2A 相互独立②24()11P B A =∣③9()22P B =④14()9P A B =∣A.4 B.3C.2D.1【答案】C 【解析】【分析】根据独立事件的概念判断①，计算条件概率判断②，根据全概率公式求解判断②④，即可回答.【详解】显然，1A ，2A ，3A 是两两互斥的事件，且()1515232P A ==++，()2215235P A ==++，而1212(())0()P A A P A P A =≠⋅，①错误；()2215235P A ==++，()214451155P A B =⨯=，所以()2411P B A =，②正确；()()()()()()1122331541349()211115101122P B P B A P A P B A P A P B A P A =⋅+⋅+⋅=⨯+⨯+⨯=，③正确；()()111552119()922P A B P A B P B ⨯===，④错误，综上：结论正确的个数为2.故选：C.二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分）9.关于x ，y 的方程2222124x y m m+=+-(其中24m ≠)表示的曲线可能是（）A.焦点在y 轴上的双曲线B.圆心为坐标原点的圆C.焦点在x 轴上的双曲线D.长轴长为的椭圆【答案】BC 【解析】【分析】根据各曲线的定义逐项验证参数的取值即可得出答案.【详解】解：对于A ：若曲线表示焦点在y 轴上的双曲线，则220m +<，无解，选项A 错误；对于B ：若曲线表示圆心为坐标原点的圆，则2224m m +=-，解得1m =±，选项B 正确；对于C ：若曲线表示焦点在x 轴上的双曲线，则240m -<，所以m>2或2m <-，选项C 正确；对于D：若曲线表示长轴长为的椭圆，则2a =a =，则22240242m m m a ⎧->⎪+>-⎨⎪=⎩或22240242m m m a⎧->⎪+<-⎨⎪=⎩，无解，选项D 错误.故选：BC.10.早在西元前6世纪，毕达哥拉斯学派已经知道算术中项，几何中项以及调和中项，毕达哥拉斯哲学家阿契塔在《论音乐》中定义了上述三类中项，其中，算术中项，几何中项的定义与今天大致相同，而今我们称2a b+为正数a ，ba ，b的几何平均数，并把这两者结合的不等式()0,02a b a b +≤>>叫做基本不等式，下列与基本不等式有关的命题中正确的是（）A.若0a >，0b >，21a b +=，则1142a b+≥B.若0a >，0b >，11133a b a b+=++，则+a b 的最小值为1C.若0a >，0b >，2210b ab +-=，则+2a b 的最小值为3+12D.0a >，0b >，4a b +=，则2222a b a b +++的最小值为2【答案】ABD 【解析】【分析】根据给定条件，利用均值不等式逐项计算判断作答.【详解】对于A ，0a >，0b >，21a b +=，则11112(2)()224222b a a b a b a b a b +=++=++≥+，当且仅当22b a a b=，即122a b ==时取等号，A 正确；对于B ，0a >，0b >，11133a b a b+=++，则1[(3)(311)]43(3a b a b a b a b a b +=++++++11(2)1433433a b a b a b a b ++=++≥+=++，当且仅当3333a b a b a b a b =++++，即12a b ==时取等号，B 正确；对于C ，0a >，0b >，2210b ab +-=，则有122b a b =-，13+222b a b b =+≥，当且仅当1322b b =，即3b =时取等号，由122b a b =-及3b =得：3a b ==，所以当3a b ==时，+2a bC 不正确；对于D ，0a >，0b >，4a b +=，则8(2)(2)a b =+++≥，当且仅当2a b ==时取等号，因此，当2a b ==时，(2)(2)a b ++取得最大值16，222222222224222()32222(2)(2)(2)(2)(2)(2)(2)(2)a b a b ab a b ab a b a b a b a b a b a b a b +++++++====≥++++++++++，所以当2a b ==时，2222a b a b +++的最小值为2，D 正确.故选：ABD11.（多选）,,a b c 分别为ABC 内角,,A B C 的对边，已知sin (3)sin b A b c B =-，且1cos 3A =，则（）A.3a c b +=B.tan A =C.ABC 的周长为4cD.ABC 的面积为29c 【答案】ABD【解析】【分析】由正弦定理得()3ba b c b =-，即可判断A 选项；由平方关系及商数关系即可判断B 选项；先由余弦定理得32b c =，再求出周长即可判断C 选项；先求得2,3a cb a ==，再求面积即可判断D 选项.【详解】由正弦定理得()3ba b c b =-，整理得3a b c =-，即3a c b +=，A 正确；由1cos 3A =可得22sin 3A ==，则sin tan cos A A A ==B 正确；由余弦定理得2222cos a b c bc A =+-，又3a b c =-，可得()2221323b c b c bc -=+-⋅，整理得32b c =，ABC 的周长为843a b c b c ++==，C 错误；由上知：3a b c =-，32b c =，可得2,3a cb a ==，则ABC 的面积为22112sin 223399bc A a a a c =⋅⋅⋅==，D 正确.故选：ABD .12.如图，正方体1111ABCD A B C D -的棱长为1，E 、F 是线段11B D 上的两个动点，且12EF =，则下列结论中正确的是（）A.AC BE⊥B.//EF 平面ABCDC.AEF △的面积与BEF △的面积相等D.三棱锥E ABF -的体积为定值【答案】ABD 【解析】【分析】证明出AC ⊥平面11DD B B ，利用线面垂直的性质可判断A 选项；利用面面平行的性质可判断B 选项；利用三角形的面积公式可判断C 选项；利用锥体的体积公式可判断D 选项.【详解】对于A ，由正方体的结构特征可知，1DD ⊥平面ABCD ，而AC ⊂平面ABCD ，则1D D AC ⊥，连接BD ，又因为四边形ABCD 为正方形，所以，AC BD ⊥，因为1DD BD D =I ，且1D D 、BD ⊂平面11DD B B ，所以，AC ⊥平面11DD B B ，因为BE ⊂平面11DD B B ，所以，AC BE ⊥，故A 正确；对于B 选项，因为平面1111//A B C D 平面ABCD ，EF ⊂平面1111D C B A ，则//EF 平面ABCD ，B 对；对于C 选项，设AC BD O = ，取11B D 的中点M ，连接OM 、AM ，由A 选项可知AC ⊥平面11BB D D ，即AO ⊥平面11BB D D ，又11B D ⊂平面11BB D D ，所以，11AO B D ⊥，又11//BB DD 且11BB DD =，所以，四边形11BB D D 为平行四边形，所以，11//BD B D 且11BD B D =，因为M 、O 分别为11B D 、BD 的中点，所以，1//DO D M 且1DO D M =，所以，四边形1DD MO 为平行四边形，则1OM DD =，因为1DD ⊥平面ABCD ，DO ⊂平面ABCD ，所以，1DD DO ⊥，所以，四边形1DD MO 为矩形，则11OM B D ⊥，又AO OM O = ，AO 、OM ⊂平面AOM ，所以，11B D ⊥平面AOM ，又AM ⊂平面AOM ，所以，11AM B D ⊥，因为11AM DD BB =>=，所以，11122AEF BEF S EF AM EF BB S =⋅>⋅=△△，C 错；对于D ，因为BEF △的面积为1111112224BEF S EF BB =⋅=⨯⨯=△，又点A 到平面BEF 的距离为定值，故三棱锥A BEF -的体积为定值，D 对.故选：ABD.第II 卷三、填空题（本题共4小题，每小题5分，共20分）13.数列{}n a 中，若11a =，12n n na a n +=+，则191k k a ==∑___________.【答案】1910##1.9【解析】【分析】依题意可得12n n a na n +=+，再利用累乘法求出数列的通项公式，最后利用裂项相消法求和即可；【详解】解：因为12n n na a n +=+，所以12n n a n a n +=+，所以111n n a n a n --=+，122n n a n a n ---=，L ，3224a a =，2113a a =，累乘可得132********143n n n n a a a a n n a a a a n n -----⨯⨯⨯⨯=⨯⨯⨯⨯+ 即()121n a a n n =+，因为11a =，所以()211211n a n n n n ⎛⎫==- ⎪++⎝⎭，所以191111111111111921222121223192022319202010k k a =⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-+-++-=-=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∑ 故答案为：191014.在622(1)x x x ⎛⎫++ ⎪⎝⎭的展开式中，x 的系数是___________（用数字作答）.【答案】240【解析】【分析】只要求出622x x ⎛⎫+ ⎪⎝⎭的展开式含x 的系数，即可得到答案；【详解】622x x ⎛⎫+ ⎪⎝⎭的展开式的通项为：()6212316622,0,1,,6rr rr r r r T C x C x r x --+⎛⎫=⋅⋅=⋅= ⎪⎝⎭，当1230r -=，即4r =时，622(1)x x x ⎛⎫++ ⎪⎝⎭展开式x 的系数为：446C 2240⋅=.当1231r -=显然不成立；故答案为：24015.已知函数()2ln f x x x ax =+存在减区间，则实数a 的取值范围为______.【答案】322ea -<【解析】【分析】函数()2ln f x x x ax =+存在减区间，则()0f x '<有解可求解．【详解】由题可知()2ln f x x x x a '=++，因为函数2()ln f x x x ax =+存在减区间，则()0f x '<在()0+∞，上有解，即2ln 0x x x a ++<有解，令()2ln g x x x x a =++，()2ln 3g x x '=+，令()0g x '>，解得32ex ->；令()0g x '<，解得320e x -<<，所以()g x 在32(0,e )-单调递减，32(e ,)-+∞单调递增，所以33332222min()(e )3ee2eg x g a a ----==-++=-+，因为2ln 0x x x a ++<有解，所以322e0a --+<，解得322e a -<．故答案为：322ea -<16.给图中A ，B ，C ，D ，E ，F 六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色．若有5种颜色可供选择，则共有_______种不同的染色方案．【答案】780【解析】【分析】首先根据使用的颜色种类分为三类，再对每种情况进行分类讨论，使用分步乘法以及分类加法即可求解.【详解】由题意可知，若满足相邻区域不同色，最少需要三种颜色，最多需要五种颜色.当有3种颜色时，则BD 同色，EC 同色，AF 同色，此时的涂色种类为111543C C C 60=种.当有4种颜色时，则有三种情况：①BD 不同色，EC 同色，AF 同色，此时涂色种类为2115322C C C 120⨯=种；②BD 同色，EC 不同色，AF 同色，此时涂色种类为2115322C C C 120⨯=种；③BD 同色，EC 同色，AF 不同色，此时涂色种类为2115322C C C 120⨯=种；即当有4种颜色时，总的涂色种类为120120120360++=种.当有5种颜色时，则有三种情况：①BD 不同色，EC 不同色，AF 同色，此时涂色种类为2215314C C C 120⨯=种；②BD 同色，EC 不同色，AF 不同色，此时涂色种类为2215314C C C 120⨯=种；③BD 不同色，EC 同色，AF 不同色，此时涂色种类为2215314C C C 120⨯=种；即当有5种颜色时，总的涂色种类为120120120360++=种.综上，总的共有60360360780++=种不同的方案.故答案为：780四、解答题（本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）17.已知直线l ：()210ax a y +-+=．（1）若直线l 在x 轴上截距和在y 轴上截距相等，求a 的值；（2）若直线l 与圆22111225x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭相切，求a 的值．【答案】（1）1；（2）4或2-．【解析】【分析】（1）分别令0x =，0y =，得到截距，解方程即可;（2）根据圆心到直线的距离等于半径列出方程求解.【详解】（1）易知直线l 的截距不能为0，令0x =，12y a=--，令0y =，1x a =-；则1112a a a-=-⇒=-故a 的值为1（2）圆心11,22⎛⎫⎪⎝⎭到直线l 的距离d ==2412445a a =⇒-+22804a a a --=⇒=或2a =-故a 的值为4或2-.18.已知数列{}n a 满足11a ＝，且2112)2(n n na n a n n ＋-+=+.（1）求23,a a ；（2）证明数列n a n ⎧⎫⎨⎬⎩⎭是等差数列，并求{}n a 的通项公式．【答案】（1）23615a a =，=（2）证明见解析，22n a n n =-【解析】【分析】（1）由递推公式直接求出23,a a ；（2）利用构造法得到121n n a a n n +-=+，即可证明n a n ⎧⎫⎨⎬⎩⎭是等差数列，并写出{}n a 的通项公式.【小问1详解】由题意可得2124a a -=，则2124a a =+，又11a =，所以26a =.由322312a a -=，得322123a a =+，所以315a =.【小问2详解】由已知得1(1)2(1)n nna n a n n +-+=+，即121n na a n n+-=+，所以数列n a n ⎧⎫⎨⎬⎩⎭是首项为111a =，公差为2d =的等差数列，则12(1)21na n n n=+-=-，所以22n a n n =-.19.某高校的大一学生在军训结束前，需要进行各项过关测试，其中射击过关测试规定：每位测试的大学生最多有两次射击机会，第一次射击击中靶标，立即停止射击，射击测试过关，得5分；第一次未击中靶标，继续进行第二次射击，若击中靶标，立即停止射击，射击测试过关，得4分；若未击中靶标，射击测试未能过关，得2分.现有一个班组的12位大学生进行射击过关测试，假设每位大学生两次射击击中靶标的概率分别为m ，0.5，每位大学生射击测试过关的概率为p .（1）设该班组中恰有9人通过射击过关测试的概率为()f p ，求()f p 取最大值时p 和m 的值；（2）在（1）的结果下，求该班组通过射击过关测试所得总分的平均数.【答案】（1）p ，m 的值分别为0.75，0.5.（2）48【解析】【分析】（1）根据已知条件列出99312()C (1)f p p p =-()01p <<，求导得9839212'()C 9(1)3(1)f p p p p p ⎡⎤=---⎣⎦()01p <<，利用导数判断函数的单调性，求出()f p 取最大值时p 的值，再根据0.50.50.75m +=，解得0.5m =即可.（2）根据题意设一位大学生通过测试所得分数的平均值，求出X 的所有可能取值，并求出每个取值所对应的概率，求得一位大学生射击过关测试所得分数的平均数()E X ,最后确定该班组通过射击过关测试所得总分的平均数即可.【小问1详解】99312()C (1)f p p p =-，01p <<，∴9839212'()C 9(1)3(1)f p p p p p ⎡⎤=---⎣⎦982123C (1)(34)p p p =--，01p <<，由'()0f p =，得0.75p =，由'()0f p >，得00.75p <<，由'()0f p <，得0.751p <<，∴()f p 在(0,0.75)上是增函数，在(0.75,1)上是减函数，∴0.75p =是()f p 的极大值点，也是()f p 的最大值点，因为()()1110.50.50.5p mm =---=+，此时，由0.50.50.75m +=，解得0.5m =.∴()f p 取得最大值时，p ，m 的值分别为0.75，0.5.【小问2详解】设一位大学生射击过关测试所得分数为随机变量X ，则X 的可能取值分别为5，4，2，则(5)0.5P X ==，(4)(10.5)0.50.25P X ==-⨯=，(2)(10.5)(10.5)0.25P X ==--=，∴一位大学生射击过关测试所得分数的平均数：()50.540.2520.254E X =⨯+⨯+⨯=.∴该班组通过射击过关测试所得总分的平均数为：12448⨯=.20.如图，在四棱锥S ABCD -中，四边形ABCD 是矩形，SAD 是正三角形，且平面SAD ⊥平面ABCD ，1AB =，P 为棱AD 的中点，四棱锥S ABCD -的体积为3．（1）若E 为棱SB 的中点，求证：//PE 平面SCD ；（2）在棱SA 上是否存在点M ，使得平面PMB 与平面SAD 所成锐二面角的余弦值为235？若存在，指出点M 的位置并给以证明；若不存在，请说明理由.【答案】（1）证明见解析；（2）存在点M ，位于AS 靠近点S 的三等分点处满足题意.【解析】【分析】（1）取SC 中点F ，连接,EF FD ，得到//PE FD ，然后利用线面平行的判定定理得到//PE 平面SCD ；（2）假设在棱SA 上存在点M 满足题意，建立空间直角坐标系，设()01AM AS λλ=≤≤，根据平面PMB 与平面SAD 的夹角的余弦值为5，则两平面法向量所成角的余弦值的绝对值等于5，求出λ，即可得出结论.【小问1详解】取SC 中点F ，连接,EF FD ，,E F 分别为,SB SC 的中点，//EF BC ∴，12EF BC =底面四边形ABCD 是矩形，P 为棱AD 的中点，//PD BC ∴，12PD BC =．//EF PD ∴，EF PD =，故四边形PEFD 是平行四边形，//PE FD \．又FD ⊂ 平面SCD ，PE ⊄平面SCD ，//PE ∴平面SCD ．【小问2详解】假设在棱SA 上存在点M 满足题意，在等边SAD 中，P 为AD 的中点，所以SP AD ⊥，又平面SAD ⊥平面ABCD ，平面SAD ⋂平面ABCD AD ＝，SP ⊂平面SAD ，SP ∴⊥平面ABCD ，则SP 是四棱锥S ABCD -的高．设()0AD m m =>，则2SP m =，ABCD S m =矩形，113323ABCD S ABCD V S SP m m 矩形四棱锥-∴=⋅=⨯=，所以2m ＝.以点P 为原点，PA ，PS的方向分别为,x z 轴的正方向，建立如图所示的空间直角坐标系，则()0,0,0P ，()1,0,0A ，()1,1,0B ，(3S ，故()1,0,0PA = ，()1,1,0PB =uu r，(3AS =- ．设()()301AM AS λλλλ==-≤≤，()13PM PA AM λλ∴=+=-．设平面PMB 的一个法向量为()1,,n x y z =，则11(1)300n PM x z n PB x y λλ⎧⋅=-+=⎪⎨⋅=+=⎪⎩ 取)13,3,1n λλλ=-．易知平面SAD 的一个法向量为()20,1,0n =u u r，1212212323cos ,7215n n n n n n -l ×\===l -l +u v u u v u v u u v u v u u v ，01λ≤≤ ，∴23λ=故存在点M ，位于AS 靠近点S 的三等分点处满足题意.21.已知双曲线()2222:10,0x y C a b a b-=>>的左，右焦点分别为()16,0F -，)26,0F ．且该双曲线过点(22,2P ．（1）求C 的方程；（2）如图．过双曲线左支内一点(),0T t 作两条互相垂直的直线分别与双曲线相交于点A ，B 和点C ，D ．当直线AB ，CD 均不平行于坐标轴时，直线AC ，BD 分别与直线x t =相交于P ．Q 两点，证明：P ，Q 两点关于x 轴对称．【答案】（1）22142x y -=（2）证明见解析【解析】【分析】（1）根据已知条件，建立关于,a b 的方程组，求解方程组即可得答案；（2）由题意，设直线AB 的方程为x my t =+，直线CD 的方程为1x y t m=-+，点()()()()11223344,,,,,,,A x y B x y C x y D x y ，联立22142x y x my t ⎧-=⎪⎨⎪=+⎩，由韦达定理可得212122224,22mt t y y y y m m --+==--，同理可得()2234342242,1212t m mt y y y y m m -+==--，由直线AC 的方程()133111y y y y x x x x --=--可得()2132131,m y y P t m y y ⎛⎫+ ⎪ ⎪+⎝⎭，同理可得()2242241,m y y Q t m y y ⎛⎫+ ⎪ ⎪+⎝⎭，然后计算0P Q y y +=即可得证.【小问1详解】解：由已知可得22226821a b a b⎧+=⎪⎨-=⎪⎩，解得224,2a b ==，所以双曲线C 的方程为22142x y -=；【小问2详解】证明：由题意，设直线AB 的方程为x my t =+，直线CD 的方程为1x y t m=-+，点()()()()11223344,,,,,,,A x y B x y C x y D x y ，由22142x y x my t ⎧-=⎪⎨⎪=+⎩，得()2222240m y mty t -++-=，则()()22222(2)424168320mt m tm t ∆=---=+->，得2224m t +>，所以212122224,22mt t y y y y m m --+==--，同理可得()2234342242,1212t m mt y y y y m m-+==--，其中,m t 满足2224t m +>，直线AC 的方程为()133111y y y y x x x x --=--，令x t =，得()131113y yy t x y x x -=-+-,又11331,x my t x y t m =+=-+，所以()2121331m y y y m y y +=+，即()2132131,m y y P t m y y ⎛⎫+ ⎪ ⎪+⎝⎭，同理可得()2242241,m y y Q t m y y ⎛⎫+ ⎪ ⎪+⎝⎭，因为()()()()()()()2222123412341324222213241324111m m y y y y y y y y my y m y y m y y m y y my y m y y ⎡⎤++++++⎣⎦+=++++()()()()()222222222221324442212122120m t t m mt mt m m m m m m y y m y y ⎡⎤---+⋅+⋅⎢⎥----⎢⎥⎣⎦==++，所以,P Q 两点关于x 轴对称.22.已知函数()()ln 2f x a x x =+-.（1）当1a =时，求()f x 的最大值；（2）设点()()11,A x f x 和()()22,B x f x 是曲线()y f x =上不同的两点，且()()12f x f x =，若12ak x x <+恒成立，求实数k 的取值范围.【答案】（1）1；（2）(],2∞-.【解析】【分析】（1）当1a =时，()ln 2f x x x =+-,求导判断函数得单调性，进而可以求出最值；（2）不妨设120x x >>，进而由题意可得1211221ln 0,1x x xk x x x -⋅-<+设12(1)x t t x =>，构造函数1()ln (1)1t g t k t t t -=⋅->+，利用导数研究函数()g t 在()1,+∞的最小值即可求出结果.【详解】（1）当1a =时，()ln 2f x x x =+-，()f x 的定义域为()0,+∞，11()1xf x x x -='-=当01x <<时，()0f x '>；当1x >时，()0f x '<，所以()f x 在()0,1上为增函数，在()1,+∞上为减函数，所以1x =是()f x 的极大值点，也是()f x 的最大值点，故()()max 11f x f ==.（2）不妨设120x x >>，由1122ln 2ln 2a x x a a x x a -+=-+，得1212ln ln x x a x x -=-由12ak x x <+，得121212ln ln x x k x x x x -⋅<+-，即1211221ln 0,1x x xk x x x -⋅-<+设12(1)x t t x =>，1()ln (1)1t g t k t t t -=⋅->+，则222212(1)1()(1)(1)k t k t g t t t t t '--+=-=-++记2()2(1)1(1)h t t k t t =--+>，24(1)44(2)k k k ∆=--=-（i ）当0k ≤时，则()h t 图像的对称轴为11t k =-≤-，所以()h t 在()1,+∞上是增函数，又()010h =>，从而当1t >时，()0h t >，所以2()()0(1)h t g t t t '=-<+，于是()g t 在()1,+∞上是减函数，所以()()10g t g <=，此时适合题意（ii ）当02k <≤时，0∆≤，则()0h t ≥恒成立，从而2()()0(1)h t g t t t '=-≤+，所以()g t 在()1,+∞上是减函数，于是()()10g t g <=，此时适合题意.（iii ）当2k >时，()h t 的对称轴方程为1t k =-，且()1420h k =-<，()2410h k k =+>，所以存在()01,2t k k ∈-，使得()00h t =，于是()h t 在()1,k -+∞内只有一个零点0t ，所以当01t t <<时，()0h t <，从而2()()0(1)h t g t t t '=->+所以()g t 在()01,t 上是增函数，于是当()01,t t ∈时，()()10g t g >=，此时不适合题意.综上，实数k 的取值范围(],2-∞【点睛】恒成立问题解题思路：（1）参变量分离：（2）构造函数：①构造函数，研究函数的单调性，求出函数的最值，解不等式即可；②构造函数后，研究函数单调性，利用单调性解不等式，转化之后参数分离即可解决问题.。

高一数学寒假作业：(二)(Word版含答案)

高一数学寒假作业（二）一、选择题，每小题只有一项是正确的。

1.已知全集{}1,2,3,4U =,集合{}{}1,2,2A B == ,则∁U (A ∪B ) =( )A ．{}134，， B ．{}34， C ． {}3 D ． {}4 2.已知集合A ＝{x|a －1≤x≤a＋2}，B ＝{x|3＜x ＜5}，则使A ⊇B 成立的实数a 的取值范围是 ( ) A.{a|3＜a≤4}＜a ＜4} D.φ3.函数的定义域为M ，的定义域为N ，则M ∩N ＝( )A ．[－2，＋∞)B ．[－2,2)C ．(－2,2)D ．(－∞，2) 4.下列式子中成立的是 ( )A.1122log 4log 6< B. 0.30.311()()23> C. 3.4 3.511())22<( D.32log 2log 3>5.下列函数是偶函数的是 ( )A. 2lg y x = B. 1()2x y = C. 21y x =- ，(11]x ∈- D. 1y x -= 6.已知函数()2030x x x fx x log ,,⎧>=⎨≤⎩, 则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是（）A ．9B ．19 C ．9- D ．19- 7.下列各个对应中,构成映射的是 ( )8.设()f x 是定义在R 上的偶函数，对任意的x R ∈，都有(2)(2)f x f x -=+，且当[2,0]x ∈-时，1()()12x f x =-，则在区间(2,6]-内关于x 的方程2()log (2)0f x x -+=的零点的个数是（）A ．1B ．2C ．3D ．49.若函数()(1)(0xxf x k a a a -=-->且1)a ≠在R 上既是奇函数，又是减函数，则()log ()a g x x k =+的图象是（）二、填空题10.函数32,1()log 1x x f x x x ⎧≤=⎨>⎩，，则(f f =__________11.若}4,3,2,2{-=A ，},|{2A t t x xB ∈==，用列举法表示B 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【答案】A
【解析】
【分析】分别求出导数，设出切点，得到切线方程，再由两点的斜率公式，结合切点满足曲线方程，运用导数求的单调区间、极值、最值即可得出a的取值范围.
【详解】设
切线：，即
切线：，即，
令
在上单调递增，在上单调递减，
所以
故选：A．
8.已知双曲线，若过点能作该双曲线的两条切线，则该双曲线离心率取值范围为（）
1.如图，I是全集，M、P、S是I的3个子集，则阴影部分所表示的集合是（）
A. B. C. D.
【答案】C
【解析】
【分析】根据Venn图表示的集合运算作答．
【详解】阴影部分在集合的公共部分，但不在集合内，表示为，
故选：C．
2.若，则z=（）
A. 1–iB. 1+iC. –iD.i
【答案】D
【解析】
（参考数据：）
A. B. C. D.
【答案】D
【解析】
【分析】根据给定条件，确定标准对数视力从下到上的项数，再利用等比数列计算作答.
【详解】依题意，以标准对数视力为左边数据组的等差数列的首项，其公差为-0.1，标准对数视力为该数列第3项，
标准对数视力对应的国际标准视力值1.0为右边数据组的等比数列的首项，其公比为，
A. B. C. D.
8.已知双曲线，若过点能作该双曲线的两条切线，则该双曲线离心率取值范围为（）
A. B. C. D.以上选项均不正确
二、多选题
9.已知向量，则下列命题正确的是（）
A.存在，使得 B.当时，与垂直
C.对任意，都有 D.当时，
10.一个质地均匀的正四面体表面上分别标有数字1，2，3，4，抛掷该正四面体两次，记事件A为“第一次向下的数字为偶数”，事件B为“两次向下的数字之和为奇数”，则下列说法正确的是（）
四、解答题
17.在△ABC中，角A，B，C的对边分别为a，b，c，已知．
（1）求的值；
（2）在边BC上取一点D，使得，求的值．
18.已知数列是公比为的等比数列，前项和为，且满足，．
（1）求数列的通项公式；
（2）若数列满足，求数列的前项和．
高三寒假作业16答案解析
一、单选题
A. B. C. D.以上选项均不正确
【答案】D
高三寒假作业16
一、单选题
1.如图，I是全集，M、P、S是I 3个子集，则阴影部分所表示的集合是（）
A. B. C. D.
2.若，则z=（）
A. 1–iB. 1+iC. –iD.i
3.若直线是圆一条对称轴，则（）
A. B. C.1D.
4.如图是标准对数远视力表的一部分．最左边一列“五分记录”为标准对数视力记录，这组数据从上至下为等差数列，公差为；最右边一列“小数记录”为国际标准视力记录的近似值，这组数据从上至下为等比数列，公比为．已知标准对数视力对应的国际标准视力准确值为，则标准对数视力对应的国际标准视力精确到小数点后两位约为（）
A. B.事件A和事件B互为对立事件
C. D.事件A和事件B相互独立
11.在正方体中，点满足，其中，，则（）
A.当时，平面
B.当时，三棱锥的体积为定值
C.当时，面积为定值
D.当时，直线与所成角的范围为
12.已知函数恰有三个零点，则下列结论中正确的是（）
A B.
C. D.
三、填空题
13. 的展开式中常数项是__________（用数字作答）．
14.某大学一寝室4人参加疫情防控讲座，4人就坐在一排有13个空位的座位上，根据防疫要求，任意两人之间需间隔1米以上（两个空位），则不同的就坐方法有_______种.
15.已知，则的最小值是_______．
16.在三棱锥中，顶点P在底面的投影为O，点O到侧面，侧面，侧面的距离均为d，若，．，且是锐角三角形，则三棱锥体积的取值范围为________．
（参考数据：）
A. B. C. D.
5.在中，．P为所在平面内的动点，且，则的取值范围是（）
A. B. C. D.
6.已知函数在区间上是增函数，且在区间上恰好取得一次最大值，则的取值范围是（）
A. B. C. D.
7.若两曲线y=x2-1与y=alnx-1存在公切线，则正实数a的取值范围为（）
【分析】先利用除法运算求得，再利用共轭复数的概念得到即可.
【详解】因，所以 .
故选：D
【点晴】本题主要考查复数的除法运算，涉及到共轭复数的概念，是一道基础题.
3.若直线是圆的一条对称轴，则（）
A. B. C.1D.
【答案】A
【解析】
【分析】若直线是圆的对称轴，则直线过圆心，将圆心代入直线计算求解．
【详解】由题可知圆心为，因为直线是圆的对称轴，所以圆心在直线上，即，解得．
故选：A．
4.如图是标准对数远视力表的一部分．最左边一列“五分记录”为标准对数视力记录，这组数据从上至下为等差数列，公差为；最右边一列“小数记录”为国际标准视力记录的近似值，这组数据从上至下为等比数列，公比为．已知标准对数视力对应的国际标准视力准确值为，则标准对数视力对应的国际标准视力精确到小数点后两位约为（）
【分析】先化简函数的解析式，再依据题意列出关于的不等式组，即可求得的取值范围.
【详解】
由，可得
由在区间上恰好取得一次最大值，可得，解之得
又在区间上是增函数，则，解之得
综上，的取值范围是
故选：B
7.若两曲线y=x2-1与y=alnx-1存在公切线，则正实数a的取值范围为（）
A. B. C. D.
【详解】解：依题意如图建立平面直角坐标系，则，，，
因为，所以在以为圆心，为半径的圆上运动，
设，，
所以，，
所以
，其中，，
因为，所以，即；
故选：D
6.已知函数在区间上是增函数，且在区间上恰好取得一次最大值，则的取值范围是（）
A. B. C标准对数视力对应的国际标准视力值为该等比数列的第3项，其大小为 .
故选：D
5.在中，．P为所在平面内的动点，且，则的取值范围是（）
A. B. C. D.
【答案】D
【解析】
【分析】依题意建立平面直角坐标系，设，表示出，，根据数量积的坐标表示、辅助角公式及正弦函数的性质计算可得；