最新人教A版必修2高中数学.3.3.8直线方程章节复习小结公开课教学设计
人教A版高中数学必修2《三章 直线与方程 小结》优质课教案_1
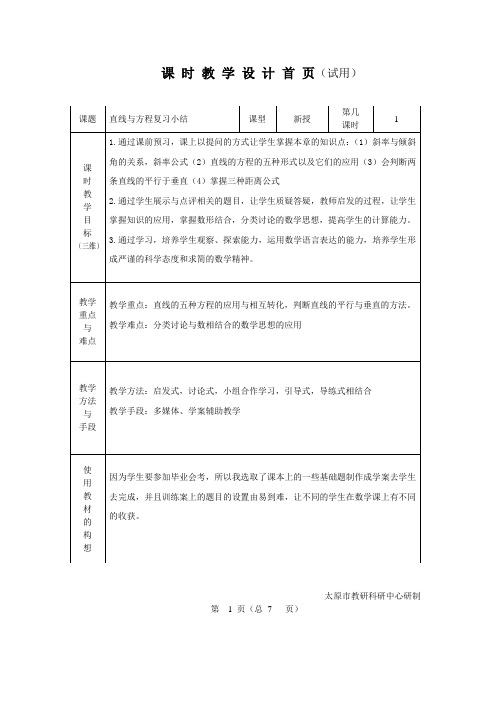
(3)求BC边上的垂直平分线所在直线的方程
2.(1)已知直线 与 垂直,求a的值
针对学生没有发现的问题引导学生质疑答疑
学生通过抢答的方式对有问题的题目进行讲解。
学生展示与点评
解:(1)
所以 ,所以BC边上的高所在的直线的方程为:
即:
(2)BC的中点坐标为(3,5)
提示学生数形结合寻找解题方法
(2)联立解得:
,所以点A(-3,3)
(2)点D(a,b),由题意得
,(1)
,(2),(1)与(2)联立得到 ,
设点C(p,q)
由题意得
,所以C(9,-13)
所以AC的方程为:
学生完善整理学案
学生进行当堂检测
太原市教研科研中心研制
第6页(总7页)
课 时 教 学 设 计 尾 页(试用)
(2)斜截式:已知直线在 轴上的截距为 和斜率 ,则直线方程为 ,它不包括垂直于 轴的直线。
(3)两点式:已知直线经过 、 两点,则直线方程为 ,它不包括垂直于坐标轴的直线。
(4)截距式:已知直线在 轴和 轴上的截距为 ,则直线方程为 ,它不包括垂直于坐标轴的直线和过原点的直线。
(5)一般式:任何直线均可写成 (A,B不同时为0)的形式。
解:(1)
解得: 或
对学生进行分数评价,鼓励学生发散思维用不同的方法去完成题目
(2)(1) 解得: 或
(2) ,解得
解:(1)点M到已知直线的距离为
,设平行于已知直线的方程为
则M到该直线的距离为 ,则
设两条直线的方程为:
则M到该直线的距离为
,解得:
或 所以,三条直线的方程为
太原市教研科研中心研制
高中数学必修二《直线与方程》教案设计

高中数学必修二《直线与方程》教案设计一、教学目标1.知识目标:o学生能够掌握直线的点斜式、两点式和一般式方程的表达形式及其相互转换。
o学生能够理解直线方程中斜率、截距的概念,并能根据给定条件求出直线方程。
o学生能够运用直线方程解决简单的几何问题,如求两直线的交点、判断两直线是否平行或垂直。
2.能力目标:o培养学生的逻辑思维能力和抽象思维能力,通过直线方程的学习,提高数学建模能力。
o提高学生的运算能力,能够熟练进行直线方程的推导和计算。
o增强学生的问题解决能力,能够运用所学知识解决实际问题。
3.情感态度价值观目标:o培养学生严谨的数学学习态度,注重逻辑推理和证明过程。
o激发学生的学习兴趣,鼓励学生积极探索数学奥秘,培养数学学习的自信心。
o培养学生的合作精神,通过小组讨论和合作学习,提高团队协作能力。
二、教学内容-重点:直线的点斜式、两点式和一般式方程的表达及相互转换;斜率、截距的概念及应用。
-难点:直线方程的应用,如求两直线的交点、判断两直线的位置关系。
三、教学方法-讲授法:用于直线方程的基本概念和理论的讲解。
-讨论法:通过小组讨论,加深学生对直线方程的理解和应用。
-案例分析法:通过具体案例分析,提高学生解决实际问题的能力。
-多媒体教学法:利用多媒体资源,如、动画等,直观展示直线方程的图形和推导过程。
四、教学资源-教材:《高中数学必修二》-教具:黑板、粉笔、直尺、圆规-多媒体资源:课件、直线方程推导动画、几何画板软件-实验器材:无需特定实验器材五、教学过程六、课堂管理1.小组讨论:每组4-5人,确保每组成员水平均衡,指定小组长负责协调讨论和记录。
2.维持纪律:明确课堂规则,如举手发言、不打断他人讲话等,对违规行为及时提醒和处理。
3.激励策略:对积极参与讨论、表现突出的学生给予表扬和奖励,如加分、小礼品等。
七、评价与反馈1.课堂小测验:每节课结束前进行小测验,检查学生对本节课内容的掌握情况。
2.课后作业:布置适量的课后作业,巩固所学知识,要求学生按时完成并提交。
高中数学人教A版必修2教案-3.2_直线的方程_教学设计_教案_2

教学准备1. 教学目标(一)知识教学点掌握直线方程的一般形式。
.(二)能力训练点1、明确直线方程一般式的形式特征;2、会根据直线方程的一般式求斜率和截距;3、会把直线方程的点斜式、两点式化为一般式。
(三)德育渗透点通过对直线方程的几种形式的特点的分析,认识事物之间的普遍联系与相互转化,培养学生看问题一分为二的辩证唯物主义观点.2. 教学重点/难点掌握直线方程的一般形式3. 教学用具4. 标签教学过程(一)引入新课点斜式、斜截式不能表示与x轴垂直的直线;两点式不能表示与坐标轴平行的直线;截距式既不能表示与坐标轴平行的直线,又不能表示过原点的直线.与x轴垂直的直线可表示成x=x0,与x轴平行的直线可表示成y=y0。
它们都是二元一次方程.我们问:直线的方程都可以写成二元一次方程吗?反过来,二元一次方程都表示直线吗?(二)直线方程的一般形式我们知道,在直角坐标系中,每一条直线都有倾斜角α.当α≠90°时,直线有斜率,方程可写成下面的形式:y=kx+b当α=90°时,它的方程可以写成x=x0的形式.由于是在坐标平面上讨论问题,上面两种情形得到的方程均可以看成是二元一次方程.这样,对于每一条直线都可以求得它的一个二元一次方程,就是说,直线的方程都可以写成关于x、y的一次方程.反过来,对于x、y的一次方程的一般形式Ax+By+C=0.(1)其中A、B不同时为零.(1)当B≠0时,方程(1)可化为这里,我们借用了前一课y=kx+b表示直线的结论,不弄清这一点,会感到上面的论证不知所云.(2)当B=0时,由于A、B不同时为零,必有A≠0,方程(1)可化为它表示一条与y轴平行的直线.这样,我们又有:关于x和y的一次方程都表示一条直线.我们把方程写为Ax+By+C=0这个方程(其中A、B不全为零)叫做直线方程的一般式.引导学生思考:直线与二元一次方程的对应是什么样的对应?直线与二元一次方程是一对一的,既一一对应。
人教A版高中数学必修二直线的方程教案新

直线的方程一、教学目标(一)知识教学点在直角坐标平面内,已知直线上一点和直线的斜率或已知直线上两点,会求直线的方程;给出直线的点斜式方程,能观察直线的斜率和直线经过的定点;能化直线方程成截距式,并利用直线的截距式作直线.(二)能力训练点通过直线的点斜式方程向斜截式方程的过渡、两点式方程向截距式方程的过渡,训练学生由一般到特殊的处理问题方法;通过直线的方程特征观察直线的位置特征,培养学生的数形结合能力.(三)学科渗透点通过直线方程的几种形式培养学生的美学意识.二、教材分析1.重点:由于斜截式方程是点斜式方程的特殊情况,截距式方程是两点式方程的特殊情况,教学重点应放在推导直线的斜截式方程和两点式方程上.2.难点:在推导出直线的点斜式方程后,说明得到的就是直线的方程,即直线上每个点的坐标都是方程的解;反过来,以这个方程的解为坐标的点在直线上.的坐标不满足这个方程,但化为y-y1=k(x-x1)后,点P1的坐标满足方程.三、活动设计分析、启发、诱导、讲练结合.四、教学过程(一)点斜式已知直线l的斜率是k,并且经过点P1(x1,y1),直线是确定的,也就是可求的,怎样求直线l的方程(图1-24)?设点P(x,y)是直线l上不同于P1的任意一点,根据经过两点的斜率公式得注意方程(1)与方程(2)的差异:点P1的坐标不满足方程(1)而满足方程(2),因此,点P1不在方程(1)表示的图形上而在方程(2)表示的图形上,方程(1)不能称作直线l的方程.重复上面的过程,可以证明直线上每个点的坐标都是这个方程的解;对上面的过程逆推,可以证明以这个方程的解为坐标的点都在直线l上,所以这个方程就是过点P1、斜率为k的直线l的方程.这个方程是由直线上一点和直线的斜率确定的,叫做直线方程的点斜式.当直线的斜率为0°时(图1-25),k=0,直线的方程是y=y1.当直线的斜率为90°时(图1-26),直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1.(二)斜截式已知直线l在y轴上的截距为b,斜率为b,求直线的方程.这个问题,相当于给出了直线上一点(0,b)及直线的斜率k,求直线的方程,是点斜式方程的特殊情况,代入点斜式方程可得:y-b=k(x-0)也就是上面的方程叫做直线的斜截式方程.为什么叫斜截式方程?因为它是由直线的斜率和它在y轴上的截距确定的.当k≠0时,斜截式方程就是直线的表示形式,这样一次函数中k和b的几何意义就是分别表示直线的斜率和在y轴上的截距.(三)两点式已知直线l上的两点P1(x1,y1)、P2(x2,y2),(x1≠x2),直线的位置是确定的,也就是直线的方程是可求的,请同学们求直线l的方程.当y1≠y2时,为了便于记忆,我们把方程改写成请同学们给这个方程命名:这个方程是由直线上两点确定的,叫做直线的两点式.对两点式方程要注意下面两点:(1)方程只适用于与坐标轴不平行的直线,当直线与坐标轴平行(x1=x2或y1=y2)时,可直接写出方程;(2)要记住两点式方程,只要记住左边就行了,右边可由左边见y就用x代换得到,足码的规律完全一样.(四)截距式例1 已知直线l在x轴和y轴上的截距分别是a和b(a≠0,b≠0),求直线l的方程.此题由老师归纳成已知两点求直线的方程问题,由学生自己完成.解:因为直线l过A(a,0)和B(0,b)两点,将这两点的坐标代入两点式,得就是学生也可能用先求斜率,然后用点斜式方程求得截距式.引导学生给方程命名:这个方程是由直线在x轴和y轴上的截距确定的,叫做直线方程的截距式.对截距式方程要注意下面三点:(1)如果已知直线在两轴上的截距,可以直接代入截距式求直线的方程;(2)将直线的方程化为截距式后,可以观察出直线在x轴和y轴上的截距,这一点常被用来作图;(3)与坐标轴平行和过原点的直线不能用截距式表示.(五)例题例2 三角形的顶点是A(-5,0)、B(3,-3)、C(0,2)(图1-27),求这个三角形三边所在直线的方程.本例题要在引导学生灵活选用方程形式、简化运算上多下功夫.解:直线AB的方程可由两点式得:即 3x+8y+15=0这就是直线AB的方程.BC的方程本来也可以用两点式得到,为简化计算,我们选用下面途径:由斜截式得:即 5x+3y-6=0.这就是直线BC的方程.由截距式方程得AC的方程是即 2x+5y+10=0.这就是直线AC的方程.(六)课后小结(1)直线方程的点斜式、斜截式、两点式和截距式的命名都是可以顾名思义的,要会加以区别.(2)四种形式的方程要在熟记的基础上灵活运用.(3)要注意四种形式方程的不适用范围.五、布置作业1.(1.5练习第1题)写出下列直线的点斜式方程,并画出图形:(1)经过点A(2,5),斜率是4;(4)经过点D(0,3),倾斜角是0°;(5)经过点E(4,-2),倾斜角是120°.解:2.(1.5练习第2题)已知下列直线的点斜方程,试根据方程确定各直线经过的已知点、直线的斜率和倾斜角:解:(1)(1,2),k=1,α=45°;(3)(1,-3),k=-1,α=135°;3.(1.5练习第3题)写出下列直线的斜截式方程:(2)倾斜角是135°,y轴上的截距是3.4.(1.5练习第4题)求过下列两点的直线的两点式方程,再化成截距式方程,并根据截距式方程作图.(1)P1(2,1)、P2(0,-3);(2)A(0,5)、B(5,0);(3)C(-4,-3)、D(-2,-1).解:(图略)六、板书设计。
高中数学第三章直线与方程复习教案新人教A版必修2
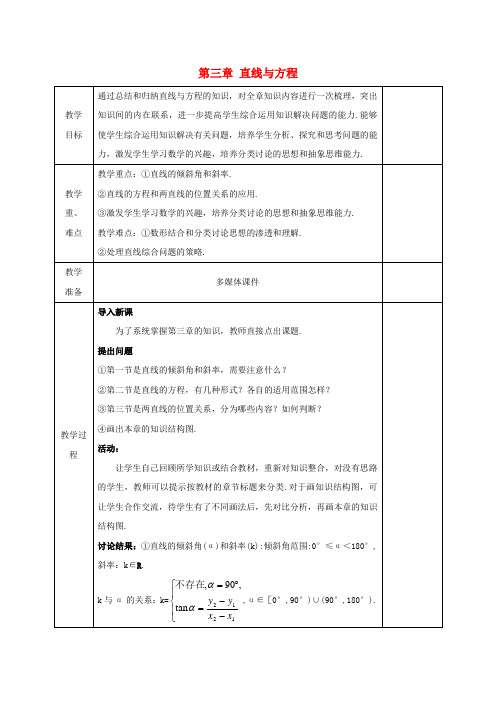
m m ;当 x=0 时,y=- . 3 4
∵直线 l 与两坐标轴围成的三角形面积为 24, ∴
1 m m ²|- |²|- |=24.∴m=±24. 3 4 2
∴直线 l 的方程为 3x+4y±24=0. 变式训练 1.设直线 l 的方程为(m -2m-3)x+(2m +m-1)y-2m+6=0,根据下列条件求 m 的值. (1)直线 l 的斜率为 1;(2)直线 l 经过定点 P(-1,-1). 解:(1)由题意得-(m -2m-3)=2m +m-1, 即 3m -m-4=0,解之,得 m=-1(舍去)或 m= (2)由题意得 (m -2m-3)³(-1)+(2m +m-1)³(-1)-2m+6=0, 即 3m +m-10=0,解之,得 m=-2 或 m=
不存在, 90, k 与 α 的关系:k= y 2 y1 ,α ∈[0°,90°)∪(90°,180°). tan x x 2 1
注意倾斜角为 90°的直线的斜率不存在(分类讨论). ②直线方程的五种形式及适用范围: (a)斜截式:y=kx+b,不含与 x 轴垂直的直线. (b)点斜式:y-y0=k(x-x0),不含与 x 轴垂直的直线. (c)两点式:
第三章 直线与方程
通过总结和归纳直线与方程的知识,对全章知识内容进行一次梳理,突出 教学 目标 知识间的内在联系,进一步提高学生综合运用知识解决问题的能力.能够 使学生综合运用知识解决有关问题,培养学生分析、探究和思考问题的能 力,激发学生学习数学的兴趣,培养分类讨论的思想和抽象思维能力. 教学重点:①直线的倾斜角和斜率. 教学 重、 难点 ②直线的方程和两直线的位置关系的应用. ③激发学生学习数学的兴趣,培养分类讨论的思想和抽象思维能力. 教学难点:①数形结合和分类讨论思想的渗透和理解. ②处理直线综合问题的策略. 教学 多媒体课件 准备 导入新课 为了系统掌握第三章的知识,教师直接点出课题. 提出问题 ①第一节是直线的倾斜角和斜率,需要注意什么? ②第二节是直线的方程,有几种形式?各自的适用范围怎样? ③第三节是两直线的位置关系,分为哪些内容?如何判断? 教学过 程 ④画出本章的知识结构图. 活动: 让学生自己回顾所学知识或结合教材,重新对知识整合,对没有思路 的学生,教师可以提示按教材的章节标题来分类.对于画知识结构图,可 让学生合作交流,待学生有了不同画法后,先对比分析,再画本章的知识 结构图. 讨论结果:①直线的倾斜角(α )和斜率(k):倾斜角范围:0°≤α <180°, 斜率:k∈R.
人教A版高中数学必修二第三章直线的方程、直线的三种形式教案新

y2 x2
y1 x1
。
【小结】求直线斜率的方法: ①定义法:已知直线的倾斜角为α ,且α ≠90°,则斜率 k=tanα ;
②公式法:已知直线过两点 P1(x1,y1)、P2(x2,y2),且 x1≠x2,则斜率 k= y2 y1 ; x2 x1
③方向向量法:若 a =(m,n)为直线的方向向量,则直线的斜率 k= n 。
,
b
三点共线,则
b
的值为(
)
A. 1
B. 1
C .2
D. 2
2
2
解:因为三点共线,所以 kAB
k AC
2 3
3 2
1
b3
2
b
1 2
2
2)直线 l1 : x my 6 0,l2 : m 2 x 3y 2m 0 相互平行,则 m 的取值范围( )
求证:不论 取何值,点 P 到直线的距离不大于 13 。
(分析)若直接运用点到直线的距离公式,将 P 到 l 的距离 d 化为关于 的函数,只需证明该函数的最大值是 13 ,
若利用直线系方程,结合图形也可获证。
21 3 11 2 2 5
解:法一:由点到直线的距离公式,得 d
由 PQ 2 12 112 13 可知命题成立。
四、总结反思
(1)两点式方程不能表示与 x 轴、 y 轴平行的直线,但行列式形式的方程能表示所有直线;
(2)设三点 A(x1, y1 ) , B(x2 , y2 ) , C(x3 , y3 ) ,则它们共线的充要条件是 A在直线BC上 。
1 3 2 1 2 2
最新人教A版必修2高中数学 第三章《直线与方程》小结与复习教案

1212x x y y k --=高中数学 第三章《直线与方程》小结与复习教案新人教A 版必修2一、教学目标1、知识与技能:(1)掌握知识结构与联系,进一步巩固、深化所学知识;(2)通过对知识的梳理,提高学生的归纳知识和综合应用知识的能力。
2、过程与方法:对本章知识进行系统的小结,直观、简明再现所学知识,化抽象为直观,易于识记,同时凸现数学知识的发展和联系。
3、情感态度与价值观:通过知识的整合、梳理,理会直线的方程及其相互联系,进一步培养学生的数形结合思想和解决问题的能力。
二、教学重点、难点重点:各知识点间的网络关系。
难点:利用直线方程相关知识解决问题。
三、教学过程(一)整合知识,发展思维1、直线的倾斜角和斜率公式:)(tan 211212x x x x y y k ≠--==α; 2、直线方程的五种形式:点斜式:)(00x x k y y -=- 两点式:121121x x x x y y y y --=-- 过点(0,b ) 过点(a ,0),(0,b )斜截式:b kx y += 截距式:1=+by a x 一般式:Ax + By + C = 03、两条直线的位置关系:(1)两条直线相交:求两条直线的交点(解方程组);两条直线垂直:12121-=⇔⊥k k l l 。
(2)两条直线平行::2121//k k l l =⇔; 点到直线的距离公式:2200B A C By Ax d +++=;两条平行直线间的距离:2221B A C C d +-=。
(二)应用举例,深化巩固例1:直线033=--y x 的倾斜角是 。
变式:(1)若20πα<<,则直线x cot α – y – 3 = 0的倾斜角是 。
练习1:若02<<-απ,则直线x cot α – y – 3 = 0的倾斜角是 。
(2)直线x sin α – y – 3 = 0的倾斜角的变化范围是 。
练习2:直线x cos α – 3y – 3 = 0的倾斜角的变化范围是 。
人教新课标版数学高一人教A版必修二 第3章直线与方程复习小结教案

第三章 直线与方程复习小结教学目标分析:知识目标:1、掌握直线的倾斜角的概念、斜率公式;2、掌握直线的方程的几种形式及其相互转化,以及直线方程知识的灵活运用;3、掌握两直线位置关系的判定,点到直线的距离公式及其公式的运用.过程与方法:能够使学生综合运用知识解决有关问题,培养学生分析、探究和思考问题的能力,激发学生学习数学的兴趣,培养分析讨论的思想和抽象思维能力。
情感目标:体会数学中数形结合思想的美.重难点分析:重点:直线知识的掌握及应用难点:数学思想方法在直线解题中的应用互动探究:一、课堂探究:知识1、直线的倾斜角与斜率1、一条直线的倾斜角()2παα≠的正切值叫做这条直线的斜率(slope ).斜率通常用小写字母k 表示,记为tan k α=.2、直线的倾斜角α的取值范围是为0απ≤<3、已知直线上两点11122212(,),(,)()P x y P x y x x ≠,直线的斜率2121y y k x x -=- 知识2、直线的方程1、直线的点斜式方程:已知直线l 经过点000(,)P x y ,且斜率为k ,则方程00()y y k x x -=-为直线的点斜式方程.2、直线的斜截式方程:直线l 与y 轴交点(0,)b 的纵坐标b 叫做直线l 在y 轴上的截距(int ercept ).直线y kx b =+叫做直线的斜截式方程.3、直线的两点式方程:已知直线上两点1112221212(,)(,)(,)P x y P x y x x y y ≠≠、,则通过这两点的直线方程为:1112122121(,)y y x x x x y y y y x x --=≠≠--. 4、直线的截距式方程:已知直线l 与x 轴的交点为(,0)A a ,与y 轴的交点为(0,)B b ,其中0,0a b ≠≠,则直线l 的方程为:1=+by a x . 5、直线方程的一般式:关于,x y 的二元一次方程0(0)Ax By c A B ++=、不同时为叫做直线的一般式方程,简称一般式( general form ). 知识3、两直线的位置关系1、两直线平行的斜率关系:两条直线有斜率且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,则它们平行,即1212//l l k k ⇔=.2、两直线垂直的斜率关系:两条直线都有斜率,如果它们互相垂直,则它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,则它们互相垂直.即12121l l k k ⊥⇔•=-知识4、距离关系1、平面上两点间的距离公式:已知平面上两点111222(,)(,)P x y P x y 、,则12||PP =.特殊地:(,)P x y与原点的距离为||OP =2、点000(,)P x y 到直线:0l Ax By C ++=的距离为:2200BA C By Ax d +++= 3、已知两条平行线直线1122:0,:0l Ax By C l Ax By C ++=++=,则12l l 与的距离为d =知识5、直线系方程的定义具有某一个共同性质的直线的集合叫做直线系,它的方程叫做直线系方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:2.3.3.8直线方程章节复习小结
课型:复习课
教学目标:进一步加深掌握直线知识,并能灵活运用知识解决有关问题
教学重点:直线方程的综合运用
教学难点:解决问题的方法与策略
教学过程:
直线与方程单元测试题
姓名-------------- 班级-------------
一.选择题
1.过点(1,3)
-y
+
x的直线方程为()P-且垂直于直线0
3
2=
A0
2=
-
+y
x
5
1
2=
-
+y
x B0
C0
2=
+
-y
x
7
5
x D0
-
2=
+y
2.已知过点(2,)
-
x平行,
2=
+y
1
-和(,4)
A m
B m的直线与直线0
则m的值为()
- C2 D10
A0 B8
3.直线13
kx y k
-+=,当k变动时,所有直线都通过定点()A(0,0)B(0,1)C(3,1)D(2,1)
4.与直线2x+3y-6=0关于点(1,-1)对称的直线是()
A.3x-2y-6=0
B.2x+3y+7=0
C. 3x-2y-12=0
D. 2x+3y+8=0
5.下列命题正确的有
①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应; ②倾斜角的范围是:0°≤α<180°,且当倾斜角增大时,斜率也增大; ③过两点A(1,2),B(m,-5)的直线可以用两点式表示;
④过点(1,1),且斜率为1的直线的方程为111
y x -=-; ⑤直线Ax+By+C=0(A,B 不同时为零),当A,B,C 中有一个为零时,这个方程不能化为截距式.
⑥若两直线平行,则它们的斜率必相等;
⑦若两直线垂直,则它们的斜率相乘必等于-1.
二.填空题
6.点(,)P x y 在直线40x y +-=上,则22x y +的最小值是________________
7.直线l 过原点且平分
A B C D 的面积,若平行四边形的两个顶点为(1,4),(5,0
B D ,则直线l 的方程为________________ 8.已知直线l 与直线3x+4y -7=0平行,并且与两坐标轴围成的三角形的面积为24,则直线l 的方程为________________
三.解答题
9.已知△ABC 的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C 的坐标.
10.把函数()y f x =在x a =及x b =之间的一段图象近似地看作直线,设a c b ≤≤,
证明:()f c 的近似值是:()f c =()()()[]f a c a b a
f b f a +--- C(c,y c )B(b,f(b))
(c,f(c))
A(a,f(a))o
y
x
11.已知直线012:=+-y x l 和点A (-1,2)、B (0,3),试在l 上找一点P ,使得PB PA +的值最小,并求出这个最小值。
答案与解析:
一. 选择题
1. A 设20,x y c ++=又过点(1,3)P -,则230,1c c -++==-,即210x y +-=
2. B 42,82
m k m m -==-=-+ 3. C 由13kx y k -+=得(3)1k x y -=-对于任何k R ∈都成立,则3010x y -=⎧⎨-=⎩
4. D 把线关于点的对称转化为点与点的对称
5. ⑤
二.填空题
6.8 22x y +可看成原点到直线上的点的距离的平方,垂直时最短:4
222d -==
7.23y x =
平分平行四边形ABCD 的面积,则直线过BD 的中点(3,2) 8.设l :3x 4y m 0++= 则当y=0得m x 3=- ; 则当x=0得m y 4=- ∵直线l 与两坐标轴围成的三角形面积为24 ∴1m m ||||24234
⋅-⋅-= ∴m 24=± ∴直线l 的方程为3x 4y 240+±=
三.解答题
9.解: ∵BH 24k 256-==- ∴AC 1k 2
=- ∴直线AC 的方程为1y 2(x 10)2
-=-+ 即x+2y+6=0 (1) 又∵AH k 0= ∴BC 所直线与x 轴垂直 故直线BC 的方程为x=6 (2)
解(1)(2)得点C 的坐标为C(6,-6)
10.证明:,,A B C 三点共线,AC AB k k ∴=
即
()()()c y f a f b f a c a b a
--=-- ()[()()]c c a y f a f b f a b a
-∴-=-- 即()[()()]c c a y f a f b f a b a
-=+-- ()f c ∴的近似值是:()()()[]f a c a b a f b f a +---. 11.解:过点B (0,3)且与直线l 垂直的直线方程为x y l 2
13:'-=-, 由⎪⎩⎪⎨⎧+-==+-321012x y y x 得:⎪⎪⎩
⎪⎪⎨⎧==51354y x ,即直线l 与直线'l 相交于点)513,54(Q , 点B (0,3)关于点)513,54(Q 的对称点为)5
11,58('B , 连'AB ,则依平面几何知识知,'AB 与直线l 的交点P 即为所求。
直线'AB 的方程为)1(1312+=-x y ,由⎪⎩⎪⎨⎧+==+-1327131012x y y x 得⎪⎪⎩
⎪⎪⎨⎧==25532514y x ,即:)25
53,2514(P , 相应的最小值为5
170)5112()581(22=-+--=‘AB .。
