【最新】人教版数学八年级上册11.2.2 三角形的外角同步练习
八年级初二上册数学人教版课时练《 三角形的外角》01(含答案)

《第十一章三角形 11.2.2三角形的外角》课时练一、选择题1.如图,在中,46C ∠=︒,将ABC 沿直线l 折叠,点C 落在点D 的位置,则12∠-∠的度数是( )A .23︒B .92︒C .46︒D .无法确定 2.如图,//AB CD ,165∠=︒,235∠=︒,则B 的度数是( )A .20︒B .25︒C .30D .35︒ 3.已知直线12//l l ,一块含30角的直角三角板如图所示放置,125∠=︒,则2∠=( )A .45︒B .50︒C .55︒D .60︒ 4.如图,直角三角形ABC 的顶点A 在直线m 上,分别度量:①①1,①2,①C ;①①2,①3,①B ;①①3,①4,①C ;①①1,①2,①3,可判断直线m 与直线n 是否平行的是( )A .①B .①C .①D .① 5.将一副三角板按如图所示摆放,直角三角尺AOB 的锐角顶点A 与另一三角尺ACD 的直角顶点重合在一起,(其中45OAB ∠=︒,60C ∠=°),直角边AD 与OB 交于点E ,若//AB CD ,则BED ∠的度数为( ).A .60︒B .65︒C .70︒D .75︒6.如图,将含30°角的直角三角板ABC 放在平行线α和b 上,①C =90°,①A =30°,若①1=20°,则①2的度数等于( )A .60°B .50°C .40°D .30°7.如图,直线//MN PQ ,点A 是MN 上一点,MAC ∠的角平分线交PQ 于点B ,若120∠=︒,2116∠=︒,则3∠的大小为( )A .136°B .148°C .146°D .138°8.如图,把ABC 纸片沿DE 折叠,点A 落在四边形BCED 的外部,1100∠=︒,244∠=︒,则A ∠的度数为( )A .32°B .30°C .28°D .26°9.如图,直线a①b ,直线AC 分别交a 、b 于点B 、C ,直线AD 交a 于点D .若①1=20°,①2=65°,则①3度数等于( )A .30°B .45°C .60°D .85°10.如图,四边形ABCD 是长方形,点F 是DA 长线上一点,G 是CF 上一点,并且ACG AGC ∠=∠,GAF F ∠=∠.若15ECB ∠=︒,则ACF ∠的度数是( )A .15︒B .20︒C .30D .45︒二、填空题 11.如图,若115EOC ∠=︒,则A B C D E F ∠+∠+∠+∠+∠+∠=____________.12.如图在直角三角形ABC 中,①ACB =90°,①A =50°,D 是AB 上的点,将①ACD 沿直线CD 翻折,使点A 恰好落在BC 上的点E 处,则①BDE =________.13.如图,直线a ①b ,一块含60°角的直角三角板ABC (①A =60°)按如图所示放置.若①1=50°,则①2的度数为__°.14.如图,AC BD ⊥于C ,E 是AB 上一点,CE CF ⊥,//,DF AB EH 平分,BEC DH ∠平分BDG ∠,则:H ∠与ACF ∠之间的数最关系为______.15.如图,在ABC 中,ABC C ∠=∠,100A ∠=︒,BD 平分ABC ∠交AC 于点D ,点E 是BC 上一个动点.若DEC 是直角三角形,则BDE ∠的度数是______.三、解答题16.小明在学习三角形的知识时,发现如下数学问题:已知线段AB ,CD 交于点E ,连结时AD ,BC .(1)如图①,若100D B ∠=∠=︒,DAB ∠的平分线与BCE ∠的平分线交于点G ,求G ∠的度数;(2)如图①,若90D B ∠=∠=︒,AM 平分DAB ∠,CF 平分BCN ∠,请判断CF 与AM 的位置关系,并说明理由.17.如图,在①ABC 中,D 是AB 上一点,E 是AC 上一点,BE ,CD 相交于点F . (1)若①A =62°,①ACD =36°,①ABE =20°,则①BFD 的度数为 °;(2)若①ADF+①AEF =180°,①FBC =①FCB ,试判断①A 与①FBC 之间的数量关系,并说明理由.18.如图,CD是①ABC的角平分线,DE①BC,交AC于点E.(1)若①A=45°,①BDC=70°,求①CED的度数;(2)若①A-①ACD=34°,①EDB=97°,求①A的度数.19.已知AM①BN,BD平分①ABN交AM于点D,E为射线BA上的点,设①ABD=α.(1)如图1,求①ADB的度数(用α表示);(2)如图2,若F为AD上的点,①EFD的平分线所在直线分别交BD、ED于点G、H,当HG//BE时,求①BEF的度数(用α表示).20.(问题背景)①MON=90°,点A、B分别在OM、ON上运动(不与点O重合).(问题思考)(1)如图①,AE、BE分别是①BAO和①ABO的平分线,随着点A、点B的运动,①AEB=.(2)如图①,若BC是①ABN的平分线,BC的反向延长线与①OAB的平分线交于点D.①若①BAO =70°,则①D = °.①随着点A 、B 的运动,①D 的大小会变吗?如果不会,求①D 的度数;如果会,请说明理由;(问题拓展)(3)在图①的基础上,如果①MON =a ,其余条件不变,随着点A 、B 的运动(如图①),①D = .(用含a 的代数式表示)21.已知ABC 中,AE 是ABC 的角平分线,72B ∠=︒,36C ∠=︒.(1)如图①,若AD BC ⊥于点D ,求DAE ∠的度数;(2)如图①,若P 为AE 上一个动点(P 不与A ,E 重合),且PF BC ⊥于点F 时,则EPF ∠=_____;(3)探究:如图①,ABC 中,已知B ,C ∠均为锐角,B C ∠>∠,AE 是ABC 的角平分线,若P 为线段AE 上一个动点(P 不与E 重合),且PF BC ⊥于点F 时,请写出EPF ∠与B ,C ∠的关系,并说明理由.22.(问题情境):如图AB //CD ,120PAB ∠=,140PCD ∠=,求APC ∠的度数. 小明的思路是:过P 作PE //AB ,通过平行线性质来求APC ∠.(1)按小明的思路,求APC ∠的度数;(2)(问题迁移):如图2,AB //CD ,点P 在射线OM 上运动,记①P AB =α,①PCD =β,当点P 在B 、D 两点之间运动时,问①APC 与α、β之间有何数量关系?请说明理由;(3)(问题应用):在(2)的条件下,如果点P 在B 、D 两点外侧运动时(点P 与点O 、B 、D 三点不重合),请直接写出①APC 与α、β之间的数量关系.23.(1)已知AB ①CD ,E 是AB 、CD 间一点,如图1,给它取名“M 型”;有结论:E A C ∠=∠+∠;如图2,给它取名“铅笔头型”,有结论:360A E C ∠+∠+∠=︒;①在图3 “M型”中,AF、CF分别平分①A、①C,则①F与①E的关系是;①在图4 “铅笔头型”中,延长EC到G,AF、CF分别平分①A、①DCG,则①F与①E的关系是;(2)若直线AB与直线CD不平行,连接EG,且EG同时平分①BEF和①FGD.①如图5,请探究①1、①2、①F之间的数量关系?并说明理由;①如图6,①1比①2的3倍多18°,①2是①F的23,求①F的度数.参考答案1.B 2.C 3.C 4.B 5.D 6.B 7.B 8.C 9.B 10.C11.230°12.10°13.11014.2①H +①ACF =180°15.30°或70°.16.(1)100°;(2)平行17.(1)62;(2)①A =2①FBC18.(1)130°;(2)55°19.(1)①ADB =α;(2)①BEF =2α20.(1)135°;(2)①45;①①D 的度数不随着点A 、B 的运动而发生变化;①D =45°;(3)12α. 21.(1)18DAE ∠=︒;(2)18°;(3)2B C EPF ∠-∠∠=. 1902∠=︒-∠F E 22.(1)100゜;(2)①APC =α+β;(3)当P 点在线段OB 上运动时,APC ∠=β-α;当P 点在射线DM 上运动时,APC ∠=α-β23.(1)①2E F ∠=∠;① ;(2)① ;①27F ∠=︒ ()1122F ∠=∠+∠。
人教版八年级数学上册《11-2-2 三角形的外角》作业同步练习题及参考答案

11.2.2 三角形的外角1.如图,直线a,b,c,d 互不平行,对它们截出的一些角的数量关系描述错误的是( ).A.∠1+∠6=∠2B.∠4+∠5=∠2C.∠1+∠3+∠6=180°D.∠1+∠5+∠4=180°2.一副三角尺按如图所示的方式叠放在一起,则∠α的度数是( ).A.165°B.120°C.150°D.135°3.如图,在△ABC 中,∠A=x°,∠B=(x+10)°,D 是BC 延长线上一点,且∠ACD=(x+70)°,则x 等于( ).A.60B.70C.80D.1004.已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2 等于( ).A.50°B.55°C.60°D.65°5.如图,∠ABC 的平分线与∠ACD 的平分线相交于点P.若∠A=60°,则∠P 等于( ).A.30°B.40°C.50°D.60°6.如图,∠B+∠C+∠D+∠E-∠A 等于( ).A.360°B.300°C.180°D.240°7.如图,∠1,∠2,∠3 的大小关系是> > .8.如图,在△ABC 中,D 是AB 上一点,E 是AC 上一点,BE 与CD 相交于点F,∠A=62°,∠ACD=35°,∠ ABE=20°,则∠BDC= ,∠BFC= .9.如图,在△ABC 中,∠A=60°,BD,CE 分别是AC,AB 上的高,H 是BD 与CE 的交点,求∠BHC 的度数.10.如图,在△ABC 中,AD 是BC 边上的高,AE 平分∠BAC,∠B=75°,∠C=45°,求∠DAE 与∠AEC 的度数.11.如图①,在△ABC 中,AD 是△ABC 的外角∠EAC 的平分线,且交BC 的延长线于点D.(1)若∠ACB=50°,∠D=15°,求∠B;(2)试探究∠ACB 与∠B 及∠D 的关系;(3)如图②,在△ABC 中,AF 是△ABC 外角∠EAB 的平分线,AF 的反向延长线交BC 的延长线于点D,∠ ACB 与∠B 及∠D 的关系仍然成立吗?为什么?①②★12.如图是一个零件的形状如图所示,按规定∠A=90°,∠B=21°,∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学知识说出其中的道理吗?13.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F 等于( ).A.360°B.720°C.540°D.240°★14.如图①,有一个五角形图案ABCDE,你能说明∠A+∠DBE+∠C+∠D+∠E=180°吗?如果点B 向下移动到AC 上(如图②)或AC 的另一侧(如图③),上述结论是否依然成立?请说明理由.答案与解析夯基达标1.A2.A 如图,∵∠2=90°-45°=45°,∴∠1=∠2-30°=15°.∴∠α=180°-∠1=165°.故选A.3.A4.B5.A 由三角形的外角性质,得∠P=∠PCD-∠PBD=1(∠ACD-∠ABC)=1∠A=30°.2 26.C ∵∠B+∠C=∠CGE=180°-∠1,∠D+∠E=∠DFG=180°-∠2,∴∠B+∠C+∠D+∠E-∠A=360°-(∠1+∠2+∠A)=180°.故选C.7.∠1 ∠2 ∠38.97°117°9.解∵BD,CE 分别是△ABC 的边AC,AB 上的高,∴∠BEH=∠ADB=90°.∵∠A=60°,∴∠ABH=30°.由三角形的一个外角等于与它不相邻的两个内角的和,得∠BHC=∠ABH+∠BEH, 即∠BHC=30°+90°=120°.培优促能10.解∠BAC=180°-∠B-∠C=180°-75°-45°=60°.∵AE 平分∠BAC,∴∠BAE=∠CAE=1×60°=30°.2∴∠AEC=∠B+∠BAE=75°+30°=105°.∵AD⊥BC,∴∠ADC=90°.∴∠DAE=∠AEC-∠ADC=105°-90°=15°.11.解(1)∵∠ACB=50°,∠D=15°,∴∠CAD=∠ACB-∠D=35°.∵AD 平分∠EAC,∴∠EAD=∠CAD=35°.∴∠B=∠EAD-∠D=20°.(2)∵∠CAD=∠ACB-∠D,AD 平分∠EAC,∴∠EAD=∠CAD=∠ACB-∠D.∴∠B=∠EAD-∠D=∠ACB-∠D-∠D=∠ACB-2∠D,即∠ACB=∠B+2∠D.(3)成立.理由如下:∵∠ACB=∠D+∠DAC,∠DAC=∠FAE,∴∠ACB=∠D+∠FAE.∵AF 平分∠EAB,∴∠FAB=∠FAE.∴∠ACB=∠D+∠FAB.∵∠FAB=∠D+∠B,∴∠ACB=∠D+∠D+∠B,即∠ACB=∠B+2∠D.12.解如图,延长CD 交AB 于点E.∵∠1=∠C+∠A,∠BDC=∠1+∠B,∴∠BDC=∠C+∠A+∠B=20°+90°+21°=131°.∵零件中∠BDC=130°,∴可以断定这个零件不合格.创新应用13.D 如图,根据三角形的外角性质可得∠1=∠A+∠C,∠2=∠B+∠D.∵∠BOF=120°,∴∠3=180°-120°=60°.根据三角形内角和定理可得∠E+∠1=180°-60°=120°,∠F+∠2=180°-60°=120°,∴∠1+∠2+∠E+∠F=120°+120°=240°,即∠A+∠B+∠C+∠D+∠E+∠F=240°.故选D.14.解在题图①中,∠A+∠C=∠DNM,①∠DBE+∠E=∠DMN,②由①+②,得∠A+∠DBE+∠C+∠E=∠DNM+∠DMN.∵∠D+∠DNM+∠DMN=180°,∴∠A+∠DBE+∠C+∠D+∠E=180°.在题图②、题图③中,上述结论仍然成立,理由与题图①完全相同.。
人教版八年级数学上册11.2.2《三角形的外角》同步练习(无答案)

11.2.2三角形的外角一、选择题1. 如图,∠ACD=120°,∠B=20°,则∠A的度数是()A.120° B.90°C.100° D.30°2.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是().A.45°B.60°C.75°D.85°3.如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF 的度数为()A.60°B.65°C.70°D.15°4.如图,在中,,,是的角平分线.则的度数是()A.95°B.100° C.105° D.110°5.在中,,与的外角度数如图所示,则x的值是( )A.60 B.65 C.70 D.806,如图,∠A=20°,∠B=30°,∠C=50°,求∠ADB的度数()A .50°B .100°C .70°D .80°7.已知等腰三角形的一个外角等于100°,则它的顶角是()A .80°或50°B .20°C .80°或20°D .不能确定8.如图,下列说法中错误的是()A .不是三角形的外角B .C . 是三角形的外角D .9.如图,在Rt△ADB中,∠D=90°,C为AD上一点,则x 可能是()A .10°B .20°C .30°D .40°10.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于()A.40°B.45°C.50°D.55°二、填空题11.在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是________.12. 如图,∠1,∠2,∠3的大小关系是_____.13.在三角形的三个外角中,钝角最多有()14.如图,把一个含30°角的直角三角尺的直角顶点放在直尺的一边上,如果∠1=20°,那么∠2的度数为()三、解答题15.证明“三角形的外角和等于360°”;如图,∠BAE、∠CBF、∠ACD 是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角∴______________.∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)∵_____________.∴∠BAE+∠CBF+∠ACD=360°请把证法补充完整。
人教版八年级数学上册 11.2.2三角形的外角 同步训练卷

人教版八年级数学上册11.2. 2三角形的外角同步训练卷一、选择题(共10小题,3*10=30)1.下列各图中,∠1是△ABC的外角的是()2.如图,∠ACD=120°,∠B=20°,则∠A的度数是()A.120°B.90°C.100°D.30°3.关于三角形的外角,下列说法中错误的是()A.一个三角形只有三个外角B.三角形的每个顶点处都有两个外角C.三角形的每个外角是与它相邻内角的邻补角D.一个三角形共有六个外角4.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=() A.35° B.95° C.85° D.75°5.将一副直角三角尺按如图所示的位置摆放,使得它们的直角边互相垂直,则∠1的度数是() A.95°B.100° C.105°D.110°6. 如图,点D在△ABC的边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是()A.24°B.59° C.60°D.69°7.如图,a∥b,若∠1=40°,∠2=55°,则∠3等于()A.85° B.95° C.105° D.115°8.下列对三角形的外角和叙述正确的是()A.三角形的外角和等于180°B.三角形的外角和就是所有外角的和C.三角形的外角和等于所有外角的和的一半D.以上都不对9.如图,点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则图中∠1,∠2,∠A的大小关系是()A.∠A>∠2>∠1B.∠A>∠1>∠2C.∠2>∠1>∠A D.∠1>∠2>∠A10.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为()A.60° B.65° C.75° D.85°二.填空题(共8小题,3*8=24)11.如图,下列各角为△ABC的外角的是_______.12. 将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是________.13.如图,平面上直线a,b分别过线段C,D两端点(数据如图),则a,b相交所成的锐角是______度.14.如图,直线a∥b,c,d是截线且交于点A,若∠1=60°,∠2=100°,则∠A=______.15.如图,∠A+∠B+∠C+∠D+∠E的度数是______.16.如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=______.17.如图,在△ABC中,∠ABC的平分线和∠ACB的外角平分线交于点D,已知∠A=80°,则∠D 的度数为________.18.如图,在△ABC中,∠B=∠C,∠CDE=1∠BAD,∠CAD=70°,则∠AED=.2三.解答题(共7小题,46分)19.(6分) 如图,AB∥CD,∠A=45°,∠C=∠E.求∠C的度数.20.(6分) 如图,DE分别交△ABC的边AB,AC于点D,E,交BC的延长线于点F,∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.21.(6分) 如图,在△ABC中,D是BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC 的度数.22.(6分) 某工厂要制作符合条件的模板.如图,要求∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测量∠BDC的度数的方法筛选出不合格的产品.若测得∠BDC的度数为150°,则这块模板是否合格?请说明理由.23.(6分)小桐把一副直角三角尺按如图的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,求∠1+∠2。
人教版八年级上册数学 11.2.2 三角形的外角 同步练习

人教版八年级上册数学11.2.2 三角形的外角 作业一、单选题1.如图将直尺与含30°角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .30B .40︒C .50︒D .60︒2.如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于( )A .105°B .120°C .110°D .115°3.如图,已知△ABC 为直角三角形,∠B =90°,若沿图中虚线剪去∠B ,则∠1+∠2=()A .90°B .135°C .270°D .315°4.下图能说明∠1>∠2的是( )A .B .C .D .5.如图,////OP QR ST 下列各式中正确的是( )A .123180∠+∠+∠=B .12390∠+∠-∠=C .12390∠-∠+∠=D .231180∠+∠-∠=6.已知,如图,在ABC ∆中,150C ︒∠=,点E 是边AB 上点,65DEF ︒∠=,则ADE BFE ∠+∠=( )A .180︒B .215︒C .205︒D .185︒7.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则图中∠β的度数是( )A .75°B .65°C .55°D .45°8.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( )A .4:3:2B .3:2:4C .5:3:1D .3:1:59.如图,将一张三角形纸片ABC 的一角折叠,使点A 落在ABC ∆处的'A 处,折痕为DE .如果A α∠=∠'CEA β∠=∠'BDA γ∠=,那么下列式子中正确的是( ∠A .2γαβ=+B .2γαβ=+C .γαβ=+D .180γαβ=--10.如图,∠ABC =∠ACB ,AD,BD,CD 分别平分△ABC 的外角∠EAC 、内角∠ABC 、外角∠ACF .以下结论:∠AD//BC ;∠∠ACB =2∠ADB ;∠DB 平分∠ADC ;∠∠ADC =90°−∠ABD ;∠∠BDC =12∠BAC .其中正确的结论有( ).A.1个B.2个C.3个D.4个二、填空题11.如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD=_____.12.从A沿北偏东60︒的方向行驶到B,再从B沿南偏西20︒方向行驶到C,则ABC∠=______. 13.如图,若AB∥CD∠∠C=60°,则∠A+∠E=_____度.14.如图,∠BCD=150°,则∠A+∠B+∠D的度数为_______.15.如图,D∠E∠F分别是△ABC三边延长线上的点,则∠D+∠E+∠F+∠1+∠2+∠3=_____度.16.如图,将一张三角形纸片ABC 的一角折叠,使点A 落在△ABC 外的A'处,折痕为DE.如果∠A =α,∠CEA′=β,∠BDA'=γ,那么α,β,γ 三个角的数量关系是__________ .三、解答题17.如图,已知DF AB ⊥于F ,且45A ︒∠=,30D ︒∠=,求ACB ∠的度数.18.已知:如图,∠XOY =90°,点A 、B 分别在射线OX 、OY 上移动(不与点O 重合),BE 是∠ABY 的平分线,BE 的反向延长线与∠OAB 的平分线相交于点C .(1)当∠OAB =40°时,∠ACB = 度;(2)随点A 、B 的移动,试问∠ACB 的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.19.如图,在ABC 中,AD 是高,AE 、BF 是角平分线,它们相交于点O ,50CAB ∠=︒,60C ∠=°.(1)求DAE ∠的度数;(2)求BOA ∠的度数.20.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.21.如图,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合).(1)如图1,若∠MON=90°,∠OBA 、∠OAB 的平分线交于点C ,则∠ACB= °; (2)如图2,若∠MON=n°,∠OBA 、∠OAB 的平分线交于点C ,求∠ACB 的度数;(3)如图2,若∠MON=n°,△AOB 的外角∠ABN 、∠BAM 的平分线交于点D ,求∠ACB 与∠ADB 之间的数量关系,并求出∠ADB 的度数;(4)如图3,若∠MON=80°,BC 是∠ABN 的平分线,BC 的反向延长线与∠OAB 的平分线交于点E .试问:随着点A 、B 的运动,∠E 的大小会变吗?如果不会,求∠E 的度数;如果会,请说明理由.答案1.C 2.D 3.C 4.C 5.D 6.B 7.A 8.C 9.A 10.D 11.30° 12.4013.60 14.150度15.180 16.γ=2α+β.17.解:∵DF AB ⊥90AFE ∴∠=︒45A ∠=︒45AEF ∴∠=︒45CED AEF ∴∠=∠=︒304575ACB D CED ∴∠=∠+∠=︒+︒=︒18.解:(1)∵∠XOY =90°,∠OAB =40°,∴∠ABY =130°,∵AC 平分∠OAB ,BE 平分∠YBA ,∴∠CAB =12∠OAB =20°,∠EBA =12∠YBA =65°,∵∠EBA =∠C+∠CAB ,∴∠C =∠EBA ﹣∠CAB =45°,故答案为45;(2)∠ACB 的大小不变化.理由:∵AC 平分∠OAB ,BE 平分∠YBA ,∴∠CAB =12∠OAB ,∠EBA =12∠YBA ,∵∠EBA =∠C+∠CAB ,∴∠C =∠EBA ﹣∠CAB =12∠YBA ﹣12∠OAB =12(∠YBA ﹣∠OAB ), ∵∠YBA ﹣∠OAB =90°,∴∠C =12×90°=45°,即:∠ACB 的大小不发生变化.19. 解:(1)∵∠CAB=50°,∠C=60°∴∠ABC=180°-50°-60°=70°,又∵AD 是高,∴∠ADC=90°,∴∠DAC=180°-90°-∠C=30°,∵AE 、BF 是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,∴∠DAE=∠DAC-∠EAF=5°,(2)∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAE=5°,∠BOA=120°.20.解[习题回顾]证明:∵∠ACB=90°,CD是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD,∵AE是角平分线,∴∠CAF=∠DAF,∵∠CFE=∠CAF+∠ACD,∠CEF=∠DAF+∠B,∴∠CEF=∠CFE;[变式思考]相等,理由如下:证明:∵AF为∠BAG的角平分线,∴∠GAF=∠DAF,∵∠CAE=∠GAF,∴∠CAE=∠DAF,∵CD为AB边上的高,∠ACB=90°,∴∠ADC=90°,∴∠ADF=∠ACE=90°,∴∠DAF+∠F=90°,∠E+∠CAE=90°,∴∠CEF=∠CFE;[探究延伸]∠M+∠CFE=90°,证明:∵C、A、G三点共线AE、AN为角平分线,∴∠EAN=90°,又∵∠GAN=∠CAM,∴∠M+∠CEF=90°,∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,∴∠CEF=∠CFE,∴∠M+∠CFE=90°.21.解(1)∵∠MON=90°,∴∠OBA+∠OAB=90°,∵∠OBA、∠OAB的平分线交于点C,∴∠ABC+∠BAC=12×90°=45°,∴∠ACB=180°-45°=135°;故答案为135;(2)在△AOB中,∠OBA+∠OAB=180°-∠AOB=180°-n°,∵∠OBA、∠OAB的平分线交于点C,∴∠ABC+∠BAC=12(∠OBA+∠OAB)=12(180°-n°),即∠ABC+∠BAC=90°-12n°,∴∠ACB=180°-(∠ABC+∠BAC)=180°-(90°-12n°)=90°+12n°;(3)∵BC、BD分别是∠OBA和∠NBA的角平分线,∴∠ABC=12∠OBA,∠ABD=12∠NBA,∠ABC+∠ABD=12∠OBA+12∠NBA,∠ABC+∠ABD=12(∠OBA+∠NBA)=90°,即∠CBD=90°,同理:∠CAD=90°,∵四边形内角和等于360°,∴∠ACB+∠ADB=360°-90°-90°=180°,由(1)知:∠ACB=90°+12n°,∴∠ADB=180°-(90°+12n°)=90°-12n°,∴∠ACB+∠ADB=180°,∠ADB=90°-12n°;(4)∠E的度数不变,∠E=40°;理由如下:∵∠NBA=∠AOB+∠OAB,∴∠OAB=∠NBA-∠AOB,∵AE、BC分别是∠OAB和∠NBA的角平分线,∴∠BAE=12∠OAB,∠CBA=12∠NBA,∠CBA=∠E+∠BAE,即12∠NBA=∠E+12∠OAB,1 2∠NBA=∠E+12(∠NBA-80°),1 2∠NBA=∠E+12∠NBA-40°,∴∠E=40°.答案第1页,总1页。
新人教版八年级数学上册11.2.2 三角形的外角 练习

11.2.2三角形的外角基础知识 一、选择题 1.(2013•襄阳)如图,在△ABC 中,D 是BC 延长线上一点,∠B=40°,∠ACD=120°,则∠A 等于( )A .60°B .70°C .80°D .90°答案:C 2.(2013•湘西州)如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD 的度数是( ) A .15° B .25° C .30° D .10°答案:A3.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( ) A.有两个锐角、一个钝角 B.有两个钝角、一个锐角 C.至少有两个钝角 D.三个都可能是锐角 答案:C4. (2012 江苏省南通市) 如图,△ABC 中,∠C =70°,若沿图中虚线截去∠C ,则∠1+∠2等于 ( )A .360°B .250°C .180°D .140° 答案:BA CB 1 25.已知△ABC,(1)如图1,若P 点是∠ABC 和∠ACB 的角平分线的交点,则∠P=90°+21∠A; (2)如图2,若P 点是∠ABC 和外角∠ACE 的角平分线的交点,则∠P=90°-∠A; (3)如图3,若P 点是外角∠CBF 和∠BCE 的角平分线的交点,则∠P=90°-21∠A . 上述说法正确的个数是( )A .0个B .1个C .2个D .3个 答案:C6.(2012•漳州)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( ) A .45° B .60° C .75° D .90°答案:C7.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A 的度数是( ) A .61° B .60° C .37° D .39°答案:C8.如图,在Rt △ADB 中,∠D=90°,C 为AD 上一点,则x 可能是( ) A .10° B .20° C .30° D .40°答案:B9.如图,∠A=34°,∠B=45°,∠C=36°,则∠DFE的度数为()A.120° B.115° C.110° D.105°答案:B10.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为()A.180° B.360° C.540° D.720°答案:B11.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A 与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()A.∠A=∠1-∠2 B.2∠A=∠1-∠2C.3∠A=2∠1-∠2 D.3∠A=2(∠1-∠2)答案:B12.如图,则∠A+∠B+∠C+∠D+∠E=()A.90 B.180 C.200 D.360答案:B13.如图,BD、CD分别平分∠ABC和∠ACE,∠A=40°,则∠D的度数是()A.20°B.30°C.40°D.60°答案:A14.如图,等边三角形ABC,P为BC上一点,且∠1=∠2,则∠3为()A.50°B.60°C.75°D.无法确定答案:B二、填空题2.如图,已知ΔABC中,∠ABC和外角∠ACE的平分线相交于点D,若∠D=400,则∠BAC的度数为 .1.如图,BP 、CP 是任意△ABC 中∠B、∠C 的角平分线,可知∠BPC=90°+21∠A,把图中的△ABC 变成图中的四边形ABCD ,BP ,CP 仍然是∠B,∠C 的平分线,猜想∠BPC 与∠A、∠D 的数量关系是 .答案:∠BPC=21(∠BAD+∠ADC).6.已知:如图,在直角坐标系中,点A ,B 分别是x 轴,y 轴上的任意两点,BE 是∠ABy 的平分线,BE 的反向延长线与∠OAB 的角平分线交于点C ,则∠ACB= .答案:45°三、解答题4.下面是有关三角形内外角平分线的探究,阅读后按要求作答:探究1:如图(1),在△ABC 中,O 是∠ABC 与∠ACB 的平分线BO 和CO 的交点,通过分析发现:∠BOC=90°+21∠A(不要求证明).探究2:如图(2)中,O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点,试分析∠BOC 与∠A 有怎样的数量关系?请说明理由.探究3:如图(3)中,O 是外角∠DBC 与外角∠ECB 的平分线BO 和CO 的交点,则∠BOC 与∠A 有怎样的数量关系?(只写结论,不需证明).结论: .解:(1)探究2结论:∠BOC=21∠A, 理由如下:∵BO 和CO 分别是∠ABC 和∠ACD 的角平分线, ∴∠1=21∠ABC,∠2=21∠ACD, 又∵∠ACD 是△ABC 的一外角, ∴∠ACD=∠A+∠ABC, ∴∠2=21(∠A+∠ABC)=21∠A+∠1, ∵∠2是△BO C 的一外角,∴∠BOC=∠2-∠1=21∠A+∠1-∠1=21∠A; (2)探究3结论∠BOC=90°-21∠A.可以编辑的试卷(可以删除)学习提示:1、通过练习发现不足。
2020-2021学年度人教版八年级数学上册11.2.2三角形的外角课时练习(含答案解析)

2020-2021学年度人教版八年级数学上册11.2.2三角形的外角课时练习一、选择题1.如图,直线//a b ,则A ∠=( )A .28︒B .35︒C .40︒D .45︒ 2.如图所示,长方形ABCD 中,点E 在CD 边上,AE ,BE 与直线L 相交α∠,β∠,构成则1∠,2∠,α∠,β∠之间的关系是( )A .12180αβ∠+∠+︒=∠+∠B .21αβ∠+∠=∠+∠C .()212αβ∠+∠=∠+∠D .12αβ∠+∠=∠-∠3.如图,A ABC CB =∠∠,AD 、BD 、CD 分别平分ABC 的外角EAC ∠、 内角ABC ∠、外角ACF ∠.以下结论:①//AD BC ;②2ACB ADB ∠=∠;③90ADC ABD ∠=︒-∠;④12BDC BAC ∠=∠.其中正确的结论有( ).A .1个B .2个C .3个D .4个4.如图,在ABC 中,点D 是BC 延长线上一点,70A ∠=︒,120ACD ∠=︒,则B 等于( ).A .60°B .80°C .70°D .50°5.如图,ABC ∆中,40A ∠=︒,20ABO ∠=︒,30ACO ∠=︒,则BOC ∠等于( )A .80︒B .90︒C .100︒D .110︒ 6.如图将直尺与含30°角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .30B .40︒C .50︒D .60︒ 7.如图,把ABC ∆绕点C 顺时针旋转某个角度α得到'',30,150A BC A ︒︒∆∠=∠=,则旋转角'BCB ∠等于( )A .30︒B .25︒C .15︒D .20︒ 8.一幅三角板,如图所示叠放在一起,则图中∠α的度数是( )A .75°B .60°C .65°D .55° 9.如图,直线AB ∥CD ,∠A =70°,∠C =40°,则∠E 等于()A .30°B .40°C .60°D .70°10.如图,在ABC ∆中,45B ∠=︒,30C ∠=︒,延长线段BA 至点E ,则EAC ∠的度数为( )A .105︒B .75︒C .70︒D .60︒二、填空题 11.一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,已知等腰三角形的底角∠3=72°,则∠1+∠2=______12.如图所示,直线12//l l ,若140∠=︒,275∠=︒,则3∠=____________︒.。
【人教版八年级数学上册同步练习试题及答案】《11.2.2三角形的外角》同步练习及答案
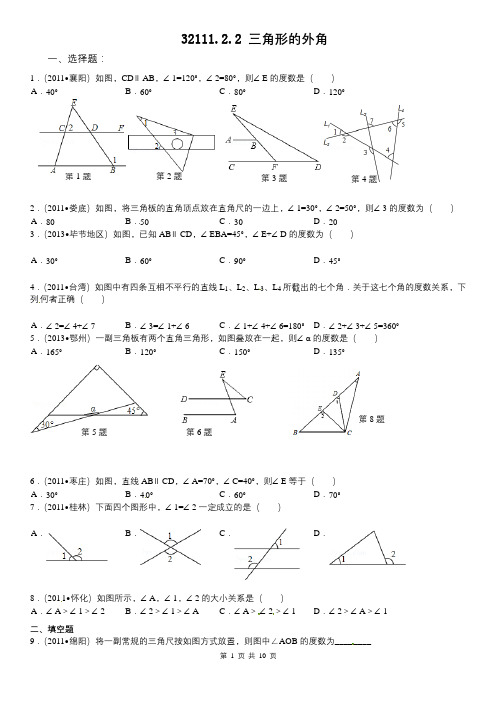
32111.2.2 三角形的外角一、选择题:A . 40° B) 3.(2013•毕节地区)如图,已知AB ∥CD ,∠EBA=45°,∠E+∠D 的度数为( ) 4.(2011•台湾)如图中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角.关于这七个角的度数关系,下列何者正确( ) 0.C1∠>∠二、填空题 9.(2011•绵阳)将一副常规的三角尺按如图方式放置,则图中∠AOB 的度数为________第1题 第2题 第3题 第4题 第5题 第6题 第8题10.(2011•泰安)如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=20°,则∠α的度数为________ 11.若三角形的外角中有一个是锐角,则这个三角形是________三角形.12.△ABC 中,若∠C-∠B=∠A ,则△ABC 的外角中最小的角是______(填“锐角”、“直角”或“钝角”). 13.如图,x=______.14.(2012•长沙)如图,在△ABC 中,∠A=45°,∠B=60°,则外角∠ACD= _________ 度. 15.(2013•黔西南州)如图,已知△ABC 是等边三角形,点B 、C 、D 、E 在同一直线上,且CG=CD ,DF=DE ,则∠E= _________ 度.16.将一副直角三角板如图放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边17.(2013•威海)将一副直角三角板如图摆放,点C 在EF 上,AC 经过点D .已知∠A=∠EDF=90°,AB=AC .∠E=30°,∠BCE=40°,则∠CDF= _____ . 18.(2013•龙岩)如图,AB ∥CD ,BC 与AD 相交于点M ,N 是射线CD 上的一点.若∠B=65°,∠MDN=135°,则∠AMB= ____ . 三、解答题:19.已知:如图,∠2是△ABC 的一个外角. 求证:∠2=∠A +∠B 证明:如图,∵∠A +∠B +∠1=180° ( ) ∠1+∠2=180° ( ) ∴∠2=∠A +∠B ( )20. (2012•贵港)如图所示,直线a ∥b ,∠1=130°,∠2=70°,求则∠3的度数.12DA第13题 第14题 第15题第17题 第18题21.已知:如图,在△ABC 中,∠B =∠C ,AD 平分外角∠EAC .求证:AD ∥BC .22.(2012•呼和浩特)如图,在△ABC 中,∠B=47°,三角形的外角∠DAC 和∠ACF 的平分线交于点E ,求∠AEC 的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新人教版数学八年级上册11.2.2 三角形的外角同步练习
要点感知1 三角形的一边与另一边的延长线组成的角叫做三角形的______.
预习练习1-1 如图所示,______是△ABC的一个外角.
要点感知2 三角形的外角等于与______的两个内角的______.
预习练习2-1 如图所示,∠A=65°,∠B=45°,则∠ACD=______.
知识点1 认识外角
1.如图,以∠AOD为外角的三角形是______
知识点2 内外角的数量关系
2.若三角形的一个外角等于和它相邻的内角,则这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.都有可能
3.如图,∠1=100°,∠C=70°,则∠A的大小是( )
A.10°
B.20°
C.30°
D.80°
4.已知△ABC的三个内角度数之比是1∶2∶3,则三个外角对应的度数之比是______.
5.求出图中的x的值
知识点3 外角定理与平行线性质的综合
6.(红河中考)如图,AB∥CD,∠D=∠E=35°,则∠B的度数为( )
A.60°
B.65°
C.70°
D.75°
7.(温州中考)如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=______度.
8.(昆明中考)如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85°
B.80°
C.75°
D.70°
9.(湘西中考)如图,一副分别含有30°和45°角的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.15°
B.25°
C.30°
D.10°
10.如图,∠α=125°,∠1=50°,则∠β的度数是______.
11.如图所示,P是△ABC内一点,延长BP交AC于点D.若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少?
挑战自我
12.如图,在折纸活动中,小明制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,求∠1+∠2的度数
参考答案
课前预习
要点感知1 外角
预习练习1-1 ∠ACD
要点感知2 它不相邻和
预习练习2-1 110°
当堂训练
1.△AOB和△COD
2.B
3.C
4.5∶4∶3
5.由图知x+80=x+x+20.解得x=60.
6.C
7.80
课后作业
8.A 9.A 10.105°11.∵∠1=∠2+∠4,∠2=∠3+∠A,∴∠1=∠3+∠A+∠4=25°+67°+40°=132°.
12.连接AA′,由图可知:∠1=∠EAA′+∠EA′A,∠2=∠DAA′+∠DA′A,∴∠1+∠2=∠EAA′+∠EA′A+∠DAA′+∠DA′A=∠EAD+∠EA′D.∵∠A=75°,∠A′=75°,∴∠1+∠2=150°.。
