浙教版初中数学九上 1.3 二次函数的专题复习 学案
中考数学二次函数复习学案(一)浙教版

⎧⎪⎨⎪⎩二次函数复习学案(一)复习目标:1、 认识二次函数是常见的简单函数之一,也是刻画现实世界变量之间关系的重要数学模型.理解二次函数的概念,掌握其函数关系式以及自变量的取值范围.2、 能正确地描述二次函数的图象,能根据图象或函数关系式说出二次函数图象的特征及函数的性质,并能运用这些性质解决问题.3、 能根据问题中的条件确定二次函数关系式,并运用二次函数及其性质解决简单的实际问题.4、 了解二次函数与一元二次方程的关系,能利用二次函数的图象求一元二次方程的近似解. 学习重点:二次函数的性质学习难点:运用二次函数的性质解决问题.5、 疑点:利用二次函数的图象求一元二次方程的近似解. 学习过程:一、本章知识梳理:1. 二次函数2()y a x h k =-+的图像和性质a >02. 二次函数c bx ax y ++=2用配方法可化成()k h x a y +-=2的形式,其中 h= , k = .3. 二次函数2()y a x h k =-+的图像和2ax y =图像的关系.顶点式:4.二次函数待定系数法确定函数解析式一般式: 顶点式的几种特殊形式.yx⑴ , ⑵ , ⑶ ,(4) . 5.二次函数与一元二次方程的关系。
6. 二次函数c bx ax y ++=2中c b a ,,的符号的确定. 二、课前热身1. 将抛物线23y x =-向上平移一个单位后,得到的抛物线解析式是 . 2. 如图1所示的抛物线是二次函数2231y ax x a =-+-的图象,那么a 的值是 .3.二次函数2(1)2y x =-+的最小值是( )A.-2B.2C.-1D.1 4.二次函数22(1)3y x =-+的图象的顶点坐标是( )A.(1,3)B.(-1,3)C.(1,-3)D.(-1,-3)5. 二次函数y ax bx c =++2的图象如图所示,则下列结论正确的是( )A.000><>c b a ,, B. 000><<c b a ,, C. 000<><c b a ,,D. 000>><c b a ,,三、典型例题1. 二次函数解析式的确定例1 求满足下列条件的二次函数的解析式 (1)图象经过A(-1,3)、B(1,3)、C(2,6);(2)图象经过A(-1,0)、B(3,0),函数有最小值-8;(3)图象顶点坐标是(-1,9),与x 轴两交点间的距离是6.例 2 已知抛物线c bx ax y ++=2与抛物线732+--=x x y 的形状相同,顶点在直线1=x 上,且顶点到x 轴的距离为5,则此抛物线的解析式为 。
浙教版九年级数学 上二次函数章节复习导学案

页 1 第页 2 第22By=x x+2 Ay=x x2﹣﹣﹣..﹣22x+1y=x y=DxC+x+2﹣.﹣.﹣例8图例7图2c?ax?bxy?,C的纵坐标为﹣2x与轴交于A、B两点,顶点8【例】如图,已知抛物线2cay?x?bx?,则下列结论正确的是现将抛物线向右平移2个单位,得到抛物线111;<b+c0;③阴影部分的面积为4;②(写出所有正确结论的序号)①_________.b>0a﹣2.=4a﹣④若c=1,则b【巩固练习】22 1m)?(?y?xm??_________.则m时,二次函数若2≤x≤1-1. 当的值为,4有最大值页 3 第题第3 第2题2)c的函数图像如图所示,则下列结论中正确的是( 3. 已知抛物线y=ax +bx+c>0 +.a+b.c<0 Da>0 A.B.b<0 C122xayxaa?1?(2)?()?3??求4. 的图像与x已知关于x的函数轴总有交点,4a的取值范围。
2m?1)x?(y??x?m).5. 抛物线与y轴交于点(0,3 轴的交点坐标;物线的解析式以及它与x(1)求抛的增大而减小?0>?②当x取什么值时,y的值随x(2)①当x取什么值时,y4【专题:二次函数的性质】2c?ax??bxy)的性质(a≠01. 二次函数最值条件图像增减性acbbacacb44?4??0222a 对称轴为=<>0 0a>0a<2ac4b???)2. 二次函数与一元二次方程的关系(判断依据:页 4 第2cax?bx?y?轴有两个公共点,那么一元二次方程的图象与“如果二次函数x【例12】20??bx?axc、m请根据你对这句话的理解,解决下面问题:若有两个不相等的实数根.”0??b)(x?a)(x1?的大小关m、nb,则a、b、axn(m<n)是关于的方程的两根,且<)系是(n<b<D.ma<.<a<m<nb Ca<m<b<n n aA.m<<b<B.【巩固练习】2的图象且m≠0)m2x+2(是常数=-函数1. 在同一直角坐标系中,y=mx+m和函数ymx,+)可能是(2),下列结论正确的是()﹣﹣2ax1(a是常数,a≠0ax2. 已知函数y= 1Aa=11 ),时,函.当数图象过点(﹣Ba=2x轴没有交点﹣.当时,函数图象与xy0Cax≥1的增大而减小.若随>,则当时,xyx0aD≤1的增大而增大随时,<.若,则当页 5 第):4,则k值为何?(,且k>0.若△ABC与△ABD的面积比为1点,其顶点为D.D C..1 B.A2的情况下,与其对的值满足1≤x≤3﹣h)为常数)+1(h,在自变量x5. 已知二次函数y=(x.应的函数值y的最小值为5,则h的值为______【补充知识点:二次函数常用公式】(浙教版教材上没讲过,但是非常有用,一定要理解性地记忆),By),(x,y)1. 两点间距离公式:点A(x,2121y????22y???xxy AB= 则AB间的距离,线段B2121y2y?xyx?Pyy?y2121坐标为2. 中点坐标公式:中点.PAB(),12P22Ay1 =k,那么3. 两平行直线解析式分别为:y=kx+b,y=kx+bkx?x221121。
【最新浙教版精选】浙教初中数学九上《1.3 二次函数的性质》word教案 (1).doc

精品【初中语文试题】1.3二次函数的性质教学目标:1.从具体函数的图象中认识二次函数的基本性质.2.了解二次函数与二次方程的相互关系.3.探索二次函数的变化规律,掌握函数的最大值(或最小值)及函数的增减性的概念,会求二次函数的最值,并能根据性质判断函数在某一范围内的增减性重点:二次函数的最大值,最小值及增减性的理解和求法. 难点:二次函数的性质的应用. 教学过程: 一. 复习引入二次函数: y=ax2 +bx + c (a ≠ 0)的图象是一条抛物线,它的开口由什么决定呢?补充: 当a 的绝对值相等时,其形状完全相同,当a 的绝对值越大,则开口越小,反之成立. 二,新课教学:1.探索填空: 根据下边已画好抛物线y= -2x 2的顶点坐标是 , 对称轴是 , 在 侧,即x_____0时, y 随着x 的增大而增大;在 侧,即x_____0时, y 随着x 的增大而减小. 当x= 时,函数y 最大值是____. 当x____0时,y<0.2. 探索填空:根据上边已画好的函数图象填空:抛物线y= 2x2的顶点坐标是 , 对称轴是 ,在 侧,即x_____0时, y 随着x 的增大而减少;在 侧,即x_____0时, y 随着x 的增大而增大. 当x= 时,函数y 最小值是____. 当x____0时,y>03.归纳: 二次函数y=ax2+bx+c(a ≠0)的图象和性质 (1).顶点坐标与对称轴 (2).位置与开口方向 (3).增减性与最值当a ﹥0时,在对称轴的左侧,y 随着x 的增大而减小;在对称轴的右侧,y 随着x 的增大而增大;当 时,函数y 有最小值 。
当a ﹤0时,在对称轴的 左侧,y 随着x 的增大而增大;在对称轴的右侧,y 随着x 的增大而减小。
当 时,函数y 有最大值4.探索二次函数与一元二次方程a2bx -=a 2bx -=a4ac 4b2-a 4ac 4b2-精品【初中语文试题】♦ 二次函数y=x 2+2x,y=x 2-2x+1,y=x 2-2x+2的图象如图所示.♦ (1).每个图象与x 轴有几个交点?♦ (2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?♦ (3).二次函数y=ax2+bx+c 的图象和x 轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?♦ 归纳: (3).二次函数y=ax2+bx+c 的图象和x 轴交点有三种情况: ♦ ①有两个交点, ♦ ②有一个交点, ♦ ③没有交点.♦ 当二次函数y=ax 2+bx+c 的图象和x 轴有交点时, 交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax 2+bx+c=0的根. 当b 2-4ac ﹥0时,抛物线与x 轴有两个交点,交点的横坐标是一元二次方程0=ax 2+bx+c 的两个根x 1与 x 2;当b 2-4ac=0时,抛物线与x 轴有且只有一个公共点;当b 2-4ac ﹤0时,抛物线与x 轴没有交点。
浙教版初中数学九年级上册 1.3 二次函数的性质 教案

“二次函数图象与性质复习(第二课时)”教学设计教材内容本节课的教学内容是期末数学总复习中的“二次函数图象与性质复习”,二次函数是初中数学的核心内容,也是重要的基础知识和重要的数学思想,不仅与其它数学知识有着密切的联系,而且还与生活中的实际问题极为广泛的应用,是联系数学知识与实际问题间的纽带和桥梁,是中考数学试卷中不可缺少的重要内容。
教学目标知识目标:1.理解二次函数的关系式;2.掌握二次函数的图象及有关性质。
能力目标:1.学会用待定系数法求二次函数关系式;2.能运用二次函数的相关知识解决简单的数学实际问题;3.培养学生数形结合、转化、函数等数学思想的能力。
情感目标:体验用数学知识解决问题的乐趣,从而培养学生学习数学的积极性。
教学重难点重点:二次函数图象与性质,能熟练运用二次函数的性质解决问题。
难点:读图、识图的能力,建立函数模型并求解。
教学过程温馨提示:每节课的所学的知识好比一颗珍珠,如果不加整理、归纳,就好比散落一地的珍珠显得杂乱;如果整理串成一串珍珠串,就美丽更有用!一.课前基础题热身练习,进一步巩固基础知识1.若二次函数2)(mxay+=与抛物线23xy=的形状相同,有最大值,且经过点(1,-12),则二次函数的解析式_______________2.已知二次函数经过(2,-6),对称轴x=1. 抛物线与x轴两交点的距离为4,二次函数的解析式______________(学生举手发言,解决问题;教师引导学生解题的关键点,指导学生正确解答的方法,并及时评价)。
【设计意图】复习课同样也要面向全体学生,针对每一个有差异的个体,适应每一个学生的不同发展的基础,要为每一个学生提供不同的发展的机会和可能,使不同的人在数学上得到不同的发展。
通过这组低起点、缓坡度、求实效的基础题训练,目的让学生学得扎实,突出数学课程的基础性和普及性,使人人获得必需的数学。
为了加强复习的有效性,以题带知识,让学生通过对问题的解决,勾起对知识的回忆,加深对知识的理解,同时还能在教学中起到及时运用→及时反馈→及时形成新知,符合学生的认知规律。
九年级数学《二次函数》总复习教案

教材:初中数学九年级上册复习目标:1.理解二次函数的概念和特征。
2.掌握二次函数的基本性质和图像的特点。
3.熟练运用二次函数解决实际问题。
4.理解抛物线的性质及其与二次函数的关系。
一、概念复习1.二次函数:通过变量的平方项表达的函数。
2.顶点:二次函数图像的最高点或最低点,表示为(a,b)。
3.对称轴:二次函数图像的对称轴,表示为x=a。
4.开口方向:二次函数图像的开口方向,由二次项的系数决定。
二、性质复习1.零点:二次函数与x轴交点的横坐标。
2.判别式:用来判断二次函数的零点个数的式子。
当Δ=b^2-4ac>0时,二次函数有两个不相等的零点。
当Δ=b^2-4ac=0时,二次函数有两个相等的零点。
当Δ=b^2-4ac<0时,二次函数没有实数零点。
3.最大值与最小值:当二次函数开口向上时,最小值是顶点的纵坐标。
当二次函数开口向下时,最大值是顶点的纵坐标。
三、图像特点复习1.开口方向:当a>0时,二次函数开口向上。
当a<0时,二次函数开口向下。
2.对称轴:对称轴与顶点的横坐标相等。
3.零点:零点是二次函数与x轴交点的横坐标。
零点的个数由判别式Δ决定。
四、实际问题复习1.利用二次函数解决实际问题的步骤:(1)明确问题中有关条件。
(2)设出二次函数的表达式。
(3)求出二次函数的最值或零点。
(4)用解出的最值或零点回答问题。
2.举例:问题:商场的营业额可以用二次函数y=2x^2+3x+4来表示,其中x表示时间(以小时计),y表示营业额(以万元计)。
求该商场的最大营业额,并在什么时间实现。
解答:(1)根据题目,得到二次函数的表达式为y=2x^2+3x+4(2)通过求导数或将二次函数表示为顶点形式,得到该二次函数的顶点为(-3/4,23/8)。
(3)所以,该商场的最大营业额为23/8万元,实现时间为-3/4小时。
五、抛物线的性质复习1. 加入二次函数的f(x)=ax^2+bx+c。
若a>0,抛物线开口向上;若a<0,抛物线开口向下。
浙教版九年级数学上册 1.3《二次函数的图像与性质》教案

二次函数的图象及性质的教学过程富阳区银湖中学 赵玲【教学学情】二次函数是初中阶段的重点知识,是高中函数的基础。
学生在已经学了函数的基础上,针对中考考纲,对学生的二次函数进行复习。
学生对二次函数的掌握存在一定的困难,因此将函数分成2节知识来进行复习,第一节是针对函数的解析式和性质展开复习。
【教学目标】1、 针对二次函数的解析式、图象、性质,让学生对二次函数的基础知识进行进一步的理解和掌握。
2、 利用函数图象,让学生感受数形结合的妙处,让学生掌握数形结合解决二次函数的方法3、 从基础知识出发,让学生逐渐打破对二次函数的恐惧,感受成功的喜悦【教学重点】二次函数的图象与性质【教学难点】利用数形结合解决问题【教学过程】一、[小题热身]1、下列函数属于二次函数的是 ( )A . 21+=x y B . ()213-=x y C. ()221x x y -+=D x x y -=21 2、在下列直角坐标系中画出二次函数4412-+-=x x y 的图象,并说说它的性质3、对于抛物线()31212++=x y ,下列结论:①抛物线开口向下,②对称轴为直线x=1,③顶点坐标(-1,3),④当x ≥1时,y 随x 的增大而减小,⑤该函数向右平移2个单位,再向下平移5个单位后的抛物线解析式为()23212-+=x y ,其中正确的结论的序号为___________________【设计意图】从二次函数的定义、图象、性质入手,让学生对二次函数的基本知识进行系统的复习。
让学生经历第2题的画图,加深对二次函数性质的理解和掌握。
【上课过程】师:生1,说说第1题判断二次函数的依据?生1:最高二次,右边是整式师:画二次函数图象的要点是什么?生2:顶点,与x 轴交点,与y 轴交点及y 轴交点的对称点师:这就是我们所说的五点法。
下面请一位同学分析下第3题。
生3:1是开口向上,因为a>0师:什么时候开口向下生一起:a<0生3: 序号2是对称轴x=-1 ,序号3对;序号4是x<-1,y 随x 增大而减小;x>-1,y 随x 增大而增大。
数学九年级上册《二次函数-复习课》教案
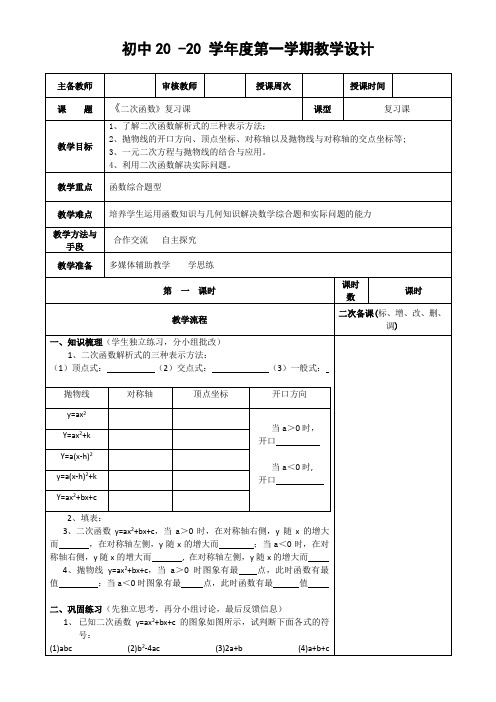
初中20 -20 学年度第一学期教学设计2、二次函数2y ax bx c =++的图像如图1,则点),(ac b M 在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3、已知二次函数y=ax 2+bx+c 的图象与x 轴交于点(-2,O)、(x 1,0),且1<x 1<2,与y 轴的正半轴的交点在点(O ,2)的下方.下列结论:①a<b<0; ②2a+c>O;③4a+c<O;④2a -b+1>O ,其中正确结论的个数为( )A 1个 B. 2个 C. 3个 D .4个4、已知:关于x 的一元二次方程ax 2+bx+c=3的一个根为x=-2,且二次函数y=ax 2+bx+c 的对称轴是直线x=2,则抛物线的顶点坐标为( ) A(2,-3) B.(2,1) C(2,3) D .(3,2) 三、拓展延伸(小组探究,合作学习) 1、已知抛物线y=x 2+(2k+1)x-k 2+k(1) 求证:此抛物线与x 轴总有两个不同的交点;(2)设A (x 1,0)和B (x 2,0)是此抛物线与x 轴的两个交点,且满足x 12+x 22= -2k 2+2k+1,①求抛物线的解析式②此抛物线上是否存在一点P ,使△PAB 的面积等于3,若存在,请求出点P 的坐标;若不存在,请说明理由。
3、已知抛物线y=12x 2+x-52.(1)用配方法求它的顶点坐标和对称轴.(2)若该抛物线与x 轴的两个交点为A 、B ,求线段AB 的长.四、课堂小结通过本节课的练习,你学到了什么知识? 五、布置作业学思练本章复习题板书设计:教学后记(反思成败、总结经。
浙教版数学九年级上册_《二次函数的性质》优质学案

1.3二次函数的性质【学习目标】1.从具体函数的图象中认识二次函数的基本性质.2.了解二次函数与二次方程的相互关系.3.探索二次函数的变化规律,.掌握函数的最大值(或最小值)及函数的增减性的概念,会求二次函数的最值,并能根据性质判断函数在某一范围内的增减性. 【课前准备】一般地,函数c bx ax y ++=2(0≠a )的图象有以下性质:二次函数c bx ax y ++=2(0≠a )的图象是一条 ,它的对称轴是直线abx 2-=,顶点坐标是(ab ac ,a b 4422--),当0>a 时, 的开口 ,顶点是抛物线上的最低点; 当0<a 时, 的开口 ,顶点是抛物线上的最 点. 【课本导学】 1.情景引入:运动员投篮时,篮球运动的路线是一条怎样的曲线?怎样计算篮球达到最高点时的高度? 2.新课学习:观察图1,图2中函数的图象,回答下列问题:(1)当自变量增大时,函数的值将怎样变化?顶点在图象的位置有什么特点? (2)判断这些函数有没有最小值或最大值.你发现这是由解析式中哪个系数决定的吗? (3)抛物线c bx ax y ++=2(0≠a )与x 轴交点的横坐标,与方程02=++c bx ax 的根有什么关系?结论: (1) (2) (3)一般的,二次函数c bx ax y ++=2(0≠a )有以下性质:条件 图象 增减性 最大(小)值0>a对称轴ab x 2-=,顶点坐标(a b ac ,a b 4422--)当a b x 2-≤时,y 随x 的增大而减少;当abx 2-≥时,y 随x 的增大而增大. 当abx 2-=时,y 达到最小值:ab ac y 442-=;无最大值.0<a对称轴abx 2-=, 顶点坐标(a b ac ,a b 4422--)当a b x 2-≤时,y 随x 的增大而增大;当abx 2-≥时,y 随x 的增大而减少. 当abx 2-=时,y 达到最大值:ab ac y 442-=;无最小值.【例题讲解】例1.已知函数2157212+--=x x y . (1)求函数图象的顶点坐标、对称轴,以及图象与坐标轴的交点坐标,并画出函数的大致图象; (2)自变量x 在什么范围内时,y 随x 的增大而增大?何时y 随x 的的增大而减少?并求出函数的最大值或最小值.例2.已知抛物线142-++=k x x y .(1)若抛物线与x 轴有两个不同的交点,求k 的取值范围; (2)若抛物线的顶点在x 轴上,求k 的值.拓展练习如图所示,抛物线322--=x x y 与x 轴交于A ,B 两点(点A 在点B 左侧),直线l 与抛物线交于A ,C 两点,其中点C 的横坐标为2. (1)求A ,B 两点的坐标及直线AC 的解析式;(2)点P 是线段AC 上的一个动点,过点P 作y 轴的平行线交抛物线于点E ,求线段PE 长度的最大值.【归纳小结】课堂作业 姓名:【A 组】 一、选择题1.已知(-1,y 1),(-2,y 2),(-4,y 3)是抛物线m x x y +--=822上的点,则( ) A.y 1<y 2<y 3 B.y 3<y 2<y 1 C.y 2>y 1>y 3 D.y 2>y 3>y 1二、填空题2.二次函数542+-=x x y 当x = 时,有最 值为 . 三、解答题3.已知二次函数6422++-=x x y .(1)求函数图象的顶点坐标、与坐标轴交点的坐标和对称轴,并画出函数的大致图象; (2)记当511.x =,22-=x ,23=x 时对应的函数值分别为y 1,y 2,y 3,试比较y 1,y 2,y 3的大小; (3)自变量x 在什么范围内时,y 随x 的增大而增大?何时y 随x 的增大而减少?并求出函数的最大值或最小值.4.二次函数12-+=bx ax y 的图象经过点(2,-1),且这个函数有最小值-3,求这个函数的关系式.5.求下列二次函数的图象与x 轴交点的坐标:(1)x x y 6322-= (2)2322+--=x x y6.篮球运动员投篮时,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为x =2.5,出手高度为2.25m ,篮筐高为3.05m.求:(1)球运动路线的函数解析式和自变量的取值范围;(2)球在运动中离地面的最大高度. 【B 组】7.如图所示,对称轴为直线27x 的抛物线经过点A (6,0)和点B (0,4). (1)求抛物线的解析式及顶点坐标;(2)设点E (x ,y )是抛物线上的一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形,求□OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值范围;(3)①当□OEAF 的面积为24时,请判断□OEAF 是否为菱形;②是否存在点E ,使□OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的专题复习
一、 考试说明的要求:
二、 复习目标
1、 认识二次函数是常见的简单函数之一,也是刻画现实世界变量之间关系的重要数学模型.理解二次函数
的概念,掌握其函数关系式以及自变量的取值范围.
2、 能正确地描述二次函数的图象,能根据图象或函数关系式说出二次函数图象的特征及函数的性质,并能
运用这些性质解决问题.
3、 能根据问题中的条件确定二次函数的关系式,并运用二次函数及其性质解决简单的实际问题.
4、 了解二次函数与一元二次方程的关系,能利用二次函数的图象求一元二次方程的近似解.
三、知识点回顾
1、二次函数的概念:形如)0(2
≠++=a c bx ax y 的函数.
2、抛物线)0(2
≠++=a c bx ax y 的顶点坐标是(a b ac a b 44,22--);对称轴是直线a
b x 2-=. 3、当a >0时抛物线的开口向上;当a <0时抛物线的开口向下.a 越大,抛物线的开口越小;a 越小,抛物线的开口越大.a 相同的抛物线,通过平移(或旋转、轴对称)一定能够重合.
4、a 、b 同号时抛物线的对称轴在y 轴的左侧;a 、b 异号时抛物线的对称轴在y 轴的右侧.抛物线与y 轴的
交点坐标是(0,C ).
5、二次函数解析式的三种形式: (1)一般式:)0(2
≠++=a c bx ax y (2)顶点式:k h x a y +-=2
)(
(3)交点式:))((21x x x x a y --=,抛物线与x 轴的交点坐标是(0,1x )和(0,2x ). 6、抛物线的平移规律:从2
ax y =到k h x a y +-=2
)(,抓住顶点从(0,0)到(h ,k ).
7、(1)当ac b 42
->0时,一元二次方程)0(02
≠=++a c bx ax 有两个实数根21,x x ,抛物线
)0(2≠++=a c bx ax y 与x 轴的交点坐标是A (0,1x )和B (0,2x )。
(2)当ac b 42
-=0时,一元二次方程)0(02
≠=++a c bx ax 有两个相等的实数根(或说一个根)
a
b x x 221-
==,抛物线)0(2
≠++=a c bx ax y 的顶点在x 轴上,其坐标是(0,2a b -).
(3)当ac b 42
-<0时,一元二次方程)0(02
≠=++a c bx ax 没有实数根,抛物线
)0(2≠++=a c bx ax y 与x 轴没有交点.
8、二次函数的最值问题和增减性:
四、例题精析
例1:函数2
2x y =、2
2x y -=、2
2
1x y =
的图象的共同特征是( ) (A )开口都向上,且都关于y 轴对称 (B )开口都向下,且都关于x 轴对称 (C )顶点都是原点,且都关于y 轴对称 (D )顶点都是原点,且都关于x 轴对称
分析:C.
【回顾】研究二次函数的图象与性质,一般从开口方向、对称轴、顶点坐标、增减性、与坐标轴的交点、最值等来观察和探究。
注意其中的规律。
例2:已知二次函数324
12
---
=x x y .(1)用配方法化为k h x a y +-=2)(的形式.(2)写出它的顶点坐标和对称轴,并画出它的图象.(3)根据图像指出:①当x 取何值时,y 随x 值的增大而减小. ②当x 取何值时,y 有最大(小)值,值是多少?③抛物线与x 、y 两坐标轴的交点坐标. ④当x 取何值时
0<y .
分析:324
12---=x x y =()
38412-+-x x =()344412-++-x =()14412
++-x
解略。
例3:已知△ABC 中,8=BC ,BC 上的高h =4,D 为BC 上一点,EF BC //,交AB 于点E ,交AC 于点F (EF 不过A 、
B ),设E 到B
C 的距离为x ,则△DEF 的面积y 关于x 的函数的图象大致为( )
分析:D
利用△AEF 与△ABC 相似,确定EF 的长,写出y 关于x 的函数关系式,确定自变量x 的取值范围,从而知晓。
例4:如图,二次函数y=x2-4x+
3的图象交x 轴于A 、B 两点,交y 轴于点C ,设抛
物线的顶点为P.
(1)求△ABC 、 △COB 的面积 (2)求四边形CAPB 的面积 分析过程见课件。
例5:一批名牌中都商场销售衬衫,平均每天可售出20件,每件赢利40元。
为了扩大销售,尽快增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,若商场每件衬衫降价x 元,商场每天的赢利为y 。
(1)你能写出x 和y 的关系吗?(2)当每件衬衫降价多少元时,商场可获得最大利润?最大利润为多少元?
分析:见导引P71页。
例6:如图有一个边长为5cm 的正方形ABCD ,和等腰三角形PQR ,PQ=PR=5cm ,QR=8cm ,点B 、C 、Q 、R 在同一直线上,当C 、Q 两点重合时,△PQR 以1cm /秒的速度向左开始匀速运动,设与正方形重合部分面
积为Scm 2。
当130≤≤t 时,求S 与t 的函数关系,并求出何时S 最大?
D
A
R
P
y y y
y
x x
x
B Q
R
R
R
R
R
五、 课堂练习
1.抛物线5)3(22+-=x y 的对称轴是 ,顶点坐标是 ;它是由抛物线2
2x y =的
图象_________________________________平移得到的。
2.当_____=x ,函数322
--=x x y 的函数值为5;
3.如果抛物线m x x y +-=62
的顶点在x 轴上,那么______=m ;
4.已知函数322
--=x x y ,则它的顶点坐标是 ,对称轴是 ;图象与y 轴的交点为 ,与x 轴的交点为 ;
5.二次函数c bx x y ++=2
的顶点坐标为(3-,1),则____________,==c b ; 6.某抛物线的顶点为1(-P ,)8-且经过点0(,)6-,则这个抛物线的解析式为 . 7、在同一直角坐标系中,一次函数c ax y +=和二次函数c ax y +=2
的图象大致为( )
8、二次函数)0(2
≠++=a c bx ax y 的图象如图所示,则
a 、
b 、
c 、ac b 42-的取值范围是( )
(A ) a >0,b <0,c <0,ac b 42
->0
(B ) a <0,b <0,c <0,ac b 42
-<0
(C ) a >0, b >0,c <0,ac b 42
->0 (D ) a >0,b <0,c >0, ac b 42
->0
9、下列图中阴影部分的面积与算式122)2
1
(|43|-++-
的结果相同的是 ( )
10、如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点A 和A 1、点B 和B 1分别关于y 轴对称,隧道拱部分BCB 1为一条抛物线,最高点C 离路面AA 1的距离为8米,点B 离路面为6米,隧道的宽度AA 1为16米;
y
x
O
第8题
x
y
O x
y
O x
y
O x
y
O
(1)求隧道拱抛物线BCB
的函数解析式;
1
(2)现有一大型运货汽车,装载某大型设备后,其宽度为4米,车载大型设备的顶部与路面的距离均为7米,他能否通过这个隧道?请说明理由。
六、作业布置
导引P74-75页,A组、B组。
