立体几何八个定理默写_含答案
立体几何所有的定理大总结(绝对全)

⽴体⼏何所有的定理⼤总结(绝对全)(⼆)异⾯直线所成⾓1.定义:不同在任何⼀个平⾯内的两条直线或既不平⾏也不相交的两条直线叫异⾯直线。
2.画法:借助辅助平⾯。
1.定义:对于异⾯直线a 和b ,在空间任取⼀点P ,过P 分别作a 和b 的平⾏线1a 和1b ,我们把1a 和1b 所成的锐⾓或者叫做异⾯直线a 和b 所成的⾓。
2.范围:(0°,90°】(★空间两条直线所成⾓范围:【0°,90°】)(三)线⾯⾓1.定义:当直线l 与平⾯α相交且不垂直时,叫做直线l 与平⾯α斜交,直线l 叫做平⾯α的斜线。
设直线l 与平⾯α斜交与点M ,过l 上任意点A ,做平⾯α的垂线,垂⾜为O ,把点O 叫做点A 在平⾯α上的射影,直线OM 叫做直线l 在平⾯α上的射影。
1.定义:把直线l 与其在平⾯α上的射影所成的锐⾓叫做直线l 和平⾯α所成的⾓。
2.范围【0°,90°】(★斜线与平⾯所成⾓范围:【0°,90°】)(三)⼆⾯⾓1.定义:(1)半平⾯:平⾯内的⼀条直线把这个平⾯分成两个部分,其中每⼀个部分叫做半平⾯。
(3)⼆⾯⾓的棱:这⼀条直线叫做⼆⾯⾓的棱。
(4)⼆⾯⾓的⾯:这两个半平⾯叫做⼆⾯⾓的⾯。
(5)⼆⾯⾓的平⾯⾓:以⼆⾯⾓的棱上任意⼀点为端点,在两个⾯内分别作垂直于棱的两条射线,这两条射线所成的⾓叫做⼆⾯⾓的平⾯⾓。
(6)直⼆⾯⾓:平⾯⾓是直⾓的⼆⾯⾓叫做直⼆⾯⾓。
1.定义:从⼀条直线出发的两个半平⾯所组成的图形叫做⼆⾯⾓。
2.表⽰:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到⾯的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
11.13期中考前最后复习【解析几何立体几何公式】默写

立体几何,解析几何基本概念默写1.直线的斜率:倾斜角不是 90的直线,它的倾斜角α的值叫做这条直线的斜率.常用k 表示,即k =,其取值范围是.倾斜角是 90的直线没有.2.已知直线的倾斜角为α,当α090≠时,k 与α的关系是;α090=时,直线斜率直线斜率k 与倾斜角α关系图像为:3、已知直线过两点,且,则斜率k =.22211121215.与直线0=++C By Ax 平行的直线方程总可以写成,与直线0=++C By Ax 垂直的直线方程总可以写成.6.直线0:,0:22221111=++=++C y B x A l C y B x A l则:⇔21//l l , ⇔⊥21l l .7、圆的标准方程:____________________,其中为圆心,为半径.8、圆的一般方程:__________________表示圆的充要条件是,其中圆心为,半径为.9.()()1122A ,,,x y B x y 为直径端点的圆方程.10、平面上两点),(),,(2211y x Q y x P 的距离=PQ ,11、点),(00y x P 到直线0:=++C By Ax l 的距离=d ,点),(00y x P 到直线:y=kx+b 的距离=d ,12、两平行直线0:,0:2211=++=++C By Ax l C By Ax l 间的距离=d .13.点),(00y x P 关于点),(b a A 的对称点为,14、),(00y x P 关于直线b kx y +=的对称点为),(y x P '',则由方程, 由此可求出y x '',.15.已知直线0=++C By Ax 与圆222)()(r b y a x =-+-,圆心),(b a 到直线0=++C By Ax 的距离为d ,则⇔直线与圆相交;⇔直线与圆相切;⇔直线与圆相离16、若圆1:221110x y D x E y F ++++=,圆2:222220x y D x E y F ++++=,若两圆相交则公共线方程为__________________17、若直线和圆相交,则相交弦的弦长公式为_________________________________________(说明公式中字母含义)18.直线与圆相交时,圆心到直线的距离为d ,圆的半径为r ,则直线被圆截得的弦长为(用,d r 表示);过P 的直线与圆O 相切,若A 为切点,则切线长_______PA =(用,PO r 表示);过圆O 外一点P 做圆O 的两条切线,切点为,A B ,则直线AB 为圆O 与__________________圆相交的公共弦。
立体几何定理大全

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
空间两直线的位置关系:空间两条直线只有三种位置关系:平行、相交、异面1、按是否共面可分为两类:〔1〕共面:平行、相交〔2〕异面:异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线间距离: 公垂线段(有且只有一条)2、假设从有无公共点的角度看可分为两类:〔1〕有且仅有一个公共点——相交直线;〔2〕没有公共点——平行或异面直线和平面的位置关系:直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为 [0°,90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a叫做平面的垂线,平面叫做直线a的垂面。
立体几何常考定理的总结(八大定理)
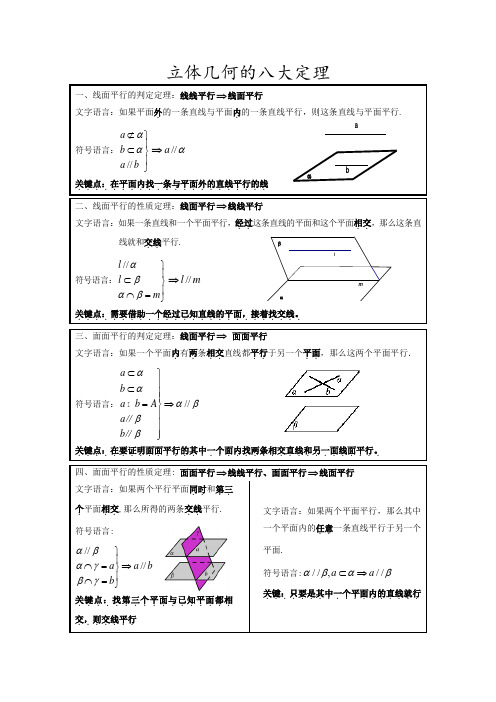
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
空间几何八定理

空间几何八定理:
1、直线与平面平行的判定定理:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行。
2、直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
3、平面与平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
4、平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行。
5、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面。
6、直线与平面垂直的性质定理:若两条直线垂直于同一个平面,则这两条直线平行。
7、平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
8、平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面。
立体几何知识点整理-答案

立体几何知识整理一、概念:1、平面:__平,无厚度,无边界,在空间延伸至无限__.2、图形文字语言符号语言公理1如果直线l上有两个点,A B在平面α上,那么直线l在平面α上.,,A lB llA Bααα∈∈⎫⇒⊂⎬∈∈⎭公理2如果不同的两个平面,αβ有一个公共点A,那么,αβ的交集是过点A的直线lA l AB A lααβ∈⋂=⎧⎧⇒⎨⎨∈∈⎩⎩公理3 不在同一直线上的三点确定一个平面公理4 平行于同一直线的两条直线互相平行//// //a bb c a c⎫⇒⎬⎭3、公理1作用:__1)证明直线在平面上2)证明点在平面上________.公理2作用:__证明三点共线(点是公共点,线是公共线)_.推论1:_一条直线和直线外的一点确定一个平面_.推论2:_两条相交的直线确定一个平面_.推论3:_两条平行的直线确定一个平面_公理3及推论作用:_确定平面的方法_.等角定理:__如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补__.4、空间中两条不重合的直线的位置关系有:__平行、相交、异面_.5、异面直线:_1)不平行不相交的两条直线2)不在任何一个平面的两条直线_.二、平行与垂直的判定与性质////a bb a a ααα⎫⎪⊂⇒⎬⎪⎭不在平面上 ,//,////a b a b a b A ββαααβ⊂⊂⎫⎪⇒⎬⎪⋂=⎭线//线 线//平面 平面//平面//,//a b a b αα⇒∃⊂ ////a a αββα⎫⇒⎬⊂⎭(一般过直线a 作截面,则//a 交线),,////,//a b a b A a b a b A a a b b ααββαβ⊂⊂⎫⎪⋂=⎪⎪''⊂⊂⇒⎬⎪'''⋂=⎪''⎪⎭////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭,,l a l b a b l a b A ααα⊥⊥⎫⎪⊂⊂⇒⊥⎬⎪⋂=⎭a a ααββ⊥⎫⇒⊥⎬⊂⎭线⊥线 线⊥平面 平面⊥平面l l a a αα⊥⎫⇒⊥⎬⊂⎭,l a a a l αβαββα⊥⎫⎪⋂=⇒⊥⎬⎪⊂⊥⎭三、求解空间中的角1、异面直线所成角异面直线所成角的定义:_对于异面直线,a b ,在空间任取一点P ,过P 分别作,a b 的平行线,a b '',把,a b ''所成的锐角或直角_.异面直线所成角的范围:__0,2π⎛⎤⎥⎝⎦__ 异面直线所成角的求法: 1)平移其中的一条或者两条至相交 2)找到异面直线所成角(或其补角) 3)放在∆中用余弦定理求角【记得写答句!!】2、直线与平面所成角若直线与平面平行,则直线与平面所成角为_0_;若直线与平面垂直,则直线与平面所成角为__2π_;若直线与平面斜交,则直线与平面所成角为_0,2π⎛⎫⎪⎝⎭_.直线与平面所成角的范围是_0,2π⎡⎤⎢⎥⎣⎦_.直线与平面所成角就是直线与_它在平面上的射影_所成角. 找直线与平面所成角的过程:1)过直线上一点(除与平面的交点)作平面的垂线,联结斜足点与垂足点(找到直线在平面上的射影)2)在直角三角形中解角(只需求两条边即可) 3、二面角二面角的平面角的范围_[]0,π_ 二面角的平面角的求解方法:1)定义法(在公共棱上取一点,分别在两个半平面上做棱的垂线)用这个方法求解二面角的平面角要会_观察两个半平面的形状_.2)三垂线法(过一个半平面上一点做另一个半平面的垂线,过垂足点做公共棱的垂线) 当_定义法很难找,又比较好做线面垂直_适用这种方法求解二面角的平面角. 四、求空间中的距离1、点到直线距离方法:1)_(直接法)过点做直线的垂线_2)_(三垂线法)过点做直线所在平面的垂线,过垂足做直线的垂线_.2、点到平面的距离方法:1)_过点做平面的垂线(垂足一般在某条线上)_2)__放在三棱锥中用等积转换__.3、直线到平面的距离适用范围:_直线与平面平行__ 方法:__转化成点到平面距离_不能取平面上与直线平行的直线,计算两平行直线的距离是因为_两平行直线之间距离大于等于直线到平面的距离_4、直线到直线的距离适用范围:__两平行直线或两异面直线_方法:__平行:转化成点到直线距离;异面:1)找公垂线(既垂直又相交)2)一直线与另一直线所在平面平行,转化为直线到平面的距离_5、平面到平面的距离适用范围:_两平行平面__方法:_转化为点到平面距离_.五、多面体1、定义棱柱的定义:_一个多面体有两个全等的多边形的面互相平行,且不在这两个面上的棱都互相平行._侧棱与底面垂直_的棱柱是直棱柱;_底面是正多边形的直棱柱_是正棱柱正四棱柱A,正方体B,四棱柱C,平行六面体D,长方体E的关系⊂⊂⊂⊂__B A E D C棱锥的定义:_一个多面体有一个多边形的面,且不在这个面上的棱都有一个公共点_._底面是正多边形,棱锥的顶点与底面中心的连线与底面垂直_的棱锥是正棱锥._各条棱都相等的三棱锥_叫做正四面体.__棱锥侧面三角形底边上的高_叫做斜高,__顶点到底面的距离_是棱锥的高.若侧棱两两垂直,则顶点在底面上的射影是底面的_垂心__;若侧棱相等,则顶点在底面上的射影是底面的_外心_;若顶点到底面各边距离相等,则顶点在底面上的射影是底面的_内心_;若侧棱与底面所成角相等,则顶点在地面上的射影是底面的_外心_2、旋转体__过旋转轴的截面_叫做轴截面1)圆柱圆柱是由__矩形(及其内部)_绕着_一条边所在的直线_旋转而成的几何体.圆柱的两个底面_全等且互相平行_,母线与母线_平行且相等__,母线与底面_垂直_.圆柱的轴截面是_矩形__.2)圆锥圆锥是由_直角三角形(及其内部)_绕着_其一条直角边所在直线_旋转而成的几何体.圆锥的母线_相交于同一点_.圆锥的的轴截面是_等腰三角形_.3)球球是由_半圆(及其内部)_绕着_直径所在直线_旋转而成的几何体._经过直径的截面_叫大圆,__不经过直径的截面_叫小圆.球面上两点,A B 的球面距离是指_经过,A B 的大圆与球面交得的劣弧长_.纬度是指_半径与赤道面所成角_,经度是_半平面与本初子午线所在半平面所成二面角_. 3、表面积与体积1)直棱柱的侧面展开图是_矩形_,若底面周长是c ,底面积是S ,侧棱长是h ,则侧面积=_ch _,全面积=_2ch S +_,体积=_Sh _.2)正棱锥的侧面都是_等腰三角形_,若正n 棱锥的底面边长是a ,底面积是S ,斜高是h ',棱锥的高是h ,则侧面积=_2n ah '_,全面积=_2n ah S '+_,体积=_13Sh _.3)圆柱的侧面展开图是_矩形_,若圆柱底面半径是r ,高是h ,则侧面积=__2rh π_,全面积=_222rh r ππ+_,体积=__2r h π_.4)圆锥的侧面展开图是_扇形_,若圆柱底面半径是r ,高是h ,母线长是l ,则侧面积=__rl π_,全面积=_2rl r ππ+_,体积=_213r h π__.5)若球的半径是R ,则球的表面积=_24R π_,体积=_343R π_.。
高中数学第八章立体几何初步知识汇总大全(带答案)

高中数学第八章立体几何初步知识汇总大全单选题1、一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设BC 的中点为M ,的中点为N ,下列结论正确的是( )A .MN//平面ABEB .MN//平面ADEC .MN//平面BDHD .MN//平面CDE答案:C解析:根据题意,得到正方体的直观图及其各点的标记字母,取FH 的中点O ,连接ON ,BO ,可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系,进而对选择支A 作出判定;根据MN 与平面BCF 的关系,利用面面平行的性质可以判定MN 与平面ADE 的关系,进而对选择支B 作出判定;利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系,进而判定C ;利用M ,N 在平面CDEF 的两侧,可以判定MN 与平面CDE 的关系,进而对D 作出判定.根据题意,得到正方体的直观图及其各点的标记字母如图所示,取FH 的中点O ,连接ON ,BO ,易知ON 与BM 平行且相等,∴四边形ONMB 为平行四边形,∴MN ‖BO ,∵BO 与平面ABE (即平面ABFE )相交,故MN 与平面ABE 相交,故A 错误;∵平面ADE ‖平面BCF ,MN ∩平面BCF =M ,∴MN 与平面ADE 相交,故B 错误;∵BO ⊂平面BDHF ,即BO ‖平面BDH ,MN ‖BO ,MN ⊄平面BDHF ,∴MN ‖平面BDH ,故C 正确;显然M ,N 在平面CDEF 的两侧,所以MN 与平面CDEF 相交,故D 错误.GH小提示:本题考查从面面平行的判定与性质,涉及正方体的性质,面面平行,线面平行的性质,属于小综合题,关键是正确将正方体的表面展开图还原,得到正方体的直观图及其各顶点的标记字母,并利用平行四边形的判定与性质找到MN 的平行线BO .2、《九章算术·商功》中,将四个面都为直角三角形的四面体称为鳖臑.如图,在鳖臑ABCD 中,AB ⊥平面BCD ,AC ⊥CD ,AC =BC +CD =2,当△BCD 的面积最大时,鳖臑ABCD 的表面积为( )A .√3+√62B .3+√62C .2+√3+√62D .3+√3+√62答案:D分析:根据题意可证明CD ⊥BC ,从而说明三角形BCD 是直角三角形,求得BD ,进而求得四个直角三角形的面积,可得答案.由题意可知:AB ⊥平面BCD ,CD ⊂平面BCD ,故AB ⊥CD ,又AC ⊥CD ,AC ∩AB =A,AB,AC ⊂平面ABC ,故CD ⊥平面ABC ,BC ⊂平面ABC ,所以S △BCD =12BC ⋅CD ≤12×(BC+CD 2)2=12 ,当且仅当BC =CD =1时取得等号, 故BD =√1+1=√2 ,由AB ⊥平面BCD ,可知AB ⊥BD,AB ⊥BC ,故AB =√AC 2−BC 2=√4−1=√3 ,所以S △ABD =12AB ⋅BD =√62,S △ABC =12AB ⋅BC =√32 , S △BCD =12BC ⋅CD =12,S △ACD =12AC ⋅CD =1,所以鳖臑ABCD 的表面积为√62+√32+12+1=3+√3+√62 , 故选:D3、在正方体ABCD −A 1B 1C 1D 1中,三棱锥A −B 1CD 1的表面积为4√3,则正方体外接球的体积为( )A .4√3πB .√6πC .32√3πD .8√6π答案:B解析:根据三棱锥的表面积进一步求出正方体的棱长,最后求出正方体的外接球的半径,进一步求出结果. 解:设正方体的棱长为a ,则B 1D 1=AC =AB 1=AD 1=B 1C =D 1C =√2a ,由于三棱锥A −B 1CD 1的表面积为4√3,所以S =4S △AB 1C =4×12×√32(√2a)2=4√3所以a =√2所以正方体的外接球的半径为√(√2)2+(√2)2+(√2)22=√62,所以正方体的外接球的体积为43π(√62)3=√6π故选:B.小提示:与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.4、如图1,已知PABC是直角梯形,AB∥PC,AB⊥BC,D在线段PC上,AD⊥PC.将△PAD沿AD折起,使平面PAD⊥平面ABCD,连接PB,PC,设PB的中点为N,如图2.对于图2,下列选项错误的是()A.平面PAB⊥平面PBC B.BC⊥平面PDCC.PD⊥AC D.PB=2AN答案:A分析:由已知利用平面与平面垂直的性质得到PD⊥平面ABCD,判定C正确;进一步得到平面PCD⊥平面ABCD,结合BC⊥CD判定B正确;再证明AB⊥平面PAD,得到△PAB为直角三角形,判定D正确;可证明平面PBC⊥平面PDC,若平面PAB⊥平面PBC,则平面PAB与平面PDC的交线⊥平面PBC,矛盾,可判断A图1中AD⊥PC,则图2中PD⊥AD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PD⊥平面ABCD,则PD⊥AC,故选项C正确;由PD⊥平面ABCD,PD⊂平面PDC,得平面PDC⊥平面ABCD,而平面PDC∩平面ABCD=CD,BC⊂平面ABCD,BC⊥CD,∴BC⊥平面PDC,故选项B正确;∵AB⊥AD,平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴AB⊥平面PAD,则AB⊥PA,即△PAB是以PB为斜边的直角三角形,而N为PB的中点,则PB=2AN,故选项D正确.由于BC⊥平面PDC,又BC⊂平面PBC∴平面PBC⊥平面PDC若平面PAB⊥平面PBC,则平面PAB与平面PDC的交线⊥平面PBC由于AB//平面PDC,则平面PAB与平面PDC的交线//AB显然AB不与平面PBC垂直,故A错误故选:A5、如图,在三棱锥A−BCD中,E,F,G分别是AB,BC,AD的中点.若∠GEF=120°,则异面直线BD与AC所成角的大小为()A.30°B.60°C.120°D.150°答案:B分析:根据异面直线所成角的定义判断.因为BD∥EG,AC∥EF,所以异面直线BD与AC所成角即∠GEF或其补角,因为异面直线所成角的范围为(0°,90°],所以异面直线BD与AC所成角的大小为60°.故选:B.6、某圆锥母线长为2,底面半径为√3,则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为()A.2B.√3C.√2D.1分析:如图截面为△SMN,P为MN的中点,设OP=x(0<x≤√3),S△SMN=√−(x2−1)2+4,进而可得面积最大值.如图所示,截面为△SMN,P为MN的中点,设OP=x(0<x≤√3)SB=2,OB=√3,∴SO=1,SP=√x2+1,MN=2√3−x2S△SMN=12MN SP=12√x2+1√3−x2=√−(x2−1)2+4当x=1时,S△SMN=2,此时截面面积最大.故选:A小提示:易错点睛:先求出面积的函数表达式进而判断最大值,本题容易误认为垂直于底面的截面面积最大.7、正方体中,点P,O,R,S是其所在棱的中点,则PQ与RS是异面直线的图形是()A.B.C.D.分析:对于A,B,D,利用两平行线确定一个平面可以证明直线PQ与RS共面,对于C,利用异面直线的定义推理判断作答.对于A,在正方体ABCD−A1B1C1D1中,连接AC,A1C1,则AC//A1C1,如图,因为点P,Q,R,S是其所在棱的中点,则有PQ//AC,RS//A1C1,因此PQ//RS,则直线PQ与RS共面,A错误;对于B,在正方体ABCD−A1B1C1D1中,连接AC,QS,PR,如图,因为点P,Q,R,S是其所在棱的中点,有AP//CR且AP=CR,则四边形APRC为平行四边形,即有AC//PR,又QS//AC,因此QS//PR,直线PQ与RS共面,B错误;对于C,在正方体ABCD−A1B1C1D1中,如图,因为点P ,Q ,R ,S 是其所在棱的中点,有RS//BB 1,而BB 1⊂平面,RS ⊄平面, 则RS//平面,PQ ⊂平面,则直线PQ 与RS 无公共点,又直线PQ 与直线BB 1相交,于是得直线PQ 与RS 不平行,则直线PQ 与RS 是异面直线,C 正确;对于D ,在正方体ABCD −A 1B 1C 1D 1中,连接A 1B ,D 1C ,PS ,QR ,如图,因为A 1D 1//BC 且A 1D 1=BC ,则四边形A 1D 1CB 为平行四边形,有A 1B//D 1C ,因为点P ,Q ,R ,S 是其所在棱的中点,有PS//A 1B ,QR//D 1C ,则PS//QR ,直线PQ 与RS 共面,D 错误. 故选:C8、下列说法中正确的是( )A .如果一条直线与一个平面平行,那么这条直线与平面内的任意一条直线平行B .平面α内△ABC 的三个顶点到平面β的距离相等,则α与β平行C .α//β,a//α,则a//βD .a//b ,a//α,b ⊄α,则b//α答案:D分析:根据线面关系,逐一判断每个选项即可.解:对于A 选项,如果一条直线与一个平面平行,那么这条直线与平面内的无数条直线平行,而不是任意的直线平行,故错误;对于B 选项,如图1,D ,E ,F ,G 分别为正方体中所在棱的中点,平面DEFG 设为平面β,易知正方体的三个顶点A ,B ,C 到平面β的距离相等,但△ABC 所在平面α与β相交,故错误;对于选项C ,a 可能在平面β内,故错误;对于选项D ,正确.11ABB A 11ABB A 11ABB A 11ABBA故选:D.多选题9、如图是正方体的平面展开图,在这个正方体中,下列结论正确的是()A.BM与ED平行B.CN⊥AFC.CN与BM成60°D.四条直线AF、BM、CN、DE中任意两条都是异面直线答案:BCD分析:还原成正方体之后根据正方体性质分析线线位置关系.根据展开图还原正方体如图所示:BM与ED不平行,所以A错误;正方体中CN⊥DM,DM//FA,所以CN⊥AF,所以B正确;CN//EB,CN与BM成角就是∠EBM,△EBM是等边三角形,所以∠EBM=60°,所以C正确;由图可得四条直线AF、BM、CN、DE中任意两条既不想交也不平行,所以任意两条都是异面直线.故选:BCD10、已知PA⊥矩形ABCD所在的平面,则下列结论中正确的是()A.PB⊥BCB.PD⊥CDC.PD⊥BDD.PA⊥BD答案:ABD分析:由PA⊥矩形ABCD,得PA⊥BD,若PD⊥BD,则BD⊥平面PAD,又BA⊥平面PAD,则过平面外一面有两条直线与平面垂直,不成立,故PD⊥BD不正确.解:∵PA⊥矩形ABCD,BD⊂矩形ABCD,∴PA⊥BD,故D正确.若PD⊥BD,则BD⊥平面PAD,又BA⊥平面PAD,则过平面外一面有两条直线与平面垂直,故PD⊥BD不正确,故C不正确;∵PA⊥矩形ABCD,∴PA⊥CD,AD⊥CD,∴CD⊥平面PAD,∴PD⊥CD,故B正确;∵PA⊥矩形ABCD,∴由三垂线定理得PB⊥BC,故A正确;故选:ABD.11、如图,在棱长均相等的正四棱锥P−ABCD中,M、N分别为侧棱PA、PB的中点,O是底面四边形ABCD对角线的交点,下列结论正确的有()A.PC//平面OMN B.平面PCD//平面OMNC.OM⊥PA D.PD⊥平面OMN答案:ABC分析:A选项,由中位线证明线线平行,推导出线面平行;B选项,在A选项的基础上证明面面平行;从而推导出D错误;由勾股定理的逆定理得到PA⊥PC,从而得到OM⊥PA.因为O为底面四边形ABCD对角线的交点,所以O为AC的中点,由M是PA的中点,可得PC∥MO,因为PC⊄在平面OMN,OM⊂平面OMN,所以PC//平面OMN,A正确;同理可推得PD//平面OMN,而PC∩PD=P,所以平面PCD//平面OMN,B正确;因为PD⊂平面PCD,故PD不可能垂直平面OMN,D错误;设该正四棱锥的棱长为a,则PA=PC=a,AC=√2a,所以PA⊥PC,因为PC∥MO,所以OM⊥PA,C正确.故选ABC.12、用平行于棱锥底面的平面去截棱锥,得到上、下两部分空间图形且上、下两部分的高之比为1:2,则关于上、下两空间图形的说法正确的是()A.侧面积之比为1:4B.侧面积之比为1:8C.体积之比为1:27D.体积之比为1:26答案:BD分析:计算出小棱锥与原棱锥的相似比,结合两个棱锥侧面积之积为相似比的平方、体积之比为相似比的立方可求得结果.依题意知,上部分为小棱锥,下部分为棱台,所以小棱锥与原棱锥的底面边长之比为1:3,高之比为1:3,所以小棱锥与原棱锥的侧面积之比为1:9,体积之比为1:27,即小棱锥与棱台的侧面积之比为1:8,体积之比为1:26.故选:BD.13、已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题正确的是()A.若m//n,m//α,则n//αB.若m//α,α∩β=n,则m//nC.若m⊥α,m⊥β,则α//βD.若m⊥α,m//n,n⊥β,则α//β答案:CD分析:根据空间中线、面的位置关系,逐一分析各个选项,即可得答案.对于A:若m//n,m//α,则n//α或n⊂α,故A错误;对于B:若m//α,α∩β=n,则m与n可平行也可异面,故B错误;对于C:若m⊥α,m⊥β,则α//β,故C正确;对于D:若m⊥α,m//n,则n⊥α,又n⊥β,则α//β,故D正确.故选:CD填空题14、已知正四棱锥的侧棱长为2√3,侧棱与底面所成的角为60°,则该四棱锥的高为_______. 答案:3解析:根据立体图形,作出直线与平面所成的角,结合线面角即可求得锥体的高.如图,过点S作SO⊥平面ABCD,连接OC,∠SCO就是侧棱与底面所成的角,×2√3=3.则∠SCO=60°,∴SO=sin60°⋅SC=√32所以答案是:3.小提示:此题考查根据线面角求线段长度,关键在于弄清正四棱锥的几何特征.15、如图所示,P 为平行四边形ABCD 所在平面外一点,E 为AD 的中点,F 为上一点,若PA//平面EBF ,则PF FC =_______答案:12##0.5分析:连接AC 交BE 于点M ,连接,由线面平行的性质得线线平行,由平行线性得结论.连接AC 交BE 于点M ,连接,∵PA//平面EBF ,PA ⊂平面,平面PAC ∩平面EBF =EM ,∴PA//EM ,又AE//BC ,∴PF FC =AM MC =AE BC =12. 所以答案是:12. 16、对于任意给定的两条异面直线,存在______条直线与这两条直线都垂直.答案:无数分析:平移一条直线与另一条相交并确定一个平面,再由线面垂直的意义及异面直线所成角判断作答. 令给定的两条异面直线分别为直线a,b ,平移直线b 到直线bʹ,使bʹ与直线a 相交,如图,则直线bʹ与a 确定平面α,点A 是平面α内任意一点,过点A 有唯一直线l ⊥α, PC FM FMPAC因此,l⊥a,l⊥bʹ,即有l⊥b,由于点A的任意性,所以有无数条直线与异面直线a,b都垂直.所以答案是:无数解答题17、如图所示,斜三棱柱ABC−A1B1C1中,点D1为A1C1上的中点.(1)求证:BC1//平面AB1D1;(2)设三棱锥A−A1B1D1的体积为V1,三棱柱ABC−A1B1C1的体积为V2,求V1V2.答案:(1)证明见解析;(2)16.分析:(1)连接A1B交AB1于点O,连接OD1,可得OD1∥BC1,由线面平行的判定定理即可证明BC1∥平面AB1D1;(2)由V1=V A−A1B1D1=12V A−A1B1C1=16V ABC−A1B1C1=16V2,即可求得结论.(1)证明:连接A1B交AB1于点O,连接OD1.则在平形四边形ABB1A1中,点O为A1B的中点,又点D1为A1C1的中点,所以OD1∥BC1,又OD1⊂平面AB1D1,B1C⊄平面AB1D1,所以BC1∥平面AB1D1.(2)V1=V A−A1B1D1=12V A−A1B1C1=16V ABC−A1B1C1=16V2所以V1V2=16.18、如图,四边形ABCD是一个半圆柱的轴截面,E,F分别是弧,AB上的一点,EF//AD,点H为线段AD的中点,且AB=AD=4,∠FAB=30°,点G为线段CE上一动点.(1)试确定点G的位置,使DG//平面CFH,并给予证明;(2)求三棱锥E−CFH的体积.答案:(1)点G为线段CE中点,证明见解析;(2)8√33.分析:(1)点G为线段CE中点,取CF中点M,证明DG//HM,再利用线面平行的判定推理作答.(2)根据给定条件,证得CE⊥平面ADEF,再结合等体积法即可求出三棱锥E−CFH的体积作答.(1)当点G为线段CE中点时,DG//平面CFH,取CF中点M,连接HM,GM,如图,则GM//EF,GM=12EF,DC因E,F分别是弧,AB上的一点,EF//AD,则EF是半圆柱的一条母线,即EF=AD,而点H为线段AD的中点,于是得GM//DH,GM=DH,即四边形DGMH为平行四边形,则DG//HM,而DG⊄平面CFH,HM⊂平面CFH,所以DG//平面CFH.(2)依题意,AB是半圆柱下底面半圆的直径,则∠AFB=90∘,而∠FAB=30°,有AF=√32AB=2√3,BF=12AB=2,显然CD是半圆柱上底面半圆的直径,则CE⊥DE,由(1)知EF是半圆柱的一条母线,则EF⊥平面CDE,而CE⊂平面CDE,即有CE⊥EF,DE∩EF=E,DE,EF⊂平面ADEF,因此,CE⊥平面ADEF,而EF//BC,EF=BC,即四边形BCEF是平行四边形,CE=BF=2,又点H为线段AD的中点,则S△EFH=12AD⋅AF=4√3,所以三棱锥E−CFH的体积V E−CFH=V C−EFH=13⋅S△EFH⋅CE=13×4√3×2=8√33.DC。
立体几何定理大全

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3: 过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.空间两直线的位置关系:空间两条直线只有三种位置关系:平行、相交、异面1、按是否共面可分为两类:(1)共面:平行、相交(2)异面:异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线.两异面直线所成的角:范围为 ( 0°,90°) esp。
空间向量法两异面直线间距离:公垂线段(有且只有一条) esp.空间向量法2、若从有无公共点的角度看可分为两类:(1)有且仅有一个公共点-—相交直线;(2)没有公共点-—平行或异面直线和平面的位置关系: 直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内-—有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直esp。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014学年高二数学---1028
立体几何“平行、垂直”定理默写
给你定理的图形语言,请写出定理的文字语言(即类似原话的叙述)、以及符号语言:
① 线面平行的判定定理——线线平行 则线面平行
文字语言: 符号语言: 图形语言:
② 面面平行的判定定理——线面平行 则面面平行
文字语言: 符号语言: 图形语言:
③ 线面平行的性质定理——线面平行 则线线平行
文字语言: 符号语言: 图形语言:
④ 面面平行的性质定理——面面平行 则线线平行
文字语言: 符号语言: 图形语言:
④ 面面平行的性质定理
α
a
b
α
a
b
βα
a
b
β
▲平行的其它结论:(1) 若面面平行,则一面内任一线平行于另一面。
(2) 等角定理:若两个角的边对应平行,则这两个角相等或互补。
⑤ 线面垂直的判定定理——线线垂直 则线面垂直
文字语言: 符号语言: 图形语言:
⑥ 面面垂直的判定定理——线面垂直 则面面垂直
文字语言: 符号语言: 图形语言:
⑦ 线面垂直的性质定理:(这个还是线面垂直的定义“线面垂直则线线垂直”有用,故用定义代替定理) 文字语言: 符号语言: 图形语言:
⑧ 面面垂直的性质定理:面面垂直 则线面垂直
αa
b
βγ
⑤ 线面垂直的判定定理 ⑥ 面面垂直的判定定理 ⑦ 线面垂直的性质定理
⑧ 面面垂直的性质定理
α
a
b
l αa
βα
a
l
文字语言: 符号语言: 图形语言:
▲垂直的其它结论:
(1)若两平行线中的一条垂直于一面,则另一条也垂直于该面。
(2)若两直线都垂直于一面,则这两直线平行。
(这个是书上的线面垂直性质定理) (3)若两平面垂直,则过一面内一点与另一面垂直的直线,必在该面内。
答案
1、八个定理——立体几何的证明的依据、更是证明的思路:
① 线面平行的判定定理——线线平行,则线面平行
文字语言: 符号语言: 图形语言: 平面外一条直线与此平面 内的一条直线平行,则此 直线与此平面平行。
② 面面平行的判定定理——线面平行,则面面平行
文字语言: 符号语言: 图形语言: 一个平面内的两条相交 直线与另一个平面平行, 则这两个平行平行。
③ 线面平行的性质定理——线面平行,则线线平行
文字语言: 符号语言: 图形语言: 一条直线与一个平面平行, 则过这条直线的任一平面 与此平面的交线与该直线
α
a
βb
α
a
b
α
a
b
β
α
a
b
βααα////a b a b a ⇒⎪⎭
⎪
⎬⎫
⊂⊄βαβαα//,,//,//⇒⎪⎭
⎪
⎬⎫
⊂相交b a b a b a b a b a a ////⇒⎪⎭
⎪
⎬⎫
=⊂βαβα
I
平行。
④ 面面平行的性质定理——面面平行,则线线平行
文字语言: 符号语言: 图形语言: 如果两个平行平面同时和 第三个平面相交,那么它 们的交线平行。
⑤ 线面垂直的判定定理——线线垂直,则线面垂直
文字语言: 符号语言: 图形语言: 一条直线与一个平面内的 两条相交直线都垂直,则 该直线与此平面垂直。
⑥ 面面垂直的判定定理——线面垂直,则面面垂直
文字语言: 符号语言: 图形语言: 一个平面过另一个平面的 垂线,则这两个平面垂直。
⑦ 线面垂直的性质定理:(用线面垂直的定义“线面垂直,则线线垂直”代替) 文字语言: 符号语言: 图形语言: 一条直线垂直于一个平面, 则这条直线垂直于这个平 面内的所有直线。
⑧ 面面垂直的性质定理:面面垂直,则线面垂直
文字语言: 符号语言: 图形语言: 两个平面垂直,则一个平 面内垂直于交线的直线与 另一个平面垂直。
α
a
b
βγ
α
a
b
l
α
a
βαa
l
b a b a ////⇒⎪⎭
⎪
⎬⎫
==γβγαβαI I αα⊥⇒⎪⎭
⎪
⎬⎫
⊂⊥⊥l b a b a b l a l 相交,,,αββα⊥⇒⎭
⎬⎫
⊂⊥a a a l a l ⊥⇒⎭
⎬⎫
⊂⊥ααα
a
β
b
βββαβα⊥⇒⎪⎭
⎪
⎬⎫
⊥⊂=⊥a b a a b ,I。
