综合领域北新国中巡回辅导二
2023年北京各区初三二模数学分类汇编-圆综合答案

如图,P为☉O外一点,PA,PB是☉O的切线,A,B为切点,点C在☉O上,连接OA,OC,AC.(1)求证:∠AOC=2∠PAC;(2)连接OB,若AC∥OB,☉O的半径为5,AC=6,求AP的长.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,点D是BC的中点,点E是AB的延长线上的一点,∠BCE=∠BOD,OD的延长线交CE于点F.(1)求证:CE是⊙O的切线;(2)若sin E=23,AC=5,求DF的长.7.(2023·北京门头沟初三二模25题)如图,AB 是⊙O 直径,弦CD ⊥AB 于E ,点F 在CD 上,且AF =DF ,连接AD ,BC .(1)求证:∠FAD =∠B ;(2)延长FA 到P ,使FP =FC ,作直线CP .如果AF ∥BC ,求证:直线CP 为⊙O的切线.AB如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得∠BFD=∠ADB.(1)求证:DF是⊙O的切线;(2)若AD=4,DE=5,求DF的长.2023.510.(2023·北京顺义初三二模24题)如图,PA ,PB 分别与⊙O 相切于A ,B 两点,AC 是⊙O 的直径.(1)求证:∠BAC=21∠APB ;(2)连接PO 交⊙O 于点D ,若AC =6,cos ∠BAC =54,求PD 的长.2023.5 11.(2023·北京昌平初三二模23题)2023.512.(2023·北京平谷初三二模24题)24.(1)解:∵BE 为O 的切线∴∠ABE=90° (1)∴∠ABC+∠EBC=90°∵AB 是直径∴∠ACB=90°∴∠A+∠ABC=90°∴∠A=∠EBC (2)∵CB CB ∴∠D=∠A∴∠D=∠EBC ··················································3(2)∵1tan D 2 ∴1tan 2EBC ∵∠ACB=90°,BC=2∴CE=1 (4)∵∠D=∠A ∴1tan 2A ∴AC=4 (5)∴AE=5Rt △AEB 中,∵F 是AE 的中点,∠ABE=90°∴12.52BF AE (6)2023.513.(2023·北京燕山地区初三二模25题)如图,AB为⊙O的直径,BC为弦,射线AM与⊙O相切于点A,过点O作OD∥BC交AM于点D,连接DC.(1)求证:DC是⊙O的切线;(2)过点B作BE⊥AB交DC的延长线于点E,连接AC交OD于点F.若AB=12,BE=4,求AF的长.。
2023年北京市部分名校中考数学备考——代数综合(学生版)

2023年北京市部分名校中考数学备考——代数综合1.(2023•海淀区人大附中开学)在平面直角坐标系xOy中,二次函数y=ax2+2ax﹣a﹣1的图象经过原点.(1)求该二次函数的解析式以及顶点坐标;(2)将该二次函数的图象在y轴左侧的部分记作W,将W绕原点旋转180°得到W',W 与W'组成一个新函数的图象.①若点B(b,1)(b≠﹣1)在该新函数图象上,求b的值;②若点(m,y1),(m+n,y2)是新函数图象上两点,若存在n≥2+,使得y1>y2,直接写出m的取值范围.2.(2023春•海淀区101月考)在平面直角坐标系中,已知抛物线y=ax2﹣2ax+a+1.(1)求抛物线的顶点坐标;(2)已知点A(﹣1,3),B(4,3),若抛物线与线段AB恰有一个公共点,求a的取值范围;(3)点P(x1,y1)在抛物线y=ax2﹣2ax+a+1上,点Q(x2,y2)在一次函数y=x+a+1的图象上,若对于任意,总存在x2≥0,使得y1≥y2,直接写出a的取值范围.3.(2023•海淀区首师大附中模拟)在平面直角坐标系xOy中,点(x0,m),(a﹣1,n),是抛物线y=ax2﹣2a2x上的点,x0≠a﹣1.(1)当x0=2,m=n时,求a和n的值;(2)若﹣4≤x0≤﹣3时,mn<0,求a的取值范围.4.(2023•海淀区玉渊潭中学模拟)在平面直角坐标系xOy中,抛物线y=ax2﹣2a2x(a≠0).(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的对称轴(用含a的式子表示);(3)若抛物线上存在两点A(a﹣1,y1)和B(a+3,y2),当y1•y2<0,求a的取值范围.5.(2023•海淀区北师大三附一模)在平面直角坐标系xOy中,点(4,3)在抛物线y=ax2+bx+3(a>0)上.(1)求该抛物线的对称轴;(2)已知m>0,当2﹣m≤x≤2+2m时,y的取值范围是﹣1≤y≤3.求a,m的值;(3)在(2)的条件下,是否存在实数n,使得当n﹣2<x<n时,y的取值范围是3n﹣3<y<3n+5.若存在,直接写出n的值;若不存在,请说明理由.6.(2023•海淀区首师大附中开学)已知抛物线y=x2﹣2ax+a2﹣2.(1)求抛物线的顶点坐标(用含a的式子表示);(2)设直线y=b与抛物线交于不同的两点A,B,若AB≤4,直接写出b的取值范围;(3)若抛物线上存在两点M(m,m)和N(n,﹣n),且当m<0,n>0时,有m+n>0,求a的取值范围.7.(2023•海淀区十九中+八一中学模拟)在平面直角坐标系中,抛物线y=a(x﹣h)2﹣4a 的顶点为点A,且0<h<3,(1)若a=2,①点A到x轴的距离为;②已知点M(﹣1,﹣6),N(3,﹣6),若抛物线与线段MN有且只有一个公共点,求h的取值范围;(2)已知点A到x轴的距离为4,此抛物线与直线y=2x+1的两个交点分别为B(x1,y1),C(x2,y2),其中x1<x2,若点D(x D,y D)在此抛物线上,当x1<x D<x2时,y D 总满足y1<y D<y2,求a的值和h的取值范围.8.(2023春•海淀区人大附中月考)在平面直角坐标系xOy中,点A(﹣4,y1),,C(m,y3)三个点在抛物线y=x2﹣2ax+c(a>0)上.(1)当a=1时,求抛物线的对称轴,并直接写出y1和y2的大小关系.(2)①若m=5,y1=y3,则a的值为;②若对于任意2≤m≤5,都满足y1>y3>y2,求a的取值范围.9.(2023•海淀区玉渊潭中学模拟)在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1(a >0).(1)若抛物线过点(4,﹣1).①求抛物线的对称轴;②当﹣1<x<0时,图象在x轴的下方,当5<x<6时,图象在x轴的上方,在平面直角坐标系中画出符合条件的图象,求出这个抛物线的表达式;(2)若(﹣4,y1),(﹣2,y2),(1,y3)为抛物线上的三点且y3>y1>y2,设抛物线的对称轴为直线x=t,直接写出t的取值范围.10.(2023春•海淀区清华附中月考)已知抛物线y=ax2+(6a﹣2)x(a>0),点(﹣3,m),(﹣1,n),(x0,t)在该抛物线上.(1)若m=n,t>0,求x0的取值范围;(2)若存在0≤x0≤1.使得n<t<m,求a的取值范围.11.(2023•海淀区清华附中开学)在平面直角坐标系中,抛物线y=ax2﹣(a+2)x+2经过点A(﹣2,t),B(m,p).(1)若t=0,①求此抛物线的对称轴;②当p<t时,直接写出m的取值范围;(3)若t<0,点C(n,q)在该抛物线上,m<n且3m+3n≤﹣4,请比较p,q的大小,并说明理由.12.(2023春•21+22中月考)在平面直角坐标系xOy中,已知抛物线y=x2﹣2tx+t2﹣t.(1)求抛物线的顶点坐标(用含t的代数式表示);(2)点P(x1,y1),Q(x2,y2)在抛物线上,其中t﹣1≤x1≤t+2,x2=1﹣t.①若y1的最小值是﹣2,求y1的最大值;②若对于x1,x2,都有y1<y2,直接写出t的取值范围.13.(2023春•西城区三十五中学月考)在平面直角坐标系xOy中,已知抛物线:y=ax2﹣2ax+4(a>0).(1)抛物线的对称轴为x=;抛物线与y轴的交点坐标为;(2)若抛物线的顶点恰好在x轴上,写出抛物线的顶点坐标,并求它的解析式;(3)若A(m﹣1,y1),B(m,y2),C(m+2,y3)为抛物线上三点,且总有y1>y3>y2,结合图象,求m的取值范围.14.(2023•海淀区清华附中模拟)在平面直角坐标系xOy中,点(4,2)在抛物线y=ax2+bx+2(a>0)上.(1)求抛物线的对称轴;(2)抛物线上两点P(x1,y1),Q(x2,y2),且t<x1<t+1,4﹣t<x2<5﹣t.①当时,比较y1,y2的大小关系,并说明理由;②若对于x1,x2,都有y1≠y2,直接写出t的取值范围.15.(2023•海淀区五十七中学二模)在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2+1与y轴交于点A.点B(x1,y1)是抛物线上的任意一点,且不与点A重合,直线y=kx+n (k≠0)经过A,B两点.(1)求抛物线的顶点坐标(用含m的式子表示);(2)若点C(m﹣2,a),D(m+2,b)在抛物线上,则a b(用“<”,“=”或“>”填空);(3)若对于x1<﹣3时,总有k<0,求m的取值范围.16.(2023•海淀区人大附中经开区校区模拟)在平面直角坐标系xOy中,抛物线y=x2﹣2bx.(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的对称轴(用含b的式子表示);(3)若抛物线上存在两点A(b﹣1,y1)和B(b+2,y2),当y1•y2<0时,求b的取值范围.17.(2023春•海淀区师达中学月考)在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(0,﹣2),(2,﹣2).(1)直接写出c的值和此抛物线的对称轴;(2)若此抛物线与直线y=﹣6没有公共点,求a的取值范围;(3)点(t,y1),(t+1,y2)在此抛物线上,且当﹣2≤t≤4时,都有|y2﹣y1|<.直接写出a的取值范围.18.(2023春•海淀区首师大附中月考)在平面直角坐标系xOy中,已知抛物线y=x2﹣2tx+t2﹣t.(1)求抛物线的顶点坐标(用含t的代数式表示):(2)点P(x1,y1),Q(x2,y2)在抛物线上,其中t﹣1≤x1≤t+2,x2=1﹣t.①若y1的最小值是﹣2,求y1的最大值;②若对于x1,x2,都有y1<y2,直接写出t的取值范围.19.(2023春•北京四中月考)已知二次函数y=ax2﹣4ax+3(a≠0).(1)求该二次函数的图象与y轴交点的坐标及对称轴.(2)抛物线过点M(﹣1,m),N(2,n),P(6,p),①判断:(m﹣3)(n﹣3)0(填“>”,“<”或“=”);②若M,N,P恰有一个点在x轴下方,求a的取值范围.20.(2023春•西城区北师大附属实验中学月考)在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.(1)求抛物线的对称轴(用含m的式子表示);(2)将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M (x1,y1),N(x2,y2)为图形G上任意两点.①当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由;②若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.21.(2023春•西城区北师大附属实验中学月考)已知:抛物线y=mx2﹣nx+2m+1(m≠0)过点A(1,0).(1)用含m代数式表示n;(2)若抛物线与x轴的另一个交点为点B,且点B在点A的左侧,求m的取值范围;(3)若m<﹣1,点、D(3,y2)、在抛物线上,请比较y1、y2、y3的大小,并说明理由.22.(2023•西城区铁路二中模拟)在平面直角坐标系中,设二次函数y=(x+a)(x﹣a﹣1)(a>0),(1)求二次函数对称轴;(2)若当﹣1≤x≤3时,函数的最大值为4,求此二次函数的顶点坐标.(3)抛物线上两点M(x1,y1),N(x2,y2)若对于t<x1<t+1,t+2<x2<t+3都有y1≠y2,求t的取值范围.23.(2023•西城区北师大二附西城实验学校模拟)在平面直角坐标系xOy中,已知抛物线y =x2﹣2ax﹣3.(1)求该抛物线的对称轴(用含a的式子表示);(2)A(x1,y1),B(x2,y2)为该抛物线上的两点,若x1=1﹣2a,x2=a+1,且y1>y2,求a的取值范围.24.(2023•西城区北师大二附西城实验学校模拟)在平面直角坐标系xOy中,点(﹣1,y1),(1,y2),(2,y3)在抛物线y=ax2+bx上.(1)若a=1,b=﹣2,求该抛物线的对称轴并比较y1,y2,y3的大小;(2)已知抛物线的对称轴为x=t,若y2<0<y3<y1,求t的取值范围.25.(2023春•西城区三帆中学月考)在平面直角坐标系xOy中,已知二次函数y=mx2﹣3mx (m≠0).(1)当二次函数经过点A(﹣1,4)时.①求该二次函数的解析式以及二次函数的顶点坐标;②一次函数y=﹣2x+b的图象经过点A,点(n,y1)在一次函数y=﹣2x+b的图象上,点(n+2,y2)在二次函数y=mx2﹣3mx的图象上.若y1<y2,求n的取值范围.(2)点M(t,y M),N(t+1,y N)在二次函数图象上,且|m|≤|y M﹣y N|≤|4m|时,求t的取值范围.26.(2023春•东城区166中学月考)已知二次函数y=ax2+bx+c(a<0)过点(﹣1,y1)和(3,y2),其对称轴为直线x=t;(1)当a=﹣1,b=4时,求此时t的值,判断y1、y2的大小关系并说明理由;(2)若在此函数上有A(m,n),且﹣1≤m≤3.①若n总是不小于y1、y2中的任何一个数,直接写出此时t的值;②当时,存在A点使得y1、y2、n三个数中最大值和最小值的差不小于1,直接写出此时t的取值范围.27.(2023•北京二中一模)在平面直角坐标系xOy中,A(﹣3,y1),B(,y2),C(m,y3)在抛物线y=﹣x2+2ax+c(a>0)上.(1)抛物线的对称轴为直线x=,直接写出y1和y2的大小关系y1y2;(2)若m=4,且y1=y3,则a的值是;(3)若对于任意1≤m≤4,都有y1<y3<y2,求a的取值范围.28.(2023•东城区171开学考)在平面直角坐标系xOy中,已知抛物线M:y=ax2﹣4ax+4a+1(a≠0)和直线l:y=.(1)抛物线M的对称轴是;(2)若直线y=n与抛物线M有两个公共点,它们的横坐标记为x1,x2,直线y=n与直线l的交点横坐标记为x3.若当﹣1<n<0时,总有x1<x3<x2,请结合函数图象,求a 的取值范围.29.(2023•东城区广渠门中学模拟)在平面直角坐标系xOy中,抛物线y=﹣x2+4mx﹣4m2﹣1与y轴交于点P.点Q(a,b)是抛物线上的任意一点,且不与点P重合,直线y=kx+b(k≠0)经过P,Q两点.(1)求抛物线的顶点坐标(用含m的式子表示);(2)若PQ∥x轴,且线段PQ长为6,求m的值;(3)若对于0<a<6时,总有k>0,求m的取值范围.30.(2023•东城区广渠门中学模拟)在平面直角坐标系xOy中,点A(﹣3,m),B(x0,n)在抛物线y=﹣x2+(2a﹣2)x﹣a2+2a上.(1)求抛物线的对称轴(用含a的式子表示);(2)若存在﹣1<x0<1,使得m<n,求a的取值范围.31.(2023•东城区广渠门中学模拟)在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+2(a >0)与y轴交于点A.(1)求点A的坐标及抛物线的对称轴;(2)当0≤x≤5时,y的最小值是﹣2,求当0≤x≤5时,y的最大值;(3)抛物线上的两点P(x1,y1),Q(x2,y2),若对于t<x1<t+1,t+2<x2<t+3,都有y1≠y2,直接写出t的取值范围.32.(2023春•东城区171中学月考)已知二次函数y=ax2﹣4ax+3(a≠0).(1)求此二次函数图象的对称轴;(2)设此二次函数的图象与x轴交于不重合两点M(x1,0)N(x2,0)(其中x1<x2),且满足x2>3﹣2x1;①直接写出x1+x2的值;②求a的取值范围.33.(2023•清华附中朝阳学校模拟)在平面直角坐标系xOy中,已知抛物线y=mx2﹣3(m ﹣1)x+2m﹣1(m≠0).(1)当m=3时,求抛物线的顶点坐标;(2)已知点A(1,2).试说明抛物线总经过点A;(3)已知点B(0,2),将点B向右平移3个单位长度,得到点C,若抛物线与线段BC 只有一个公共点,求m的取值范围.34.(2023•首师大苹果园分校模拟)在平面直角坐标系xOy中,点(m﹣2,y1),(m,y2),(2﹣m,y3)在抛物线y=x2﹣2ax+1上,其中m≠1且m≠2.(1)直接写出该抛物线的对称轴的表达式(用含a的式子表示);(2)当m=0时,若y1=y3,比较y1与y2的大小关系,并说明理由;(3)若存在大于1的实数m,使y1>y2>y3,求a的取值范围.35.(2023•石景山区京源学校模拟)在平面直角坐标系xOy中,一次函数y=﹣ax+3的图象与y轴交于点A,与抛物线y=ax2﹣2ax﹣3a(a≠0)的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.(1)求出抛物线的对称轴和点C坐标;(2)①当a=﹣1时,直接写出抛物线y=ax2﹣2ax﹣3a与图形G的公共点个数.②如果抛物线y=ax2﹣2ax﹣3a与图形G有且只有一个公共点,求出a的取值范围.36.(2023春•丰台区12中月考)在平面直角坐标系xOy中,点(2,3)在抛物线y=ax2+bx+3(a>0)上.(1)求该抛物线的对称轴;(2)已知m>0,当1﹣2m≤x≤1+m时,y的取值范围是2≤y≤6,求a,m的值;(3)在(2)的条件下,当n﹣1≤x≤n+1时,若函数值y的最大与最小值的差不超过4,直接写出n的取值范围。
2024北京各区初三二模代综汇编

2024初三二模代综汇编12024海淀二模26在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)的对称轴为x=t,点A(12t,m),B(2t,n),C(x0,y0)在抛物线上.(1)当t=2时,直接写出m与n的大小关系;(2)若对于6<x0<7,都有m<y0<n,求t的取值范围.22024西城二模26在平面直角坐标系xOy中,M(x1,y1),N(x2,y2)是抛物线y=ax2+bx+c上任意两点.设抛物线的对称轴是x=t.(1)若对于x1=2,x2=-1,有y1=y2,求t的值;(2)若对于x1≥2,都有y1<c成立,并且对于x2>1,存在y2>c,求t的取值范围.在平面直角坐标系xOy中,已知抛物线y=ax2-2amx+am2-4(a>0).(1)求该抛物线的顶点坐标(用含m的式子表示);(2)若对于该抛物线上的三个点A(m-2,y1),B(2m,y2),C(2m-2,y3),总有y1>y2>y3,求实数m的取值范围.26xOy中,抛物线y=ax2+(1-a)x-1(a≠0)的对称轴为直线x=t.a的式子表示);时,求该抛物线与x轴的公共点的坐标;(1 2,y2),(-32a-2,y3)在该抛物线上,若a>0,比较y1,y2,y3的大小,并说明理由.在平面直角坐标系xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是抛物线y=ax2-2ax-2(a>0)上的三个点.(1)求该抛物线的对称轴;(2)若对于-2<x1<-1,2<x2<3,都有y1y2<0,求证:3a-2=0;(3)若对于2<x2<3,m<x3<m+1,都有y3>y2,求m的取值范围.62024石景山二模26在平面直角坐标系xOy中,点M(2,m),N(4,n)在抛物线y=x2-2bx+c上.(1)若m=n,求b的值;(2)若点T(x0,p)在抛物线上,对于0<x0<1,都有m<p<n,求b的取值范围.在平面直角坐标系xOy中,M(x1,y1),N(x2,y2)是抛物线y=ax2+bx+c(a>0)上任意两点,其中x1<x2.(1)若抛物线经过点(4,c),1求抛物线的对称轴;2当x1+x2>4时,比较y1,y2的大小,并说明理由;(2)设抛物线的对称轴为直线x=t,若存在实数m,当t≤m时,x1=m,x2=m+1,都有y1-y2≥2,直接写出a的取值范围.82024门头沟二模26在平面直角坐标系xOy中,抛物线y=ax2+bx+c的图象经过点A(0,1a),将点A向左平移4个单位长度,得到点B,点B在抛物线上.(1)求抛物线的对称轴;(2)点B的纵坐标为-3时,求a的值;(3)已知点M(-1,1a),N(-4,-3).若抛物线与线段MN恰有一个公共点,结合函数图象,求a的取值范围.在平面直角坐标系xOy中,点(2,m)和点(4,n)在抛物线y=ax2+bx(a>0)上,设抛物线的对称轴为x=t.(1)若m=n时,求t的值;(2)已知点(-1,y1),(1,y2),(3,y3)在抛物线上.若mn<0,比较y1,y2,y3的大小,并说明理由.102024顺义二模26在平面直角坐标系xOy中,点(2m,y1),(3-m,y2)在抛物线y=x2+bx+c上.(1)当m=2时,y1=y2,求b的值;(2)若对于大于1的实数m,都有y1>y2,求b的取值范围.在平面直角坐标系xOy中,点A(-1,m)和点B(4,n)在抛物线y=ax2+bx-2(a>0)上,设抛物线的对称轴为x=t.(1)若m=1,n=6,求t的值;(2)已知点C(1,y1),D(32t,y2)在该抛物线上,若m>-2,n<-2,比较y1,y2的大小,并说明理由.122024燕山二模26在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)的对称轴为x=t.(1)若3a+2b=0,求t的值;(2)已知点(-1,y1),(2,y2),(3,y3)在该抛物线上.若a>c>0,且3a+2b+c=0,比较y1,y2,y3的大小,并说明理由.。
北师大版八年级数学下册第二章综合素质评价附答案 (1)

北师大版八年级数学下册第二章综合素质评价一、选择题(每题3分,共30分)1.2022年3月5日,李克强总理在政府工作报告中提出,今年发展主要预期目标之一是粮食产量保持在1.3万亿斤以上.若用x (万亿斤)表示我国今年粮食产量,则x 满足的关系为( )A .x ≥1.3B .x >1.3C .x ≤1.3D .x <1.32.下列式子:①7>4;②3x ≥2π+1;③3x +y >1;④x 2+3>2x ;⑤1x >4.其中是一元一次不等式的有( )A .4个B .3个C .2个D .1个3.【教材P 42习题T 1变式】【2022·宿迁】如果x <y ,那么下列不等式正确的是( )A .2x <2yB .-2x <-2yC .x -1>y -1D .x +1>y +14.不等式1-x ≥2的解集在数轴上的表示正确的是( )5.【教材P63复习题T14改编】关于x 的方程4x -2m +1=5x -8的解是负数,则m 的取值范围是( )A .m >92B .m <0C .m <92 D .m >06.方程组⎩⎨⎧x -4y =3,2x +y =6a 的解满足不等式x -y <5,则a 的取值范围是( )A .a <1B .a >1C .a <2D .a >27.【教材P 62复习题T 10改编】若不等式组⎩⎨⎧-x +4m <x +10,x +1>m的解集是x >4,则( )A .m ≤92 B .m ≤5 C .m =92 D .m =58.【2021·娄底】如图,直线y =x +b 和y =kx +4与x 轴分别相交于点A (-4,0),点B (2,0),则⎩⎨⎧x +b >0,kx +4>0的解集为( )A .-4<x <2B .x <-4C .x >2D .x <-4或x >29.【2022·上城区一模】斑马线前“车让人”,反映了城市的文明程度,但行人一般都会在红灯亮起前通过马路,某人行横道全长24 m ,小明以1.2 m /s 的速度过该人行横道,行至13处时,9 s 倒计时灯亮了,小明要在红灯亮起前通过马路,他的速度至少要提高到原来的( )A .1.1倍B .1.4倍C .1.5倍D .1.6倍10.【2022·贵阳】在同一平面直角坐标系中,一次函数y =ax +b 与y =mx +n (a <m <0)的图象如图所示,小墨根据图象得到如下结论:①在一次函数y =mx +n 的图象中,y 的值随着x 值的增大而增大; ②方程组⎩⎨⎧y -ax =b ,y -mx =n 的解为⎩⎨⎧x =-3,y =2;③方程mx +n =0的解为x =2;④当x =0时,ax +b =-1. 其中结论正确的个数是( ) A .1 B .2 C .3 D .4 二、填空题(每题3分,共24分)11.如图,天平向左倾斜,则据此列出的关于x 的不等关系为______________.12.【教材P 61复习题T 1变式】若关于x 的不等式(a -3)x >1的解集为x <1a -3,则a 的取值范围是__________.13.如图是一次函数y 1=ax +b ,y 2=kx +c 的图象,观察图象,写出同时满足y 1>0,y 2>0时x 的取值范围:__________.14.在平面直角坐标系中,若点P (m -3,m +1)在第二象限,则m 的取值范围是__________.15.不等式组⎩⎪⎨⎪⎧x -3(x -2)≤8,5-12x >2x 的整数解是__________.16.【2022春·山西期中】为了响应国家低碳生活的号召,更多的市民放弃开车选择自行车出行,市场上的自行车销量增加,某种品牌自行车专卖店抓住商机,搞促销活动对原进价为800元,标价为1 000元的某款自行车进行打折销售,若要保持利润率不低于5%,则这款自行车最多可打________折.17.【新定义题】定义一种新运算:a ※b =2a +b .已知关于x 的不等式x ※k ≥1的解集在数轴上的表示如图所示,则k =________.18.按图中程序计算,规定:从“输入一个值x ”到“结果是否≥14”为一次程序操作.若程序操作进行了两次才停止,则x 的取值范围为__________. 三、解答题(19~21题每题10分,其余每题12分,共66分) 19.解下列不等式或不等式组,并把它们的解集在数轴上表示出来: (1)15-9y <10-4y ; (2)⎩⎪⎨⎪⎧x -x -22≤1+4x3,①1+3x >2(2x -1).②20.已知关于x ,y 的二元一次方程组⎩⎨⎧2x -3y =5,x -2y =k的解满足x >y ,求k 的取值范围.21.【2022·成都】随着“公园城市”建设的不断推进,成都绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是18 km/h ,乙骑行的路程s (km)与骑行的时间t (h)之间的关系如图所示.(1)直接写出当0≤t ≤0.2和t >0.2时,s 与t 之间的函数表达式. (2)何时乙骑行在甲的前面?22.(1)解不等式5x +2≥3(x -1),并把它的解集在数轴上表示出来;(2)写出一个实数k ,使得不等式x <k 和(1)中的不等式组成的不等式组恰有3个整数解.23.【新考法题】我们可以利用学习“一次函数”时的相关经验和方法来研究函数y =|x|的图象和性质.(1)请完成下列步骤,并画出函数y=|x|的图象.①列表:x…-3 -2 -1 0 1 2 3 …y… 3 1 1 2 3 …②描点;③连线.(2)观察图象,当x________0时(填“>”“<”或“=”),y随x的增大而增大.(3)根据图象,不等式|x|<12x+32的解集为__________.24.【2022·三门峡一模】国家为了鼓励新能源汽车的发展,实行新能源积分制度,积分越高获得的国家补贴越多.某品牌的“4S”店主销纯电动汽车A(续航600千米)和插电混动汽车B,两种主销车型的有关信息如下表:车型纯电动汽车A(续航600千米) 插电混动汽车B 进价(万元/辆) 25 12售价(万元/辆) 28 16新能源积分(分/辆) 0.012R+0.8(其中R表示续航里程)2购进数量(辆) 10 25(1)3月份该“4S”店共花费550万元购进A,B两种车型,且全部售出共获得新能源积分130分,设购进A,B型号的车分别为x,y辆,则x,y分别为多少?(2)因汽车供不应求,该“4S”店4月份决定购进A,B两种车型共50辆,应环保的要求,所进车辆全部售出后获得新能源积分不得少于300分,已知每个新能源积分可获得3 000元的补贴,那么4月份如何进货才能使4S店获利最大?(获利包括售车利润和积分补贴)答案一、1.B 2.D 3.A 4.A 5.A 6.C 7.C 8.A 9.C 10.B二、11.x +2<6 12.a <3 13.-2<x <1 14.-1<m <3 15.-1,0,1 16.八四 17.318.2≤x <5 提示:由题意得⎩⎨⎧3x -1<14,3(3x -1)-1≥14,解得2≤x <5.三、19.解:(1)移项,得-9y +4y <10-15.合并同类项,得-5y <-5. 系数化为1,得y >1.不等式的解集在数轴上表示如图所示.(2)解不等式①,得x ≥45; 解不等式②,得x <3.所以原不等式组的解集为45≤x <3.不等式组的解集在数轴上表示如图所示.20.解:⎩⎨⎧2x -3y =5,①x -2y =k .②①-②,得x -y =5-k . ∵x >y ,∴x -y >0. ∴5-k >0,解得k <5.21.解:(1)s 与t 之间的函数表达式为s =⎩⎨⎧15t (0≤t ≤0.2),20t -1(t >0.2).(2)设a h 后乙骑行在甲的前面. 根据题意,得20a -1>18a , 解得a >0.5.答:0.5 h 后乙骑行在甲的前面. 22.解:(1)去括号,得5x +2≥3x -3.移项,得5x -3x ≥-3-2. 合并同类项,得2x ≥-5. 系数化为1,得x ≥-2.5. 用数轴表示解集如图所示.(2)∵实数k 使得不等式x <k 和(1)中的不等式组成的不等式组恰有3个整数解, ∴不等式组⎩⎨⎧x ≥-2.5,x <k 的解集为-2.5≤x <k .∵该不等式组恰有3个整数解,∴0<k ≤1. ∴k 可以为1.(答案不唯一) 23.解:(1)①2;0②③画函数图象如图所示.(2)>(3)-1<x <3 提示:如图,在同一平面直角坐标系中画出直线y =12x +32与y =|x |的图象,其交点的横坐标分别为-1,3.由图象可得,不等式|x |<12x +32的解集为-1<x <3. 24.解:(1)依题意得⎩⎨⎧25x +12y =550,(0.012×600+0.8)x +2y =130,解得⎩⎨⎧x =10,y =25.答:x 的值为10,y 的值为25.(2)设4月购进A 型车m 辆,则购进B 型车(50-m )辆, 依题意得⎩⎨⎧(0.012×600+0.8)m +2(50-m )≥300,50-m >0,解得1003≤m <50.设所进车辆全部售出后获得的总利润为w 万元,则w =(28-25)m +(16-12)(50-m )+0.3×[(0.012×600+0.8)m +2(50-m )]=0.8m +230,∵0.8>0,∴w 随m 的增大而增大,∴当m =49,即购进A 型车49辆,B 型车1辆时获利最大.。
第五章二元一次方程组综合训练北师大版2024—2025学年八年级上册

第五章二元一次方程组综合训练北师大版2024—2025学年八年级上册 夯实基础一.选择题(共6小题)1.已知下列方程组:(1)⎩⎨⎧-==23y y x ,(2)⎩⎨⎧=-=+4223y y x ,(3)⎪⎪⎩⎪⎪⎨⎧=--=+0131y x y x ,(4)⎪⎪⎩⎪⎪⎨⎧=-=+0131y x y x ,其中属于二元一次方程组的个数为( )A. 1B. 2C. 3D. 42.已知a b y x 352+与b a y x 4224--是同类项,则a b 的值为( )A. 2B. -2C. 1D. -13.已知方程组⎩⎨⎧-=-=+1242m ny x n y mx 的解是1{ 1x y ==-,那么m 、n 的值为( ) A. 1{ 1m n ==- B. 2{1m n == C. 3{ 2m n == D. 3{ 1m n == 4.三元一次方程组⎪⎩⎪⎨⎧=+=+=+651x z z y y x 的解是( )A.⎪⎩⎪⎨⎧===501z y xB.⎪⎩⎪⎨⎧===421z y xC.⎪⎩⎪⎨⎧===401z y xD.⎪⎩⎪⎨⎧===014z y x5.若方程组⎩⎨⎧=+=-+14346)1(y x y a ax 的解y x ,的值相等,则a 的值为( )A. -4B. 4C. 2D. 16.小亮的妈妈用28元钱买了甲、乙两种水果,甲种水果每千克4元,乙种水果每千克6元,且乙种水果比甲种水果少买了2千克,求小亮妈妈两种水果各买了多少千克?设小亮妈妈买了甲种水果x 千克,乙种水果y 千克,则可列方程组为( )A .B .C .D .二.填空题(共6小题)7.31172y x =+中,若132x =-,则y=_______. 8.由11960x y --=,用x 表示y ,得y=_______,y 表示x ,得x=_______.9.如果21{ 232x y x y +=-=,那么2426923x y x y +--+=_______. 10.如果213262310a b a b x y -++--=是一个二元一次方程,则a =__________, b =___________。
备考2023年中考数学二轮复习-一元二次方程根的判别式及应用-综合题专训及答案

备考2023年中考数学二轮复习-一元二次方程根的判别式及应用-综合题专训及答案一元二次方程根的判别式及应用综合题专训1、(2017盂.中考模拟) 某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:x …﹣3-﹣2 ﹣1 0 1 2 3 …y … 3 m ﹣1 0 ﹣1 0 3 …其中m=.(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;(3)观察函数图象,写出2条函数的性质;(4)进一步探究函数图象发现:①函数图象与x轴有个交点,所对应的方程x2﹣2|x|=0有个实数根;②方程x2﹣2|x|=2有个实数根.2、(2017长春.中考模拟) 已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0 (1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根分别为x1、x2,且满足x12+x22=10,求实数m的值.3、(2017新泰.中考模拟) 已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.(1)求k的取值范围;(2)若|x1+x2|=x1x2﹣1,求k的值.4、(2017林州.中考模拟) 已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0 (1)求证:无论k为任何实数,方程总有实数根;(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.5、(2017黄冈.中考模拟) 已知方程x2+2kx+k2﹣2k+1=0有两个实数根x1, x2.(1)求实数k的取值范围;(2)若x12+x22=4,求k的值.6、(2017鄂州.中考真卷) 关于x的方程x2﹣(2k﹣1)x+k2﹣2k+3=0有两个不相等的实数根.(1)求实数k的取值范围;(2)设方程的两个实数根分别为x1、x2,存不存在这样的实数k,使得|x1|﹣|x2|= ?若存在,求出这样的k值;若不存在,说明理由.7、(2016张家界.中考模拟) 使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0,可得x=1,我们就说1是函数y=x﹣1的零点.已知y=x2+kx﹣4(k为常数).(1)当k=0时,求该函数的零点;(2)证明:无论k取何值,该函数总有两个零点.8、(2017岳阳.中考真卷) 如图,抛物线y= x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣x﹣交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).(1)求抛物线的解析式;(2)当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.(3)设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.9、(2018广州.中考真卷) 已知抛物线。
海淀区11月进修
冯翠霞
化学
年级 活动内容 (请注明活动类型) 主讲人 刘湘 丁红霞 时间 地点 石油附中 参加对象 高一化学教师 化学高一 研究课 铝的化合物 铁的化合物 化学高二 教研活动 高二化学文科教学研究 化学高三 11月12日 星期二 上午8:30 进修学校 11月12日 任宝华 星期二 上午8:30 教材教法分析分层教研 三组学校代表 11月12日 基于考情学情分析的电解质溶液 星期二 及电化学复习策略 上午8:30 物质构成的奥秘单元整体设计 进修实验校 11月19日 (成果汇报) 王严 星期二 上午8:30 教材教法 农大附中 杨艳红 11月19日 第四章:生命中的基础有机化学物质进修实验校 高平 星期二 第五章:进入合成有机高分子化合物的时代 上午8:30 讲座 进修学校 11月19日 2013年高考分析和复习建议 支瑶 星期二 上午8:30
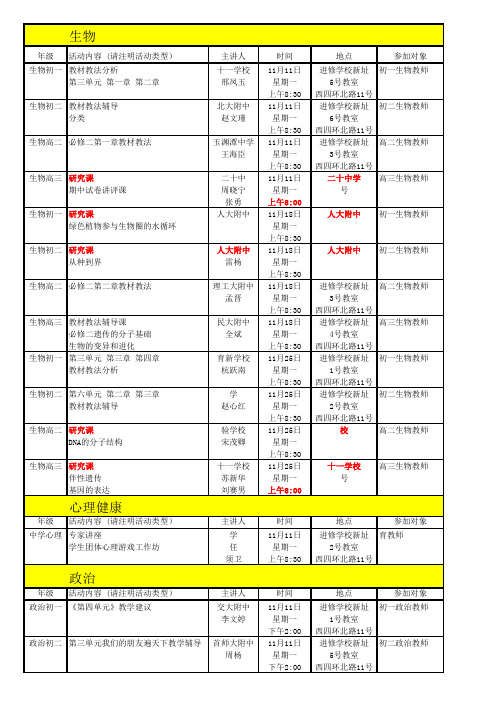
生物
年级 活动内容 (请注明活动类型) 主讲人 十一学校 邢凤玉 时间 地点 参加对象 生物初一 教材教法分析 第三单元 第一章 第二章 生物初二 11月11日 进修学校新址 初一生物教师 星期一 5号教室 上午8:30 西四环北路11号 教材教法辅导 北大附中 11月11日 进修学校新址 初二生物教师 第六单元第一章根据生物的特征进行分类 赵文瑾 星期一 6号教室 上午8:30 西四环北路11号 必修二第一章教材教法 玉渊潭中学 11月11日 进修学校新址 高二生物教师 王海臣 星期一 3号教室 上午8:30 西四环北路11号 研究课 二十中 11月11日 二十中学 高三生物教师 期中试卷讲评课 周晓宁 星期一 清河小营西路11号 张勇 上午8:00 研究课 人大附中 11月18日 人大附中 初一生物教师 绿色植物参与生物圈的水循环 星期一 上午8:30 研究课 人大附中 11月18日 人大附中 初二生物教师 从种到界 雷杨 星期一 上午8:30 必修二第二章教材教法 理工大附中 11月18日 进修学校新址 高二生物教师 孟晋 星期一 3号教室 上午8:30 西四环北路11号 教材教法辅导课 民大附中 11月18日 进修学校新址 高三生物教师 必修二遗传的分子基础 全斌 星期一 4号教室 生物的变异和进化 上午8:30 西四环北路11号 第三单元 第三章 第四章 育新学校 11月25日 进修学校新址 初一生物教师 教材教法分析 杭跃南 星期一 1号教室 上午8:30 西四环北路11号 第六单元 第二章 第三章 北达资源中学 11月25日 进修学校新址 初二生物教师 教材教法辅导 赵心红 星期一 2号教室 上午8:30 西四环北路11号 研究课 进修附属实验学校11月25日 进修附属实验学校高二生物教师 DNA的分子结构 宋茂卿 星期一 上午8:30 研究课 十一学校 11月25日 十一学校 高三生物教师 伴性遗传 苏新华 星期一 海淀区玉泉路66号 基因的表达 刘赛男 上午8:00
2023北京中考数学二模分类汇编——新定义(原卷版)

2023北京中考数学二模分类汇编——新定义1.(2023•海淀区二模)在平面直角坐标系xOy中,对于△OAB和点P(不与点O重合)给出如下定义:若边OA,OB上分别存在点M,点N,使得点O与点P关于直线MN对称,则称点P为△OAB的“翻折点”.(1)已知A(3,0),B(0,3).①若点M与点A重合,点N与点B重合,直接写出△OAB的“翻折点”的坐标;②P是线段AB上一动点,当P是△OAB的“翻折点”时,求AP长的取值范围;(2)直线与x轴,y轴分别交于A,B两点,若存在以直线AB为对称轴,且斜边长为2的等腰直角三角形,使得该三角形边上任意一点都为△OAB的“翻折点”,直接写出b的取值范围.2.(2023•西城区二模)在平面直角坐标系xOy中,给定圆C和点P,若过点P最多可以作出k条不同的直线,且这些直线被圆C所截得的线段长度为正整数,则称点P关于圆C 的特征值为k.已知圆O的半径为2,(1)若点M的坐标为(1,1),则经过点M的直线被圆O截得的弦长的最小值为,点M关于圆O的特征值为;(2)直线y=x+b分别与x,y轴交于点A,B,若线段AB上总存在关于圆O的特征值为4的点,求b的取值范围;(3)点T是x轴正半轴上一点,圆T的半径为1,点R,S分别在圆O与圆T上,点R 关于圆T的特征值记为r,点S关于圆O的特征值记为s.当点T在x轴正半轴上运动时,若存在点R,S,使得r+s=3,直接写出点T的横坐标t的取值范围.3.(2023•东城区二模)已知线段PQ是⊙G的弦,点K在直线PQ上.对于弦PQ和点K,给出如下定义:若将弦PQ绕点K逆时针旋转α(0°<α<180°)得到线段P′Q′,恰好也是⊙G的弦,则称弦PQ关于点K中心映射,点K叫做映射中心,α叫做映射角度.(1)如图1,点G是等边△ABC的中心,作⊙G交AB于点P,Q.在A,B,C三点中,弦PQ关于点中心胦射;(2)如图2,在平面直角坐标系xOy中,直线与x轴交于点E,与y轴交于点F,∠OEF的角平分线交y轴于点D.若⊙D与线段EF相交所得的弦关于点E中心映射,直接写出⊙D的半径r的取值范围;(3)在平面直角坐标系xOy中,⊙O的半径为2,线段MN是⊙O的弦.对于每一条弦MN,都有相应的点H,使得弦MN关于点H中心映射,且映射角度为60°.设点H到点O的距离为d,直接写出d的取值范围.4.(2023•朝阳区二模)在平面直角坐标系xOy中,对于图形M给出如下定义:将M上的一点(a,b)变换为点(a﹣b,a+b),M上所有的点按上述变换后得到的点组成的图形记为N,称N为M的变换图形.(1)①点(3,0)的变换点的坐标为;②直线y=x+1的变换图形上任意一点的横坐标为;(2)求直线y=2x+1的变换图形与y轴公共点的坐标;(3)已知⊙O的半径为1,若⊙O的变换图形与直线y=kx+2k(k≠0)有公共点,直接写出k的取值范围.5.(2023•丰台区二模)对于⊙W和⊙W的弦PQ,以PQ为边的正方形为PQ关于⊙W的“关联正方形”.在平面直角坐标系xOy中,已知点T(m,0),点M(m,﹣1),以点T为圆心,TM的长为半径作⊙T,点N为⊙T上的任意一点(不与点M重合).(1)当m=0时,若直线y=x+t上存在点在MN关于⊙T的“关联正方形”上,求t的取值范围;(2)若点A在MN关于⊙T的“关联正方形”上,点B(﹣m+2,3)与点A的最大距离为d,当d取最小值时,直接写出此时m和d的值.6.(2023•石景山区二模)在平面直角坐标系xOy中,对于点M(不与点O重合)和线段PQ,给出如下定义:连接OM,平移线段OM,使点M与线段PQ的中点M′重合,得到线段O′M”,则称点O′为线段PQ的“中移点”.已知⊙O的半径为1.(1)如图,点P(﹣1,0),点Q(m,4),①点M为⊙O与y轴正半轴的交点,,求m的值;②点M为⊙O上一点,若在直线y=x+3上存在线段PQ的“中移点”O′,求m的取值范围.(2)点Q是⊙O上一点,点M在线段OQ上,且OM=t(0).若P是⊙O 外一点,点O′为线段PQ的“中移点”,连接OO′,当点Q在⊙O上运动时,直接写出OO′长的最大值与最小值的差(用含t的式子表示).7.(2023•大兴区二模)在平面直角坐标系中,已知点A(﹣r,0),B(r,0).点P为平面内一点(不与点A,点B重合),若△ABP是以线段AB为斜边的直角三角形,则称点P 为线段AB的直点.(1)若r=1,①在点,P2(0,1),P3(﹣1,﹣1)这三个点中,点是线段AB的直点;②点P为线段AB的直点,点C(﹣1,1),求CP的取值范围;(2)点D在直线y=x﹣1上,若点D的横坐标x D满足2<x D<4,点P为线段AB的直点,且DP=1,直接写出r的取值范围.8.(2023•顺义区二模)在平面直角坐标系xOy中,已知点P,直线l与图形G.连接点P 与图形G上任意一点Q,取PQ的中点M,点M关于直线l的对称点为N,所有的对称点组成的图形W称为图形G关于点P及直线l的“对应图形”.已知点A(4,0).(1)对于直线l:x=a,若直线y=﹣2x﹣4关于点A及直线l的“对应图形”与直线y =﹣2x﹣4的交点在x轴的上方,求a的取值范围;(2)已知点B(0,4),C(﹣4,0),D(6,4),直线l:x=﹣1,⊙T的圆心T(t,0),半径为2.若存在⊙T关于点D及直线l的“对应图形“与△ABC的边有交点,直接写出t的取值范围.9.(2023•门头沟区二模)在平面直角坐标系xOy中,线段AB=4,点M,N在线段AB上,且MN=2,P为MN的中点,如果任取一点Q,将点Q绕点P顺时针旋转180°得到点Q′,则称点Q′为点Q关于线段AB的“旋平点”.(1)如图1,已知A(﹣1,0),B(3,0),Q(1,2),如果Q′(a,b)为点Q关于线段AB的“旋平点”,画出示意图,写出a的取值范围;(2)如图2,⊙O的半径为3,点A,B在⊙O上,点Q(1,0),如果在直线x=m上存在点Q关于线段AB的“旋平点”,求m的取值范围.10.(2023•昌平区二模)在平面直角坐标系xOy中,对于点P,点Q和直线l,点P关于l 的对称点P′,点Q是直线l上一点,将线段P′Q绕点P′逆时针旋转90°得到P′K,如果线段P′K与直线l有交点,称点K是点P关于直线l和点Q的“双垂点”.(1)若P(2,1),点K1(1,1),K2(1,0),K3(1,﹣2)中是点P关于x轴和点Q 的“双垂点”的是;(2)若点Q(0,5),点P,K是直线y=x+3上的点,点K是点P关于y轴和点Q的“双垂点”,求P点的坐标;(3)点P在以(0,t)为圆心,1为半径的圆M上,直线l:y=x+2,若圆M上存在点K是点P关于直线l和点Q的“双垂点”,直接写出t的取值范围.11.(2023•平谷区二模)在平面直角坐标系xOy中,对于△OAB,其中,B(2,0),给出如下定义:将OA边绕点O逆时针旋转60°得到线段OC,连接BC,BC与△OAB的过点A的高线交于点P,将点P关于直线y=kx+b(k≠0)对称得到点Q,我们称Q为△OAB的留缘点.(1)若k=1,b=0,请在图中画出△OAB的留缘点Q,并求出点Q的坐标;(2)已知M(﹣3,0),N(﹣3,5),若线段MN上存在△OAB的留缘点,求b的取值范围.12.(2023•房山区二模)在平面直角坐标系xOy中,有图形W和点P,我们规定:若图形W上存在点M、N(点M和N可以重合),满足PM=PN,其中点P′是点P关于x轴的对称点,则称点P是图形W的“对称平衡点”.(1)如图1所示,已知,点A(0,2),点B(3,2).①在点P1(0,1),P2(1,﹣1),P3(4,1)中,是线段AB的“对称平衡点”的是;②线段AB上是否存在线段AB的“对称平衡点”?若存在,请求出符合要求的“对称平衡点”的横坐标的范围,若不存在,请说明理由.(2)如图2,以点A(0,2)为圆心,1为半径作⊙A.坐标系内的点C满足AC=2,再以点C为圆心,1为半径作⊙C,若⊙C上存在⊙A的“对称平衡点”,直接写出C点纵坐标y c的取值范围.13.(2023•燕山二模)在平面直角坐标系xOy中,⊙O的半径为2.对于直线l和线段BC,给出如下定义:若将线段BC关于直线l对称,可以得到⊙O的弦B′C(B′,C′分别是B,C的对应点),则称线段BC是以直线l为轴的⊙O的“关联线段”,例如,图1中线段BC是以直线l为轴的⊙O的“关联线段”.(1)如图2,点B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.①在线段B1C1,B2C2,B3C3中,以直线l1:y=x+4为轴的⊙O的“关联线段”是;②在线段B1C1,B2C2,B3C3中,存在以直线l2:y=﹣x+b为轴的⊙O的“关联线段”,求b的值;(2)已知直线l3:y=﹣x+m(m>0)交x轴于点A,在△ABC中,AB=6,BC=2,若线段BC是以直线l3为轴的⊙O的“关联线段”,直接写出m的最大值与最小值,以及相应的AC的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有鑑於泰北華人村落地處偏遠,部份 有鑑於泰北華人村落地處偏遠, 村落師資嚴重缺乏, 村落師資嚴重缺乏,許多當地教師於 高中畢業後,隨即投入教職工作, 國、高中畢業後,隨即投入教職工作, 如此年輕有為之青年教師卻沒有持續 進修學習之機會與課程, 進修學習之機會與課程,許多老師在 畢業後即等於停止進修, 畢業後即等於停止進修,打罵教育仍 是一般泰北教師最拿手之之教育方式, 是一般泰北教師最拿手之之教育方式, 雖泰北孩童學生從不曾有反抗、 雖泰北孩童學生從不曾有反抗、辱罵 或毆打老師之情況發生, 或毆打老師之情況發生,但對學生之 學習興趣培養, 學習興趣培養,閱讀或讀書習慣之養 卻有不良之影響。 成,卻有不良之影響。
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
黃書亞:「我跟他說要擦手的,然後 他就拿肥皂給我。」記者:「但是你 要的是衛生紙?」黃書亞:「對對對, 我就說不是這個。」 短短1個月的義工行,黃書亞和妹妹體 驗深刻,決定下個月再提出申請,繼續 到泰北服務,他們還說,如果有機會的 話,希望一輩子都待在那裡,照顧這群 等待救援的弱勢族群。
送愛到泰北
去年七月底范老師回台北,拿了兩大袋 的手工布包來找我,她說,這是泰北阿 卡族少女做的。由於當地是著名的金三 角毒品之鄉,家境貧窮或父母本身吸毒 的,這些少女常被賣到色情場所以改善 家中經濟。一位外國神父,不忍年輕的 生命遭遇如此不幸,將她們集合在一起, 指導她們做手工藝品,然後將作品拿到 山下城市義賣,再把收入聘請老師教她 們讀書識字,並苦口婆心地勸告少女們, 再窮再苦絕不販賣自己的身體。
泰北文教服務概況報導
;其二為49年後從中國逃出來的人, 越過邊界進入泰北山區。泰國政府面 對這群華人發給他們難民證,畫區域 給他們居住,所以這些華人只能居住 在山區,很難有進一步的發展。
泰北文教服務概況報導
泰北山區大約有一百多個華人難民村,生活 皆多普遍貧苦落後;加上這些華人村地處於邊境交 界地帶,資訊傳遞不易、少有外來文化刺激,居民教 育程度及基本醫療知識生活自理能力低,也因此無 法教育下一代子女。 「無國籍難民」,一個嶄新的名詞,被冠在了他們 的身上,但是,曾幾何時他們都是有國籍、身份、 家園和希望的人們,如今,他們在甚麼都失去的同 時,還要遭受到旁人的歧視…。
泰北文教服務項目
認養學生學費 認養教師薪資補助 營養餐補助 師資培訓 學校行政補助 捐助電腦、電腦師、青年志工的最大福報
送愛到泰北
一個偶然,在報上看到一則新聞,經 常利用寒暑假前往泰北中文學校服務 的范老師,在退休後,為了能更進一 步照顧孤苦貧困的華人小孩,毅然變 賣台北家產,隻身到泰北的清萊省開 辦一所育幼院,讓他們可以接受良好 完整的教育,由於孩子們都來自鄉下 破碎家庭,財力窘困,所以范老師每 年兩次回台義賣,募集教育經費和圖 書、文具、衣物等。
泰北(金三角) 泰北(金三角)海外服務 Northern-Thai (Golden Triangle) Overseas Voluntary Service
泰北(金三角) 泰北(金三角)海外服務 Northern-Thai (Golden Triangle) Overseas Voluntary Service
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
記者:「那裡買來的嗎?」泰北義工黃 書亞:「對!那裡買回來的。」
拿出籐球,這是新竹國三女學生黃書亞, 在泰北當義工期間,帶回來紀念品。她 說過去這1個月,和妹妹跑到泰北,照 顧貧困家庭,過程點滴在心頭
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
送愛到泰北
這份工作看似容易,沒什麼多大的麻煩,實 際上也帶給我不小的挫折和煩惱。有些人好 心拎來一整袋的衣物、書籍,放在我辦公室 的桌上,常常等到我下班的時候,桌上桌下 已堆積如山,坐在位子上,兩腳都不知該往 那兒擺,只得趕忙稍做分類和整理。卻又發 現,有的衣服已經泛黃甚至破舊,有的書本 也一張一張準備分家了,回收的鉛筆只有無 名指的長度。想想:花了錢,寄的是這樣的 物品給人,對方收到後,會是什麼樣的心情 呢?將心比心之後,我也就果斷的做了取捨, 沒寄出去又還可以用的,再請班上小朋友幫 忙消耗。歷經幾個回合,現在的心境比較能 包容而不是犯嘀咕,整理裝箱的時候也能心 平氣和,不再視為負擔。
送愛到泰北
范老師感動神父的悲愍,所以也從泰北扛了 好幾袋回來,希望找有心人幫忙義賣;她找 上了我,可是我卻很困難地搖搖頭拒絕了。 寄寄包裹尚可勝任,拿著手工布包賣給人家, 我實在開不了口,一點勇氣都沒有。范老師 笑一笑,她說我可以試一試,但不要有壓力, 助人是很快樂的事。我稍稍想了一下:「如 果我是山上的少女,多麼希望有人可以從旁 助我一臂之力。」念頭一轉,我接下了范老 師手中的袋子,開始我的義賣處女秀。
美麗的世界由你我來開創
Q2: 成為台灣世界青年志工協會的志 成為台灣世界青年志工協會的志 台灣世界青年志工協會 或會員), 工(或會員 ,需要繳會費嗎? 或會員 需要繳會費嗎? 不用! 不用!我們歡迎有志青年加入並 參與我們志願服務的工作, 參與我們志願服務的工作,無須繳交 任何費用或會費。試想, 任何費用或會費。試想,若空有一群 固定繳會費的會員, 固定繳會費的會員,但卻不參與志願 服務的活動,這絕非我們所樂見的。 服務的活動,這絕非我們所樂見的。
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
泰北文教服務宗旨
服務宗旨: 1.『心懷大愛做小事』幫助『他們』能自力 更生。 2.為協助華人村達成中華文化傳承目標,召 募志工深入泰北深山叢林,尋找最貧困的村 莊和學校去幫助他們;同時對泰北難民村展 開醫療、技訓、修路、建校舍、接電工程、 認養教師和學生、探訪家庭、各項濟貧、扶 困等關懷工作。
送愛到泰北
經過進一步的接觸和了解,我發現了 源頭,很興奮地找了也是非常熱心公 益的設備組長一起共襄盛舉。我告訴 自己每個月少買一件衣服,就可以省 下八百元,把募來的教科書、文具、 衣物等,湊齊了二十公斤, 用菜籃車 拖到郵局,裝箱打包以後,扛上櫃檯 再寄出。就是這樣的因緣,一趟又一 趟,一箱又一箱,開啟了「送愛到泰 北」,連郵局的工作人員知道了這個 緣起,服務時不僅用心也更有耐心, 還不斷地讚嘆隨喜。
黃書亞:「他們的水龍頭就掛在牆上, 所以他們就直接站過去,然後就直接站 在那邊,不脫衣服洗澡的。」 深入泰北地區,黃書亞和妹妹當義工老 師,教小朋友學中文,剛開始不能適應 當地氣侯和食物,還出現頭痛、身體不 舒服的狀況。
勇哉! 勇哉!國三女 到泰北照料貧困童 記者:侯力元 新竹 報導
黃書亞:「就是因為一下下雨,一下出 太陽,一下冷一下熱,所以很難過,就 頭痛、頭暈這樣,喉嚨發炎。」 泰北的生活困苦,每餐一菜一湯,有的 時候,白飯配個辣椒和鹽巴就是一餐, 吃不飽的生活,姐妹倆第一次體驗,不 過最讓她們困擾的是溝通問題,不會講 泰語的他們,只能比手劃腳,結果還鬧 出笑話。
服務內容: 1、全程住宿當地服務據點,體驗當地生活 及文化。 2、協助當地中文教育、農作、新年活動及 衛生教育知識傳遞等。 3、依當地需求機動性服務。 服務對象: 泰北服務遊學團--泰北華人戒毒村失依兒童 及青少年。 招生對象:15歲以上之學生或社會大眾。15 ~18歲者鼓勵家長陪同參與。
泰北(金三角) 泰北(金三角)海外服務 Northern-Thai (Golden Triangle) Overseas Voluntary Service 教師活動知能研習 Teacher Activity Training 教師活動知能研習活動主要之內容為利用團 康活動之教學與創作, 康活動之教學與創作,有助當地教師在教學 課程能有更加生動活潑, 課程能有更加生動活潑,提高孩童學習中文 之興趣。課程內容包括:團體動力、 之興趣。課程內容包括:團體動力、傳統唱 音樂唱跳、掌聲歡呼、民俗遊戲、基本/ 跳、音樂唱跳、掌聲歡呼、民俗遊戲、基本 團體舞蹈、啦啦隊舞蹈、綜藝舞蹈、 團體舞蹈、啦啦隊舞蹈、綜藝舞蹈、學生輔 導教育、校園美化及班級經營、運動武術、 導教育、校園美化及班級經營、運動武術、 團體競賽/遊戲 肢體開發、戲劇實務、 遊戲、 團體競賽 遊戲、肢體開發、戲劇實務、舞台 實務、主持技巧、相聲、脫口秀、 實務、主持技巧、相聲、脫口秀、360度行 度行 動劇、默劇等課程。 動劇、默劇等課程。
送愛到泰北
在八月初的返校日,我將各式各樣的 布包提到了學校,準備大顯身手,沒 想到前一晚的沙盤推演,在看到了同 事之後,我不但說不出話來,還把布 包藏到桌底下,深怕被人發現我在做 生意。眼看著時間一分一秒的過去, 我除了乾著急,使不出任何招式,真 懊惱自己的不量力。
送愛到泰北
也不知過了多久,突然念頭一閃,找個伴一 起來吆喝吧,不要獨自去承擔那份緊張和尷 尬了。果真馬上出現戲劇性的變化,同事們 紛紛好奇探個頭,手裡挑來撿去,跟著問東 問西,我大略描述了泰北阿卡族少女的情況, 沒一會兒功夫,很多人慷慨認購,布包一個 一個的少了,我的心情也漸漸地開了。因為 這個開端,想幫助他人的信心和勇氣增強了, 所以接下來的義賣活動就很順利地推展出去, 善心不斷地傳送擴大。
美麗的世界由你我來開創
常見問題: 常見問題: Q1: 如何加入台灣世界青年志工協會 如何加入台灣世界青年志工協會 志工行列? 志工行列? 只要你曾報名參與協會之志願服 務活動,即是我們的生力軍喔! 務活動,即是我們的生力軍喔!亦可 與協會聯絡,留下聯絡資料, 與協會聯絡,留下聯絡資料,若有新 活動消息, 活動消息,便會馬上透過電子郵件或 寄信給你。 寄信給你。
綜合領域北新國中巡迴輔導二
服務學習:泰北經驗分享 報告人:安和國中謝明勳老師 2007.04.02
泰北文教服務概況報導
緣起: 在泰北、緬甸交界區散居著一群人, 他們有著和我們一樣的皮膚,留著和 我們一樣的血液 ,卻過著和我們截然不同的生活。 這些人的來源有二,其一為當時 國民政府部隊,從中國雲南撤入泰國 北部,安營與當地的 少數民族通婚,這些就是泰北華人難 民村的開闢者
