2013上半年运筹学第一次作业
运筹学1

16/10
若将目标函数变为max Z = 2x1 + 4x2 ,则表示目标函数的等值线与约束 条件x1 + 2x2 ≤8的边界线x1 + 2x2 = 8平行。当Z值由小变大时,与线段Q 2Q3重合,如图1.3所示,线段Q2Q3上任意一点都使Z取得相同的最大值, 即这个线性规划问题有无穷多最优解。
17/10
运筹学第一次作业指导
储宜旭
이 문서는 나눔글꼴로 작성되었습니다. 설치하 기
运筹学
2/10
3/10
4/10
5/10
实际问题线性规划模型的基本步骤: (1) 确定决策变量。这是很关键的一步,决策变量选取 得当,不仅会使线性规划的数学模型建得容易,而且 求解比较方便。 (2) 找出所有限制条件,并用决策变量的线性等式或不 等式来表示,从而得到约束条件。一般可用表格形式 列出所有的限制数据,然后根据所列出的数据写出相 应的约束条件,以避免遗漏或重复所规定的限制要求。 (3) 把实际问题所要达到的目标用决策变量的线性函数 来表示,得到目标函数,并确定是求最大值还是最小 值。
10/10
11/10
12/10
线性规划问题的图解法
为了给后面的线性问题的基本理论提供较直观的几何说明, 先介绍线性规划问题的图解法。 我们把满足约束条件和非负条件的一组解叫做可行解,所有 可行解组成的集合称为可行域。 图解法的一般步骤如下。 (1) 建立平面直角坐标系。 (2) 根据线性规划问题的约束条件和非负条件画出可行域。 (3) 作出目标函数等值线Z = c(c 为常数),然后根据目标函 数平移等值线至可行域边界,这时目标函数与可行域的交点 即最优解。
运筹学第一次作业

练习一1、 某厂接到生产A 、B 两种产品的合同,产品A 需200件,产品B 需300件。
这两种产品的生产都经过毛坯制造与机械加工两个工艺阶段。
在毛坯制造阶段,产品A 每件需要2小时,产品B 每件需要4小时。
机械加工阶段又分粗加工与精加工两道工序,每件产品A 需粗加工4小时,精加工10小时;每件产品B 需粗加工7小时,精加工12小时。
若毛坯生产阶段能力为1700小时,粗加工设备拥有能力为1000小时,精加工设备拥有能力为3000小时。
又加工费用在毛坯、粗加工、精加工时分别为每小时3元、3元、2元。
此外在粗加工阶段允许设备可进行500小时的加班生产,但加班生产时间内每小时增加额外成本4、5元。
试根据以上资料,为该厂制订一个成本最低的生产计划。
解:设正常生产A,B 产品数12,x x ,加班生产A,B 产品数34,x x13241324341324min 3(22444477)7.5(47)2(10101212)z x x x x x x x x x x x x x x =+++++++++++++.s t 13241212121220030024170047100010123000475000i x x x x x x x x x x x x x +≥⎧⎪+≥⎪⎪+≤⎪+≤⎨⎪+≤⎪+≤⎪⎪≥⎩且为整数,i=1,2,3,42、 对某厂I ,Ⅱ,Ⅲ三种产品下一年各季度的合同预订数如下表所示。
时为15000小时,生产I 、Ⅱ、Ⅲ产品每件分别需时2、4、3小时。
因更换工艺装备,产品I 在2季度无法生产。
规定当产品不能按期交货时,产品I ,Ⅱ每件每迟交一个季度赔偿20元,产品Ⅲ赔偿10元;又生产出来产品不在本季度交货的,每件每季度的库存费用为5元。
问:该厂应如何安排生产,使总的赔偿加库存的费用为最小(要求建立数学模型,不需求解)。
解:设x ij 为第j 季度产品i 的产量,s ij 为第j 季度末产品i 的库存量,d ij 为第j 季度产品i 的需求量。
运筹学第一次作业

先用单纯形法求出最优解,然后分析在下列各种条件下,最优解分别有什么变化?(1)约束条件①的右端常数由20变为30;(2)约束条件②的右端常数由90变为70;(3)目标函数中X 3的系数由13变为8;(4) X 1的系数列向量由 变为; (5)增加一个约束条件③⎪⎩⎪⎨⎧≥≤++≤++-++-=0x ,x ,x )2(90x 10x 4x 12)1(20x 3x x .t .s x 13x 5x 5Z max 321321321321⎪⎪⎭⎫ ⎝⎛-121⎪⎪⎭⎫ ⎝⎛50)3(50x 5x 3x 2321≤++在上述线性规划问题的第①、②个约束条件中分别加入松弛变量X4,X5得列出此问题的初始单纯形表,并进行迭代计算,由表可知,线性规划问题的最优解X*=(0,20,0,0,10)T,目标函数最优值z*=5×20=100。
(1) 列出单纯形表,并利用对偶单纯形法求解,由表可知,线性规划问题的最优解变为X*=(0,0,9,3,0)T,目标函数最优值z*=13×9=117。
(2)列出单纯形表,并利用对偶单纯形法求解由表可知,线性规划问题的最优解变为X*=(0,5,5,0,0)T,目标函数最优值z*=5×5+13×5=90。
(3)x3为非基变量,其检验数变为σ3=8-5×3-0×(-2)=-7<0,所以线性规划问题的最优解不变。
(4) x1在最终单纯形表中的系数列向量变为P'1=B-1,从而x1在最终单纯形表中的检验数变为(X1X2X3)=(0200)f max=100所以线性规划问题的最优解不变(5)增加一个约束条件:2x1+3x2+5x3≤50。
在约束条件③中加入松弛变量x6,得2x1+3x2+5x3+x6=50,加入原单纯形表,并进行迭代计算。
由表中计算结果可知,目标函数最优值。
运筹学第1次及目标规划

第一次实验要求:建模并求解(excel规划求解)1、合理下料问题.现要做100套钢架,每套由长2.8米、2.2米和1.8米的元钢各一根组成,已知原材料长6.0米,问应如何下料,可以使原材料最省?如果每套钢架由2.8米的元钢1根、2.2米的元钢2根、1.8米的元钢3根,则如何修改数学模型?2、配料问题.某工厂要用三种原材料甲、乙、丙混合调配出三种不同规格的产品A、B、C.已知产品的规格要求、产品单价、每天能供应的原材料数量及原材料单价(分别见表1和表2),问该厂应如何安排生产,使利润收入为最大?表1表23、连续投资问题.某部门在今后五年内考虑给下列项目投资,已知:项目A,从第一年到第四年每年年初需要投资,并于次年末回收本利115%;项目B,第三年初需要投资,到第五年末能回收本利125%,但规定最大投资额不超过4万元;项目C,第二年初需要投资,到第五年末能回收本利140%,但规定最大投资额不超过3万元;项目D,五年内每年初可购买公债,于当年末归还,并加利息6%.该部门现有资金10万元,问它应如何确定给这些项目每年的投资额,使到第五年末拥有的资金的本利总额为最大?4、购买汽车问题.某汽车公司有资金600 000元,打算用来购买A、B、C三种汽车.已知汽车A每辆为10 000元,汽车B每辆为20 000元,汽车C每辆为23 000元.又汽车A每辆每班需一名司机,可完成2 100吨·千米;汽车B每辆每班需两名司机,可完成3 600吨·千米;汽车C每辆每班需两名司机,可完成3 780吨·千米.每辆汽车每天最多安排三班,每个司机每天最多安排一班.限制购买汽车不超过30辆,司机不超过145人.问:每种汽车应购买多少辆,可使每天的吨·千米总数最大?5、人员安排问题.某医院根据日常工作统计,每昼夜24小时中至少需要如下表所示数量的护士,护士们分别在各时段开始时上班,并连续工作8小时,向应如何安排各个时段开始上班工作的人数,才能使护士的总人数最少?目标规划实验要求:建模并求解(1-5选2个,6-12选3个)【案例6.1】升级调资问题.某高校领导在考虑本单位员工的升级调资方案时,依次考虑如下的目标:(1)年工资总额不超过900万元;(2)每级的人数不超过定编规定的人数;(3)副教授、讲师、助教级的升级面尽可能达到现有人数的20%;助教级不足编制的人数可直接聘用应届毕业研究生.教授级人员中有10%要退休.有关资料见表6.6,请为该领导拟定满意的方案.表6.6【案例6.2】农场生产计划问题.友谊农场有3万亩农田,欲种植玉米、大豆和小麦三种农作物.各种作物每亩需施化肥分别为0.12吨、0.20吨、0.15吨.预计秋后玉米每亩可收获500kg,售价为0.24元/千克,大豆每亩可收获200千克,售价为1.20元/千克,小麦每亩可收获300千克,售价为0.70元/千克.农场年初规划时考虑如下几个方面:P1:销售收入不低于350万元;P2:总产量不低于1.25万吨;P3:小麦产量以0.5万吨为宜;P4:大豆产量不少于0.2万吨;P5:玉米产量不超过0.6万吨;P6:农场现能提供5 000吨化肥;若不够,可在市场高价购买,但希望高价采购量愈少愈好.试就该农场生产计划建立数学模型.【案例6.3】多目标运输问题.已知有三个产地给四个销地供应某种产品,产销地之间的供需量和单位运价,见表6.7有关部门在研究调运方案时依次考虑以下七项目标,并规定其相应的优先等级:P1:B4是重点保证单位,必须全部满足其需要;P2:A3向B1提供的产量不少于120;P3:每个销地的供应量不小于其需要量的80%;P4:所订调运方案的总运费不超过最小运费调运方案的20%;P5:因路段的问题,尽量避免安排将A2的产品运往B4;P6:给B1和B3的供应率要相同;P7:力求总运费最省.试求满意的调运方案.表6.7【案例6.4】电台节目安排问题.一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间.据有关规定,该台每天允许广播12小时,其中商业节目用以赢利,每分钟可收入250美元,新闻节目每分钟需支出40美元,音乐节目每播一分钟费用为17.50美元.根据规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目.问每天的广播节目该如何安排?优先级如下:P1:满足规定要求;P2:每天的纯收入最大.试建立该问题的目标规划模型.【案例6.5】混合配方问题.某酒厂用三种等级的原料酒I、II、III兑制成三种混合酒(A、B、C牌).这些原料酒的供应量受到严格限制,它们每日的供应量分别为1 500千克,2 000千克和1 000千克,供应价格分别为18元/千克,13.5元/千克和9元/千克.三种混合酒的配方及售价见表6.8.表6.8厂长确定:首先必须按规定比例兑制混合酒;其次是获利最大;再次是混合酒A每天至少生产2 000千克.试建立数学模型.6、公司决定使用100万元新产品开发基金开发A,B,C三种新产品.经预测估计,开发A,B,C三种新产品的投资利润率分别为5%,6%,8%.由于新产品开发有一定风险,公司研究后确定了如下优先顺序目标:第一,A产品至少投资30万元;第二,为分散投资风险,任何一种新产品的开发投资不超过开发基金总额的35%;第三,应至少留有10%的开发基金,以备急用;第四,使总的投资利润最大.试建立投资方案的目标规划模型.7、某电子制造公司生产两种立体声耳机,一种为普及型,装配一个需1小时,另一种为豪华型,每个装配时间为2小时.正常的装配作业每周限定为40小时.市场调查表明,每周生产量普及型不超过30件,豪华型不超过15件.净利润普及型为每件40元,豪华型每件60元.已知公司经理对优先级的排序如下:P1:总利润最大;P2:装配线尽可能少加班;P3:销售耳机尽可能多;试建立此问题的目标规划模型.8、某工厂生产甲、乙两种产品,单位甲产品可获利6元,单位乙产品可获得4元.生产过程中每单位甲、乙产品所需机器台时数分别为2和3个单位,需劳动工时数分别为4和2个单位.该厂在计划期内可提供100个单位的机器台时数和120个劳动工时数,如果劳动力不足尚可组织工人加班.该厂制定了如下目标:第一目标:计划期内利润达180元;第二目标:机器台时数充分利用;第三目标:尽量减少加班的工时数;第四目标:甲产品产量达22件,乙产品产量达18件.上述四个目标分别为四个不同的优先等级.请列出该目标规划问题的数学模型,并用图解法、单纯形法(表格形式)分别求解之.9、已知单位牛奶、牛肉、鸡蛋中的维生素及胆固醇含量等有关数据如下表,如果只考虑三种食物,并且设立了下列三个目标:第一,满足三种维生素的每日最小需要量;第二,使每日摄入的胆固醇最少;第三,使每日购买食品的费用最少.要求建立问题的目标规划模型.10、某工厂生产白布、花布两种产品,其生产率皆为1 000米/小时;其利润分别为1.5元/米和2.5元/米;每周正常生产时间为80小时(加班时间不算在内).第一目标:充分利用正常生产时间进行生产;第二目标:每周加班时数不超过10小时;第三目标:销售花布要求达到70 000米,白布达45 000米;第四目标:每周利润达15万元.试建立上述问题的数学模型.11、某工厂生产唱机和录音机两种产品,每种产品均需经A、B两个车间的加工才能完成.表中给出了全部已知条件,要求尽可能实现的目标有以下六个:第一目标:仓库费用每月不超过4 600元;第二目标:唱机每月售出50台;第三目标:勿使A、B车间停工(权系数由两车间的生产费用决定);第四目标:车间A加班不超过20小时;第五目标:录音机每月售出80台;第六目标:车间A、B加班时数的总和要限制(权系数由两车间的生产费用决定).试列出该问题的目标规划数学模型.12、某公司下设三个工厂,生产同一种产品,现在要把三个工厂生产的产品运送给四个订户.工厂的供应量、订户的需求量以及从三个工厂到四个订户的单位运费如表所示(表格中方格内数字为单位运费).现在要作出一个产品调运计划,依次满足下列各项要求:p1:订户4的订货量首先要保证全部予以满足;p2:其余订户的订货量满足程度应不低于80%;p3:工厂3调运给订户1的产品量应不少于15个单位;p4:因线路限制,工厂2应尽可能不分配给订户4;p5:订户1和订户3的需求满足程度应尽可能平衡;p6:力求使总运费最小.试建立上述问题的目标规划模型.。
运筹学考试复习资料

《运筹学课程》第一次作业 第一题:某工厂生产某一种型号的机床,每台机床上需要2.9m 、2.1m 、1.5m 的轴、分别为1根、2根、1根。
这些轴需用同一种圆钢制作,圆钢的长度为7.4m 。
如果要生产100台机床,问应如何安排下料,才能用料最省?试建立其线性规划模型。
第二题:用图解法求解,线性规划问题⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0,52426155..2max 212121221x x x x x x x t s x x Z 第一题:求以下各图的最小支撑树(1)(2)第二题:表1《运筹学课程》第二次作业第一题:用图解法求解下列线性规划问题,并指出问题是具有唯一最忧解、多重最优解、无界解或无可行解.第二题:将下列线性规划模型的一般形式转化为标准型(1)()⎪⎪⎩⎪⎪⎨⎧∞-∞∈≥≤++=+-≥+-+-=,321321321321321,0,1036345..32max x x x x x x x x x x x x t s x x x Z (2)()⎪⎩⎪⎨⎧-∞∞∈≥≤-≤-+--=++-+-=,,0,0824..22min 321321321321x x x x x x x x x t s x x x Z第三题:用单纯型法求解线性规划问题,并用图解法进行验证注:按照我上课所讲例题的求解步骤进行(参照课件),好好理解单纯型法的基本原理,做题时先不要使用单纯型法的表格形式。
第四题:自己亲自动手推到一下单纯型法中的检验数,参照课件中29-31页。
第一题:(1)求点v 1到图中个点的最短路;(2)指出v 1不可到达哪些点。
第二题:已知某地区的交通网络如图所示,图中点代表居民小区,边表示公路,l ij为小区间公路距离,问该地区中心医院应建在哪个小区较为合适。
第一题:用最简单方法求解该线性规划问题(提示:求出该问题的对偶问题,然后用单纯型法求解对偶问题,可减少计算量,从最后一张单纯形表获得原问题的最优解)第二题:表1第三题:已知产销平衡问题,见表2表2分别用“最小元素法”和“伏格尔法”求该问题的初始基可行解,并求出这两个基可行解的目标函数值。
运筹学第一次作业详解
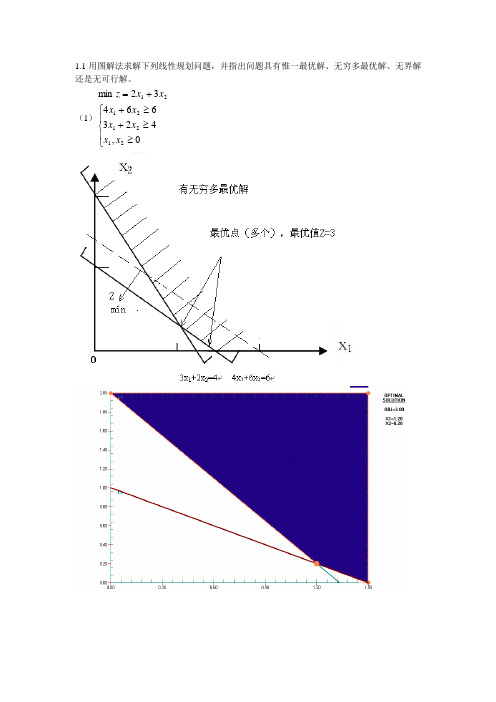
1.1用图解法求解下列线性规划问题,并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。
(1)⎪⎩⎪⎨⎧≥≥+≥++=0,42366432min 21212121x x x x x x x x z(2)⎪⎩⎪⎨⎧≥≥+≤++=0,12432223max 21212121x x x x x x x x z(3)⎪⎩⎪⎨⎧≤≤≤≤≤++=83105120106max 212121x x x x x x z(4)⎪⎩⎪⎨⎧≥≤+-≥-+=0,2322265max 21212121x x x x x x x x z1.2将下述线性规划问题化成标准形式。
(1)⎪⎪⎩⎪⎪⎨⎧≥≥-++-≤+-+-=-+-+-+-=无约束4,03,2,12321422245243min 4321432143214321x x x x x x x x x x x x x x x x x x x x z解:令z z -=',''4'44x x x -=⎪⎪⎩⎪⎪⎨⎧≥=-+-++-=+-+-+=-+-+-+-+-=0,,,,,,232142222455243'max 65''4'43216''4'43215''4'4321''4'4321''4'4321x x x x x x x x x x x x x x x x x x x x x x x x x x x x x z (2)⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束3,02,016324322min 21321321x x x x x x x x x x x x z解:令z z -=',1'1x x -=,''3'33x x x -=⎪⎩⎪⎨⎧≥=++-+=-+++-+=0,,,,6243322'max 4''3'32'14''3'32'1''3'32'1''3'32'1x x x x x x x x x x x x x x x x x x z1.3对下述线性规划问题找出所有基解,指出哪些是基可行解,并确定最优解。
2013《运筹学》考试题及其答案

T()
15
{10}
oo
11
00
00
6
P( )+Wi
j
10+0
10
+4
10+0
10+0
10+0
T()
15
14
{11}
00
00
7
P( )+Wi
j
11+0
11+0
11+0
11+9
T()
15
{14}
00
20
8
P( )+Wi
j
14+o
14+
1
14+o
T()
{15}
{15}
11
9
P( )+wi
j
15+
4
T()
0
1
0
3/5
1/5
0
6/5
0
X3
0
0
1
1
1
1
0
rj(-z)
0
0
0
1/5
—M+7/5
——M
18
/5
表中所有检验数rj0,根据最优解定理,问题存在唯一的最优解X(3,§,0,0,0,0)t,目标函
5 5
数的最优值maxz43 618。
555
二、试用表上作业法求解下列运输问题的最优解。
'产
B1
B2
B3
B4
初始值
T(
)
{0}
00
00
oo
oo
OO
oo
运筹学一试题1

(可不抄题,答案必须写在我校统一配发的专用答题纸上!)一、 (13分) 某汽车公司有资金600000元,打算用来购买A 、B 、C 三种汽车。
已知汽车A 每辆为10000元,汽车B 每辆为20000元,汽车C 每辆为23000元。
又汽车A 每辆每班需一名司机,可完成2100吨-公里;汽车B 每辆每班需两名司机,可完成3600吨-公里;汽车C 每辆每班需两名司机,可完成3780吨-公里。
每辆汽车每天最多安排三班,每个司机每天最多安排一班。
限制购买汽车不超过30辆,司机不超过145人。
问:每种汽车应购买多少辆,可使每天的吨-公里总数最大?要求建立这个问题的线性规划模型。
(不用求解)二、 (16分) 考虑线性规划问题max Z = x 1 + x 2 + x 3 + x 4约束条件 x 1 + x 2 ≤ 2x 3 + x 4 ≤ 5x j ≥ 0 j = 1, 2, 3, 4(1) 求此线性规划问题的全体最优基可行解; (2) 确定任意最优解的表达式。
三、 (12分) 判断下列说法是否正确,为什么?(1) 若线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;(2) 若线性规划的对偶问题无可行解,则原问题也一定无可行解; (3) 如果线性规划的原问题和对偶问题都具有可行解,则该线性规划问题一定具有最优解;(4) 已知线性规划问题 max Z = CX , AX ≤ b , X ≥ 0 。
若X ~是它的一个基解,Y ~是其对偶问题的一个基解,则恒有b Y ~X ~C ≤。
四、 已知线形规划问题min Z = 8x 1 + 6x 2 + 3x 3 + 6x 4约束条件 x 1 + 2x 2 + x 4 ≥33x 1 + x 2 + x 3 + x 4≥6 x 3 + x 4≥2 x 1 + x 3 ≥2 x 1,x 2,x 3,x 4≥0 (1) 写出其对偶问题;(2) 已知原问题最优解为X *=(1,1,2,0),试根据对偶理论,直接求出对偶问题的最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.填空题
1.节点、箭线是网络计划图的基本元素。
2. 一般的排队系统由 _输入过程__,排队规则__,_服务机构___组成。
3.等待制的服务规有:__先到先服务__,__后到先服务__,__随机服务__,有优先权的服务_。
4. ___具有对策行为_的模型称为对策模型。
5. 对策模型包含的基本要素有:__局中人_______、_策略集_、___赢得函数___。
二.名词解释
(1)策略:一局对策中,可供局中人选择的一个实际可行的完整的行动方案。
(2)局中人:在一个对策行为(或一局对策)中,有权决定自己行动方案的对策参加者。
(3)主观概率:,是由决策者对事件的了解去确定,而这样确定的概率反映了决策者对事件出现的信念程度。
(4)先验概率:是指根据以往经验或专家评估分析得到的概率。
(5)决策树:有些决策问题,当进行决策后又产生一些新情况,并需要进行新的决策,又接着又有一些新情况,又需要进行新的决策,这样决策,情况,决策……构成一个序列,这就是序列决策。
描述序列决策的有力工具之一是决策树,决策树是由决策点,事件点及结果成的树形图。
三.解答题
1.某厂有大量同一型号的车床,当这种车床损坏后或送机修车间或由机修车间派人来修理。
已知该车床损坏率服从泊松分布,平均每天2台。
又机修车间对每台
损坏车床的修理时间为负指数分布的随机变量,平均每台的修理时间为,天。
但是一个与机修人员编制及维修设备好坏(即与机修车间每年开支费用K)有关的函数。
已知
又知机器损坏后,每台每天的生产损失为400元,每个月工作天数为22天,
试决定使该厂生产最经济的K及值。
解:设机器损坏造成的生产损失S 1;(2)机修车间的开支S 2。
要使整个系统最经济,就是要使S = S 1 +S 2为最小。
以一个月为期进行计算如下: S 1=(正在修理和待修机器数)×(每台每天的生产损失)×(每个月的工作日数)=
S2 = K / 12
令 ,得
K =16430元 μ=17.65
2.某修理店只有一个修理工人,来修理的顾客到达次数服从泊松分布,平均每小时4人,修理时间服从指数分布,平均需6分钟,求:
(1)修理店空闲的时间概率
(2)店内有3个顾客的概率
(3)店内至少一名顾客的概率
(4)在店内顾客平均数
(5)在店内平均逗留时间
(6)等待服务的顾客平均数
(7)平均等待修理的时间
(8)必须在店内耗费15分钟以上的概率。
解:本例可看成一个M/M/1/∞/∞排队问题,其中
(1)修理店空闲概率 240022880088008800010001000119s L ..K .K .λλμλλ⎛⎫⎛⎫⎛⎫⨯⨯=⨯=⨯=⨯ ⎪ ⎪ ⎪-+--⎝⎭⎝⎭⎝⎭
2880012000119S K /.K .⎛⎫=⨯+ ⎪-⎝⎭21176000001012000119dS .dK (.K .)
⨯=-=-
(2)店内有3个顾客的概率
(3)店内至少有1个顾客的概率
(4)在店内的顾客平均数
Ls= /( - )=4/(10-4)=0.667人
(5)在店内的平均逗留时间
Ws=1 =1/(10-4)=0.167h
(6)等待服务的顾客平均数
Lq= / =4*0.4/(10-4)=0.267人
(7)平均等待修理(服务)时间
(8)必须在店内消耗15分钟以上的概率
P(T>15)= exp(/4)=exp(-(10-4)/4)=exp(-1.5)=0.223 2. 用线性规划求下列矩阵对策
A=
解:求解问题可化成两个互为对偶的线性规划问题
min(x1+x2+x3)
3x
1-1x
2
-3X
31
≥
-3x
1+3x
2
-1x
31
≥
-4x
1-3x
2
+3x
31
≥
x 1,x
2
,x
30
≥
max(y1+y2+y3)
3y1-1y2-3y31
≤
-3y1+3y2-1y31
≤
-4y1-3y2+3y31
≤
y1+y2+y30
≥
四.证明题
1.证明如下序列不可能是某个简单图的次的序列:
(1)7,6,5,4,3,2
(2)6,6,5,4,3,2,1
(3)6,5,5,4,3,2,1
证明:
1.已知定理:∑∈v v v d)(=2q,而在此序列中,∑)(v d=27,为奇数,所以此序
列不可能为图的次的序列。
又知定理:奇点的个数应为偶数,而在此序列中,奇点7,5,3为奇数个,所以此序列不可能为图的次的序列。
2.在序列中,奇点5,3,1为奇数个,所以此序列不可能为图的次的序列。
3.对于七顶点的图,假定d(v1)=6,d(v2)=5,d(v7)=1,并假设G为简单图,则
v1存在与其它六个点的连线(包含与v7),v2与v1间存在边e12,而v7次为1,所以必不与v1外的其它点相连,因而v2 与除v1,v7外的四点间各有一连线。
假设G(V,E)为简单位图,则余下的v3,v4,v5,v6中任一点(用vi 表示)已确定存在ei,ei2,无ei7,对于d(vi)=5的该点来说,必与除 v7外的每一点都有连线,由此推论,v4,v5,v6都同时与v1,v2,v3,相连,即v4,v5,v6的次至少是3,这与d(v6)=2相矛盾。
故假设不成立,该图中可能有环或多重边,非简单图的次的序列。
