完全二叉树定义完全二叉树
二叉树基本知识

二叉树基本知识:
1.二叉树的定义:二叉树是每个结点最多有两个子树的树结构,它有五种基本形态:
二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
2.二叉树的性质:若规定根结点的层数为1,则一颗非空二叉树的第i层上最多有2^(i-1)
(i>0)个结点。
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结
点数是2^K -1 (k >= 0)个。
对任何一颗二叉树,如果其叶子结点个数为n0,度为2的非叶子结点个数为n2,则有n0=n2+1。
3.二叉树的分类:二叉树有两大类,一是普通二叉树,二是特殊二叉树。
普通二叉树
是指除了满二叉树和完全二叉树之外的二叉树,特殊二叉树包括满二叉树和完全二叉树。
满二叉树是指所有层都完全填满的二叉树,而完全二叉树是指只有最下面两层结点度数可以小于2,并且最下面一层的叶子结点都位于本层中间位置的二叉树。
4.二叉树的遍历:二叉树的遍历主要有三种方法,分别是前序遍历、中序遍历和后序
遍历。
前序遍历是先访问根结点,然后遍历左子树,最后遍历右子树;中序遍历是先遍历左子树,然后访问根结点,最后遍历右子树;后序遍历是先遍历左子树,然后遍历右子树,最后访问根结点。
完全二叉树深度公式

完全二叉树深度公式
完全二叉树深度公式:在完全二叉树中,具有n个结点的完全二叉树深度为(log2n)+1,其中(log2n)+1是向下取整。
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
(1)所有的叶结点都出现在第k层或k-l层(层次最大的两层)
(2)对任一结点,如果其右子树的最大层次为L,则其左子树的最大层次为L或L+l。
1。
完美二叉树,完全二叉树和完满二叉树

完美⼆叉树,完全⼆叉树和完满⼆叉树树在数据结构中占有⾮常重要的地位。
本⽂从树的基本概念⼊⼿,给出完美(Perfect)⼆叉树,完全(Complete)⼆叉树和完满(Full)⼆叉树的区别。
如果学习过⼆叉树,但是对这三种⼆叉树并没有深⼊的理解,或者完全被国产数据结构教科书所误导(只听说过满⼆叉树和完全⼆叉树)的朋友不妨花点时间耐着性⼦将本⽂仔细阅读N(>=1)遍。
1. 的基本概念1.1 树的定义A tree is a (possibly non-linear) data structure made up of nodes or verticesand edges without having any cycle. The tree with no nodes is called the nullor empty tree. A tree that is not empty consists of a root node and potentiallymany levels of additional nodes that form a hierarchy.树是由结点或顶点和边组成的(可能是⾮线性的)且不存在着任何环的⼀种数据结构。
没有结点的树称为空(null或empty)树。
⼀棵⾮空的树包括⼀个根结点,还(很可能)有多个附加结点,所有结点构成⼀个多级分层结构。
[注:本⽂将node⼀律译为"结点"(⽽不是"节点"),因为joint或connection是节点,⽽node是结点。
关于"结点"与"节点"请⾃⾏搜索浙江⼤学陈⽔福教授的⽂章--"360度"解读如何正确应⽤"结点"与"节点"]A simple unordered tree; in this diagram, the node labeled 7 has two children,labeled 2 and 6, and one parent, labeled 2. The root node, at the top,has no parent. 上图是⼀棵⽆序的树⽰例。
完全二叉树深度计算方法

完全二叉树深度计算方法完全二叉树是一种特殊的二叉树结构,它是指除了最后一层外,其他所有层的节点数都达到最大值,并且最后一层的节点都集中在左边。
在计算完全二叉树的深度时,我们可以采用多种方法。
一种常用的方法是递归法。
递归法的基本思想是将问题分解成更小的子问题,然后通过递归调用解决子问题。
对于完全二叉树来说,可以通过递归的方式来计算左子树和右子树的深度,然后取两者中的较大值加1即可得到整棵树的深度。
具体的实现方法如下:1. 判断树是否为空,如果为空则返回0。
2. 递归计算左子树的深度,将结果保存在变量left_depth中。
3. 递归计算右子树的深度,将结果保存在变量right_depth中。
4. 返回left_depth和right_depth中的较大值加1,即为整棵树的深度。
下面是一个使用递归法计算完全二叉树深度的示例代码:```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef get_tree_depth(root):if root is None:return 0left_depth = get_tree_depth(root.left)right_depth = get_tree_depth(root.right)return max(left_depth, right_depth) + 1```除了递归法外,还可以使用迭代法来计算完全二叉树的深度。
迭代法的基本思想是利用栈或队列来存储节点,通过循环遍历栈或队列中的节点,直到遍历完所有节点为止。
具体的实现方法如下:1. 判断树是否为空,如果为空则返回0。
2. 创建一个空的队列,并将根节点入队。
3. 初始化深度为0。
4. 循环遍历队列中的节点,每次遍历一层节点时,深度加1。
二叉树

6-2-2 二叉树的基本操作与存储实现
1、二叉树的基本操作 Initiate(bt)
Create(x, lbt, rbt)
InsertL(bt, x, parent) InsertR(bt, x, parent) DeleteL(bt,parent) DeleteR(bt,parent)
Search(bt,x)
BiTree DeleteL(BiTree bt, BiTree parent){ BiTree p; if(parent==NULL||parent->lchild==NULL){ cout<<“删除出错”<<endl; return NULL; } p=parent->lchild; parent->lchild =NULL; delete p; return bt ; }
a b c e 0 1 2 3 4 5 a b c d e ^ 6 7 8 9 10 ^ ^ ^ f g
d
f
g
特点:结点间关系蕴含在其存储位置中。浪费空间, 适于存满二叉树和完全二叉树。
二、链式存储结构 1、二叉链表存储法
A
B C E G D B A ^
lchild data rchild
F
^ C ^ typedef struct BiTNode { DataType data; struct BiTNode *lchild, *rchild; }BiTNode, *BiTree; ^ E
二叉树的五种基本形态
A
A
A B
A
B 空二叉树
B
C 左、右子树 均非空
只有根结点 的二叉树
右子树为空
左子树为空
数据结构中各种树
数据结构中各种树阅读⽬录 数据结构中有很多树的结构,其中包括⼆叉树、⼆叉搜索树、2-3树、红⿊树等等。
本⽂中对数据结构中常见的⼏种树的概念和⽤途进⾏了汇总,不求严格精准,但求简单易懂。
1. ⼆叉树 ⼆叉树是数据结构中⼀种重要的数据结构,也是树表家族最为基础的结构。
⼆叉树的定义:⼆叉树的每个结点⾄多只有⼆棵⼦树(不存在度⼤于2的结点),⼆叉树的⼦树有左右之分,次序不能颠倒。
⼆叉树的第i层⾄多有2i-1个结点;深度为k的⼆叉树⾄多有2k-1个结点;对任何⼀棵⼆叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
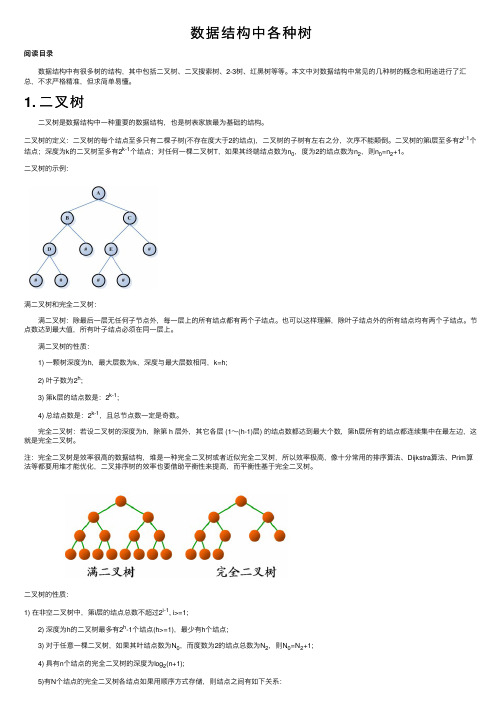
⼆叉树的⽰例:满⼆叉树和完全⼆叉树: 满⼆叉树:除最后⼀层⽆任何⼦节点外,每⼀层上的所有结点都有两个⼦结点。
也可以这样理解,除叶⼦结点外的所有结点均有两个⼦结点。
节点数达到最⼤值,所有叶⼦结点必须在同⼀层上。
满⼆叉树的性质: 1) ⼀颗树深度为h,最⼤层数为k,深度与最⼤层数相同,k=h; 2) 叶⼦数为2h; 3) 第k层的结点数是:2k-1; 4) 总结点数是:2k-1,且总节点数⼀定是奇数。
完全⼆叉树:若设⼆叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最⼤个数,第h层所有的结点都连续集中在最左边,这就是完全⼆叉树。
注:完全⼆叉树是效率很⾼的数据结构,堆是⼀种完全⼆叉树或者近似完全⼆叉树,所以效率极⾼,像⼗分常⽤的排序算法、Dijkstra算法、Prim算法等都要⽤堆才能优化,⼆叉排序树的效率也要借助平衡性来提⾼,⽽平衡性基于完全⼆叉树。
⼆叉树的性质:1) 在⾮空⼆叉树中,第i层的结点总数不超过2i-1, i>=1; 2) 深度为h的⼆叉树最多有2h-1个结点(h>=1),最少有h个结点; 3) 对于任意⼀棵⼆叉树,如果其叶结点数为N0,⽽度数为2的结点总数为N2,则N0=N2+1; 4) 具有n个结点的完全⼆叉树的深度为log2(n+1); 5)有N个结点的完全⼆叉树各结点如果⽤顺序⽅式存储,则结点之间有如下关系: 若I为结点编号则如果I>1,则其⽗结点的编号为I/2; 如果2I<=N,则其左⼉⼦(即左⼦树的根结点)的编号为2I;若2I>N,则⽆左⼉⼦; 如果2I+1<=N,则其右⼉⼦的结点编号为2I+1;若2I+1>N,则⽆右⼉⼦。
二叉树

7.1.2
二叉树的五种基本形态
Ф
左子树
(a) (b) (c)
右子树
(d)
左子树
(e)
右子树
7.1.3
两种特殊形态的二叉树
结点拥有的子树数称为该结点的度(degree)。度为零的结点称 为叶子(leaf),其余结点称为分支结点(branch)。树中结点的最大的 度称为树的度。显然,二叉树结点的度可能为0、1或2。 根结点的层次(level)为1,其余结点的层次等于该结点的双亲结 点的层次加1。树中结点的最大层次称为该树的高度或深度。 1.满二叉树 2.完全二叉树
7.6
本章小结
本章讨论了二叉树数据类型的定义以及实现方法。二叉树是 以两个分支关系定义的层次结构,结构中的数据元素之间存在着一 对多的关系,因此它为计算机应用中出现的具有层次关系或分支关 系的数据,提供了一种自然的表示方法。 二叉树是有明确的左子树和右子树的树形结构,因此当用二 叉树来描述层次关系时,其左孩子表示下属关系,而右孩子表示的 是同一层次的关系。 二叉树的遍历算法是实现各种操作的基础。遍历的实质是按 某种规则将二叉树中的数据元素排列成一个线性序列,二叉树的线 索链表便可看成是二叉树的一种线性存储结构,在线索链表上可对 二叉树进行线性化的遍历,即不需要递归,而是从第一个元素起, 逐个访问后继元素直至后继为空止。因此,线索链表是通过遍历生 成的,即在遍历过程中保存结点之间的前驱和后继的关系。
7.1.4
二叉树的几个特性
由二叉树的定义、形态,我们很容易的得出下面二叉树的 一些特性。 性质1 在二叉树的第i 层上至多有 2i-1 个结点(i≥1)。 性质2 深度为k的二叉树中至多含有2k-1 个结点(k≥1)。 性质3 对任何一棵二叉树 T,如果其终端结点数为,度为 2的结点数为,则。 性质4 具有n个结点的完全二叉树的深度为 log2n+1。 性质5 如果对一棵有 n 个结点的完全二叉树(其深度为 log2n+1)的结点按层序(从第1层到第 log2n+1 层,每层从左到 右)从1起开始编号。
已知一颗完全二叉树共有768个结点,则该树的深度为

根据定义,一棵完全二叉树是指没有空结点且每个结点有2个或0个子节点,但它必须符合以下条件:所有叶子结点都必须出现在同一层上,并且从左往右依次排列。
因此,如果已知一棵完全二叉树的结点数为768,根据方法,可以知道该树的深度为9层。
要研究这道题,首先要了解完全二叉树的定义及特性。
完全二叉树是一种满足以下条件的二叉树:每一个结点都有2个或0个子节点,并且从左到右依次排列,即叶子结点都出现在同一层上;此外,它的深度(层数)和节点数量也是有规律的。
根据完全二叉树的定义,我们可以得出结论:对于一颗完全二叉树,其深度与其节点数量有一定的关系,具体来讲,当一棵完全二叉树的结点数量为2^n-1时,其深度为n;而当结点数量不等于2^n-1时,其深度大于n,而小于n+1。
因此,本题中用768个结点来表示一棵完全二叉树,因为2^8-1=255,因此该树的深度大于8,而小于9,最终我们可以得出,该树的深度为9层。
以上就是关于已知一颗完全二叉树共有768个结点,则该树的深度为题的分析介绍,从完全二叉树的定义出发,利用关系式计算,最终得出该树的深度为9层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完全二叉树定义完全二叉树(Complete Binary Tree)若设二叉树的深度为h,除第h 层外,其它各层(1~h-1) 的结点数都达到最大个数,第h 层所有的结点都连续集中在最左边,这就是完全二叉树.完全二叉树是由满二叉树而引出来的.对于深度为K的,有N个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树.若一棵二叉树至多只有最下面的两层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,则此二叉树成为完全二叉树.完全二叉树特点叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或L+1;出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:var tree:array[1..n]of longint;{n:integer;n>=1}对于tree[i],有如下特点:(1)若i为奇数且i>1,那么tree的左兄弟为tree[i-1];(2)若i为偶数且i1,tree的双亲为tree[i div 2];(4)若2*i
满二叉树(Full Binary Tree):
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点(最后一层上的无子结点的结点为叶子结点)。
也可以这样理解,除叶子结点外的所有结点均有两个子结点。
节点数达到最大值。
所有叶子结点必须在同一层上.
一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
它的叶子数是: 2^h
第k层的结点数是: 2^(k-1)
总结点数是: 2^k-1 (2的k次方减一)
总节点数一定是奇数。
完全二叉树(Complete Binary Tree)
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。
对于深度为K的,有N个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
