初中数学竞赛 知识点和真题 第31讲 极端原理
极_端_原_理

1.11 极 端 原 理极端原理就是一种从特殊对象看问题的方法,它以对象数量上的极端情况,比如最大值、最小值、最长、最短等为出发点,寻找解题的突破口和答案. 极端原理作为一种解题的思想在几何、数论、组合、图论等方面都有着广泛的应用,利用这个简单而又通俗的原理可以解决不少与存在性有关的数学问题和其他问题. 但在具体解题中,需要我们具体问题具体分析.在应用极端原理时,我们要利用如下的事实: 性质1 有限个数中一定有最大数和最小数; 性质2 无限个正整数中有最小数;性质3 无限个实数不一定有最大数或最小数.例1 平面上给定100个点,已知其中任意两点的距离不超过1,且任意三点所成的三角形是钝角三角形.证明:这100个点被一个半径为12的圆覆盖. 证 在这100个点中,每两点有一个距离,这有限个数(100992⨯个)中,一定有一个最大数(性质1),不妨设A ,B 两点间的距离最大(如果最大的距离不止一个,任取一个即可),以线段AB 为直径作一个圆,由题设,1AB ≤,所以,此圆的半径12≤.在其余的98个点中任取一点C ,因为AB AC ≥,AB BC ≥,又由题设知△ABC 是钝角三角形,如图1所示,所以∠C 一定是钝角,于是点C 位于以AB 为直径的圆内,也就是说这100个点都被这个圆所覆盖.图1CBA例2 空间中给出了8个点,其中任意4个点都不在同一平面上,在它们之间连以17条线段.证明:这些线段至少形成了一个三角形.证 每一个点都连出了若干条线段(至多为7条),不妨设连出线段数目最多的点为A ,它共连出了n 条线段.如果所有17条线段都没有形成三角形,那么与A 相连的n 个点之间彼此都没有线段相连,而其余的(7-n )个点中,每一点所连出的线段条数不多于n 条,因此,线段的总数目不超过22(7)8(4)1616,n n n n nn +-=-+=--+≤这与已知的有17条线段矛盾.从而命题成立.说明 其实本题的结论可加强为“三角形的数目不少于4个”,这个问题较难,留给有兴趣的读者思考.例3 设有(7)n n ≥个圆,其中任意3个圆都不两两相交(包括相切),求证:一定可以找到一个圆,它至多能与5个圆相交.证 设这n 个圆中半径最小的圆(如有多个,任取其中一个即可)为1O . 若1O 与6个(或多于6个)的圆234567,,,,,O O O O O O 都相交,则连接121317,,,OO OO OO ,如图2所示,于是1,2,,6∠∠∠ 中至少有一个不大于60 ,不妨设213160O OO ∠=∠≤,连接23O O ,设123,,O O O 的半径分别为123,,R R R ,1213,R R R R ≤≤.因为12,O O 相交,故它们的连心距不超过两圆半径之和,即1212OO R R ≤+23R R ≤+.同理131323OO R R R R ≤+≤+.又在123O O O ∆中,160∠≤ ,故在23,O O ∠∠中必有一个大于等于60. 设2601O ∠≥≥∠,则1323OO O O ≥,即2323R R O O +≥,所以2O 与3O 相交,从而123,,O O O 两两相交,这与题设矛盾!例4 平面上有(5)n n≥个点. 将他们用红、蓝两色染色. 设任何3个同色点不共线.求证:存在一个三角形使得(1)它的三个顶点涂有相同颜色;(2)这三角形至少有一条边上不包含另一种颜色的点.证由于点数5n≥,且所有的点只染两种颜色,所以,至少有三点同色.因此,存在三个顶点同色的三角形.我们在这些顶点同色的三角形中取一个面积最小的三角形.如果这个三角形的每一条边上都有一个另一种颜色的点,那么我们就找到了另一个三个顶点同色的三角形,而且,这个三角形具有更小的面积,这是不可能的.因此题设的三角形一定存在.说明本题证明中使用了极端原理.我们考虑的是面积,是一种很好的想法,值得我们仔细体会.例5 证明:不定方程33324x y z +=没有正整数解(x ,y ,z ) .证 用反证法.假设方程有正整数解,设111(,,)x y z 是所有正整数解中使x 最小的一组解.由于33311124x y z +=, 所以,31x 是偶数,故1x 是偶数.设122x x =,则333211824x y z +=, 即33321142x y z +=, 故1y 是偶数.设122y y =,则333221482x y z +=, 即33322124x y z +=, 故1z 是偶数.设122z z =,则333222248x y z +=, 即 33322224x y z +=,所以,222(,,)x y z 也是原方程的一组正整数解,且21x x <,矛盾.所以,原方程没有正整数解.例6 设正整数a ,b ,k 满足221a b k ab +=-,求证:k =5. 证 对每一个满足上述方程的k ,设00,a b 是满足2200001a b k a b +=-,且00a b +最小的一组a ,b ,不妨设00a b ≥.若00a b =,则220020002211a b k a b a +==+--,由于2011,2a -≠,故k 不是整数.若00a b >,关于a 的一元二次方程22000a b ka b k -++=的一个根为0a ,由韦达定理知,另一个根a '是正整数,于是,由00a b +最小的性知,a '0a ≥,于是22000a a a b k '≤=+,故 222200000(1)21k a b a a a ≥-≥--=-.当01b =时,2000012111a k a a a +==++--,所以,011a -=或者2,从而k =5. 当02b ≥时,有22222000000002(1)(21)441a a b k a b a a a >+=-≥-=-+,所以 202(1)1a -<,这不可能.综上所述,k =5.例7 若干个人聚会,其中某些人彼此认识,已知如果某两人在聚会者中有相同数目的熟人,那么他俩便没有共同的熟人.证明:若聚会者中有人至少有2010个熟人,则必然也有人恰好有2010个熟人.证 我们考虑(聚会者中)熟人最多的某个人(如果这样的人不止一个,那么任取其中一个),记为A ,设A 共认识n 个人,这些熟人依次记为12,,,n B B B .由于12,,,n B B B 中任意两个人i B 与j B 都认识A ,即是他俩的共同熟人,因此(由题设推出)i B 与j B 的熟人数目不等.此外,12,,,n B B B 的熟人数目均不会超过n (这里用到了n 的“最大性”!),于是他们的熟人数目恰好是1,2,…,n .现在已知有人至少认识2010人,这意味着n ≥2010,所以,数2010在上述数列中出现,于是12,,,n B B B 中恰好有人有2010个熟人.1.给定平面上不全在一条直线上的n个点,则必有一条直线恰好通过这n个点中的两个点.2.在一次乒乓球循环赛中,n(n≥3)名选手中没有全胜的.证明:一定可以从中找出三名选手A,B,C,有A胜B,B胜C,C胜A.。
中考数学1轮总复习学案 第31讲 几何变换考题典练

21世纪教育网 –中小学教育资源及组卷应用平台 21世纪教育网 第九章 第二部分核心演练 第31讲 几何变换考题典练 核心能力: 1 熟练运用平移对称旋转解决相关的几何问题 2 熟练运用平移 旋转 对称 位似等几何变换构建常见几何模型解决问题 核心方法: 熟练运用几何变换构图补形,借助方程思想,函数思想,分类讨论,数形结合等基本思想方法进行推理 旋转策略:1相似,锐角三角函数及勾股定理是解决这类问题的利器, 2利用平移或轴对称补全等,或者利用旋转补形成一拖二,回到角含半角型,一线三等角(K)型,中心对称型,对角互补及共顶点等边型等基本几何模型, 3 常见顺势延长或连结或作平行或作垂直等辅助线进行补形; 4利用全等或相似或锐角三角函数导出线段比例关系或者借助勾股定理,设元建立方程求解; 核心典例 典题1(正方形内”十字结构):如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,
求证: (1)∠DNP=∠DAP;(2)PC=2BN;(3)DNDCDP为常数;(4)MN=MF+NE. (5)若正方形的边长为6,求线段DM长度的最小值
典题2(一线三等角) ( 2017岳阳)问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1,△BND的面积为S2. (1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1•S2= ; (2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1•S2的值; (3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α. (Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1•S2的表达式(结果用a,b和α的三角函数表示). (Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1•S2的表达式,不必写出解答过程. 21世纪教育网 –中小学教育资源及组卷应用平台 21世纪教育网 典题3(角含半角) (2017烟台)【操作发现】(1)如图1,△ABC为等边三角形,现将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF. ①求∠EAF的度数;②DE与EF相等吗?请说明理由; 【类比探究】(2)如图2,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF,请直接写出探究结果:①求∠EAF的度数;②线段AE,ED,DB之间的数量关系.
专题31 极值点偏移问题的研究(解析版)

专题31 极值点偏移问题的研究一、题型选讲题型一、常见的极值点偏移问题常见的极值点偏移问题主要有以下几种题型:1. 若函数)(x f 存在两个零点21,x x 且21x x ≠,求证:0212x x x >+(0x 为函数)(x f 的极值点); 2. 若函数)(x f 中存在21,x x 且21x x ≠满足)()(21x f x f =,求证:0212x x x >+(0x 为函数)(x f 的极值点);3. 若函数)(x f 存在两个零点21,x x 且21x x ≠,令2210x x x +=,求证:0)('0>x f ; 例1、(2019无锡期末)已知函数f(x)=e x -a2x 2-ax(a>0).(1) 当a =1时,求证:对于任意x>0,都有f(x)>0 成立;(2) 若函数y =f(x)恰好在x =x 1和x =x 2两处取得极值,求证:x 1+x 22<ln a.思路分析 (1)利用导数分别讨论函数 和 的单调性即可;(2)直接证明比较困难,需要利用分析法,通过代数变形,换元等方法将问题转化为熟悉的不等式问题,再通过构造函数,结合常用不等式 ,利用导数进行证明.(1)由f(x)=e x -12x 2-x,则f′(x)=e x -x -1,令g(x)=f′(x),则g′(x)=e x -1,(3分)当x>0,g′(x)>0,则f′(x)在(0,+∞)上单调递增,故f′(x)>f′(0)=0,所以f(x)在(0,+∞)上单调递增,(5分)进而f(x)>f(0)=1>0,即对于任意x>0,都有f(x)>0.(6分)(2) f′(x)=e x -ax -a,因为x 1,x 2为f(x)的两个极值点,所以⎩⎪⎨⎪⎧f′(x 1)=0,f′(x 2)=0.即⎩⎪⎨⎪⎧e x 1-ax 1-a =0,e x 2-ax 2-a =0.两式相减,得a =⎩⎪⎨⎪⎧e x 4-ax 1-a =0,e x 2-ax 2-a =0.两式相减,得a =e x 1-e x 2x 1-x 2,(8分)则所证不等式等价x 1+x 22<ln e x 1-e x 2x 1-x 2,即e x 1-x 22<e x 1-x 2-1x 1-x 2,(12分)令t =x 1-x 2,t>0,所以证不等式只需证明: e t 2<e t -1t →t e t2-e t +1<0,(14分) 设φ(t)=t e t 20⎝⎛⎭⎫t2+1≥0,所以φ′(t)≤0,所以φ(t)在(0,+∞)单调递减,φ(t)<φ(0)=0. 所以x 1+x 22<ln a.(16分)例2、(2018常州期末)已知函数f(x)=ln x(x +a )2,其中a 为常数.(1) 若a =0,求函数f(x)的极值;(2) 若函数f(x)在(0,-a)上单调递增,求实数a 的取值范围;(3) 若a =-1,设函数f(x)在(0,1)上的极值点为x 0,求证:f(x 0)<-2.思路分析 第一小问,利用导函数求单调性、极值、值域的一般步骤,必须掌握!也是解决后面问题的基础;第二小问,由函数在(0,-a)上的单调性得出导函数在特定区间的符号,转化为含参数的恒成立问题;第三小问,关键是找到零点的大致范围,还是利用导数求最大值、最小值的方法.规范解答 (1) 当a =0时,f(x)=ln xx 2,定义域为(0,+∞).f′(x)=1-2ln x x 3,令f′(x)=0,得x =e .当x 变化时,f′(x),f(x)的变化情况如下表:所以当x =e 时,f(x)的极大值为12e ,无极小值.(4分)(2) f′(x)=1+ax-2ln x (x +a )3,由题意f′(x)≥0对x∈(0,-a)恒成立.因为x∈(0,-a),所以(x +a)3<0,所以1+ax -2ln x≤0对x∈(0,-a)恒成立.所以a≤2x ln x -x 对x∈(0,-a)恒成立.(6分)令g(x)=2x ln x -x,x∈(0,-a),则g′(x)=2ln x +1.∈若0<-a≤e -12,即0>a≥-e -12,则g′(x)=2ln x +1<0对x∈(0,-a)恒成立,所以g(x)=2x ln x -x 在(0,-a)上单调递减,则a≤2(-a)ln (-a)-(-a),所以ln (-a)≥0,所以a≤-1与a≥-e -12矛盾,舍去;∈若-a>e -12,即a<-e -12,令g′(x)=2ln x +1=0,得x =e -12,当0<x<e -12时,g′(x)=2ln x +1<0,所以g(x)=2x ln x -x 单调递减,当e -12<x<-a 时,g′(x)=2ln x +1>0,所以g(x)=2x ln x -x 单调递增,所以当x =e -12时,g(x)min =g(e -12)=2e -12·lne -12-e -12=-2e -12,所以a≤-2e -12.综上,实数a 的取值范围是(-∞,-2e -12].(10分)(3) 当a =-1时,f(x)=ln x(x -1)2,f′(x)=x -1-2x ln x x (x -1)3.令h(x)=x -1-2x ln x,x∈(0,1),则h′(x)=1-2(ln x +1)=-2ln x -1,令h′(x)=0,得x =e -12.∈当e -12≤x<1时,h′(x)≤0,所以h(x)=x -1-2x ln x 单调递减,h(x)∈(0,2e -12-1],x∈(0,1),所以f′(x)=x -1-2x ln x x (x -1)3<0恒成立,所以f(x)=ln x (x -1)2单调递减,且f(x)≤f(e -12).(12分)∈当0<x≤e -12时,h′(x)≥0,所以h(x)=x -1-2x ln x 单调递增,其中h ⎝⎛⎭⎫12=12-1-2·12·ln 12=ln 4e>0, h(e -2)=e -2-1-2e -2·lne -2=5e2-1<0,所以存在唯一x 0∈⎝⎛⎭⎫e -2,12,使得h(x 0)=0,所以f′(x 0)=0, 当0<x<x 0时,f′(x)>0,所以f(x)=ln x(x -1)2单调递增;当x 0<x≤e -12时,f′(x)<0,所以f(x)=ln x (x -1)2单调递减,且f(x)≥f(e -12),(14分) 由∈和∈可知,f(x)=ln x(x -1)2在(0,x 0)上单调递增,在(x 0,1)上单调递减,所以当x =x 0时,f(x)=ln x(x -1)2取极大值.因为h(x 0)=x 0-1-2x 0ln x 0=0,所以ln x 0=x 0-12x 0,所以f(x 0)=ln x 0(x 0-1)2=12x 0(x 0-1)=12⎝⎛⎭⎫x 0-122-12.又x 0∈⎝⎛⎭⎫e -2,12∈⎝⎛⎭⎫0,12,所以2⎝⎛⎭⎫x 0-122-12∈⎝⎛⎭⎫-12,0,所以f(x 0)=12⎝⎛⎭⎫x 0-122-12<-2.(16分)例3、(2018南通、扬州、淮安、宿迁、泰州、徐州六市二调)设函数f(x)=x -a sin x(a>0).(1) 若函数y =f(x)是R 上的单调增函数,求实数a 的取值范围; (2) 设a =12,g (x )=f (x )+b ln x +1(b ∈R ,b ≠0),g ′(x )是g (x )的导函数.∈若对任意的x >0,g ′(x )>0,求证:存在x 0,使g (x 0)<0;∈若g (x 1)=g (x 2)(x 1≠x 2),求证:x 1x 2<4b 2.思路分析 (1) 由题意,f′(x)≥0对x∈R 恒成立,可考虑参数分离求参数范围;(2)∈根据x >0,g ′(x )>0,知g (x )为增函数,根据基本初等函数的性质得出必须有b >0,当然要说明理由,再寻找支撑点x 0的值,x →0时,b ln x 下降的程度大于x ,而-12sin x 在固定范围,所以使b ln x 足够小即可;∈用(1)的结论和g (x 1)=g (x 2)(x 1≠x 2),构建不等式-2b >x 2-x 1ln x 2-ln x 1>0,然后运用放缩和换元的策略,转化为证明一元函数的单调性,即可证明.规范解答 (1) 由题意,f ′(x )=1-a cos x ≥0对x ∈R 恒成立,(1分) 因为a >0,所以1a ≥cos x 对x ∈R 恒成立,因为(cos x )max =1,所以1a≥1,从而0<a ≤1.(3分)(2) ∈g (x )=x -12sin x +b ln x +1,所以g ′(x )=1-12cos x +bx.若b <0,则存在-b 2>0,使g ′⎝⎛⎭⎫-b 2=-1-12cos ⎝⎛⎭⎫-b 2<0,不合题意,所以b >0.(5分)取x 0=e -3b,则0<x 0<1.此时g (x 0)=x 0-12sin x 0+b ln x 0+1<1+12+b lne -3b +1=-12<0.所以存在x 0>0,使g (x 0)<0.(8分)∈依题意,不妨设0<x 1<x 2,令x 2x 1=t ,则t >1.由(1)知函数y =x -sin x 单调递增,所以x 2-sin x 2>x 1-sin x 1.从而x 2-x 1>sin x 2-sin x 1.(10分) 因为g (x 1)=g (x 2),所以x 1-12sin x 1+b ln x 1+1=x 2-12sin x 2+b ln x 2+1,所以-b (ln x 2-ln x 1)=x 2-x 1-12(sin x 2-sin x 1)>12(x 2-x 1).所以-2b >x 2-x 1ln x 2-ln x 1>0.(12分)下面证明x 2-x 1ln x 2-ln x 1>x 1x 2,即证明t -1ln t >t ,只要证明ln t -t -1t <0 (*).设h (t )=ln t -t -1t (t >1),所以h ′(t )=-(t -1)22t t <0在(1,+∞)上恒成立.所以h (t )在(1,+∞)上单调递减,故h (t )<h (1)=0,从而(*)得证.所以-2b >x 1x 2,即x 1x 2<4b 2.(16分)例4、(2018南通、泰州一调)已知函数g(x)=x 3+ax 2+bx(a,b∈R )有极值,且函数f (x )=(x +a )e x 的极值点是g (x )的极值点,其中e 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)(1) 求b 关于a 的函数关系式;(2) 当a >0时,若函数F (x )=f (x )-g (x )的最小值为M (a ),证明:M (a )<-73.思路分析 (1) 易求得f(x)的极值点为-a -1,则g′(-a -1)=0且g′(x)=0有两个不等的实数解,解之得b与a 的关系.(2) 求导得F′(x)=(x +a +1)(e x -3x +a +3),解方程F′(x)=0时,无法解方程e x -3x +a +3=0,构造函数h(x)=e x -3x +a +3,证得h(x)>0,所以-a -1为极小值点,而且得出M(a),利用导数法证明即可.规范解答 (1) 因为f′(x)=e x +(x +a)e x =(x +a +1)e x ,令f′(x)=0,解得x =-a -1.列表如下:所以x =-a -1时,f(x)取得极小值.(2分)因为g′(x)=3x 2+2ax +b,由题意可知g′(-a -1)=0,且Δ=4a 2-12b>0,所以3(-a -1)2+2a(-a -1)+b =0,化简得b =-a 2-4a -3.(4分)由Δ=4a 2-12b =4a 2+12(a +1)(a +3)>0,得a≠-32.所以b =-a 2-4a -3⎝⎛⎭⎫a≠-32.(6分) (2) 因为F(x)=f(x)-g(x)=(x +a)e x -(x 3+ax 2+bx),所以F′(x)=f′(x)-g′(x)=(x +a +1)e x -[3x 2+2ax -(a +1)(a +3)]=(x +a +1)e x -(x +a +1)(3x -a -3)=(x +a +1)(e x -3x +a +3).(8分)记h(x)=e x -3x +a +3,则h′(x)=e x -3,令h′(x)=0,解得x =ln 3.列表如下:所以x =ln 3时,h(x)取得极小值,也是最小值,此时,h(ln 3)=e ln 3-3ln 3+a +3=6-3ln 3+a=3(2-ln 3)+a =3ln e 23+a>a>0.(10分)所以h(x)=e x -3x +a +3≥h(ln 3)>0,令F′(x)=0,解得x =-a -1.列表如下:所以x =-a -1时,F(x)取得极小值,也是最小值.所以M(a)=F(-a -1)=(-a -1+a)e-a -1-[(-a -1)3+a(-a -1)2+b(-a -1)]=-e-a -1-(a +1)2(a +2).(12分)令t =-a -1,则t<-1,记m(t)=-e t -t 2(1-t)=-e t +t 3-t 2,t<-1,则m′(t)=-e t +3t 2-2t,t<-1.因为-e -1<-e t <0,3t 2-2t>5,所以m′(t)>0,所以m(t)单调递增.(14分) 所以m(t)<-e -1-2<-13-2=-73,即M(a)<-73.(16分)题型二、构造函数的极值点偏移问题(1)求出函数)(x f 的极值点0x ;(2)构造一元差函数)()()(00x x f x x f x F --+=;(3)确定函数)(x F 的单调性;(4)结合0)0(=F ,判断)(x F 的符号,从而确定)(0x x f +、)(0x x f -的大小关系.例5、(2017苏州期末)已知函数f (x )=(ln x -k -1)x (k ∈R ).(1) 当x >1时,求函数f (x )的单调区间和极值;(2) 若对于任意x ∈[e,e 2],都有f (x )<4ln x 成立,求实数k 的取值范围; (3) 若x 1≠x 2,且f (x 1)=f (x 2),证明:x 1x 2<e 2k .. 思路分析 (1) 只要注意对k 的讨论. (2) 分离出k ,转化为k >K (x )恒成立问题.(3) 先说明0<x 1<e k<x 2,从而只要证e k<x 2<e 2k x 1,只要证f (x 1)=f (x 2)<f ⎝⎛⎭⎫e 2k x 1.转化为关于x 1的不等式对0<x 1<e k 恒成立问题.规范解答 (1) f ′(x )=ln x -k ,其中x >1.(1分)∈若k ≤0,则x >1时,f ′(x )>0恒成立,f (x )在(1,+∞)上单调递增,无极值;(2分) ∈若k >0,则f (x )在(1,e k ]上单调递减,在[e k ,+∞)上单调递增,(4分) 有极小值f (e k )=-e k ,无极大值.(5分)(2) 问题可转化为k >⎝⎛⎭⎫1-4x ln x -1对x ∈[e,e 2]恒成立.(7分) 设K (x )=⎝⎛⎭⎫1-4x ln x -1,则K ′(x )=4x 2ln x +⎝⎛⎭⎫1-4x 1x =4x 2(ln x -1)+1x. 当x ∈[e,e 2]时,K ′(x )≥1x >0,所以K (x )在[e,e 2]上单调递增,K (x )max =K (e 2)=1-8e 2.(9分)所以实数k 的取值范围是⎝⎛⎭⎫1-8e 2,+∞.(10分) (3) 因为f ′(x )=ln x -k ,所以f (x )在(0,e k ]上单调递减,在[e k ,+∞)上单调递增.不妨设0<x 1<e k<x 2.要证x 1x 2<e 2k ,只要证x 2<e 2kx 1.因为f (x )在[e k,+∞)上单调递增,所以只要证f (x 1)=f (x 2)<f ⎝⎛⎭⎫e 2kx 1,即要证(ln x 1-k -1)x 1<(k -ln x 1-1)e2kx 1.(12分)令t =2(k -ln x 1)>0,只要证(t -2)e t +t +2>0.设H (t )=(t -2)e t +t +2,则只要证H (t )>0对t >0恒成立.H ′(t )=(t -1)e t +1,H ″(t )=t e t >0对t >0恒成立.所以H ′(t )在(0,+∞)上单调递增,H ′(t )>H ′(0)=0.(14分)所以H (t )在(0,+∞)上单调递增,H (t )>H (0)=0. 综上所述,x 1x 2<e 2k .(16分)例6、(2019南通、泰州、扬州一调)已知函数f(x)=ax +ln x(a∈R ).(1) 讨论f (x )的单调性;(2) 设f (x )的导函数为f ′(x ),若f (x )有两个不相同的零点x 1,x 2.∈求实数a 的取值范围;∈证明:x 1f ′(x 1)+x 2f ′(x 2)>2ln a +2.思路分析 (1)求导函数f′(x),对a 分类讨论,确定导函数的正负,即可得到f(x)的单调性(2)∈根据第(1)问的函数f(x)的单调性,确定a>0,且f(x)min =f(a)<0,求得a 的取值范围,再用零点判定定理证明根的存在性.∈ 对所要证明的结论分析,问题转化为证明x 1x 2>a 2,不妨设0<x 1<a<x 2,问题转化为证明x 1>a 2x 2,通过对f(x)的单调性的分析,问题进一步转化为证明f ⎝⎛⎭⎫a 2x 2>f(x 2),构造函数,通过导数法不难证得结论.解:(1)f(x)的定义域为(0,+∞),且f′(x)=x -ax2.(1.1)当a≤0时,f′(x)>0成立,所以f(x)在(0,+∞)为增函数;(2分)(1.2)当a>0时,(i )当x>a 时,f′(x)>0,所以f(x)在(a,+∞)上为增函数;(ii )当0<x<a 时,f′(x)<0,所以f(x)在(0,a)上为减函数.(4分)(2)∈由(1)知,当a≤0时,f(x)至多一个零点,不合题意;当a>0时,f(x)的最小值为f(a),依题意知f(a)=1+ln a<0,解得0<a<1e.(6分)一方面,由于1>a,f(1)=a>0,f(x)在(a,+∞)为增函数,且函数f(x)的图像在(a,1)上不间断.所以f(x)在(a,+∞)上有唯一的一个零点. 另一方面, 因为0<a<1e ,所以0<a 2<a<1e .f(a 2)=1a +ln a 2=1a +2ln a,令g(a)=1a +2ln a,当0<a<1e 时,g′(a)=-1a 2+2a =2a -1a 2<0,所以f(a 2)=g(a)=1a+2ln a>g ⎝⎛⎭⎫1e =e -2>0 又f(a)<0,f(x)在(0,a)为减函数,且函数f(x)的图像在(a 2,a)上不间断.所以f(x)在(0,a)有唯一的一个零点. 综上,实数a 的取值范围是⎝⎛⎭⎫0,1e .(10分) ∈ 设p =x 1f′(x 1)+x 2f′(x 2)=1-a x 1+1-ax 2=2-⎝⎛⎭⎫a x 1+a x 2. 又⎩⎨⎧ln x 1+a x 1=0,ln x 2+a x 2=0,则p =2+ln (x 1x 2).(12分)下面证明x 1x 2>a 2.不妨设x 1<x 2,由∈知0<x 1<a<x 2. 要证x 1x 2>a 2,即证x 1>a 2x 2.因为x 1,a 2x 2∈(0,a),f(x)在(0,a)上为减函数,所以只要证f ⎝⎛⎭⎫a 2x 2>f(x 1).又f(x 1)=f(x 2)=0,即证f ⎝⎛⎭⎫a 2x 2>f(x 2).(14分) 设函数F(x)=f ⎝⎛⎭⎫a 2x -f(x)=x a -a x -2ln x +2ln a(x>a). 所以F′(x)=(x -a )2ax 2>0,所以F(x)在(a,+∞)为增函数.所以F(x 2)>F(a)=0,所以f ⎝⎛⎭⎫a 2x 2>f(x 2)成立. 从而x 1x 2>a 2成立.所以p =2+ln (x 1x 2)>2ln a +2,即x 1f′(x 1)+x 2f′(x 2)>2ln a +2成立.(16分)解题反思 1. 第(2)∈中,用零点判定定理证明f(x)在(0,a)上有一个零点是解题的一个难点,也是一个热点问题,就是当0<a<1e 时,要找一个数x 0<a,且f(x 0)>0,这里需要取关于a 的代数式,取x 0=a 2,再证明f(a 2)>0,事实上由(1)可以得到x ln x≥-1e ,而f(a 2)=1a +ln a 2=1+2a ln a a>0即可.2. 在(2)∈中证明x 1x 2>a 2的过程,属于构造消元构造函数方法,将两个变量x 1,x 2转化为证明单变量的问题,这一处理方法,在各类压轴题中,经常出现,要能领悟并加以灵活应用二、达标训练1、(2018常州期末)已知函数f(x)=ln x(x +a )2,其中a 为常数.(1) 若a =0,求函数f(x)的极值;(2) 若函数f(x)在(0,-a)上单调递增,求实数a 的取值范围;(3) 若a =-1,设函数f(x)在(0,1)上的极值点为x 0,求证:f(x 0)<-2.思路分析 第一小问,利用导函数求单调性、极值、值域的一般步骤,必须掌握!也是解决后面问题的基础;第二小问,由函数在(0,-a)上的单调性得出导函数在特定区间的符号,转化为含参数的恒成立问题;第三小问,关键是找到零点的大致范围,还是利用导数求最大值、最小值的方法.规范解答 (1) 当a =0时,f(x)=ln xx 2,定义域为(0,+∞).f′(x)=1-2ln x x 3,令f′(x)=0,得x =e .当x 变化时,f′(x),f(x)的变化情况如下表:所以当x =e 时,f(x)的极大值为12e ,无极小值.(4分)(2) f′(x)=1+ax-2ln x (x +a )3,由题意f′(x)≥0对x∈(0,-a)恒成立.因为x∈(0,-a),所以(x +a)3<0,所以1+ax -2ln x≤0对x∈(0,-a)恒成立.所以a≤2x ln x -x 对x∈(0,-a)恒成立.(6分)令g(x)=2x ln x -x,x∈(0,-a),则g′(x)=2ln x +1.∈若0<-a≤e -12,即0>a≥-e -12,则g′(x)=2ln x +1<0对x∈(0,-a)恒成立,所以g(x)=2x ln x -x 在(0,-a)上单调递减,则a≤2(-a)ln (-a)-(-a),所以ln (-a)≥0,所以a≤-1与a≥-e -12矛盾,舍去;∈若-a>e -12,即a<-e -12,令g′(x)=2ln x +1=0,得x =e -12,当0<x<e -12时,g′(x)=2ln x +1<0,所以g(x)=2x ln x -x 单调递减,当e -12<x<-a 时,g′(x)=2ln x +1>0,所以g(x)=2x ln x -x 单调递增,所以当x =e -12时,g(x)min =g(e -12)=2e -12·lne -12-e -12=-2e -12,所以a≤-2e -12.综上,实数a 的取值范围是(-∞,-2e -12].(10分)(3) 当a =-1时,f(x)=ln x(x -1)2,f′(x)=x -1-2x ln x x (x -1)3.令h(x)=x -1-2x ln x,x∈(0,1),则h′(x)=1-2(ln x +1)=-2ln x -1,令h′(x)=0,得x =e -12.∈当e -12≤x<1时,h′(x)≤0,所以h(x)=x -1-2x ln x 单调递减,h(x)∈(0,2e -12-1],x∈(0,1),所以f′(x)=x -1-2x ln x x (x -1)3<0恒成立,所以f(x)=ln x (x -1)2单调递减,且f(x)≤f(e -12).(12分)∈当0<x≤e -12时,h′(x)≥0,所以h(x)=x -1-2x ln x 单调递增,其中h ⎝⎛⎭⎫12=12-1-2·12·ln 12=ln 4e>0, h(e -2)=e -2-1-2e -2·lne -2=5e2-1<0,所以存在唯一x 0∈⎝⎛⎭⎫e -2,12,使得h(x 0)=0,所以f′(x 0)=0,当0<x<x 0时,f′(x)>0,所以f(x)=ln x(x -1)2单调递增;当x 0<x≤e -12时,f′(x)<0,所以f(x)=ln x (x -1)2单调递减,且f(x)≥f(e -12),(14分)由∈和∈可知,f(x)=ln x(x -1)2在(0,x 0)上单调递增,在(x 0,1)上单调递减,所以当x =x 0时,f(x)=ln x(x -1)2取极大值.因为h(x 0)=x 0-1-2x 0ln x 0=0,所以ln x 0=x 0-12x 0,所以f(x 0)=ln x 0(x 0-1)2=12x 0(x 0-1)=12⎝⎛⎭⎫x 0-122-12.又x 0∈⎝⎛⎭⎫e -2,12∈⎝⎛⎭⎫0,12,所以2⎝⎛⎭⎫x 0-122-12∈⎝⎛⎭⎫-12,0,所以f(x 0)=12⎝⎛⎭⎫x 0-122-12<-2.(16分) 2、(2017南京学情调研)已知函数f (x )=ax 2-bx +ln x ,a ,b ∈R .(1) 当a =b =1时,求曲线y =f (x )在x =1处的切线方程; (2) 当b =2a +1时,讨论函数f (x )的单调性;(3) 当a =1,b >3时,记函数f (x )的导函数f ′(x )的两个零点是x 1和x 2 (x 1<x 2),求证:f (x 1)-f (x 2)>34-ln2.思路分析 (1) 通过求出f ′(1),f (1)的值,利用点斜式求出切线的方程;(2) 研究单调性,通过求出导函数f ′(x ),然后研究f ′(x )的正负,分类讨论,确定分类的标准是a ≤0,a >0,在a >0时,再按12a <1,12a =1,12a>1分类;(3) 要证明此不等式,首先要考察x 1,x 2的范围与a ,b 的关系,由已知求出f ′(x )=2x 2-bx +1x (x >0),因此x 1,x 2是方程g (x )=2x 2-bx +1=0的两根,x 1x 2=12,粗略地估计一下,由于g ⎝⎛⎭⎫12=3-b 2<0,g (1)=3-b <0,因此有x 1∈⎝⎛⎭⎫0,12,x 2∈(1,+∞),由此可知f (x )在[x 1,x 2]上为减函数,从而有f (x 1)-f (x 2)>f ⎝⎛⎭⎫12-f (1),这里f ⎝⎛⎭⎫12-f (1)=b 2-34-ln2>34-ln2,正好可证明题设结论.规范解答 (1) 因为a =b =1,所以f (x )=x 2-x +ln x , 从而f ′(x )=2x -1+1x.因为f (1)=0,f ′(1)=2,所以曲线y =f (x )在x =1处的切线方程为y -0=2(x -1),即2x -y -2=0.(3分) (2) 因为b =2a +1,所以f (x )=ax 2-(2a +1)x +ln x ,从而f ′(x )=2ax -(2a +1)+1x =2ax 2-(2a +1)x +1x =(2ax -1)(x -1)x,x >0.(5分)当a ≤0时,若x ∈(0,1),则f ′(x )>0;若x ∈(1,+∞),则f ′(x )<0,所以f (x )在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.(7分)当0<a <12时,由f ′(x )>0得0<x <1或x >12a ;由f ′(x )<0得1<x <12a ,所以f (x )在区间(0,1)和⎝⎛⎭⎫12a ,+∞上单调递增,在区间⎝⎛⎭⎫1,12a 上单调递减. 当a =12时,因为f ′(x )≥0(当且仅当x =1时取等号),所以f (x )在区间(0,+∞)上单调递增.当a >12时,由f ′(x )>0得0<x <12a 或x >1;由f ′(x )<0得12a <x <1,所以f (x )在区间⎝⎛⎭⎫0,12a 和(1,+∞)上单调递增,在区间⎝⎛⎭⎫12a ,1上单调递减.(10分) (3) 证法1 因为a =1,所以f (x )=x 2-bx +ln x ,从而f ′(x )=2x 2-bx +1x(x >0).由题意知,x 1,x 2是方程2x 2-bx +1=0的两个根,由根与系数的关系可得x 1x 2=12.记g (x )=2x 2-bx +1,因为b >3,所以g ⎝⎛⎭⎫12=3-b 2<0,g (1)=3-b <0,所以x 1∈⎝⎛⎭⎫0,12,x 2∈(1,+∞),且bx i =2x 2i +1(i =1,2),(12分)所以f (x 1)-f (x 2)=(x 21-x 22)-(bx 1-bx 2)+ln x 1x 2=-(x 21-x 22)+ln x 1x 2. 因为x 1x 2=12,所以f (x 1)-f (x 2)=x 22-14x 22-ln(2x 22),x 2∈(1,+∞).(14分) 令t =2x 22∈(2,+∞),φ(t )=f (x 1)-f (x 2)=t 2-12t-ln t .因为φ′(t )=(t -1)22t 2≥0,所以φ(t )在区间(2,+∞)上单调递增,所以φ(t )>φ(2)=34-ln2,即f (x 1)-f (x 2)>34-ln2.(16分)证法2 因为a =1,所以f (x )=x 2-bx +ln x ,从而f ′(x )=2x 2-bx +1x(x >0).由题意知,x 1,x 2是方程2x 2-bx +1=0的两个根.记g (x )=2x 2-bx +1,因为b >3,所以g ⎝⎛⎭⎫12=3-b 2<0,g (1)=3-b <0,所以x 1∈⎝⎛⎭⎫0,12,x 2∈(1,+∞),且f (x )在[x 1,x 2]上为减函数.(12分)所以f (x 1)-f (x 2)>f ⎝⎛⎭⎫12-f (1)=14-b 2+ln 12-(1-b )=-34+b2-ln2. 因为b >3,所以f (x 1)-f (x 2)>-34+b 2-ln2>34-ln2.(16分)3、已知函数()()2ln 2,g x x ax a x a R =-+-∈.(1)求()g x 的单调区间;(2)若函数()()()212f x g x a x x =++-, 1212,()x x x x <是函数()f x 的两个零点, ()f x '是函数()f x 的导函数,证明: 1202x x f +⎛⎫<⎪⎝⎭'. 【解析】试题分析:(1)先求函数导数,根据导函数是否变号进行讨论,当0a ≤时, ()0g x '>, ()g x 递增,当0a >时,导函数有一零点,导函数先正后负,故得增区间为10,a ⎛⎫⎪⎝⎭,减区间为1,a⎛⎫+∞ ⎪⎝⎭;(2)利用分析法先等价转化所证不等式:要证明1202x x f +⎛⎫<⎪⎝⎭',只需证明121212ln ln 20x x x x x x --<+- 12(0)x x <<,即证明()1212122ln ln x x x x x x ->-+,即证明12112221ln 1x x xx x x ⎛⎫- ⎪⎝⎭>+,再令()120,1x t x =∈,构造函数()()1ln 22h t t t t =+-+,利用导数研究函数()h t 单调性,确定其最值: ()h t 在()0,1上递增,所以()()10h t h <=,即可证得结论. 试题解析:(1) ()g x 的定义域为()0,+∞, ()()122g x ax a x-'=+- 当0a ≤时, ()0g x '>, ()g x 递增当0a >时, ()()()()()2221211122ax a x x ax g x ax a x x x-+-++-'+=-+-==()()10,0,xg x g x a '<递增; ()()1,0,x g x g x a'><递减 综上:∈当0a >时, ()g x 的单调增区间为10,a ⎛⎫ ⎪⎝⎭,单调减区间为1,a ⎛⎫+∞ ⎪⎝⎭当0a ≤时, ()g x 的单调增区间为()0,+∞即证明()1212122ln ln x x x x x x ->-+,即证明()12112221ln *1x x xx x x ⎛⎫- ⎪⎝⎭>+令()120,1x t x =∈,则()()1ln 22h t t t t =+-+ 则()1ln 1h t t t +'=-, ()2110h t t t -'=<' ∈()h t '在()0,1上递减, ()()10h t h ''>=,∈()h t 在()0,1上递增, ()()10h t h <=所以()*成立,即1202x x f +⎛⎫<⎪⎝⎭' 4、已知函数()ln (,f x ax x b a b =+为实数)的图像在点()()1,1f 处的切线方程为1y x =-. (1)求实数,a b 的值及函数()f x 的单调区间;(2)设函数()()1f x g x x+=,证明()()1212()g x g x x x =<时, 122x x +>.5、过点P(−1,0)作曲线f(x)=e x的切线l.(1)求切线l的方程;(2)若直线l与曲线y=a f(x) (a∈R)交于不同的两点A(x1,y1),B(x2,y2),求证:x1+x2<−4.试题分析:(1)先根据导数几何意义求切线斜率y′|x=0=1,再根据点斜式求切线方程y=x+1.因为x1≠x2,不妨设x1<−2,x2>−2.设g(x)=f(x)−f(−4−x),则g′(x)=f′(x)+f′(−4−x)=(x+2)e x(1−e−2(2+x)),当x>−2时,g′(x)>0,g(x)在(−2,+∞)单调递增,所以g(x)>g(−2)=0,所以当x>−2时,f(x)>f(−4−x).因为x2>−2,所以f(x2)>f(−4−x2),从而f(x1)>f(−4−x2),因为−4−x2<−2,f(x)在(−∞,−2)单调递减,所以x1<−4−x2,即x1+x2<−4.。
例析-极端原理-在中考数学中的应用

例析”极端原理”在中考数学中的应用极端原理是一种从特殊对象看问题的方法,它以对象数量上的极端情况(如最大值、最小值、最长、最短等),图形的极限、边缘位置,问题的特殊之处为出发点,寻求解题的突破口和答案.极端原理作为一种解题的思想,在几何,组合,图论,数论等方面都有着广泛的应用.利用这个简单而通俗的原理,可以解决不少与存在性有关的数学问题和极值问题。
在近几年的河南中考数学试题中我们也常会碰到一些求极值的情况,大致分为三类:(1)常利用”小羊喝水原理”解决两条线段之和最短的问题.解决的策略是利用轴对称、构造全等三角形将两条线段的求和问题改造成一条线段,再根据”两点之前线段最短”来说明最短. (2)利用函数的增减性结合自变量的取值范围去确定函数值或自变量值的最大值或最小值.(3)利用图形的极端点或极端位置来取得极端值.下面我以几个中考题为例对如何利用图形的极端点或极端位置来解决极端值问题:例1.(2009 河南第14题)动手操作:在矩形纸片abcd中,ab=3,ad=5.如图1所示,折叠纸片,使点a落在bc边上的a’处,折痕为pq,当点a’在bc边上移动时,折痕的端点p、q也随之移动.若限定点p、q分别在ab、ad边上移动,则点a’在bc边上可移动的最大距离为__________。
分析:说到最值,同学们很容易想到运用函数的有关知识,先找到函数关系式,再利用函数的增减性结合自变量的取值范围去确定函数值的最大值或最小值.我们知道要利用函数必先找到两个变量之间的关系,因为点p、q都为动点,所以要找出ba’与哪个量之间具有明显的函数关系确实困难.于是,我们从另一侧面来进行分析说明.(1)若要得到ba’的最大值,我们可让点a’离点b尽可能远.如图2所示:我们沿∠abc的角平分线折叠,使点a落在bc边上的点a’处.由于点p在ab上移动,当点p与点b重合时点a’离点b 最远,此时ba’=ba=3,即点a’离点b的最远距离为3.(2)接下来探索点a’何时离点b最近.从图2开始,当点a’在bc上向点b靠近的过程中点p和点q位置的变化情况,不难看出,点p会从点b向点a运动,点q会从图②中的位置向点c运动.因为点q只能在ac上运动,所以当点q到点c时达到极限位置,如图3所示,此时点a’离点b最近.由折叠可知da’=da=5,在由勾股定理得,所以 .即点a’离点b的最近距离为1.综合上面两种情况可知,点a’在bc边上移动的最大距离为2.点评:我们通过图形在运动变化过程中的两种极端位置,分别找出点a’离点b的最远位置和最近位置,为解题找到出路,从而化难为易.例2.(2010 河南第15题)如图4,rt△abc中,∠c=90°,∠abc=30°,ab=6.点d在ab边上,点e是bc边上一点(不与点b、c重合),且da=de,则ad的取值范围是________。
2025年中考数学一轮复习课件:第31讲解直角三角形

答案:解:由题意,得∠CHA=∠CHB=90°,CH=60,所以∠A
=60°,∠B=45°.
在Rt△ACH中,AH=
= =20
°
在Rt△BCH中,BH=
= =60.
°
所以AB=AH+BH=20 +60.
答:A,B之间的距离是(20 +60)米.
在Rt△ABC中,∠ACB=45°,所以AB=BC·tan45°=a m.
在Rt△ADB中,∠ADB=42°,所以AB=BD·tan42°≈0.9(22-a)m,
则a=0.9(22-a),解得a≈10.4,所以AB=BC=10.4 m,
即乌当惜字塔AB的高度约为10.4 m.
(2)由(1)得BC=AB=10.4 m,所以BD=CD-BC=22-10.4=11.6(m).
×
=15(米).
在Rt△CAD中,AD=15 米,∠CAD=60°.
因为tan∠CAD=
,所以CD=AD·tan∠CAD=15
所以BC=BD+CD=15+45=60(米).
答:这栋高楼的高BC为60 米.
× =45(米),
12.一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑
.
11.如图,小强从热气球上的A点测量一栋高楼顶部的仰角∠DAB=30°,测量这栋高
楼底部的俯角∠DAC=60°,热气球与高楼的水平距离AD为15 米,求这栋高楼的
高BC.
答案:解:在Rt△BAD中,AD=15 米,∠DAB=30°.
因为tan∠DAB=
,所以BD=AD·tan∠DAB=15
初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)

初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)第 1 页板块一梅涅劳斯定理及其逆定理梅涅劳斯定理:如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点,那么1AF BD CE FB DC EA=.这条直线叫ABC △的梅氏线,ABC △叫梅氏三角形.证法一:如左图,过C 作CG ∥DF证法二:如中图,过A 作AG BD ∥交DF 的延长线于G三式相乘即得:1AF BD CE AG BD DCFB DC EA BD DC AG=??=.证法三:如右图,分别过A B C 、、作DE 的垂线,分别交于123H H H 、、.则有123AH BH CH ∥∥,所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ??=??=.梅涅劳斯定理的逆定理:若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点,如果1AF BD CE FB DC EA=,则F 、D 、E 三点共线.【例1】如图,在ABC △中,AD 为中线,过点C 任作一直线交AB 于点F ,交AD 于点E ,求证::2:AE ED AF FB =.【解析】∵直线FEC 是ABD △的梅氏线,∴1AE DC BF ED BC FA ??=.而12DC BC =,∴112AE BF ED FA ??=,即2AE AF ED BF=.习题1. 在△ABC 中,D 是BC 的中点,经过点D 的直线交AB于点E ,交CA 的延长线于点F .求证:FA EAFC EB=.【解析】直线截ABC △三边于D 、E 、F 三点,应用梅氏定理,知1CD BE AFDB EA FC=,又因为BD BC =,所以1BE AF EA FC ?=,即FA EAFC EB=.习题2. 如图,在△ABC 中,90ACB ∠=?,AC BC =.AM 为BC 边上的中线,CD AM ⊥于点D ,CD 的延长线交AB 于点E .求AEEB.【解析】由题设,在Rt AMC △中,CD AM ⊥,2AC CM =,由射影定理224AD AD AM AC DM DM AM CM===?.对ABM △和截线EDC ,由梅涅劳斯定理,1AE BC MD EB CM DA ??=,即21114AE EB ??=.所以2AE EB=.知识导航夯实基础梅涅劳斯定理与塞瓦定理【例2】如图,在ABC △中,D 为AC 中点,BE EF FC ==,求证:::5:3:2BM MN ND =.【解析】∵直线AE 是BCD △的梅氏线,∵直线AF 是BCD △的梅氏线,习题3. 如图,在ABC △中,D 为BC 的中点,::4:3:1AE EF FD =.求::AG GH AB .【解析】∵HFC 是ABD △的梅氏线,∵D 为BC 的中点,::4:3:1AE EF FD =,∵GEC 是ABD △的梅氏线,【例3】过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ,交CB 的延长线于点D .求证:1BE CFEA FA+=.【解析】作直线AG 交BC 于M ,同理,2CF DCFA DM=,而2BD DC BD BD BM +=++2()2BD BM DM =+=【例4】如图,点D 、E 分别在ABC △的边AC 、AB 上, AE EB =,23AD DC =,BD 与CE 交于点F ,40ABC S =△.求AEFD S .【解析】对ECA △和截线BFD ,由梅氏定理得:1EF CD AB FC DA BE ??=,即32121EF FC ??=,所以13EF FC =.所以1148BFE BEC ABC S S S ==△△△,进而211140115840AEFD ABD BEF ABC S S S S ??=-=-==△△△.习题4. 如图,在ABC △中,三个三角形面积分别为5,8,10.四边形AEFD 的面积为x ,求x的值.【解析】对ECA △和截线BFD ,由梅氏定理得:1CD AB EF DA BE FC ??=,即1823115152x x +??=+,解得22x =.【备选】如图,ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形,其中三个小三角形的面积如图所示,求ABC △的面积.【解析】对ABD △和截线COF ,由梅氏定理得:1AF BC DO FB CD OA ??=,即41132BC CD ??=,所以32BC CD =,所以3BCBD=.所以33105315ABC ABD S S ==?=△△.【例5】如图,在ABC △中,A ∠的外角平分线与边BC 的延长线交于点P ,B ∠的平分线与边CA 交于点Q ,C ∠的平分线与边AB 交于点R ,求证:P 、Q 、R 三点共线.【解析】 AP 是BAC ∠的外角平分线,则BQ 是ABC ∠的平分线,则 CR 是ACB ∠的平分线,则??①②③得非常挑战探索提升第 3 页因R 在AB 上,Q 在CA 上,P 在BC 的延长线上,则根据梅涅劳斯定理的逆定理得:P 、Q 、R 三点共线.习题5. 证明:不等边三角形的三个角的外角平分线与对边的交点是共线的三个点.【解析】如图,CD BE AF 、、分别为三角形ABC 的三个外角平分线,分别交AB AC BC 、、于D E F 、、.过C 作BE 的平行线,则BCP CBE EBD CPB ∠=∠=∠=∠,所以BPC △是等腰三角形.则PB CB =.则有:CE PB CBEA BA BA ==.同理AD AC DB CB =;BF BA FC AC=.所以1CE AD BF CB AC BA EA DB FC BA CB AC ??=??=.所以D E F 、、共线.板块二塞瓦定理及其逆定理塞瓦定理:如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ,如图,那么1BD CE AFDC EA FB=.通常称点P 为ABC △的塞瓦点.证明:∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线,两式相乘即可得:1BD CE AFDC EA FB=.塞瓦定理的逆定理:如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上,并且1BD CE AF DC EA FB=,那么AD 、BE 、CF 相交于一点(或平行).证明:⑴ 若AD 与BE 相交于一点P 时,如图,作直线CP 交AB 于'F .由塞瓦定理得:'1BD CE AF DC EA F B=',又已知1BD CE AF DC EA FB ??=,∴AF AF FB F B'=',∴'F 与F 重合∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点.⑵ 若AD 与BE 所在直线不相交,则AD ∥BE ,如图.∴BD EA DC AC=,又已知1BD CE AF DC EA FB ??=,∴1EA CE AF AC EA FB ??=,即CE FB AC AF=.说明:三线平行的情况在实际题目中很少见.【例6】(1)设AX BY CZ ,,是ABC △的三条中线,求证:AX BY CZ ,,三线共点.探索提升知识导航(2)若AX BY CZ ,,为ABC △的三条内角平分线.求证:AX BY CZ ,,三线共点.【解析】(1)由条件知,BX XC YC YA ZA ZB ===,,.∴1BX CY AZXC YA ZB=,根据塞瓦定理的逆定理可得三条中线AX BY CZ ,,共点.这个点称为这个三角形的重心.(2)由三角形内角平分线定理得:BX AB CY BC AZ ACXC AC YA BA ZB BC===,,.三式分别相乘,得:1BX CY AZ AB BC ACXC YA ZB AC AB BC=??=.根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ,,共点,这个点称为这个三角形的内心.习题6. 若AX BY CZ ,,分别为锐角ABC △的三条高线,求证:AX BY CZ ,,三线共点.【解析】由ABX CBZ △∽△得:BX AB BZ BC =;由BYA CZA △∽△得:AZ ACAY AB =;由AXC BYC △∽△可得:YC BC CX AC =.所以1BX AZ YC AB AC BCBZ AY CX BC AB AC=??=.根据塞瓦定理的逆定理可得三条高线AX BY CZ ,,共点.对直角三角形、钝角三角形,同样也可以证得三条高线共点.我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心.【例7】如图,M 为ABC △内的一点,BM 与AC 交于点E ,CM 与AB 交于点F ,若AM 通过BC 的中点D ,求证:EF BC ∥.【解析】对ABC △和点M 应用塞瓦定理可得:1AF BD CEFB DC EA=.又因为BD DC =,所以1AF CE FB EA ?=.进而AF AEFB EC=,所以EF BC ∥.习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ,两条对角线交于N .求证:直线MN必平分梯形的两底.∵1MD AQ BC DA QB CM=(由塞瓦定理得)板块三梅涅劳斯定理、塞瓦定理综合【备选】如图,E 、F 分别为ABC △的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF 交于点P ,AP 的延长线交BC 于点D .求:AP PD 的值.【解析】∵P 为ABC △的塞瓦点.∵EPB 为ACD △的梅氏线,【备选】如图,四边形ABCD 的对边AB 和DC ,DA 和CB 分别相交于点L K ,,对角线AC 与BD 交于点M .直线KL 与BD 、AC 分别交于点F G 、.求证:KF KGLF LG=.【解析】对DKL △与点B 应用塞瓦定理得:1DA KF LCAK FL CD=.对DKL △和截线ACG 应用梅涅劳斯定理可得:1DA KG LCAK GL CD=.非常挑战进而可得KF KGLF LG.第 5 页。
31类比与联想
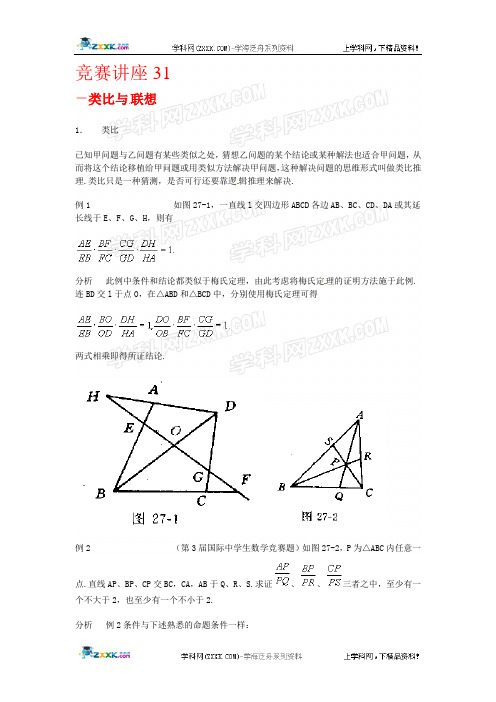
竞赛讲座31-类比与联想1.类比已知甲问题与乙问题有某些类似之处,猜想乙问题的某个结论或某种解法也适合甲问题,从而将这个结论移植给甲问题或用类似方法解决甲问题,这种解决问题的思维形式叫做类比推理.类比只是一种猜测,是否可行还要靠逻辑推理来解决.例1 如图27-1,一直线l交四边形ABCD各边AB、BC、CD、DA或其延长线于E、F、G、H,则有分析此例中条件和结论都类似于梅氏定理,由此考虑将梅氏定理的证明方法施于此例.连BD交l于点O,在△ABD和△BCD中,分别使用梅氏定理可得两式相乘即得所证结论.例2 (第3届国际中学生数学竞赛题)如图27-2,P为△ABC内任意一点.直线AP、BP、CP交BC,CA,AB于Q、R、S.求证、、三者之中,至少有一个不大于2,也至少有一个不小于2.分析例2条件与下述熟悉的命题条件一样:“P为△ABC内任意一点.直线AP、BP、CP交BC、CA、AB于Q、R、S.求证:”这说明可将这个命题的结论用于例2,由知中至少有一个不大于,不妨设≤即3PQ≤AQ.而AQ=AP+AQ,∴AP≥2PQ,∴≥2,即不小于2.[来源:学§科§网Z§X§X§K]同理可证三式中至少有一个不大于2.2.联想[来源:学科网ZXXK]由前面的例题的解决,我们看到类比是与联想交织在一起的.事实上不论用什么方法解决问题都少不了运用“联想”.根据问题之间的相似性、接近性、对比性进行由此及彼的联想,从而将某个已知的结论和方法的全部或部分移植给所研究的新问题是解决问题的一种基本思想方法.[来源:学#科#网]例3 已知0<a<1,0<b<1.求证:+≥分析观察待证式左端,它的每个根式都使我们想到Rt△ABC中的等式a2+b2=c2,激起我们构造平面图形利用几何方法证明这个不等式的大胆想法.[来源:学|科|网]如图27-3,作边长为1的正方形ABCD,分别在AB、AD上取AE=a,AG=b,过E、G分别作AD、AB的平行线,交CD、BC于F、H,EF、GH交于O点.由题设条件及作图可知,△AOG、△BO E、△COF、△DOG皆为直角三角形.∴OC=再连结对角形AC,BD,易知AC=BD=,OA+OC≥AC,OB+OD≥BD,∴≥合理的联想是以正确的观察为基础的.观察所研究的问题的特征和规律,联想似曾相识的问题,便可以迅速地找到一个解决新问题的模式.例4 (柯西不等式)()·()≥(a1b1+a2+b2+…+a n b n)2(其中等号当时成立).分析设a=,c=,b=2(a1b1+a2+b2+…+a n b n),求证不等式变为b2-4ac≤0,这不就是一元二次方程的判别式吗?于是构造下面无相异实根的实系数一元二次方程解此题便是十分自然的事了.设f(x)=()x2-2(a1b1+…+a n b n)·x+(),变形为f(x)=(a1x-b1)2+…+(a n x+b n)2≥0.这说明方程f(x)=0仅当时有相等实根,否则无实根,故f(x)=0的判别式不大于0,即()()≥(a1b1+…+a n b n)2.对于一般性的命题联想它的特殊情况,从研究特殊情形入手常可以找到解决一般问题的方法.例5 (第18届全苏中学生数学竞赛题)数学x(≠0)和y使得对任意的n≥1,数都是某整数的平方数,求这样的x和y.解从最简单的情形入手.如果,那么A是大于40的两位数,并且它的末位数字是2或8,可以验证仅当A=68或98时,A2的百位数6,即682=4624;982=9604.现在来看一般情况,=4·+2(10n+…+10+1)+2=4·10n+1·[来源:学.科.网Z.X.X.K]==[(2·10n+1+4)/3]2==66…682.[来源:学_科_网Z_X_X_K]=(10n-1)10n+2+6·10n+1+4=(10n+1-2)2=.∴x=4,y=2 或x=9,y=0.例6 设P1,P2,…,P n依次为△ABC中∠BAC的n等分线与BC的交点,求证分析先考虑n=2的情形,即“设P1为△ABC的∠BAC的平分线与BC的交点,求证”.这是三角形内角平分线性质,证法很多.因考虑到要证的一般情形的结论是线段的乘积的比,故我们利用三角形的面积公式来证.如图27-4,在△ABP1和△ACP1中,∵∠BAP1=∠CAP1且BP1与CP1边上的高相等,∴即[来源:]再考虑n=3的情形,即“设P1,P2为△ABC的∠BAC的三等分角线与BC的交点,求证[来源:学。
第一讲-极端原理

第3讲 极端原理纵观整个数学历史的发展过程,人们在生产生活和社会实践中,不断地提出自己的猜想,然后努力对提出的猜想加以印证,在一个一个的数学问题不断被解决的过程中,一种种新的思维方式不断的诞生了,从而在一方面推动了社会的进步,另一方面也促进了人们思维品质的提高。
我们在解决数学竞赛问题的时候,往往也需要从多侧面,多角度进行思考。
1893年,数学家塞尔维斯特提出猜想:有限点集N 中含n 个元素,其中n ≥3,所含点不都在同一直线上,则必有一条直线只过点集中的两个点。
为了这一猜想的圆满证明,人们经历了一个漫长的过程,直到1933年,数学家伽莱才给出了对这一问题较为完整的一个证明。
但还是显得很麻烦。
又50年过去了,人们终于找到了一种简单明确的证明方法,使这一问题得到了圆满的解决,这就是极端原理。
例一:有限点集N 中含n 个元素,其中n ≥3,所含点不都在同一直线上,试证有一条直线只过点集中的两个点。
证明:任取一条直线过点集中不只一点,则点集中还有有限个不在该直线上的点,在这有限个点中,总有一点到该直线的距离小于或等于其他各点到该直线的距离,我们取这一点和这条直线作一个点线对的组合,可知这样的组合有有限个,找到其中点线距最小的一组,在这一组中的直线必定只过两点。
若上述直线过三点P 1、P 2、P 3,点P 为到该直线距离最近的点,将点P 与P 1、P 2、P 3中距离最远的点相连则剩下的两点中必有一点到所连直线的距离小于点P 到该直线的距离,如图所示: 例二:有十六个城市参加的足球邀请赛,每一市都派出甲、乙两队参赛,规则规定,同一城市的两队之间不进行比赛,不同城市的两队之间最多比赛一场,比赛若干天后,经统计发现,除A 市的甲队外,其他各队已比赛过的场次各不相同,问A 市的乙队已赛过多少场?3 2 1 P分析:①共32只球队,某队最多可赛30场②统计了31只球队,31只球队比赛的场次分别为0、1、2、3、……、30③运用极端原理的思想对31只已统计的球队进行配对解:将已赛过K 场的球队记为:L (K ),则L (30)已赛过自己该赛的每一场,即与它不同城市的30个队均赛过至少一场;则L (30)与L (0)来自同一城市,同理,L (29)与L (1)来自同一城市,……,L(16)与L(14)来自同一城市,因此L(15)必为A 市乙队,于是可知, A 市乙队已赛15场.例三:试证:任意四面体中,一定可以找到一个顶点,使从这个顶点出发的三条棱可以组成一个三角形的三条边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第31讲极端原理
我们要证明存在具有某种性质的对象,极端原
理告诉我们去找使某函数最大或最小的对象。
——A·恩格尔知识方法扫描
让我们先看一个有趣的放硬币游戏.
两人相继轮流往一张圆桌上平放一枚同样大小的硬币,条件是后放的硬币不能压在先放的硬币上,直到桌子上再也放不下一枚硬币为止。
谁放入了最后一枚硬币谁获胜。
问:先放的人有没有必定取胜的策略?
这是一个古老而值得深思的难题.当有人向一位确有才能的数学家提出这个难题时,引出了如下一段意味深长的对话:
数学家:这有什么难?如果圆桌小到只能容纳一枚硬币,那么先放的人当然能够取胜。
提问者:这还用你讲?简直废话!
数学家:不!这是一个很重要的特殊情况,它的解决将导致一般问题的解决.提问者:怎么解决?
数学家:我先将第一枚硬币放在桌子的中心,利用圆桌的对称性,我就可以获胜.不管是圆桌还是方桌,也不管是桌子有多大,只要有一个对称中心就行.数学家独具慧眼,能从一般性问题中一下子找到一个极易求解的极端情形,并能将极端情形下的解法推向一般,轻而易举地解决了上述难题,而且还作了推广.
这位数学家大概是这样思考的:
一般性的问题比较复杂,先将其极端化,注意到所放硬币总数1
n≥,取其极端情形1
n=即假设桌子小到只能放下一枚硬币,得出特殊问题的解,即先占中心者为胜.然后根据圆桌的对称性,先放者把硬币放在中心位置O,若后放者把硬币放在C处,则先放者把硬币放在中心位置O的对称点C'处,这样只要后放者能放下硬币,先放者总能根据对称性,放下硬币,最后获胜.
这种思考问题的方法称为极端原理.
从问题的极端情况考虑,对于数值问题来说,就是指取它的最大或最小值,如最大或最小的数、最大或最小距离、最大或最小边(角、面积)、得分最多或最少的队员等;对于一个动点来说,指的是线段的端点,三角形的顶点等等。
极端化的假设实际上也为题目增加了一个条件,求解也就会变得容易得多。
经典例题解析
例1设有n(n≥2)名选手进行比赛,任两选手都进行一场比赛,每场比赛均决出胜负.求证:存在选手A,使得其他的任一选手,或是输给A,或是输给被A打败的某一名选手.
证明要寻找的选手A,依直觉,应是“实力”最强的选手.因此,在这n
名选手中,设取胜的场次最多的一名选手为A(考虑极端!).下面证明他满足题目的要求.
对其他的任一选手B ,若B 不是输给A ,即B 胜A.因B 战胜的对手不多于A 战胜的对手,故除A 、B 之外,A 战胜的对手必多于B 战胜的对手,从而,必存在选手C ,是A 战胜的,但不是B 战胜的,即B 输给被A 打败的选手C .故结论成立.
评 注 例1的解法关键是抓住了“取胜的场次最多的一名选手”,利用这一点,解决了我们“无从着手”的难处,使解题简捷明快.
例2 把1600颗花生,分给100只猴子.证明:不管怎样分,至少有4只猴子得到的花生一样多.并设计一种分法,使得没有5只猴子得到的花生一样多.并设计一种分法,使得没有5只猴子得到一样多的花生.
分析与解 要使没有4只猴子得到的花生一样多,我们考虑极端情况:最经济(即所用花生数目最少)的分法是3只得0颗,3只得1颗,…,3只得32颗,还有一只得33颗,这样分需花生数3×(0+1+2+…+32)+33=1617已经超过了花生总数1600颗.所以不管怎样分,至少有4只猴子分得的花生一样多.
没有5只猴子一样多的分法是很多的,例如,对前述极端情况稍作调整可得到一种分法:4只得0颗,3只得1颗,3只得2颗,…,3只得31颗,2只得32颗,还有一只得48颗,共计3×(0+1+2+…+32)-32+48=1600(颗),
例3 平面上给定n 个点(n ≥3),任三点不共线,求证:在这n 个点中存在三个点A 、B 、C ,使其余n-3个点都在△ABC 之外.
分 析 此题有多种思考方法,其中最自然的想法是:面积越小的三角形,其内的点越少,而形外的点越多,所以要使其余n-3个点都在△ABC 之外,自然取面积最小的三角形.
证 明 在n 个点中任取两点B 、C ,作线段BC ,则其余n-2个点都不在BC 所在的直线上,以BC 为底边,其余n-2个点为顶点可得n-2个三角形,取面积最小的,记为△ABC 即为所求,事实上,如果△ABC 内还有—点A ′,则S BC A '∆<S ABC ∆,这与S ABC ∆最小矛盾.
评 注 本题还可从以下几种极端状态着手:
(1)取其余n-2个点到直线BC 的距离最小的一点A ,则△ABC 即为所求;
(2)其余n-2个到BC 的视角最大的点设为A ,则△ABC 为所求;
(3)以B 为顶点,旋转BC ,首先交到的点(或说旋转角最小的点)设为A ,则△ABC 为所求.
以上四种思考方法,从不同角度取定一个几何量,在系统自身状态不断变化时考虑极端情况(最大或最小),使问题迎刃而解.
例4 平面上有n 个点,其中任三点都可组成三角形,且其面积均不超过1,证明存在一个面积不超过4的三角形,它能覆盖住所有n 个点.
分 析 由于面积越大的三角形,覆盖的点越多,所以我
们自然地会想到:从取面积最大的三角形入手.
证 明 平面上由n 个点组成的三角形的数目是有限的,其
中必有一个面积最大的三角形,设为△ABC ,过各顶点分别作
对边的平行线,可得一个新△A ′B ′C ′.如图,
S C B A '''∆=4S ABC ∆,
∵S ABC ∆≤1,∴S C B A '''∆≤4.
平面上所有的n 个点全被△A ′B ′C ′覆盖住,否则设△A ′B ′C ′外有一点P ,则有S PBC ∆>S ABC ∆,这与S ABC ∆最大矛盾.
评 注 由以上三例的分析、证明,我们不难发现利用极端性原理的步骤:选取适当的量——考虑极端状态——反证法证明.
例5 平面上给定n 个点,其中没有三点共线.证明:存在通过其中三个点的圆,它的内部(圆上除外)不包含任何一个已知点.
证明 给定的n 个点总存在具有最小距离的两个
点,不妨设为A 、B .以线段AB 为直径画O ,则其余的2n -个点与A 、B 的距离均不小于AB ,它们都位于O
的外面,将这2n -个点分别与点A 、B 连结,所得视角
依大小顺序排成一列,有
122180.n AP B AP B AP B -∠≤∠≤≤∠<
现过A 、B 、2n P -三点作圆(如图所示),显然该圆内部不包含任何一个已知点,即为所求.
例6 在凸五边形ABCDE 的边和对角线中,没有互相平行的线段.延长边AB 和对角线CE ,使之相交于某个点,然后在边AB 上标上一个箭头,使之指向交点的方向.依此办法把五条边都标上箭头.求证:必有两个箭头指向五边形的同一个顶点.
证 明 考查由凸五边形的每三个相邻顶点所成的五个三角形,其中必有面积最小者.设△ABC 的面积最小.下面证明:BC 边上箭头必指向B 点.
由于DA 不平行于BC(如图),再由S ABC ∆的最小性知S ABC ∆<
S DBC ∆.设M 、N 分别是由A 及D 向BC 所引垂线的垂足,于是DN
>AM .所以,直线AD 与直线BC 交点在CB 的延长线上,且位于
B 的一方.从而,依箭头的标法,B
C 边上的箭头指向B .
同理,AB 边上的箭头指向B .结论得证.
例7 晚会上(2)n n ≥对男女青年双双起舞,设任何一个男青年都未与全部女青年跳过舞,而每个女青年至少与一个男青年跳过.求证:必有两男12,b b 及两女12,g g ,使得1b 与1g ,2b 与2g 跳过舞而1b 与2g ,2b 与1g 均未跳过.
证法1 记与之跳过舞的女青年数最多的男青年之一为1b ,因1b 未与全部女青年跳过,故可找到女青年2g 未与1b 跳过.因2g 至少与一个男青年跳过舞,故存在2b (1b ≠)与2g 跳过.如果凡事与1b 跳过舞的女青年都与2b 跳过,则与2b 跳过舞的P 2 P 1 P K
A B P n -2= C。
