《1.1 空间几何体的结构》测试题
专题14 空间几何体的结构、面积与体积(练)【解析版】

第一篇热点、难点突破篇专题14空间几何体的结构、面积与体积(练)【对点演练】一、单选题1.(2022秋·北京·高三统考阶段练习)已知圆柱的上、下底面的中心分别为1O,2O,过直O O的平面截该圆柱所得的截面是面积为12的正方形,则该圆柱的体积为()线12A.B.12πC.D.则该圆台的体积为()A.36πB.40πC.42πD.45πOO的长度===,1O为ABC的外接圆的圆心,球O的表面积为64π,则1AB BC AC为()B.2C.D.3A【答案】C【分析】由已知求得球O的半径4r=,即可求R=,根据正弦定理求出ABC外接圆半径2出结果.O的半径为r,球O的半径为R.【详解】设圆1依题意得ABC 为等边三角形,则由正弦定理得O 的表面积为如图,根据球的截面性质得2d OA ==的扇形,则该圆锥的侧面积为( ) A .π B .3π2C D .点作球O 的截面,则最小截面的面积为( ) A .3π B .4πC .5πD .6π子,其形状可以看成一个正四面体.广东流行粽子里放蛋黄,现需要在四角状粽子内部放入一个蛋黄,蛋黄的形状近似地看成球,当这个蛋黄的表面积是9π时,则该正四面体的高的最小值为()A.4B.6C.8D.10实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为()A.3:2B.5:4C.5:3D.4:3一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为,则该圆锥的体积为( )A .B .C .D .9π中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),若458h r =,则S 占地球表面积的百分比约为( ) A .26% B .34% C .42% D .50%【答案】C【分析】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,得AOC α∠=,在直角三角形中求出cos α后,可计算两者面积比.【详解】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,如图,则AOC α∠=,r OE =,CE h =,OA CA ⊥,二、填空题10.(2022秋·江苏徐州·高三期末)已知圆柱的高为8,该圆柱内能容纳半径最大的球的表面积为36π,则圆柱的体积为______.【答案】72π【分析】先分析半径最大的球不可能为圆柱的内切球,所以此球是与圆柱侧面与下底面相切的球,就能求出圆柱底面半径,然后根据圆柱的体积公式可得.【详解】圆柱内能容纳半径最大的球的表面积为36π,设此球半径为r,则24π36π3r r=⇒=如果圆柱有内切球,又因为圆柱的高为8,所以内切球半径为43>,说明这个圆柱内能容纳半径最大的球,与圆柱侧面和下底面相切,与上底面相离,易得圆柱底面半径为3,圆柱的体积为2π3872π⋅⨯=故答案为:72π【冲刺提升】一、单选题1.(2022秋·广东东莞·高三统考期末)已知一个装满水的圆台形容器的上底半径为6,下底半径为1,高为,若将一个铁球放入该容器中,使得铁球完全没入水中,则可放入的铁球的体积的最大值为()A.B.C D.108π【答案】B【分析】作出体积最大时的剖面图,分析出此时圆与上底,两腰相切,建立合适直角坐标系,()53,05<<t=-533)32332=模拟预测)某工厂要生产容积为为侧面成本的2倍,为使成本最小,则圆柱的高与底面半径之比应为()A.1B.1C.2D.4 2圆柱上下底的总面积为3.(2022·浙江·模拟预测)如图,正方体1111的棱长为1,,E F 分别为棱BC ,11的中点,则三棱锥1B AEF -的体积为( )A .524B .316C .29D .181AB ES =因为正方体ABCD A B C D -的棱长为1, 所以111(,1,0),(0,1,1),(1,22AE AB AF =-==-的法向量为(,,)n x y z =112n AE x n AB y z ⎧⋅=-⎪⎨⎪⋅=+⎩所以(2,1,1)n =-,F 平面1AB E 的距离为2AF n n-+⋅=又因为1AB =,121122AB EAB S⎫==⋅⎪⎭所以三棱锥故选:AF ,G ,H 分别是SA ,SB ,BC ,AC 的中点,则四边形EFGH 面积的取值范围是( ) A .()0,∞+ B .⎫∞⎪⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭D .1,2⎛⎫+∞ ⎪⎝⎭【答案】B【分析】画出图形,求出,EF HG ,说明EFHG 是矩形,结合图形,说明S 点在ABC 平面时,面积最小,求出即可得到范围 【详解】如图所示:由正三棱锥S ABC -的底面边长是2,因为E 、F 、G 、H 分别是SA 、SB 、BC 、AC 的中点,设ABC 的中心为SC OA >=所以EFGH 所以四边形且4BC =,6BD =,面ABC 与面BCD 夹角正弦值为1,则空间四边形ABCD 外接球与内切球的表面积之比为( )A B C D 【答案】C【分析】根据空间四边形ABCD 的线面关系可得DB ⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱中,根据圆柱的外接球半径求得空间四边形ABCD 的外接球半径R ,又根据内切球的几何性质用等体积法可求得空间四边形ABCD 的内切球半径r ,即可得空间四边形ABCD 外接球与内切球的表面积之比.【详解】解:面ABC 与面BCD 夹角正弦值为1,∴面ABC ⊥面BCD ,又面ABC ⋂面BCD BC =,DB BC DB ⊥⊂面BCD ,DB ∴⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱12O O 中,如下图所示:点在上底面圆周上,ABC三个顶点在下底面圆周上,则圆柱O O的外接球即空间四边连接OA,则球心为为正ABC4sin6032BC=︒1111333ABC ABD ADC BCDS r S r S r S r⋅+⋅+⋅+⋅,,所以()22142132832ADCS=⨯⨯-=,44612ABC ABD ADC BCDS S S S⨯⨯⨯=+++⨯外接球与内切球的表面积之比为6.(2022秋·湖南长沙·高三长郡中学校考阶段练习)三棱锥A BCD -中,AB BC AD CD BD AC ======,则三棱锥A BCD -的外接球的表面积为( )A .20πB .28πC .32πD .36π23AB AD ==且E 为BD 中点,AE BD ∴⊥,AE AB ∴=又AE CE =120, 过BCD △的外心作平面同理过ABD △l l O ''=,易知连接O E ',O 为BCD △又在OO E '中,603=,∴得27O C O O ''=,即外接球半径7=,故外接球表面积28π=.故选:B7.(2022秋·天津河东·高三统考期末)一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的两个底面和三个侧面都相切,若棱柱的体积为)A.16πB.4πC.8πD.32π8.(2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.则该截角四面体的表面积是______.正六边形每个内角均为2π111A B C 中,点P 在棱1BB 上,且1PA PC ⊥,当1APC 的面积取最小值时,三棱锥-P ABC 的外接球的表面积为______.【答案】28π时,1APC 面积取得最小值,补形后三棱锥的外接球,求出外接球半径和表面积【详解】由勾股定理得:AB =,则16PA =(7x y ++1APC S =2169y +,即2x =其中长方体的外接球的直径为,平面PAB ⊥平面PCD ,则P ABCD -体积的最大值为__________.PO ⊥平面ABCD ,PE CD⊥CD平面POE∴⊥,CD OE底面ABCD是边长为∴⊥,CD BCOE⊂平面ABCD OE BC∴,同理可得:OF∥O E F三点共线故,,∥,且有EF BC设平面PAB⋂平面∥AB CD AB,∴∥∥l AB⊥PE CD平面PAB∴⊥平面PEPF⊂平面∴⊥PE PF不妨设PE22∴+x y且2OP=-即2y m11.(2023·广西梧州·统考一模)边长为1的正方形ABCD 中,点M ,N 分别是DC ,BC 的中点,现将ABN ,ADM △分别沿AN ,AM 折起,使得B ,D 两点重合于点P ,连接PC ,得到四棱锥P AMCN -.(1)证明:平面APN ⊥平面PMN ;(2)求四棱锥P AMCN -的体积. ,所以PMN 为直角三角形,即PMN S=111111222AMN ABN ADM CMN ABCD S S S S S =---=-⨯⨯⨯-⨯正方形设点P 到平面AMN 的距离为h ,由A PMN P V V --=1133PMN AMN S PA S h ⋅=⋅△△,即13188h ⨯=,得h =)AMN MCN S S h +=AMCN 的体积为全国·高三对口高考)如题图,是圆锥底面的圆心,ABC 是底面的内接正三角形.P 为DO 上一点,90APC ∠=︒.(1)求证:PC ⊥平面PAB ;(2)若DO =.求三棱锥-P ABC 的体积. 因为ABC 是底面的内接正三角形,CO AB ⊥,PO OC ⋂AB ⊥平面PC ⊂平面AB PC ⊥,PA AB A =,⊥平面PAB(2)解:设圆锥的母线为l,底面半径为r,则圆锥的侧面积为ππ,即,=603所以,在等腰直角三角形APC。
高中数学必修2知识点加例题加课后习题

高中数学必修二第一章 空间几何体1.1空间几何体的结构 1、棱柱定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱'''''E D C B A ABCDE -几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
2、棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
3、棱台定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如四棱台ABCD—A'B'C'D'几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点4、圆柱定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
5、圆锥定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
6、圆台定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
人教A版高中数学必修2第一章 空间几何体1.1 空间几何体的结构习题

1.1空间几何体的结构一.判断正误(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;()(2)圆锥顶点与底面圆周上任意一点的线段是圆锥的母线;(对)(3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;()(4)圆柱的任意两条母线所在的直线是互相平行的.(对)(5)棱垂直于底面的棱柱是直棱柱(对)(6)底面是正多边形的棱柱是正棱柱(7)棱柱的侧面都是平行四边形.(对)(8)有两个面平行,其余各面都是平行四边形的几何体叫棱柱(9)有一个面是多边形,其余各面都是三角形的几何体叫棱锥(10)由五个面围成的多面体一定是四棱锥(11)棱台各侧棱的延长线交于一点(对)(12)棱柱的侧棱都相等,侧面都是全等的平行四边形;(13)存在每个面都是直角三角形的四面体;(对)(14)棱台的侧棱延长后交于一点.(对)(15)棱柱的侧面可以是三角形(16)正方体和长方体都是特殊的四棱柱(对)(17)棱柱的各条棱都相等(18)所有的几何体的表面都展成平面图形(19)有两个平面互相平行,其余各面都是四边形的多面体一定是棱柱;(20)有一个面是多边形,其余各面都是三角形的多面体一定是棱锥;(21)用一个面去截棱锥,底面与截面之间的部分叫棱台;(22)侧面都是长方形的棱柱叫长方体.(23)多面体至少有四个面(对)(24)有两个侧面是矩形的棱柱是直棱柱;(25)各侧面都是正方形的棱柱一定是正棱柱;(26)一个三棱锥四个面可以都为直角三角形.(对)(27)有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱(对)(28)直角三角形的一边为轴旋转一周所得的旋转体是圆锥;(29)以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;(30)一个平面截圆锥,得到一个圆锥和一个圆台.(31)两底面互相平行,其余各面都是梯形,侧棱延长线交于一点的几何体是棱台(对)(32)如图,在透明塑料制成的长方体ABCD﹣A1B1C1D1容器内装进一些水,将容器底面一边BC固定于底面上,再将容器倾斜,随着倾斜度的不同,有下列三个说法:①水的形状始终是棱柱形状;②水面形成的四边形EFGH的面积不改变;③当E∈AA1时,AE+BF是定值.其中正确说法是.(写出所以正确说法的序号)【答案】①③(33)若正棱锥底面边长与侧棱长相等,则该棱锥一定不是()A.三棱锥B.四棱锥C.五棱锥D.六棱锥【答案】D二.多面体和旋转体表面上的最短距离问题1.已知侧棱长为2的正三棱锥S﹣ABC如图所示,其侧面是顶角为20°的等腰三角形,一只蚂蚁从点A出发,围绕棱锥侧面爬行两周后又回到点A,则蚂蚁爬行的最短路程为.【答案】2.如图所示,在三棱柱ABC ﹣A 1B 1C 1中,AA 1⊥底面A 1B 1C 1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC 1=,P 是BC 1上一动点,则A 1P+PC 的最小值是 .【答案】3.如图:已知正三棱锥P ﹣ABC ,侧棱PA ,PB ,PC 的长为2,且∠APB=30°,E ,F 分别是侧棱PC ,PA 上的动点,则△BEF 的周长的最小值为( )【答案】C .224.如图,直三棱柱111C B A ABC -中,1=AB ,2=BC ,5=AC ,31=AA ,M 为线段1BB 上的一动点,则当1MC AM +最小时,△1AMC 的面积为______。
高一数学必修2__1.1空间几何体的结构(练习题)
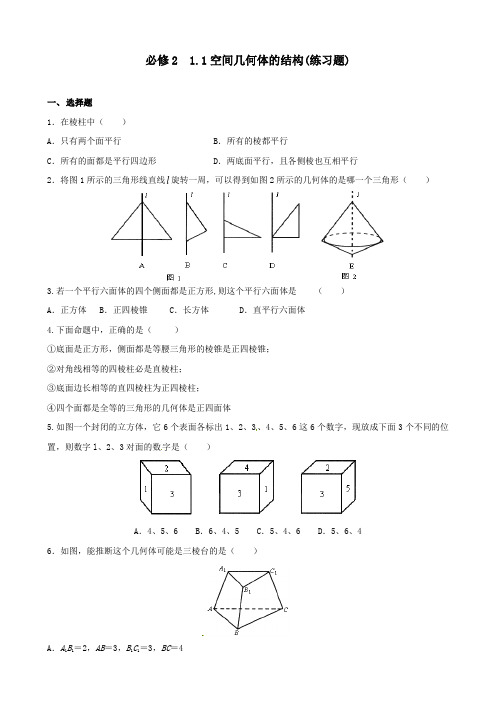
必修2 1.1空间几何体的结构(练习题)一、选择题1.在棱柱中()A.只有两个面平行 B.所有的棱都平行C.所有的面都是平行四边形 D.两底面平行,且各侧棱也互相平行2.将图1所示的三角形线直线l旋转一周,可以得到如图2所示的几何体的是哪一个三角形()3.若一个平行六面体的四个侧面都是正方形,则这个平行六面体是()A.正方体 B.正四棱锥C.长方体D.直平行六面体4.下面命题中,正确的是()①底面是正方形,侧面都是等腰三角形的棱锥是正四棱锥;②对角线相等的四棱柱必是直棱柱;③底面边长相等的直四棱柱为正四棱柱;④四个面都是全等的三角形的几何体是正四面体5.如图一个封闭的立方体,它6个表面各标出1、2、3、4、5、6这6个数字,现放成下面3个不同的位置,则数字l、2、3对面的数字是()A.4、5、6 B.6、4、5 C.5、4、6 D.5、6、46.如图,能推断这个几何体可能是三棱台的是()A.A1B1=2,AB=3,B1C1=3,BC=4B.A1B l=1,AB=2,B l C l=1.5,BC=3,A1C1=2,AC=3C.A l B l=1,AB=2,B1C l=1.5,BC=3,A l C l=2,AC=4D.AB=A1B1,BC=B1C1,CA=C1A17.有下列命题(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;(3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;(4)圆柱的任意两条母线所在的直线是互相平行的.其中正确的是()A.(1)(2) B.(2)(3) C.(1)(3) D.(2)(4)8.下列命题中错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.圆锥的轴截面是所有过顶点的截面中面积最大的一个C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面是全等的等腰三角形9.一个三棱锥四个面中,是直角三角形的最多有()A.1个 B.2个 C.3个 D.4个10.图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是_______________.(注:把你认为正确的命题的序号都填上)11.高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是_______________.三、解答题12.察以下几何体的变化,通过比较,说出他们的特征.13.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,母线长为10cm,求圆锥的母线长__________.。
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
人教版数学高一第一章空间几何体单元测试精选(含答案)3

【答案】 2 1 3 4 2
评卷人 得分
三、解答题
试卷第 8页,总 11页
40.一张长为10cm ,宽为 5cm 的矩形纸,以它为侧面卷成一个圆柱,求该圆柱的体积.
125
【答案】
cm3 或 125
cm3 .
π
2π
41.如图所示,在四边形 ABCD 中, A0, 0 , B 1,0 , C 2,1 , D 0,3 ,将四边
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
【答案】A
8.如图所示,观察四个几何体,其中判断正确的是( ).
A.(1)是棱台 C.(3)是棱锥 【答案】C
B.(2)是圆台 D.(4)不是棱柱
试卷第 2页,总 11页
9.一个球的内接正方体的表面积为 54,则球的表面积为( )
1
PB1= A1B1,则多面体 P-BCC1B1 的体积为( )
4
A.
8 3
C.4
【答案】B
16
B.
3
D.5
评卷人 得分
二、填空题
27.圆台的上底面半径为 2,下底面半径为 3,截得此圆台的圆锥的高为 6,则此圆台
的体积为____________.
【答案】 38 π 3
28.已知在三棱锥 P ABC 中,侧面与底面所成的二面角相等,则点 P 在平面 ABC 内的射影一定是 ABC 的__________心.
所示),则其侧视图的面积是 ( )
A.4 3cm2
B.2 3 cm2
C.8 cm2
D.4 cm2
【答案】A 21.若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为( )
1.1.1空间几何体的结构特征

.
(1)
.
定义 表示方法 棱柱ABCD A1 B1C1 D1 棱柱AC1 斜棱柱 侧棱与底面是否垂直 直棱柱—正棱柱 三棱柱 分类 棱柱 四棱柱 底面边数 五棱柱 侧棱都相等,侧面都是平行四边形 性质 两个底面与平行于底面的截面是全等多边形 过不相邻的两条侧棱的截面是平行四边形
思考题2:
1、侧棱不垂直于底面且底面为三角形 斜三棱柱 的棱柱叫做___________; 2、侧棱垂直于底面且底面为四边形的 直四棱柱 棱柱叫做____________; 3、侧棱垂直于底面且底面为正五边形 正五棱柱 的棱柱叫做____________。
练习.在球内有相距14cm 的两个平行截面,它们的面 积分别是 64πcm2 和 36πcm2,求球的表面积。
1.1.1空间几何体的结构特征
简单几何体
简单多面体
简单旋转体
棱 柱
棱ห้องสมุดไป่ตู้锥
棱 台
球
圆 柱
圆 锥
圆 台
思考题1 例1:下列命题中正确的是( D ) A、有两个面平行,其余各面都是四 边形的几何体叫棱柱。 B、有两个面平行,其余各面都是平 行四边形的几何体叫棱柱。(举例) C、有两个侧面是矩形的棱柱是直棱 柱。(举例) D、有两个相邻侧面垂直与底面的棱 柱是直棱柱。
高一数学空间几何体试题答案及解析
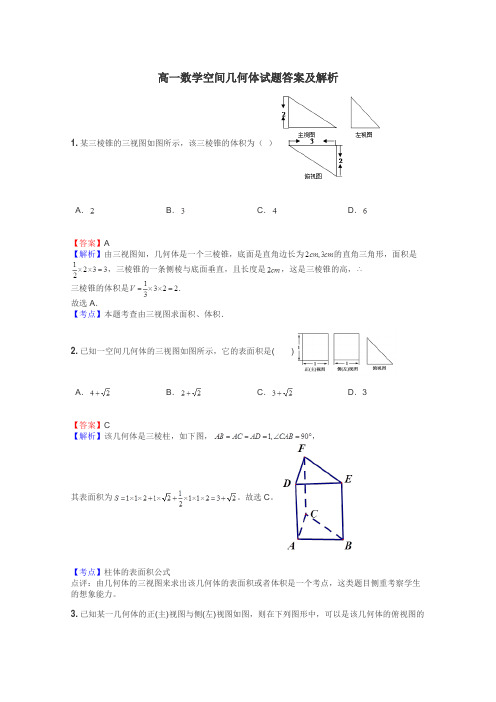
高一数学空间几何体试题答案及解析1.某三棱锥的三视图如图所示,该三棱锥的体积为()A.B.C.D.【答案】A【解析】由三视图知,几何体是一个三棱锥,底面是直角边长为的直角三角形,面积是,三棱锥的一条侧棱与底面垂直,且长度是,这是三棱锥的高,三棱锥的体积是.故选A.【考点】本题考查由三视图求面积、体积.2.已知一空间几何体的三视图如图所示,它的表面积是()A.B.C.D.3【答案】C【解析】该几何体是三棱柱,如下图,,其表面积为。
故选C。
【考点】柱体的表面积公式点评:由几何体的三视图来求出该几何体的表面积或者体积是一个考点,这类题目侧重考察学生的想象能力。
3.已知某一几何体的正(主)视图与侧(左)视图如图,则在下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①③④⑤D.①②③④【答案】D【解析】俯视图为⑤的几何体的侧视图如下,这与题目不相符,而①②③④符合题意。
故选D。
【考点】三视图点评:本题考查简单空间图形的三视图,考查空间想象能力,是基础题.4.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中,是的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求出该几何体的体积;(2)若是的中点,求证:∥平面;(3)求证:平面⊥平面.【答案】(1)4 (2)主要证明∥ (3)主要证明平面【解析】解:(1)由题意可知,四棱锥中,平面平面,,所以,平面,又,,则四棱锥的体积为.(2)连接,则∥,∥,又,所以四边形为平行四边形,∴∥,∵平面,平面,所以,∥平面.(3)∵,是的中点,∴⊥,又在直三棱柱中可知,平面平面,∴平面,由(2)知,∥,∴平面,又平面,所以,平面平面.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定.点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是由面面垂直的性质定理可得AB⊥平面ACDE,(2)的关键是分析出四边形ANME为平行四边形,即AN∥EM,(3)的关键是熟练掌握空间线线垂直,线面垂直与面面垂直之间的相互转化.5.如图是长方体被一平面所截得到的几何体,四边形为截面,长方形为底面,则四边形的形状为( )A.梯形B.平行四边形C.可能是梯形也可能是平行四边形D.不确定【答案】B【解析】因为,长方体中相对的平面互相平行,所以,被平面截后,EF,GH平行且相等,GF,EH 平行且相等,故四边形的形状为平行四边形,选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《1.1 空间几何体的结构》测试题
一、选择题:
1.下左图是由右侧哪个平面图形旋转得到的( ).
考查目的:考查旋转体的概念、简单组合体的特征.
答案:A.
解析:几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得.
2.下列说法正确的是( ).
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
考查目的:考查棱柱、棱锥和棱台的概念和几何特征.
答案:D.
解析:棱台也有两个面平行,其余各面都是四边形,所以排除A;又根据下图排除B,C;只有D符合棱台的定义.
3.(2011广东文)正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( ).
A.20
B.15
C.12
D.10
考查目的:考查空间想象能力及体对角线的概念.
答案:D.
解析:选上底面内的每个顶点,与下底面内不在同一侧面内的两个顶点的连线,可构成正五棱柱的对角线,所以共10条.
二、填空题
4.轴截面是等边三角形的圆锥,它的侧面展开图的圆心角等
于 .
考查目的:考查圆锥的结构,圆锥展开图与圆锥相应量的关系.
答案:.
解析:设圆锥的底面半径为R,则母线长为2R,所以展开所得的扇形半径为2R,弧长为,所以圆心角为.
5.已知棱长都相等的正三棱锥内接于一个球,某学生画出四个过球心的平面截球与正三棱锥所得的图形,如下图所示界面图形正确的是 .
考查目的:考查组合体的特征和组合体的截面图形.
答案:⑴⑵⑶.
解析:因为正三棱锥与球面只有四个公共点,即四个顶点,过正三棱锥的任意三个顶点所做的平面不可能过球心.
6.在长方体中,AB=5,BC=4,,则一只小虫从A点沿长方体的表面爬到点的最短距离是.
考查目的:考查长方体的结构特征,长方体展开图的特征.
答案:.
解析:将长方体展开成为平面图形,在矩形,和中连结,求得对角线长分别为,和,所以小虫从A点沿长方体的表面爬到点的最短距离是.
三、解答题:
7.根据下列对于几何结构特征的描述,说出几何体的名称:
⑴由7个面围成,其中两个面是互相平行且全等的五边形,其他面都是全等的矩形;
⑵一个等腰三角形绕着底边上的高所在的直线旋转形成的封闭曲面所围成的图形;
⑶一个等腰直角三角形绕着底边上所在的直线旋转形成的封闭曲面所围成的图形.
考查目的:考查简单几何体的概念.
答案:⑴五棱柱;⑵圆锥;⑶两个底面重合的全等圆锥.
解析:根据多面体和旋转体的概念可得.
8.若一个几何体有两个面平行,且其余各面均为梯形,则它一定是棱台,此命题是否正确,说明理由.
考查目的:考查棱台的概念,台体与椎体的关系.
答案:不一定,如图所示的多面体的侧棱延长线没有交与一点.
解析:棱台是由平行与棱锥底面的平面截成的.。
