字典树和kmp
字典树(Trie树)实现与应用

字典树(Trie树)实现与应⽤⼀、概述 1、基本概念 字典树,⼜称为单词查找树,Tire数,是⼀种树形结构,它是⼀种哈希树的变种。
2、基本性质根节点不包含字符,除根节点外的每⼀个⼦节点都包含⼀个字符从根节点到某⼀节点。
路径上经过的字符连接起来,就是该节点对应的字符串每个节点的所有⼦节点包含的字符都不相同 3、应⽤场景 典型应⽤是⽤于统计,排序和保存⼤量的字符串(不仅限于字符串),经常被搜索引擎系统⽤于⽂本词频统计。
4、优点 利⽤字符串的公共前缀来减少查询时间,最⼤限度的减少⽆谓的字符串⽐较,查询效率⽐哈希树⾼。
⼆、构建过程 1、字典树节点定义class TrieNode // 字典树节点{private int num;// 有多少单词通过这个节点,即由根⾄该节点组成的字符串模式出现的次数private TrieNode[] son;// 所有的⼉⼦节点private boolean isEnd;// 是不是最后⼀个节点private char val;// 节点的值TrieNode(){num = 1;son = new TrieNode[SIZE];isEnd = false;}} 2、字典树构造函数Trie() // 初始化字典树{root = new TrieNode();} 3、建⽴字典树// 建⽴字典树public void insert(String str) // 在字典树中插⼊⼀个单词{if (str == null || str.length() == 0){return;}TrieNode node = root;char[] letters = str.toCharArray();//将⽬标单词转换为字符数组for (int i = 0, len = str.length(); i < len; i++){int pos = letters[i] - 'a';if (node.son[pos] == null) //如果当前节点的⼉⼦节点中没有该字符,则构建⼀个TrieNode并复值该字符{node.son[pos] = new TrieNode();node.son[pos].val = letters[i];}else//如果已经存在,则将由根⾄该⼉⼦节点组成的字符串模式出现的次数+1{node.son[pos].num++;}node = node.son[pos];}node.isEnd = true;} 4、在字典树中查找是否完全匹配⼀个指定的字符串// 在字典树中查找⼀个完全匹配的单词.public boolean has(String str){if(str==null||str.length()==0){return false;}TrieNode node=root;char[]letters=str.toCharArray();for(int i=0,len=str.length(); i<len; i++){int pos=letters[i]-'a';if(node.son[pos]!=null){node=node.son[pos];}else{return false;}}//⾛到这⼀步,表明可能完全匹配,也可能部分匹配,如果最后⼀个字符节点为末端节点,则是完全匹配,否则是部分匹配return node.isEnd;} 5、前序遍历字典树 // 前序遍历字典树.public void preTraverse(TrieNode node){if(node!=null){System.out.print(node.val+"-");for(TrieNode child:node.son){preTraverse(child);}}} 6、计算单词前缀的数量 // 计算单词前缀的数量public int countPrefix(String prefix){if(prefix==null||prefix.length()==0){return-1;}TrieNode node=root;char[]letters=prefix.toCharArray();for(int i=0,len=prefix.length(); i<len; i++){int pos=letters[i]-'a';if(node.son[pos]==null){return 0;}elsenode=node.son[pos];}}return node.num;} 完整代码:package com.xj.test;public class Trie{private int SIZE = 26;private TrieNode root;// 字典树的根class TrieNode // 字典树节点{private int num;// 有多少单词通过这个节点,即由根⾄该节点组成的字符串模式出现的次数private TrieNode[] son;// 所有的⼉⼦节点private boolean isEnd;// 是不是最后⼀个节点private char val;// 节点的值TrieNode(){num = 1;son = new TrieNode[SIZE];isEnd = false;}}Trie() // 初始化字典树{root = new TrieNode();}// 建⽴字典树public void insert(String str) // 在字典树中插⼊⼀个单词{if (str == null || str.length() == 0){return;}TrieNode node = root;char[] letters = str.toCharArray();//将⽬标单词转换为字符数组for (int i = 0, len = str.length(); i < len; i++){int pos = letters[i] - 'a';if (node.son[pos] == null) //如果当前节点的⼉⼦节点中没有该字符,则构建⼀个TrieNode并复值该字符 {node.son[pos] = new TrieNode();node.son[pos].val = letters[i];}else//如果已经存在,则将由根⾄该⼉⼦节点组成的字符串模式出现的次数+1{node.son[pos].num++;}node = node.son[pos];}node.isEnd = true;}// 计算单词前缀的数量public int countPrefix(String prefix){if(prefix==null||prefix.length()==0){return-1;}TrieNode node=root;char[]letters=prefix.toCharArray();for(int i=0,len=prefix.length(); i<len; i++){int pos=letters[i]-'a';if(node.son[pos]==null){return 0;}else{node=node.son[pos];}return node.num;}// 打印指定前缀的单词public String hasPrefix(String prefix){if (prefix == null || prefix.length() == 0){return null;}TrieNode node = root;char[] letters = prefix.toCharArray();for (int i = 0, len = prefix.length(); i < len; i++){int pos = letters[i] - 'a';if (node.son[pos] == null){return null;}else{node = node.son[pos];}}preTraverse(node, prefix);return null;}// 遍历经过此节点的单词.public void preTraverse(TrieNode node, String prefix){if (!node.isEnd){for (TrieNode child : node.son){if (child != null){preTraverse(child, prefix + child.val);}}return;}System.out.println(prefix);}// 在字典树中查找⼀个完全匹配的单词.public boolean has(String str){if(str==null||str.length()==0){return false;}TrieNode node=root;char[]letters=str.toCharArray();for(int i=0,len=str.length(); i<len; i++){int pos=letters[i]-'a';if(node.son[pos]!=null){node=node.son[pos];}else{return false;}}//⾛到这⼀步,表明可能完全匹配,可能部分匹配,如果最后⼀个字符节点为末端节点,则是完全匹配,否则是部分匹配return node.isEnd;}// 前序遍历字典树.public void preTraverse(TrieNode node){if(node!=null){System.out.print(node.val+"-");for(TrieNode child:node.son){preTraverse(child);}}}public TrieNode getRoot(){return this.root;}public static void main(String[]args){Trie tree=new Trie();String[]strs= {"banana","band","bee","absolute","acm",};String[]prefix= {"ba","b","band","abc",};for(String str:strs){tree.insert(str);}System.out.println(tree.has("abc"));tree.preTraverse(tree.getRoot());System.out.println();//tree.printAllWords();for(String pre:prefix){int num=tree.countPrefix(pre);System.out.println(pre+"数量:"+num);}}}View Code 执⾏结果截图:三、简单应⽤ 下⾯讲⼀个简单的应⽤,问题是这样的: 现在有⼀个英⽂字典(每个单词都是由⼩写的a-z组成),单词量很⼤,⽽且还有很多重复的单词。
数据结构kmp算法

数据结构kmp算法
KMP算法是一种字符串匹配算法,它的全称是Knuth-Morris-Pratt算法。
它的作用是在一个主串中查找一个模式串的出现位置。
该算法的时间复杂度为O(n+m),其中n为主串的长度,m为模式串的长度。
KMP算法的核心是利用已匹配的信息来减少比较次数,以达到提高匹配效率的目的。
具体地,KMP算法采用了一种称为“部分匹配表”的数据结构。
该表用于存储模式串中每个前缀子串的最长公共前后缀长度。
KMP算法的实现过程如下:首先,通过预处理生成部分匹配表,然后从主串的第一个字符开始,依次与模式串进行比较。
如果当前字符匹配成功,则继续比较下一个字符;如果匹配失败,则利用部分匹配表中的信息,移动模式串的位置,直到找到一个新的匹配位置或者模式串到达末尾。
最终,如果找到了模式串在主串中的出现位置,则返回该位置,否则返回-1。
需要注意的是,部分匹配表中的每个元素,都是对应模式串的一个前缀子串的最长公共前后缀长度。
因此,当一个字符匹配失败时,我们可以利用部分匹配表中的信息,跳过已经匹配过的前缀,直接从前缀的最长公共前后缀的下一个位置开始比较。
这样就能够减少比较次数,提高匹配效率。
总之,KMP算法是一种高效的字符串匹配算法,它利用部分匹配表来减少比较
次数,提高匹配效率。
该算法的时间复杂度为O(n+m),其中n为主串的长度,m为模式串的长度。
因此,KMP算法被广泛应用于字符串匹配、文本编辑、自然语言处理等领域。
kmp算法原理

kmp算法原理KMP算法(Knuth-Morris-Pratt算法)是一种用于快速搜索字符串中某个模式字符串出现位置的算法,由Knuth, Morris 和 Pratt于1977年提出。
KMP算法的工作方式如下:首先,给定一个主串S和一个模式串P,KMP算法的第一步就是先构造一个新的模式串P,其中的每一项存储着P中每一个字符前面由不同字符串组成的最长前缀和最长后缀相同的子串。
接着,在S中寻找P,它会从S的第一个字符开始,如果匹配上,就继续比较下一个字符,如果不匹配上,就根据P中相应位置上保存的信息跳到特定位置,接着再开始比较,如此不断循环下去,直到从S中找到P为止。
KMP算法的思路特别巧妙,比较效率很高,它的复杂度为O(m+n),其中m为主串的长度,n为模式串的长度。
它取代了以前的暴力搜索算法,极大地提高了程序的性能。
KMP算法的实现过程如下:(1)首先确定模式串P的每一个字符,构造模式串P的next数组:next[i]存储P中第i个字符之前最长相同前缀和后缀的长度(P中第i个字符之前最长相同前缀和后缀不包括第i个字符);(2)接着从S中的第一个字符开始比较P中的每一个字符,如果字符不匹配,则采用next数组中保存的信息跳到特定位置,而不是暴力比较,以此不断循环,直到从S中找到P为止。
KMP算法是由Don Knuth, Vaughan Pratt和James Morris在1977年提出的。
它的思想是利用之前遍历过的P的信息,跳过暴力比较,可以把字符串搜索时间从O(m×n)降低到O(m+n)。
KMP算法在很多领域有着重要的应用,如文本编辑,模式匹配,编译器设计与多项式字符串匹配等等,都是不可或缺的。
多模算法简介
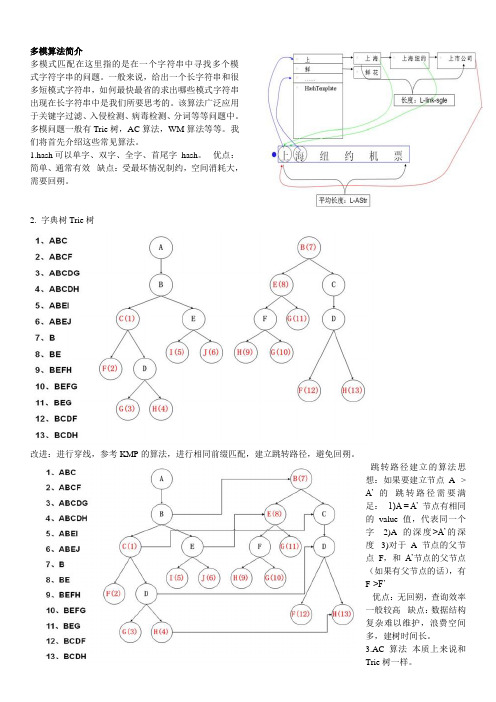
多模算法简介多模式匹配在这里指的是在一个字符串中寻找多个模式字符字串的问题。
一般来说,给出一个长字符串和很多短模式字符串,如何最快最省的求出哪些模式字符串出现在长字符串中是我们所要思考的。
该算法广泛应用于关键字过滤、入侵检测、病毒检测、分词等等问题中。
多模问题一般有Trie树,AC算法,WM算法等等。
我们将首先介绍这些常见算法。
1.hash 可以单字、双字、全字、首尾字hash。
优点:简单、通常有效缺点:受最坏情况制约,空间消耗大,需要回朔。
2.字典树Trie树改进:进行穿线,参考KMP的算法,进行相同前缀匹配,建立跳转路径,避免回朔。
跳转路径建立的算法思想:如果要建立节点A ->A’ 的跳转路径需要满足:1)A = A’ 节点有相同的value值,代表同一个字2)A的深度>A’的深度3)对于A节点的父节点F,和A’节点的父节点(如果有父节点的话),有F->F’优点:无回朔,查询效率一般较高缺点:数据结构复杂难以维护,浪费空间多,建树时间长。
3.AC算法本质上来说和Trie树一样。
转向函数:建立一个根据输入字符转变状态的有限自动机失效函数:当出现状态无法根据输入字符继续走时,需要根据失效函数转化当前状态。
失效函数的建立需要满足:节点r深度之前都已建立失效函数f。
则若有g(r, a) = s,回朔r’=f( r )直至找到g(r’, a) 存在,则将f(s)=g(r’, a)。
和Trie树是一致的。
实际上,如果某状态节点r对输入字符a无路径,则可以将该节点的失效函数f( r )指向的状态节点r’的g(r’, a)作为g(r, a)。
这样在搜索中就不需要专门考虑失效节点的问题了,只需要沿着转向函数一直走。
输出函数:某状态代表着匹配某模式的结束,因此输出函数的值就是匹配成功模式的集合。
因为模式之间可能会有互包含,因此可能有多个成功匹配的模式。
AC算法比Trie树数据结构简单,因此运用广泛。
字典树等等

字典樹的性質
從根節點往下走訪到的每個節點都可能代 表一個字串(字串長度為節點深度-1),不 一定僅限於葉子(為什麼?)。 而每個字串的共同前綴 都只會儲存一次,有著 共同前綴的字串們會被 擺在一起,並從代表從 最長共同前綴以下才開 始分歧。
字典樹的資料結構實作
因為不知道之後字串的數量與長度,所以 通常用指標實現,在節點中加入指向子節 點的指標(亦代表子節點的字元)*Next, 同時,為了判斷字串是存在,在節點中記 錄字串出現次數的count。
1
a b c d e …
查詢字串“ace”
0 a b c d e …
指標尚未建立 查尋失敗
0 a b c d e …
0
a b c d e …
1 a b c d e …
1
a b c d e …
釋放記憶體
當字典樹用完之後,記得要將記憶體釋放, 否則再開一個字典樹的時候空間會不夠用。 釋放的方式可以用遞迴輕鬆實現,釋放記 憶體的複雜度是O(節點個數)。
圖示
0 a b c d e …
虛擬碼
STRUCT TRIE{ 1. INT count ; 2. STRUCT TRIE *Next [|Σ|] ; };
建立一棵字典樹
雖然是以指標建立的,但是還必須要有根 節點才有辦法進行接下來的一連串動作, 需要注意的是,當新增一個節點時(包括 現在的根結點以及之後的子孫),記得要 把裡面的東西歸零。
I’m ROOT!!
CREATE-A-TRIE() 1. root ← new TRIE*
0
a b c d e …
將字串插入/刪除
每個字串都一定會有一個獨一無二的節點 (包含空字串)。 當我們需要加入字串或從字典樹中刪除字 串的時候,就只需要更動該節點的count 值即可。這個節點會在一個深度為長度 +1的節點,可以用O(length)的時間找到 這個節點!
18个查找函数

18个查找函数查找函数是计算机编程中常用的工具之一,用于在给定数据集中快速找到目标元素。
这些函数广泛应用于各种编程语言和领域,包括数据处理、数据库查询、图形算法等。
本文将介绍18个常见的查找函数,并逐步回答与之相关的问题。
1. 线性查找(Linear Search)线性查找是最简单的一种查找方法,它逐个地比较目标元素与数据集中的每个元素,直到找到目标或遍历完整个数据集。
但是,线性查找的时间复杂度较高,适用于小规模数据集或未排序的数据。
问题1:线性查找的时间复杂度是多少?答:线性查找的时间复杂度为O(n),其中n是数据集的大小。
2. 二分查找(Binary Search)二分查找是一种高效的查找算法,要求数据集必须是有序的。
它通过将数据集分成两半,并与目标元素进行比较,从而逐步缩小查找范围。
每次比较都可以将查找范围缩小一半,因此该算法的时间复杂度较低。
问题2:二分查找要求数据集必须是有序的吗?答:是的,二分查找要求数据集必须是有序的,这是保证算法正确性的前提。
3. 插值查找(Interpolation Search)插值查找是对二分查找的改进,它根据目标元素与数据集中最大和最小元素的关系,估算目标所在位置,并逐步逼近目标。
这种方法在被查找的数据集分布较为均匀时能够显著提高查找效率。
问题3:何时应该使用插值查找而不是二分查找?答:当被查找的数据集分布较为均匀时,插值查找能够提供更好的性能。
而对于分布不均匀的数据集,二分查找可能更适用。
4. 斐波那契查找(Fibonacci Search)斐波那契查找是一种利用斐波那契数列的性质进行查找的算法。
它类似于二分查找,但将查找范围按照斐波那契数列进行划分。
这种方法在数据集较大时能够降低比较次数,提高查找效率。
问题4:为什么使用斐波那契数列进行划分?答:斐波那契数列具有递增的性质,能够将查找范围按照黄金分割比例进行划分,使得划分后的两部分大小接近,提高了查找的效率。
AC自动机基础入门

在树中插入单词
在这里的操作对于不同的题目 一般有3种不同的操作。 1:s[ind].count++; 这个是在解决出现总次数的时 候是这样处理的。 2:s[ind],count=1; 这个是在ac自动机上进行dp的 时候经常用的。 3.新加一个标记id。 这个是在处理有哪些单词出现 过。
void make_fail() { qin = qout = 0; int i, ind, ind_f; for(i = 0; i < 26; i++) { if(s[0].next[i] != -1) { q[qin++] = s[0].next[i]; } } while(qin != qout) { ind = q[qout++]; for(i = 0; i < 26; i++) { //找之后的子节点 if(s[ind].next[i] != -1) { q[qin++] = s[ind].next[i]; ind_f = s[ind].fail; while(ind_f > 0 && s[ind_f].next[i] == -1) ind_f = s[ind_f].fail; if(s[ind_f].next[i] != -1) ind_f = s[ind_f].next[i]; s[s[ind].next[i]].fail = ind_f;//子节点的fail根据父节点fail指针的搞定 } } }
AC自动机
by 李翔
AC自动机
• 不是accept自动机。
• 是Aho-Corasick 造出来的。所以你懂的
用途
• 字符串的匹配问题 • 多串的匹配问题 • 例如给几个单词 acbs,asf,dsef, • 再给出一个 很长的文章,acbsdfgeasf • 问在这个文章中,总共出现了多少个单词, 或者是单词出现的总次数。
kmp字典树

KMP自匹过程void getnext(){int i=0,j=-1;next[0]=-1;while(i<m){if(j==-1||b[i]==b[j]){i++;j++;next[i]=j;}else j=next[j];}}1.循环节 if (l%(l-next[l])==0) 循环节最大个数为l/(l-next[l])2.A和B匹配j=-1;for(i=0;i<n;i++){while(j>-1&&b[j+1]!=a[i]) j=next[j];if(b[j+1]==a[i]) j++;if(j==m-1)break;}字典树主程序中需要加root=(Trie *) malloc (sizeof (Trie)); for (int i=0;i<MAX;i++)root->next[i]=NULL;Trie的数据结构定义:1 2 3 4 5 6 7 8 #define MAX 26typedef struct Trie {Trie *next[MAX];int v;//根据需要变化};Trie *root;next是表示每层有多少种类的数,如果只是小写字母,则26即可,若改为大小写字母,则是52,若再加上数字,则是62了,这里根据题意来确定。
v可以表示一个字典树到此有多少相同前缀的数目,这里根据需要应当学会自由变化。
Trie的查找(最主要的操作):(1) 每次从根结点开始一次搜索;(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;(3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
这里给出生成字典树和查找的模版:生成字典树:1 2 3 4 5 6 7 8 910111213 void createTrie(char*str){int len =strlen(str);Trie *p = root, *q;for(int i=0; i<len;++i){int id = str[i]-'0';if(p->next[id]==NULL){q =(Trie *)malloc(sizeof(Trie)); q->v =1;//初始v==1for(int j=0; j<MAX;++j)q->next[j]=NULL;1415161718192021222324 p->next[id]= q;p = p->next[id];}else{p->next[id]->v++;p = p->next[id];}}// p->v = -1; //若为结尾,则将v改成-1表示(视情况而定) }接下来是查找的过程了:1 2 3 4 5 6 7 8 9101112131415 int findTrie(char*str){int len =strlen(str);Trie *p = root;for(int i=0; i<len;++i){int id = str[i]-'0';//根据需要选择是减去'0'还是'a',或者是'A'p = p->next[id];if(p ==NULL)//若为空集,表示不存以此为前缀的串return0;if(p->v ==-1)//字符集中已有串是此串的前缀return-1;}return-1;//此串是字符集中某串的前缀}释放空间1 2 3 4 5 6 7 8 910111213 int dealTrie(Trie* T){int i;if(T==NULL)return0;for(i=0;i<MAX;i++){if(T->next[i]!=NULL)dealTrie(T->next[i]);}free(T);return0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 如果a[i+1]==b[j+1],i和j各加1,什么时候
KMP算法的运行过程
• i = 1 2 3 4 5 6 7 8 9 …… • A=abababaabab… • B=ababacb
j=1234 567 如果a[i+1]!=b[j+1],这时候怎么办? j=5时,a[i+1]!=b[j+1],我们要把j改成比它 小的值j’。改成多少合适呢?
-1,i=0; next[i]={Max{k|0<k<i,其中 ‘0~k-1’ 与‘i-k+1~i-1’ 相匹配}; 0,其他;
KMP算法的运行过程
• 我们用两个指针i和j分别表示,A[i-j+ 1..i]与
B[1..j]完全相等。也就是说,i是不断增加的, 随着i的增加j相应地变化,且j满足以A[i]结尾 的长度为j的字符串正好匹配B串的前 j个字符 (j当然越大越好),现在需要检验A[i+1]和 B[j+1]的关系。 j==m,就说B是A的子串(B串已经整完了)
ba b band abc
Sample Output 2 3 1 0
虽然可以用map, 可是太慢了~ Map方法大家自 己想想哈~
初步分析
假设单词表容量为M,需要统计的前缀数 量为N,单词的平均长度为L,则常规算法 的时间复杂度是? Question: 如果单词表容量很大->查找效率? ->低 更有效率的方法:字典树
j=nest[j]; //对应字符不等,移动到next[j]
}
if(j>T_len) return 1;//匹配成功
else return 0;//匹配不成功
}
求next数组
void getNext(Sstring S){ int i=0,j=-1; next[0]=-1; while(i<len){
用途:数据库里学的索引等以及电子目录查找等
空 词 典
插 入 A
插 入 AN
插 入 ASP
插 入 AS
插 入 ASC
插 入 ASCII
插 入 BAS
插 入 BASIC
Trie的查找(最主要的操作)
(1)在trie树上进行检索总是始于根结点。
(2)取得要查找关键词的第一个字母,并根据该字母 选择对应的子树并转到该子树继续进行检索。
• 通俗地讲,next[i]保存了以s[i]为结尾的后缀与
定义
•
字符串: a b a b a c b next[i] :-1 0 0 1 2 3 0 0
•
•
字符串: a b c a b a b c a b c a b c a b next[i]: -1 0 0 0 1 2 1 2 3 4 5 3 4 5 3 4 5
示例—(HDOJ-1247)
题意:输入一些字符串,输出由别的两个单 词组成的单词。
Sample Input a ahat hat Sample Output ahat hatword
hatword
hziee word
分析:
虽然还是可以用map,但是map太慢了~
前者是字典树的代码,31ms,代码长度1729KB 后者是map的代码 ,359ms,代码长度529KB Map方便,代码好写,但是慢!因为stl都慢! 字典树运行快!效率高! 一旦数据加强或时限变小,则map会TLE了
定义
• next: 为对应模式串的数组 • 设字符串为 s1s2s3...sm ,其中s1,s2,s3,...
si,... sm均是字符,则next[i]=m,当且仅当满 足如下条件:字符串s1s2...sm equals 字符串 s(i-m+1)...si-1 si 并且s1s2...sm s(m+1) unequals s(i-m) s(i-m+1)...si-1 si。 模式串前缀的最长匹配数。
思路:
将每个单词枚举每个分开的位置,比如 ahat可以分成 a hat ah at aha t 这三组,查找这三组单词只要有一组同时存在则 输出ahat;比如a和hat都存在于单词表中。
字典树和map的作用就是查找单词是否存在
Map的方法
• 以上两道例题的参考代码都是动态申请 • 空间,用的指针。 • 以下是一个非指针的字典树的模板, • 不喜欢指针的同学可以看看,数组模
KMP算法的运行过程
• i = 1 2 3 4 5 6 7 8 9 …… • A=abababaabab… • B= ababacb
j= next: 1234 567 0012300
遇到不匹配的时候,KMP算法则将字符串B向后移 动到next[i]位后,重新匹配
KMP算法的运行过程
• i = 1 2 3 4 5 6 7 8 9 …… • A=abababaabab… • B= ababacb
KMP算法的运行过程
• i = 1 2 3 4 5 6 7 8 9 …… • A=abababaabab… • B= ababacb
j= 1234 567
next: 0 0 1 2 3 0 0
暴力算法则将字符串B向后移动一位后,重新匹配
KMP算法的运行过程
• i = 1 2 3 4 5 6 7 8 9 …… • A=abababaabab… • B= ababacb
if(j==m){//模式串匹配到最后一个字母,则表示匹配成功
printf(“匹配成功\n”); return ;} } printf(“无法匹配 ”); }
KMP算法
• 作为一种无回溯的算法,它是高效的,
待会儿你将看到它的时间复杂度为 O(m+n),空间复杂度也为O(m+n)
Hale Waihona Puke • 而且,它很容易理解,代码也很短
ACM暑假培训
字典树、KMP 扩展:扩展kmp、AC自动机、后缀数组
负责任:彭文文 指导人:孟祥凤 哈尔滨理工大学ACM集训队
参考学习资料
图书:
《算法导论》(第二版) ,机械工业出版社,P557~P568 《算法竞赛入门经典训练指南》,P208~P214
练习题:
字典树:
Hdu1075(简单) Hdu1251(简单) Hdu4099(难!字典树+大数相加) KMP: hdu1686(给两个字符串a,s,判断a在s里出现的个数 ) hdu3336(稍难,kmp+dp,给一个字符串,输出所有字符串前缀的总个数)
时间复杂度分析
• 由于while循环的不确定性,好像时间复杂
度很高.
• 但事实上,我们可以看到无论是j还是temp,
它只在程序的最后+1,故最多+n(+m)。因 而while循环最多-n(-m),因而算法的复杂度 都是线性的.
• next的复杂度O(m),KMP的复杂度为O(n)
示例—(hrbust-1309)
拟 提
• 指针,优点是静态开辟,时间快,但 • 前开辟较大的内存,比较耗内存。 • 仅供参考:
相关练习
• HDOJ-1075What Are You Talking About • HDOJ-1251统计难题 • HDOJ-1298T9 • HDOJ-1800 Flying to the Mars • ZOJ-1109
KMP算法
它是:在一个长字符串中匹配一个短 子串的无回溯算法。
定义
• s: 模式串 , m: 模式串的长度 • text: 要匹配的字符串, n:text的长度 • text中能找到与s完全一样的子串,例如:
abcabca中含有abc;认为text与模式串 匹配,当然text也可能与模式串有多处匹 配 s:abc 则text与s 匹配的位置有3和6
(3)接着取得要查找关键词的第二个字母,并进一步 选择对应的子树进行检索。
(4) ... 关键词的所有字母已被取出,则读取附在该结点上 的信息,即完成查找。
Trie的数据结构定义
• • • • •
struct dictree {
dictree *child[26]; //总共26个字母,所以孩子最多 26个! int n; //根据需要变化,可以用来标记是不是尾节 点或者出现次数等!
题意:输入两个字符串s和t,查找字符串s中 是否有t这个字符串。
Sample Input
abcdefg abcde abcde bcdef
Sample Output
yes no
剩下的几页有点小小难噢~不过大家如果真正理解了 kmp,剩下的也好理解喽~课下自学哈~
So easy!
关于next的一个性质
j=
next:
1234 567
0012300
遇到不匹配的时候,KMP算法则将字符串B向后移 动到next[i]位后,重新匹配
KMP伪代码
int KMP(Sstring S,Sstring T){ int i=0,j=0; while( i<=S_len && j<=T_len ) { if(S[i]==T[j] || j==-1) else { ++i;++j; }//匹配则向后移动一位
查找效率分析
• •
•
在trie树中查找一个关键字的时间和树中包含的 结点数无关,而取决于组成关键字的字符数。 (对比:二叉查找树的查找时间和树中的结点 数有关O(log2N)。)
如果要查找的关键字可以分解成字符序列且不 是很长,利用trie树查找速度优于二叉查找树。
若关键字长度最大是5,则利用trie树,利用5次 比较可以从265=11881376个可能的关键字中 检索出指定的关键字。而利用二叉查找树至少 要进行log2265=23.5次比较。
