《数学建模与数学实验》上机报告
数学建模基础实验报告(3篇)
第1篇一、实验目的本次实验旨在让学生掌握数学建模的基本步骤，学会运用数学知识分析和解决实际问题。
通过本次实验，培养学生主动探索、努力进取的学风，增强学生的应用意识和创新能力，为今后从事科研工作打下初步的基础。
二、实验内容本次实验选取了一道实际问题进行建模与分析，具体如下：题目：某公司想用全行业的销售额作为自变量来预测公司的销售量。
表中给出了1977—1981年公司的销售额和行业销售额的分季度数据（单位：百万元）。
1. 数据准备：将数据整理成表格形式，并输入到计算机中。
2. 数据分析：观察数据分布情况，初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立：利用统计软件（如MATLAB、SPSS等）进行线性回归分析，建立公司销售额对全行业的回归模型。
4. 模型检验：对模型进行检验，包括残差分析、DW检验等，以判断模型的拟合效果。
5. 结果分析：分析模型的拟合效果，并对公司销售量的预测进行评估。
三、实验步骤1. 数据准备将数据整理成表格形式，包括年份、季度、公司销售额和行业销售额。
将数据输入到计算机中，为后续分析做准备。
2. 数据分析观察数据分布情况，绘制散点图，初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立利用统计软件进行线性回归分析，建立公司销售额对全行业的回归模型。
具体步骤如下：（1）选择合适的统计软件，如MATLAB。
（2）输入数据，进行数据预处理。
（3）编写线性回归分析程序，计算回归系数。
（4）输出回归系数、截距等参数。
4. 模型检验对模型进行检验，包括残差分析、DW检验等。
（1）残差分析：计算残差，绘制残差图，观察残差的分布情况。
（2）DW检验：计算DW值，判断随机误差项是否存在自相关性。
5. 结果分析分析模型的拟合效果，并对公司销售量的预测进行评估。
四、实验结果与分析1. 数据分析通过绘制散点图，观察数据分布情况，初步判断数据适合使用线性回归模型进行拟合。
2. 模型建立利用MATLAB进行线性回归分析，得到回归模型如下：公司销售额 = 0.9656 行业销售额 + 0.01143. 模型检验（1）残差分析：绘制残差图，观察残差的分布情况，发现残差基本呈随机分布，说明模型拟合效果较好。
数学实验与数学建模上机实习任务
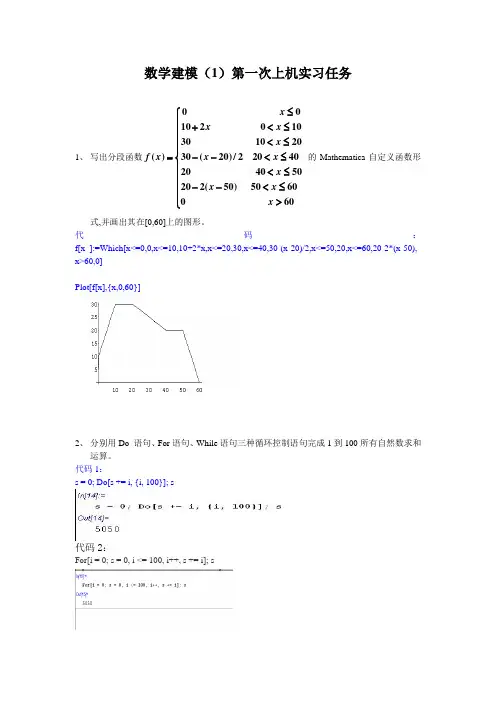
数学建模（1）第一次上机实习任务1、 写出分段函数00102010301020()30(20)/22040204050202(50)5060060x x x x f x x x x x x x ≤⎧⎪+<≤⎪⎪<≤⎪=--<≤⎨⎪<≤⎪--<≤⎪⎪>⎩ 的Mathematica 自定义函数形式,并画出其在[0,60]上的图形。
代码：f[x_]:=Which[x<=0,0,x<=10,10+2*x,x<=20,30,x<=40,30-(x-20)/2,x<=50,20,x<=60,20-2*(x-50),x>60,0]Plot[f[x],{x,0,60}]2、 分别用Do 语句、For 语句、While 语句三种循环控制语句完成1到100所有自然数求和运算。
代码1：s = 0; Do[s += i, {i, 100}]; s代码2：For[i = 0; s = 0, i <= 100, i++, s += i]; s代码3： i = 0; s = 0; While[i <= 100, s += i; i++]; s3、按要求绘制下列函数图形。
（1） s i n ()z x y =，1010,1010x y -≤≤-≤≤。
代码： Plot3D[Sin[x*y],{x,-10,10},{y,-10,10}]（2）在同一坐标系中画出下列三个函数2sin(),,x y x x y e y x =+==的图形，并给坐标横轴和纵轴分别标记为x 和y ，自变量范围为：2020x -≤≤，第一个输出曲线是绿色且线宽为0.06，第二个输出曲线为蓝色，第三个输出曲线为虚线。
代码：Plot[{Sin[x]+x,Exp[x],x^2,x},{x,-20,20},AxesLabel->{"x","y"},PlotStyle->{{RGBColor[0,1,0],T hickness[0.06]},{Dashing[{0.5,0.3}]},{RGBColor[0,0,1]}}]。
数学建模上机实验报告3
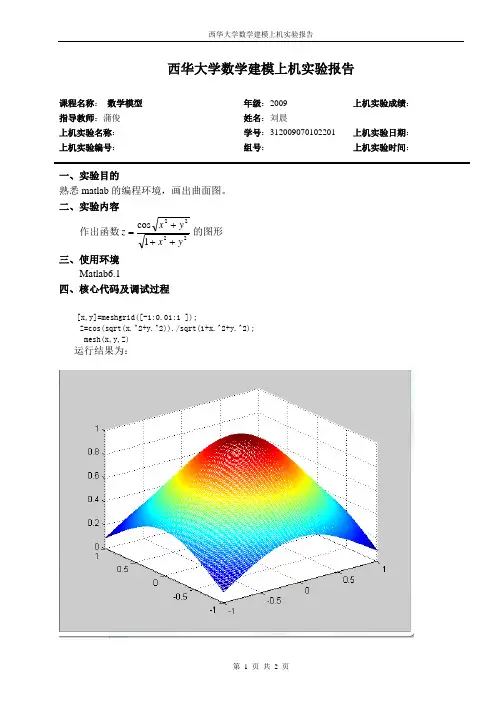
一、实验目的 实验目的 熟悉 matlab 的编程环境，画出曲面图。 二、实验内容 作出函数 z = cos x 2 + y 2 1+ x2 + y2 的图形
三、使用环境 Matlab6.1 四、核心代码及调试过程
[x,y]=meshgrid([-1:0.01:1 ]); Z=cos(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2); mesh(x,y,Z)运行结来自为：第 1 页 共 1 页
西华大学数学建模上机实验报告
五、总结
通过本次实验上机，我基本掌握了对三维图像的画法和 matlab 的编程环,并了解且掌握了画出其图像的函 数。
第 2 页 共 2 页
西华大学数学建模上机实验报告
西华大学数学建模上机实验报告
课程名称 课程名称： 数学模型 名称 指导教师：蒲俊 指导教师 上机实验名称 上机实验名称： 名称 上机实验编号： 上机实验编号 年级：2009 姓名：刘晨 姓名 学号：312009070102201 学号 组号： 上机实验日期： 上机实验日期 上机实验时间： 上机实验时间 上机实验成绩： 上机实验成绩
《数学建模与数学实验》上机实验报告
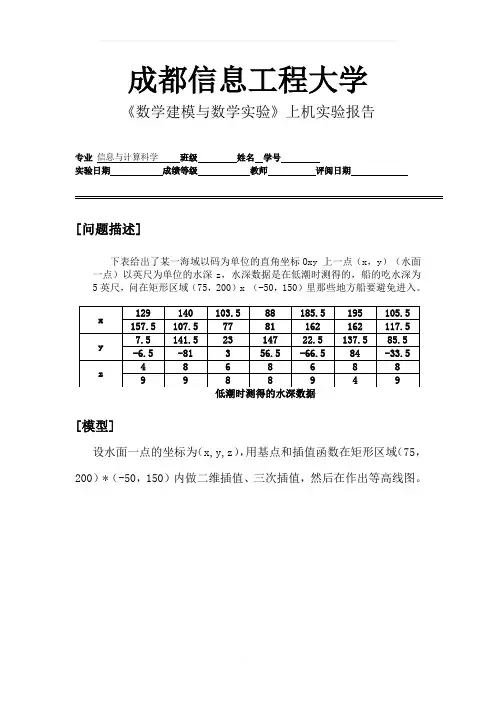
成都信息工程大学《数学建模与数学实验》上机实验报告专业信息与计算科学班级姓名学号实验日期成绩等级教师评阅日期[问题描述]下表给出了某一海域以码为单位的直角坐标Oxy 上一点（x，y）（水面一点）以英尺为单位的水深z，水深数据是在低潮时测得的，船的吃水深为5英尺，问在矩形区域（75，200）x （-50，150）里那些地方船要避免进入。
[模型]设水面一点的坐标为（x,y,z），用基点和插值函数在矩形区域（75，200）*（-50，150）内做二维插值、三次插值，然后在作出等高线图。
[求解方法]使用matlab求解：M文件：water.mx=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5];y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];cx = 75:0.5:200;cy = -50:0.5:150;[cx,cy]=meshgrid(cx,cy);作出曲面图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> meshz(cx,cy,cz)>> xlabel('X'),ylabel('Y'),zlabel('Z')>>作出等高线图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> figure(2)>> contour(cx,cy,cz,[-5,-5],'r')>> hold on>> plot(x,y,'*')>> xlabel('X'),ylabel('Y')[结果]插值结果等值图：[结果分析及结论]根据等值图可看出：红色区域为危险区域，所以船只要避免进入。
《数学建模与数学实验》上机实验报告
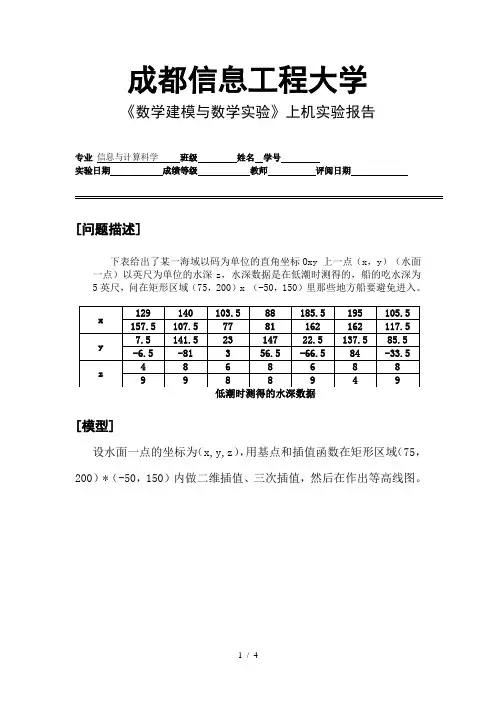
成都信息工程大学《数学建模与数学实验》上机实验报告专业信息与计算科学班级姓名学号实验日期成绩等级教师评阅日期[问题描述]下表给出了某一海域以码为单位的直角坐标Oxy 上一点（x，y）（水面一点）以英尺为单位的水深z，水深数据是在低潮时测得的，船的吃水深为5英尺，问在矩形区域（75，200）x （-50，150）里那些地方船要避免进入。
[模型]设水面一点的坐标为（x,y,z），用基点和插值函数在矩形区域（75，200）*（-50，150）内做二维插值、三次插值，然后在作出等高线图。
[求解方法]使用matlab求解：M文件：water.mx=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5];y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.584 -33.5];z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];cx = 75:0.5:200;cy = -50:0.5:150;[cx,cy]=meshgrid(cx,cy);作出曲面图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> meshz(cx,cy,cz)>> xlabel('X'),ylabel('Y'),zlabel('Z')>>作出等高线图：代码如下：>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> figure(2)>> contour(cx,cy,cz,[-5,-5],'r')>> hold on>> plot(x,y,'*')>> xlabel('X'),ylabel('Y')[结果]插值结果等值图：[结果分析及结论]根据等值图可看出：红色区域为危险区域，所以船只要避免进入。
数学建模实习报告
数学建模实习报告一、实习目的数学建模主要是将显示对象的信息加以翻译、归纳的产物。
通过对数学模型的假设、求解、验证，得到数学上的解答，在经过翻译回到现实对象，给出分析、决策的结果。
数学建模对我们并不陌生，在我们的日常生活和工作中，经常会用到有关建模的概念。
例如，我们平时出远门，会考虑一下出行的路线，以达到既快速又经济的目的；一些厂长为了获得更大的利润，往往会策划出一个合理安排生产和销售的最优方案......这些问题和建模都有着很大的联系。
通过数学建模培训，就会知道解决问题的原理。
学习更多的数学方面的知识及其应用，数学建模的过程可以培养我们全面、多角度考虑问题的能力，使我们的逻辑推理能力和量化分析能力得到很好的锻炼和提高，它还可以让我了解多种数学软件以及如何运用数学软件对模型求解。
二、实习内容（一）实习单位简介西安财经学院统计学院数学建模组是以信息与计算科学系主任王培勋教授为组长的指导教师组，每年都组队参加高教社杯全国大学生数学建模竞赛，并取得了优异的成绩。
今年我院数学建模参赛队员的选拔是经过学生自愿报名、考试选拔、集中培训等环节来进行的。
30 名最后入选的学生，组建了10个队，经过一个暑假的培训，基本全部掌握了数学软件的计算机程序设计方法，掌握了常用的数学建模方法。
在三天三夜的竞赛过程中，各参赛小组学员勇于拼搏，力争创新，在规定的七十二小时内顺利完成了答卷。
（二）实习内容数学建模是运用数学思想、方法和知识解决实际问题的过程，它为我们学生提供了自主学习的空间，有助于我们体验数学在解决实际问题中的价值和作用，体验数学与日常生活和其他学科的联系，体验综合运用知识和方法解决实际问题的过程，增强应用意识；有助于激发我们学习数学的兴趣，发展我们的创新意识和实践能力。
数学建模与数学实验开创了大学生把数学理论和专业知识有机结合的新途径，是培养学生分析问题、解决问题和使用计算机进行科学计算的有效方法，是培养学生创新能力和实践能力的有效手段。
西安交通大学数学建模上机实验报告
问题一某大型制药厂销售部门为了找出某种注射药品销量与价钱之间的关系,通过市场调查搜集了过去30个销售周期的销量及销售价钱的数据,如表.按照这些数据至少成立两个数学模型, 作出图形,比较误差。
问题分析：该问题是通过已知的过去30个销售周期的销量及销售价钱的 数据，来寻觅一个最能反映该药销量与价钱之间的函数曲 线。
在数学上归结为最佳曲线拟合问题。
大体思想：曲线拟合问题的提法:已知一组二维数据，即平面上的n 个点),x i i y （ i=1,2,3.....n ，i x 互不相同，寻求一个函数)(f y x =，使)(x f 在某中准则下与所有数据点最为接近，即曲线拟合得最好。
最小二乘法是解决曲线拟合最常常利用的方式.大体思路：1122 ()()()()m m f x a r x a r x a r x =+++令其中rk(x) 是事前选定的一组函数，ak 是待定系数(k=1,2,…,m,m ＜n), 拟合准则是使n 个点(xi,yi) (i=1,2…,n)，与y=f(xi)的距离 的平方和最小，称最小二乘法准则。
一、系数的肯定22111 (,,)[()]n nm ii i i i J a a f x y δ====-∑∑记求m a a ,,1 使得使J 达到最小.0 (1,,)kJ k m a ∂==∂ 取得关于 m a a ,,1 的线性方程组：11111()[()]0 ()[()]0nmi k k i i i k n mm i k k i i i k r x a r x y r x a r x y ====⎧-=⎪⎪⎪⎨⎪⎪-=⎪⎩∑∑∑∑ 1 ,,().m a a f x 解出，即得散点图： 程序： x=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; y=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; plot(x,y,'r.')通过观察，结合实际情形。
数学建模上机实验报告4
西华大学数学建模基础实验报告课程名称： 数学建模基础 年级： 实验成绩： 指导教师姓名：实验名称：数据拟合与线性规划 学号： 实验日期： 实验编号： 组号：实验时间：一、实验目的学习简单的数据拟合与线性规划。
找出函数关系，解决最值问题。
二、实验内容1．已知飞机下轮廓线上数据如下（1）作数据的点图形。
（2）确定X 和 Y 之间的近似关系。
2．已知下列数据为录像机磁带的测试数据 试求出下列关系bn an t +=23．用MATLAB 或 Lingo 求解线性规划问题6543218121110913min x x x x x x z +++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤++≤++=+=+=+6,,2,1,09003.12.15.08001.14.0500600400x ..654321635241 i x x x x x x x x x x x x t s i4．用MATLAB 或 Lingo 求解线性规划问题m a x 6543216.064.072.032.028.04.0x x x x x x z +++++=85003.003.003.001.001.001.0..654321≤+++++x x x x x x t s70005.002.041≤+x x 10005.002.052≤+x x 90008.003.063≤+x x6,2,10 =≥j x j 5．用MATLAB 或 Lingo 求解线性规划问题X 0 3 5 7 9 11 12 13 14 15 Y1.21.72.02.12.01.81.21.01.6321436min x x x z ++= 120..321=++x x x t s 301≥x5002≤≤x203≥x三、使用环境MATLAB7.0四、核心代码、调试过程及结果1．题（1）X=[0 3 5 7 9 11 12 13 14 15] Y=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6] plot(X,Y,'*')(2)x=polyfit(X,Y,2) x =-0.0249 0.4416 0.0683 >> x=polyfit(X,Y,3) x =0.0012 -0.0517 0.5939 -0.0541>> x=polyfit(X,Y,4) x =0.0004 -0.0123 0.0769 0.2146 0.03003.C=[13 9 10 11 12 8];A=[0.4 1.1 1 0 0 0;0 0 0 0.5 1.2 1.3];b=[800;900];Aeq=[1 0 0 1 0 0;0 1 0 0 1 0;0 0 1 0 0 1]; beq=[400;600;500];VLB=[0;0;0;0;0;0];VUB=[];[x,fval]=linprog(C,A,b,Aeq,beq,VLB,VUB) Optimization terminated.x =1.6518e-0126004.4013e-0134001.4351e-012500fval =138004.c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08];b=[850;700;100;900];Aeq=[]; beq=[];vlb=[0;0;0;0;0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)>> xxgh4Optimization terminated.x =1.0e+004 *3.50000.50003.00000.00000.00000.0000fval =-2.5000e+0045.c=[6 3 4]’;A=[0 1 0];b=[50];Aeq=[1 1 1];beq=[120];vlb=[30,0,20];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)>> xxgh5Optimization terminated.x =30.000050.000040.0000fval =490.0000五、总结通过这个上机，我对MA TLAB解决简单的线性规划问题只能说有初步的了解，但是还是编程起来很吃力。
数学建模实验报告3
1 2 A = 14 1 13 3
1
2 1 1 7 1 5 1 5
4 7 1 2 3
3 5 1 2 1 1
3 5 1 3 1 1
2.(幂法 算法与编程 幂法)算法与编程 幂法 function [lambda,x,k]=Pow_Meth(A,x0,eps,N) %幂法求成对比较阵 A 的主特征值 lambda 及其特征向量 x 幂法求成对比较阵 的主特征值 为迭代初始向量， 为预先给定的精度,N %x0 为迭代初始向量，eps 为预先给定的精度 为最大迭代次数 %k 为迭代次数 n=length(x0); x0=x0/sum(x0); %初始向量 x0 归一化 初始向量 for k=1:N x1=A*x0; x=x1/sum(x1);%归一化 归一化 err=max(abs(x-x0)); if err<=eps break; end x0=x; end lambda=sum(x1./x0)/n; 主程序： 主程序： A=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1;1/3 1/5 3 1 1]; x0=[0.2 0.2 0.2 0.2 0.2]'; eps=1e-5;N=100; [lambda,x,k]=Pow_Meth(A,x0,eps,N)
1 1 2 1 解：层次分析模型 A = 4 1 4 17
2 1 1 3 1 2 1 4
4 3 1 1 2 1
7 2 4 2 1 1 3 1 1 3 4
3.算法与编程 算法与编程 function [lambda,x,k]=Pow_Meth(A,x0,eps,N) %幂法求成对比较阵 A 的主特征值 lambda 及其特征向量 x 幂法求成对比较阵 %x0 为迭代初始向量，eps 为预先给定的精度 为最大迭代次数 为迭代初始向量， 为预先给定的精度,N %k 为迭代次数 n=length(x0); x0=x0/sum(x0); %初始向量 x0 归一化 初始向量 for k=1:N x1=A*x0; x=x1/sum(x1);%归一化 归一化 err=max(abs(x-x0)); if err<=eps break; end x0=x; end lambda=sum(x1./x0)/n;
数学模型上机实验报告
《数学模型》上机实验报告2014-2015学年第二学期专业：信息与计算科学班级：信计122姓名：司后君学号：20121211057上机实验1--证券投资(P130-1)一、问题（1）1、决策变量：投资a,b,c,d,e,的资金分别为x1,x2,x3,x4,x52、目标函数：设获利最大值为z,z=0.043*x1+0.027*x2+0.025*x3+0.022*x4+0.045*x53、约束条件：(2*x1+2*x2+x3+x4+5*x5)/(x1+x2+x3+x4+x5)<=1.4(9*x1+15*x2+4*x3+3*x2+2*x5)/(x1+x2+x3+x4+x5)<=5X2+x3+x4>=400X1+x2+x3+x4+x5<=10004、Lindo/Lingo程序:model:max=0.043*x1+0.027*x2+0.025*x3+0.022*x4+0.045*x5;(2*x1+2*x2+x3+x4+5*x5)/(x1+x2+x3+x4+x5)<=1.4;(9*x1+15*x2+4*x3+3*x2+2*x5)/(x1+x2+x3+x4+x5)<=5;X2+x3+x4>=400;X1+x2+x3+x4+x5<=1000;end5、程序运行结果: Local optimal solution found.Objective value: 31.45000Infeasibilities: 0.000000Extended solver steps: 5Total solver iterations: 26Variable Value Reduced CostX1 400.0000 0.000000X2 0.000000 0.2275000E-01X3 350.0000 0.000000X4 250.0000 0.000000X5 0.000000 0.3550000E-01Row Slack or Surplus Dual Price1 31.45000 1.0000002 0.000000 14.250003 0.000000 0.75000004 200.0000 0.0000005 0.000000 0.3145000E-016、结果说明：由运行结果可知目标函数值为31.4万元，x1投资400万元，x3投资350万元，x4投资250万元。
《数学建模与数学实验》实验报告实验五：线性规划模型实验
《数学建模与数学实验》实验报告实验五：线性规划模型实验专业、班级数学09B 学号094080144 姓名徐波课程编号实验类型验证性学时 2实验（上机）地点同析楼4栋404 完成时间2012-6-10任课教师李锋评分一、实验目的及要求掌握数学软件lingo的基本用法和一些常用的规则，能用该软件进行基本线性规划运算，并能进行的编程，掌握线性规划模型的。
二、借助数学软件，研究、解答以下问题某电力公司经营两座发电站，发电站分别位于两个水库上，已知发电站A可以将A的一万m^3 的水转换成400千度电能，发电站B能将水库B的一万立方米转化成200千度电能。
发电站A，B每个月最大发电能力分别是60000千度，35000千度，每个月最多有50000千度能够以200元/千度的价格出售，多余的电能只能够以140元/千度的价格出售，水库A,B的其他有关数据如下：水库A 书库B水库最大蓄水量2000 1500水源本月流入水量200 40水源下月流入水量130 15水库最小蓄水量1200 800水库目前蓄水量1900 850设计该电力公司本月和下月的生产计划。
本月的情况：解:设本月高价卖出的水量是u，低价卖出的数量是v，A,B书库用来发电的水量好似xa，xb，从水库里放走的水量是ya，yb，水库月末剩余的水量分别是za，zb；建立模型如下：目标函数：、Max=200u+140v约束条件：每个月发电量与卖电量相等：400*x1+200*x2=u+v;水库发电后剩余水量及消耗水量与发电前的水量守恒：X1+y1+z1=2100;X2+y2+z2=890+x1+y1;其他约束条件：400*x1a<=60000;200*x1a<=35000;1200<=z1a<=2000;800<=z2a<=1500;u1<=50000;现在进行两个月同时计算：设本月和下月高价卖出的水量是u1，u2，低价卖出的水量是v1,v2，A,B水库用来发电的水量是xa1,xa2,xb1,xb2,从水库直接放走的水量分别是ya1,ya2,yb1,yb2,水库月末剩余水量分别是za1,za2,zb1,zb2.建立模型如下：目标函数：Max=200*(u1+u2)+140*(v1+v2)约束条件：每个月发电量与卖电量相等：400*xa1+200*xb1=u1+v1;400*xa2+200*xb2=u2+v2;水库发电后剩余水量及消耗水量与发电前的水量守恒：xa1+ya1+za1=2100;xb1+yb1+zb1=890+xa1+ya1;xb2+yb2+zb2=zb2+15+xa2+ya2;xa2+ya2+za2=za1+130;其他约束条件：400*xa1<=60000;400*xa2<=60000;200*xb1<=35000;200*xb2<=35000;1200<=za1<=2000;1200<=za2<=2000;800<=zb1<=1500;800<=zb2<=1500;u1<=50000;u2<=50000;编程实现如下：model:max=200*u+140*v;400*x1+200*x2=u+v;X1+y1+z1=2100;X2+y2+z2=890+x1+y1;400*x1<=60000;200*x2<=35000;Z1>=1200;Z1<=2000;Z2>=800;Z2<=1500;u<=50000;end解得：Global optimal solution found.Objective value: 0.1630000E+08Total solver iterations: 5Variable Value Reduced Cost U 50000.00 0.000000V 45000.00 0.000000X1 150.0000 0.000000 X2 175.0000 0.000000 Y1 0.000000 0.000000 Z1 1950.000 0.000000 Y2 0.000000 0.000000 Z2 865.0000 0.000000Row Slack or Surplus Dual Price1 0.1630000E+08 1.0000002 0.000000 -140.00003 0.000000 0.0000004 0.000000 0.0000005 0.000000 140.00006 0.000000 140.00007 750.0000 0.0000008 50.00000 0.0000009 65.00000 0.00000010 635.0000 0.00000011 0.000000 60.000000编程实现如下：model:max=200*(u1+u2)+140*(v1+v2);400*x1a+200*x2a-u1+v1=0;400*x1b+200*x2b=u2+v2;X1a+y1a+z1a=2100;X2b+y2b+z2b=zb2+15+x1b+y1b;X2a+y2a+z2a=890+x1a+y1a;X1a+y1b+z1b=z1a+130;400*x1a<=60000;400*x1b<=60000;200*x2a<=35000;200*x2b<=35000;Z1a<=2000;Z1a>=1200;Z1b<=2000;Z1a>=1200;Z2a<=1500;Z2a>=800;Z2b>=800;Z2b<=1500;u1<=50000;u2<=50000;end解得：Global optimal solution found.Objective value: 0.3330000E+08Total solver iterations: 0Variable Value Reduced Cost U1 50000.00 0.000000 U2 50000.00 0.000000 V1 50000.00 0.000000 V2 45000.00 0.000000 X1A 0.000000 56000.00 X2A 0.000000 28000.00 X1B 150.0000 0.000000 X2B 175.0000 0.000000 Y1A 900.0000 0.000000 Z1A 1200.000 0.000000 Y2B 0.000000 0.000000 Z2B 800.0000 0.000000 ZB2 810.0000 0.000000 Y1B 0.000000 0.000000 Y2A 990.0000 0.000000 Z2A 800.0000 0.000000 Z1B 1330.000 0.000000Row Slack or Surplus Dual Price1 0.3330000E+08 1.0000002 0.000000 140.00003 0.000000 -140.00004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 60000.00 0.0000009 0.000000 140.000010 35000.00 0.00000011 0.000000 140.000012 800.0000 0.00000013 0.000000 0.00000014 670.0000 0.00000015 0.000000 0.00000016 700.0000 0.00000017 0.000000 0.00000018 0.000000 0.00000019 700.0000 0.00000020 0.000000 340.000021 0.000000 60.00000由上可知，最大值是0.3260000E+08，每月A,B厂发电用水量是150,175,150,175三、本次实验的难点分析实验过程中遇到了一些问题：对掌握lingo的基本用法有所欠缺，本实验中存在偏差。
数学实验与数学建模实验报告
数学实验与数学建模实验报告学院：湘雅医学院专业班级：不告诉你姓名：郝甍学号：完成时间：2012年6月22日承诺书本人承诺所呈交的数学实验与数学建模作业都是本人通过学习自行进行编程独立完成，所有结果都通过上机验证，无转载或抄袭他人，也未经他人转载或抄袭。
若承诺不实，本人愿意承担一切责任。
承诺人：2012年 6 月20 日注意事项如下：1、2012年6月22日(第十八周星期五)之前，将电子文档发送到邮箱：xuanyunqin@（word文档命名：姓名＋学号＋数学实验作业）2、2012年6月22日(第十八周星期五)，将实验报告电子打印稿交到物理楼数学实验室办公室，过时不再受理。
谢谢同学们合作!!!数学实验学习体会（每个人必须要写1500字以上，占总成绩的20%）通过几周的学习，我对MATLAB数学实验与建模有了更生的认识。
我感受到MATLAB强大的运算能力和实用性。
但最深刻的感受就是：要不断地用它。
MATLAB是个好工具，但如果不用他来解决问题，只知道一点语法，那是连皮毛都没有学到的。
还有就是程序设计，对于程序的运行效率非常有帮助。
有的时候，编出来的程序能够运行，但是耗时太长，程序虽然没有错，但是不是和实际应用。
这就需要对程序的结构和算法问题进行改进，要时刻思考多动脑，找到十一的解题途径。
还有就是学习MATLAB要多动手，找一个习题实际操作一下或者找一个实际的程序来动手编一下，才能更好地对MATLAB有所了解，进一步巩固知识。
要在编程的过程中学习，程序需要什么只是再去补充，变成是一点一点积累的，需做一些随手笔记，我就是在这个时候有所懈怠才发懵的。
当然，除了要去用它以外，辅导书可以很大程度上提高我们的知识与技能，通过模仿别人编写的程序，可以大大加快我们掌握它的进度，并且学到一些课堂中所没有的知识.实验一图形的画法1. 做出下列函数的图像：（1）)2sin()(22--=xxxxy，22≤≤-x（分别用plot、fplot）（2）22/9/251x y+=（用参数方程）(3) 在同一图形窗口中，画出四幅不同图形（用subplot命令）：1cos()y x=，2sin(/2)y x pi=-，23cos()y x x pi=-，sin()4xy e=（]2,0[π∈x）（1）>> x=-2:0.001:2;>> y=x.^2.*sin(x.^2-x-2);>> plot(x,y)>> fplot('x.^2.*sin(x.^2-x-2)',[-2,2])（2）>> t=0:0.001:2*pi;>> x=9*cos(t);>> y=25*sin(t);>> plot(x,y)（3）>> x=0:0.01:2*pi;>> figure(1);>> subplot(2,2,1);>> y1=cos(x);>> plot(y1);>> subplot(2,2,2);>> y2=sin(x-pi/2);>> plot(y2);>> subplot(2,2,3);>> y3=(x.^2).*cos(x-pi);>> plot(y3);>> subplot(2,2,4);>> y4=exp(sin(x));>> plot(y4)2作出极坐标方程为)cos1(2tr-=的曲线的图形.>> t=linspace(-2*pi,2*pi,1000);>> r=2*(1-cos(t));>> plot(r) 图1.1.1 图1.1.2图1.1.33 作出极坐标方程为10/t e r =的对数螺线的图形.>> t=0:0.01:2*pi; >> polar(t,exp(t/10))4 绘制螺旋线⎪⎩⎪⎨⎧===t z t y t x ,sin 4,cos 4在区间［0，π4］上的图形.在上实验中，显示坐标轴名称。
《数学建模与实验》实验报告
4.绘制颜色为蓝色，数据点用五角星标识的函数 在(0,5)上的虚线图。
5.在0≤x≤2区间内，绘制曲线y1=2e^(-0.5x)和y2=cos(4πx)，并给图形添加图形标注。
实
验
步
骤
1.在[-2，2]中，以/50为步长取点在同一图形窗口绘出蓝色实线型的Y1=sin(2x)和红色线型的Y2=cos(2x)。
>>subplot(2,2,1);plot(x,y1,'b'),title(' y1=5*x.^1+6');
>>subplot(2,2,2);plot(x,y2,'r'),title(' y2=5*x.^2+6');
>>subplot(2,2,3);plot(x,y3,'k'),title(' y3=5*x.^3+6');
《数学建模与实验》实验报告
实验名称
MATLAB软件绘图
班级
姓名
学号
实验目的
1．熟悉MATLAB基本命令与操作；
2．掌握MATLAB的绘图命令；
实验内容
1.在[-2，2]中，以/50为步长取点在同一图形窗口绘出蓝色实线型的Y1=sin(2x)和红色线型的Y2=cos(2x)。
2.分割图形窗口为4块，分别用不同颜色在第K块上绘y=5x^k+6，并在每一块上标明函数表达式.
>> y2=cos(4*pi*x);
>> plot(x,y1,'-',x,y2,'o');
>>legend('y1','y2')
初中数学建模实验报告(3篇)
第1篇一、实验背景随着科学技术的飞速发展，数学建模作为一种重要的科学研究方法，越来越受到人们的重视。
初中数学建模实验旨在培养学生运用数学知识解决实际问题的能力，提高学生的创新思维和团队协作能力。
本实验以某市居民出行方式选择为研究对象，通过建立数学模型，分析不同因素对居民出行方式的影响。
二、实验目的1. 理解数学建模的基本概念和步骤。
2. 学会运用数学知识分析实际问题。
3. 培养学生的创新思维和团队协作能力。
4. 提高学生运用数学知识解决实际问题的能力。
三、实验方法1. 收集数据：通过网络、调查问卷等方式收集某市居民出行方式选择的相关数据。
2. 数据处理：对收集到的数据进行整理、清洗和分析，为建立数学模型提供依据。
3. 建立模型：根据数据分析结果，选择合适的数学模型，如线性回归模型、多元回归模型等。
4. 模型求解：运用数学软件或编程工具求解模型，得到预测结果。
5. 模型验证：将预测结果与实际数据进行对比，验证模型的准确性。
四、实验过程1. 数据收集：通过问卷调查的方式，收集了500份某市居民的出行方式选择数据，包括出行距离、出行时间、出行目的、出行方式等。
2. 数据处理：对收集到的数据进行整理和清洗，剔除无效数据，得到有效数据490份。
3. 建立模型：根据数据分析结果，选择多元回归模型作为本次实验的数学模型。
4. 模型求解：利用SPSS软件对多元回归模型进行求解，得到以下结果：- 模型方程：Y = 0.05X1 + 0.03X2 + 0.02X3 + 0.01X4 + 0.005X5 + 0.002X6 + 0.001X7 + 0.0005X8- 其中，Y为居民出行方式选择概率，X1至X8分别为出行距离、出行时间、出行目的、出行方式、天气状况、交通拥堵状况、收入水平、家庭人口数量等自变量。
5. 模型验证：将模型预测结果与实际数据进行对比，结果显示模型具有较高的预测准确性。
五、实验结果与分析1. 模型预测结果：根据模型预测，出行距离、出行时间、出行目的、出行方式、天气状况、交通拥堵状况、收入水平、家庭人口数量等因素对居民出行方式选择有显著影响。
《数学建模与实验》实验报告
1、输入数据： >> x=[20 25 30 35 40 45 50 55 60 65]'; 实 X=[ones(10,1) x]; Y=[13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3]'; [b,bint,r,rint,stats]=regress(Y,X) 验 b,bint,stats 得出结果： >> b = 步 9.1212 0.2230 bint = 骤 8.0211 0.1985 Stats = 0.9821 439.8311 0.0000 10.2214 0.2476
2 ˆ t 得回归模型： s 9.1329 65.8896 489.2946t
《数学建模与实验》实验报告
实验名称 班级 实验目的 数学 09-1 实验六 MATLAB 回归分析 姓名 学号 25 号
1.熟悉 MATLAB 基本命令； 2.掌握回归分析的方法。 1、考察温度 x 对产量 y 的影响，测得下列 10 组数据：
温度（℃） 20 产量（kg） 13.2 25 15.1 30 16.4 35 17.1 40 17.9 45 18.7 50 19.6 55 21.2 60 22.5 65 24.3
从残差图可以看出，所有数据的残差离零点均较近，且残差 的置信区间均包含零点，这说明回归模型 y=9.1212+0.2230x 能较好的符合原始数据. 预测及作图： >> z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r') 当 x=42℃时，产量估值 z=18.4885 . 预测区间：[16.3581，20.6206]（置信度 95%） 2、作二次多项式回归： >>xi =0:2:20; yi =[0.6 2.0 4.4 7.5 11.8 17.1 23.3 31.2 39.6 49.7 61.7]; [p,S]=polyfit(xi, yi,2) 得到结果： p= 0.1403 S= R: [3x3 double] df: 8 normr: 1.1097
数学建模实验报告
《数学建模实验报告》Lingo软件的上机实践应用简单的线性规划与灵敏度分析学号：班级:姓名：日期：2010—7—21数学与计算科学学院一、实验目的：通过对数学建模课的学习，熟悉了matlab和lingo等数学软件的简单应用，了解了用lingo软件解线性规划的算法及灵敏性分析。
此次lingo上机实验又使我更好地理解了lingo程序的输入格式及其使用，增加了操作连贯性，初步掌握了lingo软件的基本用法，会使用lingo计算线性规划题，掌握类似题目的程序设计及数据分析。
二、实验题目（P55课后习题5）：某工厂生产A、2A两种型号的产品都必须经过零件装配和检验两道工序，1如果每天可用于零件装配的工时只有100h，可用于检验的工时只有120h，各型号产品每件需占用各工序时数和可获得的利润如下表所示：（1)试写出此问题的数学模型，并求出最优化生产方案.（2）对产品A的利润进行灵敏度分析1（3）对装配工序的工时进行灵敏度分析（4)如果工厂试制了A型产品，每件3A产品需装配工时4h,检验工时2h，可获3利润5元，那么该产品是否应投入生产？三、题目分析：总体分析：要解答此题，就要运用已知条件编写出一个线性规划的Lingo 程序，对运行结果进行分析得到所要数据；当然第四问也可另编程序解答.四、 实验过程：(1)符号说明设生产1x 件1A 产品,生产2x 件2A 产品.（2）建立模型目标函数：maxz=61x +42x 约束条件：1） 装配时间：21x +32x <=100 2） 检验时间：41x +22x <=120 3） 非负约束：1x ，2x >=0所以模型为： maxz=61x +42xs.t 。
⎪⎩⎪⎨⎧>=<=+<=+0,1202410032212121x x x x x x（3）模型求解：1）程序model:title 零件生产计划; max=6*x1+4＊x2; 2*x1+3*x2<=100; 4*x1+2＊x2<=120； end附程序图1：2）计算结果Global optimal solution found。
专业数学建模实验报告一
Solve[4*x^3+a*b*x^2+2*a*b*x+a*b0,x]
{{x-((a b)/12)-(24 ab-a2b2)/(12 (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3)+1/12 (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3},{x-((a b)/12)+((1+ ) (24 ab-a2b2))/(24 (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3)-1/24 (1- ) (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3},{x-((a b)/12)+((1- ) (24 ab-a2b2))/(24 (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3)-1/24 (1+ ) (-216 ab+36 a^2 b^2-a^3 b^3+24 )1/3}}
（一）利用中心差分公式，即 ，借助数学软件，从P10表1中的数据出发，重新计算教材P11中的表2和P12表3。
[主要使用的Mathematica语句：Table，Fit及循环控制语句]
【解】：给出你的计算或分析步骤、结ห้องสมุดไป่ตู้，列出必要的程序清单等
P11表2
程序代码如下：
%人口数据处理拟合
data1=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4 281.4];
数学建模与数学实验
数学建模与数学实验在当今的科学和技术领域，数学的应用日益广泛且深入。
数学建模与数学实验作为数学与实际问题相结合的重要手段，正发挥着越来越关键的作用。
数学建模，简单来说，就是将现实世界中的实际问题转化为数学问题，并通过建立数学模型来解决。
它就像是一座桥梁，连接着抽象的数学理论和具体的现实情境。
比如，在交通规划中，我们需要考虑如何优化道路布局以减少拥堵。
这时候，就可以通过数学建模，将道路的流量、车辆的速度、路口的通行能力等因素用数学语言描述出来，然后运用数学方法进行分析和求解，从而得出最佳的规划方案。
数学建模的过程并非一蹴而就，而是一个复杂且充满挑战的过程。
首先，需要对问题进行深入的理解和分析，明确问题的本质和要求。
这就像是医生在诊断病情，必须先了解患者的症状、病史等信息，才能做出准确的判断。
接下来，要对问题进行合理的简化和假设。
因为现实问题往往非常复杂，包含众多的因素，如果不进行简化，很难建立有效的数学模型。
但简化的同时也要注意不能过度，否则会导致模型与实际情况偏差过大。
然后，就是选择合适的数学工具和方法来建立模型。
这就如同选择合适的工具来完成一项工作，只有选对了工具，才能高效地解决问题。
数学实验则是对数学建模的补充和验证。
它通过实际的操作和计算，来检验模型的正确性和有效性。
在数学实验中，我们可以利用计算机软件和工具，对建立的数学模型进行数值计算、模拟仿真等操作。
例如，在研究物体的运动轨迹时，可以通过数学实验来模拟不同初始条件下物体的运动情况，从而验证所建立的数学模型是否能够准确地描述物体的运动规律。
数学实验不仅能够帮助我们验证模型，还能让我们更加直观地理解数学模型所描述的现象。
有时候，抽象的数学公式和理论可能让人感到难以理解，但通过数学实验，将其转化为具体的图像、数据等，就能让人更容易接受和掌握。
数学建模与数学实验对于培养我们的创新能力和解决实际问题的能力具有重要意义。
在解决实际问题的过程中，我们需要不断地思考、尝试新的方法和思路，这无疑能够激发我们的创新思维。
数学建模与创新数学实验实验报告(统一模板)
《数学建模与创新数学实验》课程实验报告姓名学号完成时刻年月日基础教学学院数学教学部实验目的：1、 掌握Matlab 的大体操作和大体运算。
2、 掌握模糊集和隶属度函数概念。
3、 掌握模糊评价方式的适用范围和一般步骤。
一、大体编程（第1题15分，第2题5分，第三题20分，共40分）要求：写出完成下列运算的程序，并给出计算结果。
（#表示学号的最后一名 ##表示学号的后两位）1. 别离将数字6，向量[]1#3和矩阵1234#6789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦录入给变量x ，a 和M ，并计算 （1）x 与a 的乘积；（2）a 的共轭转置b ；（3）M 与b 的乘积；（4）M 的特征值p 。
clear all;clcx=6;a=[1 6 3];M=[1 2 3;4 6 6;7 8 9];>> x*aans =6 36 18>> b=a'b =163>> M*bans =225882>> p=eig(M)p =2.叙述如何将给定类型的数据文件,,读入matlab，并别离赋值给变量DataTxt, DataXls和DataMat。
DataTxt=textread(‘’)DataXls=xlsread(‘’)DataMat=importdata('')3.假定在C:\MATLAB7\work目录下存储有图片数据，，……,。
利用matlab自带函数imread，编程将这些图片读入matlab，并赋值给变量DataPicclear all;clcA1=imread(‘C:\MATLAB7\work\’)A2= imread(‘C:\MATLAB7\work\’)A3= imread(‘C:\MATLAB7\work\’)A4= imread(‘C:\MATLAB7\work\’)A5= imread(‘C:\MATLAB7\work\’)A6= imread(‘C:\MATLAB7\work\’)A7= imread(‘C:\MATLAB7\work\’)A8= imread(‘C:\MATLAB7\work\’)A9= imread(‘C:\MATLAB7\work\’)A 10= imread(‘C:\MATLAB7\work\’)DataPic=[A1,A2,A3,A4,A5,A6,A7,A8,A9,A10]二、模糊综合评价（60分）按照教材第6章：模糊综合评价决策建模，回答以下问题：1、设论域{}123456{,,,,,}40,50,60,70,80,90X x x x x x x ==表示六个身高均为170cm 的学生的体重（单位：千克），X 上的一个模糊集“胖子”(记作M )的隶属函数概念为 40()9040M x x μ-=-． (1) 编写一个matlab 函数,用于计算体重为x 千克学生的隶属度,给出程序;(2) 用序偶表示法表示模糊集M .2、设()0.30.350.1R =，0.30.50.20.20.20.20.30.40.2S ⎛⎫ ⎪= ⎪ ⎪⎝⎭，编程计算T R S =．3、以同窗购买电脑或衣饰为例，说明模糊综合评价方式的一般步骤。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《数学建模与数学实验》上机报告（第 1 次）一、上机训练目的、题目或内容（简述综述）等题目一：数学软件（MathType5.2、MATLAB 、Maple、Mathematica4.0、LINGO8.0）安装调试；基本命令使用（变量赋值、定义函数、过程控制、绘图命令、拟合、线性规划、非线性规划）；高等数学实验（绘图，极限，求导，积分，解微分方程）；线性代数实验（矩阵基本运算，线性方程组求解，解超定方程组，优化命令）。
调试运行给定的两个程序：题目二：1、以两种方式打开MATLAB 工作窗口，进入MATLAB 6.0 的工作环境，并尝试用不同的方式退出。
（这个在报告里面说明方法就可以）2、尝试、熟悉MATLAB 6.0 的各栏菜单以及各个工具栏的功能。
（自己掌握，报告里面就不写了）3、绘制函数y=cos(5x+2)/sin(3x+1) 的图像，并求解当x=2 时的函数值。
4、练习并熟练掌握MATLAB 的帮助命令，学会利用MATLAB 的帮助信息。
5、求矩阵Ａ=的行列式、逆的特征根；Ｂ=，解方程ＢＸ=6、两个矩阵Ａ=Ｂ=将矩阵改为3行3列的矩阵，作加、减、乘和除（左除，右除）运算，同事运用数组运算法则进行运算，比较二者计算结果有何异同。
二、数学模型或求解分析或算法描述程序命令图形等题目一：1) c=[6,3,4];A=[0,1,0];b=[50];Aeq=[1,1,1];beq=[120];vlb=[30,0,20];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)2) function f=fun3(x);f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2x0=[1;1];A=[2 3 ;1 4]; b=[6;5];Aeq=[];beq=[];VLB=[0;0]; VUB=[];[x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,VLB,VUB)题目二：3. x=2;y=cos(5*x+2)./sin(3*x+1)x=[-10:0.01:10];y=cos(5*x+2)./sin(3*x+1);plot(x,y)5. A=[8 1 -5 1;9 -3 0 -6;-5 2 -1 2;0 4 -7 6]det(A)inv(A)[V,D]=eig(A)6.B=[1 3 5;2 4 6; 7 8 9;1 0 1]b=[1;2;3;1]X=B\b三、结果或结论或截图四、结果分析讨论或评价、推广、小结等运用数学软件求解相关数学问题更加简便，省去了繁琐的计算过程，所求的结果也准确可靠。
可以广泛推广到各个领域应用。
《数学建模与数学实验》上机报告（第 2 次）一、上机训练目的、题目或内容（简述综述）等题目三：1、创建一个表达式Ζ= ,并求当x=1,y=2是的z值。
2、按照的步长间隔绘制函数在0时的曲线。
3、用曲面画图命令surf表现函数的图像。
4、作函数的图标，并用所有的修饰命令进行修饰。
5、计算积分：（1）（2）6、求函数的导数（1）（2）题目四：1、用while循环写一个1~200之间的整数和。
2、编写一个M文件，画出下列分段函数所表示的曲面。
=二、数学模型或求解分析或算法描述程序命令图形等题目三：1、 x=1;y=2;z=(sqrt(4*x^2+1)+0.5457*exp(-0.75*x^2-3.75*y^2-1.5*x))/(2*sin(3*y)-1)2、 x=0:0.1:1;y=x.*exp(-x);plot(x,y);3、[x,y]=meshgrid(-1:0.02:1);z=x.^2+y.^2;surf(x,y,z)axis equal4、y=tan(sin(x))-sin(tan(x));plot(x,y)xlabel('x')ylabel('y')title('这是一个图','fontsize',20);5、(1)syms xy=int((exp(x)-1)^4)*exp(x);yy=int(y,x,0,1)(2)syms xy=(2*x)/(x^2+1);yy=int(y,x,0,inf)6、(1)syms xf=sym(2^(x/log10(x)));diff(f)(2)syms x af=(1/2*a)*(log10(sqrt(a^2+x^2)/a+x)-a/(a+x));diff(f)题目四：start=1en=200sum=0while start<=ensum = start + sum;start = start + 1;endsum三、结果或结论或截图题目三：1、2、3、4、5、(1)(2)6、(1)(2)题目四：四、结果分析讨论或评价、推广、小结等《数学建模与数学实验》上机报告（第 3 次）一、上机训练目的、题目或内容（简述综述）等题目五：利用Matlab 求解线性规划问题线性规划是一种优化方法，Matlab 优化工具箱中有现成函数linprog 对如下式描述的LP 问题求解：% min f'x% s.t .(约束条件)：Ax<=b% (等式约束条件)：Aeqx=beq% lb<=x<=ublinprog 函数的调用格式如下：x=linprog(f,A,b)x=linprog(f,A,b,Aeq,beq)x=linprog(f,A,b,Aeq,beq,lb,ub)x=linprog(f,A,b,Aeq,beq,lb,ub,x0)x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)[x,fval]=linprog(…)[x, fval, exitflag]=linprog(…)[x, fval, exitflag, output]=linprog(…)[x, fval, exitflag, output, lambda]=linprog(…)其中：x=linprog(f,A,b)返回值x 为最优解向量。
x=linprog(f,A,b,Aeq,beq) 作有等式约束的问题。
若没有不等式约束，则令A=[ ]、b=[ ] 。
x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options) 中lb ,ub 为变量x 的下界和上界，x0 为初值点，options 为指定优化参数进行最小化。
Options 的参数描述：Display 显示水平。
选择’off’不显示输出；选择’Iter’显示每一步迭代过程的输出；选择’final’显示最终结果。
MaxFunEvals 函数评价的最大允许次数Maxiter 最大允许迭代次数TolX x 处的终止容限[x,fval]=linprog(…) 左端fval 返回解x 处的目标函数值。
[x,fval,exitflag,output,lambda]=linprog(f,A,b, Aeq,beq,lb,ub,x0) 的输出部分：exitflag 描述函数计算的退出条件：若为正值，表示目标函数收敛于解x 处；若为负值，表示目标函数不收敛；若为零值，表示已经达到函数评价或迭代的最大次数。
output 返回优化信息：output.iterations 表示迭代次数；output.algorithm 表示所采用的算法；outprt.funcCount 表示函数评价次数。
lambda 返回x 处的拉格朗日乘子。
它有以下属性：lambda.lower-lambda 的下界；lambda.upper-lambda 的上界；lambda.ineqlin-lambda 的线性不等式；lambda.eqlin-lambda 的线性等式。
1 某厂生产甲乙两种口味的饮料,每百箱甲饮料需用原料6 千克,工人10 名,可获利10 万元;每百箱乙饮料需用原料5 千克,工人20 名,可获利9 万元.今工厂共有原料60 千克,工人150 名,又由于其他条件所限甲饮料产量不超过8 百箱.问如何安排生产计划,即两种饮料各生产多少使获利最大.进一步讨论:1)若投资0.8 万元可增加原料1 千克,问应否作这项投资.2)若每百箱甲饮料获利可增加1 万元,问应否改变生产计划.2 某农场I、II、III 等耕地的面积分别为100 hm2、300 hm2 和200 hm2，计划种植水稻、大豆和玉米，要求三种作物的最低收获量分别为190000kg、130000kg 和350000kg。
I、II、III 等耕地种植三种作物的单产如表5.1.4 所示。
若三种作物的售价分别为水稻1.20 元/kg，大豆1.50 元/kg，玉米0.80 元/kg。
那么，（1）如何制订种植计划，才能使总产量最大？（2）如何制订种植计划，才能使总产值最大？表 1题目六：无约束优化问题求下列函数的极小点，极小值（1）（2）（3）二、数学模型或求解分析或算法描述程序命令图形等题目五：c=[-10 -9];A=[6 5;10 20;1 0];b=[61;150;800];Aeq=[];beq=[];vlb=[0;0];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)2）c=[-11 -9];A=[6 5;10 20;1 0];b=[60;150;8];Aeq=[];beq=[];vlb=[0;0];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)2c=[11 9 9 8 6 6 14 12 10];A=[11000 9500 9000 0 0 0 0 0 0;0 0 0 8000 6800 6000 0 0 0;0 0 0 0 0 0 14000 12000 10000]; Aeq=[1 0 0 1 0 0 1 0 0;0 1 0 0 1 0 0 1 0;0 0 1 0 0 1 0 0 1];beq=[100 200 300];vlb=[0;0;0;0;0;0;0;0;0];vub=[];b=[190000 130000 350000];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)题目六：1）[xos,yos]=fminsearch('x(1)^2+4*x(2)^2+9*x(3)^2-2*x(1)+18*x(2)',[0 0 0]) 2）[xos,yos]=fminsearch('x(1)^2+3/2*x(2)^2-2*x(1)*x(2)+x(1)-2*x(2)',[0 0 0])3）[xos,yos]=fminsearch('(x(1)-1)^4+x(2)^2',[0 1 0])三、结果或结论或截图题目五：题目六：1、2、3、四、结果分析讨论或评价、推广、小结等《数学建模与数学实验》上机报告（第 4 次）一、上机训练目的、题目或内容（简述综述）等题目七：某公司有5 个建筑工地要开工，每个工地的位置（用平面坐标系a，b 表示，距离单位：千米）及水泥日用量d(吨)由下表给出。