函数的图象变换(习题)
函数的图像变换习题

1D escribe how the graph of y = f(x) is transformed to give the graph ofa y = f(x− 1)b y = f(x) − 3c y = 2f(x)d y = f(4x)e y = −f(x)f y = 15f(x) g y = f(−x) h y = f(23x)2The diagram shows the curve with equation y = f(x) which crosses the coordinate axes at the points (0, 3) and (4, 0).Showing the coordinates of any points of intersection with the axes, sketch on separate diagrams the graphs ofa y = 3f(x)b y = f(x + 4)c y = −f(x)d y = f(12x)3Find and simplify an equation of the graph obtained whena the graph of y = 2x + 5 is translated by 1 unit in the positive y-direction,b the graph of y = 1 − 4x is stretched by a factor of 3 in the y-direction, about the x-axis,c the graph of y = 3x + 1 is translated by 4 units in the negative x-direction,d the graph of y = 4x− 7 is reflected in the x-axis.4The diagram shows the curve with equation y = f(x) which has a turning point at (2, 4) andcrosses the y-axis at the point (0, 6).Showing the coordinates of the turning point and of any points of intersection with the axes,sketch on separate diagrams the graphs ofa y = f(x) − 3b y = f(x + 2)c y = f(2x)d y = 12f(x)5D escribe a single transformation that would map the graph of y = x3 onto the graph ofa y = 4x3b y = (x− 2)3c y = −x3d y = x3 + 56D escribe a single transformation that would map the graph of y = x2 + 2 onto the graph ofa y = 2x2 + 4b y = x2− 5c y = 19x2 + 2 d y = x2 + 4x + 67Find and simplify an equation of the graph obtained whena the graph of y = x 2 + 2x is translated by 1 unit in the positive x -direction,b the graph of y = x 2 − 4x + 5 is stretched by a factor of 13in the x -direction, about the y -axis. c the graph of y = x 2 + x − 6 is reflected in the y -axis,d the graph of y = 2x 2 − 3x is stretched by a factor of 2 in the x -direction, about the y -axis. 8f(x ) ≡ x 2 − 4x .a Find the coordinates of the turning point of the graph y = f(x ).b Sketch each pair of graphs on the same set of axes showing the coordinates of the turning point of each graph.i y = f(x ) and y = 3 + f(x ) ii y = f(x ) and y = f(x − 2) iii y = f(x ) and y = f(2x )9Sketch each pair of graphs on the same set of axes.a y = x 2 and y = (x + 3)2b y = x 3 and y = x 3 + 4c y = 1x and y = 12x −d y and y 10a Describe two different transformations, each of which would map the graph ofy = 1x onto the graph of y = 13x .b Describe two different transformations, each of which would map the graph ofy = x 2 onto the graph of y = 4x 2 .11f(x ) ≡ (x + 4)(x + 2)(x − 1).Showing the coordinates of any points of intersection with the axes, sketch on separate diagrams the graphs ofa y = f(x )b y = f(x − 4)c y = f(−x )d y = f(2x )12T he curve y = f(x ) is a parabola and the coordinates of its turning point are (a , b ).Write down, in terms of a and b , the coordinates of the turning point of the grapha y = 3f(x )b y = 4 + f(x )c y = f(x + 1)d y = f(13x ) 13x )The diagram shows the curve with equation y = f(2x ) which crosses the coordinate axes at the points (−2, 0) and (0, 1).Showing the coordinates of any points of intersection with the coordinate axes, sketch on separate diagrams the curvesa y = 3f(2x )b y = f(x )。
高一数学三角函数图象变换试题答案及解析

高一数学三角函数图象变换试题答案及解析1.为了得到函数的图像,只需将函数的图像( )A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【答案】B【解析】先用诱导公式将化为= =,由平移知识知,只需将函数的图像向右平移个长度单位,故选B.考点:诱导公式;平移变换2.为了得到函数的图像,只需把函数的图像()A.向右平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向左平移个长度单位【答案】B【解析】=sin2(x-),为了得到函数的图象,只需将的图象向右平移个单位即可,故选A.【考点】函数y=Asin(ωx+φ)的图象变换.三角函数图像的平移.3.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的僻析式是( )A.B.C.D.【答案】C【解析】将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),可得函数,再将所得的图象向左平移个单位,得函数,即故选C.【考点】函数y=Asin(ωx+φ)的图象变换.4.函数(其中,的图象如图所示,为了得到的图象,可以将的图象A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度【答案】A【解析】由图知,,∴,∴.又由图可得,∵,∴,∴,∴为了得到的图象,可以将的图象向右平移个单位长度,故选A.【考点】1、三角函数的图象;2、函数的图象变换.5.要得到函数y=cos()的图像,只需将y=sin的图像( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】A【解析】本题考查三角函数的图像平移问题,要注意将函数解析式变为,然后根据“左加右减”的口诀平移即可.【考点】三角函数图像平移.6.函数的图象向右平移个单位后与函数的图象重合.则的解析式是( )A.B.C.D.【答案】C【解析】根据反方向知:的图像向左平移个单位后得到,根据左加右减的平移原理得到:,故选C.【考点】的图像变换7.函数的最小正周期为()A.B.C.D.【答案】【解析】由三角函数的最小正周期得.解决这类问题,须将函数化为形式,在代时,必须注意取的绝对值,因为是求最小正周期.【考点】三角函数的周期计算8.将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为()A.B.C.0D.【答案】B【解析】根据题意,由于将函数的图象沿轴向左平移个单位后,得到,故可知的一个可能取值为,故答案为B.【考点】三角函数的图象变换点评:主要是考查了三角函数的图象变换的运用,属于基础题。
(word版)高中数学三角函数y=Asin(ωx+φ)图像变换练习题

三角函数y =Asin(ωx +φ)图像练习题一、单选题1. 函数f(x)=2sin(ωx +φ)(ω>0,−π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( )A. 2,−π3 B. 2,−π6 C. 4,−π6 D. 4,π32. 为了得到函数y =sin (2x +π3)的图象,只需要把函数y =sinx 的图象上( )A. 各点的横坐标缩短到原来的12,再向左平移π3个单位长度 B. 各点的横坐标缩短到原来的12,再向左平移π6个单位长度 C. 各点的横坐标伸长到原来的2倍,再向左平移π3个单位长度 D. 各点的横坐标伸长到原来的2倍,再向左平移π6个单位长度3. 要得到函数y =sinx +cosx 的图象,只需把函数y =√2sin (x −π12)的图象( )A. 向左平移π3个单位长度 B. 向右平移π3个单位长度 C. 向左平移13个单位长度D. 向右平移13个单位长度4. 要得到函数y =3sin (2x +π4)的图象,只需将y =3sin2x 的图象( )A. 向左平移π8个单位 B. 向右平移π8个单位 C. 向左平移π4个单位D. 向右平移π4个单位5. 已知函数f(x)=Msin(ωx +φ)(M >0,ω>0,|φ|<π2)在半个周期内的图象如图所示,则函数f(x)的解析式为( )A. f(x)=2sin(x +π6) B. f(x)=2sin(2x −π6)C. f(x)=2sin(x−π6)D. f(x)=2sin(2x+π6)6.为得到函数y=cos(x+π3)的图象,只需将函数y=sinx的图象()A. 向左平移π6个单位长度 B. 向右平移π6个单位长度C. 向左平移5π6个单位长度 D. 向右平移5π6个单位长度7.函数y=Asin(ωx+φ)在一个周期上的图象如图所示,则函数的解析式是()A. y=2sin(x2−23π)B. y=2sin(x2+43π)C. y=2sin(x2+23π)D. y=2sin(x2−π3)8.设ω>0,函数y=sin(ωx+π3)+2的图象向右平移4π3个单位长度后与原图象重合,则ω的最小值是().A. 23B. 43C. 32D. 39.如图所示,函数f(x)=Asin(2x+φ)(其中A>0,|φ|<π2)的图象过点(0,√3),则f(x)的图象的一个对称中心是()A. (−π3,0)B. (−π6,0)C. (π6,0)D. (π4,0)10.将函数y=sinωx(ω>0)的图象向左平移π6个单位长度,平移后的图象如图所示,则平移后的图象所对应的函数解析式为()A. y=sin(x+π6)B. y=sin(x−π6)C. y=sin(2x+π3)D. y=sin(2x−π3)11.将函数f(x)=sin(x+φ)图象上所有点的横坐标变为原来的1ω(ω>1)(纵坐标不变),得函数g(x)的图象.若g(π6)=1,g(2π3)=0,且函数g(x)在(π6,π2)上具有单调性,则ω的值为()A. 2B. 3C. 5D. 712.设函数的最小正周期为π,则下列说法正确的是()A. 函数f(x)的图象关于直线x=π3对称B. 函数f(x)的图象关于点(π12,0)对称C. 函数f(x)在(−5π12,π12)上单调递减D. 将函数f(x)的图象向右平移5π12个单位,得到的新函数是偶函数13.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π2),其图象相邻的最高点之间的距离为π,将函数y=f(x)的图象向左平移π12个单位长度后得到函数g(x)的图象,且g(x)为奇函数,则()A. f(x)的图象关于点(π6,0)对称 B. f(x)的图象关于点(−π6,0)对称C. f(x)在(−π6,π3)上单调递增 D. f(x)在(−2π3,−π6)上单调递增14.已知曲线C1:y=cosx,C2:y=sin(2x+2π3),则下面结论正确的是()A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C215.已知曲线y=sin(2x+π6)向左平移φ(φ>0)个单位,得到的曲线y=g(x)经过点(−π12,1),则()A. 函数y=g(x)的最小正周期T=π2B. 函数y=g(x)在[11π12,17π12]上单调递增C. 曲线y=g(x)关于直线x=π6对称D. 曲线y=g(x)关于点(2π3,0)对称16.若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π)的图象如图所示,则函数y=f(x)的解析式为()A. y=32sin(2x+π6)B. y=32sin(2x−π6)C. y=32sin(2x+π3)D. y=32sin(2x−π3)二、多选题17.已知函数f(x)=sin(2x+π3),将其图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若函数g(x)为奇函数,则φ的值可以为()A. π12B. π6C. π3D. 2π318.为了得到函数y=cos(2x+π4)的图象,只要把函数y=cosx图象上所有的点()A. 向左平移π4个单位长度,再将横坐标变为原来的2倍B. 向左平移π4个单位长度,再将横坐标变为原来的12倍C. 横坐标变为原来的12倍,再向左平移π8个单位长度 D. 横坐标变为原来的12倍,再向左平移π4个单位长度19. 已知函数f(x)=2cos 2ωx +√3sin2ωx −1(ω>0)的最小正周期为π,则下列说法正确的有( )A. ω=2B. 函数f(x)在[0,π6]上为增函数C. 直线x =π3是函数y =f(x)图象的一条对称轴 D. 点(512π,0)是函数y =f(x)图象的一个对称中心20. 将函数f(x)的图象向右平移π6个单位长度,再将所得函数图象上的所有点的横坐标缩短到原来的23,得到函数g(x)=Asin(ωx +φ)(A >0,ω>0,|φ|<π2)的图象.已知函数g(x)的部分图象如图所示,则下列关于函数f(x)的说法正确的是( )A. f(x)的最小正周期为π,最大值为2B. f(x)的图象关于点(π6,0)中心对称 C. f(x)的图象关于直线x =π6对称 D. f(x)在区间[π6,π3]上单调递减第II 卷(非选择题)三、解答题21. 已知函数f(x)=4cos xsin (x +π6)−1.(1)求f(x)的最小正周期;(2)求f(x)在区间[−π6,π4]上的最大值和最小值.22.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,−π2<φ<π2)的部分图象如图所示.(1)求函数f(x)的解析式;(2)若x∈[−53,53],求函数f(x)的值域.23.已知函数f(x)=2√3sinxcosx−cos(2x+π3)−cos(2x−π3).(Ⅰ)求f(π2)的值.(Ⅱ)求函数f(x)在区间[−π12,5π12]上的最大值和最小值.24.已知函数y=12sin (2x+π6),x∈R.(1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的简图;(3)该函数的图象可由y=sin x(x∈R)的图象经过怎样的平移和伸缩变换得到⋅25.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图像如图所示:(1)求函数f(x)的解析式;(2)将函数y=f(x)的图像上各点的横坐标缩短到原来的12,纵坐标不变,得到函数y=g(x)的图像,求函数y=g(x)在区间[0,π4]上的最大值及函数取最大值时相应的x 值.26.已知函数f(x)=cos2x+sin(2x−π6).(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)当x∈[0,π]时,求函数f(x)的单调递增区间.27.已知函数f(x)=2cos(x−π3)+2sin(3π2−x).(1)求函数f(x)的单调递减区间;(2)求函数f(x)的最大值,并求f(x)取得最大值时的x的取值集合;(3)若f(x)=65,求cos(2x−π3)的值.28.已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<π)的部分图像如图所示.(I)求f(x)的解析式;(II)在△ABC中,角A、B、C的对边分别为a,b,c,a=1,c=2,f(A)=1,求b的值.29.已知函数f(x)=√3sinxcosx+sin2x−12.(1)求f(x)的单调递增区间;(2)若A∈(π12,π3),f(A)=13,求cos(2A−5π6)的值.30.已知函数f(x)=4sinxcos(x+π3)+√3.(1)求函数f(x)的最小正周期及单调增区间;(2)求函数f(x)在区间[−π4,π6]上的值域和取得最大值时相应的x的值.答案和解析1.【答案】A本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.结合图象由周期求出ω,由特殊点的坐标求出φ的值.【解答】解:由题意可知T=2×(11π12−5π12)=π,∴ω=2,x=5π12时,函数取得最大值2,可得:2sin(2×5π12+φ)=2,,即,又∵−π2<φ<π2,所以φ=−π3.故选A.2.【答案】B本题考查了函数y=Asin(ωx+φ)的图象的伸缩平移,属于基础题.根据函数图象伸缩平移变换法则即可得到答案.【解答】解:y=sinx图象上各点的横坐标缩短到原来的12,得到y=sin2x的图象,再向左平移π6个单位长度得到y=sin[2(x+π6)]=sin(2x+π3)的图象,故选B.3.【答案】A【分析】本题主要考查函数y=Asin(ωx+φ)的图象的平移变换,辅助角公式,属于基础题.由辅助角公式,根据函数y=Asin(ωx+φ)的图象的平移变换可得答案.【解答】解:y =sinx +cosx,则要得到函数y =sinx +cosx 的图象,只需把函数y =√2sin (x −π12)的图象向左平移π3个单位长度. 故选A .4.【答案】A本题考查函数y =Asin(ωx +φ)的图象变换规律,属于基础题.由y =3sin (2x +π4)=3sin [2(x +π8)],根据左加右减的平移原理,即可得到结果. 【解答】解:y =3sin (2x +π4)=3sin [2(x +π8)],因此将函数y =3sin2x 的图象向左平移π8个单位,即可得到函数y =3sin (2x +π4)的图象. 故选A .5.【答案】A【分析】本题主要考查由函数y =Asin(ωx +φ)的部分图象求解析式,属于基础题. 由函数的最值求出A ,由周期求出ω,由五点法作图求出φ的值.【解答】解:由图象知M =2. 设函数f(x)的最小正周期为T , 则14T =π3−(−π6)=π2,可知T =2π,ω=2πT=1,将(π3,2)代入f(x)的解析式得sin(π3+φ)=1, 又|φ|<π2,可得φ=π6,故函数f(x)的解析式为f(x)=2sin(x +π6). 故选A .6.【答案】C本题考查了函数y =Asin(ωx +φ)的图象与性质、函数图象的变换的相关知识,属于基础题.根据函数y=Asin(ωx+φ)的图象变换的规则可得结论.【解答】解:故选C.7.【答案】C本题考查三角函数y=Asin(ωx+φ)的图象和性质,涉及诱导公式应用,属于基础题.依题意,根据图象求得A=2,ω=12,根据五点作图法得进而求得结果.【解答】解:由图知A=2,T2=8π3−2π3=2π=πω,ω=12,y=2sin(12x+φ),根据五点作图法知,代入得,,所以,k∈Z,故选C.8.【答案】C本题考查函数y=Asin(ωx+φ)的图象和性质,属于基础题.函数y=sin(ωx+π3)+2的图象向右平移4π3个单位长度后与原图象重合,可判断出4π3是此函数周期的整数倍,由此能求出ω的表达式,判断出它的最小值.【解答】解:由函数的图象向右平移4π3个单位长度后与原图象重合,得4π3是此函数周期的整数倍.又ω>0,∴2πω⋅k=4π3(k∈Z,且k>0),∴ω=3k2(k∈Z,且k>0),∴ωmin=32.故选C.9.【答案】B【解答】解:由函数图象可知A=2,由于图象过点(0,√3),可得2sinφ=√3,即sinφ=√32,由于|φ|<π2,解得φ=π3,即有f(x)=2sin(2x+π3).由2x+π3=kπ,k∈Z,解得x=kπ2−π6,k∈Z,故f(x)的图象的对称中心是(kπ2−π6,0),k∈Z,当k=0时,f(x)的图象的一个对称中心是(−π6,0).故选B.10.【答案】C本题考查三角函数图像的平移变换,函数的解析式,属于基础题.由三角函数图像的平移得为,代入点,得,得ω=2,从而得解析式.【解答】解:函数y=sinωx(ω>0)的图象向左平移π6个单位长度,则平移后的图象所对应的函数解析式为,代入点,得,,k∈Z,当k=0时,ω=2,即解析式为y=sin(2x+π3).故选C.11.【答案】B本题考查函数y=Asin(ωx+φ)的图象与性质,属于中档题.根据题意得出,得出ω=2n−1(n∈N∗),由函数g(x)在(π6,π2)上具有单调性,得出π2−π6⩽T2=πω,即可求出结果.【解答】解:由题意得,g(x)=sin(ωx+φ),最小正周期T=2πω,若g(π6)=1,g(2π3)=0,,∴ω=2n−1(n∈N∗),∵函数g(x)在(π6,π2)上具有单调性,∴π2−π6⩽T2=πω,解得ω⩽3,又ω>1,ω=2n−1(n∈N∗),∴ω=3.故选B.12.【答案】D本题考查函数y=Asin(ωx+φ)的图象与性质,正弦、余弦函数的图象与性质,属于中档题.先根据函数f(x)=12sin(ωx+π3)(ω>0)的最小正周期为π,求出ω=2,再根据选项逐一判断即可.【解答】解:∵函数f(x)=12sin(ωx+π3)(ω>0)的最小正周期为π,∴2πω=π,解得ω=2,则f(x)=12sin(2x+π3),对于A.当x=π3时,f(π3)=12sin(2×π3+π3)=0,∴函数f(x)的图象关于点(π3,0)对称,故A不正确;对于B.当x=π12时,f(π12)=12sin(2×π12+π3)=12,∴函数f(x)的图象关于直线x=π12对称,故B不正确;对于C.f(x)=12sin(2x+π3)的单调递减区间满足:2kπ+π2≤2x+π3≤2kπ+3π2,k∈Z,解得kπ+π12≤x≤kπ+7π12,k∈Z,k=−1时不符合,故C不正确;对于D.将函数f(x)的图象向右平移5π12个单位,得到新函数为g(x)=f(x−5π12)=1 2sin(2x−π2)=−12cos2x,是偶函数,故D正确.故选D.13.【答案】C本题考查三角函数的图象的性质,属一般题.根据题意求出函数解析式,然后验证对称性和单调性.【解答】解:f(x)=2sin(ωx +φ)(ω>0,|φ|<π2),其图象相邻最高点之间距离为,ω=2, 所以将函数y =f(x)的向左平移π12个单位长度后,,因为g(x)为奇函数, 所以,则,则,当,,当,,故A ,B 错误;当x ∈(−π6,π3)时,,所以f(x)在(−π6,π3)单调递增,故C 正确;当x ∈(−2π3,−π6)时,,所以f(x)在(−2π3,−π6)单调递减,故D 错误; 故选C .14.【答案】D本题考查三角函数的图象变换、诱导公式的应用. 利用三角函数的伸缩变换以及平移变换转化求解即可.【解答】解:把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变, 得到函数y =cos2x 图象,再把得到的曲线向左平移π12个单位长度, 得到函数y =cos2(x +π12)=cos(2x +π6) =sin(2x +2π3)的图象,即曲线C 2,故选D .15.【答案】D本题主要考查函数y =Asin(ωx +φ)的图象变换规律,三角函数的图象和性质,属于基础题.利用函数y =Asin(ωx +φ)的图象变换规律求得g(x)的解析式,再利用余弦函数的图象和性质,可得结论.【解答】解:把曲线y=sin(2x+π6)向左平移φ(φ>0)个单位,得到的曲线y=g(x)=sin(2x+2φ+π6),由于所得曲线经过点(−π12,1),∴sin(−π6+2φ+π6)=sin2φ=1,,,∵φ>0,,,,,故g(x)=cos(2x+π6)的最小正周期为2π2=π,故A错误;在[11π12,17π12]上,2x+π6∈[2π,3π],故函数y=g(x)在[11π12,17π12]上单调递减,故B错误;当x=π6时,g(x)=0,故g(x)的图象关于点(π6,0)对称,故C错误;当x=2π3时,g(x)=0,故g(x)的图象关于点(2π3,0)对称,故D正确,故选:D.16.【答案】D由图象求y=Asin(ωx+φ)(A>0,ω>0)解析式的方法;(1)A可由图象上最高点和最低点的纵坐标确定;(2)ω可由图象上最高点与最低点的横坐标确定,先求出最小正周期T,再由T=2πω求出ω;(3)φ可以由某一点处的函数值求得,要注意φ的范围.【解答】解:设f(x)的最小正周期为T,则12T=2π3−π6=π2,T=π,∴ω=2πT =2.又由图象可得A=32,∴f(x)=32sin(2x+φ).∵f(5π12)=32sin(2×5π12+φ)=32,∴5π6+φ=2kπ+π2,k∈Z,即φ=2kπ−π3,k∈Z,又|φ|≤π,∴φ=−π3,∴y=f(x)=32sin(2x−π3).故选D.17.【答案】BD【解析】【分析】本题考查了函数y=Asin(ωx+φ)的图象与性质的相关知识,试题难度较易由题意将函数f(x)图象向右平移φ(φ>0)个单位长度后,得到的图象对应的解析式g(x),又函数g(x)为奇函数,即可得出φ的值【解答】解:将函数f(x)图象向右平移φ(φ>0)个单位长度后,得到的图象对应的解析式为g(x)=sin[2(x−φ)+π3]=sin(2x−2φ+π3).由g(x)为奇函数可得−2φ+π3=kπ(k∈Z),故φ=π6−kπ2(k∈Z),又φ>0,结合选项,所以φ的值可以为π6,23π.故应选BD.18.【答案】BC【分析】本题考查函数y=Asin(ωx+φ)的图象与性质,函数图象的平移伸缩变换,属于基础题.依据函数y=Asin(ωx+φ)的图象平移伸缩变换的规则逐一判定即可.【解答】解:对于A,把函数y=cosx图象上所有的点向左平移π4个单位长度,可得函数,再将横坐标变为原来的2倍,可得函数,故A错误;对于B,把函数y=cosx图象上所有的点向左平移π4个单位长度,可得函数,再将横坐标变为原来的12倍,可得函数,故B正确;对于C,把函数y=cosx图象上所有的点横坐标变为原来的12倍,可得函数y=cos 2x,再向左平移π8个单位长度,可得函数,故C正确;对于D,把函数y=cosx图象上所有的点横坐标变为原来的12倍,可得函数y=cos 2x,再向左平移π4个单位长度,可得函数,故D错误.故选BC.19.【答案】BD本题考查三角函数的性质应用,考查两角和与差的三角函数公式,辅助角公式及二倍角公式应用,属基础题.依题意,根据两角和与差的三角公式及二倍角公式化简函数,再根据三角函数的性质求解即可.【解答】解:,因最小正周期为π得ω=1,故A错误,当时,,得函数f(x)在[0,π6]上为增函数,故B正确;当,,所以直线x=π3不是函数y=f(x)图象的一条对称轴,故C 错误;当,,得点(512π,0)是函数y=f(x)图象的一个对称中心,故D正确;故选BD.20.【答案】ACD本题考查三角函数的图象与性质,涉及正弦函数图象与性质的应用,属于中档题.先由函数图象得出g(x)的解析式,再由函数图象的变换得出f(x)的解析式,借助正弦函数的图象与性质得出答案即可.【解答】解:由图可知,A=2,T=4×(2π9−π18)=2π3,∴ω=2πT=3,又由g(2π9)=2,可得2π9×3+φ=π2+2kπ(k∈Z),且lφ|<π2,∴φ=−π6,∴g(x)=2sin(3x −π6),将函数g(x)的图象上所有点的横坐标伸长到原来的32,可得函数,再将函数图象向左平移π6个单位长度,得到函数,∴f(x)=2sin(2x +π6),∴f(x)的最小正周期为π,最大值为2,A 正确. 令2x +π6=kπ,k ∈Z ,得,∴函数f(x)图象的对称中心为(kπ2−π12,0)(k ∈Z), 由kπ2−π12=π6,得k =12,不符合k ∈Z ,B 错误; 对于选项C ,令2x +π6=π2+kπ(k ∈Z),得x =π6+kπ2(k ∈Z),∴函数f(x)图象的对称轴为直线x =π6+kπ2(k ∈Z),当k =0时,x =π6,故C 正确;当x ∈[π6,π3]时,2x +π6∈[π2,5π6],∴f(x)在区间[π6,π3]上单调递减,D 正确. 故选ACD .21.【答案】解:(1)因为f(x)=4cos xsin (x +π6)−1=4cos x (√32sin x +12cos x)−1=√3sin 2x +2cos 2x −1 =√3sin 2x +cos 2x=2sin (2x +π6), 所以f(x)的最小正周期为π; (2)因为−π6≤x ≤π4, 所以−π6≤2x +π6≤2π3.故当2x +π6=π2,即x =π6时,f(x)取得最大值2; 当2x +π6=−π6,即x =−π6时,f(x)取得最小值−1.【解析】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,属于中档题.(1)利用二倍角和两角和与差以及辅助角公式将函数化为y=Asin(ωx+φ)的形式,即可求出函数的最小正周期;(2)先根据x的取值范围求得2x+π6的范围,再由正弦函数的性质即可求出函数的最大值和最小值.22.【答案】解:(1)由图象知函数的最大值为1,即A=1,T2=3−(−1)=4,即周期T=8,即2πω=8,得ω=π4,则f(x)=sin(π4x+φ),由五点对应法得π4×1+φ=π2,得φ=π4,即f(x)=sin(π4x+π4).(2)若x∈[−53,53 ],则π4x+π4∈[−π6,2π3],∴当π4x+π4=−π6时,即x=−53时,f(x)最小,最小值为f(−53)=−12,当π4x+π4=π2时,即x=1时,f(x)最大,最大值为f(1)=1,∴f(x)的值域为[−12,1].【解析】本题主要考查三角函数的图象和性质,利用图象法求出函数的解析式以及结合三角函数的最值性质是解决本题的关键.难度不大.(1)根据函数图象先求出A和周期,结合周期公式求出ω,利用五点对应法求出φ即可求出函数的解析式.(2)求出角的范围,结合三角函数的最值关系进行求解即可.23.【答案】解:(Ⅰ;(Ⅱ)f(x)=2√3sinxcosx−cos(2x+π3)−cos(2x−π3)=√3sin2x−12cos2x+√32sin2x−12cos2x−√32sin2x=√3sin2x −cos2x =2sin(2x −π6),因为x ∈[−π12,5π12]∴−π3≤2x −π6≤2π3,∴2sin(2x −π6)∈[−√3,2]. 即函数f(x)在区间[−π12,5π12]上的最大值为2,最小值为−√3.【解析】本题考查三角函数的化简与求值,考查三角函数的性质,属基础题. (Ⅰ)将代入化简即可;(Ⅱ)利用辅助角公式化简得到f(x),由x 的取值范围得出2x −π6的范围,再由正弦函数的性质得出最值即可.24.【答案】解:(1)函数y =12sin (2x +π6)的振幅为12,周期为π,初相为π6.(2)列表:描点画图(如图所示):(3)函数y =sinx 的图象向左平移π6个单位长度,得到函数y =sin (x +π6)的图象, 再保持纵坐标不变,把横坐标缩短为原来的12倍,得到函数y =sin (2x +π6)的图象, 再保持横坐标不变,把纵坐标缩短为原来的12倍,得到函数y =12sin (2x +π6)的图象.【解析】本题主要考查了三角函数的图象和性质以及“五点法”作图和图象的平移和伸缩变换,属于基础题.(1)结合振幅、周期、初相的定义可得; (2)按照列表、描点、连线的步骤求解画图;(3)由y =sinx (x ∈R )的图象左移π6个单位得到数y =sin (x +π6),x ∈R 的图象,然后横坐标再伸缩得到y =sin (2x +π6),x ∈R 的图象,最后纵坐标再伸缩得到y =12sin (2x +π6),x ∈R 的图象.25.【答案】解:(1)如图可知,A =2,T =4×[π12−(−π6)]=π,∴ω=2πT=2.∵{2sin (2×π12+φ)=2|φ|<π2,∴φ=π3,即函数解析式为;(2)根据图象平移原则得g (x )=2sin (4x +π3), ∵x ∈[0,π4],∴4x +π3∈[π3,4π3],∴2sin (4x +π3)∈[−√3,2], 当,即x =π24时,函数g(x)在区间[0,π4]上的最大值为2.【解析】本题考查了三角函数的图象与性质的应用,求出函数f(x)的解析式是关键,属于中档题.(1)利用三角函数的图象,得出振幅A 与周期T ,代入特殊点求出φ,即可求出函数解析式;(2)根据图像平移,得到函数g(x)的解析式,最后利用正弦型函数的性质求出结果.26.【答案】解:(Ⅰ)函数f(x)=cos2x +sin(2x −π6)=cos2x +√32sin2x −12cos2x =sin(2x +π6),故它的最小正周期为2π2=π.(Ⅱ)令2kπ−π2≤2x +π6≤2kπ+π2,k ∈Z , 得kπ−π3≤x ≤2kπ+π6,k ∈Z ,∴函数的增区间为[kπ−π3,2kπ+π6],k∈Z,∵x∈[0,π],∴函数的增区间为[0,π6]、[2π3,π].【解析】本题主要考查两角和差的三角公式,正弦函数的周期性和单调性,属于基础题.(Ⅰ)由题意利用两角和差的三角公式化简函数f(x)的解析式,可得它的最小正周期.(Ⅱ)由题意利用正弦函数的单调性,求出函数f(x)的单调递增区间.27.【答案】解:f(x)=2cosxcosπ3+2sinxsinπ3−2cosx=cosx+√3sinx−2cosx=√3sinx−cosx=2sin(x−π6 ).(1)令2kπ+π2≤x−π6≤2kπ+32π(k∈Z),∴2kπ+2π3≤x≤2kπ+5π3(k∈Z),∴f(x)的单调递减区间为[2kπ+2π3,2kπ+5π3](k∈Z).(2)f(x)取最大值2时,x−π6=2kπ+π2(k∈Z),则x=2kπ+2π3(k∈Z).∴f(x)的最大值是2,取得最大值时的x的取值集合是{x|x=2kπ+2π3,k∈Z}.(3)∵f(x)=65,∴2sin(x−π6)=65,∴sin(x−π6)=35.∴cos(2x−π3)=1−2sin2(x−π6)=1−2×(35)2=725.【解析】本题考查了函数y=Asin(ωx+φ)的图象与性质,诱导公式,两角和与差的三角函数公式和二倍角公式,属于中档题.利用诱导公式和两角差的余弦函数公式得f(x)=√3sinx−cosx,即.(1)利用函数y=Asin(ωx+φ)的单调性,计算得结论;(2)利用函数y=Asin(ωx+φ)的最值,计算得结论;(3)利用题目条件得,再利用余弦的二倍角公式,计算得结论.28.【答案】解:(1)由最值可确定A=2,周期T=2×(π3+π6)=π⇒ω=2,又f(π3)=2,即,,即,∵|φ|<π,∴φ=−π6,所以f(x)=2sin (2x−π6);(2)f(A)=2sin (2A−π6)=1⇒sin (2A−π6)=12⇒2A−π6=π6或5π6,故A=π6或π2,当A=π2时,三角形为直角三角形,此时a>c,这与题目条件a=1,c=2矛盾,所以舍掉;当A=π6时,由余弦定理得:a2=b2+c2−2bccos A⇒b2−2√3b+3=0,解得b=√3.【解析】本题考查函数y=Asin(ωx+φ)的图象与性质,余弦定理,考查运算化简的能力,属于中档题.(1)由图可得A=2,,可得ω=2,再由f(π3)=2,结合|φ|<π可得φ,从而可得f(x)的解析式;(2)由(1)及f(A)=1,求得A=π6或π2,按A讨论结合余弦定理可得.29.【答案】解:(1)f(x)=√3sinxcosx+sin2x−12=√32sin2x+1−cos2x2−12=sin(2x−π6 ),令−π2+2kπ≤2x−π6≤π2+2kπ,k∈Z.解得,k∈Z.所以f(x)的单调增区间为[−π6+kπ,π3+kπ](k∈Z).(2)由(1)得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6)=13,令θ=2A−π6,则0<θ<π2,所以sinθ=13,cosθ=2√23,则cos(2A−56π)=cos(θ−23π)=cosθcos23π+sinθsin23π=2√23×(−12)+13×√32=√3−2√26.【解析】本题考查了函数y=Asin(ωx+φ)的图象与性质和三角恒等变换,是中档题。
初中数学专题复习(函数图像变换)

初中数学专题复习(函数图像变换)一.一次函数的图像变换1.(2020•宿迁)如图,在平面直角坐标系中,Q是直线y=﹣x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为()A.B.C.D.解:作QM⊥x轴于点M,Q′N⊥x轴于N,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N在△PQM和△Q′PN中,∴△PQM≌△Q′PN(AAS),∴PN=QM,Q′N=PM,设Q(m,﹣),∴PM=|m﹣1|,QM=|﹣m+2|,∴ON=|3﹣m|,∴Q′(3﹣m,1﹣m),∴OQ′2=(3﹣m)2+(1﹣m)2=m2﹣5m+10=(m﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′的最小值为,当m=2时,OQ′2有最小值为5,故选:B.2.(2020•湖北)如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a 于点P1,过点P1作x轴的平行线交直线b于点P2,过点P2作y轴的平行线交直线a于点P3,过点P3作x轴的平行线交直线b于点P4,…,按此作法进行下去,则点P2020的横坐标为21010.解:∵点P(1,0),P1在直线y=x上,∴P1(1,1),∵P1P2∥x轴,∴P2的纵坐标=P1的纵坐标=1,∵P2在直线y=﹣x上,∴1=﹣x,∴x=﹣2,∴P2(﹣2,1),即P2的横坐标为﹣2=﹣21,同理,P3的横坐标为﹣2=﹣21,P4的横坐标为4=22,P5=22,P6=﹣23,P7=﹣23,P8=24…,∴P4n=22n,∴P2020的横坐标为2=21010,故答案为:21010.3.(2020•锦州)如图,过直线l:y=上的点A1作A1B1⊥l,交x轴于点B1,过点B1作B1A2⊥x轴.交直线l于点A2;过点A2作A2B2⊥l,交x轴于点B2,过点B2作B2A3⊥x轴,交直线l于点A3;…按照此方法继续作下去,若OB1=1,则线段A n A n﹣1的长度为3×22n﹣5.(结果用含正整数n的代数式表示)解:∵直线l:y=x,∴直线l与x轴夹角为60°,∵B1为l上一点,且OB1=1,∴OA1=cos60°•OB1=OB1=,OB1=cos60°•OA2,∴OA2=2OB1=2,∴A2A1=2﹣=∵OA2=2,∴OB2=2OA2=4,∴OA3=2OB2=8,∴A3A2=8﹣2=6,…A n A n﹣1=3×22n﹣5故答案为3×22n﹣5.4.(2020•南宁)如图1,在平面直角坐标系中,直线l1:y=x+1与直线l2:x=﹣2相交于点D,点A是直线l2上的动点,过点A作AB⊥l1于点B,点C的坐标为(0,3),连接AC,BC.设点A的纵坐标为t,△ABC的面积为s.(1)当t=2时,请直接写出点B的坐标;(2)s关于t的函数解析式为s=,其图象如图2所示,结合图1、2的信息,求出a与b的值;(3)在l2上是否存在点A,使得△ABC是直角三角形?若存在,请求出此时点A的坐标和△ABC的面积;若不存在,请说明理由.解:(1)如图1,连接AG,当t=2时,A(﹣2,2),设B(x,x+1),在y=x+1中,当x=0时,y=1,∴G(0,1),∵AB⊥l1,∴∠ABG=90°,∴AB2+BG2=AG2,即(x+2)2+(x+1﹣2)2+x2+(x+1﹣1)2=(﹣2)2+(2﹣1)2,解得:x1=0(舍),x2=﹣,∴B(﹣,);(2)如图2可知:当t=7时,s=4,把(7,4)代入s=中得:+7b﹣=4,解得:b=﹣1,如图3,过B作BH∥y轴,交AC于H,由(1)知:当t=2时,A(﹣2,2),B(﹣,),∵C(0,3),设AC的解析式为:y=kx+n,则,解得,∴AC的解析式为:y=x+3,∴H(﹣,),∴BH=﹣=,∴s===,把(2,)代入s=a(t+1)(t﹣5)得:a(2+1)(2﹣5)=,解得:a=﹣;(3)存在,设B(x,x+1),分两种情况:①当∠CAB=90°时,如图4,∵AB⊥l1,∴AC∥l1,∵l1:y=x+1,C(0,3),∴AC:y=x+3,∴A(﹣2,1),∵D(﹣2,﹣1),在Rt△ABD中,AB2+BD2=AD2,即(x+2)2+(x+1﹣1)2+(x+2)2+(x+1+1)2=22,解得:x1=﹣1,x2=﹣2(舍),∴B(﹣1,0),即B在x轴上,∴AB==,AC==2,∴S△ABC===2;②当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴△ABD是等腰直角三角形,∴AB=BD,∵A(﹣2,t),D(﹣2,﹣1),∴(x+2)2+(x+1﹣t)2=(x+2)2+(x+1+1)2,(x+1﹣t)2=(x+2)2,x+1﹣t=x+2或x+1﹣t=﹣x﹣2,解得:t=﹣1(舍)或t=2x+3,Rt△ACB中,AC2+BC2=AB2,即(﹣2)2+(t﹣3)2+x2+(x+1﹣3)2=(x+2)2+(x+1﹣t)2,把t=2x+3代入得:x2﹣3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(﹣2,9),B(3,4),∴AC==2,BC==,∴S△ABC===10;当x=0时,如图6,此时,A(﹣2,3),AC=2,BC=2,∴S△ABC===2.5.(2020•哈尔滨)已知:在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OA=OB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为y=x,过点C作CM⊥y轴,垂足为M,OM=9.(1)如图1,求直线AB的解析式;(2)如图2,点N在线段MC上,连接ON,点P在线段ON上,过点P作PD⊥x轴,垂足为D,交OC于点E,若NC=OM,求的值;(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若∠DHE=∠DPH,GQ﹣FG =AF,求点P的坐标.解:(1)∵CM⊥y轴,OM=9,∴y=9时,9=x,解得x=12,∵AC⊥x轴,∴A(12,0),∵OA=OB,∴B(0,﹣12),设直线AB的解析式为y=kx+b,则有,解得,∴直线AB的解析式为y=x﹣12.(2)如图2中,∵∠CMO=∠MOA=∠OAC=90°,∴四边形OACM是矩形,∴AO=CM=12,∵NC=OM=9,∴MN=CM﹣NC=12﹣9=3,∴N(3,9),∴直线ON的解析式为y=3x,设点E的横坐标为4a,则D(4a,0),∴OD=4a,把x=4a,代入y=x中,得到y=3a,∴E(4a,3a),∴DE=3a,把x=4a代入,y=3x中,得到y=12a,∴PD=12a,∴PE=PD﹣DE=12a﹣3a=9a,∴=.(3)如图3中,设直线FG交CA的延长线于R,交y轴于S,过点F作FT⊥OA于T.∵GF∥x轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR,∴∠OFR=∠R=∠AOS=∠BSG=90°,∴四边形OSRA是矩形,∴OS=AR,∴SR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°﹣45°=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵OF⊥FQ,∴∠OSR=∠R=∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠QFR+∠FQR=90°,∴∠OFS=∠FQR,∴△OFS≌△FQR(AAS),∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB=45°,∴SF=SB=QR,∵∠SGB=∠QGR,∠BSG=∠R,∴△BSG≌△QRG(AAS),∴SG=GR=6,设FR=m,则AR=m,AF=m,QR=SF=12﹣m,∵GQ﹣FG=AF,∴GQ=×m+6﹣m=m+6,∵GQ2=GR2+QR2,∴(m+6)2=62+(12﹣m)2,解得m=4,∴FS=8,AR=4,∵∠OAB=∠FAR,FT⊥OA,FR⊥AR,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT是矩形,∴OT=SF=8,∵∠DHE=∠DPH,∴tan∠DHE=tan∠DPH,∴=,由(2)可知DE=3a,PD=12a,∴=,∴DH=6a,∴tan∠PHD===2,∵∠PHD=∠FHT,∴tan∠FHT==2,∴HT=2,∵OT=OD+DH+HT,∴4a+6a+2=8,∴a=,∴OD=,PD=12×=,∴P(,).二.反比例函数的图像变换6.(2020•赤峰)如图,点B在反比例函数y=(x>0)的图象上,点C在反比例函数y=﹣(x>0)的图象上,且BC∥y轴,AC⊥BC,垂足为点C,交y轴于点A.则△ABC的面积为()A.3B.4C.5D.6解:过B点作BH⊥y轴于H点,BC交x轴于D,如图,∵BC∥y轴,AC⊥BC,∴四边形ACDO和四边形ODBH都是矩形,=|﹣2|=2,∴S矩形OACDS矩形ODBH=|6|=6,=2+6=8,∴S矩形ACBH∴△ABC的面积=S矩形ACBH=4.故选:B.7.(2020•朝阳)如图,在平面直角坐标系中,一次函数y=x+4的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)的图象上,则k的值为()A.﹣12B.﹣42C.42D.﹣21解:∵当x=0时,y=0+4=4,∴A(0,4),∴OA=4;∵当y=0时,,∴x=﹣3,∴B(﹣3,0),∴OB=3;过点C作CE⊥x轴于E,∵四边形ABCD是正方形,∴∠ABC=90°,AB=BC,∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,∴∠CBE=∠BAO.在△AOB和△BEC中,,∴△AOB≌△BEC(AAS),∴BE=AO=4,CE=OB=3,∴OE=3+4=7,∴C点坐标为(﹣7,3),∵点C在反比例函数的图象上,∴k=﹣7×3=﹣21.故选:D.8.(2020•西宁)如图,一次函数y=﹣x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点C (﹣2,m).(1)求反比例函数的解析式;(2)若点P在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,请直接写出所有符合条件的P点坐标.解:(1)∵点C(﹣2,m)在一次函数y=﹣x+1的图象上,把C点坐标代入y=﹣x+1,得m=﹣(﹣2)+1=3,∴点C的坐标是(﹣2,3),设反比例函数的解析式为,把点C的坐标(﹣2,3)代入得,,解得k=﹣6,∴反比例函数的解析式为;(2)在直线y=﹣x+1中,令x=0,则y=1,∴B(0,1),由(1)知,C(﹣2,3),∴BC==2,当BC=BP时,BP=2,∴OP=2+1,∴P(0,2+1),当BC=PC时,点C在BP的垂直平分线,∴P(0,5),即满足条件的点P的坐标为(0,5)或(0,).9.(2020•湖北)如图,直线AB与反比例函数y=(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.(1)填空:反比例函数的关系式为y=;(2)求直线AB的函数关系式;(3)动点P在y轴上运动,当线段PA与PB之差最大时,求点P的坐标.解:(1)将点A坐标(6,1)代入反比例函数解析式y=,得k=1×6=6,则y=,故答案为:y=;(2)过点A作AC⊥x轴于点C,过B作BD⊥y轴于D,延长CA,DB交于点E,则四边形ODEC是矩形,设B(m,n),∴mn=6,∴BE=DE﹣BD=6﹣m,AE=CE﹣AC=n﹣1,∴S△ABE==,∵A、B两点均在反比例函数y=(x>0)的图象上,∴S△BOD=S△AOC==3,∴S△AOB=S矩形ODEC﹣S△AOC﹣S△BOD﹣S△ABE=6n﹣3﹣3﹣=3n﹣m,∵△AOB的面积为8,∴3n﹣m=8,∴m=6n﹣16,∵mn=6,∴3n2﹣8n﹣3=0,解得:n=3或﹣(舍),∴m=2,∴B(2,3),设直线AB的解析式为:y=kx+b,则,解得:,∴直线AB的解析式为:y=﹣x+4;(3)如图,根据“三角形两边之差小于第三边可知:当点P为直线AB与y轴的交点时,PA﹣PB有最大值是AB,把x=0代入y=﹣x+4中,得:y=4,∴P(0,4).10.(2020•济南)如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,2),反比例函数y=(x>0)的图象与BC,AB分别交于D,E,BD=.(1)求反比例函数关系式和点E的坐标;(2)写出DE与AC的位置关系并说明理由;(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.解:(1)∵B(2,2),则BC=2,而BD=,∴CD=2﹣=,故点D(,2),将点D的坐标代入反比例函数表达式得:2=,解得k=3,故反比例函数表达式为y=,当x=2时,y=,故点E(2,);(2)由(1)知,D(,2),点E(2,),点B(2,2),则BD=,BE=,故==,===,∴DE∥AC;(3)①当点F在点C的下方时,当点G在点F的右方时,如下图,过点F作FH⊥y轴于点H,∵四边形BCFG为菱形,则BC=CF=FG=BG=2,在Rt△OAC中,OA=BC=2,OC=AB=2,则tan∠OCA===,故∠OCA=30°,则FH=FC=1,CH=CF•cos∠OCA=2×=,故点F(1,),则点G(3,),当x=3时,y==,故点G在反比例函数图象上;②当点F在点C的上方时,同理可得,点G(1,3),同理可得,点G在反比例函数图象上;综上,点G的坐标为(3,)或(1,3)都在反比例函数图象上.三.二次函数的图像变换11.(2020•河北)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.12.(2020•贵港)如图,对于抛物线y1=﹣x2+x+1,y2=﹣x2+2x+1,y3=﹣x2+3x+1,给出下列结论:①这三条抛物线都经过点C(0,1);②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到;③这三条抛物线的顶点在同一条直线上;④这三条抛物线与直线y=1的交点中,相邻两点之间的距离相等.其中正确结论的序号是①②④.解:①当x=0时,分别代入抛物线y1,y2,y3,即可得y1=y2=y3=1;①正确;②y1=﹣x2+x+1,y3=﹣x2+3x+1的对称轴分别为直线x=,x=,由x=向右平移1个单位得到x=,②正确;③y1=﹣x2+x+1=﹣(x﹣)2+,顶点坐标(,),y2=﹣x2+2x+1=﹣(x﹣1)2+2,顶点坐标为(1,2);y3=﹣x2+3x+1=﹣(x﹣)2+,顶点坐标为(,),∴顶点不在同一条直线上,③错误;④当y=1时,则﹣x2+x+1=1,∴x=0或x=1;﹣x2+2x+1=1,∴x=0或x=2;﹣x2+3x+1=1,∴x=0或x=3;∴相邻两点之间的距离都是1,④正确;故答案为①②④.13.(2020•巴中)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B左侧),交y轴正半轴于点C,M为BC中点,点P为抛物线上一动点,已知点A坐标(﹣1,0),且OB=2OC=4OA.(1)求抛物线的解析式;(2)当△PCM≌△POM时,求PM的长;=5S△BCP时,求点P的坐标.(3)当4S△ABC解:(1)∵A(﹣1,0),∴OA=1,又∵OB=2OC=4OA,∴OC=2,OB=4,∴B(4,0),C(0,2),∵点B,点C,点A在抛物线上,∴解得:,、∴抛物线解析式为:;(2)连接OM,∵M为BC中点,∴M(2,1),∵△PCM≌△POM,∴CM=OM,PC=PO,∴MP是OC的垂直平分线,∴PM∥x轴,∴点P的纵坐标为1,当y=1时,代入,解得:,∴或,∴PM=或;(3)∵S△ABC=×AB×OC=5,4S△ABC=5S△BCP,∴S△BCP=4,∵B(4,0),C(0,2),∴直线BC解析式为y=﹣x+2,当点P在BC上方时,如图2,过点P作PE⊥x轴,交BC于点E,设点P(p,﹣p2+p+2),则点E(p,﹣p+2),∴PE=﹣p2+2p,∴4=×4×(﹣p2+2p),∴p=2,∴点P(2,3);当点P在BC下方时,如图3,过点P作PE⊥x轴,交BC于点E,∴PE=p2﹣2p,∴4=×4×(p2﹣2p),∴p=2±2,∴点P或;综上,点P的坐标为:(2,3)或或.14.(2019•衡阳)在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为(﹣1010,10102).解:∵A点坐标为(1,1),∴直线OA为y=x,A1(﹣1,1),∵A1A2∥OA,∴直线A1A2为y=x+2,解得或,∴A2(2,4),∴A3(﹣2,4),∵A3A4∥OA,∴直线A3A4为y=x+6,解得或,∴A4(3,9),∴A5(﹣3,9)…,∴A2019(﹣1010,10102),故答案为(﹣1010,10102).15.(2020•西宁)如图1,一次函数的图象与两坐标轴分别交于A,B两点,且B点坐标为(0,4),以点A为顶点的抛物线解析式为y=﹣(x+2)2.(1)求一次函数的解析式;(2)如图2,将抛物线的顶点沿线段AB平移,此时抛物线顶点记为C,与y轴交点记为D,当点C的横坐标为﹣1时,求抛物线的解析式及D点的坐标;(3)在(2)的条件下,线段AB上是否存在点P,使以点B,D,P为顶点的三角形与△AOB相似,若存在,求出所有满足条件的P点坐标;若不存在,请说明理由.解:(1)∵抛物线解析式为y=﹣(x+2)2,∴点A的坐标为(﹣2,0),设一次函数解析式为y=kx+b(k≠0),把A(﹣2,0),B(0,4)代入y=kx+b,得,解得,∴一次函数解析式为y=2x+4;(2)∵点C在直线y=2x+4上,且点C的横坐标为﹣1,∴y=2×(﹣1)+4=2,∴点C坐标为(﹣1,2),设平移后的抛物线解析式为y=a(x﹣h)2+k(a≠0),∵a=﹣1,顶点坐标为C(﹣1,2),∴抛物线的解析式是y=﹣(x+1)2+2,∵抛物线与y轴的交点为D,∴令x=0,得y=1,∴点D坐标为(0,1);(3)存在,①过点D作P1D∥OA交AB于点P1,∴△BDP1∽△BOA,∴P1点的纵坐标为1,代入一次函数y=2x+4,得,∴P1的坐标为(,1);②过点D作P2D⊥AB于点P2,∴∠BP2D=∠AOB=90°,又∵∠DBP2=∠ABO(公共角),∴△BP2D∽△BOA,∴,∵直线y=2x+4与x轴的交点A(﹣2,0),B(0,4),又∵D(0,1),∴OA=2,OB=4,BD=3,∴,∴,∴,过P2作P2M⊥y轴于点M,设P2(a,2a+4),则P2M=|a|=﹣a,BM=4﹣(2a+4)=﹣2a,在Rt△BP2M中,∴,解得(舍去),∴,∴,∴P2的坐标为(,),综上所述:点P的坐标为:(,1)或(,).。
函数图象变换

函数图象变换1、平移变换2、对称变换①y=f(-x)与y=f(x)关于y轴对称;②y=-f(x)与y=f(x)关于x轴对称;③y=-f(-x)与y=f(x)关于原点对称;④y=f-1(x)与y=f(x)关于直线y=x对称;⑤y=|f(x)|的图象可将y=f(x)的图象在x轴下方的部分以x轴为对称轴翻折到x轴上方,其余部分不变.⑥y=f(|x|)的图象:可将y=f(x),x≥0的部分作出,再利用偶函数关于y轴的对称性.三、伸缩变换①y=Af(x)(A>0)的图象,可将y=f(x)图象上每一点的纵坐标伸(A>1)缩(0<A<1)到原来的A倍,横坐标不变而得到.②y=f(ax)(a>0)的图象,可将y=f(x)的图象上每一点的横坐标伸(0<a<1)缩(a>1)到原来的,纵坐标不变而得到.三、初等函数及图象(大致图象)【高考试题剖析】1.当a>1时,在同一坐标系中,函数y=a-x与y=log a x的图象是( )【答案】A2.若函数f(x-1)=x2-2x+3(x≤1)则函数f-1(x)的草图是( )【解析】f(x-1)=(x-1)2+2 ①f(x)=x2+2 ②又∵①式中x≤1,∴x-1≤0,故②式中函数自变量x≤0,由②式得:x=-,即f-1(x)=- (x≥2).【答案】C3.已知函数f(x)=ax3+bx2+cx+d的图象如图2—6,则( )A.b∈(-∞,0)B.b∈(0,1)C.b∈(1,2)D.b∈(2,+∞)【解析】由题知f(x)=0有三个根0,1,2.∴f(x)=ax3+bx2+cx+d=ax(x-1)(x-2)=ax3-3ax2+2ax.∴b=-3a,∵a>0,∴b<0.【答案】A4.若函数y=f(x)的图象过点(1,0),则它的反函数的图象必经过点_____.【解析】点(1,0)关于直线y=x的对称点是(0,1).【答案】(0,1)5.要得到y=lg(3-x)的图象,只需作y=lgx关于_____轴对称的图象,再向_____平移3个单位而得到.【解析】由y=lgx的图象关于y轴对称得y=lg(-x)的图象,要得y=lg(3-x)即y=lg[-(x-3)]的图象,需将y=lg(-x)的图象向右平移3个单位.【答案】y 右【典型例题精讲】[例1]已知y=f(x)的图象如图2—7所示,则下列式子中能作为f(x)的解析式是( )A.B.x2-2|x|+1C.|x2-1|D.【解析】当f(x)=时,其图象恰好是上图.【答案】A[例2]画出函数y=lg|x+1|的图象.【解】y=lg|x+1|.[例3]要将函数y=的图象通过平移变换得到y=的图象,需经过怎样的变换?【解】y=-1,先沿x轴方向向左平移1个单位,再沿y轴方向向上平移1个单位,即可得到y=的图象.[例4]方程kx=有两个不相等的实根,求实数k的取值范围.【解】设y1=kx ①y2= ②方程①表示过原点的直线,方程②表示半圆,其圆心(2,0),半径为1,如图2—9.易知当OA与半圆相切时, ,故当0≤k<时,直线与半圆有两个交点,即0≤k<时,原方程有两个不相等的实根.[例5]作函数f(x)=x+的图象.【分析】f(x)=x+不能由已知函数图象变换得到,故需对函数f(x)的性质进行研究.【解】函数的定义域是(-∞,0)∪(0,+∞),∵f(-x)=-f(x),∴f(x)是(-∞,0)∪(0,+∞)上的奇函数,又|f(x)|=|x+|=|x|+≥2,当且仅当|x|=1时等号成立,∴当x>0时y≥2;当x<0时,y≤-2;当x∈(0,1)时函数为减函数,且急剧递减;当x∈[1,+∞)时函数为增函数,且缓慢递增,又x≠0,y≠0,∴图象与坐标轴无交点,且y轴是渐近线,作出第一象限的函数的图象,再利用对称性可得函数在定义域上的图象,如图2—10所示.【评述】(1)熟悉各种基本函数图的“原型”是函数作图的一项基本功;先研究函数的性质,再利用性质作图则能减少作图的盲目性,提高图象的准确性.(2)与图象有关的“辅助线”要用虚线作,以起到定形、定性、定位、定量的作用.【综合能力训练】1.f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示.令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )A.若a<0,则函数g(x)的图象关于原点对称B.若a=-1,-2<b<0,则方程g(x)=0有大于2的实根C.若a≠0,b=2,则方程g(x)=0有两个实根D.若a≥1,b<2,则方程g(x)=0有三个实根【解析】将f(x)图象上每点的纵坐标变为原来的a倍,横坐标不变,再将所得图象向上(b>0)或向下(b<0)平移|b|个单位,得g(x)=af(x)+b的图象.【答案】B2.(2007.全国Ⅱ)把函数y=ex的图象按向量=(2,3)平移,得到y=f(x)的图象,则f(x)= ( )(A)e x-3+2 (B)e x+3-2 (C)e x-2+3 (D)e x+2-3【答案】C3.(2008·菏泽模拟)如图为函数y=m+的图象,其中m,n为常数,则下列结论正确的是 ( )(A)m<0,n>1 (B)m>O,n>l(C)m>O,0<n<1 (D)m<0,0<n<1【答案】D4.(2008.安庆模拟)函数y=e-|x-1|的图象大致是( )【答案】D5.在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为x=0,y=0,2x+3y=30,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是( )A.95 B.91 C.88D.75【解析】画出图象,补形做出长方形AOBC,共有整点数11×16=176,而六点(0,10),(3,8),(6,6),(9,4),(12,2),(15,0)在长方形的对角线上,所以符合题意的点数为(176+6)×=91.【答案】B6.将函数y=logx的图象沿x轴方向向右平移一个单位,得到图象C,图象C1与C关于原点对称,图象C2与C1关于直线y=x对称,那么C2对应的函数解析式是_____.【解析】C:y=log(x-1);由-y=log(-x-1)得C1:y=log2(-x-1);求C1的反函数得y=-1-2x.【答案】y=-1-2x7.若函数y=|-x2+4x-3|的图象C与直线y=kx相交于点M(2,1),那么曲线C与该直线有 个交点.【解析】(数形结合法)作y=|-x2+4x-3|的图象,知其顶点在M(2,1).过原点与点M(2,1)作直线y=kx,如图.∴曲线C与直线y=kx有四个交点.【答案】48.作函数y=()|x-1|的图象.【解】(1)y=故它在区间[1,+∞)上的图象,可由y=2-x(x≥0)的图象沿x轴方向向右平移1个单位得到;在区间(-∞,1)上的图象,可由y=2x(x<0)的图象沿x轴方向向右平移1个单位得到.9.已知函数y=f(x)(x∈R)满足f(a+x)=f(a-x),求证y=f(x)的图象关于直线x=a对称.【证明】设p(x0,y0)是y=f(x)图象上的任一点,则有y0=f(x0),设点P关于直线x=a的对称点为p′(x′,y′),则有,即 由y0=f(x0)y′=f[a-(a-x′)]=f(x′).即点p′(x′,y′)也在y=f(x)的图象上.∴y=f(x)的图象关于直线x=a对称.【评述】本题的结论应熟记.10.画出函数y=的图象,并利用此图象判定方程=x+a有两个不同的实数解时,实数a所满足的条件.【解】图象是抛物线y2=2x+1在y≥0上的部分.把y=x+a代入y2=2x+1,得(x+a)2=2x+1,即x2+2(a-1)x+a2-1=0,由Δ=0得a=1,此时直线与抛物线相切.又因抛物线顶点是(-,0),可知当直线过点(-,0)时,即a=时直线与抛物线有两交点,故当≤a <1时直线与此抛物线有两个交点,即原方程有两不同实数解.。
函数图像变换练习题

函数图像变换练习题函数图像变换练习题函数图像变换是数学中的重要概念,它帮助我们理解函数的性质和变化规律。
通过对函数图像进行变换,我们可以观察到函数在平移、伸缩和翻转等操作后的形态变化。
在这篇文章中,我们将通过一些练习题来加深对函数图像变换的理解。
1. 平移变换平移变换是指将函数图像沿着坐标轴的方向进行平移。
具体而言,平移变换可以分为水平平移和垂直平移两种情况。
练习题1:考虑函数f(x) = x^2,将其沿x轴方向平移3个单位,请画出平移后的函数图像。
解答:对于函数f(x) = x^2,进行水平平移3个单位后的函数可以表示为f(x-3) = (x-3)^2。
通过计算可知,平移后的函数图像与原函数相比,在x轴上整体向右平移了3个单位。
2. 伸缩变换伸缩变换是指将函数图像沿着坐标轴的方向进行拉伸或压缩。
具体而言,伸缩变换可以分为水平伸缩和垂直伸缩两种情况。
练习题2:考虑函数f(x) = x^2,将其在x轴方向进行压缩,使得函数图像变为原来的一半宽度,请画出压缩后的函数图像。
解答:对于函数f(x) = x^2,进行在x轴方向的压缩后的函数可以表示为f(2x) = (2x)^2。
通过计算可知,压缩后的函数图像与原函数相比,在x轴上整体变窄了一半。
3. 翻转变换翻转变换是指将函数图像沿着坐标轴进行翻转。
具体而言,翻转变换可以分为水平翻转和垂直翻转两种情况。
练习题3:考虑函数f(x) = x^2,将其进行水平翻转,请画出翻转后的函数图像。
解答:对于函数f(x) = x^2,进行水平翻转后的函数可以表示为f(-x) = (-x)^2。
通过计算可知,翻转后的函数图像与原函数相比,在y轴上对称翻转。
通过以上练习题,我们可以看到函数图像在不同的变换下发生了形态上的变化。
这些变换可以帮助我们更好地理解函数的性质和变化规律。
在实际应用中,函数图像变换也被广泛应用于物理、工程和经济等领域。
除了上述的平移、伸缩和翻转变换,函数图像还可以进行其他的变换,如旋转和剪切等。
第7节 函数的图象(经典练习及答案详解)

第7节函数的图象知识梳理1.利用描点法作函数的图象步骤:(1)确定函数的定义域;(2)化简函数解析式;(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等);(4)列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等),描点,连线.2.利用图象变换法作函数的图象(1)平移变换(2)对称变换y=f(x)的图象y=-f(x)的图象;y=f(x)的图象y=f(-x)的图象;y=f(x)的图象y=-f(-x)的图象;y=a x(a>0,且a≠1)的图象y=log a x(a>0,且a≠1)的图象.(3)伸缩变换(4)翻折变换1.记住几个重要结论(1)函数y=f(x)与y=f(2a-x)的图象关于直线x=a对称.(2)函数y=f(x)与y=2b-f(2a-x)的图象关于点(a,b)中心对称.(3)若函数y=f(x)对定义域内任意自变量x满足:f(a+x)=f(a-x),则函数y=f(x)的图象关于直线x=a对称.而言,如果x的系数不是1,常需把系数提出2.图象的左右平移仅仅是相对于...x.来,再进行变换.而言的,利用“上加下减”进行.3.图象的上下平移仅仅是相对于...y.诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)当x∈(0,+∞)时,函数y=|f(x)|与y=f(|x|)的图象相同.()(2)函数y=af(x)与y=f(ax)(a>0且a≠1)的图象相同.()(3)函数y=f(x)与y=-f(x)的图象关于原点对称.()(4)若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.()答案(1)×(2)×(3)×(4)√解析(1)令f(x)=-x,当x∈(0,+∞)时,y=|f(x)|=x,y=f(|x|)=-x,两者图象不同,(1)错误.(2)中两函数当a≠1时,y=af(x)与y=f(ax)是由y=f(x)分别进行横坐标与纵坐标伸缩变换得到,两图象不同,(2)错误.(3)y=f(x)与y=-f(x)的图象关于x轴对称,(3)错误.2.(多选题)若函数y=a x+b-1(a>0,且a≠1)的图象经过第一、三、四象限,则下列选项中正确的有()A.a>1B.0<a<1C.b>0D.b<0答案AD解析因为函数y=a x+b-1(a>0,且a≠1)的图象经过第一、三、四象限,所以其大致图象如图所示.由图象可知函数为增函数,所以a>1,当x=0时,y=1+b-1=b<0,故选AD.3.在2 h内将某种药物注射进患者的血液中,在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减,能反映血液中药物含量Q随时间t变化的图象是()答案B解析依题意知,在2 h内血液中药物含量Q持续增加,停止注射后,Q呈指数衰减,图象B适合.4.(2019·全国Ⅰ卷)函数f(x)=sin x+xcos x+x2在[-π,π]的图象大致为()答案D解析 ∵f (-x )=sin (-x )-x cos (-x )+(-x )2=-f (x ),且x ∈[-π,π],∴f (x )为奇函数,排除A.当x =π时,f (π)=π-1+π2>0,排除B ,C ,只有D 满足. 5.(2021·长沙检测)已知图①中的图象对应的函数为y =f (x ),则图②中的图象对应的函数为( )A.y =f (|x |)B.y =f (-|x |)C.y =|f (x )|D.y =-|f (x )|答案 B解析 观察函数图象可得,②是由①保留y 轴左侧及y 轴上的图象,然后将y 轴左侧图象翻折到右侧所得,结合函数图象的对称变换可得变换后的函数的解析式为y =f (-|x |).6.(2020·重庆联考)已知函数f (x )的图象如图所示,则函数g (x )=log2f (x )的定义域是________.答案 (2,8]解析 当f (x )>0时,函数g (x )=log 2f (x )有意义,由函数f (x )的图象知满足f (x )>0时,x ∈(2,8].考点一 作函数的图象【例1】作出下列函数的图象: (1)y =⎝ ⎛⎭⎪⎫12|x |;(2)y =|log 2(x +1)|;(3)y =x 2-2|x |-1.解 (1)先作出y =⎝ ⎛⎭⎪⎫12x 的图象,保留y =⎝ ⎛⎭⎪⎫12x 图象中x ≥0的部分,再作出y =⎝ ⎛⎭⎪⎫12x的图象中x >0部分关于y 轴的对称部分,即得y =⎝ ⎛⎭⎪⎫12|x |的图象,如图①实线部分.(2)将函数y =log 2x 的图象向左平移一个单位,再将x 轴下方的部分沿x 轴翻折上去,即可得到函数y =|log 2(x +1)|的图象,如图②.(3)∵y =⎩⎪⎨⎪⎧x 2-2x -1,x ≥0,x 2+2x -1,x <0,且函数为偶函数,先用描点法作出[0,+∞)上的图象,再根据对称性作出(-∞,0)上的图象,得图象如图③.感悟升华 1.描点法作图:当函数解析式(或变形后的解析式)是熟悉的基本函数时,就可根据这些函数的特征描出图象的关键点直接作出.2.图象变换法:若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出,并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响.【训练1】分别作出下列函数的图象: (1)y =sin |x |;(2)y =2x -1x -1. 解 (1)当x ≥0时,y =sin|x |与y =sin x 的图象完全相同,又y =sin|x |为偶函数,图象关于y 轴对称,其图象如图①.(2)y =2x -1x -1=2+1x -1,故函数的图象可由y =1x 的图象向右平移1个单位,再向上平移2个单位得到,如图②所示. 考点二 函数图象的辨识1.(2020·浙江卷)函数y =x cos x +sin x 在区间[-π,π]的图象大致为( )答案 A解析 因为f (x )=x cos x +sin x ,则f (-x )=-x cos x -sin x =-f (x ),又x ∈[-π,π],所以f (x )为奇函数,其图象关于坐标原点对称,则C ,D 错误.且x =π时,y =πcos π+sin π=-π<0,知B 错误;只有A 满足. 2.(2021·重庆诊断)函数f (x )=x cos ⎝ ⎛⎭⎪⎫x -π2的图象大致为( )答案 A解析 根据题意,f (x )=x cos ⎝ ⎛⎭⎪⎫x -π2=x sin x ,定义域为R ,关于原点对称.有f (-x )=(-x )sin(-x )=x sin x =f (x ),即函数y =f (x )为偶函数,排除B ,D.当x ∈(0,π)时,x >0,sin x >0,有f (x )>0,排除C.只有A 适合. 3.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x ≤1,log 13x ,x >1,则函数y =f (1-x )的大致图象是( )答案 D解析 法一先画出函数f (x )=⎩⎨⎧3x ,x ≤1,log 13x ,x >1的草图,令函数f (x )的图象关于y 轴对称,得函数f (-x )的图象,再把所得的函数f (-x )的图象,向右平移1个单位,得到函数y =f (1-x )的图象(图略),故选D.法二 由已知函数f (x )的解析式,得y =f (1-x )=⎩⎨⎧31-x,x ≥0,log 13(1-x ),x <0,故该函数过点(0,3),排除A ;过点(1,1),排除B ;在(-∞,0)上单调递增,排除C.选D.4.函数f (x )的部分图象如图所示,则f (x )的解析式可以是( )A.f (x )=x +sin xB.f (x )=cos xxC.f (x )=x ⎝ ⎛⎭⎪⎫x -π2⎝ ⎛⎭⎪⎫x -3π2D.f (x )=x cos x 答案 D解析 从图象看,y =f (x )应为奇函数,排除C ; 又f ⎝ ⎛⎭⎪⎫π2=0,知f (x )=x +sin x 不正确;对于B,f(x)=cos xx ,得f′(x)=-x sin x-cos xx2,当0<x<π2时,f′(x)<0,所以f(x)=cos xx 在⎝⎛⎭⎪⎫0,π2上递减,B不正确;只有f(x)=x cos x满足图象的特征.感悟升华 1.抓住函数的性质,定性分析:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从周期性,判断图象的循环往复;(4)从函数的奇偶性,判断图象的对称性.2.抓住函数的特征,定量计算:从函数的特征点,利用特征点、特殊值的计算分析解决问题.考点三函数图象的应用角度1研究函数的性质【例2】(多选题)(2021·滨州一模)在平面直角坐标系xOy中,如图放置的边长为2的正方形ABCD沿x轴滚动(无滑动滚动),点D恰好经过坐标原点.设顶点B(x,y)的轨迹方程是y=f(x),则对函数y=f(x)的判断正确的是()A.函数y=f(x)是奇函数B.对任意的x∈R,都有f(x+4)=f(x-4)C.函数y=f(x)的值域为[0,22]D.函数y=f(x)在区间[6,8]上单调递增答案BCD解析由题意得,当-4≤x<-2时,点B的轨迹为以(-2,0)为圆心,2为半径的14圆;当-2≤x <2时,点B 的轨迹为以原点为圆心,22为半径的14圆; 当2≤x <4时,点B 的轨迹为以(2,0)为圆心,2为半径的14圆,如图所示; 以后依次重复,所以函数f (x )是以8为周期的周期函数.由图象可知,函数f (x )为偶函数,故A 错误;因为f (x )的周期为8,所以f (x +8)=f (x ),即f (x +4)=f (x -4),故B 正确; 由图象可知,f (x )的值域为[0,22],故C 正确;由图象可知,f (x )在[-2,0]上单调递增,因为f (x )在[6,8]的图象和在[-2,0]的图象相同,故D 正确.故选BCD.角度2 函数图象在不等式中的应用【例3】 (1)若函数f (x )=log 2(x +1),且a >b >c >0,则f (a )a ,f (b )b ,f (c )c 的大小关系是( ) A.f (a )a >f (b )b >f (c )c B.f (c )c >f (b )b >f (a )a C.f (b )b >f (a )a >f (c )cD.f (a )a >f (c )c >f (b )b(2)(2020·北京卷)已知函数f (x )=2x -x -1,则不等式f (x )>0的解集是( ) A.(-1,1) B.(-∞,-1)∪(1,+∞) C.(0,1)D.(-∞,0)∪(1,+∞)答案 (1)B (2)D解析 (1)由题意可得,f (a )a ,f (b )b ,f (c )c 分别看作函数f (x )=log 2(x +1)图象上的点(a ,f (a )),(b ,f (b )),(c ,f (c ))与原点连线的斜率.结合图象可知,当a >b >c >0时,f (a )a <f (b )b <f (c )c .(2)在同一平面直角坐标系中画出h (x )=2x ,g (x )=x +1的图象如图.由图象得交点坐标为(0,1)和(1,2). 又f (x )>0等价于2x >x +1, 结合图象,可得x <0或x >1.故f (x )>0的解集为(-∞,0)∪(1,+∞).故选D.角度3 求参数的取值范围【例4】 (1)已知函数f (x )=⎩⎪⎨⎪⎧2x ,x ≥2,(x -1)3,x <2.若关于x 的方程f (x )=k 有两个不同的实根,则实数k 的取值范围是________.(2)已知函数f (x )=|x 2+3x |,x ∈R .若方程f (x )-a |x -1|=0恰有4个互异的实数根,则实数a 的取值范围为________. 答案 (1)(0,1) (2)(0,1)∪(9,+∞)解析 (1)画出分段函数f (x )的图象如图所示,结合图象可以看出,若f (x )=k 有两个不同的实根,也即函数y =f (x )的图象与y =k 有两个不同的交点,k 的取值范围为(0,1). (2)设y 1=f (x )=|x 2+3x |,y 2=a |x -1|.在同一直角坐标系中作出y 1=|x 2+3x |, y 2=a |x -1|的图象如图所示.由图可知f (x )-a |x -1|=0有4个互异的实数根等价于y 1=|x 2+3x |与y 2=a |x -1|的图象有4个不同的交点,且4个交点的横坐标都小于1,所以①⎩⎪⎨⎪⎧y =-x 2-3x ,y =a (1-x )(-3<x <0)有两组不同解.消去y 得x 2+(3-a )x +a =0,该方程有两个不等实根x 1,x 2,∴⎩⎪⎨⎪⎧Δ=(3-a )2-4a >0,-3<a -32<0,(-3)2+(3-a )×(-3)+a >0,02+(3-a )×0+a >0,∴0<a <1.②⎩⎪⎨⎪⎧y =x 2+3x ,y =a (x -1)(x >1)有两组不同解. 消去y 得x 2+(3-a )x +a =0有两不等实根x 3、x 4, ∴Δ=a 2-10a +9>0,又∵x 3+x 4=a -3>2,x 3x 4=a >1, ∴a >9.综上可知,0<a <1或a >9.感悟升华 1.利用函数的图象研究函数的性质对于已知或易画出其在给定区间上图象的函数,其性质(单调性、奇偶性、周期性、最值(值域)、零点)常借助于图象研究,但一定要注意性质与图象特征的对应关系.2.利用函数的图象可解决某些方程和不等式的求解问题,方程f(x)=g(x)的根就是函数f(x)与g(x)图象交点的横坐标;不等式f(x)<g(x)的解集是函数f(x)的图象位于g(x)图象下方的点的横坐标的集合,体现了数形结合思想.【训练2】(1)设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.(2)(2020·徽州一中期中)已知奇函数f(x)在x≥0时的图象如图所示,则不等式xf(x)<0的解集为________.(3)(多选题)(2021·淄博模拟)关于函数f(x)=|ln|2-x||,下列描述正确的有()A.函数f(x)在区间(1,2)上单调递增B.函数y=f(x)的图象关于直线x=2对称C.若x1≠x2,但f(x1)=f(x2),则x1+x2=4D.函数f(x)有且仅有两个零点答案(1)[-1,+∞)(2)(-2,-1)∪(1,2)(3)ABD解析(1)如图作出函数f(x)=|x+a|与g(x)=x-1的图象,观察图象可知,当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).(2)∵xf(x)<0,∴x和f(x)异号,由于f(x)为奇函数,补齐函数的图象如图.当x∈(-2,-1)∪(0,1)∪(2,+∞)时,f(x)>0,当x∈(-∞,-2)∪(-1,0)∪(1,2)时,f(x)<0,∴不等式xf(x)<0的解集为(-2,-1)∪(1,2).(3)函数f(x)=|ln|2-x||的图象如图所示,由图可得,函数f(x)在区间(1,2)上单调递增,A正确;函数y=f(x)的图象关于直线x=2对称,B正确;若x1≠x2,但f(x1)=f(x2),则x1+x2的值不一定等于4,C错误;函数f(x)有且仅有两个零点,D正确.函数图象的活用直观想象是发现和提出问题,分析和解决问题的重要手段,在数学研究的探索中,通过直观手段的运用以及借助直观展开想象,从而发现问题、解决问题的例子比比皆是,并贯穿于数学研究过程的始终,而数形结合思想是典型的直观想象范例.一、根据函数图象确定函数解析式【例1】(2021·长沙检测)已知某函数的图象如图所示,则下列函数中,与图象最契合的是()A.y =sin(e x +e -x )B.y =sin(e x -e -x )C.y =cos(e x -e -x )D.y =cos(e x +e -x )答案 D解析 由函数图象知,函数图象关于y 轴对称,∵y =sin(e x -e -x )为奇函数,图象关于原点对称,B 不正确; 又-1<f (0)<0,但sin 2>0,cos 0=1,故A ,C 不正确; 只有y =cos(e x +e -x )满足图象特征.故选D.素养升华 函数解析式与函数图象是函数的两种重要表示法,图象形象直观,解析式易于研究函数性质,可根据需要,相互转化.二、由图象特征研究函数性质求参数【例2】设函数f (x )=⎩⎨⎧-x 2+4x ,x ≤4,log 2x ,x >4,若函数y =f (x )在区间(a ,a +1)上单调递增,则实数a 的取值范围是( ) A.(-∞,1] B.[1,4]C.[4,+∞)D.(-∞,1]∪[4,+∞) 答案 D解析 作出函数f (x )的图象如图所示,由图象可知,要使f (x )在(a ,a +1)上单调递增, 需满足a ≥4或a +1≤2. 因此a ≥4或a ≤1.素养升华 1.运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.2.图象形象地显示了函数的性质,因此,函数性质的确定与应用及一些方程、不等式的求解常与图象数形结合研究.A级基础巩固一、选择题1.(2020·天津卷)函数y=4xx2+1的图象大致为()答案A解析令f(x)=4xx2+1,则f(x)的定义域为R,且f(-x)=-4xx2+1=-f(x),因此,函数为奇函数,排除C,D.当x=1时,f(1)=42=2>0,排除B.故选A.2.(2021·江南十校模拟)函数f(x)=x cos x2x+2-x在⎣⎢⎡⎦⎥⎤-π2,π2上的图象大致为()答案C解析根据题意,有f(-x)=-x cos x2x+2-x=-f(x),且定义域关于原点对称,则在⎣⎢⎡⎦⎥⎤-π2,π2上,f (x )为奇函数,其图象关于原点对称,排除A ,B ; 又在区间⎝ ⎛⎭⎪⎫0,π2上,x >0,cos x >0,2x >0,2-x >0,则f (x )>0,排除D ,只有C 适合.3.若函数f (x )=a x -a -x (a >0且a ≠1)在R 上为减函数,则函数y =log a (|x |-1)的图象可能是( )答案 D解析 由f (x )在R 上是减函数,知0<a <1.又y =log a (|x |-1)是偶函数,定义域是(-∞,-1)∪(1,+∞).∴当x >1时,y =log a (x -1)的图象由y =log a x 的图象向右平移一个单位得到.因此D 正确.4.下列函数中,其图象与函数y =ln x 的图象关于直线x =1对称的是( ) A.y =ln(1-x ) B.y =ln(2-x ) C.y =ln(1+x ) D.y =ln(2+x )答案 B解析 法一 设所求函数图象上任一点的坐标为(x ,y ),则其关于直线x =1的对称点的坐标为(2-x ,y ),由对称性知点(2-x ,y )在函数f (x )=ln x 的图象上,所以y =ln(2-x ).法二 由题意知,对称轴上的点(1,0)在函数y =ln x 的图象上也在所求函数的图象上,代入选项中的函数表达式逐一检验,排除A ,C ,D ,选B.5.(2021·豫北名校联考)已知f (x )是定义在R 上的奇函数,当x >0时,f (x )=3-2x ,则不等式f (x )>0的解集为( )A.⎝ ⎛⎭⎪⎫-32,32B.⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫32,+∞ C.⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫0,32 D.⎝ ⎛⎭⎪⎫-32,0∪⎝ ⎛⎭⎪⎫32,+∞ 答案 C解析 根据题意,f (x )是定义在R 上的奇函数,当x >0时,f (x )=3-2x ,可得其图象如图,且f (0)=0,f ⎝ ⎛⎭⎪⎫32=f ⎝ ⎛⎭⎪⎫-32=0,则不等式f (x )>0的解集为⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫0,32.6.若函数f (x )=⎩⎨⎧ax +b ,x <-1,ln (x +a ),x ≥-1的图象如图所示,则f (-3)=( ) A.-12 B.-54 C.-1D.-2答案 C解析 由图象知⎩⎪⎨⎪⎧ln (a -1)=0,b -a =3,得⎩⎪⎨⎪⎧a =2,b =5.∴f (x )=⎩⎪⎨⎪⎧2x +5,x <-1,ln (x +2),x ≥-1.故f (-3)=5-6=-1.7.(多选题)(2021·山东新高考模拟)对于函数f (x )=lg(|x -2|+1),下列说法正确的是( )A.f (x +2)是偶函数B.f (x +2)是奇函数C.f (x )在区间(-∞,2)上是减函数,在区间(2,+∞)上是增函数D.f (x )没有最小值 答案 AC解析 f (x +2)=lg(|x |+1)为偶函数,A 正确,B 错误.作出f (x )的图象如图所示,可知f (x )在(-∞,2)上是减函数,在(2,+∞)上是增函数;由图象可知函数存在最小值0,C 正确,D 错误.8.若函数y =f (x )的图象的一部分如图(1)所示,则图(2)中的图象所对应的函数解析式可以是( )A.y =f ⎝ ⎛⎭⎪⎫2x -12B.y =f (2x -1)C.y =f ⎝ ⎛⎭⎪⎫12x -12D.y =f ⎝ ⎛⎭⎪⎫12x -1答案 B解析 函数f (x )的图象先整体往右平移1个单位,得到y =f (x -1)的图象,再将所有点的横坐标变为原来的12,得到y =f (2x -1)的图象. 二、填空题9.若函数y =f (x )的图象过点(1,1),则函数y =f (4-x )的图象一定经过点________. 答案 (3,1)解析 由于函数y =f (4-x )的图象可以看作y =f (x )的图象先关于y 轴对称,再向右平移4个单位长度得到.点(1,1)关于y 轴对称的点为(-1,1),再将此点向右平移4个单位长度为(3,1).所以函数y =f (4-x )的图象过定点(3,1).10.在平面直角坐标系xOy 中,若直线y =2a 与函数y =|x -a |-1的图象只有一个交点,则a 的值为________. 答案 -12解析 函数y =|x -a |-1的大致图象如图所示,∴若直线y =2a 与函数y =|x -a |-1的图象只有一个交点, 只需2a =-1,可得a =-12.11.使log 2(-x )<x +1成立的x 的取值范围是________. 答案 (-1,0)解析 在同一直角坐标系内作出y =log 2(-x ),y =x +1的图象,知满足条件的x ∈(-1,0).12.已知函数f (x )在R 上单调且其部分图象如图所示,若不等式-2<f (x +t )<4的解集为(-1,2),则实数t 的值为________. 答案 1解析 由图象可知不等式-2<f (x +t )<4, 即f (3)<f (x +t )<f (0).又y =f (x )在R 上单调递减,∴0<x +t <3,不等式解集为(-t ,3-t ). 依题意,得t =1.B 级 能力提升13.若直角坐标系内A ,B 两点满足:(1)点A ,B 都在f (x )的图象上;(2)点A ,B 关于原点对称,则称点对(A ,B )是函数f (x )的一个“和谐点对”,(A ,B )与(B ,A )可看作一个“和谐点对”.已知函数f (x )=⎩⎪⎨⎪⎧x 2+2x (x <0),2e x (x ≥0),则f (x )的“和谐点对”有( ) A.1个 B.2个C.3个D.4个答案 B解析 作出函数y =x 2+2x (x <0)的图象关于原点对称的图象(如图中的虚线部分),看它与函数y =2e x (x ≥0)的图象的交点个数即可,观察图象可得交点个数为2,即f (x )的“和谐点对”有2个.14.(2020·潍坊质检)已知函数f (x )是定义在R 上的偶函数,且对任意的x ∈R ,f (x +2)=f (x ),当0≤x ≤1时,f (x )=x 2.若直线y =x +a 与函数f (x )的图象在[0,2]内恰有两个不同的公共点,则实数a 的值是( ) A.0 B.0或-12 C.-14或12D.0或-14答案 D解析 因为f (x +2)=f (x ),所以函数f (x )的周期为2,如图所示:由图知,直线y =x +a 与函数f (x )的图象在区间[0,2]内恰有两个不同的公共点时,直线y =x +a 经过点(1,1)或与曲线f (x )=x 2(0≤x ≤1)相切于点A ,则1=1+a ,或方程x 2=x +a 只有一个实数根.所以a =0或Δ=1+4a =0,即a =0或a =-14.15.(多选题)(2021·日照模拟)设f (x )是定义在R 上的函数,若存在两个不相等的实数x 1,x 2,使得f ⎝ ⎛⎭⎪⎫x 1+x 22=f (x 1)+f (x 2)2,则称函数f (x )具有性质P .那么下列函数中,具有性质P 的函数为( ) A.f (x )=⎩⎪⎨⎪⎧1x ,x ≠0,0,x =0B.f (x )=|x 2-1|C.f (x )=x 3+xD.f (x )=2|x |答案 ABC解析 对于A ,在函数f (x )的图象上取A (-1,-1),B (0,0),C (1,1),有f (0)=f (-1)+f (1)2成立,故A 正确; 对于B ,在函数f (x )的图象上取A (-2,1),B (0,1),C (2,1),有f (0)=f (-2)+f (2)2成立,故B 正确; 对于C ,在函数f (x )的图象上取A (1,2),B (0,0),C (-1,-2),有f (0)=f (-1)+f (1)2成立,故C 正确; 对于D ,因为f (x )=2|x |,f (x 1)+f (x 2)2=2|x 1|+2|x 2|2≥2|x 1|·2|x 2|=2|x 1|+|x 2|2≥2|x 1+x 22|=f ⎝ ⎛⎭⎪⎫x 1+x 22,又x 1≠x 2,所以f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2恒成立,故D 错误.故选ABC.16.已知函数f (x )=|log 3x |,实数m ,n 满足0<m <n ,且f (m )=f (n ),若f (x )在[m 2,n ]上的最大值为2,则n m =________.答案 9解析 如图,作出函数f (x )=|log 3x |的图象,观察可知0<m <1<n且mn =1.若f (x )在[m 2,n ]上的最大值为2,从图象分析应有f (m 2)=2,∴log 3m 2=-2,∴m 2=19.从而m =13,n =3,故n m =9.。
函数图像的平移变换练习题
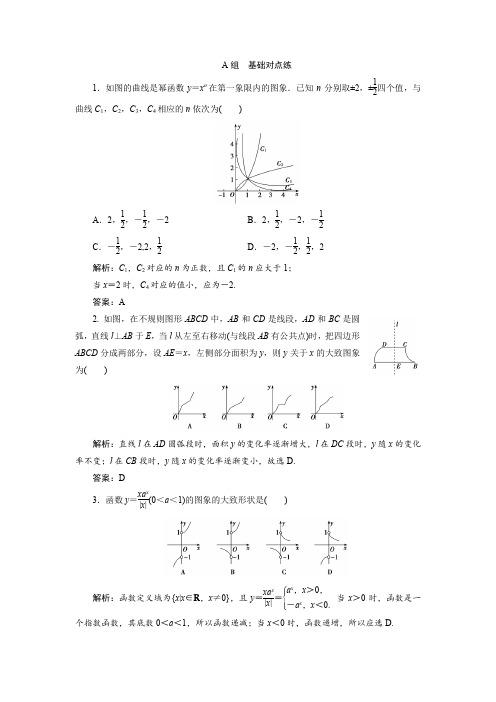
A 组 基础对点练1.如图的曲线是幂函数y =x n 在第一象限内的图象.已知n 分别取±2,±12四个值,与曲线C 1,C 2,C 3,C 4相应的n 依次为( )A .2,12,-12,-2B .2,12,-2,-12C .-12,-2,2,12D .-2,-12,12,2解析:C 1,C 2对应的n 为正数,且C 1的n 应大于1; 当x =2时,C 4对应的值小,应为-2. 答案:A2. 如图,在不规则图形ABCD 中,AB 和CD 是线段,AD 和BC 是圆弧,直线l ⊥AB 于E ,当l 从左至右移动(与线段AB 有公共点)时,把四边形ABCD 分成两部分,设AE =x ,左侧部分面积为y ,则y 关于x 的大致图象为( )解析:直线l 在AD 圆弧段时,面积y 的变化率逐渐增大,l 在DC 段时,y 随x 的变化率不变;l 在CB 段时,y 随x 的变化率逐渐变小,故选D.答案:D3.函数y =xa x|x |(0<a <1)的图象的大致形状是( )解析:函数定义域为{x |x ∈R ,x ≠0},且y =xa x |x |=⎩⎪⎨⎪⎧a x ,x >0,-a x ,x <0.当x >0时,函数是一个指数函数,其底数0<a <1,所以函数递减;当x <0时,函数递增,所以应选D.答案:D4.函数f (x )=ln ⎝⎛⎭⎫x -1x 的图象是( )解析:自变量x 满足x -1x =x 2-1x >0,当x >0时可得x >1,当x <0时可得-1<x <0,即函数f (x )的定义域是(-1,0)∪(1,+∞),据此排除选项A 、D 中的图象.当x >1时,函数x -1x单调递增,故f (x )=ln ⎝⎛⎭⎫x -1x 单调递增. 答案:B5. (2018·武昌调研)已知函数f (x )的部分图象如图所示,则f (x )的解析式可以是( )A .f (x )=2-x 22xB .f (x )=cos xx 2C .f (x )=-cos 2xxD .f (x )=cos xx解析:A 中,当x →+∞时,f (x )→-∞,与题图不符,故不成立;B 为偶函数,与题图不符,故不成立;C 中,当x →0+时,f (x )<0,与题图不符,故不成立.选D.答案:D6.函数f (x )的图象向右平移1个单位长度,所得图象与曲线y =e x 关于y 轴对称,则f (x )=( )A .e x +1 B .e x -1 C .e-x +1 D .e-x -1解析:与曲线y =e x 关于y 轴对称的图象对应的函数为y =e -x ,将函数y =e -x 的图象向左平移1个单位长度即得y =f (x )的图象,∴f (x )=e-(x +1)=e-x -1,故选D.答案:D7.函数f (x )=2ln x 的图象与函数g (x )=x 2-4x +5的图象的交点个数为( )A .3B .2C .1D .0解析:在同一直角坐标系下画出函数f (x )=2ln x 与函数g (x )=x 2-4x +5=(x -2)2+1的图象,如图所示.∵f (2)=2ln 2>g (2)=1,∴f (x )与g (x )的图象的交点个数为2.故选B. 答案:B 8.若函数y =2-x +1+m 的图象不经过第一象限,则m 的取值范围是________.解析:由y =2-x +1+m ,得y =⎝⎛⎭⎫12x -1+m ;函数y =⎝⎛⎭⎫12x -1的图象如所示,则要使其图象不经过第一象限,则m ≤-2. 答案:(-∞,-2]9. 函数f (x )=⎩⎪⎨⎪⎧ax +b ,x ≤0,log c ⎝⎛⎭⎫x +19,x >0的图象如图所示,则a +b +c =________.解析:由图象可求得直线的方程为y =2x +2.又函数y =log c ⎝⎛⎭⎫x +19的图象过点(0,2),将其坐标代入可得c =13,所以a +b +c =2+2+13=133. 答案:13310.(2018·枣庄一中模拟)已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=x 2-2x ,如果函数g (x )=f (x )-m (m ∈R )恰有4个零点,则m 的取值范围是________.解析:f (x )的图象如图所示,g (x )=0即f (x )=m , y =m 与y =f (x )有四个交点, 故m 的取值范围为(-1,0). 答案:(-1,0)11.若函数f (x )=⎩⎨⎧1x ,x <0,⎝⎛⎭⎫13x,x ≥0,则不等式-13≤f (x )≤13的解集为__________.解析:函数f (x )=⎩⎨⎧1x ,x <0,⎝⎛⎭⎫13x,x ≥0和函数g (x )=±13的图象如图所示.当x <0时,是区间(-∞,-3],当x ≥0时,是区间[1,+∞),故不等式-13≤f (x )≤13的解集为(-∞,-3]∪[1,+∞).答案:(-∞,-3]∪[1,+∞)B 组 能力提升练1.函数y =(x 3-x )2|x |的图象大致是( )解析:由于函数y =(x 3-x )2|x |为奇函数,故它的图象关于原点对称,当0<x <1时,y <0;当x >1时,y >0,故选B.答案:B2.(2018·临沂模拟)已知a 是常数,函数f (x )=13x 3+12·(1-a )x 2-ax +2的导函数y =f ′(x )的图象如图所示,则函数g (x )=|a x -2|的图象可能是( )解析:∵f (x )=13x 3+12(1-a )x 2-ax +2,∴f ′(x )=x 2+(1-a )x -a ,由函数y =f ′(x )的图象可知-1-a2>0,∴a >1,则函数g (x )=|a x -2|的图象是由函数y =a x 的图象向下平移2个单位,然后将x 轴下方的图象翻折到x 轴上方得到的,故选D.答案:D3.函数f (x )=ax 3+bx 2+cx +d 的图象如图所示,则下列结论成立的是( )A .a >0,b <0,c >0,d >0B .a >0,b <0,c <0,d >0C .a <0,b <0,c >0,d >0D .a >0,b >0,c >0,d <0解析:∵函数f (x )的图象在y 轴上的截距为正值,∴d >0.∵f ′(x )=3ax 2+2bx +c ,且函数f (x )=ax 3+bx 2+cx +d 在(-∞,x 1)上单调递增,(x 1,x 2)上单调递减,(x 2,+∞)上单调递增,∴f ′(x )<0的解集为(x 1,x 2),∴a >0,又x 1,x 2均为正数,∴c 3a >0,-2b3a >0,可得c >0,b <0.答案:A4.(2018·石家庄模拟)设f (x )=|3x -1|,c <b <a ,且f (c )>f (a )>f (b ),则下列关系中一定成立的是( )A .3c >3aB .3c >3bC .3c +3a >2D .3c +3a <2解析: 画出f (x )=|3x -1|的图象,如图所示,要使c <b <a ,且f (c )>f (a )>f (b )成立,则有c <0,且a >0.由y =3x 的图象可得0<3c <1<3a .∴f (c )=1-3c ,f (a )=3a -1,∵f (c )>f (a ), ∴1-3c >3a -1,即3a +3c <2. 答案:D5.已知函数f (x )=-2x 2+1,函数g (x )=⎩⎪⎨⎪⎧log 12x ,x >02x ,x ≤0,则函数y =|f (x )|-g (x )的零点的个数为( )A .2B .3C .4D .5解析:函数y =|f (x )|-g (x )的零点的个数,即|f (x )|-g (x )=0的根的个数,可得|f (x )|=g (x ),画出函数|f (x )|,g (x )的图象如图所示,观察函数的图象,则它们的交点为4个,即函数y =|f (x )|-g (x )的零点个数为4,选C.答案:C6. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A BCD 中,AB ⊥平面BCD ,且BD ⊥CD ,AB =BD =CD ,点P 在棱AC 上运动,设CP 的长度为x ,若△PBD 的面积为f (x ),则f (x )的图象大致是( )解析: 如图,作PQ ⊥BC 于Q ,作QR ⊥BD 于R ,连接PR ,则由鳖臑的定义知PQ ∥AB ,QR ∥CD .设AB =BD =CD =1,则CP AC =x 3=PQ1,即PQ =x 3,又QR 1=BQ BC =APAC =3-x 3,所以QR =3-x 3,所以PR =PQ 2+QR 2=⎝⎛⎭⎫x 32+⎝ ⎛⎭⎪⎫3-x 32=332x 2-23x +3,所以f (x )=362x 2-23x +3=66⎝⎛⎭⎫x -322+34,故选A. 答案:A7.若关于x 的不等式4a x -1<3x -4(a >0,且a ≠1)对于任意的x >2恒成立,则a 的取值范围为( )A.⎝⎛⎭⎫0,12B.⎝⎛⎦⎤0,12 C .[2,+∞)D .(2,+∞)解析:不等式4a x -1<3x -4等价于a x -1<34x -1.令f (x )=a x -1,g (x )=34x -1,当a >1时,在同一坐标系中作出两个函数的图象,如图1所示,由图知不满足条件;当0<a <1时,在同一坐标系中作出两个函数的图象,如图2所示,则f (2)≤g (2),即a 2-1≤34×2-1,即a ≤12,所以a 的取值范围是⎝⎛⎦⎤0,12,故选B.答案:B8.已知函数f (x )=x 2-2(a +2)x +a 2,g (x )=-x 2+2(a -2)x -a 2+8.设H 1(x )=max{f (x ),g (x )},H 2(x )=min{f (x ),g (x )}(max{p ,q }表示p ,q 中的较大值,min{p ,q }表示p ,q 中的较小值).记H 1(x )的最小值为A ,H 2(x )的最大值为B ,则A -B =( )A .a 2-2a -16B .a 2+2a -16C .-16D .16解析:f (x )=g (x ),即x 2-2(a +2)x +a 2=-x 2+2(a -2)x -a 2+8,即x 2-2ax +a 2-4=0,解得x =a +2或x =a -2.f (x )与g (x )的图象如图.由图及H 1(x )的定义知H 1(x )的最小值是f (a +2), H 2(x )的最大值为g (a -2),A -B =f (a +2)-g (a -2)=(a +2)2-2(a +2)2+a 2+(a -2)2-2(a -2)·(a -2)+a 2-8=-16. 答案:C9.若函数f (x )=(2-m )xx 2+m的图象如图所示,则m 的取值范围为( )A .(-∞,-1)B .(-1,2)C .(0,2)D .[1,2)解析:根据题图可知,函数图象过原点,即f (0)=0,所以m ≠0.当x >0时,f (x )>0,所以2-m >0,即m <2.函数f (x )在[-1,1]上是单调递增的,所以f ′(x )≥0在[-1,1]上恒成立,则f ′(x )=(2-m )(x 2+m )-2x (2-m )x (x 2+m )2=(m -2)(x 2-m )(x 2+m )2≥0,∵m -2<0,(x 2+m )2>0,∴只需x 2-m ≤0在[-1,1]上恒成立即可,∴m ≥(x 2)max ,∴m ≥1.综上所述:1≤m <2,故选D. 答案:D10.设函数f (x )=⎩⎪⎨⎪⎧2-x -1, x ≤0,x 12, x >0.若f (x 0)>1,则x 0的取值范围是________.解析: 在同一直角坐标系中,作出函数y =f (x )的图象和直线y =1,它们相交于(-1,1)和(1,1)两点,由f (x 0)>1,得x 0<-1或x 0>1.答案:(-∞,-1)∪(1,+∞)11.定义在R 上的函数f (x )=⎩⎪⎨⎪⎧lg|x |,x ≠0,1, x =0,关于x 的方程y =c (c 为常数)恰有三个不同的实数根x 1,x 2,x 3,则x 1+x 2+x 3=________.解析: 函数f (x )的图象如图,方程f (x )=c 有三个根,即y =f (x )与y =c 的图象有三个交点,易知c =1,且一根为0,由lg|x |=1知另两根为-10和10,∴x 1+x 2+x 3=0.答案:012.(2018·咸阳模拟)已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >0,3x ,x ≤0,关于x 的方程f (x )+x -a =0有且只有一个实根,则实数a 的取值范围是________.解析:方程f (x )+x -a =0有且只有一个实根,等价于函数y =f (x )与y =-x +a 的图象有且只有一个交点.结合下面函数图象可知a >1.答案:(1,+∞)13.(2018·湖北百所重点学校联考)设函数f (x )对任意实数x 满足f (x )=-f (x +1),且当0≤x ≤1时,f (x )=x (1-x ),若关于x 的方程f (x )=kx 有3个不同的实数根,则k 的取值范围是__________.解析:因f (x )=-f (x +1),故f (x +2)=f (x ),即函数f (x )是周期为2的周期函数,画出函数y =f (x ),x ∈[0,1]的图象,再借助函数满足的条件f (x )=-f (x +1)及周期性,画出函数y =f (x )的图象如图,易知仅当直线y =kx 位于l 1与l 2之间(不包括l 1、l 2)或与l 3重合时满足题意,对y =x (1-x )求导得y ′=1-2x ,y ′|x =0=1,∴l 2的斜率为1.以下求l 3的斜率:当1≤x ≤2时,易得f (x )=-f (x -1)=-(x -1)[1-(x -1)]=x 2-3x +2,令x 2-3x +2-kx =0,得x 2-(3+k )x +2=0,令Δ=(3+k )2-8=0,解得k =-3±22,由此易知l 3的斜率为-3+2 2.同理,由2≤x ≤3时,f (x )=-x 2+5x -6,可得l 1的斜率为5-2 6.综上,5-26<k <1或k =-3+22,故应填(5-26,1)∪{-3+22}.答案:(5-26,1)∪{-3+22}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的图象变换(习题)
1.函数y=-2x2的图象是由函数y=-2x2+4x+6的图象经过怎样的变换得到的?
()
A.向左平移1个单位长度,向上平移8个单位长度
B.向右平移1个单位长度,向上平移8个单位长度
C.向左平移1个单位长度,向下平移8个单位长度
D.向右平移1个单位长度,向下平移8个单位长度
4.若函数(1)
x
y a b
=-+(a>0,且a≠1)的图象在第一、三、四象限,则必有()
A .0<a <1,b >0
B .0<a <1,b <0
C .a >1,b <0
D .a >1,b >
5. 若函数()y f x =与()y f x =的图象相同,则()f x 可能是( )
A .1y x -=
B .2x y =
C .2log y x =
D .21y x =-
6. 当0<a <1时,函数()log ()a f x x =-与()1g x ax =-的图象的交点在( )
A . 第四象限
B .第三象限
C .第二象限
D .第一象限
7. 在同一平面直角坐标系内,函数1()3x f x -=与1()3x g x +=的图象关于( )
A .y 轴对称
B .x 轴对称
C .原点对称
D .直线x =1对称
f (x -1)的函数 f (-x )的函数 |f (x )|的函数 f (|x |)的函数
A B C D
10. 将()y f x =的图象向右平移1个单位长度,所得图象与y =ln x 关于y 轴对称,
则()y f x =的解析式为( ) A .()ln(1)f x x =+ B .()ln(1)f x x =- C .()ln(1)f x x =-+ D .()ln(1)f x x =--
11. 若函数22()(1)()f x x x ax b =-++的图象关于直线x =-2对称,则a ,b 的值分
别为( ) A .15,8 B .8,15
C .3,4
D .-3,-4
12. 已知函数()y f x =的图象关于直线x =1对称,且在[1)+∞,上单调递减,
(0)0f =,则(1)0f x +>的解集为( )
A . (1)+∞,
B .(1)(1)-∞-+∞,,
C .(1)-∞-,
D .(11)-,
13. 已知函数()
y f x =的图象与ln y x =的图象关于x 轴对称,则
(2)f
=_____________.
15.若函数2x a
=的图象的对称轴是直线x=2,则a的值为__________.
y--+
【参考答案】
1. C
2. B
3. C
4. D
5. B
6. C
7. A
8. A
9. C
10.D
11.B
12.D
13.-ln 2
14.
1
() 2
+∞,
15.2。
