河南省郑州外国语中学2019-2020学年第一学期七年级上期第一次月考数学试卷及答案
2019-2020学年河南省郑州外国语中学七年级(上)第一次月考数学试卷 (含答案解析)

2019-2020学年河南省郑州外国语中学七年级(上)第一次月考数学试卷一、选择题(本大题共10小题,共30.0分)1.在有理数−4、0、3、−23、3.14中,非负整数的个数有()A. 1个B. 2个C. 3个D. 4个.2.由5个小立方体搭成如图所示的几何体,从左面看到的平面图形是()A. B. C. D.3.北京时间2019年4月10日人类首次直接拍摄到黑洞的照片,它是一个“超巨型”质量黑洞,位于室女座星系团中一个超大质量星系−M87的中心,距离地球5500万光年.数据“5500万光年”用科学记数法表示为()A. 5500×104光年B. 055×108光年C. 5.5×103光年D. 5.5×107光年4.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是()A. B.C. D.5.下列计算正确的是()A. (−3)2=6B. −3−3=0C. −3×2=−6D. (−2)2=−46.若a与−2互为相反数,则a的倒数是()A. 2B. −2C. 12D. −127.在一个正方体容器内分别装入不同量的水,再把容器按不同方式倾斜一点,容器内水面的形状不可能是()A. B. C. D.8.下列判断正确的是()A. |−2|=−2B. |a|=aC. −|−2|<0D. −3<−49.若|ab|=ab,则必有()A. a>0,b<0B. a<0,b<0C. ab>0D. ab≥010.计算:(−3)+(−2)=()A. 5B. −5C. −1D. 1二、填空题(本大题共5小题,共15.0分)11.比–1小–2的数是_______.12.13.笔尖在纸上快速滑动写出了一个又一个汉字,这说明了______________;硬币在桌面上快速转动时,看上去像球,这说明了_______________。
2019-2020郑州外国语中学七年级数学上册第一次月考试卷(含答案)

一、选择题1.下列说法正确的是()A .所有的整数都是正数B .不是正数的数一定是负数C .0不是最小的有理数D .正有理数包括整数和分数2.全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000000千瓦是《政府工作报告》中确定的重点任务之一.将数据15000000用科学记数法表示为()A .15×106B .1.5×107C .1.5×108D .0.15×1083.下列各组数中,互为相反数的是()A.211)与(-- B.112与)(- C.212与D22-与4.如图,的倒数在数轴上表示的点位于下列两个点之间()A .点E 和点FB .点F 和点GC .点G 和点HD .点H 和点I5.质检员抽查某种零件的质量,超过规定长度的记为正数,短于规定长度的记为负数,检查结果如下:第一个为0.13豪米,第二个为﹣0.12毫米,第三个为﹣0.15毫米,第四个为0.11毫米,则质量最差的零件是()A .第一个B .第二个C .第三个D .第四个6.在﹣0.1428中用数字3替换其中的一个非0数码后,使所得的数最大,则被替换的字是()A .1B .2C .4D .87.已知a ,b ,c 在数轴上的位置如图所示,化简|a+c|﹣|a ﹣2b|﹣|c+2b|的结果是()郑州外国语中学201-209学年上期七年级第一次月考20(数学)A .4b+2cB .0C .2cD .2a+2c 8.绝对值大于2且小于5的所有的整数的和是()A .7B .﹣7C .0D .59.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB ,则线段AB 盖住的整点的个数是()A.2018或2019B.2019或2020C.2020或2021D.2021或202210.若ab <0,且a >b ,则a ,|a ﹣b|,b 的大小关系为()A .a >|a ﹣b|>bB .a >b >|a ﹣b|C .|a ﹣b|>a >bD .|a ﹣b|>b >a二、填空题11.一艘潜艇正在﹣50米处执行任务,其正上方10米处有一条鲨鱼在游弋,则鲨鱼所处的高度为米.()_____2,021x 2.122=+=++-y x y 则若13.若|a|=3,|-b|=|-7|,且ab>0,则a-b=______.14.设n 是正整数,则n11)(--的值是________.积为______.和为为______ ,的整数有_____个2018绝对值小于 15.16.在,﹣(﹣1),3.14,﹣|﹣8﹣22|,﹣3,﹣32,﹣(﹣)3,0中有理数有m 个,自然数有n 个,分数有k 个,负数有t 个,则m ﹣n ﹣k+t=.17.已知a 的倒数是﹣,b 与c 互为相反数,m 与n 互为倒数,则b ﹣a+c ﹣mn=.18.定义一种新运算:a ※b=,则当x=3时,2※x ﹣4※x 的结果为.19.观察下列算式:32=9,33=27,34=81,35=243,…,那么32016的末位数字为20.如果|a|=﹣a ,那么正确的是_________①﹣a 一定是非负数,②﹣a 一定是负数,③|a|一定是正数,④|a|不能是0三、解答题.+5,2,-,2-,|-2.5|,0表示下列各数画一条数轴一条数轴, 21.2”把这些数连接起来并用“:<22.计算下列各题6.32.53.44.15.11+--+-)()())((329449812-÷⨯÷-()()(313261324-⨯-÷---9.03.05453342222-÷--⨯-+-+-)()()()(23.已知三个有理数a ,b ,c 的积是正数,它们的和是负数,当x=++时,求代数式:2005x19﹣2008x+2010的值.24.某自行车厂一周计划生产700辆自行车,平均每天生产100辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):星期一二三四五六日增减+5﹣2﹣7+13﹣11+18﹣9(1)根据记录可知前四天共生产辆;(2)产量最多的一天比产量最少的一天多生产辆;(3)该厂实行计件工资制,生产一辆车给工人60元,超额完成任务每辆奖10元,少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?郑州外国语中学201-209学年上期七年级第一次月考数学试题答案及解析一.选择题(共10小题)1.下列说法正确的是()A.所有的整数都是正数B.不是正数的数一定是负数C.0不是最小的有理数D.正有理数包括整数和分数【考点】有理数.【分析】根据分类:,,采用排除法求解.【解答】解:负整数不是正数,A错误;0既不是正数也不是负数,B错误;没有最小的有理数,C正确;正有理数包括正整数和正分数,D错误;故选:C.2.全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000000千瓦是《政府工作报告》中确定的重点任务之一.将数据15000000用科学记数法表示为()A.15×106B.1.5×107C.1.5×108D.0.15×108【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n 是负数.【解答】解:将15000000用科学记数法表示为:1.5×107.20故选:B .3.下列各组数中,互为相反数的是()A.211)与(-- B.112与)(- C.212与D22-与解答:选A4.如图,的倒数在数轴上表示的点位于下列两个点之间()A .点E 和点FB .点F 和点GC .点G 和点HD .点H 和点I【考点】数轴;倒数.【分析】根据倒数的定义即可判断;【解答】解:的倒数是,∴在G 和H 之间,故选:C .5.质检员抽查某种零件的质量,超过规定长度的记为正数,短于规定长度的记为负数,检查结果如下:第一个为0.13豪米,第二个为﹣0.12毫米,第三个为﹣0.15毫米,第四个为0.11毫米,则质量最差的零件是()A .第一个B .第二个C .第三个D .第四个【考点】正数和负数.【分析】根据无论正负,绝对值最大的零件与规定长度偏差最大进行答题.【解答】解:由于|0.11|<|﹣0.12|<|0.13|<|﹣0.15|,所以﹣0.15毫米与规定长度偏差最大.故选:C .6.在﹣0.1428中用数字3替换其中的一个非0数码后,使所得的数最大,则被替换的字是()A.1B.2C.4D.8【考点】有理数大小比较.【分析】对负数来说,绝对值大的反而小,因此用3代替其中的一个数字,使她的绝对值最小即为正确选项.【解答】解:逐个代替后这四个数分别为﹣0.3428,﹣0.1328,﹣0.1438,﹣0.1423.﹣0.1328的绝对值最小,只有C符合.故选:C.7.已知a,b,c在数轴上的位置如图所示,化简|a+c|﹣|a﹣2b|﹣|c+2b|的结果是()A.4b+2c B.0C.2c D.2a+2c【考点】数轴;15:绝对值.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.【解答】解:由数轴上点的位置得:b<a<0<c,且|b|>|c|>|a|,∴a+c>0,a﹣2b>0,c+2b<0,∴原式=a+c﹣a+2b+c+2b=2c+4b.故选:A.8.绝对值大于2且小于5的所有的整数的和是()A.7B.﹣7C.0D.5【考点】绝对值;19:有理数的加法.【分析】绝对值大于2且小于5的整数绝对值有3,4.因为±3的绝对值是3,±4的绝对值是4,又因为互为相反数的两个数的和是0,所以,绝对值大于2而小于5的整数的和是0.【解答】解:因为绝对值大于2而小于5的整数为±3,±4,故其和为﹣3+3+(﹣4)+4=0.故选:C.9.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB ,则线段AB 盖住的整点的个数是()A .2018或2019B .2019或2020C .2020或2021D .2021或2022解答:B .10.若ab <0,且a >b ,则a ,|a ﹣b |,b 的大小关系为()A .a >|a ﹣b |>bB .a >b >|a ﹣b |C .|a ﹣b |>a >bD .|a ﹣b |>b >a【考点】绝对值.【分析】根据所给条件,分析a ,b 的正负值,然后再比较大小.【解答】解:∵ab <0,且a >b ,∴a >0,b <0∴a ﹣b >a >0∴|a ﹣b |>a >b 故选:C .二.填空题(共5小题)11.一艘潜艇正在﹣50米处执行任务,其正上方10米处有一条鲨鱼在游弋,则鲨鱼所处的高度为﹣40米.【考点】11:正数和负数.【分析】由于在其上方,那么一定比﹣50米的高度高.【解答】鲨鱼所处的高度为﹣50+10=﹣40米.()_____2,021x 2.122=+=++-y x y 则若解答:-3.513.若|a|=3,|-b|=|-7|,且ab>0,则a-b=______.解答:±414.设n 是正整数,则n11)(--的值是________.解答:0或2积为______. 和为为______,的整数有_____个2018绝对值小于 15.解答:40350016.在,﹣(﹣1),3.14,﹣|﹣8﹣22|,﹣3,﹣32,﹣(﹣)3,0中有理数有m个,自然数有n个,分数有k个,负数有t个,则m﹣n﹣k+t=6.【考点】12:有理数;14:相反数.【分析】根据题意得出m、n、k、t的值,计算可得.【解答】解:数列中有理数有8个,自然数有2个,分数有3个,负数有3个,∴m=8、n=2、k=3、t=3,则m﹣n﹣k+t=8﹣2﹣3+3=6,故答案为:617.已知a的倒数是﹣,b与c互为相反数,m与n互为倒数,则b﹣a+c﹣mn= 1.【考点】相反数;倒数;代数式求值.【分析】根据倒数的定义求出a,根据互为相反数的两个数的和等于0可得b+c=0,根据互为倒数的两个数的积等于1可得mn=1,然后代入代数式进行计算即可得解.【解答】解:∵a的倒数是﹣,∴a=﹣2,∵b与c互为相反数,∴b+c=0,∵m与n互为倒数,∴mn=1,∴b﹣a+c﹣mn=0﹣(﹣2)﹣1=2﹣1=1.故答案为:1.18.定义一种新运算:a※b=,则当x=3时,2※x﹣4※x的结果为8.【考点】45:整式的加减—化简求值.【分析】原式利用已知的新定义化简,计算即可得到结果.【解答】解:当x=3时,原式=2※3﹣4※3=9﹣(4﹣3)=9﹣1=8,故答案为:819.观察下列算式:32=9,33=27,34=81,35=243,…,那么32016的末位数字为1.【考点】1Q :尾数特征;37:规律型:数字的变化类.【分析】从运算的结果可以看出尾数以3、9、7、1四个数字一循环,用2016除以4,余数是几就和第几个数字相同,由此解决问题即可.【解答】解:已知31=3,末位数字为3,32=9,末位数字为9,33=27,末位数字为7,34=81,末位数字为1,35=243,末位数字为3,36=729,末位数字为9,37=2187,末位数字为7,38=6561,末位数字为1,…由此得到:3的1,2,3,4,5,6,7,8,…次幂的末位数字以3、9、7、1四个数字为一循环,又∵2016÷4=504,∴32016的末位数字与34的末位数字相同是1.故答案为:1.20.如果|a|=﹣a ,那么正确的是_________①﹣a 一定是非负数,②﹣a 一定是负数,③|a|一定是正数,④|a|不能是0解答:①三.解答题.+5,2,-,2-,|-2.5|,0表示下列各数画一条数轴一条数轴, 21.2”把这些数连接起来并用“: 22.计算下列各题6.32.53.44.15.11+--+-)(=-6)())((329449812-÷⨯÷-=0.5()()(313261324-⨯-÷---=59.03.05453342222-÷--⨯-+-+-)()()()(=-20.123.已知三个有理数a ,b ,c 的积是正数,它们的和是负数,当x=++时,求代数式:2005x 19﹣2008x +2010的值.【考点】33:代数式求值.【分析】先确定a 、b 、c 的符号,求出x 的值,再代入求出即可.【解答】解:∵三个有理数a ,b ,c 的积是正数,它们的和是负数,∴a 、b 、c 两个数是负数,一个是正数,∴x=++=﹣1﹣1+1=﹣1,∴2005x 19﹣2008x +2010=2005×(﹣1)19﹣2008×(﹣1)+2010=2013.24.某自行车厂一周计划生产700辆自行车,平均每天生产100辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):星期一二三四五六日增减+5﹣2﹣4+13﹣10+16﹣9(1)根据记录可知前四天共生产312辆;(2)产量最多的一天比产量最少的一天多生产26辆;(3)该厂实行计件工资制,生产一辆车给工人60元,超额完成任务每辆奖15元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少元?【考点】11:正数和负数.【分析】(1)根据有理数的加法,可得答案;(2)根据有理数的减法,可得答案;(3)根据有理数的乘法,可得工资与奖金,根据有理数的加法,可得答案.【解答】解:(1)+5﹣2﹣4+13=12,300+12=312,则前四天共生产312辆自行车,故答案为:312;(2)16﹣(﹣10)=26,则这一周产量最多的一天比产量最少的一天多生产26辆自行车,故答案为:26;(3)解:12﹣10+16﹣9=9(辆)700+9=709(辆)60×709+15×9=42675(元)答:该工厂一周的工资总额为42675元.。
河南省郑州枫杨外国语中学2019-2020学年度七年级上学期第一次月考数学试卷(含答案)

河南省郑州枫杨外国语中学2019-2020学年度七年级上学期第一次月考数学试卷(时间:90 分钟满分:100 分)一 、 选 择 题 ( 每 题3 分 , 共 30 分 )1.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引 入负数.如果收入 100 元记作+100 元.那么﹣80 元表示( )A .支出 20 元B .收入 20 元C .支出 80 元D .收入 80 元2.380 亿这个数据用科学记数法表示为( )A .3.8×109B .3.8×1010C .3.8×1011D .3.8×10123.若 x ,y 为有理数,下列各式成立的是( )A .(﹣x )3=x 3B .(﹣x 4)=x 4C .(x ﹣y )3=(y ﹣x )3D .﹣x 3=(﹣x )34.当 a 、b 互为相反数时,下列各式一定成立的是( ) A .B .C .a +b =0D . a ⨯ b <0 5.如图所示,下列图形绕直线 l 旋转 360°后,能得到空心圆柱的是()D.6.以下命题正确的是()A .如果|a |+|b |=0,那么 a 、b 都为零B .如果 ab ≠0,那么 a 、b 不都为零C .如果 ab =0,那么 a 、b 都为零D .如果|a |+|b |≠0,那么 a 、b 均不为零7.如图,点 A 、B 表示的数分别是 a 、b ,点 A 在 0 和 1 对应的两点(不包括这两点)之间移动,点 B 在﹣3, ﹣2 对应的两点之间移动,下列四个代数式的值可能比 2019 大的是()A .﹣B .b ﹣aC .(a ﹣b )2D. 8.若 a < b < 0 < c < d ,则以下四个结论中,正确的是( ) A . a + b + c + d 一定是正数. B . d + c - a - b 可能是负数. C . d - c - b - a 一定是正数. D . c - d - b - a 一定是正数.9.若 m 满足方程 2019 - m = 2019 + m ,则 m - 2020 等于( ).A .m - 2020 B .- m - 2020 C .m + 2020 D .- m +202010.若 a 、b 有理数,下列判断: ①a 2+(b +1)2 总是正数;②a 2+b 2+1 总是正数;③9+(a ﹣b )2 的最小值为 9;④1﹣(ab +1)2 的最大值是 0. 其中正确的个数是( )A .1B .2C .3D .4二、填空题(每题 3 分,共 24 分)11.在太阳系九大行星中,离太阳最近的水星由于没有大气,白天在阳光的直接照射下,表面温度高达 427℃,夜晚则低至﹣170℃,则水星表面昼夜的温差为℃.12.下图是计算机计算程序,若开始输入 x =﹣2,则最后输出的结果是.13.已知|a |=3,且 a = - a ,则 a 3+a 2+a +1=.14. a 为有理数,满足 - a = 2a - 3 ,求a = .15.如图所示的是一个正方体的展开图,它的每一个面上都写有一个数,并且相对的两个面的两个数字之和为 10,那么 a +b ﹣2c =.16.如图,将 4×3 的网格图剪去 5 个小正方形后,图中还剩下 7 个小正方形,为了使余下的部分(小正方形之间至少要有一条边相连)恰好能折成一个正方体,需要再剪去 1 个小正方形,则应剪去的小正方形的编号是.(第 15 题图)(第 16 题图)17.现有一列数 a 1 , a 2 , a 3 ,…, a 98 , a 99 , a 100 ,其中a 3 = 9,a 7 = -7 ,a 98 = -1 ,且满足任意相邻三个数的和为常数,则 a 1 + a 2 + a 3 + + a 99 + a 100 的值为.18.某工厂某周计划每日生产自行车 100 辆,由于每日上班人数不一定相等,工人实行轮休,实际每日生 产量与计划量相比情况如表(增加的为正数,减少的为负数),则本周实际生产总量为辆.星期一 二 三 四 五 六 七 增加/辆﹣1+3﹣2+4+7﹣5﹣10三、解答题(共 6 大题,共 46 分) 19.计算(每小题 3 分,共 12 分):20.(6 分)画出数轴,在数轴上表示下列各数,并用“>”号连接起来. ﹣,0,1.5, - - 3 , - 2 2 .21.(6 分)如果 a 、b 互为相反数,c 、d 互为倒数,|m |=2,|n |=1,且 mn <0,求式子22.(6 分)有理数 a 、b 在数轴上的对应点位置如图所示,化简|a +1|+|2﹣b |+|a +b ﹣1|.23.(6 分)2019 年 8 月 9 日台风利马奇登陆,给多地造成严重影响.为民排忧解难的解放军驾着冲锋舟沿一条南北方向的河流营救灾民,早晨从 A 地出发,晚上最后到达 B 地,约定向北为正方向,当天航行依次记录如下(千米):14,﹣9,18,﹣7,13,﹣6,10,﹣5求:(1)B 地在 A 地的南面,还是北面?与 A 地相距多少千米? (2)这一天冲锋舟离 A 地最远多少千米?(3)若冲锋舟每千米耗油 0.5 升,油箱容量为 30 升,则途中至少需要补充多少升油?24.(10 分)已知a、b 满足(a﹣2)2+|ab+6|=0,c=2a+3b,且有理数a、b、c 在数轴上对应的点分别为A、B、C.(1)则a=,b=,c=.(2)点D 是数轴上A 点右侧一动点,点E、点F 分别为CD、AD 中点,当点D 运动时,线段EF 的长度是否发生变化,若变化,请说明理由,若不变,请求出其值;(3)若点A、B、C 在数轴上运动,其中点C 以每秒1 个单位的速度向左运动,同时点A 和点B 分别以每秒3 个单位和每秒2 个单位的速度向右运动.请问:是否存在一个常数m 使得m•AB﹣2BC 不随运动时间t 的改变而改变.若存在,请求出m 和这个不变化的值;若不存在,请说明理由.- 28答案参考一、选择题1——5 CBDCD 6——10 AACDB二、填空题11、59712、-1713、-2014、1 或315、3816、517、2618、696三、解答题13 8 19、(1) ;(2)12 3 ;(3) -;(4) -973 9920、1.5 > 0 >-1 221、-9 >--3 >-22 >-51422、原式= - 2a - 2b + 223、解:(1)∵14+(﹣9)+18+(﹣7)+13+(﹣6)+10+(﹣5)=28∴B 地在A 地的北面,与A 地相28 千米;(2)∵0+14=14;14+(﹣9)=5;5+18=23;23+(﹣7)=16;16+13=29;29+(﹣6)=23;23+10=33;33+(﹣5)=28;∴这一天冲锋舟离A 地最远33 千米;(3)(14+9+18+7+13+6+10+5)×0.5﹣30=82×0.5﹣30=41﹣30=11(升).答:途中至少需要补充11 升油.24、解:(1)∵a、b 满足(a﹣2)2+|ab+6|=0,∴a﹣2=0 且ab+6=0.解得a=2,b=﹣3.∴c=2a+3b=﹣5.(2)如图,当点D 运动时,线段EF 的长度不发生变化,理由如下:∵点E、点F 分别为CD、AD 中点,∴ED =CD,FD =AD,∴EF=ED﹣FD =CD ﹣AD =AC =×7=3.5,∴当点D 运动时,线段EF 的长度不发生变化,其值为3.5;(3)假设存在常数m 使得m•AB﹣2BC 不随运动时间t 的改变而改变.则依题意得:AB=5+t,2BC=4+6t.所以m•AB﹣2BC=m(5+t)﹣(4+6t)=5m+mt﹣4﹣6t 与t 的值无关,即m﹣6=0,解得m=6,所以存在常数m,m=6 这个不变化的值为26.故答案是:2;﹣3;﹣5.。
2019-2020年七年级数学上第一次月考数学试题含答案.docx

2019-2020 年七年级数学上第一次月考数学试题含答案一、 (本大 共 8 个小 ,每小 3 分,共 24 分.在每小 出的四个 中,只有一 符合 目要求. )1. 3 的相反数是()A .1B . 3C.1 D . 3332.某市 2015 年元旦的最高气温 2℃,最低气温 - 8℃,那么 天的最高气温比最低气温高( ▲ )A .10℃B . -6 ℃C. 6 ℃D . - 10℃3.下列各 数中,两个数相等的是()A . 32 与 23B. 23 与 ( 2)3C . 32 与 ( 3) 2D2. 2 ( 3) 与 2 ( 3)24. 等于其本身的数有()A . 1 个B . 2 个C . 0 个D .无数个5.如果 ab0 , ab 0 ,那么下列各式中一定正确的是()A . a b 0B .aC . b a 0D .abb6、如 所示是 算机程序 算,若开始 入x1, 最后 出的 果是()输入×(- 4)—(— 1) >10YES出NOA . 5 B. -19C. 77D. 877. 已知 : 22222 ,3 3 323, 4 4424, 55 525, ⋯,33 8 8 15152424若 10b 102b符合前面式子的 律, ab 的 ---------()aaA.109B.140C.179D.2108.等 △ ABC 在数 上的位置如 所示,点 A 、C 的数分 0 和- 1,若△ ABC 点沿 方向在数 上 翻 ,翻 1 次后,点 B 所 的数 1, 翻2009 次后,点 B ( ▲ )A .不 任何数B. 的数是 2007C . 的数是 2008D . 的数是 2009二、填空 (本大 共 10 个小 ,每小3 分,共 30 分.) 9. 若 x 2 =81, x= 。
10.省 划重建校舍3890000平方米, 3890000用科学 数法表示.11.如果 a 2(b1) 2 0 ,那么 (ab) 2014.12. 不大于6 的整数的 是.13. 如果一个数的平方等于它的本身, 个数是 。
2020-2021学年河南省郑州外国语中学七年级上学期第一次月考数学试卷

2020-2021学年河南省郑州外国语中学七年级上学期第一次月考数学试卷一、选择题(本大题共10小题,共30.0分)1. 如果−4m 表示向西运动4米,那么向东运动2米应记作( )A. +2mB. −2mC. +4mD. −4m 2. 2019年江西正在建设新高铁--昌赣高铁,全长415公里,耗资532亿元,计划在2020年全线通车.将532亿用科学记数法表示应为( )A. 53.2×109B. 5.32×1010C. 0.532×1011D. 5.32×109 3. 某天的温度上升了−2℃的意义是( )A. 上升了2℃B. 没有变化C. 下降了−2℃D. 下降了2℃ 4. a ,b 在数轴上位置如图所示,则a ,b ,−a ,−b 的大小顺序是( )A. −a <b <a <−bB. b <−a <−b <aC. −a <−b <b <aD. b <−a <a <−b 5. 如图,在数轴上点A 和点B 之间的整数的和是A. 3B. 5C. 7D. 9 6. 在−2,−9,0,2四个数中,最大的数是( )A. 2B. −2C. 0D. −9 7. 下列各组数中,相等的一组是( )A. (−3)2与−32B. (−2)3与−23C. 23与32D. (23)2与223 8. 已知a <b ,则下列不等式的变形不正确的是( )A. a +c <b +cB. −a +1<−b +1C. 3a <3bD. a 2<b 2 9. 在实数0、−√3、tan45°、−1中,最大的是( )A. 0B. −√3C. tan45°D. −110.有理数a,b在数轴上的位置如图所示,则在a+b,a−b,ab,a3,a2b3这五个数中,正数的个数是()A. 2B. 3C. 4D. 5二、填空题(本大题共5小题,共15.0分)11.若“神舟十一号”火箭发射点火前15秒记为−15秒,那么发射点火后10秒应记为______ 秒.12.−53的倒数的绝对值是______ .13.如果规定a※b=a×(a−b),则8※(−2)=______ .14.用加减乘除四种运算计算“24点”:①2,3,−6,9:______ ;②3,−5,7,13:______ .15.数列1,1,2,3,5,8,13,21,34,55,…的排列规律是:前两个数是1,从第三个数开始,每一个数都是它前面两个数的和,这个数列叫做斐波那契数列.在斐波那契数列的前2012个数中共有个偶数.三、计算题(本大题共2小题,共16.0分)16.计算:(1)991819×(−12);(2)(134−78−712)×(−117);(3)0.7×149+234×(−15)+0.7×59−14×15;(4)(79−56+718)×36−6×1.45+3.95×6;(5)(12020−1)×(12019−1)×(12018−1)×…×(11000−1).17.出租车司机小王在一段东西方向的公路上营运,若规定向东为正,向西为负,小王这一天所走的路程如下:(单位:千米)+6,−5,+7,−4,−5,+3,−5,−4,+8,+9(1)将最后一批乘客送到目的地时,小王在出发地的什么方向?距离出发地多远?(2)若出租车每公里耗油0.08升,则这一天出租车总共耗油多少升?四、解答题(本大题共5小题,共39.0分)18. 在数轴上画出表示下列各数的点:−22,−|−2.5|,−(−312),0,−(−1)2005,+|+5|比较这些数的大小,并用“<”号将所给的数按从小到大的顺序连接起来.19. 已知|a|=6,b =3,ab <0,求a +b 的值.20. 股民王海上星期六买进某公司的股票3000股,每股17元,下表为本周内每日股票的涨跌情况(单位:元)星期一 二 三 四 五 六 每股涨跌+4 +4.5 −1 −2.5 −6 +2 试问:(1)本周内,每股的最高价是多少元?最低价是多少元?分别是星期几?(2)以上星期六为0点,画出本周内股票价格涨跌情况的折线图.21. 计算、解方程(1)(13)+56−(−76)−53; (2)(−4)2×(−34)+30÷(−6);(3)x−23+1=3x+14.22. 把下列各数在数轴上表示出来,并把它们按从小到大的顺序用“<”号连接起来.A :|−1.5|,B :(−1)3,C :+(−2.5),D :−(−3).【答案与解析】1.答案:A解析:解:东、西为两个相反方向,如果−4m表示向西运动4米,那么向东运动2米应记作+2m.故选:A.根据正数和负数的意义解答.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示,“正”和“负”相对.本题考查了正数和负数.明确正数和负数,相反意义的量用正数和负数表示是解题的关键.2.答案:B解析:解:532亿=53200000000=5.32×1010,故选:B.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.此题主要考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.答案:D解析:本题主要考查了正数与负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.在一般情况下,温度上升一般用正数表示,上升的度数是负数,则表示与上升相反意义的量,即下降了2℃.解:上升一般用正数表示,则温度上升了−2℃的意义是下降了2℃,故选D.4.答案:D解析:解:从数轴上可以看出b<0<a,|b|>|a|,∴−a<0,−a>b,−b>0,−b>a,即b<−a<a<−b,故选:D.从数轴上a、b的位置得出b<0<a,|b|>|a|,推出−a<0,−a>b,−b>0,−b>a,根据以上结论即可得出答案.。
2024--2025学年河南省郑州市北师大版七年级上册 数学期中试卷 (A)

2024--2025学年河南省郑州市北师大版七年级上册数学期中试卷(A )1.在-(-2)、|-1|、-|0|,-22,(-3)2,-(-4)5中正数有()A .1个B .2个C .3个D .4个2.下列各组数中,结果相等的是()A.与B.与C.与D.与3.人类已知最大的恒星是盾牌座UY,它的规模十分巨大,如果将盾牌座UY 放在太阳系的中心,它的表面将接近土星轨道,半径约等于1.43344937×109km.那么这个数的原数是()A .143344937kmB .1433449370kmC .14334493700kmD .1.43344937km4.下列选项中,两个单项式属于同类项的是()A .a 3与b 3B .-2a 2b与ba2C .x2y 与-xy2D .3x 2y 与-4x2yz5.已知整式的值为6,则整式的值为()A .0B .12C .14D .186.如图是一个正方体的表面展开图,则这个正方体是()A.B.C.D .7.如图,从边长为的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的另一边长是()A.B .C .D .68.若,则多项式的值为()A .B .5C.D .9.如图,将数轴上-6与6两点间的线段六等分,这五个等分点所对应数依次为,,,,,则下列正确的是()A.B.C.D.10.如图,一个立方体的六个面上分别标着连续的自然数,若相对两个面上所标之数的和相等,则这六个数的和为()A.69B.75C.78D.8111.在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记作+0.22,那么小东跳出了3.85米,记作______.12.一个棱柱有12个顶点,所有的侧棱长的和是48cm,则每条侧棱长是____cm.13.已知多项式x|m|+(m﹣2)x﹣10是二次三项式,m为常数,则m的值为_____.14.将一个边长为a的正方形纸片[如图(1)]剪去两个小长方形,得到一个如图(2)所示的“”形图案,则这个“”形图案的周长为____.15.如果关于的多项式与多项式的次数相同,则=_________.16.计算(1)(2).17.化简,求值:,其中,.18.一个几何体由几个完全相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示该位置的小正方体的个数.(1)请画出从正面看、从左面看到的这个几何体的形状图;(2)若小正方体的棱长为1,求这个几何体的表面积.19.某种箱装水果的标准质量为每箱10千克,现抽取8箱样品进行检测,称重如下(单位:千克):10.2,9.9,9.8,10.1,9.6,10.1,9.7,10.2.为了求得这8箱样品的总质量,我们可以选取一个基准质量进行简化运算.(1)你认为选取的这个恰当的基准质量为______千克;(2)根据你选取的基准质量,用正、负数填写下表;(超过基准质量的部分记为正数,不足基准质量的部分记为负数)原质量(千克)10.29.99.810.19.610.19.710.2与基准质量的差距(千克)(3)这8箱样品的总质量是多少?20.如图,两摞完全相同的课本整齐地叠放在讲台上,请根据图中所给出的信息,回答下列问题:(1)每本课本的厚度为cm.(2)若有一摞上述规格的课本x本整齐地叠放在讲台上,请用含x的代数式表示出这摞课本的顶部距离地面的高度.(3)当时,求课本的顶部距离地面的高度.21.【问题情境】某综合实践小组计划进行废物再利用的环保小卫士活动.他们准备用废弃的宣传单制作成装垃圾的无盖纸盒.【操作探究】(1)若准备制作一个无盖的正方体纸盒,如图(1),图形经过折叠能围成一个无盖正方体纸盒.(填A,B,C,或D)(2)如图(2)是小明的设计图,把它折成一个无盖正方体纸盒后与“保”字所在面相对的面上的文字是.(3)如图(3),有一张边长为20cm的正方形废弃宣传单,小华将其四个角各剪去一个边长为4cm小正方形后,折成无盖长方体纸盒.求这个无盖长方体纸盒的底面积和容积.22.某中学准备在网上订购一批篮球和跳绳,查阅后发现篮球每个售价为120元,跳绳每根售价为25元.现有甲、乙两家网店均提供包邮服务,并提出了各自的优惠方案.甲网店:买一个篮球送一根跳绳;乙网店:篮球和跳绳都按定价的付款.已知要购买篮球40个,跳绳x根.(1)若在甲网店购买,则需付款元;若在乙网店购买,则需付款元;(用含x的代数式表示)(2)当时,在哪家网店购买较为合算?(3)当时,你认为还有更为省钱的购买方案吗?如果没有,请说明理由;如果有,请写出你的购买方案,并计算需要付款的金额.23.已知点A,B在数轴上分别表示a,b.任务要求(1)对照数轴填写下表:a 83b 404A ,B 两点间的距离48124问题探究(2)若A ,B 两点间的距离记为d ,试问d 和a ,b 有何数量关系.问题拓展(3)当x 等于多少时,的值最小,最小值是多少?(4)若点C 表示的数为x ,当点C 在什么位置时,|x-1|+|x-5|的值最小,最小值是多少?。
河南省郑州外国语中学2020-2021学年七年级上期第一次月考数学试卷

郑州外国语中学2020-2021学年七年级上学期第一次月考数学试卷(时间:60分钟 分值:100分)一、选择题(每小题3分,共30分)1.在一条南北方向的路道上,张强先向北走了10米,此时他的位置记作+10米.又向南走了13米,此时他的位置在( )A . +23 米处B . +13米处C . -3米处D .-23米处2.随着我国综合国力的提升,中华文化影响日益增强,学中文的外国人越来越多,中文已成为英国居民的第二外语,美国常讲中文的人口约有2100000人,请将2100000用科学记数法表示为( )A .70.2110⨯B . 62.110⨯C . 52110⨯D . 72.110⨯3.2020年3月抗击“新冠肺炎”居家学习期间,小华计划每天背诵6个汉语成语.将超过的个数记为正数,不足的个数记为负数,某-周连续 5天的背诵记录如下: +4, 0, +5,-3,+2,则这5天他共背诵汉语成语( )A .38个B .36个C .34个D .30个4.数轴上到点-2的距离为5的点表示的数为( )A . -3B .-7C .3或-7D .5或-35.在数轴上,点A ,B 在原点O 的同侧,分别表示数a , 1,将点A 向左平移3个单位长度,B 得到点C .若点C 与点B 互为相反数,则a 的值为( )A . 3B .2C . -1D .06.若a >0,b <0,a +b >0. 则a ,b ,-a ,-b 按照从小到大的顺序用“<"连接起来,正确的是( )A .-a <b <-b <aB . a >-b >b >-aC . b <-a <-b <aD . -a <-b <b <a7.下列各组数中,数值相等的是( )A . -22和(-2)2B . 212-和212⎛⎫- ⎪⎝⎭C . (-2) 2和22D . -212⎛⎫- ⎪⎝⎭和212-8.若a -b >0,则下列各式中一定正确的是( )A . a <bB . ab <0C .0a b> D . -a <-b 9.下列说法中:①0是最小的的整数;②有理数不是正数就是负数;③正整数、负整数、正分数、负分数统称为有理数;④非负数就是正数;⑤-2π是有理数;⑥平方等于它本身的数有±1;⑦无限小数都不是有理数;⑧正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )A . 7个B .6个C . 5个D .4个10.一只小球落在数轴上的某点P 0,第一次从P 0向左跳1个单位到P 1,第二次从P 1向右跳2个单位到 P 2,第三次从P 2向左跳3个单位到P 3,第四次从P 3向右跳4个单位到P 4……若按以上规律跳了100次 时,它落在数轴上的点P 100所表示的数恰好是2019,则这只小球的初始位置点P 0所表示的数( )A .1969B .1968C .-1969D .-1968二、填空题(每小题3分,共15分)11.检查商店出售的袋装白糖,白糖每袋按规定重500g .一袋白糖重499g .就记作- 1,如果一袋白糖重503g ,应记作 .12.下列四组有理数的比较大小:①-1<-2,②-(-1)>(-2),③56+-67⎛⎫<-- ⎪⎝⎭,④56-67<-,正确的序号是_ .13.定义:对任何有理数a ,b ,都有22a b a ab b ⊗=++,若已知()()22230a b -++=,则a b ⊗= .14.根据“二十四点”游戏的规则,用仅含有加、减、乘、除及括号的运算式,使2,-3,-4,4的运算结果等于24: (只要写出一个算式即可).15.观察算式::3'+2=5;32+2=11;33+2=29;34+2=83;35+2=245;36+2=731;....,则32019+2019的个位数字是_ .三、解答题(共55分)16.(8分)计算:(1) ()()()324252846+-⨯--÷+-(2) ()24113111237341224⎛⎫⎛⎫----+-+-÷- ⎪ ⎪⎝⎭⎝⎭17.(6分)请在数轴上表示下列各数:3--,4,-1. 5,-5,122并将它们用“>”连接起来18.(6分)己知|x|=3,|y|=7.(1)若x <y ,求x +y 的值:(2)若xy <0. 求x -y 的值.19.(8分)己知:数轴上有理数m 所表示的点到原点的距离为3个单位长度,a 、b 互为相反数且都不为零,c 、d 互为倒数,求2333a a b cd m b ⎛⎫++-- ⎪⎝⎭的值.20.(9分)某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位: km ):(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?(3)若该出租车的计价标准为:行驶路程不超过3km 收费10元,超过3km 的部分按每千米加1.8元收 费,在这过程中该驾驶员共收到车费多少元?21.(9分)观察这些等式1123523236++==⨯;11347343412++==⨯;11459454520++==⨯; (1)请在理解上面计算方法的基础上,把下面两个数表示成两个分数的和的形式(分别写出表示的试程和结果)1342= = ,1772= = . (2)利用以上所得的规律进行计算:35791113151726122030425672-+-+-+-.22. (9分) 数轴上从左到右有A ,B ,C 三个点,点C 对应的数是10,AB = BC =20.(1)点A 对应的数是 .点B 对应的数是 .(2)若数轴上有一点D ,且BD =4,则点D 表示的数是什么?(3)动点P 从A 出发,以每秒4个单位长度的速度向终点C 移动,同时,动点Q 从点B 出发,以每秒1个单位长度的速度向终点C 移动,设移动时间为t 秒.当点P 和点Q 间的距离为8个单位长度时,求t 的值.郑州外国语中学2020-2021学年七年级上期第一次月考数学试卷答案参考一、选择题1. C2. B3.A4. C5. B6. A7. C8. D9. A 10. A二、填空题11. +3g 12. ④ 13. 7 14. ()()()3442-⨯-⨯÷ 15. 6三、解答题16. 解:⑴7; ⑵-10.17. 解:4 > 122 > -1.5 > 3-- > -518. 解:(1)4或10(2)10或-1019. 解:根据题意得:m =±3,a +b =0,a b =-1,cd =1, 则原式=3(a +b )+ a b-3cd -m 2=0-1-3-9=-13. 20. 解:(1)5+2+(-4)+(-3)+10=10(km )答:接送完第五批客人后,该驾驶员在公司的南边10千米处.(2)(5+2+|-4|+|-3|+10)×0.2=24×0.2=4.8(升)答:在这个过程中共耗油4.8升.(3)[10+(5-3)×1.8]+10+[10+(4-3)×1.8]+10+[10+(10-3)×1.8]=68(元)答:在这个过程中该驾驶员共收到车费68元.21. 解:(1)136711426767+==+⨯,178911728989+==+⨯; (2) 111111111111112233445566778=+--++--++--++原式=119-=89.22. 解:(1)∵AB =BC =20,点C 对应的数是10,点A 在点B 左侧,点B 在点C 左侧, ∴点B 对应的数为10-20=-10,点A 对应的数为-10-20=-30.故答案为:-30;-10.(2)由于点B 对应的数为-10,BD =4,所以点D 表示的数为-14或-6;(3)当运动时间为t 秒时,点P 对应的数是4t -30,点Q 对应的数是t -10.故答案为:4t -30;t -10.依题意,得:|t -10-(4t -30)|=8,∴20-3t =8或3t -20=8,解得:t =4或t =283. ∴t 的值为4或283.。
2019-2020郑州外国语中学数学中考第一次模拟试卷(含答案)
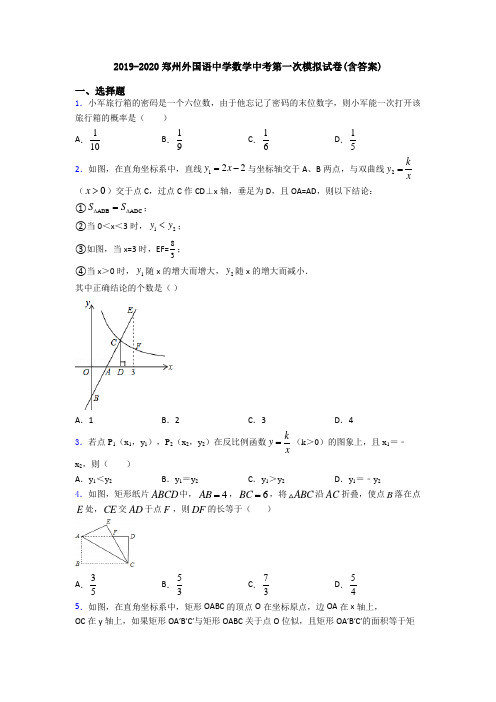
k x
( x 0 )交于点 C,过点 C 作 CD⊥x 轴,垂足为 D,且 OA=AD,则以下结论:
① SΔADB SΔADC ;
②当 0<x<3 时, y1 y2 ;
③如图,当 x=3 时,EF= 8 ; 3
④当 x>0 时, y1 随 x 的增大而增大, y2 随 x 的增大而减小.
其中正确结论的个数是( )
【详解】
解:∵四边形 ABMO 是圆内接四边形,∠BMO=120°,
∴∠BAO=60°,
∵∠AOB=90°,
∴AB 是⊙C 的直径, ∴∠ABO=90°-∠BAO=90°-60°=30°, ∵点 A 的坐标为(0,3), ∴OA=3, ∴AB=2OA=6, ∴⊙C 的半径长=3,故选:C 【点睛】 本题考查的是圆内接四边形的性质、圆周角定理及直角三角形的性质,熟知圆内接四边形 对角互补的性质是解答此题的关键.
x 的方程 x2=42+(6-x)2,解方程求出 x 即可. 【详解】
∵矩形 ABCD 沿对角线 AC 对折,使△ABC 落在△ACE 的位置, ∴AE=AB,∠E=∠B=90°, 又∵四边形 ABCD 为矩形, ∴AB=CD,
∴AE=DC, 而∠AFE=∠DFC, ∵在△AEF 与△CDF 中,
AFE=CFD
(1)求抛物线的解析式;
(2)点 D 是抛物线上一点,连接
BD、CD,满足 SDBC
3S 5
ABC ,求点 D 的坐标;
(3)点 E 在线段 AB 上(与 A、B 不重合),点 F 在线段 BC 上(与 B、C 不重合),是
否存在以 C、E、F 为顶点的三角形与△ABC 相似,若存在,请直接写出点 F 的坐标,若不
故选 A.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郑州外国语中学2019-2020 学年七年级上期第一次月考数学试
卷
(时间:60 分钟分值:100 分)
一、选择题(每小题3 分,共30 分)
1.下列说法正确的是( ) A.一个有理数不是正数就
是负数 B.0 是最小的数
C.一个有理数不是整数就是分数
D.1 是最小的整数
2.右图是某兴趣社制作的模型,则从左面看到的图形为( )
正面
A.B.C.D.
3.北京时间2019 年4 月10 日21 点整,天文学家召开全球新闻发布会,宣布首次直接拍摄到黑洞的照片,这颗黑洞位于代号为M87 的星系当中,距离地球5300 万光年之遥,质量相当于60 亿颗太阳,其中5300
万这个数据可以用科学记数法表示为( )
A. 5.3×108
B. 5.3x×107
C. 5.3×103
D. 53×102
4. 下面四个图形中,经过折叠能围成如右图所示的几何图形的是( )
A.B.C.D.
5.下列运算中,正确的是( )
A. -3-2=-1
B. (-3)2=-6
C. (- 1
)x(-2)=0 D. 6÷(-
1
)=-12
2 2
6. 如果a,b 互为相反数,x,y 互为倒数,m 的倒数等于它本身,则6(a+b)+m2-3xy 的值是(
) A. -2 B. -1 C. 0
D.1
7. 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是( )
A.B.C.D.
8.下列说法正确的是( )
A. 若|a|=a,则a>0;
B. 若a2=b2,则a=b;
C. 若0<a<1,则a3<a2<a
D. 若a>b,则1 < 1 .
a b
a b ab
9.已知a、b 为有理数,且b>0,
则的值是( )
a b ab
A. 3 B. -1 C. -3 D. 3 或-1
10. 小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆“游戏,现在将-1、2、-3、4、-5、6、-7、8 分别填入图中的圆圆内,使横、竖以及内外两围上的4 个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中
a+b 的值为( )
A. -6 或-3 B. -8 或1 C. -1 或-4 D.1 或-1
二、填空题(每小题3 分,共15 分)
11. 比1 小2 的数是.
12. 笔尖在纸上快速滑动写出了一个字母S,用数学知识解释为.
13. 试判断1+7+72+73+74+…+72019 的个位数字是.
14. 某校园餐厅把 WIFI 密码做成了数学题,小亮在厅就餐时,
思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那
么他输入的密码是.
15. 已知数轴上两点A、B 对应的数分别为-1,3,点P 为数轴上一动点,其对应的数为x 当P 到点A、B 的距离之和为7 时,则对应的数x 的值为.
三、解答题(共55 分)
16.(8 分)计算:
17.(9 分)如果| a+1| (b-
2)2=0. (1)求a,b 的值;
(2)求(a+b)2020+a2019 的值.
18. 用小立方块搭成的几何体,从正面看的主视图和从上面看的俯视图如下,问这样的几何体有可能?它最多需要小立方块,最少需要小立方块,画出最少、最多时从左面看到的左视图. (答案不唯一时,画出一种即可)
最多时的左视图最少时的左视图
19.(9 分)十一假期到了,王老师一家四口驾小轿车去省博物馆参观.早上从家里出发,向东走了 5 千米到超市买东西,然后又向东走了 3 千米到省博物馆,下午从博物馆出发向西走了 11.5 千米到同事张老师家做客. 晚上返回家里.
(1)若以王老师家为原点,向东为正方向,用1 个单位长度表示1 千米,请将王老师家、超市、省博物馆
和张老师家的位置在下面数轴上分别用点A、B、C、D 表示出来;
(2)张老师家与王老师所去的超市相距多少千米?
(3)若小轿车每千米耗油0.12 升,求王老师一家从出发到返回家,小轿车的耗油量.
20.(9 分)定义☆运算,观察下列运算:
(+5)☆(+14)=+19,(-13)☆(-7)=+20,
(-2)☆(+15)=-17,(+18)☆(-7)=-25,
0☆(-19)=+19,(+13)☆0=+13.
⑴请你认真思考上述运算,归纳☆运算的法则:
两数进行☆运算时,同号,异号.
特别地,0 和任何数进行☆运算,或任何数和0 进行☆运算,.
⑵计算:(+17)☆[0☆(-16)]= ;
⑶若2×(2☆a)-1=3a,求a 的值.
21.(11 分)国庆节“十一”假期,我市嵩山风景区迎来了客流高峰期,经查仅9 月30 日一天的游客人数达到了5(万人),在7 天假期中每天旅游的人数变化如下表:(正数表示比前一天多的人数,负数表示比前一天少的人数.)
日期10 月1
日10 月2
日
10 月3
日
10 月4
日
10 月5
日
10 月6
日
10 月7
日
人数变化单位:万人+1.2 +0.6 +0.8 -0.6 -0.4 +0.6 -1.4
⑴求出10 月1-7 日每天的游客人数并完成下面7 天游客人数记录表:
日期 1 2 3 4 5 6 7
游客人数(万人)
⑵假定该景区的门票是每人100 元,请你计算“十一”黄金周期间该景区的门票收入是多少元?(用科学记数
法表示)
⑶以9 月30 日的游客人数为0 点,在下图中画折线统计图表示这7 天的游客人数情
况.日期
日期 1
2
3
4
5
6
7 游客人数(万人)
6.2
6.8
7.6
7
6.6
7.2
5.8
一、选择题
郑州外国语中学 2019-2020 学年七年级上期第一次月考数学试卷答案参考
1. C
2. D
3.B
4. B
5. D
6. A
7. D
8. C
9. D 10. A 二. 填空题
11. -1 12. 点动成线 13. 7 14. 143549 15. -2.5 或 4.5 三、解答题
16. 解:⑴0; ⑵-16.
17. 解:⑴a=-1,b=2;⑵0.
18. 解:共有 3 种可能;最多有 8 块小立方体;最少 7 块小立方体. 最多需要 8 个小正方体,从左边看几何体得到的图形如图(1)
所示; 最少需要 7 个正方体,从左面看该几何体得到的图形如图(2)或(3)所示,答案不唯
一.
19. 解:⑴如图. ⑵5-(-3.5)=8.5;⑶11.5×2×0.12=2.76(升).
20. 解:⑴(+5)☆(+14)=+19,(-13)☆(-7)=+20,两正数或两负数进行☆运算时,结果为正数. (-2)☆(+15)=-17,(+18)☆(-7)=-25,一正数一负数进行☆运算时,结果为负数.
∴两数进行☆运算时,同号得正,异号得负. 0☆(-19)=+19,(+13)☆0=+13,0 和一个负数进行☆运算时, 结果为正数;一个正数和 0 进行☆运算时,结果为正数; ∴0 和任何数进行☆运算,或任何数和 0 进行☆运算,结果为正数. 故答案为:得正;得负;结果为正数.
⑵(+17)☆[0☆(-16)]=(+17)☆(+16)=+33,故答案为:+33; ⑶①若 a <0,则 2☆a=-(2+|a|)=-(2-a)=-2+a ,∴2×(-2+a)-1=3a ,解得:a=-5, ②若 a=0,则 2☆a=+2,∴2×2-1=3a ,解得:a=1,不成立; ③若 a >0,则 2☆a=+(2+a)=2+a ,∴2×(2+a)-1=3a ,解得:a=3;综上所述,a 的值为-5 或 3. 21. 解:⑴求出 10 月 1-7 日每天的游客人数并完成下面 7 天游客人数记录表:
⑵6.2+6.8+7.6+7+6.6+7.2+5.8=40 万人,100×40=4000(万元); 4000 万元=4×107 元; ⑶如图.。
