杨辉三角队列实现
c语言杨辉三角形代码

c语言杨辉三角形代码杨辉三角形是中国古代数学中较为重要的数学问题之一,也是计算机领域中经典的问题之一。
它形成一个三角形,数字排列成三角形形状,其中每个数字等于它上方两数字之和。
以下是一个用C语言编写的杨辉三角形代码:#include <stdio.h>int main() {int rows, coef = 1;printf("请输入行数: ");scanf("%d", &rows);for (int i = 0; i < rows; i++) {for (int space = 1; space <= rows - i; space++)printf(" ");for (int j = 0; j <= i; j++) {if (j == 0 || i == 0)coef = 1;elsecoef = coef * (i - j + 1) / j;printf("%4d", coef);}printf("\n");}return 0;}在这个代码中,我们首先定义一个整数变量rows来表示杨辉三角形的行数。
然后通过用户输入来获取杨辉三角形的行数。
接着我们使用两个嵌套循环来打印杨辉三角形。
外层循环用来控制打印的行数。
内层循环用来打印每一行的数字。
在内层循环中,首先使用一个循环打印空格,使得每行的数字能够居中显示。
其次,在这个循环中,我们使用一个if语句来判断当前位置是否为杨辉三角形的边界,也就是第一个数字和每一行的最后一个数字。
如果是边界上的数字,我们将其设置为1,否则就使用前一行的数字通过组合公式计算当前位置的数字。
最后我们在内层循环的末尾打印一个换行符,以便换行显示下一行。
运行以上代码,将会看到打印出指定行数的杨辉三角形。
这个代码是很简单但有效的实现了杨辉三角形的打印。
杨辉三角实验报告
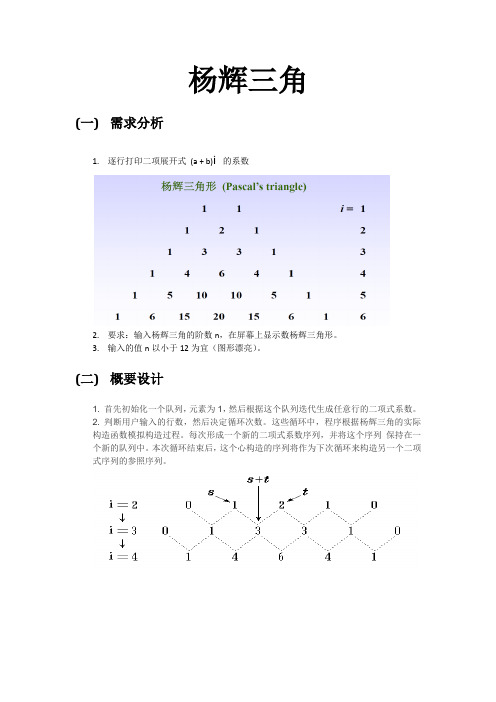
杨辉三角(一)需求分析1.逐行打印二项展开式(a + b)i 的系数2.要求:输入杨辉三角的阶数n,在屏幕上显示数杨辉三角形。
3.输入的值n以小于12为宜(图形漂亮)。
(二)概要设计1. 首先初始化一个队列,元素为1,然后根据这个队列迭代生成任意行的二项式系数。
2. 判断用户输入的行数,然后决定循环次数。
这些循环中,程序根据杨辉三角的实际构造函数模拟构造过程。
每次形成一个新的二项式系数序列,并将这个序列保持在一个新的队列中。
本次循环结束后,这个心构造的序列将作为下次循环来构造另一个二项式序列的参照序列。
(三)详细设计1.定义队列结点typedef struct QNode{int data;struct QNode *next;}QNode ,*QueuePtr;typedef struct {QueuePtr front;QueuePtr rear;}LinkQueue;2.基本操作函数原型●队列初始化void InitQueue(LinkQueue *Q){Q->front =Q->rear = (QueuePtr)malloc(sizeof(QNode));if(!Q->front) printf("OVERFLOW");Q->front->next= NULL;}●插入元素e为新的队尾元素void EnQueue(LinkQueue *Q,int e){QNode *p;p = (QueuePtr)malloc(sizeof(QNode));if(!p) printf("OVERFLOW");p->data = e;p->next = NULL;Q->rear->next = p;Q->rear = p;}●void DeQueue(LinkQueue *Q){ QNode *p;if(Q->front == Q->rear) printf("ERROR");Q->front->next = Q->front->next->next;}●美化形状for(i = 1;i <= n; i++){printf("\n");c=i;for(b=1;b<=n-c;c++){printf(" ");}}●根据上行系数求下行系数for (j=1;j<=i+2;j++){t = q->front->next->data;DeQueue (q);EnQueue (q,s+t);s = t;if (j!=i+2) printf("%3d ",s);}(四)调试分析1.美化形状时,第一次的输出空格的个数和位置考虑的有瑕疵,导致图像歪歪曲曲的。
用队列方法输出杨辉三角

/*用队列方法输出杨辉三角。
*/#include<iostream.h>#include<iomanip.h>#include<stdlib.h>#define ElemType int/*-----LNode的结点类型定义-----*/struct LNode{ElemType data; //值域LNode* next; //链接指针域};/*-----队列的链接存储结构的定义-----*/struct LinkQueue{LNode* front; //队首指针LNode* rear; //队尾指针};/*------1.初始化链队-----*/void InitQueue(LinkQueue& HQ){HQ.front=HQ.rear=NULL; //把队首和队尾指针置为空}/*-----2.向链队中插入一个元素------*/void EnQueue(LinkQueue& HQ, ElemType item){LNode* newptr=new LNode; //得到一个新的结点newptr->data=item; //把item 的值赋给新结点的值域newptr->next=NULL; //把新结点的指针域置为空if(HQ.rear==NULL) //若链队为空,则新结点既是队首又是队尾{HQ.front=HQ.rear=newptr;}else //若链队非空,则新结点被链接到队尾并修改队尾指针{HQ.rear=HQ.rear->next=newptr;}}/*-------3.从队列中删除一个元素-------*/ElemType OutQueue(LinkQueue& HQ){if(HQ.front==NULL) //若链队为空则终止运行{cerr<<"链队为空,无法删除!"<<endl;exit(1);}ElemType temp=HQ.front->data; //暂存队首元素以便返回LNode* p=HQ.front; //暂存队首指针以便收回队首指针HQ.front=p->next; //使队首指针指向下一个结点if(HQ.front==NULL) //若删除后链队为空,则使队尾指针为空{HQ.rear=NULL;}delete p; //回收原队首结点return temp; //返回被删除的队首元素}void YanyHuiTriangular(LinkQueue& HQ, int n){int i,j; //i,j 都是循环变量int first,second; //first,second 分别记录上一行的两个累加数EnQueue(HQ,1);for(i=1; i<n+1; i++){ //第 0 至 n-1 行元素分别入列,并输出;最后第 n 行入列first=0; second=0;//控制每行前头空格的输出for(j=0; j<n-i+1; j++){cout<<setw(3)<<' ';}for(j=0; j<i; j++){second=OutQueue(HQ);cout<<setw(3)<<second<<setw(3)<<' ';EnQueue(HQ,first+second);first=second;}cout<<endl; //输完一行,回车EnQueue(HQ,second);}//最后输出最后一行元素(即第 n 行出列)for(j=0; j<n+1; j++){cout<<setw(3)<<OutQueue(HQ)<<setw(3)<<' '; }cout<<endl;}void main(){LinkQueue LQ;InitQueue(LQ);cout<<"用队列输出杨辉三角!"<<endl<<endl; int n;cout<<"请输入要输出多少行杨辉三角:"; cin>>n;YanyHuiTriangular(LQ,n);}。
数据结构实验报告(杨辉三角-约瑟夫环)

数据结构实验报告实验一杨辉三角形(Pascal’s triangle)一、需求分析1.输入的形式和输入值的范围本程序中,需输入的杨辉三角级数level为正整数,由键盘输入,以回车结束2.输出的形式通过屏幕输出杨辉三角3.程序所能达到的功能用户从键盘输入需要的杨辉三角级数,从屏幕输出杨辉三角4.测试数据输入:5输出: 1 11 2 11 3 3 11 4 6 4 11 5 10 10 5 1二、概要设计以链队列结构实现该实验1.抽象数据类型定义ADT Queue {数据对象:D = { ai | ai∈ElemSet , i = 1,2,…,n,n≥0 }数据关系:R1={<ai-1,ai> | ai-1 , ai∈D, i=2,…,n}约定其中ai端为队列头,an端为队列尾基本操作:InitQueue ( &Q )操作结果:构造一个空队列QDestroyQueue ( &Q )初始条件:队列Q已存在操作结果:队列Q被销毁,不再存在ClearQueue ( &Q )初始条件:队列Q已存在操作结果:将Q清为空队列QueueEmpty ( Q )初始条件:队列Q已存在操作结果:若Q为空队列,则返回TRUE,否则FALSEQueueLength ( Q )初始条件:队列Q已存在操作结果:返回Q的元素个数,即队列长度GetHead ( Q , &e )初始条件:Q为非空队列操作结果:用e返回Q的队头元素EnQueue ( &Q , e )初始条件:队列Q已存在操作结果:插入元素e为Q的新队尾元素DeQueue ( &Q , &e )初始条件:Q为非空队列操作结果:删除Q的队头元素,并用e返回其值QueueTraverse ( Q , visit( ) )初始条件:Q已存在且非空操作结果:从队头到队尾,依次对Q的每个数据元素调用函数visit( )。
杨辉三角形实验报告

题目:编写程序,根据输入的行数,屏幕显示杨辉三角形(Pascal’s triangle)班级:自动化05 姓名:刘丽丽学号:10054107 完成日期:2011.12.20 一.需求分析1、本演示程序中,利用顺序队列打印杨辉三角。
杨辉三角的特点是两个腰上的数字都为1,其它位置上的数字是其上一行中与之相邻的两个整数之和,故在打印过程中,第i行上的元素要由第i-1行中的元素来生成。
这是一个基于队列的操作来实现杨辉三角不断生成的过程。
2、此次输出的杨辉三角不需要只有一个1的第一行,但只需对输出实际杨辉三角的程序稍作修改即可;3、在计算机终端上显示"提示信息"之后,由用户在键盘上输入演示程序中需要输入的数据,以“回车符”为结束标志。
相应的输入数据和运算结果显示在其后。
4、程序执行的命令包括:1)构造顺序队列;2)分析第 i 行元素与第 i+1行元素的关系目的是从前一行的数据可以计算下一行的数据 从第i 行数据计算并存放第i+1行数据5、 测试数据输入行数 n=3; 输出结果为:1 11 2 1 1 3 3 1二. 概要设计链队列的抽象数据类型定义为: ADT Queue{ 数据对象 :D={ai| ai ∈Elemset ,i=1,2,3,···n ,n >=0}11i = 1 1 2 121 3 3 13 14 6 4 141510 10 5 15 1 6152015 6 16数据关系:R={<ai-1 ,ai>| ai-1 ,ai∈D,i=1,2,···n} (约定其中ai端为队列头,an端为队列尾)基本操作:InitQueue(&Q)操作结果:构造一个空队列DestroyQueue(&Q)初始条件:队列已存在操作结果:队列被销毁ClearQueue(&Q)初始条件:队列已存在操作结果:将Q清空QueueEmpty(Q)若队为空,则返回为TRUE,否则返回为FALSE。
杨辉三角队列实现

杨辉三⾓队列实现杨辉三⾓显⽰问题描述:编写程序,根据输⼊的⾏数,屏幕显⽰杨辉三⾓。
基本要求:(1)⾏数不⼤于20⾏。
(2)基于队列的操作来实现杨辉三⾓的不断⽣成过程。
(注:不要⽤其它的公式计算的⽅法或者⼆维数组来实现)(3)基于数组实现队列的物理数据结构需求分析:1、输⼊形式:输⼊⼀个整数n ,0<=n<=202、输出形式:打印出来前(n+1)⾏的杨辉三⾓数列3、功能实现:输出前20层的杨辉三⾓序列4、样例输⼊输出:(数据加强版)输⼊:10输出:1 n=11 1 n=21 2 1 n=31 3 3 1 n=41 4 6 4 1 n=51 5 10 10 5 1 n=61 6 15 20 15 6 1 n=71 7 21 35 35 21 7 1 n=81 8 28 56 70 56 28 8 1 n=91 9 36 84 126 126 84 36 9 1 n=105、效率分析:O(n)抽象数据类型( ADT):抽象数据结构描述:Typedef struct {Int q[MaxSize];//存放队列中的元素Int front,rear;//front和rear分别是指向队头和队尾的指针}Queue;队列的基本操作:V oid InitQueue(Queue Q) function:构造⼀个空队列V oid EnQueue(Queue Q,int x) :function:将元素x⼊队V oid DeQueue(Queue Q,int x):function:删除队头元素,并⽤x返回其值Bool QueueEmpty(Queue Q) function:判断队列是否为空概要设计:既然要⽤到队列来打印杨辉三⾓,那么肯定会利⽤到队列FILO的性质(First In Lase Out),由于是要打印⼀个数列,那么肯定要利⽤已经进队的元素在其出队之前完成杨辉三⾓的递归性----即利⽤要出队的元素来不断地构造新的进队的元素,即在第N⾏出队的同时,我们来构造杨辉三⾓的第N+1⾏,从⽽实现打印杨辉三⾓的⽬的。
使用队列实现杨辉三角

使⽤队列实现杨辉三⾓使⽤队列实现杨辉三⾓杨辉三⾓的特点:除了第⼀⾏,其他⾏两端都为1;从第三⾏开始可以看出,除了两端,其中每个数都是元素本⾝上⾯对着的两个数的和;奇数⾏有奇数个数,偶数⾏有偶数个数,都是n个数每⾏数从左端开始看到中间都是升序,都是正序。
想要⽤代码来实现杨辉三⾓最简单的⽅法就是使⽤两个数组来实现,互相承载结果,并将数组打印出来。
但结合杨辉三⾓的特点,正序可以想到⽤队列的问题来解决。
解决⽅案:可以想到,作为开端的1可以看成是0和1的和,因此开始可以将队列设成这样(此处是以3⾏为例⼦)设定变量a和b来作为队列第⼀个元素和第⼆个元素的载体。
在a获取了第⼀个元素后将第⼀个元素移出队列,然后让b获取新的第⼀个元素,然后将a和b加起来,并将结果移进队列中,并将结果打印出来然后重复上述步骤,可以得到:要能够获取第⼆⾏的值,我在第⼀⾏中进⾏两次和运算即可,第⼀轮到此也就可以停⽌了。
然后,让⼀个0⼊列,再次重复上⾯的步骤,具体流程⼤概是这样:遇到的问题:最初的原代码:package ch15;import java.util.Scanner;/*** Created by Funny_One on 2017/10/13.*/public class YangHuiTriangle {public static void main(String[] args) {CircularArrayQueue<Integer> queue = new CircularArrayQueue();Scanner sca = new Scanner(System.in);System.out.println("需要显⽰的⾏数:");int n = sca.nextInt();queue.enqueue(0);queue.enqueue(1);System.out.println(1);for(int times =0;times<n;times++){queue.enqueue(0);for(int i=1;i<queue.size()-1;i++){int a,b=0,c;if(queue.size()==1){a = b;b = queue.first();c = a + b;queue.enqueue(c);System.out.print(c);}else {a=queue.first();queue.dequeue();b = queue.first();queue.dequeue();c = a+b;queue.enqueue(c);System.out.print(c+" ");}}System.out.println();}}}运⾏的结果是:可以见到,其中出现的问题有:问题1:每⼀⾏只有⼀个元素;问题2:每个元素都是1;问题3: 不只有三⾏;在我进⾏调试之后,发现这些问题的原因是:问题1的原因:在我的代码中,当a和b将数据获取之后,⼀个1⼊列,1被打印出来,同时两个数被移出队列。
数据结构之杨辉三角(队列实现)(C++版)

数据结构之杨辉三⾓(队列实现)(C++版)#include <iostream>#include <stdlib.h>#include <windows.h>#include <string>#define MAXLISTSIZE 100 //预设的存储空间最⼤容量#define TRUE 1#define FALSE 0using namespace std;typedef int ElemType;typedef struct{ElemType *elem; //存储空间基址 int rear; //队尾指针 int front; //队头指针int queuesize; //允许的最⼤存储空间,以元素为单位 }Queue;void InitQueue(Queue &Q, int maxsize){//构造⼀个最⼤存储空间为 maxsize 的空队列 Q if (maxsize == 0)maxsize = MAXLISTSIZE;Q.elem = new ElemType[maxsize]; //为循环队列分配存储空间 if (!Q.elem) exit(1); //存储分配失败Q.queuesize = maxsize;Q.front = Q.rear = 0;} //InitQueuebool EnQueue(Queue &Q, ElemType e){// 若当前队列不满,这在当前队列的尾元素之后,插⼊元素 e 为新的队列尾元素,并返回TRUE,否则返回FALSEif((Q.rear + 1) % Q.queuesize == Q.front)return FALSE;Q.elem[Q.rear] = e;Q.rear = (Q.rear+1) % Q.queuesize;return TRUE;}bool DeQueue(Queue &Q, ElemType &e){//若队列不空,则删除当前队列Q中的头元素,⽤ e 返回其值,并返回TRUE,否则返回 FALSE if (Q.front == Q.rear)return FALSE;e = Q.elem[Q.front];Q.front = (Q.front+1) % Q.queuesize;return TRUE;}bool GetHead(Queue Q, ElemType &e){//若队列不空,则⽤ e 返回队⾸元素,并返回TRUE,否则返回 FALSEif (Q.front == Q.rear)return FALSE;e = Q.elem[Q.front];return TRUE;}int QueueLength(Queue Q){//返回队列Q中元素个数,即队列的长度return((Q.rear-Q.front+Q.queuesize) % Q.queuesize);}bool QueueEmpty(Queue Q){if(Q.front == Q.rear)return TRUE;elsereturn FALSE;}int main(void){//打印输出杨辉三⾓的前n(n>0)⾏int n, i, k;Queue Q;ElemType s, e;cout << "请输⼊杨辉三⾓的⾏数:";cin >> n;/* for(i = 1; i <= n; i++)cout << ' ';cout<< '1' << endl; // 在中⼼位置输出杨辉三⾓最顶端的"1"*/ InitQueue(Q, n+3); // 设置最⼤容量为 n+3 的空队列EnQueue(Q, 0); // 添加⾏界值EnQueue(Q, 1);EnQueue(Q, 1); // 第⼀⾏的值⼊队列k = 1;while(k < n){ // 通过循环队列输出前 n-1 ⾏的值for(i = 1; i <= n - k; i++)cout<< ' '; // 输出n-k个空格以保持三⾓型EnQueue(Q, 0); // ⾏界值"0"⼊队列do { // 输出第 k ⾏,计算第 k+1 ⾏DeQueue(Q, s);GetHead(Q, e);if(e) cout<< e << ' '; //若e为⾮⾏界值0,则打印输出 e 的值并加⼀空格else cout << endl; //否则回车换⾏,为下⼀⾏输出做准备EnQueue(Q, s+e);}while(e!=0);k++;}//whileDeQueue(Q, e); //⾏界值"0"出队列while (!QueueEmpty(Q)){ //单独处理第 n ⾏的值的输出DeQueue (Q, e);cout << e << ' ';}//whilecout << endl;}//yanghui。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网上看了许多杨辉三角队列实现的代码,结果运行时都或多或少有点小问题,为此我提供一份自己运行正确的。
程序无误,细心做一下
注意,这是做成三个文件运行的
第一个文件命名 stdafx.h
#include<stdio.h>
#include<malloc.h>
#define Max 50
struct queue
{
int *base;
int front;
int rear;
};
typedef struct queue *SqQueue;
SqQueue InitQueue();//队列的初始化
int EnQueue(SqQueue Q,int e);//数据进队(从队尾传值)
int DeQueue(SqQueue Q);//数据出队(返回队头)
void YHPrint(SqQueue Q,int n);//打印杨辉三角
void jiemian();//界面函数,方便调用(个人习惯)
第二个文件命名为 stdafx.c
#include "stdafx.h"
int GetQueueFirstData(SqQueue Q)
{ return Q->base[Q->front];
}
int isEmptyQueue(SqQueue Q)
{ if(Q->front=Q->rear)
return 1;
else
return 0;
}
SqQueue InitQueue()
{ SqQueue Q;
Q=(SqQueue)malloc(sizeof(struct queue));
if (Q==NULL)
return NULL;
Q->base=(int *)malloc(Max*sizeof(int));
if(Q->base==NULL)
return NULL;
Q->front=Q->rear=0;
return Q;
}
int EnQueue(SqQueue Q,int e)
{
if((Q->rear+1)%Max==Q->front)
return 0;
Q->base[Q->rear]=e;
Q->rear=(Q->rear+1)%Max;
return 1;
}
int DeQueue(SqQueue Q)
{ int e;
if(Q->front==Q->rear)
return 0;
e=Q->base[Q->front];
Q->front=(Q->front+1)%Max;
return e;
}
void YHPrint(SqQueue Q,int n)
{
int i,j,k,s1;
int s2;
for(i=1;i<=n;i++)
{
for(k=0;k<n-i;k++)
printf(" ");
for(j=1,s1=0;j<i;j++)
{
s2=DeQueue(Q);
printf("%d",s1+s2);
printf(" ");
EnQueue(Q,s1+s2);
s1=s2;
}
printf("1");
EnQueue(Q,1);
printf("\n");
}
}
void jiemian()
{
int n,t;
SqQueue Q;
printf("杨辉三角:执行请输入:1,退出请输入:2!\n");
scanf("%d",&t);
do{
switch(t)
{
case 1:{
Q=InitQueue();
printf("请输入杨辉三角的层数:\n");
scanf("%d",&n);
YHPrint(Q,n);
};break;
case 2:printf("欢迎再次使用!");break;
default:printf("输入错误:");break;
}
if(t==1)
{
printf("你还想继续使用吗?继续请输入:1,退出请输入:2!\n");
scanf("%d",&t);
}
}while(t==1);
}
第三个主程序命名 succeed.c
就可以了,这样模块化。
#include "stdafx.c"
int main()
{
jiemian();
return 0;
}
程序无误,细心做一下
给代码链接,自己运行
Qq网盘
/1bb49fc61d3aea83a13fc8f1783cab87百度云
/s/1geKPYsr。
