《化简含有字母的式子》综合练习2
《化简含有字母的式子》综合练习2
《化简含有字母的式子》综合练习
基础练习:
1、直接写出得数。
3m-m= 8x-7x=
2x+3x= 9y-4y=
5m+2m= 4a+a=
7a-3a+a= 8m+2m-9m=
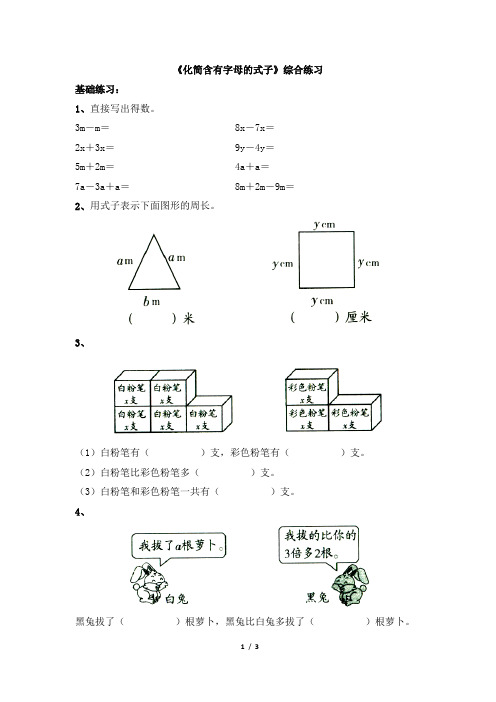
2、用式子表示下面图形的周长。
3、
(1)白粉笔有()支,彩色粉笔有()支。
(2)白粉笔比彩色粉笔多()支。
(3)白粉笔和彩色粉笔一共有()支。
4、
黑兔拔了()根萝卜,黑兔比白兔多拔了()根萝卜。
5、
(1)用式子表示出苹果树比梨树多多少棵?
(2)当a=4,b=5时,苹果树比梨树多多少棵?
综合练习:
6、一辆汽车每小时行驶m千米,从甲地到乙地共用4小时,从乙地到丙地共用5小时。
(1)用式子表示出从甲地到丙地一共有多少千米?当m=90时,路程是多少?(2)你还能提出什么问题?并用式子表示出来。
7、在一个长a厘米、宽b厘米的长方形内画一个最大的正方形。
(1)用式子表示出正方形的面积和剩下的面积。
(2)当a=12,b=4时,剩下部分的面积是多少平方厘米?
8、如图,这个较大的长方形是由宽为a的4个完全相同的小长方形拼成的,用式子比啊搜出大长方形的周长。
8.3 化简含有字母的式子(教案)苏教版五年级上册数学

教案:化简含有字母的式子一、教学目标1. 让学生理解化简含有字母的式子的意义,掌握化简的方法。
2. 培养学生运用数学符号进行表达和交流的能力。
3. 培养学生观察、分析、抽象、概括的能力。
二、教学重点与难点1. 教学重点:掌握化简含有字母的式子的方法。
2. 教学难点:理解化简含有字母的式子的意义,能正确进行化简。
三、教学过程1. 导入利用生活中的例子,如小明和小红分别有a个苹果和b个苹果,他们一共有多少个苹果?引导学生理解字母可以表示数,从而引出化简含有字母的式子。
2. 新课导入(1)展示例题:化简下列各式a a a ab b b b b(2)引导学生观察、分析,发现规律:多个相同的字母相加,可以用乘法表示。
a a a a = 4ab b b b b = 5b(3)讲解化简含有字母的式子的意义:将含有字母的式子简化为更简洁的形式,便于计算和表达。
3. 演练与巩固(1)让学生独立完成以下练习:c c c = 3cd d d d d d = 6d(2)同桌互相检查,讨论解题过程。
4. 拓展与应用(1)让学生尝试化简以下式子:2a 3a4b-2b(2)引导学生运用乘法分配律进行化简:2a 3a = (2 3)a = 5a4b-2b = (4-2)b = 2b5. 课堂小结让学生回顾本节课所学内容,总结化简含有字母的式子的方法。
6. 课后作业(1)完成教材P46页练习题1、2、3。
(2)预习下一节课内容:解方程。
四、教学反思本节课通过实例导入,引导学生理解化简含有字母的式子的意义,掌握化简的方法。
在教学过程中,注重学生的观察、分析、抽象、概括能力的培养,让学生在演练与巩固环节充分练习,提高解题能力。
同时,拓展与应用环节引导学生运用乘法分配律进行化简,提高学生的数学思维水平。
总体来说,本节课达到了教学目标,但还需在课后关注学生的学习情况,及时进行辅导与答疑。
重点关注的细节:化简含有字母的式子的方法及其意义化简含有字母的式子是数学中一个基础而重要的概念,它要求学生不仅理解字母代表的数学意义,而且要能够灵活运用各种数学性质和法则来简化表达式。
数学人教五年级上册《第五单元_第04课时_化简含有字母的式子例5》(说课稿)

数学人教五年级上册《第五单元_第04课时_化简含有字母的式子例5》(说课稿)一. 教材分析人教五年级上册《第五单元_第04课时_化简含有字母的式子例5》这一课时,是在学生已经掌握了四则运算、代数知识的基础上进行教学的。
本课时主要让学生学习如何化简含有字母的式子,通过具体的例子让学生理解并掌握化简的方法。
教材通过例5引导学生运用所学的知识解决实际问题,进一步培养学生的逻辑思维能力和解决问题的能力。
二. 学情分析五年级的学生已经具备了一定的数学基础,对四则运算和代数知识有一定的了解。
但是,学生在解决含有字母的式子问题时,还存在着一定的困难。
因此,在教学本课时,教师需要针对学生的实际情况进行引导,让学生在理解的基础上掌握化简含有字母的式子的方法。
三. 说教学目标1.知识与技能目标:学生能够理解并掌握化简含有字母的式子的方法,能够运用所学的知识解决实际问题。
2.过程与方法目标:通过小组合作、讨论交流的方式,培养学生的团队协作能力和表达能力。
3.情感态度与价值观目标:学生能够感受到数学与生活的联系,激发学习数学的兴趣。
四. 说教学重难点1.教学重点:学生能够理解并掌握化简含有字母的式子的方法。
2.教学难点:学生能够灵活运用所学的知识解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、小组合作法、讨论交流法等。
2.教学手段:利用多媒体课件、黑板、粉笔等。
六. 说教学过程1.导入新课:通过一个实际问题,引导学生思考如何化简含有字母的式子,激发学生的学习兴趣。
2.自主学习:学生通过阅读教材,理解并掌握化简含有字母的式子的方法。
3.合作交流:学生分组讨论,分享各自的方法和心得,培养团队协作能力和表达能力。
4.教师讲解:教师针对学生的讨论情况进行讲解,引导学生正确理解并掌握化简方法。
5.巩固练习:学生进行课堂练习,教师及时给予指导和反馈。
6.拓展提高:学生通过解决实际问题,运用所学的知识,提高解决问题的能力。
七年级数学下册综合算式专项练习题代数式的化简练习

七年级数学下册综合算式专项练习题代数式的化简练习代数式的化简在数学中是一个重要的基本概念和技巧。
通过化简代数式,我们可以简化复杂的表达式,使其更加简洁、清晰,并且便于进行计算和推导。
下面是一些七年级数学下册综合算式专项练习题,帮助我们理解和熟练运用代数式的化简方法。
1. 化简代数式:(1) 化简表达式:3x + 2y + x - y(2) 化简表达式:2a^2 + 3a^2 - 4a + a^2 - a(3) 化简表达式:5(x + y) - 3(2x - y)(4) 化简表达式:2(2x - 3y) + 3(4x + 2y)(5) 化简表达式:3(x + y) - 2(2x - 3y) + 4(3x - y)2. 合并同类项:(1) 合并同类项:2xy + 3yx - 4yx - xy(2) 合并同类项:3a^2 - 2a + a^2 + a - a^2(3) 合并同类项:5(x + y) - 3(2x - y) + 2x - 4y(4) 合并同类项:2(2x - 3y) + 3(4x + 2y) - 5x + 2y(5) 合并同类项:3(x + y) - 2(2x - 3y) + 4(3x - y) + 2(2x - y)3. 移项和分配律:(1) 移项和分配律:4x + 3 = 2x + 6(2) 移项和分配律:2(a - 3) + 3(a + 2) = 5a - 6(3) 移项和分配律:3(2x + 1) - 2(x - 3) = 4x + 11(4) 移项和分配律:5(3x - 2) + 2(2x + 1) - 4(x - 3) = 10x + 15(5) 移项和分配律:4(2x + 3) + 3(3x - 2) - 2(4x + 1) = 3x - 14. 二次项的化简:(1) 化简表达式:(x + 3)^2(2) 化简表达式:(2x - 1)^2(3) 化简表达式:(a + b)(a - b)(4) 化简表达式:(2x + 3)^2 - (x - 2)^2(5) 化简表达式:(3x - 2y)(3x + 2y)通过以上的练习题,我们可以熟悉基本的代数式化简的方法和技巧,并且掌握合并同类项、移项和分配律,以及二次项的化简等知识点。
化简含有字母的式子教程

化简含有字母的式子
执教:施玲利
小华用小棒摆了a个三角形;
小芳用小棒也摆了a个正方形。
……
……
看了这幅图,你能提出什么问题? ①小华和小芳一共用了多少根小棒? ②小芳比小华多用了多少根小棒?
化简: 4 a- a =4×a-1×a =(4-1)a =3a
x千克 x千克 x千克
x x千克 千克
xx 千克 千克
小芳一分钟跳的个数-小明一分钟跳的个数=小芳比小明多跳的个数
b
2b+b =3b
(2b-b 2+1)b =b =3b
( 2-1)b =b
这是红旗小学的荷花池和凉亭的平面图。 (1)荷花池和凉亭的面积一共有多大?
荷花池的面积+凉亭的面积=总面积 总的长度×宽=总面积
(2)当a=4时,求荷花池和凉亭的面积共是多少 平方米?
x千克 x 千克
x 千克 x千克 x千克 千克
苹果有( 5x )千克,梨有( 3x )千 克,苹果和梨共有( 8x )千克,苹 果比梨多( 2x )千克。
5x43;冬冬到学校的路程=明明家到冬冬家的路程 明明和冬冬一分钟共行的路程×时间=明明到冬冬家的路程
明明从家出发,每分行70米,a分可到学校; 冬冬从家出发,每分行80米,a分也可到学校。 从明明家到冬冬家一共( 150a )米。
70a+80a =150a
(70+80)a =150a
小明和小芳跳绳,小明一分钟跳了b个,小芳一分 钟跳的个数是小明的2倍。两人一分钟共跳 (3b) 个。 两人跳了一分钟,小芳比小明多跳( )个。
试一试:
b×8= 8b
x×3= 3x
1×x= x
c×d= cd
最新苏教版小学四年级下册数学精品化简含有字母的式子

最新苏教版小学数学精品课
计下面各题。
4x+5x= 9x
7x +3x=
10x
9x -6x=
6a-5a=
3x
a
4a -2a= 2b+7b= 8y+y= 7x -x=
2a 9b 9y 6x
最新苏教版小学数学精品课
明明从家出发,每分行65米,a 分可到学校;冬冬从家出发,每分行
75米,a分也可到学校。从明明家到冬冬家一共有(
最新苏教版小学数学精品课
…… ……
小华用小棒摆了a个三角形,小芳用小棒摆了a个正方形。他们两人一 共用了多少根小棒?
小华用了3a根,小芳用了4a 根,一共用了(3a+4a)根。
摆一个三角形和一个正方 形要用7根,一共用了7a根。
最新苏教版小学数学精品课
…… ……
小华用小棒摆了a个三角形,小芳用小棒摆了a个正方形。他们两人一 共用了多少根小棒?
3a+4a =(3+4)a =7a
实际上是应用了乘法分配 律。
答:他们一共用了7a根小棒。 最新苏教版小学数学精品课
小芳比小华多用了多少根小棒? 4a-3a
=(4-3)a =a
答:小芳比小华多用了a根小棒。
最新苏教版小学数学精品课
…… ……
苹果有( )5千x克,梨有( )千克,苹果3和x 梨共有 ( )千克,苹果比梨多( 8x )千克。
实验准 备室 米
a
12米
4米
(2)、当a=8时,求科学实验室和实验准备室的面积一共是多少平 方米。
16×8=128(平方米)
答:一共是128平方米。 最新苏教版小学数学精品课
你知道最早有意识地系统使用字母来表示 数的人是谁吗?他就是法国数学家韦达一生致 力于数学的研究,做出了很多重要贡献,成为 那个时代最伟大的数学家。自从韦达系统使用 字母表示数后,引出了大量的数学发现,解决 了很多古代的复杂问题。
含字母的式子化简

含字母表示的式子(化简)一、下面的式子都能化简吗?把能化简的进行化简并写出答案7a-3 6y-x 8a+9b 8b+9b 5m+4m20x+5x+6x 19c+5+2c 3a+4+5b 3a+3b 3.2x+2-1.2x二、填空题1、明明从家出发,每分钟行60米,b分钟可到学校;冬冬从家出发,每分钟行75米,b 分钟也可到学校。
从明明家到冬冬家一共米。
2、一种笔记本的单价是x元,小强买了7本,晓刚买了3本。
小强比小刚多用了元,当x=1.5时。
小强比小刚多用了元3、铺设一条长4千米的自来水管道,已经铺了7天,每天铺x米。
先用含有字母的式子表示还没有铺的米数,再计算当x=500时,还剩米没有铺。
甲、乙两车同时从A、B两地相向而行,甲车的速度是100千米/时,乙车的速度是80千米/时,经过t小时两车相遇。
A、B两地的路程是千米。
当t=5时,A、B两地的路程是千米5、一件衣服a元,一条裤子的价钱比一件衣服贵8元,一套衣服需要多少。
6、三个连续自然数,中间的一个是a,它前面的数是 ,后面的数是含字母表示的式子(化简)二、下面的式子都能化简吗?把能化简的进行化简并写出答案7a-3 6y-x 8a+9b 8b+9b 5m+4m20x+5x+6x 19c+5+2c 3a+4+5b 3a+3b 3.2x+2-1.2x二、填空题1、明明从家出发,每分钟行60米,b分钟可到学校;冬冬从家出发,每分钟行75米,b 分钟也可到学校。
从明明家到冬冬家一共米。
2、一种笔记本的单价是x元,小强买了7本,晓刚买了3本。
小强比小刚多用了元,当x=1.5时。
小强比小刚多用了元3、铺设一条长4千米的自来水管道,已经铺了7天,每天铺x米。
先用含有字母的式子表示还没有铺的米数,再计算当x=500时,还剩米没有铺。
甲、乙两车同时从A、B两地相向而行,甲车的速度是100千米/时,乙车的速度是80千米/时,经过t小时两车相遇。
A、B两地的路程是千米。
八年级数学下册综合算式专项练习题代数式化简

八年级数学下册综合算式专项练习题代数式化简代数式化简是数学中的重要概念之一,它可以简化复杂的代数表达式,使其更易于计算和理解。
在八年级数学下册中,综合算式专项练习题中涉及了一些代数式化简的例题。
本文将通过解析具体的练习题,详细说明代数式化简的方法和步骤。
例一:化简表达式:3x + 2x + 5y - 2y解析:这个表达式中包含了多个项,其中每个项有不同的系数和变量。
要化简这个表达式,首先将其中相同的项合并在一起,然后计算它们的系数的和。
3x + 2x + 5y - 2y = (3 + 2) x + (5 - 2) y= 5x + 3y所以,化简后的表达式为5x + 3y。
例二:化简表达式:2(a + b) - (3a - 4b)解析:这个表达式中包含了括号,其中的项之间还存在加减法运算。
要化简这个表达式,首先根据分配律将括号内的表达式展开,然后根据运算规则合并项。
2(a + b) - (3a - 4b) = 2a + 2b - 3a + 4b= -a + 6b所以,化简后的表达式为-a + 6b。
通过以上两个例题可以看出,代数式化简的关键在于合并同类项,以及根据需要展开括号,并根据运算规则进行合并。
下面我们来解析更多的例题。
例三:化简表达式:4x^2 - 6xy + 3x^2 + 2xy解析:这个表达式中包含了变量的平方项和混合项。
要化简这个表达式,首先合并同类项。
4x^2 - 6xy + 3x^2 + 2xy = (4x^2 + 3x^2) + (-6xy + 2xy)= 7x^2 - 4xy所以,化简后的表达式为7x^2 - 4xy。
例四:化简表达式:(a + b)^2 - (a^2 + 2ab + b^2)解析:这个表达式涉及了平方项和括号运算,要化简这个表达式,需要根据平方公式展开括号,并合并同类项。
(a + b)^2 - (a^2 + 2ab + b^2) = a^2 + 2ab + b^2 - a^2 - 2ab - b^2= 0所以,化简后的表达式为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《化简含有字母的式子》综合练习
基础练习:
1、直接写出得数。
3m-m= 8x-7x=
2x+3x= 9y-4y=
5m+2m= 4a+a=
7a-3a+a= 8m+2m-9m=
2、用式子表示下面图形的周长。
3、
(1)白粉笔有()支,彩色粉笔有()支。
(2)白粉笔比彩色粉笔多()支。
(3)白粉笔和彩色粉笔一共有()支。
4、
黑兔拔了()根萝卜,黑兔比白兔多拔了()根萝卜。
5、
(1)用式子表示出苹果树比梨树多多少棵?
(2)当a=4,b=5时,苹果树比梨树多多少棵?
综合练习:
6、一辆汽车每小时行驶m千米,从甲地到乙地共用4小时,从乙地到丙地共用5小时。
(1)用式子表示出从甲地到丙地一共有多少千米?当m=90时,路程是多少?(2)你还能提出什么问题?并用式子表示出来。
7、在一个长a厘米、宽b厘米的长方形内画一个最大的正方形。
(1)用式子表示出正方形的面积和剩下的面积。
(2)当a=12,b=4时,剩下部分的面积是多少平方厘米?
8、如图,这个较大的长方形是由宽为a的4个完全相同的小长方形拼成的,用式子比啊搜出大长方形的周长。
