数学月刊二月号 戴老师立体几何练习120分
江苏省盱眙县新马中学2013届高考数学二轮复习精品训练立体几何

江苏省盱眙县新马中学2013届高考数学二轮复习精品训练:立体几何本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知三条不重合的直线l n m 、、,两个不重合的平面βα、,有下列命题: ① 若m ∥n ,n ⊂α,则m ∥α;②若l⊥α,m ⊥β,且l ∥m ,则α∥β③若m ⊂α,n ⊂α,m //β,n ∥β,则α∥β④若α⊥β,αβ=m ,n ⊂β,n ⊥m ,则n ⊥α其中正确命题的个数为( )A .1个B .2个C .3个D .4个【答案】B2.用斜二测画法画一个水平放置的平面图形为如下图的一个正方形,则原来图形的形状是( )【答案】A3.一个水平放置的三角形的斜二测直观图是等腰直角三角形O B A ''',若1=''B O ,那么原∆ABO 的面积是( )A .12B C D .【答案】C4.过球心的10个平面,其中任何三个平面都不交于同一条直线,它们将球面分成( )A .92部分B .1024部分C .516部分D .100部分 【答案】A5.一个组合体的三视图如下,则其体积为( )A.12πB.16πC.20πD.28π【答案】C6.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )【答案】D7.如图,平面α⊥平面β,α∩β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )A.当|CD|=2|AB|时,M,N两点不可能重合B.M,N两点可能重合,但此时直线AC与l不可能相交C.当AB与CD相交,直线AC平行于l时,直线BD可以与l相交D.当AB,CD是异面直线时,直线MN可能与l平行【答案】B8.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大时,其高的值为( )A.B C D.【答案】D9.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰三角形,且直角边长为1,那么这个几何体的体积为( )A .1B .12C .13D .16【答案】D10.已知直线l ⊥平面α,直线m β平面⊂,给出下列命题:①α∥.m l ⊥⇒β ②l⇒⊥βα∥m. ③l ∥m βα⊥⇒ ④α⇒⊥m l ∥β,其中正确的命题是( )A .①③B .②③④C .②④D .①②③【答案】A11.给出命题:(设βα、表示平面,l 表示直线,C B A 、、表示点) ⑴若ααα⊂∈∈∈∈l l B B A lA 则,,,,;⑵若AB B B A A =∈∈∈∈βαβαβα 则,,,,;⑶若αα∉∈⊄A l A l则,,;⑷若 重合与,则不共线、、,且、、,、、βαβαC B A C B A C B A ∈∈。
南京郑和外国语学校高中数学选修2-1第二章《空间向量与立体几何》测试(有答案解析)

一、选择题1.在四棱锥P ABCD -中,PD ⊥平面ABCD ,四边形ABCD 为正方形,2AB =,E 为PB 的中点,若3cos ,3DP AE =,则PD =( )A .1B .32C .3D .22.长方体1111ABCD A BC D -,110AB AA ==,25AD =,P 在左侧面11ADD A 上,已知P 到11A D 、1AA 的距离均为5,则过点P 且与1AC 垂直的长方体截面的形状为( )A .六边形B .五边形C .四边形D .三角形3.在四棱锥O ﹣ABCD 中,底面ABCD 是平四边形,设OA a =,OB b =,OC c =,则BD 可表示为( )A .a c b +-B .a +2b c -C .c b a +-D .a c +-2b4.如图为一正方体的平面展开图,在这个正方体中,有以下结论:①AN GC ⊥,②CF 与EN 所成的角为60︒,③BD //MN ,④二面角E BC N --的大小为45︒,其中正确的个数是( )A .1B .2C .3D .45.如图,点P 在正方体1111ABCD A BC D -的面对角线1BC 上运动,则下列四个结论:①三棱锥1A D PC -的体积不变; 1//A P ②平面1ACD ; 1DP BC ⊥③;④平面1PDB 平面1ACD .其中正确的结论的个数是( )A .1个B .2个C .3个D .4个6.正方体ABCD —A ′B′C′D′中,AB 的中点为M ,DD′的中点为N ,则异面直线B′M 与CN 所成角的大小为 A .0°B .45°C .60 °D .90°7.在直三棱柱111ABC A B C -中,1111122AA A B B C ==,且AB BC ⊥,点M 是11AC 的中点,则异面直线MB 与1AA 所成角的余弦值为( ) A .13B .223C .324D .128.如图,将边长为2的正方体ABCD 沿对角线BD 折起,得到三棱锥1A BCD -,则下列命题中,错误的为( )A .直线BD ⊥平面1AOCB .1A B CD ⊥C .三棱锥1A BCD -2D .若E 为CD 的中点,则//BC 平面1AOE 9.如图,已知正三棱柱111ABC A B C -的棱长均为2,则异面直线1A B 与1BC 所成角的余弦值是( )A .32B .12C .14D .010.如图,在棱长为2的正方体1111ABCD A BC D -中,点E F 、分别是棱AB 、BC 的中点,则点1C 到平面1B EF 的距离等于( )A .23B .223C .233D .4311.如图所示,平行六面体1111ABCD A BC D -中,以顶点A 为端点的三条棱长都为1,且两两夹角为60︒.求1BD 与AC 夹角的余弦值是( )A 3B 6C .217D 21 12.如图,在四棱柱1111ABCD A BC D -中,底面ABCD 为正方形,侧棱1AA ⊥底面ABCD ,3AB =,14AA =,P 是侧面11BCC B 内的动点,且1AP BD ⊥,记AP 与平面11BCC B 所成的角为θ,则tan θ的最大值为( )A .43B .53C .2D .259二、填空题13.ABC △中,90C ∠︒=,60A ∠︒=,2AB =,M 为AB 中点,将BMC △沿CM 折叠,当平面BMC ⊥平面AMC 时,A ,B 两点之间的距离为_____.14.在正方体1111ABCD A B C D -中,M 、N 分别是11A B 、11A C 的中点,则异面直线BM 与AN 所成角的余弦值为______.15.已知三棱柱ABC ﹣A 1B 1C 1中,AA 1⊥面ABC ,AB ⊥AC ,且AA 1=AB=AC ,则异面直线AB 1与BC 1所成角为_____.16.空间四边形ABCD 的两条对棱AC 、BD 的长分别为5和4,则平行于两条对棱的截面四边形EFGH 在平移过程中,周长的取值范围是__________.17.已知αβ⊥,平面α与平面β的法向量分别为m ,n ,且(1,2,5)m =-,(3,6,)n z =-,则z =__________.18.直线1:(3)30l a x y ++-=与直线2:5(3)40l x a y +-+=,若的方向向量是的法向量,则实数_____.19.已知平行六面体中,则____.20.在正方体ABCD -A 1B 1C 1D 1中,下列给出四个命题: (1)四边形ABC 1D 1的面积为1AB BC (2)11AD A B 与的夹角为60°;(3)22111111111111()3();(4)()0AA A D A B A B AC A B A D ++=⋅-=; 则正确命题的序号是______.(填出所有正确命题的序号)三、解答题21.在四棱台1111ABCD A BC D -中,底面ABCD 是边长为2的菱形,1111AAA B ==,120BAD ∠=︒,1AA ⊥平面ABCD .(1)E 是棱AD 的中点,求证:1//B E 平面11CDD C ;(2)试问棱AD 上是否存在点M ,使得二面角111M A B D --的余弦值是5719?若存在,求点M 的位置;若不存在,请说明理由.22.如图,平行四边形ABCD 中,26AD AB ==,,E F 分别为,AD BC 的中点.以EF 为折痕把四边形EFCD 折起,使点C 到达点M 的位置,点D 到达点N 的位置,且NF NA =.(1)求证:平面AFN ⊥平面NEB ; (2)若23BE =F 到平面BEM 的距离.23.如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,4PD =,底面ABCD 是边长为2的正方形,E ,F 分别为PB ,PC 的中点.(1)求证:平面ADE ⊥平面PCD ;(2)求直线BF 与平面ADE 所成角的正弦值.24.如图,在四棱锥P ABCD -中,PD ⊥底面ABCD ,底面ABCD 是边长为2的正方形,PD DC =,F ,G 分别是PB ,AD 的中点.(Ⅰ)求证:GF ⊥平面PCB ;(Ⅱ)求平面PAB 与平面PCB 的夹角的大小;(III )在线段AP 上是否存在一点M ,使得DM 与平面ADF 所成角为30︒?若存在,求出M 点坐标,若不存在,请说明理由.25.如图,在直三棱柱111ABC A B C -中,12AA AB AC ===,AB AC ⊥,M 是棱BC 的中点,点P 在线段A 1B 上.(1)若P 是线段1A B 的中点,求直线MP 与平面11ABB A 所成角的大小; (2)若N 是1CC 的中点,平面PMN 与平面CMN 所成锐二面角的余弦值为53737,求线段BP 的长度.26.如图,已知四棱锥P ABCD -的底面是菱形,对角线AC ,BD 交于点O ,4OA =,3OB =,4OP =,OP ⊥底面ABCD ,设点M 是PC 的中点.(1)直线PB 与平面BDM 所成角的正弦值. (2)点A 到平面BDM 的距离.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】由已知以D 为原点建立空间直角坐标系,设(0,0,)P a ,求得,DP AE 的坐标,由数量积公式可得答案. 【详解】由已知DP DA DC 、、两两垂直,所以以D 为原点,建立如图所示的坐标系,设(0)PD a a =>,则(0,0,)P a ,(2,0,0)A ,连接BD 取中点F ,连接EF ,所以//EF PD ,EF ⊥平面ABCD , 所以(1,1,)2a E ,所以(0,0,)DP a =,(1,1,)2a AE =-,由3cos ,3DP AE =,得2232cos ,3114a DP AE DP AE DP AE a a ⋅===⋅⋅++, 解得2a =. 故选:D.【点睛】本题考查了空间向量的数量积公式的应用,关键点是建立空间直角坐标系,由数量积公式求得a ,考查了学生的空间想象力.2.B解析:B 【分析】以D 为坐标原点建立如图所示的空间直角坐标系,先利用向量找出截面与11A D 、AD 和AB 的交点,再过Q 作//QF MN 交11B C 于F ,过F 作//EF QM ,交1BB 于E ,即可判断截面形状. 【详解】以D 为坐标原点建立如图所示的空间直角坐标系,则()()()120,0,5,25,0,10,0,10,0P A C ,()125,10,10AC ∴=--, 设截面与11A D 交于(),0,10Q Q x ,则()20,0,5Q PQ x =-,()12520500Q A C PQ x ∴⋅=---=,解得18Q x =,即()18,0,10Q ,设截面与AD 交于(),0,0M M x ,则()20,0,5M PM x =--,()12520500M AC PM x ∴⋅=--+=,解得22Mx =,即()22,0,0M , 设截面与AB 交于()25,,0N N y ,则()3,,0N MN y =,1253100N AC MN y ∴⋅=-⨯+=,解得7.5Ny =,即()25,7.5,0N ,过Q 作//QF MN ,交11B C 于F ,设(),10,10F F x ,则()18,10,0F QF x =-, 则存在λ使得QF MN λ=,即()()18,10,03,7.5,0F x λ-=,解得22F x =,故F 在线段11B C 上,过F 作//EF QM ,交1BB 于E ,设()25,10,E E z ,则()3,0,10E EF z =--, 则存在μ使得EF QM μ=,即()()3,0,104,0,10E z μ--=-,解得 2.5E z =,故E 在线段1BB 上,综上,可得过点P 且与1AC 垂直的长方体截面为五边形QMNEF . 故选:B.【点睛】本题考查截面的形状的判断,解题的关键是先利用向量找出截面与11A D 、AD 和AB 的交点,即可利用平面的性质找出其它点的位置.3.D解析:D 【分析】作出图形,根据条件得出BD BA BC =+,再得到BA a b =-,BC c b =-,即可求解, 得到答案. 【详解】如图所示,在四棱锥O ABCD -中,底面ABCD 是平行四边形,则BD BA BC =+, 在OAB ∆中,BA OA OB a b =-=-, 在OBC ∆中,BC OC OB c b =-=-, 故选:D.【点睛】本题主要考查了向量的线性运算,以及向量的加法的几何意义,其中解答中熟记向量的运算法则是解答的关键,着重考查了推理与计算能力,属于基础题.4.C解析:C 【分析】根据题意画出正方体直观图,建立空间直角坐标系,计算0AN GC ⋅=,由此判断①正确.根据线线角的知识,判断②正确.根据线线的位置关系,判断③错误.根据二面角的知识,判断④正确. 【详解】画出正方体的直观图,如下图所示,设正方体边长为2,以,,DA DC DG 分别为,,x y z 轴建立空间直角坐标系.则()()()()2,0,0,0,2,2,0,0,2,0,2,0A N G C ,所以()()2,2,20,2,20AN GC ⋅=-⋅-=,所以AN GC ⊥,故①正确.由于//EN AC ,所以CF 与EN 所成的角为FCA ∠,而在FAC ∆中,AF FC CA ==,也即FAC ∆是等边三角形,故60FCA ∠=,所以②正确.由于//EN AC ,而AC 与BD 相交,故,BD MN 不平行,③错误.由于,EB BC FB BC ⊥⊥,所以EBF ∠即是二面角E BC N --的平面角.EBF ∆是等腰直角三角形,所以45EBF ∠=,故④正确. 综上所述,正确的命题个数为3个. 故选:C.【点睛】本小题主要考查空间线线、面面的位置关系有关命题的真假性判断,属于中档题. 5.C解析:C【分析】利用空间中线线、线面、面面间的位置关系求解.【详解】对于①,由题意知11//AD BC ,从而1//BC 平面1AD C ,故BC 1上任意一点到平面1AD C 的距离均相等,所以以P 为顶点,平面1AD C 为底面,则三棱锥1A D PC -的体积不变,故①正确;对于②,连接1A B ,11AC ,111//AC AD 且相等,由于①知:11//AD BC ,所以11//BAC 面1ACD ,从而由线面平行的定义可得,故②正确;对于③,由于DC ⊥平面11BCBC ,所以1DC BC ⊥,若1DP BC ,则1BC ⊥平面DCP ,1BC PC ⊥,则P 为中点,与P 为动点矛盾,故③错误;对于④,连接1DB ,由1DB AC ⊥且11DB AD ⊥,可得1DB ⊥面1ACD ,从而由面面垂直的判定知,故④正确.故选C .【点睛】本题考查命题真假的判断,解题时要注意三棱锥体积求法中的等体积法、线面平行、垂直的判定,要注意使用转化的思想.6.D解析:D【分析】以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴建立空间直角坐标系,利用向量1(1,0,2)B M =--,(2,0,1)CN =-的数量积为0,即可求解.【详解】以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴建立空间直角坐标系如图所示, 设正方体1111ABCD A BC D -的棱长为2,由图可知(1,0,0)M ,1(2,0,2)B ,(2,2,0)C ,(0,2,1)N ,所以1(1,0,2)B M =--,(2,0,1)CN =-所以1cos ,0B M CN 〈〉=所以异面直线B M '与CN 所成的角为90︒.故本题正确答案为D .【点睛】本题主要考查了异面直线所成角,属于基础题.7.B解析:B【分析】以B 为原点,BA 为x 轴,BC 为y 轴,1BB 为z 轴,建立空间直角坐标系,求得11,1,22MB ⎛⎫=--- ⎪⎝⎭,()10,? 02AA =,,利用空间向量夹角余弦公式能求出异面直线MB 与1AA 所成角的余弦值.【详解】在直三棱柱111ABC A B C -中,1111122AA A B B C ==,且AB BC ⊥,点M 是11AC , ∴以B 为原点,BA 为x 轴,BC 为y 轴,1BB 为z 轴,建立空间直角坐标系, 设11111222AA A B B C ===, 则11,1,22M ⎛⎫ ⎪⎝⎭,(0,00B ,),(1,00A ,),1(1,02A ,), 11,1,22MB ⎛⎫=--- ⎪⎝⎭,1(0,02AA ,)=, 设异面直线MB 与1AA 所成角为θ, 则1122cos 1824MB AA MB AA θ⋅===⋅⋅ ∴异面直线MB 与1AA 22B . 【点睛】本题主要考查异面直线所成角的余弦值的求法,是基础题.求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.8.B解析:B【分析】通过线线垂直证得线面垂直,进而得到A 正确;对于B 选项先假设成立,再推出矛盾进而得到结果不正确;C 根据四棱锥的形状得到球心位置,进而得到半径;由线面平行的判定定理得到线面平行.【详解】因为ABCD 是正方形,故得到BD AC ⊥,折叠之后得到1BD OA ⊥,BD OC ⊥,1O A OC O ⋂= 故得到BD ⊥面1AOC ,进而得到A 选项正确; 假设1A B CD ⊥,又因为11A B A ⊥D ,进而得到1A B ⊥面1ACE ,则11A B AC ⊥,三角形1A BC ,BC=2=1 2,A B =不可能满足直角关系,故B 错误.三棱锥1A BCD -,的外接球的球心在O 点处,因为OC=OD=OB=O 1A ,此时球的半径为C 正确;若E 为CD 的中点,则//BC OE ,OE 在平面1AOE 内,故得到//BC 平面1AOE ,D 正确;故答案为B.【点睛】直线与平面垂直的概念是利用直线与直线垂直的概念定义的,要注意定义中的“任何一条直线”这个词,它与“所有直线”是同义词,但与“无数条直线”不同,2.如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面.符号语言如下:a b b a αα⎫⇒⊥⎬⊥⎭. 9.C解析:C【分析】建立空间直角坐标系,结合空间向量的结论求解异面直线所成角的余弦值即可.【详解】以AC 的中点O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则:()10,1,2A -,)B,)12B ,()0,1,0C , 向量()13,1,2A B =-,()12B C =--, 11cos ,A B BC <>1111A B B C A B BC ⋅=⨯=14=. 本题选择C 选项.【点睛】本题主要考查异面直线所成的角的求解,空间向量的应用等知识,意在考查学生的转化能力和计算求解能力.10.D解析:D【分析】建立空间直角坐标系,找到平面1B EF 的法向量,利用向量法求点到平面的距离求解即可.【详解】以1D 为坐标原点,分别以11D A ,11D C ,1D D 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,则1(2,2,0)B ,1(0,2,0)C ,(2,1,2)E ,(1,2,2)F .设平面1B EF 的法向量为(,,)n x y z =,1(0,1,2)B E =-1(1,0,2)B F =-则1100n B E n B F ⎧⋅=⎪⎨⋅=⎪⎩,即2020y z x z -+=⎧⎨-+=⎩ 令1z =,得(2,2,1)n =.又11(2,0,0)BC =-, ∴点1C 到平面1B EF 的距离1122|||243||221n B C h n ⋅-===++, 故选:D . 【点睛】 本题用向量法求点到平面的距离,我们也可以用等体积法求点到平面的距离,当然也可以找到这个垂线段,然后放在直角三角形中去求.11.B解析:B【分析】以1,,AB AD AA 为空间向量的基底,表示出1BD 和AC ,由空间向量的数量积求出向量的夹角的余弦值即得.【详解】 由题意11111cos 602AB AD AB AA AD AA ⋅=⋅=⋅=⨯⨯︒=. 以1,,AB AD AA 为空间向量的基底,AC AB AD =+,111BD AD AB AD AA AB =-=+-,221111()()AC BD AB AD AD AA AB AB AD AB AA AB AD AD AA AB AD ⋅=+⋅+-=⋅+⋅-++⋅-⋅1=, 222()23AC AB AD AB AB AD AD =+=+⋅+=222211111()2222BD AD AA AB AD AA AB AD AA AD AB AA AB =+-=+++⋅-⋅-⋅=, ∴11116cos ,632AC BD AC BD AC BD ⋅<>===⋅⋅.∴1BD 与AC 夹角的余弦值为66. 故选:B .【点睛】本题考查用空间向量法求异面直线所成的角,解题时选取空间基底,把其他向量用基底表示,然后由数量积的定义求得向量的夹角,即得异面直线所成的角. 12.B 解析:B【分析】建立空间直角坐标系,利用向量法能求出线面角的正切值的最大值.【详解】 以1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系,设(,3,)P x z ,则1(3,3,),(3,3,4)AP x z BD =-=--,11,0AP BD AP BD ⊥∴⋅=,33(3)3340,4x z z x ∴---⨯+=∴=, 22225||(3)6916BP x z x x ∴=-+=-+225488191625255x ⎛⎫=-+ ⎪⎝⎭, ||5tan ||3AB BP θ∴=,tan θ∴的最大值为53. 故选:B .【点睛】本题主要考查的是线面所成角,解题的关键是找到线面所成角的平面角,是中档题.二、填空题13.【解析】【分析】取MC 中点O 连结AOBO 推导出AC =BM =AM =CM =1AO =BO =AO ⊥MCAO ⊥平面BMCAO ⊥BO 由此能求出AB 两点之间的距离【详解】取MC 中点O 连结AOBO ∵△ABC 中∠C =解析:102【解析】【分析】 取MC 中点O ,连结AO ,BO ,推导出AC =BM =AM =CM =1,AO =32,BO =72,AO ⊥MC ,AO ⊥平面BMC ,AO ⊥BO ,由此能求出A ,B 两点之间的距离.【详解】取MC 中点O ,连结AO ,BO ,∵△ABC 中,∠C =90°,∠A =60°,AB =2,M 为AB 中点,∴AC =BM =AM =CM =1,∴AO 2131()2- BO 22011172cos120121422BM MO BM OM ⎛⎫+-⨯⨯⨯+-⨯⨯⨯-= ⎪⎝⎭ AO ⊥MC ,将△BMC 沿CM 折叠,当平面BMC ⊥平面AMC 时,AO ⊥平面BMC ,∴AO ⊥BO ,∴A ,B 两点之间的距离|AB |=223710442BO AO +=+=, 故答案为:102. 【点睛】 本题考查两点间距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.14.【解析】【分析】由题意设正方体的棱长为2建立如图所示空间直角坐标系利用空间向量求解即可得到答案【详解】设正方体的棱长为2建立如图所示空间直角坐标系则0211异面直线BM 与AN 所成角的余弦值为故答案为 解析:3010【解析】【分析】由题意,设正方体的棱长为2,建立如图所示空间直角坐标系,利用空间向量求解,即可得到答案.【详解】设正方体的棱长为2,建立如图所示空间直角坐标系,则A(2,0,0),B(2,2,0),M(2,1,2),N(1,1,2),()BM 0,1,2∴=-,()AN 1,1,2=-,BM AN330cos BM,AN 1056BM AN ⋅∴===⨯⋅. ∴异面直线BM 与AN 所成角的余弦值为3010. 故答案为3010.【点睛】本题主要考查了空间向量在立体几何中的应用,其中解答中根据几何体的结构特征,建立适当的空间直角坐标系,利用向量的夹角公式求解是解答的关键,着重考查了推理与运算能力,属于基础题.15.【解析】连结A1B ∵AA1⊥面ABC 平面A1B1C1∥面ABC ∴AA1⊥平面A1B1C1∵A1C1⊂平面A1B1C1∴AA1⊥A1C1∵△ABC 与△A1B1C1是全等三角形AB ⊥AC ∴A1B1⊥A1 解析:2π 【解析】连结A 1B , ∵AA 1⊥面ABC ,平面A 1B 1C 1∥面ABC ,∴AA 1⊥平面A 1B 1C 1,∵A 1C 1⊂平面A 1B 1C 1,∴AA 1⊥A 1C 1,∵△ABC 与△A 1B 1C 1是全等三角形,AB ⊥AC ,∴A 1B 1⊥A 1C 1,∵A 1B 1∩AA 1=A 1,∴A 1C 1⊥平面AA 1B 1B ,又∵AB 1⊂平面AA 1B 1B ,∴A 1C 1⊥AB 1,∵矩形AA 1B 1B 中,AA 1=AB ,∴四边形AA 1B 1B 为正方形,可得A 1B ⊥AB 1,∵A 1B∩A 1C 1=A 1,∴AB 1⊥平面A 1BC 1,结合BC 1⊂平面A 1BC 1,可得AB 1⊥BC 1,即异面直线AB 1与BC 1所成角为2π. 故答案为2π.16.【解析】如图所示设∴∴∴周长又∵∴周长的范围为故答案为: 解析:(8,10)【解析】如图所示,设DH GH k DA AC ==, ∴1AH EH k DA BD==-, ∴5GH k =,4(1)EH k =-,∴周长82k =+.又∵01k <<,∴周长的范围为(8,10).故答案为:(8,10).17.3【详解】∵且平面与平面的法向量分别为∴解得:解析:3 【详解】∵αβ⊥,且平面α与平面β的法向量分别为m ,n , ∴(1,2,5)(3,6,)31250m n z z ⋅=-⋅-=--+=, 解得:3z =.18.【解析】试题分析:由题意得:即考点:两直线垂直【名师点睛】在研究直线平行与垂直的位置关系时如果所给直线方程含有字母系数时要注意利用两直线平行与垂直的充要条件:(1)l1∥l2⇔A1B2-A2B1=0 解析:2-【解析】试题分析:由题意得:12l l ⊥,即5(3)302a a a ++-=⇒=- 考点:两直线垂直 【名师点睛】在研究直线平行与垂直的位置关系时,如果所给直线方程含有字母系数时,要注意利用两直线平行与垂直的充要条件:(1)l 1∥l 2⇔A 1B 2-A 2B 1=0且A 1C 2-A 2C 1≠0(或B 1C 2-B 2C 1≠0);(2)l 1⊥l 2⇔A 1A 2+B 1B 2=0,这样可以避免对字母系数进行分类讨论,防止漏解与增根. (3与,0l Ax By C ++=平行的直线可设为0Ax By C ++=',与,0l Ax By C ++=垂直的直线可设为0Bx Ay C -+='19.【解析】试题分析:因为在平行六面体中所以则考点:本题考查的知识点是点线面间的距离计算考查空间两点之间的距离运算根据已知条件构造向量将空间两点之间的距离转化为向量模的运算是解答本题的关键 解析:【解析】试题分析:因为在平行六面体中,,所以,则.考点:本题考查的知识点是点、线、面间的距离计算,考查空间两点之间的距离运算,根据已知条件,构造向量,将空间两点之间的距离转化为向量模的运算,是解答本题的关键.20.(1)(3)(4)【分析】结合正方体图形分别对四个命题进行判断【详解】⑴由面故所以四边形的面积为正确⑵是等比三角形又因为异面直线与所成的夹角为但是向量的夹角为故错误⑶由向量的加法可以得到则故正确⑷由解析:(1) (3) (4) 【分析】结合正方体图形,分别对四个命题进行判断 【详解】⑴由AB ⊥面11BBCC ,故1AB BC ⊥,所以四边形11ABC D 的面积为1AB BC 正确 ⑵1ACD 是等比三角形,160ADC ∠∴=︒,又因为11A B D C ,∴异面直线1AD 与1A B 所成的夹角为60︒,但是向量11AD A B 与的夹角为120︒,故错误⑶由向量的加法可以得到111111AA A D A B AC ++=,()221113AC A B =,则 ()()2211111113AA A D A B A B ++=,故正确⑷111111A B A D D B -=,由11D B ⊥面11AC C ,故111D B AC ⊥,可得111)0AC D B ⋅=,故正确 【点睛】本题主要考查的是用向量的知识和方法研究正方体中的线线位置关系以及夹角和面积,用到向量的加减法,夹角及向量的数量积,熟练掌握正方体中的线线位置关系及夹角与向量的有关知识方法是做好本题的关键。
甘肃省甘南藏族自治州2024高三冲刺(高考数学)统编版(五四制)测试(预测卷)完整试卷

甘肃省甘南藏族自治州2024高三冲刺(高考数学)统编版(五四制)测试(预测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖.在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:小张说:“甲或乙团队获得一等奖”;小王说:“丁团队获得一等奖”;小李说:“乙、丙两个团队均未获得一等奖”;小赵说:“甲团队获得一等奖”.若这四位同学中有且只有两位预测结果是对的,则获得一等奖的团队是( )A.甲B.乙C.丙D.丁第(2)题已知复数z满足,则在复平面内z对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限第(3)题若,则“”是“”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件第(4)题如图,在四棱锥中,,,,P为侧棱SA的中点,则四棱锥外接球的表面积为()A.B.C.D.第(5)题2022年4月23日是第27个世界读书日,以引导全民阅读为出发点,弘扬中华优秀文化,传承中华悠久文明,我校高一年级部举行了“培养阅读习惯,分享智慧人生”为主题的读书竞赛活动.如图所示的茎叶图是甲、乙两个代表队各7名队员参加此次竞赛的成绩,乙队成绩的众数为,则下列关于这两个代表队成绩的叙述中,其中错误的是()A.甲队的众数大于乙队的众数B.甲队的中位数大于乙队的中位数C.甲队的平均数小于乙队的平均数D.甲队的方差小于乙队的方差第(6)题正项等比数列中,,若,则的最小值等于()A.1B.C.D.第(7)题已知空间向量,,则向量在向量上的投影向量是()A.B.(2,﹣1,2)C.D.(1,﹣2,1)第(8)题已知集合,,则中元素的个数为()A.0B.1C.2D.无数个二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题在封闭的四棱锥内有一个半径为的球,为正方形,的面积为1,,则()A.PA的最小值为B.该球球面不能与该四棱锥的每个面都相切C.若,则的最大值为D.若,则的最大值为第(2)题定义在上的偶函数满足,且当时,若关于的不等式的整数解有且仅有9个,则实数m的取值可以是()A.B.C.D.第(3)题设定义在R上的函数满足:①:②对任意实数满足;③存在大于零的常数m,使得,且当时,.则()A.B.当时,C.函数在R上没有最值D.任取三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知关于的不等式对任意均成立,则实数的取值范围为_____.第(2)题已知椭圆C的焦点、都在x轴上,P为椭圆C上一点,的周长为6,且,,成等差数列,则椭圆C的标准方程为______.第(3)题已知双曲线的一个焦点坐标为,且该焦点到双曲线渐近线的距离为,则双曲线的标准方程为________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题2023年9月26日,第十四届中国(合肥)国际园林博览会在合肥骆岗公园开幕.本届园博会以“生态优先,百姓园博”为主题,共设有5个省内展园、26个省外展园和7个国际展园,开园面积近3.23平方公里.游客可通过乘坐观光车、骑自行车和步行三种方式游园.(1)若游客甲计划在5个省内展园和7个国际展园中随机选择2个展园游玩,记甲参观省内展园的数量为,求的分布列及数学期望;(2)为更好地服务游客,主办方随机调查了500名首次游园且只选择一种游园方式的游客,其选择的游园方式和游园结果的统计数据如下表:游园方式观光车自行车步行游园结果参观完所有展园808040未参观完所有展园20120160用频率估计概率.若游客乙首次游园,选择上述三种游园方式的一种,求游园结束时乙能参观完所有展园的概率.第(2)题在直角坐标系中,曲线的参数方程为(为参数).以原点为极点,轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.(1)求的普通方程和的直角坐标方程;(2)若与有公共点,求实数的取值范围.第(3)题已知函数.(1)当时,求函数在处的切线方程;(2)若函数在定义域上单调增,求的取值范围;(3)若函数在定义域上不单调,试判定的零点个数,并给出证明过程.第(4)题已知且在上单调递增,.(1)当取最小值时,证明恒成立.(2)对,,使得成立,求实数的取值范围.第(5)题如图,在平面直角坐标系中,已知椭圆()的上顶点为,圆经过点.(1)求椭圆的方程;(2)过点作直线交椭圆于,两点,过点作直线的垂线交圆于另一点.若△PQN的面积为3,求直线的斜率.。
江苏省涟水县第一中学数学必修二导练:第课时 立体几何复习苏教 缺答案

立体几何复习一.填空题:(5分×14=70分)1.两个平面可以将空间分成________部分.2.三条直线两两平行,则过其中任意两条直线最多可确定_______________个平面. 3.在正方体1111ABCD A B C D -各个表面的对角线中,与1AD 所成角为60的直线 有_______条.4.异面直线所成角的取值范围为________,斜线与平面所成角的取值范围为________, 直线与平面所成角的取值范围为________________.5.用长、宽分别是π3与π的矩形硬纸卷成圆柱的侧面,则圆柱底面的半径为________. 6.一个边长为a 的正三角形,绕它的一条边旋转一周,所得几何体的体积是_______. 7.一个正方体的内切圆柱与外接圆柱的表面积之比是_______.8.若A α∉,α∈B ,6AB =,AB 与α所成的角为45,则A 到α的距离是_____. 9.若两条直线a ,b 分别在两个平行平面内,则a ,b 的位置关系是____________. 10.经过平面α外一点和平面α内一点与平面α垂直的平面有_________________个. 11.一平面截一球得到半径是3cm 的圆面,球心到这个平面的距离是4cm ,则该球的体积是_________________.12.若两个平行平面的距离等于10,夹在这两个平面间的线段AB 长为20,则AB 与这两个平面所成角为________________.13.如图,在三棱锥111ABC A B C -中,AB ,BC ,1BB 两两垂直且12ABBCBB ,11E D ,分别是棱1111C B B A ,的中点,则1AD 与1CE 所成角的大小是_________.14.如图,三角形AOC 是边长为1的等腰三角形,则它直观图的面积为_____________.1C1A1B ABC1D1E13题14题二.解答题:15.在正三棱锥S ABC -中,求证:SA BC ⊥.(14分)B C17.如图,三棱锥S ABC -中,已知SA BC ⊥,SA BC a ==,SA DE ⊥,BC DE ⊥,且DE b =,求三棱锥S ABC -的体积.(14分)18.如图,三棱锥A BCD -中,,E G 分别是BC ,AB 的中点,F 在CD 上,H 在AD 上,且有::2:3DF FC DH HA ==. 试确定EF ,GH ,BD 的位置关系.(16分)A B C D E S BCDG A H EF19.如图,在正方体1111ABCD A B C D -中,E 为1DD 的中点.求证:(1)1//BD 平面EAC ;(2)平面EAC ⊥平面1AB C .(16分)C ABDE 1A1B1C 1D。
2020江苏高考数学填空题专项拔高专题01 立体几何中的常见计算问题(解析版)
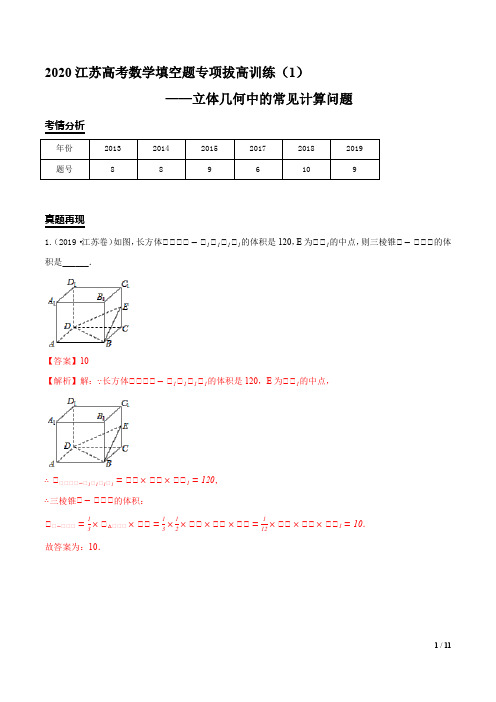
2020江苏高考数学填空题专项拔高训练(1)——立体几何中的常见计算问题考情分析真题再现1.(2019·江苏卷)如图,长方体的体积是120,E为的中点,则三棱锥的体积是______.【答案】10【解析】解:长方体的体积是120,E为的中点,,三棱锥的体积:.故答案为:10.2.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为______.【答案】【解析】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:.故答案为:.3.(2017·江苏卷)如图,在圆柱内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱的体积为,球O的体积为,则的值是______.【答案】【解析】解:设球的半径为R,则球的体积为,圆柱的体积为,则.故答案为.核心要点1.求几何体的表面积及体积问题,可以多角度、多方位的考虑,熟记公式是关键所在,求三棱锥的体积,等体积转化是常用的方法,转化的原则是其高易求,底面放在已知几何体的某一面上。
2.求不规则几何体的体积,常用分割或补形的思想,将不规则的几何体转化为规则几何体以易于求解。
拔高训练1.(2019·南通模拟改编)如图,在直三棱柱-中,若四边形是边长为4的正方形,且,,M是的中点,则三棱锥-的体积为______ .【答案】4【解析】解:在直三棱柱中,若四边形是边长为4的正方形,且,,,,,,,平面,平面,是的中点,,三棱锥的体积:.故答案为4.2.(2019·苏北四市一模改编)圆锥的侧面展开图是半径为3,圆心角为的扇形,则这个圆锥的高是______.【答案】【解析】解:设此圆锥的底面半径为r,根据圆锥的侧面展开图扇形的弧长等于圆锥的底面周长可得,,即,则圆锥的高为:.故答案为.3.(2019·扬州模拟)若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为3,圆心角为的扇形,则该圆锥的体积为______.【答案】【解析】解:如图:圆锥PO沿模型PB剪开,侧面展开图扇形的圆心角,半径,则扇形弧长为.设圆锥PO的底面半径为r,则,得.圆锥的高.该圆锥的体积为.故答案为:.4.(2019·苏州校级模拟)若一圆锥的底面半径为3,体积是,则该圆锥的侧面积等于______.【答案】【解析】解:由已知得到圆锥的体积,解得,所以圆锥的母线长度为,所以圆锥的侧面积为.故答案为.5.(2019·泰州模拟)已知直四棱柱底面是边长为2的菱形,侧面对角线的长为,则该直四棱柱的侧面积为______.【答案】【解析】解:如图所示,直四棱柱底面ABCD是边长为2的菱形,侧面对角线的长为,侧棱长为;该直四棱柱的侧面积为.故答案为:.6.(2019·徐州调研)已知正四棱柱的底面边长为3cm,侧面的对角线长是,则这个正四棱柱的体积是______.【答案】54【解析】解:设正四棱柱的高为h,正四棱柱的底面边长为3cm,侧面的对角线长是,,解得,这个正四棱柱的体积故答案为:54.7.(2019·南通校级模拟)如图,在直三棱柱中,,,,,点D为侧棱上的动点,当最小时,三棱锥的体积为______ .【答案】【解析】解:将直三棱柱展开成矩形,如图,连结,交于D,此时最小,,,,,点D为侧棱上的动点,当最小时,,此时三棱锥的体积:.故答案为:.8.(2019·扬州二模改编)如图,平面ABC,,,,,E,F分别为AB,PC的中点,则三棱锥的体积为______.【答案】【解析】解:平面ABC,,,,,E,F分别为AB,PC的中点,,F到平面ABC的距离,三棱锥的体积为:.故选:.9.(2019·无锡校级模拟)已知正四棱锥的体积是,高为4cm,则该四棱锥的侧面积是______.【答案】60【解析】解:设正四锥的底面边长为a,则,解得,四棱锥的斜高为,四棱锥的侧面积.侧故答案为:60.10.(2019·苏州校级模拟)如图,平面ABC,,,,,E,F分别为AB,PC的中点,则三棱锥的体积为_______ .【答案】【解析】,,,,E为AB的中点,,,平面ABC,F分PC的中点,到平面ABC距离为,,故答案为.11.(2019·南京模拟)已知圆锥的高是底面半径的2倍,侧面积为,若正方形ABCD内接于底面圆O,则四棱锥侧面积为.【答案】【解析】解:圆锥的高是底面半径的2倍,侧面积为,设底面半径为r,则高为2r,母线长,圆锥的侧面积,解得,正方形ABCD内接于底面圆O,,四棱锥侧面积为:.故答案为:.12.(2019·徐州模拟)在棱长为3的正方体中,P在线段上,且,M为线段上的动点,则三棱锥的体积为________.【答案】【解析】解:棱长为3的正方体中,P、M分别为线段,上的点,,到面的距离到面的距离,M为线段上的点,,.故答案为:.13.(2019·南通三模改编)如图,直三棱柱的六个顶点都在半径为1的半球面上,,侧面是半球底面圆的内接正方形,则侧面的面积为______.【答案】【解析】解:直三棱柱的六个顶点都在半径为1的半球面上,,故B,侧面边长为,故AB,故侧面的面积,故答案为:.14.(2019·无锡模拟)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸若盆中积水深九寸,则平地降雨量是____________寸.注:平地降雨量等于盆中积水体积除以盆口面积;一尺等于十寸【答案】3【解析】解:如图,由题意可知,天池盆上底面半径为14寸,下底面半径为6寸,高为18寸.因为积水深9寸,所以水面半径为寸则盆中水的体积为立方寸.所以则平地降雨量等于寸.故答案为3.15.(2019·连云港校级模拟)如图,是棱长为a的正方体,M,N分别为棱和的中点,则三棱锥的体积为.【答案】【解析】解:由题意,三棱锥体积为故答案为.11 / 11。
文科小综合--立体几何

2019届高三文科数学小综合专题练习一一立体几何东莞高级中学曾环望老师提供1、(2019揭阳)某师傅需用合板制作一个工作台,工作台由主体和附属两部分组成,主体部分全封闭,附属部分是为了防止工件滑出台面而设置的三面护墙,其大致形状的三视图如右图所示(单位长度:cm),贝U按图中尺寸,做成的工作台用去的合板的面积为(制作过程合板的损耗和合板厚度忽略不计)()2A. 40000 cmA.①② B .①③ C .①④ D.②④5、(2009北江中学)已知是两个不同的平面,m n是两条不同的直线,给出下列命题:①若ml e m :_「,则I.:;②若m 二:;,n 二:jm〃:,n〃:,则-// -;③如果m二”,n二:,m> n是异面直线,那么n与〉相交;④若:二m,n//m,且n -■, n 二,则n〃:且n〃:.其中正确的命题是()A.①②B.②③C.③④D.①④40800cm2C. 1600(22 ,17)cm2D. 241600cm2、(2009广东五校)在下列关于直线m与平面:- ■-的命题中,真命题是((A)若丨[,且鳥.1】,则I(B)若I _ 一:,且〉// 1 ,则I _ :(C)若:-Q - = m,且l_m ,则丨// :•3、(2009番禺)一个几何体的三视图如右图,其中主视图和左视图都是边长为1的正三角形, 那么这个几何体的侧面积为(4、(2019惠州调研二文)F列四个几何体中, 每个几何体的三视图有且仅有两个视图相同的是()•二、填空题6、(2009北江中学)如图是一个空间几何体的主视图、左视图、俯视图,女口果主视图、左视图所对应的三角形皆为边长为2的正三角形,俯视图对应的四边形为正方形,那么这个几何体的体积为 _________________ •7、表面积为16二的球的内接正方体的体积为______________ •8、一个平面四边形的斜二测化法的直观图是一个边长为1的正方形,则原平面四边形的面积为.9、将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了10、在一个密封的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是 ________________ •三、解答题11、已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.(1)求四棱锥P-ABCD的体积;(2)是否不论点E在何位置,都有BD _ AE ?证明你的结论;12、如图,已知AB _平面ACD , DE —平面ACD, △ ACD为等边三角形,AD =DE =2AB , F 为CD 的中点.(1) 求证:AF //平面BCE ;(2) 求证:平面BCE _平面CDE ;EEF6为 PD 、AB 的中点,且 PA =AB -1 , BC =2 ,(1) 求四棱锥E - ABCD 的体积; (2) 求证:直线AE //平面PFC15、(2009广东揭阳)如图,已知ABCD -A^GQ 是底面为正方形的长方体,• AD 1A^ = 60 , AD^ 4 ,点P 是AD 1上的动点.B(1) 试判断不论点P 在AD 1上的任何位置,是否都有平面B 1PA 1垂直于平面AA 1D 1 ?并证明你的结论;(2) 当P 为AD 1的中点时,求异面直线 AA 与B,P 所成角的余弦值;B13、( 09广东四校文期末) 直三棱柱 ABC-ABG 中,AC=BC=AA=2 , . ACB = 90 . E 为BB ,的中点,D 点在AB 上且DE —.,3 . (1) 求证:CD 丄平面AABB ; (2) 求三棱锥A —CDE 的体积•14、( 09北江中学文期末)如图,在底面是矩形的四棱锥P-ABCD 中,PA_ 面 ABCD , E 、F 为别DD 116、(2009广东潮州期末)如图,在四棱锥 P —ABCD 中,底面为直角梯形, AD//BC,. BAD =90 ,BEPA 垂直于底面 ABCD ,PA = AD = AB =2BC =2 ,M , N 分别为PC , PB 的中点。
温州中学高一年级暑期数学试题训练立体几何参考答案

温州中学高一年级暑期数学试题训练—立体几何参考答案一.选择题1~5 DCDCC 6~10 DCCBD 11~15 BCCAC 16~17 BC 二.填空题1.(1/2,1)2.1:83.(1)(2)4.20π5.(1)(4)(5)6.(0,-1,0)7.88.8π9.(1)12 (2)3 10.900 11.arctan 5. 三.解答题1. (Ⅰ)略;(Ⅱ)4,49.2.(Ⅰ)∵PA ⊥底面ABC ,∴PA ⊥BC .又90B C A ︒∠=,∴AC ⊥BC . ∴BC ⊥平面PAC .(Ⅱ)∵D 为PB 的中点,DE//BC ,∴12D E B C =,又由(Ⅰ)知,BC ⊥平面PAC , ∴DE ⊥平面PAC ,垂足为点E .∴∠DAE 是AD 与平面PAC 所成的角, ∵PA ⊥底面ABC ,∴PA ⊥AB ,又PA=A B , ∴△ABP 为等腰直角三角形,∴12AD AB =, ∴在Rt △ABC 中,60ABC ︒∠=,∴12BC AB =.∴在Rt △ADE 中,2sin 24D E BCD AE ADAD∠===,∴A D 与平面PAC 所成的角的大小2arcsin 4.(Ⅲ)∵AE//BC ,又由(Ⅰ)知,BC ⊥平面PAC ,∴DE ⊥平面PAC ,又∵AE ⊂平面PAC ,PE ⊂平面PAC ,∴DE ⊥AE ,DE ⊥PE , ∴∠AEP 为二面角A D E P --的平面角,∵PA ⊥底面ABC ,∴PA ⊥AC ,∴90PAC ︒∠=.∴在棱PC 上存在一点E ,使得AE ⊥PC ,这时90A E P ︒∠=, 故存在点E 使得二面角A D E P --是直二面角.3. (I )作MN ∥SD 交CD 于N ,作NE AB ⊥交A B 于E ,连ME 、NB ,则MN ⊥面ABCD ,M E AB ⊥,2NE AD ==设MN x =,则NC EB x ==,在R T M E B ∆中, 60MBE ∠=︒3M E x ∴=。
2023-2024学年江苏省高中数学人教A版选修一空间向量与立体几何强化训练-2-含解析

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年江苏省高中数学人教A 版选修一空间向量与立体几何强化训练(2)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)-49-91. 设,且,则xz 等于 ( )A. B. C. D.A ∈a ,a ∈α⇒A ∈αA ∈a ,a ⊄α⇒A ∉αA ∉a ,a ⊄α⇒A ∉αA ∈a ,a ⊂α⇒A ⊂α2. 已知点A ,直线a ,平面α,以下叙述正确的是( )A. B. C.D. 3.如图,在四棱锥P ﹣ABCD 中,底面ABCD 是正方形,E 为PD 中点,若=,= ,=,则=( )A. B. C.D.4. 已知点 , , 则()A. B.C. D.①④①③②③④②③5. 设m ,n 是两条不同的直线, , , 是三个不同的平面.有下列四个命题:①若 , , , 则;②若 , , 则;③ 若 , , , 则;④ 若 , , , 则 .其中错误命题的序号是( )A. B. C. D.6. 已知,,若,且BP平面ABC,则实数x,y,z分别为( )A. B. C. D.7. 在四棱锥中,底面是正方形,为的中点,若,则()A. B. C. D.-668. 已知空间向量a=(-1,1,3),b=(2,-2,x),若a∥b,则实数x的值是()A. B. C. D.9. 定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体中,,,,则异面直线与之间的距离是()A. B. C. D.110. 已知向量=(-1,0,2),=(1,1,0),且+k与2-相互垂直,则k值为( )A. B. C. D.11. 在三菱锥中,平面ABC,,D,E,F分别是棱AB,BC,CP的中点,,,则直线PA与平面DEF所成角的正弦值为()A. B. C. D.12. 在四棱锥中,,,,则该四棱锥的高为()A. B. C. D.阅卷人得分二、填空题(共4题,共20分)13. 如图,在空间四边形中,和为对角线,为的重心是上一点,以为基底,则.14. 过球O表面上一点A引三条长度相等的弦AB,AC,AD,且AB,AC,AD两两夹角都为60°,若,则该球的体积为.15. 已知直线l与平面垂直,直线的一个方向向量为,向量与平面平行,则.16. 在棱长为1正方体中,为线段的中点,则到平面的距离为;17.如图所示,矩形ABCD的边AB=a,BC=2,PA⊥平面ABCD,PA=2,现有数据:①a= ;②a=1;③a= ;④a=2;⑤a=4;(1) 当在BC边上存在点Q,使PQ⊥QD时,a可能取所给数据中的哪些值?请说明理由;(2) 在满足(1)的条件下,a取所给数据中的最大值时,求直线PQ与平面ADP所成角的正值;(3) 记满足(1)的条件下的Q点为Q n(n=1,2,3,…),若a取所给数据的最小值时,这样的Q有几个?试求二面角Q n﹣PA ﹣Q n+1的大小.18. 在如图所示的多面体中,平面,,,,,,,是的中点.(1) 求证:平面;(2) 求二面角的余弦值.19. 在图中,和都是直角三角形,, .将沿折起,使得,如图 .(1) 证明:平面平面;(2) 若分别为的中点,求二面角的大小.20. 如图所示,四边形为菱形,,二面角为直二面角,点是棱的中点.(1) 求证:;(2) 若,当二面角的正切值为时,求直线与平面所成的角.21. 在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为矩形,点E,F,M,S分别为棱PB,AD,AB,CD的中点,G为线段EM的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.(1) 确定N的位置,并求线段NG的长;(2) 平面CEF与PA交于点K,求三棱锥B﹣CKN的体积.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)(3)18.(1)(2)(1)(2)20.(1)(2)21.(1)(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴老师立体几何练习120分第Ⅰ卷 (选择题 共50分)一、选择题(10×5′=50′)1.如图,设O 是正三棱锥P-ABC 底面三角形ABC 的中心, 过O 的动平面与P-ABC 的三条侧棱或其延长线的交点分别记 为Q 、R 、S ,则PSPR PQ 111++ ( )A.有最大值而无最小值B.有最小值而无最大值C.既有最大值又有最小值,且最大值与最小值不等D.是一个与平面QRS 位置无关的常量2.在正n 棱锥中,相邻两侧面所成的二面角的取值范围是 ( ) A.⎪⎭⎫ ⎝⎛ππ-,1n n B.⎪⎭⎫ ⎝⎛ππ-,2n n C.⎪⎭⎫ ⎝⎛π2,0 D.⎪⎭⎫ ⎝⎛π-π-n n n n 1,2 3.正三棱锥P-ABC 的底面边长为2a ,点E 、F 、G 、H 分别是P A 、PB 、BC 、AC 的中点,则四边形EFGH 的面积的取值范围是 ( )A.(0,+∞)B.⎪⎪⎭⎫⎝⎛+∞,332a C.⎪⎪⎭⎫ ⎝⎛+∞,632a D.⎪⎭⎫ ⎝⎛+∞,212a 4.已知二面角α-a -β为60°,点A 在此二面角内,且点A 到平面α、β的距离分别是AE =4,AF =2,若B ∈α,C ∈β,则△ABC 的周长的最小值是 ( )A.43B.27C.47D.23 5.如图,正四面体A-BCD 中,E 在棱AB 上,F 在棱CD 上, 使得FDCFEB AE ==λ(0<λ<+∞),记f (λ)=αλ+βλ,其中αλ表示EF 与AC 所成的角,βλ表示EF 与BD 所成的角,则 ( )A.f (λ)在(0,+∞)单调增加B.f (λ)在(0,+∞)单调减少C.f (λ)在(0,1)单调增加,在(1,+∞)单调减少D.f (λ)在(0,+∞)为常数6.直线a ∥平面β,直线a 到平面β的距离为1,则到直线a 的距离与平面β的距离都等于54的点的集合是 ( )A.一条直线B.一个平面C.两条平行直线D.两个平面 7.正四棱锥底面积为Q ,侧面积为S ,则它的体积为 ( ) A.)(6122Q S Q - B.)(3122Q S Q - C.)(2122Q S Q - D.S Q 318.已知球O 的半径为R ,A 、B 是球面上任意两点,则弦长|AB |的取值范围为 ( ) A.[0,2R ] B.(0,2R ] C.(0,2R ) D.[R ,2R ]9.已知平面α∩平面β=l ,m 是平面α内的一条直线,则在平面β内 ( ) A..一定存在直线与直线m 平行,也一定存在直线与直线m 垂直 B.一定存在直线与直线m 平行,但不一定存在直线与直线m 垂直 C.不一定存在直线与直线m 平行,但一定存在直线与直线m 垂直D.不一定存在直线与直线m 平行,也不一定存在直线与 直线m 垂直10.如图为一个简单多面体的表面展开图(沿图中虚线折第1题图第5题图第10题图叠即可还原),则这个多面体的顶点数为 ( )A.6B.7C.8D.9 二、填空题(4×4′=16′)11.边长为a 的等边三角形内任一点到三边距离之和为定值,这个定值为 ;推广到空间,棱长为a 的正四面体内任一点到各面距离之和为 .12.在△ABC 中,AB =9,AC =15,∠BAC =120°,其所在平面外一点P 到A 、B 、C 三个顶点的距离都是14,则P 点到直线BC 的距离为 .13.已知将给定的两个全等的正三棱锥的底面粘在一起,恰得到一个所有二面角都相等的六面体,并且该六面体的最短棱的长为2,则最远的两顶点间的距离是 .14.有120个等球密布在正四面体A-BCD 内,问此正四面体的底部放有 个球. 三、解答题(4×10′+14′=54′)15.定直线l 1⊥平面α,垂足为M ,动直线l 2在平面α内过定点N ,但不过定点M .MN =a 为定值,在l 1、l 2上分别有动线段AB =b ,CD =c .b 、c 为定值.问在什么情况下四面体ABCD 的体积最大?最大值是多少?16.如图所示,已知四边形ABCD 、EADM 和MDCF 都是边长为a 的正方形,点P 、Q 分别是ED 和AC 的中点,求:(1)PM 与所成的角; (2)P 点到平面EFB 的距离; (3)异面直线PM 与FQ 的距离.17.如图,在梯形ABCD 中,AB ∥CD ,∠ADC =90°,3AD =DC =3,AB =2,E 是CD 上一点,满足DE =1,连结AE ,将△DAE 沿AE 折起到△D 1AE 的位置,使得∠D 1AB =60°,设AC 与BE 的交点为O .(1)试用基向量AB ,AE ,1AD 表示向量1OD(2)求异面直线OD 1与AE 所成的角.(3)判断平面D 1AE 与平面ABCE 是否垂直,并说明理由.18.如图,在斜棱柱ABC —A 1B 1C 1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点B 1在底面ABC 上的射影O 恰好是AB 的中点.(1)求证:B 1C ⊥C 1A ;(2)求二面角C 1-AB-C 的大小.第16题图第17题图3a.19.如图所示,在三棱锥P-ABC中,P A=PB=PC,BC=2a,AC=a,AB=3a,点P到平面ABC的距离为2(1)求二面角P-AC-B的大小;(2)求点B到平面P AC的距离.第19题图戴老师立体几何练习参考答案一、选择题1.D 设正三棱锥P-ABC 中,各棱之间的夹角为α,棱与底面夹角为β,h 为点S 到平面PQR 的距离,则V S-PQR =31S △PQR ·h =31(21PQ ·PR ·sin α)·PS ·sin β,另一方面,记O 到各平面的距离为d ,则有V S-PQR =V O-PQR +V O-PRS +V O-PQS =31S △PQR ·d +31S △PRS·d +31S △PQS ·d =3d ·21·PQ ·PR ·sin α+3d ·21PS ·PR ·sin α+3d ·21·PQ ·PS ·sin α.故有PQ ·PR ·PS ·sinβ=d (PQ ·PR +PR ·PS +PQ ·PS ),即PS PR PQ 111++=dβsin =常量.2.B 设正n 棱锥的高为h ,相邻两侧面所成二面角为θ.当h →0时,正n 棱锥的极限为正n 边形,这时相邻两侧面所成二面角为平面角,即二面角θ→π.当h →∞时,正n 棱锥的极限为正n 棱柱,这时相邻两侧面所成二面角为正n 边形的内角,即θ→n n 2-π.故选B.3.B 如图,易知四边形EFGH 为矩形,当P →底面△ABC 的中心O 时,矩形EFGH →矩形E 1F 1GH .G H F E S 11矩形 =E 1F 1·F 1G =a ·33a =33a 2.即S 矩形EFGH →33a 2.当P →∞时,S 矩形EFGH →∞. ∴S 矩形EFGH ∈⎪⎪⎭⎫⎝⎛+∞,332a .故选B.4.C 如图,∵a ⊥AE ,a ⊥AF ,∴a ⊥平面AEF .设a 交平面AEF 于点G ,则∠EGF 是二面角α-a -β的平面角,∠EGF =60°,∠EAF =120°,且易知当△ABC 的周长最小时,B ∈EG ,C ∈FG .设点A 关于平面α的对称点为A ′,点A 关于平面β的对称点为A ″,连结A ′A ″,分别交线段EG 、FG 于点B 、C ,则此时△ABC 的周长最短,记为l .由中位线定理及余弦定理得l =2EF =2︒⨯⨯-+120cos 2422422=47.5.D 因为ABCD 是正四面体,故AC ⊥BD ,作EG ∥AC 交BC 于G ,连结GF ,则αλ=∠GEF ,且FDCFEB AE GB CG ==, ∴GF ∥BD ,故GF ⊥EG ,且βλ=∠EFG ,∴f (λ)=αλ+βλ=90°为常数. 6.C 这两条直线在距a 为51的平面上,分布在a 在该平面上的射影的两侧. 7.A 设正四棱锥各棱长均为1,则Q =1,S =3,此时,正四棱锥的高h =22,∴V =31Qh =62,将Q =1,S =3代入选择支,知A 正确.8.B 考虑A 、B 两点在球面上无限靠近但又不重合,及A 、B 两点应为直径的两端点时的情况.点评 若忽视几何里的两点、两直线、两平面等均应是相异的两元素,就会误选A,球的最长弦就是直径,但球没有第3题图解第4题图解最短弦.9.C 若m ∥l ,则β内必有与m 平行的直线;若m 与l 相交,则β内无直线与m 平行.∴不一定存在直线与直线m 平行,排除A 、B.又β内一定存在与m 在β内的射影垂直的直线,由三垂线定理知,β内一定存在直线与m 垂直,故选C.10.B 本题考查简单多面体的表面展开与翻折,着重考查考生的空间想像能力,该多面体是正方体切割掉一个顶点,故有7个顶点. 二、填空题11.a 23;36a 本题通过等积找规律. 12.727 分析 P 点到A 、B 、C 距离相等,故P 点在平面ABC 上的射影是三角形ABC 的外心,故可由△ABC 的已知条件求出△ABC 外接圆半径,进而求得P 点到平面ABC 的距离,及外心到直线BC 的距离,从而最终解决问题.解 记P 点在平面ABC 上的射影为O ,则AO 、BO 、CO 分别是P A 、PB 、PC 在平面ABC 上的射影 ∵P A=PB=PC ,∴OA=OB=OC , ∴O 为△ABC 的外心.在△ABC 中,BC =15915922⨯++=21 由正弦定理,2R =︒120sin 21,∴R =73P 点到平面ABC 的距离为()7371422=-.O 点到直线BC 的距离OD =327221)37(22=⎪⎭⎫⎝⎛+ (D 为BC 边的中点) ∵OP ⊥平面ABC ,OD ⊥BC ,∴PD ⊥BC . ∴P 到BC 的距离PD =727327722=⎪⎭⎫ ⎝⎛+. 13.3 如图所示,作CE ⊥AD ,连结EF ,易证EF ⊥AD , 则∠CEF 为面ADF 和面ACD 所成二面角的平面角.设G 为 CD 的中点,同理∠AGB 为面ACD 和面BCD 所成二面角的 平面角,由已知∠CEF =∠AGB .设底面△CDF 的边长为2a ,侧棱AD 长为b .在△ACD 中,CE ·b =AG ·2a ,所以CE =baa b baAG 2222⋅-=⋅在△ABC 中,易求得AB =22222342332a b a b -=⎪⎪⎭⎫⎝⎛-,由△CEF ∽△AGB 得CEAGCF AB =,即aba b a b aa b 22342222222⋅--=-解得b =34a ,因此b =2时,2a =3,∴最远的两顶点间距离为3. 14.36 正四面体ABCD 的底部是正△BCD ,假设离BC 边最近的球有n 个,则与底面△BCD 相切的球也有n 排,各排球的个数分别为n 、n -1、…、3、2、1,这样与底面相切的球共有1+2+…+n =2)1(+n n 个.由于正四面体各面都是正三角形.因此,正四面体内必有n 层球,自上而下称为:第1层、第2层、…第n 层,那么第n -1层,第n -2层,…第2层,第1层球的个数分别是:1+2+…+n =2)1(+n n 、1+2+…+n -1=2)1(nn -, 1+2=232⨯,1=221⨯ ∴,1202212)1(2)1(=⨯++-++n n n n第13题图解即61n (n +1)(n +2)=120. 即(n -8)(n 2+11n +90)=0,∴n =8,因此正四面体内共有8层小球,其底部所放球数为298⨯=36(个). 三、解答题15.分析 在四面体ABCD 的基础上,补上一个三棱锥B-MCD . 解 如图,连结MC 、MD ,则∵AM ⊥平面MDC ,BM ⊥平面MDC∴V A-BCD =V A-MDC -V B-MDC =31S △MDC ·(AM-BM )=31S △MDC ·AB 设M 到CD 的距离为x ,则S △MDC =21CD ·x =21cx ,∴V A-BCD =31×21cx ·b =61bcx∵x ≤MN =a ,∴当x =a 时,即MN 为l 1与l 2的公垂线时,V A-BCD 最大,它的最大值为61abc .点评 x ≤MN ,包含x =MN ,也包含x<MN ,垂线段小于斜线段.16.解 建立空间直角坐标系,使得D (0,0,0),A (a ,0,0),B (a ,a ,0),C (0,a ,0),M (0,0,a ),E (a ,0,a ),F (0,a ,a ), 则由中点坐标公式得P (2a ,0,2a ),Q (2a ,2a,0), (1) 所以PM =(-2a ,0,2a ),FQ (2a ,-2a ,-a ),PM ·FQ =(-2a )×2a +0+2a ×(-a )=-43a 2, 且|PM |=22a ,|FQ |=26a ,所以cos PM ,FQ 23262243||||2-=⨯-=a a aFQ PM . 故得两向量所成的角为150°;(2) 设n =(x ,y ,z )是平面EFB 的单位法向量,即|n |=1,n ⊥平面EFB ,所以n ⊥EF ,且n ⊥BE ,又=(-a ,a ,0),=(0,-a ,a ),即有⎪⎩⎪⎨⎧=-=+-=++,0,0,1222az ay ay ax z y x 得其中的一个解是⎪⎪⎪⎩⎪⎪⎪⎨⎧===;33,33,33z y x ∴n =⎪⎪⎭⎫⎝⎛33,33,33,=⎪⎭⎫ ⎝⎛2,0,2a a , 设所求距离为d ,则d =|PE ·n |=a 33; (3) 设e =(x 1,y 1,z 1)是两异面直线的公垂线上的单位方向向量, 则由=⎪⎭⎫ ⎝⎛-2,0,2a a ,=⎪⎭⎫ ⎝⎛--a a a ,2,2,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=+-=++.022,022,111111212121az y a x az a x a z y x 求得其中的一个e =⎪⎪⎭⎫ ⎝⎛-33,33,33,第15题图解而MF =(0,a ,0),设所求距离为m ,则m =|MF ]·e |=|-33a |=33a . 17.解 (1)根据已知,可得四边形ABCE 为平行四边形,所以O 为BE 中点. AD AD AD OD 2121)(211111--=+-=-=. (2).1)2(2145cos 222145cos 21)2121(211-=-︒⨯⨯-︒⨯⨯=⋅--=⋅AD OD ∵(1OD )2=(1AD -21-21)2=23, ∴|1OD |=26. ∴cos<1OD ,332261||||11-=⨯-=⋅AE OD , 所以OD 1与AE 所成角为arccos33. (3)设AE 的中点为M ,则1=1AD -21AE . ∵1MD ·=1AD ·-21·=1×2×cos60°-21×2×2cos45°=0, ∴1MD ⊥.1MD ·=1AD ·-21AE =2cos 45°-21×(2)2=0,∴1MD ⊥. 所以MD 1垂直于平面ABCE 内两条相交直线,∴MD 1⊥平面ABCE .而D 1M 平面AD 1E ,所以平面AD 1E ⊥平面ABCE .18.(1)解法一 连结BC 1、CO ,∵B 1O ⊥平面ABC ,CO ⊥AB ,∴B 1C ⊥AB , 又∵在菱形BB 1C 1C 中,B 1C ⊥BC 1, ∴B 1C ⊥平面ABC 1,∴B 1C ⊥C 1A .(2)作C 1Q ⊥平面ABC 于Q 点,连接AQ ,∴∠C 1CQ 是侧棱与底面所成的角,即∠C 1CQ =60°, 在△C 1CQ 中,CQ =21CC 1=AO ,C 1Q =23CC 1, 由BC ,B 1C 1,OQ 平行且相等,又∵CO ⊥AB ,∴QA ⊥AB ,∴C 1A ⊥AB ,∴∠QAC 1是二面角C 1-AB -C 的平面角, 在△AQC 1中,C 1Q =AQ ,∴∠QAC 1=45°解法二 (1)以O 为原点,OC 所在直线为x 轴,AB 所在直线为y 轴,建立空间直角坐标系,如图, ∵B 1O ⊥平面ABC ,∴∠B 1BO 是侧棱与底面所成角,∴∠B 1BO =60°.设棱长为2a ,则OB 1=3a ,BO =a ,又CO 为正三角形的中线,∴CO =3a . 则A (0,a ,0),B (0,-a ,0),C (3a ,0,0),B 1(0,0,3a ),C 1(3a ,a ,3a ). B 1=(3a ,0,-3a ),C 1=(-3a ,0,-3a).第18题图解(1)第18题图解(2)∵C B 1·A C 1=-3a 2+0+3a 2=0,∴B 1C ⊥C 1A .(2)在△C 1AB 中,|C 1|=6a ,|1BC |=|(3a ,2a ,3a )|=10a ,||=2a , ∴S △C 1AB =6a 2,作C 1Q ⊥平面ABC 于Q 点,则Q (3a ,a ,0). ∴S △ABQ =3a 2,设二面角C 1-AB-C 的平面角为θ, 则cos θ=221=∆∆ABC ABQ S S . 二面角C 1-AB -C 的平面角为45°.19.(1)解法一 由条件知△ABC 为直角三角形,∠BAC =90°,∵P A=PB=PC ,∴点P 在平面ABC 上的射影是△ABC 的外心,即斜边BC 的中点E ,取AC 中点D ,连结PD 、DE 、PE ,PE ⊥平面ABC .DE ⊥AC (∵DE ∥AB ).∴AC ⊥PD ,∠PDE 为二面角P-AC-B 的平面角. tan PDE =32323==a a DEPE , ∴∠PDE =60°,故二面角P-AC-B 的平面角为60°.解法二 设O 为BC 的中点,则可证明PO ⊥面ABC ,建立如图空间直角坐标系, 则A ⎪⎪⎭⎫⎝⎛-0,23,21a a ,B (-a ,0,0),C (a ,0,0),P ⎪⎭⎫ ⎝⎛a 230,0, AC 中点D ⎪⎪⎭⎫⎝⎛-0,43,43a a , =⎪⎪⎭⎫ ⎝⎛-0,23,23a a ,=⎪⎪⎭⎫ ⎝⎛-a a a 23,43,43 ∵AB ⊥AC ,P A =PC ,PD ⊥AC ,cos<,>即为二面角P-AC -B 的余弦值.而cos<,DP >=21491631690434904323)43)(23(22222=++⨯+++⨯+--a a a a a a a a a 二面角P-AC-B 的平面角为60° (2)解法一 PD =a a a DE PE 349432222=+=+, S △APC =21·AC ·PD =223a第19题图解设点B 到平面P AC 的距离为h ,则由V P-ABC =V B-APC 得31·S △ABC ·PE =31·S △APC ·h ,h =a a aa a S PE S APC ABC 2323233212=⋅⋅⋅=⋅∆∆. 故点B 到平面P AC 的距离为a 23. 解法二 点E 到平面P AC 的距离容易求得,为43a ,而点B 到平面P AC 的距离是其2倍, ∴点B 到平面P AC 的距离为a 23.。
