长方体表面,怎样爬最短?
08 立体图形上的最短路径问题

第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1.基本思路:立体图形平面化,即化“曲”为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4.解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,13AB cm ==所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C’处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC’(在面ADD’A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与BB’C’C 相连,连接AC’,使E 点在AC’上(如图2))(412810')('2222cm CC BC AB AC =+=++= 所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可.试题解析:解:如下图所示,把圆柱的半侧面展开成矩形,点S ,F 各自所在的母线为矩形的一组对边上下底面圆的半周长为矩形的另一组对边.该矩形上的线段SF 即为所求的最短路线. 过点S 作点F 所在母线的垂线,得到SEF Rt ∆.34SF cm ==【难度】较易【例题4】(2015·红河期末)如下图,有一圆锥形粮堆,其主视图是边长为6m 的正三角形ABC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路程是__________m (结果不取近似值)【答案】【解析】试题分析:求小猫经过的最短距离,首先应将其侧面展开,将问题转化为平面上两点间的距离的问题,根据展开图中扇形的弧长与圆锥底面周长相等可求展开图的扇形圆心角度数,故可得出展开图中90BAP ∠=︒,即可用勾股定理求出小猫经过的最短距离BP 长.试题解析:解:作出圆锥侧面展开后的扇形图如下图,设该扇形的圆心角度数为n , 由展开扇形圆弧长等于底面圆周长,可得180n AC BC ππ⋅=⋅, 再由6AC BC m ==,可得180n =︒, 故在展开的平面图形中,1180902BAC ∠=⨯︒=︒点B 到P 的最短距离为 )BP m ===【难度】一般类型三 通过轴对称来转化【例题5】桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A 处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B 处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在位置?【答案】15厘米【解析】试题分析:把圆柱展开,得到矩形形状,A B 、的最短距离就是线段'BA 的长,根据勾股定理解答即可 试题解析:解:如图所示,作A 点关于杯口的对称点'A则'15BA ==厘米【难度】较易三、实战演练类型一 通过平移来转化1.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm 、3dm 、2dm .A 和B 是这个台阶上两个相对的端点,点A 处有一只蚂蚁,想到点B 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B 的最短路程为 dm .【答案】25dm【解析】试题分析:先将图形平面展开,再根据勾股定理进行解答试题解析:解:如图,三级台阶平面展开图为长方形,长为20dm ,宽为(2+3)×3dm ,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B 点最短路程为xdm ,由勾股定理可得x 2=202+[(2+3)×3]2,解得x =25.即蚂蚁沿着台阶面爬行到点B 的最短路程为25dm .【难度】较易类型二 通过旋转来转化2.(2015·陕西)有一个圆柱形油罐,已知油罐周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周造梯子,正好到达A 点的正上方B 处,问梯子最短有多长?【答案】13m【解析】试题分析:把圆柱沿AB 侧面展开,连接AB ,再根据勾股定理得出结论试题解析:解:展开图如图所示,12AC m =,5BC m =13AB m ===【难度】较易3.有一个圆柱体,如图,高4cm ,底面半径5cm ,A 处有一小蚂蚁,若蚂蚁欲爬行到C 处蚂蚁爬行的最短距离 .)cm【解析】试题分析:圆柱展开就是一个长方形,根据两点之间线段最短可求试题解析:解:∵4AB =,BC 为底面周长的一半,即5BC π=∴)AC cm ===【难度】较易4.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线-螺旋前进的,难道植物也懂得数学? 阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm ,绕一圈升高(即圆柱的高)40cm ,则它爬行一周的路程是多少?(2)如果树干的周长是80cm ,绕一圈爬行100cm ,它爬行10圈到达树顶,则树干高多少?【答案】(1)50cm ;(2)6m【解析】试题分析:(1)如下图,将圆柱展开,可知底面圆周长,即为AC 的长,圆柱的高即为BC 的长,求出AB 的长即为葛藤树的最短路程(2)先根据勾股定理求出绕行1圈的高度,再求出绕行10圈的高度,即为树干高 试题解析:解:(1)如图,O 的周长为30cm ,即AC =30cm高是40cm ,则BC =40cm ,由勾股定理得50AB cm ==故爬行一周的路程是50cm(2)O 的周长为80cm ,即AC =80cm绕一圈爬行100cm ,则AB=100cm ,高BC =60cm∴树干高=60×10=600cm =6m故树干高6m【难度】一般5.(2015·江阴市)如图,一个无盖的正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从盒外的B 点沿正方形的表面爬到盒内的M 点,蚂蚁爬行的最短距离是 ( )A B C .1 D .2+【答案】B【解析】试题分析:根据已知得出蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是如图BM的长度,进而利用勾股定理求出试题解析:解:∵蚂蚁从盒外的B点沿正方体的表面爬到盒内的M点∴蚂蚁爬行的最短距离是如图BM的长度∵无盖的正方体盒子的棱长为2,BC的中点为M∴1224A B=+=11A M=∴BM=故选:B【难度】较易6.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示,若沿OA剪开,则得到的圆锥侧面展开图为()【答案】C【解析】试题分析:要求小蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线. 试题解析:解:∵C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A∴侧面展开图BO 为扇形对称轴,连接AC 即是最短路线∵另一只小蚂蚁绕着圆锥侧面爬行到点B ,作出C 关于OA 的对称点,再利用扇形对称性得出关于BO 的另一对称点,连接即可.故选C【难度】一般7.(2014·枣庄)图①所示的正方体木块棱长为6cm ,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A 爬行到顶点B 的最短距离为 cm .【答案】(cm【解析】试题分析:要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果试题解析:解:如答图,易知△BCD 是等腰直角三角形,△ACD 是等边三角形,在Rt △BCD 中,CD ==,∴12BE CD ==,在Rt △ACE 中,AE ==,∴从顶点A 爬行到顶点B 的最短距离为(cm【难度】一般8.一个圆锥的母线长为QA =8,底面圆的半径r =2,若一只小蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到A 点,则蚂蚁爬行的最短路线长是________(结果保留根式)【答案】【解析】解:设圆锥的展开图扇形’QAA 的中心角'AQA ∠的度数为n ,则 822180n ππ⨯⨯⨯=,解得:90n = 即'90AQA ∠=在'Rt AQA 中,根据勾股定理'AA =【难度】一般9.如图,圆锥的主视图是等边三角形,圆锥的底面半径为2cm ,假若点B 有一只蚂蚁只能沿圆锥的表面爬行,它要想吃到母线AC 的中点P 处的食物,那么它爬行的最短路程是多少?【答案】【解析】试题分析:根据圆锥的主视图是等边三角形可知,展开图是半径是4的半圆,点B 是半圆的一个端点,而点P 是平分半圆的半径的中点,根据勾股定理就可求出两点B 和P 在展开图中的距离,就是这只蚂蚁爬行的最短距离试题解析:解:设圆锥的展开图的圆心角为n , 则422180n ππ⨯⨯⨯=, 解得:180n =︒ 即'180CAC ∠=︒在展开图中,'BA CC ⊥,4BA =,2AP =由勾股定理得,BP =点评:本题主要考查了圆锥的侧面展开图的计算,正确判断蚂蚁爬行的路线,把曲面的问题化为平面的问题是解题的关键【难度】较难10.(1)如图○1,一个无盖的长方体盒子的棱长分别为3BC cm =,4AB cm =,15AA cm =,盒子的内部顶点1C 处有一只昆虫甲,在盒子的内部顶点A 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点1C 处静止不动,请计算A 处的昆虫乙沿盒子内壁爬行到昆虫甲1C 处的最短路程,并画出其最短路径,简要说明画法(2)如果(1)问中的长方体的棱长分别为6AB BC cm ==,114AA cm =,如图○2,假 设昆虫甲从盒内顶点1C 以1厘米/秒的速度在盒子的内部沿棱1C C 向下爬行,同时昆虫乙从 盒内顶点A 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕 捉到昆虫甲?【答案】(1)1A E C →→就是最短路径 (2)5秒【解析】解:(1)如图二,将上表面展开,使上表面与前表面在同一平面内,即11A A D 、、三点共线,111538AA A D +=+= 114D C =根据勾股定理得1AC =如图三,将右侧面展开,使右侧面与下面在同一平面内,即1A B B 、、三点共线 1459AB BB +=+=,113B C =根据勾股定理得1AC =如图四,将右侧面展开,使右侧面与前表面在同一平面内,即A B C 、、三点共线. 437AB BC +=+=,15CC =根据勾股定理得1AC.在图四中,∵1ABE ACC ∽ ∴1BE AB CC AC= ∴457BE =,207BE =如图一,在1BB 上取一点E ,使207BE =,连接AE ,1EC ,1A E C →→就是最短路径 (2)如图五,设1C F x =,则3AF x =,5CF x =-在Rt ACF 中,根据勾股定理得222AF AC CF =+即:()()()22236614x x =++-解得:15x =,2172x =- ∵0x >∴5x =所以,昆虫至少需要5秒才能捉到昆虫甲.点评:在长方体中,经过它的表面,从一个顶点到另一个与它相对的顶点的最短距离是:在 长、宽、高中,以较短的两条边的和作为一条直角边,最长的边作为另一条直角边,斜边即 为最短路线长【难度】较难11.如图,A 是高为10cm 的圆柱底面圆上一点,一只蜗牛从A 点出发,沿30°角绕圆柱侧面爬行,当他爬到顶上时,他沿圆柱侧面爬行的最短距离是( )A. 10cmB. 20cmC. 30cmD. 40cm【答案】B试题分析:将圆柱侧面展开,连接AB ,根据三角函数求出AB 的长即可试题解析:解:根据题意得,10BC cm =,30BAC ∠=︒ ∴13010202A BC Sin cmB =÷︒=÷= 故选B .【难度】一般12.如图,是一个长4m ,宽3m ,高2m 的有盖仓库,在其内壁的A 处(长的四等分)有一只壁虎,B 处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为( )A .4.8B .5 D【答案】C【解析】有两种展开方法:①长方体展开成如图所示,连接A B 、,②将长方体展开成如图所示,连接A B 、【难度】较易13.(2015-2016·内蒙古包头)如图,长方体的长为15 cm,宽为10 cm,高为20 cm,点B 距离C点5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是cm.【答案】25【解析】试题分析:要求正方体中两点之间的最短路径,最直接的作法就是将正方体展开,然后利用两点之间线段最短解答.试题解析:解:如图:(1(2(3所以需要爬行的最短距离是25.【难度】较难14.已知:如图,一个玻璃材质的长方体,其中6,4,8===BF BC AB ,在顶点E 处有一块爆米花残渣,一只蚂蚁从侧面BCSF 的中心沿长方体表面爬行到点E .则此蚂蚁爬行的最短距离为 .【解析】试题分析:要求蚂蚁爬行的最短距离,需要将立体图形转化为平面图形,将E 、O (设面BCSF 的中心为点O )所在的两个面展开,但展开图并非只有一种,而是两种,需要利用“两点之间,线段最短”,来一一求出线段EO 的长度,然后比较两种情况的结果,找出最短路径 试题解析:解:设面BCSF 的中心为点O ,根据题意,最短路径有下列两种情况:○1如图1,沿SF 把长方体的侧面展开,蚂蚁爬行的最短距离==○2如图2,沿BF 把长方体的侧面展开,蚂蚁爬行的最短距离==∵【难度】较难15.如图,圆柱形容器中,高为1.2m ,底面周长为1m ,在容器内壁..离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁..,离容器上沿0.3m 与蚊子相对..的点A 处,则壁虎捕捉蚊子的最短距离为 m (容器厚度忽略不计).【答案】1.3m【解析】试题分析:将容器侧面展开,建立A 关于EF 的对称点A’,根据两点之间线段最短可知A ’B 的长度即为所求试题解析:解:要求壁虎捉蚊子的最短距离,实际上是求在EC 上找一点P ,使P A+PB 最短, 过点A 作EC 的对称点A ’,连结A ’B ,则A ’B 与EF 的交点P 就是所求的点P因为两点之间,线段最短,A’B 的长即为壁虎捕捉蚊子的最短距离∵底面周长为1m∴'0.5A D m =, 1.2BD m =' 1.3A B m =【难度】一般类型三 通过轴对称来转化16.一只蚂蚁欲从圆柱形桶外的A 点爬到桶内的B 点处寻找食物,已知点A 到桶口的距离AC 为12cm ,点B 到桶口的距离BD 为8cm ,CD 的长为15cm ,那么蚂蚁爬行的最短路程是多少?【答案】25cm【解析】试题分析:如图,作点B 关于CD 的对称点B’,连结AB ’, 交CD 于点P ,连结PB ,则最短路线应该 是沿AP 、PB ’ 即可试题解析:解:如下图所示,作点B 关于CD 的对称点'B ,连结'AB ,交CD 于点P ,则蚂蚁的爬 行路线'A P B →→ 为最短,且'AP PB AP PB +=+在'Rt AEB 中,15AE CD ==,''=12820EB ED DB AC BD =++=+=由勾股定理知 '25AB =所以,蚂蚁爬行的最短路程是25cm【难度】一般。
【暑假分层作业】第04练 几何最短路径问题或折叠中的应用-2022年八年级数学(人教版)

第04练几何最短路径问题或折叠中的应用一、单选题1.如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体的对角顶点G处,若AB=3cm,BC=5cm,BF=6cm,则最短的爬行距离是()A.10 B.14 C.106D.130【答案】A【解析】【分析】把长方体展开,根据两点之间线段最短得出最短路线AG,根据勾股定理,即可求出AG长度;【详解】把长方体展开有三种情况:当蜘蛛从A出发到EF上再到G时,如下图所示=,5BC cm∴==,FG BC cm5∴=+=,BG cm5611()在Rt ABG中,22+=;311130()AG cm当蜘蛛从A出发到BF上再到G时,如下图所示3AB cm =,5BC cm =,358()AG cm ∴=+=,6BF cm =,6CG BF cm ∴==,在Rt ABG 中,228610()AG cm =+=,当蜘蛛从A 出发到EH 上再到G 时,如下图所示6=AE cm ,=3EF cm 5=FG cm ,∴AF=9cm ,在Rt AFG 中,2295106()=+=AG cm ,13010610>>.故选:A .【点睛】本题考查勾股定理的应用,掌握两点之间线段最短是解题的关键.2.如图,圆柱的高为4cm ,底面半径为3πcm ,在圆柱下底面的A 点处有一只蚂蚁,它想吃到上底面B 处的食物,已知四边形ADBC 的边AD 、BC 恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是( )cm .A .5B .5πC .3+4πD .3+8π【解析】【分析】如图,先把圆柱体沿着直线AC 剪开,得到矩形如图示:可得线段AB 的长度为所求的最短距离,再利用勾股定理可得答案.【详解】解:把圆柱体沿着直线AC 剪开,得到矩形如下:则线段AB 的长度为所求的最短距离.由题意得圆柱的高为:4,cm 底面半径为3cm π,1134,=2=3,22AC BC C ππ∴==⨯⨯底面圆 2222345,AB AC BC ∴=+=+=所以蚂蚁至少要爬行5cm 路程才能吃到食物.故选:A【点睛】本题考查平面展开最短路径问题,弄懂圆柱展开图是长方形,根据两点之间线段最短是解题的关键.3.如图是一个三级台阶,它的每一级的长,宽,高分别是20dm,3dm,2dm ,A 和B 是这个台阶相对的端点,点A 处有一只蚂蚁,想到B 处去吃食物,则这只蚂蚁爬行的最短距离为( )A .25dmB .26dmC .24dmD .27dm【答案】A【解析】【分析】 先将图形平面展开,再由勾股定理根据两点之间线段最短进行解答.解:三级台阶平面展开图为长方形,长为20dm ,宽为(2+3)×3dm ,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B 点最短路程为x dm ,由勾股定理得:x 2=202+[(2+3)×3]2=252, 解得x =25.故选:A .【点睛】本题的是平面展开-最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题4.如图所示折叠直角三角形纸片的直角,使点C 落在斜边AB 上的点E 处,已知CD =1,∠B =30︒,则AC 的长是( )A .1B .2C 3D .3【答案】C【解析】【分析】 由三角形的内角和可得60BAC ∠=︒,由折叠可得,30B BAD ∠=∠=︒,继而求出30CAD ∠=︒,再根据含30度角的直角三角形的性质可得22AD CD ==,再利用勾股定理求解即可.【详解】90,30C B ∠=︒∠=︒,60BAC ∴∠=︒,由折叠可得,30B BAD ∠=∠=︒,30CAD ∴∠=︒,在Rt ACD △中,1CD =,22AD CD ∴==, 由勾股定理得223AC AD CD =-=,故选:C .【点睛】本题考查了三角形的内角和定理,折叠的性质,含30度角的直角三角形的性质,勾股定理,熟练掌握知识点是解题的关键.5.如图,在Rt △ABC 中,∠ACB =90°, AB =5,AC =3,点D 是BC 上一动点,连接AD ,将△ACD 沿AD 折叠,点C 落在点E 处,连接DE 交AB 于点F ,当∠DEB 是直角时,DF 的长为( ).A .5B .3C .32D .34【答案】C【解析】【分析】 如图,由题意知90AED C ∠=∠=︒,3AE AC ==,DE CD =,90AED DEB ∠=∠=︒,可知A EB 、、三点共线,E 与F 重合,在Rt ABC 中,由勾股定理得22BC AB AC =-,求BC 的值,设DF DE CD x ===,4BD x =-,在Rt BDE 中,由勾股定理得222BE BD DE =-,计算求解即可.【详解】解:如图,∵DEB ∠是直角∴90DEB ∠=︒由题意知90AED C ∠=∠=︒,3AE AC ==,DE CD =∴90AED DEB ∠=∠=︒∴A E B 、、三点共线∴E 与F 重合在Rt ABC 中,由勾股定理得224BC AB AC =-=设DF DE CD x ===,4BD x =-在Rt BDE 中,由勾股定理得222BE BD DE =-即()22224x x =--解得32x = ∴DF 的长为32故选C .【点睛】本题考查了折叠的性质,勾股定理等知识.解题的关键在于明确A E B 、、三点共线,E 与F 重合.6.如图,Rt ABC 中,90,4,6B AB BC ∠=︒==,将ABC 折叠,使点C 与AB 的中点D 重合,折痕交AC 于点M ,交BC 于点N ,则线段CN 的长为( ).A .73B .83C .3D .103【答案】D【解析】【分析】由折叠的性质可得DN =CN ,根据勾股定理可求DN 的长,即可得出结果.【详解】解:∵D 是AB 中点,AB =4,∴AD =BD =2,∵将△ABC 折叠,使点C 与AB 的中点D 重合,∴DN=CN,∴BN=BC-CN=6-DN,在Rt△DBN中,DN2=BN2+DB2,∴DN2=(6-DN)2+4,∴DN=103,∴CN=DN=103,故选:D.【点睛】本题考查了翻折变换、折叠的性质、勾股定理,熟练运用折叠的性质是本题的关键.二、填空题7.长方体的长为15cm,宽为10cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是_________.【答案】25cm【解析】【分析】要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.【详解】解:只要将长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如图1:∵长方体的宽为10,高为20,点B与点C的距离是5,∴BD=CD+BC=10+5=15,AD=20,在直角三角形ABD中,根据勾股定理得:AB22221520BD AD+=+;只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图2:∵长方体的宽为10,高为20,点B离点C的距离是5,∴BD=CD+BC=20+5=25,AD=10,在直角三角形ABD中,根据勾股定理得:AB=22222510529BD AD+=+=;只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如图3:∵长方体的宽为10,高为20,点B离点C的距离是5,∴AC=CD+AD=20+10=30,在直角三角形ABC中,根据勾股定理得:AB=2222305537AC BC+=+=;∵25529537<<∴蚂蚁爬行的最短距离是25cm,故答案为:25cm.【点睛】此题考查了轴对称-最短路线问题,本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可,正确掌握勾股定理及长方体的不同展开方式是解题的关键.8.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为32πm的半圆,其边缘AB=CD=15m,点E在CD上,CE=3m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为_____m.(边缘部分的厚度忽略不计)【答案】20【解析】【分析】要求滑行的最短距离,需将该U 型池的侧面展开,进而根据“两点之间线段最短”得出结果.【详解】解:如图是其侧面展开图:AD =1322ππ=16(m ), AB =CD =15m .DE =CD -CE =15-3=12(m ),在Rt △ADE 中,AE =2222161220AD DE +=+=(m ).故他滑行的最短距离约为20m .故答案为:20.【点睛】本题考查了平面展开-最短路径问题,本题就是把U 型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.9.如图,海上救援船要从A 处到海岸l 上的M 处携带救援设备,再回到海上C 处对故障船实施救援,使得行驶的总路程AM CM +为最小.已知救援船和故障船到海岸l 的最短路径分别为AB 和CD ,20BD =海里,60AMB ∠=°,救援船的平均速度是25节(1节=1海里/小时),则这艘救援船从A 处最快到达故障船所在C 处的时间为 ________小时.【答案】1.6【解析】【分析】作A 关于BD 的对称点Q ,连接CQ 即可,求出AM +CM =QC ,根据勾股定理求出CQ 即可.【详解】解:作A 关于BD 的对称点Q ,连接CQ ,交BD 于M ,则此时点M 为所求;∴AM +CM =QM +CM =CQ ,过Q 作QR ⊥CD ,交CD 的延长线于R ,则四边形BQRD 是矩形,所以BD =QR ,BQ =DR ,∵A 、Q 关于BD 对称,∴AB =BQ =DR ,∵∠AMB =60°,30A ∴∠=︒ ∴223AB AM BM BM -∴BM 3,AM =2BM ,CM =2MD ∴AM +CM =2BD =2×20=40(海里),即CQ =40(海里),∵救援船的速度是25节(1节=1海里/小时),∴这艘救援船最快4025=1.6(小时)到达故障船. 故答案为:1.6.【点睛】本题考查了轴对称−最短路线问题,能找出点M 的位置是解此题的关键. 10.如图,在Rt ABC 中,90,3,4B AB BC ∠=︒==.将ABC 折叠,使点B 恰好落在边AC 上,与点B '重合,AE 为折痕,则EB C '的周长为__________.【答案】6【解析】【分析】首先利用勾股定理求出AC=5,根据折叠得到B’C=2,求出三角形的周长.【详解】解:R t△ABC中,∠B=90°,∴AC=2222+=+=,AB BC345由折叠知AB’=AB=3,∴B’C=AC-AB’=5-3=2,∴△B’EC的周长为B’C+EC+B’E=B’C+EC+BE=B’C+CB=2+4=6,故答案为6.【点睛】本题考查折叠的性质以及勾股定理,解决问题的关键是分清折叠前后的对应的关系.11.如图,小明将一张正方形纸片对折,使得AB与CD重合,折痕为EF,展开后再沿BH 折叠,使得点C刚好落在折痕EF上的C′处,若CH=1cm,则BC= _____cm.3【解析】【分析】连接CC′,证明△BCC′是等边三角形,再由折叠的性质得到∠HBC=∠HBC′=30°,利用含30度角的直角三角形的性质求解即可解决问题.【详解】解:如图,连接CC ′,由折叠的性质知,折痕为EF 是BC 的垂直平分线,∴BC ′=CC ′,又由折叠的性质知,BC = BC ′,∠HBC =∠HBC ′,∴BC ′=CC ′=BC ,∴△BCC ′是等边三角形,∴∠C ′BC =60°,∴∠HBC =∠HBC ′=30°,在Rt △HBC 中,∠HBC =30°,CH =1cm ,∴HB =2cm ,∴BC =2222213BH CH -=-=(cm ),故答案为:3.【点睛】本题考查了翻折变换的性质,等边三角形的判定和性质,勾股定理,解决本题的关键是掌握翻折的性质.12.如图,CD 是△ABC 的中线,将△ACD 沿CD 折叠至A CD '△,连接AA '交CD 于点E ,交CB 于点F ,点F 是A E '的中点.若EDA '△的面积为12,8A B '=,则点F 到AC 的距离为______.【答案】365【解析】【分析】过点F 作FH ⊥AC 于点H ,由翻折的性质可知S △AA 'D =24,由D 为AB 的中点,则S△AA'B=2S△AA'D=48,得AA'=12,再通过AAS证明△A'BF≌△ECF,得CE=A'B=8,在Rt△CAE 中,由勾股定理求出AC的长,最后通过面积法即可求出FH的长.【详解】解:如图,过点F作FH⊥AC于点H,根据翻折的性质得:AD=A'D,AA'⊥CD,AE=A'E,∵CD是△ABC的中线,∴CD=BD,∴AD=BD=A'D,∴∠AA'B=90°,又∵S△A'DE=12,∴S△ADE=12,∴S△ADA'=24,又∵D为AB的中点,∴S△AA'B=2S△AA'D=48,即12×AA′×A′B=48,∴AA'=12,又∵F为A'E的中点,∴A'F=EF,在△A'BF与△ECF中,A F EFCFE BFACEF BA F'=⎧⎪∠='⎨⎪∠=∠'⎩,∴△A'BF≌△ECF(AAS),∴CE=A'B=8,∵AA'=2A'E,A'E=2EF=6,∴EF=3,AF=9,在Rt△CAE中,由勾股定理得:CA=22AE CE+=10,在△CAF中,CA•HF=AF•CE,∴HF=9810⨯=365,即点F到AC的距离为365,故答案为:365.【点睛】本题主要考查了翻折的性质,全等三角形的判定与性质,勾股定理等知识,运用等积法求垂线段的长是解题的关键.三、解答题13.如图,是用棱长为1cm的两个正方体拼成的新几何体,求一只蚂蚁从顶点A出发沿着新几何体的表面爬行到顶点B的最短路程是多少cm?【答案】22cm【解析】【分析】根据两点之间线段最短,将组合体图形转化为平面图形,进而勾股定理求解即可【详解】解:如图,将组合体的上底面展开,点B到了点B'的位置,蚂蚁沿A D B→→所在的直线运动到B'路程最短,∴22222222AB AC B C'=++若按以下方式展开,则2AB'=+=1310>1022即蚂蚁从顶点A出发到顶点B的最短路程是22cm.【点睛】本题考查了勾股定理的应用,将立体图形转化为平面图形是解题的关键.14.吴老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路径长.(1)如图1,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;(2)如图2,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表而爬到点C1处;(3)如图3,是一个底面周长为10cm,高为5cm的圆柱体,一只蚂蚁欲从圆柱体底面上的点A沿圆柱体侧面爬到点C处.【答案】(1)蚂蚁需要爬行的最短路径长为55;(2)蚂蚁需要爬行的最短路径长为234;(3)蚂蚁需要爬行的最短路径长为52.【解析】【分析】(1)根据正方体的侧面展开图,利用勾股定理求出AC1的长即可得答案;(2)分横向展开和竖向展开两种情况,分别利用勾股定理求出AC1的长,比较即可得答案;(3)画出圆柱侧面展开图,利用勾股定理求出AC的长即可得答案.【详解】(1)正方体的侧面展开图如图所示:AC 1为蚂蚁需要爬行的最短路径长,∵正方体的棱长为5cm ,∴AC =10,CC 1=5,∴AC 1=22221105AC CC +=+=55cm .∴蚂蚁需要爬行的最短路径长为55cm .(2)分两种情况:①如图,当横向展开时:AC =10,CC 1=6,∴AC1=22221106AC CC +=+=234cm ,②如图,当竖向展开时:AD =11,DC 1=5,∴AC1=22221115AD DC +=+=146cm ,∵234<146,∴蚂蚁需要爬行的最短路径长为234cm .(3)圆柱侧面展开图如图所示:∵圆柱底面周长为10cm ,高为5cm ,∴BC =5,AB =5,∴AC =222255AB BC +=+=52cm ,∴蚂蚁需要爬行的最短路径长为52cm .【点睛】本题考查立体图形的侧面展开图及勾股定理,熟记各立体图形的侧面展开图是解题关键. 15.如图直角三角形纸片中,∠C =90°,AB =10,BC =8,AC =6,沿点B 的直线折叠这个三角形,使点C 在AB 边上的点E 处,折痕为BD .(1)求△ADE 的周长;(2)求DE 的长.【答案】(1)8;(2)83【解析】【分析】(1)根据折叠的性质可得BE =BC =8,DE =CD ,则AE =AB -BE =2,即可得到△ADE 的周长=AD +AE +DE =AD +DE +AE =AC +AE =8;(2)设CD =DE =x ,则AD =AC -CD =6-x ,由折叠的性质可知∠DEB =∠C =90°,则∠DEA =90°,即可得到222AD AE DE =+,则()22262x x -=+,由此求解即可.【详解】解:(1)由折叠的性质可知,BE =BC =8,DE =CD ,∴AE =AB -BE =2,∴△ADE 的周长=AD +AE +DE =AD +DE +AE =AC +AE =8;(2)设CD =DE =x ,则AD =AC -CD =6-x ,由折叠的性质可知∠DEB =∠C =90°,∴∠DEA =90°,∴222AD AE DE =+,∴()22262x x -=+, 解得83x =, ∴83DE =. 【点睛】本题主要考查了折叠的性质,勾股定理,解题的关键在于能够熟练掌握折叠的性质. 16.矩形ABCD 在平面直角坐标系的位置如图所示,F 为AB 上一点,将BCF △沿CF 折叠,使点B 恰好落在AD 与y 轴的交点E 处.连接CE ,若,AE AB 的长满足24(8)0AE AB -+-=.(1)求点A ,B 的坐标;(2)求点D 的坐标;(3)在平面内是否存在点P ,使以E ,F ,C ,P 为顶点的四边形为平行四边形?若存在,直接写出点P 的坐标;若不存在,请说明理由.【答案】(1)A (-4,8)B (-4,0)(2)D (6,8)(3)P 1(2,-3)、P 2(10,3)、P 3(-10,13)【解析】【分析】(1)通过算术平方根、平方数的非负性求出AE 、AB 的值;(2)设未知边,通过勾股定理构建等式,再求出未知边,从而求出坐标;(3)分三种情况讨论:CF 作对角线;CE 作对角线;EF 作对角线.(1)24(8)0AE AB --=得:AE -4=0且AB -8=0∴AE =4AB =8∴A (-4,8)B (-4,0)(2)解:设AE 为x ,根据勾股定理有:()22284x x --=解得:x =3设ED 为y ,根据勾股定理有:()22284y y +=+ 解得:y =6∴D (6,8)(3)∵点E 到点F :(0-4,8-3)=F (-4,5)∴P 1=(6-4,0-3)=(2,-3)∵点F 到点E :(—4+4,5+3)=E (0,8)∴P 2=(6+4,0+3)=(10,3)∵点C 到点E :(6-6,0+8)=E (0,8)∴P 3=(-4-6,5+8)=(-10,13)【点睛】本题考查直角坐标系和勾股定理、动点问题,掌握相应知识和技能是本题关键. 17.如图是三个全等的直角三角形纸片,且::3:4:5AC BC AB =,按如图的三种方法分别将其折叠,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在角的两边重合,记折叠后不重叠部分面积分别为123,,S S S .(1)若3AC =,求1S 的值.(2)若1213S S +=,求①单个直角三角形纸片的面积是多少?②此时3S 的值是多少?【答案】(1)32(2)①36;②367【解析】【分析】 (1)设DE =CE =x ,则BE =4-x ,依据S △ABE =12AB ×DE =12BE ×AC ,即可得到x 的值,进而得出S 1的值.(2)①如图1,依据S△ABE=12AB×DE=12BE×AC,即可得到DE=32x,进而得出S1=32x2;如图2,依据S△ABN=12AB×HN=12AN×BC,即可得到EN=43x,进而得出S2=x2,再根据S1+S2=13,即可得到x2=6,进而得出单个直角三角形纸片的面积.②如图3,由折叠可得,AC=CF=3x,所以BF=BC-CF=4x-3x=x,则S3=13S△CMF=13S△ACM,所以S3=17ABCS,即可求解.(1)解:∵AC∶BC∶AB=3∶4∶5,AC=3,∴BC=4,AB=5,由折叠可得,DE=CE,∠ADE=∠C=90°,AD=AC=3,设DE=CE=x,则BE=4﹣x,∵S△ABE=12AB×DE=12BE×AC,∴AB×DE=BE×AC,即5x=3(4﹣x),解得x=32,∴S1=12BD×DE=13222⨯⨯=32.(2)解:由AC:BC:AB=3:4:5,可设AC=3x,BC=4x,AB=5x,①如图1,由折叠可得,AD=AC=3x,BD=5x-3x=2x,DE=CE,∠ADE=∠C=90°,∵S△ABE=12AB×DE=12BE×AC,∴AB×DE=BE×AC,即5x×DE=(4x-DE)×3x,解得DE=32 x,∴S1=12BD×DE=12×2x×32x=32x2;如图2,由折叠可得,BC=BH=4x,HN=CN,∴AH=x,AN=3x-HN,∵S△ABN=12AB×HN=12AN×BC,∴AB×HN=AN×BC,即5x×HN=(3x-HN)×4x,解得HN=43 x,∴S 2=12AH ×HN =12×x ×43x =23x 2, ∵S 1+S 2=13,∴32x 2+23x 2=13, 解得x 2=6,∴S △ABC =12×3x ×4x =6x 2=36.答:单个直角三角形纸片的面积是36;②如图3,由折叠可得,AC =CF =3x ,∴BF =BC -CF =4x -3x =x ,∴S 3=13S △CMF =13S △ACM , ∴S 3=17ABC S =367, 答:此时S 3的值为367. 【点睛】本题主要考查了翻折变换(折叠问题),折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决问题的关键是利用面积法求得某些线段的长度.18.如图,M ,N 分别为锐角AOB ∠边OA ,OB 上的点,把AOB ∠沿MN 折叠,点O 落在AOB ∠所在平面内的点C 处.(1)如图1,点C 在AOB ∠的内部,若20CMA ∠=︒,50CNB ∠=︒,求AOB ∠的度数.(2)如图2,若45AOB ∠=︒,2ON =C 在直线OB 上方,CM 与OB 交于点E ,且MN ME =,求折痕MN 的长.(3)如图3,若折叠后,直线MC OB ⊥,垂足为点E ,且5OM =,3ME =,求此时ON 的长.【答案】(1)35O ∠=︒(2)2MN =(3)52ON =或10 【解析】【分析】(1)根据折叠知,()1180802OMN CMN CMA ∠=∠=︒-∠=︒,65ONM ∠=︒根据三角形内角和定理即可求得答案;(2)根据MN ME =,由等边对等角可得ENM MEN ∠=∠,设OMN CMN x ∠=∠=度,根据三角形内角和为180°,建立一元一次方程解方程求解即可求得30OMN ∠=︒,过N 作NH OM ⊥于H ,根据勾股定理求得1NH =,根据含30度角的直角三角形的性质即可求得MN 的长;(3)①当点C 在OB 上方时,②当点C 在OA 下方时,设ON x =,则4NE OE ON x =-=-,勾股定理求解即可;(1)由折叠知,()1180802OMN CMN CMA ∠=∠=︒-∠=︒, 同理得65ONM ∠=︒,∴18035OMN ONM AOB =︒-∠-∠=∠︒.(2)如图,∵MN ME =,∴ENM MEN ∠=∠,设OMN CMN x ∠=∠=度,∵45AOB ∠=︒,∴(45)ENM MEN x ∠=∠=+度,∴()245180x x ++=,解得30x =,即30OMN ∠=︒,过N 作NH OM ⊥于H ,∵2ON =∴1NH =,∴2MN =.(3)当点C 在OB 上方时,如图3-1∵5OM =,3ME =,直线MC OB ⊥,∴4OE =,设ON x =,则4NE OE ON x =-=-,又由折叠知:5CM OM ==,CN ON x ==,∴532CE CM ME =-=-=,在Rt CNE 中,根据勾股定理,得()22242x x -+= 解得52x =,即52ON =;当点C 在OA 下方时,如图3-2由折叠知:CM OM =,CN ON =,∴538CE CM ME =+=+=,设ON x =,则4NE ON OE x =-=-,在Rt CNE 中,根据勾股定理,得()22248x x -+=,解得10x =,即10ON =.【点睛】本题考查了折叠的性质,三角形内角和定理,等边对等角求角度,勾股定理,分类讨论是解题的关键.1.如图,在纸片ABC ∆中,1230AB AC B ︒==∠=,,折叠纸片,使点B 落在AC 的中点D处,折痕为EF ,则DEF ∆的面积为( )A 493B .3C .3D 563 【答案】A【解析】【分析】过点D 作AB 的垂线,垂足为G ,过D 作CF 的垂线,垂足为H ,过A 作BC 的垂线,垂足为N , 分别求出△DEA 和△DFC 的面积,利用S △DEF =12×(S △ABC -S △DEA -S △DFC )可得结果.【详解】解:过点D 作AB 的垂线,垂足为G ,∵∠BAC =120°,∴∠GAC =60°,∠GDA =30°,∴AG =11324AD AC ==,DG 2233AD AG -= 设AE =x , 则BE =12-x =DE ,在Rt △DGE 中,222DE GE GD =+,即()()2212327x x -=++,解得:x =185, ∴S △ADE =12DG ×AE =1183325⨯⨯2735过D 作CF 的垂线,垂足为H ,过A 作BC 的垂线,垂足为N ,∵30B ,∴AN =12AB =6,BN 2212663 ,∴BC =123设DF =y ,则CF =123y ,DH =132CD =,CH 2233CD DH -= 则有222DH FH DF +=,即(222312333y y +-=, 解得:143y 则S △DFC =111433311322DH CF ⎛⋅=⨯⨯= ⎝⎭ ∴S △DEF =12 ×(S △ABC -S △DEA -S △DFC )=1122DEA DFC BC AN S S ⎛⎫⨯⋅⋅-- ⎪⎝⎭△△=112712363113225⎛⎫⨯⨯⨯-- ⎪⎝⎭ = 4935故选A .【点睛】此题主要考查了翻折变换以及勾股定理、等腰三角形的性质等知识,正确得出AE 、BF 的长是解题关键.2.如图,把等边ABC ∆沿着DE 折叠,使点B 恰好落在AC 边上的点B '处,且DB AC '⊥,若6cm B C '=,则AE =_____cm .【答案】333【解析】【分析】先根据30°直角三角形的特点求出CD 、B D ',再根据折叠求出BC 的长,最后证明90B EA '∠=︒即可利用30°直角三角形的特点求出AE .【详解】∵等边三角形ABC ∆∴60∠=∠=∠=︒A B C ,AC BC =∵DB AC '⊥,6cm B C '=∴30B DC '∠=︒∴212CD B C '==∴2263DB CD B C ''+∵折叠∴60B EB D ,63DB BD '==∴30AB E '∠=︒,1263AC BC DC BD ==+=+∴18090B EA A AB E ''∠=-∠-∠=︒,663AB AC B C ''=-=+∴13332AE AB '==+ 故答案为:333+【点睛】本题考查折叠的性质、勾股定理、30°的直角三角形的性质、等边三角形的性质,证明90B EA '∠=︒是解题的关键.3.如图,一透明圆柱形无盖容器高12cm ,底面周长24cm ,在杯口点B 处有一滴蜂蜜,此时一只蚂蚁在杯外壁底部与蜂蜜相对的A 处.(1)若蜂蜜固定不动,求蚂蚁吃到蜂蜜所爬行的最短路线长;(2)若该蚂蚁刚出发时发现B 处的蜂蜜正以0.5cm /s 的速度沿杯内壁下滑,它便沿最短路径在8秒钟时吃到了蜂蜜,求此蚂蚁爬行的平均速度.【答案】(1)122cm ;(2)2.5cm /s【解析】【分析】(1)先将圆柱的侧面展开,再根据勾股定理求解即可;(2)根据勾股定理得到蚂蚁所走的路程,于是得到结论.【详解】(1)如图所示.∵圆柱形玻璃容器,高12cm ,底面周长为24cm ,∴AD =12cm ,∴AB 22221212AD BD =+=+=122(cm ).答:蚂蚁要吃到食物所走的最短路线长度是122cm ;(2)∵AD =12cm ,∴蚂蚁所走的路程2212(124)=++=20,∴蚂蚁的平均速度=20÷8=2.5(c m/s ).【点睛】本题考查了平面展开﹣最短路径问题,将图形展开,利用勾股定理进行计算是解题的关键.4.定义:若a ,b ,c 是△ABC 的三边,且2222a b c +=,则称△ABC 为“方倍三角形”.(1)对于①等边三角形②直角三角形,下列说法一定正确的是___.A. ①一定是“方倍三角形”B. ②一定是“方倍三角形”C. ①②都一定是“方倍三角形”D. ①②都一定不是“方倍三角形”(2)若Rt△ABC是“方倍三角形”,且斜边3AB=,则该三角形的面积为___;(3)如图,△ABC中,120ABC∠=,45ACB∠=,P为AC边上一点,将△ABP沿直线BP 进行折叠,点A落在点D处,连结CD,AD,若△ABD为“方倍三角形”,且AP=2,求BC的长.【答案】(1)A(2)2231【解析】【分析】(1)直接利用“方倍三角形”的定义对等边三角形和直角三角形分别判断即可;(2)根据勾股定理和“方倍三角形”的定义求得直角三角形的三边长,即可求得直角三角形的面积;(3)根据题意可得△ABP≌△DBP,根据“方倍三角形”定义可得△ABD为等边三角形,从而证明△APD为等腰直角三角形,可得AP=DP2,延长BP交AD于点E,根据勾股定理求出BE的长,根据△PBC为等腰直角三角形,即可求得结论.(1)对于①等边三角形,三边相等,设边长为a,则2222a a a+=,根据“方倍三角形”定义可知:等边三角形一定是“方倍三角形”;对于②直角三角形,三边满足关系式:222+=a b c,根据“方倍三角形”定义可知:直角三角形不一定是“方倍三角形”;故选:A故答案为:A ;(2)设Rt △ABC 其余两条边为a ,b , 则满足223a b +=,根据“方倍三角形”定义,还满足:2232a b +=, 联立解得1a b =⎧⎪⎨=⎪⎩则Rt △ABC ;(3) 由题意可知:ABP DBP ≅, ∴,BA BD ABP DBP =∠=∠, 根据“方倍三角形”定义可知: 222222BA BD AD BA +==, ∴AD AB BD ==,∴△ABD 为等边三角形,60BAD ∠=, ∴30ABP DBP ∠=∠=, ∴90PBC ∠=,∵45CPB ∠=,∴18045135APB ∠=-=, ∴90DPC ∠=,∵2,1045ABC ACB ∠=∠=, ∴15BAC ∠=,∴45CAD ∠=,∴△APD 为等腰直角三角形,∴AP DP ==∴2AD =.延长BP 交AD 于点E ,如图,∵ABP PBD∠=∠,∴BE AD⊥,112PE AD AE===,∴22413BE AB AE=-=-=∴31PB BE PE=-=,∵45CPB PCB∠=∠=,∴△PBC为等腰直角三角形,∴31PC BC=.【点睛】本题考查了翻折变换、等边三角形的性质,解决本题的关键是掌握等边三角形的性质.。
《勾股定理的应用》--长方体表面上的最短路径问题教学设计

17.3.勾股定理的应用---长方体表面上最短路径问题一、学生知识状况分析本节将利用勾股定理解决立体图形表面上两顶点间最短距离问题,需要学生了解空间图形、对长方体进行展开实践操作活动.学生在学习七年级下正(长)方体展开图已经有了一定的认知上,已经基本具备解决本课题问题所需的知识基础和活动经验.二、教学任务分析本节是义务教育课程标准人教版教科书八年级(下)第十七章《勾股定理的应用》延伸的课题学习,具体内容是运用勾股定理解决长方体表面两顶点间最短路径问题.在这问题的解决过程中,需要经历立体图形转化为平面图形的过程,通过操作、观察、对比,培养学生的分析、归纳应用等能力;在探究活动具体一定的难度,在突破难点时需要具有学生敢于探索、勇于思考的精神,有助于锻炼学生独立思考,力闯难关的勇气.也通过转化思想、对比方法培养学生学习数学的基本素养。
三、教学设计:(一)教学目标:知识与技能:1、熟练运用勾股定理解决实际问题;2.通过立体图形转化为平面图形,能找出最短路线;过程与方法:1.强化转化思想和对比方法,培养学生分析、归纳、解决问题的能力;2.构建直角三角形模型,回归平面几何本源;情感态度与价值观:在教学过程中培养学生动手实践、观察、分析、归纳的习惯,体会知识的形成过程和获得知识的成就感;增强学生应用数学知识解决实际问题的经验,培养学生解决问题的能力,激发学生学习的兴趣和信心。
(二)教学重难点:1、教学重点:知识形成过程,并有效运用勾股定理解决实际问题。
2、教学难点:通过转化思想把立体图形转化为平面图形,构建直角三角形模型,并分情况讨论,得出结论的探究的过程。
(三)课前准备:课件、长方体盒子、线、两颗螺丝。
(四)教法、学法:引导---探究---归纳演示操作,引发思考,分类讨论,对比分析,达成结论。
(五)教学过程分析本节课设计了八个环节.第一环节:复习巩固;第二环节:问题呈现;第三环节:探索新知;第四环节:解决问题;第五环节:课堂练习;第六环节:课堂小结;第七环节:课后作业.第八环节:课后反思。
中考专题1——立体图形中的最短路径问题

中考复习专题1——立体几何中的最短路径问题姓名:(蚂蚁沿阶梯、正方体、长方体、圆柱、圆锥外侧面吃食问题)1、台阶问题如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?2、圆柱问题有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?变式1:有一圆柱形油罐,已知油罐底面圆周长是12m,高AB是5m,要从点A处开始绕油罐一周建造梯子,正好到达A点的正上方B处,问梯子最短有多长?变式2:桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖。
问小虫至少爬多少厘米才能到达蜜糖所在的位置。
ABABcABD C D 1C 1①421AC 1=√42+32=√25;②A B B 1CA 1C 1412AC 1=√62+12=√37;A B 1D 1D A 1C 1③412AC 1=√52+22=√29 .3、正方体问题 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B的最短距离是( ). (A )3 (B ) 5 (C )2 (D )14、长方体问题 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析:展开图如图所示,372925<<路线①即为所求。
小结:长、宽、高中,较短的两条边的和作为一条直角边,最长的边作为另一条直角边, 斜边长即为最短路线长。
5、圆锥问题 如图,已知O 为圆锥的顶点,MN 为圆锥底面的直径,一只蜗牛从M 点出发,绕圆锥侧面爬行到N 点时,所爬过的最短路线的痕迹(虚线)在侧面展开图中的位置是( ).A BABA’ABCABC211AB A 1B 1D CD 1C 124ACB D练习:1、现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm ,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
几何体表面的最短路线问题

体顶点A处有一个蚂蚁,现要向顶点B爬行,求最短
路线长.
B
7
侧面展 开图
左
B
3
3 A5
A7
5
AB2 (5 7)2 32 153
B 结论:
AB最短 b c 2 a 2 `
A
长:a, 宽:b, 高:c 且a > b > c > 0
第三项:爬柱子
比赛规则:在圆柱侧面从A走到B,所走路线最 短者获胜.
5
12
立体图形
转化 展开
平面图形
数学思想:转化思想
数学原理:两点之间线段最短
当堂检测:
1.如图,蚂蚁从台阶A处爬到B处它的最短距离是( B ).
A 20 B 25 C 30 D 35
2.如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只
蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短
2
如图,台阶的长、宽、高分别是30,2,8,求 从A到B所走的的最短距离是 50 .
第二项:翻方块
比赛规则:在方体表面从A走到B,所走路线最 短者获胜.
B
A
如图,方块是边长为1的正方体,求从A到B所走
的最短路线长是
。
第二项:翻方块
如图,方块是边长为1的正方体,求从A到B所走
的最短路线长是
。
B
B
B
答:最短距离是20厘米
路径长为 13
cm.
3.有一个长方体,它的长、宽、高分别为10cm,6cm,12cm.在
顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.已知蚂 蚁沿长方体表面爬行的速度是3cm/s,问蚂蚁能否在7秒内获取到食物? 并说明理由.
长方体中最短路线

E C D F A B
思维方法和过程
前面 后面
A点
左面 下面
右面 上面
B点
E C D F A B
思维方法和过程
前面 A 后面 A
A点
左面 B
右面 B 上面 B
B点
B 下面
E C D F A B
思维方法和过程
前面 A A点 左面 B 下面 C 后面 A 右面 B 上面 C B点
①前面和右面;②前面和上面;③左面和上面; ④左面和后面;⑤下面和右面;⑥下面和后面.
方法一
1、展开前面和右面 2、连接AC' 则AC'为最短路径 由勾股定理得 AC'= 前面 右面
2 2
C '
C'
5 1
26
A
方法二
1、展开前面和上面 2、连接AC' 则AB2为最短路径 由勾股定理得 AB2= 前面 上面
则AC'为最短路径
由勾股定理得 AC'=
A
4
2
2 2 5
2
C'
方法六
1、展开下面和后面
2、连接AC'
则AC'为最短路径 由勾股定理得 AC'= 3 3
2 2
A
3 2
C'
总结
从A到B共有六种最短路径 最短路径为 2 3
B
A
问题二
1.如图所示的长方体中,长BF=7cm, 宽AB=5cm,高AC=5cm,一只蚂蚁从点A沿着 长方体的外表面爬行到点E的最短路程为( )
从A到B走最短路径要走几个面?
①前面和右面;②前面和上面;③左面和上面; ④左面和后面;⑤下面和右面;⑥下面和后面.
立体图形上最短距离问题

立体图形上最短距离问题金水初中刘彬在北师大版数学的七年级和八年级的教材中都涉及到了物体在几何体表面爬行时的最短距离问题,这对于一些刚刚接触几何体的同学是个很难理解的问题。
实际在数学上就是在几何体表面点到点的最短距离的问题。
结合教学实际,我总结了教材和练习中最常见的几种最短距离问题,主要涉及到了正方体、长方体和圆柱,以及它们几种简单的变形,特总结如下,希望能对这方面的问题,帮助解决学生的困惑,能使学生掌握这方面的知识.同一个面最短距离最简单,主要是连线,借助勾股定理来解决,在下面的介绍简单介绍,重点说不在同一个面的问题。
这几个几何体中正方体最简单,下面先从正方体开始说起.一、正方体和长方体中最短距离例1、如图,一只蚂蚁在正方体表面爬行(1)、当蚂蚁从正方体的一个顶点A Array爬到顶点B,怎样爬距离最短?分析:由于顶点A和顶点B在同一个平面上,所以连接,利用勾股定理直接求解即可。
(2)如图,如果蚂蚁要从边长为1 cm的正方体顶点A爬到顶点C分析:由于顶点A和顶点C不在同一个平面上,所以要求最短距离需要将正方体展开,在展开的表面上利用勾股定理求出最短距离. 解:将正方体展开,下面是其四连面的一部分,这是A与C的位置如图所示,这时AC的长度就是长方形的对角线的长度。
所以 AC的长所以在正方体中求最短距离相对来说还是比较简单的。
(3)如果将正方体换成边长AD=2CM,宽DF=3cm,高AB=1cm的长方体,蚂蚁仍需从顶点A沿表面爬到顶点E的位置,请你说明这只蚂蚁沿怎样的路线爬行距离最短?为什么?分析:由于长方体每边的长短不一样,所以在展开图中就有三种不同的形式,三种情况下结果就会不一样解:方案一:将面ABCD沿DC展开和面CDEF在同一个平面中,如图,这时BE的长度为2+3=5,EF的长度为1,所以AE==方案二:将面ADCF沿DF展开和面CDEF在同一个平面,如图,这时AC=2+1=3,EF=3所以AE=BABA方案三:将面ADFG 沿FG 展开 和面EFGH 在同一个平面中,如图,这时DE=3+1=4,EH=2。
08 立体图形上的最短路径问题
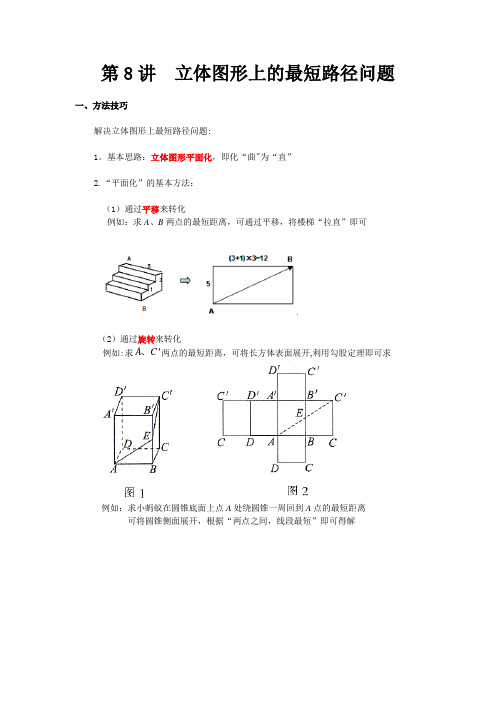
第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1。
基本思路:立体图形平面化,即化“曲"为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4。
解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,2251213AB cm =+=所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C'处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC'(在面ADD'A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与BB’C’C 相连,连接AC’,使E 点在AC'上(如图2))(412810')('2222cm CC BC AB AC =+=++=所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体表面,怎样爬最短
重庆市广益中学 秦大忠
八年级(上)北师大版初中数学实验教材第一章第三节研究了蚂蚁在圆柱表面爬行路程最短的问题。
研究中既用到了初一的展开与折叠、两点之间线段最短,又用到了刚学到的勾股定理。
若蚂蚁在长方体表面爬行,结果又会怎样呢?看完下面三组同学的解答,再仔细想一想,聪明的你肯定会明白的。
问题 如右图,有一块长方体ABCD-EFGH 石料,
其长AB=5dm ,宽BC=4dm ,高AE=3dm ,在地面上
H 处有一只蚂蚁,长方体的顶点B 处有一只受伤的小
昆虫,蚂蚁想在最短的时间内捕捉住小昆虫,需要爬
行的最短路程是多少?
甲组同学的解答是:
解:如右图,将长方体的面BCGF 沿CG 展开,
则点B 至点B1的位置,在矩形DB1F1H 中,HB1的
长就是爬行的最短路程。
由勾股定理得: 221111F B HF HB +=
=2
211)1(F B GF HG ++
=2
23)45(++
=310 (蚂蚁爬行的实际路线是折线HB ) 乙组同学的解答是:
解:如右图,将长方体的面DCGH 沿DC 展开, 则点B 至点B1的位置,在矩形HGB1A1中,HB1的 长就是爬行的最短路程。
由勾股定理得:
2211GB HG HB +=
=2
2
)1(CB GC HG ++
=2
2)43(5++
=74 (蚂蚁爬行的实际路线是折线HB )
丙组同学的解答是:
解:如右图,将长方体的面ABDC 沿AD 展开, 则点B 至点B1的位置,在矩形HEB1C1中,HB1的 长就是爬行的最短路程。
由勾股定理得:
2
211EB HE HB +=
B1
F1
=2
2)1(EB EA HE ++
=2
2)35(4++
=54 (蚂蚁爬行的实际路线是折线HB )
看了以上三组同学的解答,是不是都有道理?之前你做这类题时有没有类似的经历。
但事实:908074 告诉我们,74才是最小的,所代表的距离才最短;这个解答是沿长方体的最长边展开的。
一般地,长方体ABCD-EFGH 的长CD=a , 宽BC=b ,高DH=c ,且c <b <a ,则从H 到B 的 最短路程的计算应沿CD (或AB )展开。
H B =2
211GB HG HB +=
=2
2)1(CB GC HG ++
=2
2)(c b a ++
聪明的同学,你现在明白了吗?
特别地,当长方体变为棱长为a 的正方体时,其他条件不变,其最短路程为:
a a a a 5)(22=++。
