第一学期初三数学期中考试题102810(附答案)
九年级第一学期期中考试数学试卷(含参考答案)

九年级第一学期期中考试数学试卷(含参考答案)学校:___________班级:___________姓名:___________考号:___________一、选择题:本大题共10小题,每小题3分,共30分.1.在下列方程中是一元二次方程的是()A.x2-2x y+y2=0B. x2-2x=3C. x(x +3)= x2-1D. x + =02.将二次函数y= x2的图象向右平移2个单位,再向上平移1个单位,所得图象的表达式是()A.y=(x- 2)2+1B.y= (x +2)2+1C. (x- 2)2-1D.y= (x +2)2- 13.一元二次方程x2-2x +5=0的根的情况是()A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.无法判断4.对于二次函数y= - (x- 2)2-3,下列说法正确的是()B A.当x >0时,y随x的增大而增大 B.当x =2时,y有最大值- 3C.图象的顶点坐标为(-2,-7)D.图象与x轴有两个交点5.用配方法解方程x2- 6x- 3=0时,原方程应变形为()A. (x +3)2=3B. (x +3)2=12C. (x- 3)2=3D. (x- 3)2=126.已知函数y=(x- 1)2+2,当函数值y随x的增大而减小时,x的取值范围是()A x <1 B. x >1 C. x >-2 D. - 2< x <47.若x1,x2是一元二次方程2x2- 9x +4=0的两根,则x1+ x2的值是()A. - 2B.2C.D. - 28.二次函数y=ax2+b x+c(a≠0)的图像如图所示,则函数值y>0时,x的取值范围是()A. x <-1B. x >3C. -1< x <3D. x <-1 或x >3第8题图第10题图9.某经济开发区,今年一月份工业产值达50亿元,第一季度总产值为175 亿元,二月、三月平均增长率是多少?若设平均每月的增长率为x,根据题意,可列方程为()A.50(1+x)2=175B.50+50(1+x)+50(1+x)2=175C.50 (1+x) +50(1+x)2= 175D.50+50(1+x)2=17510.已知二次函数y=ax2+b x+c(a≠0)的图像如图所示,对称轴为直线x=2.则下列结论中正确的是()A a bc>0 B.4a-b=0 C.9a+3b+c<0 D.5a+c>0二、填空题:本大题共5小题,每小题3分,共15分.11.方程x2= x的解是____________12.当k______时,y=( k +3)x2- k x+2是关于x的二次函数.13.抛物线y=2(x +1)2-3,的顶点坐标为________,对称轴为直线______14.已知x=1是方程x2+ax-b=0的一个根,则a-b+2023=_____15如图,一段抛物线:y=-x(x -2)(0≤x≤2),记为C1,它与x轴交于点O,A1;将C绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C6,若P(11,m)在第6段抛物线C6上,则m的值为=____三、解答题(一):本大题共3小题,第16 题10分,第17、18题7分,共24分.16.计算:用适当方法解方程:(1)(x +1)2=5x+5 (2)x2- 4x- 5=017.某次聚会上,同学们互相送照片,每人给每个同学一张照片,一共送出90张照片,问一共有多少位同学参加了聚会?18.已知抛物线y= x2- 2x- 3.(1)求抛物线与两坐标轴的交点坐标(2)求它的顶点坐标。
九年级上册数学期中试卷【含答案】

九年级上册数学期中试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()A. a/2B. a√2C. 2aD. a√32. 下列哪个数是无理数?()A. √9B. √16C. √3D. √13. 下列哪个数是实数?()A. √-1B. 3/0C. ∞D. -54. 一次函数y=2x+3的图像是一条()A. 水平线B. 垂直线C. 斜线D. 曲线5. 二元一次方程组x+y=5, x-y=3的解为()A. x=4, y=1B. x=2, y=3C. x=3, y=2D. x=1, y=4二、判断题(每题1分,共5分)1. 任何两个有理数的和仍然是有理数。
()2. 任何两个实数的积一定是实数。
()3. 一元二次方程的解一定是实数。
()4. 一次函数的图像一定是一条直线。
()5. 二元一次方程组一定有解。
()三、填空题(每题1分,共5分)1. 若a+b=5, a-b=1,则a=_____, b=_____.2. 若x²-5x+6=0,则x=_____, x=_____.3. 一次函数y=kx+b的图像是一条_____.4. 二元一次方程组的解法有_____, _____.5. 实数包括_____, _____, _____.四、简答题(每题2分,共10分)1. 解释什么是有理数。
2. 解释什么是无理数。
3. 解释什么是实数。
4. 解释一次函数的图像是一条直线的原因。
5. 解释二元一次方程组有解的条件。
五、应用题(每题2分,共10分)1. 已知一个正方形的边长为a,求它的面积。
2. 已知一个长方形的长为a,宽为b,求它的面积。
3. 已知一次函数y=kx+b的图像过点(1, 3),(2, 5),求k和b的值。
4. 已知二元一次方程组x+y=5, x-y=3,求x和y的值。
5. 已知一元二次方程x²-5x+6=0,求它的解。
六、分析题(每题5分,共10分)1. 分析什么情况下两个有理数的和是无理数。
九年级(上)期中(全册)考试数学试题(含答案)
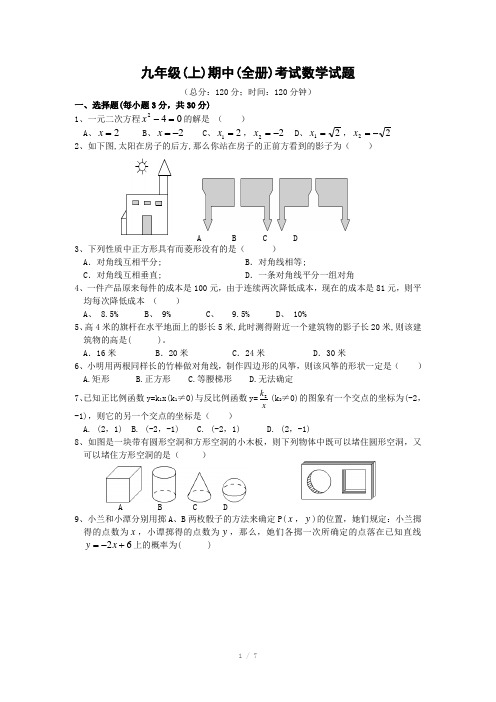
九年级(上)期中(全册)考试数学试题(总分:120分;时间:120分钟)一、选择题(每小题3分,共30分)1、一元二次方程042=-x 的解是 ( )A 、2=xB 、2-=xC 、21=x ,22-=xD 、21=x ,22-=x2、如下图,太阳在房子的后方,那么你站在房子的正前方看到的影子为( )A B C D3、下列性质中正方形具有而菱形没有的是( )A .对角线互相平分;B .对角线相等;C .对角线互相垂直;D .一条对角线平分一组对角4、一件产品原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本 ( )A 、 8.5%B 、 9%C 、 9.5%D 、 10%5、高4米的旗杆在水平地面上的影长5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是( )。
A .16米B .20米C .24米D .30米6、小明用两根同样长的竹棒做对角线,制作四边形的风筝,则该风筝的形状一定是( )A.矩形B.正方形C.等腰梯形D.无法确定7、已知正比例函数y=k 1x(k 1≠0)与反比例函数y=2k x (k 2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )A. (2,1)B. (-2,-1)C. (-2,1)D. (2,-1)8、如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )A B C D9、小兰和小潭分别用掷A 、B 两枚骰子的方法来确定P(x ,y )的位置,她们规定:小兰掷得的点数为x ,小谭掷得的点数为y ,那么,她们各掷一次所确定的点落在已知直线62+-=x y 上的概率为( )A 、366B 、181C 、121D 、91 10、在同一直角坐标系中,函数y=kx-k 与k y x =(k ≠0)的图象大致是( )二、填空题(每题4分,共24分)11、若反比例函数x k y =的图象经过点(2-,3),则xk y =的图象在 象限。
期中试卷数学九年级上册【含答案】

期中试卷数学九年级上册【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = x² 4x + 3,则f(2)的值为:A. 0B. 1C. -1D. 22. 下列函数中,奇函数是:A. f(x) = x³B. f(x) = x²C. f(x) = |x|D. f(x) = x² + 13. 若直线y = 2x + 3与x轴相交,则交点的坐标是:A. (0, 3)B. (-3/2, 0)C. (3/2, 0)D. (3, 0)4. 下列哪个图形不是正比例函数的图像?A. 直线通过原点,斜率为正B. 直线通过原点,斜率为负C. 抛物线D. 直线不通过原点5. 若一组数据的平均数为10,且其中5个数为6,剩余5个数的平均数为12,则这组数据的总数为:A. 60B. 70C. 80D. 90二、判断题(每题1分,共5分)6. 任何两个奇函数的乘积一定是偶函数。
()7. 一次函数的图像一定是直线。
()8. 二次函数的图像一定是抛物线。
()9. 若一组数据的方差为0,则这组数据中的所有数都相等。
()10. 两条平行线的斜率一定相等。
()三、填空题(每题1分,共5分)11. 若函数f(x) = x² 4x + 4,则f(x)的最小值为______。
12. 一次函数y = 2x 3与y轴的交点坐标为______。
13. 若一组数据的平均数为10,标准差为2,则这组数据的方差为______。
14. 若直线y = 3x + 2与x轴相交,则交点的坐标为______。
15. 二次函数y = x² 4x + 3的顶点坐标为______。
四、简答题(每题2分,共10分)16. 解释什么是正比例函数。
17. 什么是二次函数的顶点?18. 简述一次函数图像的性质。
19. 解释什么是数据的平均数。
20. 什么是直线的斜率?五、应用题(每题2分,共10分)21. 某商店进行打折活动,原价为x元的商品打8折后售价为0.8x元。
九年级上册数学期中考试试卷【含答案】

九年级上册数学期中考试试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()A. a/2B. a√2C. 2aD. a√32. 下列哪个是无理数?()A. √9B. √16C. √3D. √13. 下列哪个数是虚数?()A. 3B. -5C. √-1D. 04. 二项式展开式(x+y)^3的项数为()A. 2B. 3C. 4D. 55. 下列哪个图形不是中心对称图形?()A. 正方形B. 矩形C. 圆D. 正三角形二、判断题(每题1分,共5分)6. 任何两个奇数之和都是偶数。
()7. 一元二次方程的解可以是两个相同的实数根。
()8. 函数y=2x+3的图像是一条直线。
()9. 所有的正方形都是矩形。
()10. 对角线互相垂直的四边形一定是菱形。
()三、填空题(每题1分,共5分)11. 若a、b是不为0的实数,且a+b=0,则a和b的关系是_________。
12. 一个等差数列的第5项是10,第10项是20,则这个数列的公差是_________。
13. 若一个圆的半径为r,则它的直径是_________。
14. 二项式展开式(x+y)^4中x^2y^2的系数是_________。
15. 一个正六边形的内角和是_________度。
四、简答题(每题2分,共10分)16. 简述一元二次方程的求解公式。
17. 什么是等差数列?给出一个等差数列的例子。
18. 什么是相似三角形?相似三角形的性质有哪些?19. 什么是中心对称图形?给出一个中心对称图形的例子。
20. 什么是概率?如何计算一个事件的概率?五、应用题(每题2分,共10分)21. 一个长方形的长是10cm,宽是5cm,求它的面积和周长。
22. 解方程:2x-5=3x+4。
23. 一个等差数列的第1项是3,公差是2,求第10项。
24. 一个圆的半径是7cm,求它的周长和面积。
25. 抛掷一个正方体,求得到一个偶数面的概率。
初三数学上册期中考试卷及答案

初三数学上学期期中试卷附参考答案 (答题时间:100分钟,满分:120分)一、选择题:(每题4分,共32分)1.计算()23-的结果是 ( )A.3B.3-C.3±D.9 2.下列各式中与2是同类二次根式的是 ( ) A. 12 B. 24 C. 32 D. 233.下列运算中正确的是 ( )A .523=+B .82)8()2(-⨯-=-⨯-C .322944=D =4.一元二次方程0422=-+x x 的根的情况是 ( )A .有两个相等的实数根B .有两个不相等的实数根C .只有一个相等的实数根D .没有实数根 5.用配方法解一元二次方程0782=++x x ,则方程可变形为 ( )A .9)4(2=-xB .57)8(2=+xC .16)8(2=-xD .9)4(2=+x 6.在某次同学聚会上,每两人都互赠了一件礼物,所有人共送了210份礼物,设 有x 人参加这次聚会,则列出方程正确的是 ( )A.210)1(=-x xB.2102)1(=-x x C. 210)1(=+x x D.2102)1(=+x x7的结果是 ( )A .B .10C ..20 8.已知a 为实数,下列式子一定有意义的是 ( )A 二、填空题:(每题3分,共24分)9.2-x 在实数范围内有意义,则x 的取值范围是.10.一元二次方程0132=--x x 的解是 .11.等腰三角形两边的长分别为方程02092=+-x x 的两根,则三角形的周长是.12. 关于x 的一元二次方程04)2(22=-+-+m mx x m 有一根为0,则m= .13.实数a 在数轴上的位置如图所示,化简|1|a -= .14.a 是实数,且a -4+︱a 2-2a -8︱=0,则a 的值是__________. 15. 把a ab (b >0)中根号外的因式移入根号内得__________. 16. 要使式子x3-x 有意义,则x 的取值范围是__________.三、解答题:(共64分) 17.计算:(每题5分,共10分)(1)()22832264÷+- (2)253230÷⨯18.(本题6分)已知关于x 的方程0102=-+kx x 的一个解与分式方程5252=-+x x 的解相等. (1)求k 的值; (2)求方程0102=-+kx x 的另一个解.19.(本题6分)先化简,再求值:)2(24422x x x x x +÷+++,其中3=x20.(本题6分)已知a 、b 、c 在数轴上的位置如图所示,化简:a 2-︱a +b ︱+(c -a )2+(b +c )2.21.(本题7分)大众电影院为吸引学生观看电影,推出如下的收费标准:-112a 第13题江南中学组织初三学生观看电影,共支付给电影院3750元,请问共组织了多少学生观看电影?22.(9分)已知33x y =+=-22x y xy +的值.23.(10分)用适当方法解下列方程:(1)(2-3x )(x +4)=(3x -2)(1-5x ); (2)14x 2+52x -6=0.24.(10分)先化简,再求值:x 2(3-x )+x (x 2-2x )+1,其中x = 3一、选择题:(每题3分,共24分)1.A 2.C 3.D 4.B 5.D 6.A 7. 8. 二、填空题:(每题2分,共16分) 9.2≥x 10.2133,213321-=+=x x 11.13或14 12.2 13.1 14.22- 15.40° 16.2三、解答题:(共60分)17.(1)()22832264÷+- =232+化简83正确得1分,832264+-计算正确得2分,得出正确答案得2分,共5分 (2)253230÷⨯=22 乘法计算正确得2分,除法计算正确得2分,得出正确答案得1分,共5分18.(1)k= -3 计算出x=5得2分,计算出k=-3得2分,共4分. (2)另一个解为 -2 计算正确得2分. 19. )2(24422x x x x x +÷+++=xx x x x 1)2(12)2(2=+⋅++当3=x 时,原式=33。
九年级上学期数学期中考试卷及答案精选全文

可编辑修改精选全文完整版第一学期期中考试九年级数学试题1. 计算()23-的结果是()A.3B.3- C.3±2. 若P(x;-3)与点Q(4;y)关于原点对称;则x+y=()A、7B、-7C、1D、-13. 下列二次根式是最简二次根式的是()4. 一元二次方程22350xx++=的根的情况是( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法判断5. 用配方法解方程0142=++xx;则配方正确的是()A、3)2(2=+x B、5)2(2-=+xC、3)2(2-=+x D、3)4(2=+x6. 如图;AB、AC都是圆O的弦;OM⊥AB;ON⊥AC;垂足分别为M、N;如果MN=3;那么BC=(). A. 4 B.5 C. 6 D.7二、填空题(共8小题;每小题3分;满分24分)7. 2-x在实数范围内有意义;则x的取值范围是.8. 221x-=的二次项系数是 ;一次项系数是 ;常数项是 .9. 一只蚂蚁沿图中所示的折线由A点爬到了C点;则蚂蚁一共爬行了______cm.(图中小方格边长代表1cm)NMOCBA10. 关于x 的一元二次方程04)2(22=-+-+m mx x m 有一根为0;则m= . 11. 对于任意不相等的两个数a;b;定义一种运算*如下:ba b a b a -+=*;如523232*3=-+=;那么)5(*3-= .12. 有4个命题:①直径相等的两个圆是等圆;②长度相等的两条弧是等弧;③圆中最大的弦是通过圆心的弦;④在同圆或等圆中;相等的两条弦所对的弧是等弧;其中真命题是_________。
13. 有两个完全重合的矩形;将其中一个始终保持不动;另一个矩形绕其对称中心O 按逆时针方向进行旋转;每次均旋转22.5︒;第.2.次.旋转后得到图①;第.4.次.旋转后得到图②…;则第20次旋转后得到的图形与图①~图④中相同的是____. (填写序号)14. 等腰三角形两边的长分别为方程02092=+-x x 的两根;则三角形的周长是 .三、解答题(共4小题;每小题6分;共24分) 15. 解方程:x(x-2)+x-2=016. 计算:0)15(282218-+--图① 图② 图③ 图④ OOOO17. 下面两个网格图均是4×4正方形网格;请分别在两个网格图中选取两个白色的单位正方形并涂黑;使整个网格图满足下列要求. 18. 如图;大正方形的边长515+;小正为方形的边长为515-;求图中的阴影部分的面积.四、(本大题共2小题;每小题8分;共16分)19. 数学课上;小军把一个菱形通过旋转且每次旋转120°后得到甲的图案。
九年级第一学期期中数学测试卷参考答案

第一学期九年级数学期中卷答案与评分标准(满分150分,考试时间100分钟)一 、选择题:(本大题共8题,满分24分)1.C ; 2.B ; 3.C ; 4.A ; 5.C ; 6.D ;二、填空题:(本大题共12题,满分48分)7.4; 8.203; 9.AD BC =; 10.52; 11.5a b -+ ; 12.133 ; 13.5e -; 14.65°、115°; 15.12 ; 16.53; 17.5.1; 18.12-; 三.(本大题共7题,满分78分)19. (本题满分10分)解:原式=222-+ -------------------------------------------(8分) =11323-+ ---------------------------------------(1分) =136-----------------------------(1分) 20.(本题满分10分)解:(1) ∵ AD ⊥BC ,BE ⊥AC ,∴ ∠BDF=∠ADC=∠BEC=90°-----------------------(2分)∴ ∠C+∠DBF=90°,∠C+∠DAC=90°∴ ∠DBF=∠DAC , ------------------------------(2分)∴ △ACD ∽ △BFD ------------------------------(1分)(2) ∵ tan ∠ABD=1,∠ADB=90°∴1AD BD = ,即AD=BD------------------------------(2分)∵ △ACD ∽ △BFD,∴ 1AC AD BF BD == ------------------------------(2分)∴ BF=AC=3 ------------------------------(1分)21. (本题满分10分)解:(1)b a AC +=------------------------------(2分) 2233CE a b =--------------------------------(2分) 12FB a b =-----------------------------(2分) (2)画图正确3分,结论1分22.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)证明:(1)ABC ∆、ADC ∆---------------------(4分)(2) ∵∠ACD =∠B ∠A=∠A ∴△ACD ∽ △ABC ---------------------(1分) ∴2()S ADC DC S ABC BC∆=∆ ---------------------(2分) ∴1849S ABC S ABC ∆-=∆---------------------(2分) ∴1625S ABC ∆=--------(1分)23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)(1)证明:∵∠AFD =∠BEC ∴∠AFB =∠AEC-----------------(2分)∵DA=DB ∴∠ABF =∠EAC-----------------(2分)∴ABF ∆ ≌AEC ∆ ∴AF =CE----------------(2分)(2)∵∠AFB =∠AEC ,∠BAF =∠EAF ∴AEF ∆ ∽ ABF ∆-----------(2分) ∴BF AF EF AE= ------------------------(1分) ∵ABF ∆ ≌AEC ∆ ,BF =AE------------------------(1分)∴BF AFEF BF=,即AFEFBF⋅=2---------------------------(2分)24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(,3)小题满分4分) 证明:(1)设y kx b=+ ----------------------(1分)把A(0 ,6)、 B(8 ,0)代入解析式,得34k=-,6b= ------(2分)∴364y x=-+ ----------------------(1分)(2)延长BE交y轴于点G∵AE是∠BAO的平分线, BE⊥AE∴∠BAE =∠OAE,∠AEB =∠AEG=90°,AE=AE∴ABE∆≌AGE∆-----------------------------------(1分)∴点E是BG的中点----------------------------(1分)又∵EM⊥x轴,即EM∥y轴∴12BM BEOB BG== ------------------------------(2分)即M为OB的中点其它方法酌情给分(3)∵AG=AB=10 ∴OG=4 , ME=2 ,OM=4 ∴E(4,-2)--------------(1分)当EN∥MB 得N(323,-2)--------------(1分)当MN∥EB 得N(325,65)--------------(2分)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 证明:(1)∵将∆ABC折叠,恰使点A落在边BC上点D处,∴∠A=∠EDF又∵∠B=∠A=∠EDF,且∠B+∠BED=∠EDF+∠FDC ∴∠BED=∠FDC----------(2分)∵∠B=∠C,∠BED=∠FDC,∴△BDE∽△CFD--------------------(2分)(2)∵△BDE∽△CFD∴BDE CFD C BE C DC∆∆= ------------------------------------------(2分) ∵∆ABC 沿EF 折叠,使点A 落在边BC 上点D 处∴AE=ED ,AF=FD∴1BDE C BE ED BD BA BD x ∆=++=+=+2CFD C DF FC CD AC CD x ∆=++=+=----------------------(2分) ∴212x y x-=- ,(01x << )--------------------------------(2分) 其它方法酌情给分(3)当∠BED=90° ,2x y =∴1BD =- ---------------(2分)当∠BDE=90° ,2y x =∴2BD =----------------(2分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1第一学期初三数学期中考试题卷一、选择题:(每小题4分,共32分)1、下列图形中,是中心对称图形的是( )2、下列等式成立的是( ) A .9494+=+ B .3327= C . 3333=+ D .4)4(2-=-3、下列各式中是一元二次方程的是( ) A .x x 112=+ B .1)1)(1(2+=--+x x x x C .1322-+x x D .1212=+x x 4、下列二次根式中属于最简二次根式的是( ) A .44+a B .48 C .14 D .ba5x 的取值范围是( ) A.x ≥﹣25 B.x ≤25 C. x ≥25 D. x ≤- 256、关于关于x 的一元二次方程220x x +-=的根的情况是( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .无实数根 D .无法判断7、三角形两边的长分别是8和6,第三边的长是方程x ²-12x +20=0的一个实数根,则三角形的周长是( )A . 24B . 26或16C . 26D . 168、某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为x ,则可列方程为( )A 、225(1)64x +=B 、225(1)64x -=C 、264(1)25x +=D 、264(1)25x -=二、填空题(每小题4分,共20分)9、若点A (a –2,3)与点B (4,–3)关于原点对称,则a= 。
10、已知x =‐1是方程x 2-ax +6=0的一个根,则a =____________。
11.若2<x<3,化简x x -+-3)2(2的正确结果是 _。
12.如图(11),△ABC 绕点A 旋转后到达△ADE 处,若∠BAC =120°,∠BAD =30°,则∠DAE =__________,∠CAE =__________。
a ※b =ba ba -+,如3※2=52323=-+.那么12※4= 。
三、解答题:(每小题7分,共35分) 14、.计算:101()(2π--++︱-6︱15、计算:482)681(26--16、解方程:2450x x +-=17、解方程:(23)46x x x +=+18、已知a 、b 、c 满足054)3(2=-+-+-c b aA B DC2求:(1)a 、b 、c 的值;(2)试问以a 、b 、c 为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.四、解答题(每小题9分,共27分)19、.当m 为何值时,一元二次方程222(41)210x m x m -++-=。
① 有两个不相等的实数根?② 有两个相等的实数根? ③ 没有实数根?20、如图14,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,ABC △的顶点均在格点上,点C 的坐标为(41)-,.①把ABC △向上平移5个单位后得到对应的111A B C △,画出111A B C △,并写出1C 的坐标; ②以原点O 为对称中心,再画出与111A B C △关于原点O 对称的222A B C △,并写出点2C 的坐标.21、如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?五、解答题(每小题12分,共36分)22、已知关于x 的方程012)14(2=-+++k x k x 。
(1)求证此方程一定有两个不相等的实数根。
(2)设1x 、2x 是方程的两个实数根,且(1x -2)(2x -2)=23-k ,求k 的值。
23、某百货大楼服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元。
为了迎接“十·一”国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。
经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件。
要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少?24、(一位同学拿了两块45三角尺MNK △,ACB △做了一个探究活动:将MNK △ 的直角顶点M 放在ABC △的斜边AB 的中点处,设4AC BC ==.B图(1)N图(2)N图(3)第24题图△,则重叠部分的面积为,周长(1)如图(1),两三角尺的重叠部分为ACM为.△绕顶点M逆时针旋转45,得到图26(2),此时重叠部分的面(2)将图(1)中的MNK积为,周长为.△绕M旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此(3)如果将MNK时重叠部分的面积为.AD ,求出重叠部分图形的周长.(4)在图(3)情况下,若13班级__________________ 姓名_________________ 考号________________17.解:Array 18、解四、解答题(本大题共3小题,每小题9分, 共27分)19.解:20.解:24、(1)如图(1),两三角尺的重叠部分为ACM △,则重叠部分的面积为 ,周长为 .(2)将图(1)中的MNK △绕顶点M 逆时针旋转45,得到图(2),此时重叠部分的面积为 ,周长为 .(3)如果将MNK △绕M 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 .(4)在图(3)情况下,若1AD ,求出重叠部分图形的周长.B图(1)N 图(2)N图(3)第24题图第一学期初三数学期中考答题卷第一题:选择题(请把你认为正确的选项填到对应的空格里,每题只有一个正确答案)第二题:填空题(本题包括5小题,每小题4分,共20分,请把你认为正确的答案填到对应的空格里)9.-2 10. -7 11. 1 12. 1200 300 13.12三、解答题(本题包括5小题,每小题7分,共35分)14.解:原式=-2+1+2-6=-5 15.解: 原式=6×1216.解:(x +5)(x-1)=0 ∴x +5=0或x-1=0 ∴x 1=-5,x 2=117.解:x(2x+3)-2(2x+3)=0 ∴(2x+3)(x-2)=0 ∴2x +3=0或x-2=0 ∴x 1=-32,x 2=2 18、解:(1) 054)3(2=-+-+-c b a又(a-3)2≥0≥,5c -0≥∴a-3=0,b-4=0,c-5=0.∴a=3,b=4,c=5.(2)能构成三角形,它的周长l=3+4+5=12四、解答题(本大题共3小题,每小题9分, 共27分)19.解:a=2,b=-(4m+1),c=2m2-1∴∆=b2-4ac=()41m-+⎡⎤⎣⎦2-4×2×(2m2-1)=8m+9∴当8m+90,即m>98-时,原方程有两个不相等的实数根;∴当8m+9=0,即m=98-时,原方程有两个相等的实数根;∴当8m+9<0,即m<98-时,原方程没有实数根。
20.解:(1)点C1 的坐标是(4,4),图略。
(2)、点C2 的坐标是(—4,—4),图略。
21、解:设小路的宽为x米,依题意得:(32-2x)(15-x)=78×15×32整理,得x2-31x+30=0解得x1=1,x2=30(不合题意,舍去)答:小路的宽为1米。
五、解答题(本大题共3小题,每小题12分,共36分)22、(1)证明:a=1,b=4k+1,c=2k-1∴=b2-4ac=(4k+1)2-4×1×(2k-1)=16k2+5k2≥0, ∴16k2+5>0, 即>0,∴原方程一定有两个不相等的实数根。
(2)解:依题意得1212(41),21x x k x x k+=-+=-又(1x-2)(2x-2)=23-k,∴12122(423x x x x k -++=-)即 212[(41)]42k k k --⨯-++=-解得k =—123、解:设每件童装应降价x 元,依题意得: (40(208)12004xx -+⨯=) 整理得:212302000,10,20x x x x -+===解得因为商家为了扩大销售量,增加盈利,尽快减少库存,所以10x =不符合题意舍去。
答:每件童装应降价20元。
24、(1)如图(1),两三角尺的重叠部分为ACM △,则重叠部分的面积为 4 ,周长为.(2)将图(1)中的MNK △绕顶点M 逆时针旋转45,得到图(2),此时重叠部分的面积为 4 ,周长为 8 .(3)如果将MNK △绕M 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 4 .(4)在图(3)情况下,若1AD =,求出重叠部分图形的周长.B图(1)N图(2) N图(3)第24题图。
