空间几何体(超级完美版)
(完整版)高中数学空间几何体知识点总结

空间几何体知识点总结一、空间几何体的结构特征1.柱、锥、台、球的结构特征由若干个平面多边形围成的几何体称之为多面体。
围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体称之为旋转体,其中定直线称为旋转体的轴。
(1)柱棱柱:一般的,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱;棱柱中两个互相平行的面叫做棱柱的底面,简称为底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点。
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……注:相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:棱柱的性质:①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形;③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
圆柱:以矩形的一边所在的直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱;旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形。
棱柱与圆柱统称为柱体;(2)锥棱锥:一般的有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥;这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱。
底面是三角锥、四边锥、五边锥……的棱柱分别叫做三棱锥、四棱锥、五棱锥……正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。
注:棱锥的性质:①平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;②正棱锥各侧棱相等,各侧面是全等的等腰三角形;③正棱锥中六个元素,即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边长一半,构成四个直角三角形。
(完整版)空间几何体练习题含答案
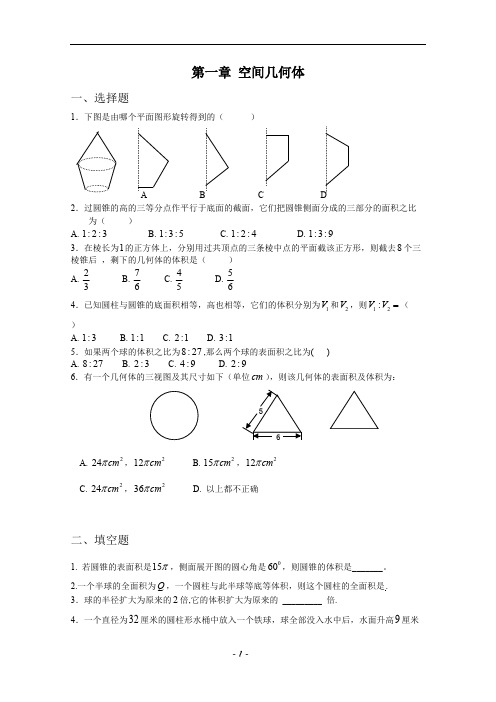
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
空间立体几何【完整版】

·
L
异面直线: 不同在任何一个平面内,没有公共点。 2 公理 4:平行于同一条直线的两条直线互相平行。 符号表示为:设 a、b、c 是三条直线 a∥ b c∥ b =>a∥c
强调:公理 4 实质上是说平行具有传递性,在平面、空间这个性质都适用。 公理 4 作用:判断空间两条直线平行的依据。 3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 4 注意点: ① a'与 b'所成的角的大小只由 a、b 的相互位置来确定,与 O 的选择无关,为简便,点 O 一般取在两直线中的一条上; (0, ② 两条异面直线所成的角θ∈
A
α
L
A
B
B∈α 公理 1 作用:判断直线是否在平面内 (2)公理 2:过不在一条直线上的三点,有且只有一个平面。 符号表示为:A、B、C 三点不共线 => 有且只有一个平面α, 使 A∈α、B∈α、C∈α。
A B
α·
·
C
·
公理 2 作用:确定一个平面的依据。 (3)公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共 直线。 符号表示为:P∈α∩β =>α∩β=L,且 P∈L 公理 3 作用:判定两个平面是否相交的依据 2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系: 共面直线 相交直线:同一平面内,有且只有一个公共点; 平行直线:同一平面内,没有公共点; β α
2 2
3 圆锥的表面积 S rl r 5 球的表面积 S 4R
2
2
(二)空间几何体的体积 1 柱体的体积 3 台体的体积
V S底 h
2 锥体的体积
V
1 S底 h 3
高中数学必修2《空间几何体》共25页文档

•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
ห้องสมุดไป่ตู้
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
空间几何体的结构课件(共46张PPT)

S
C
B
D
A
四棱锥:S-ABCD
P
Q C
B
D
A
×
其他的三棱锥底面的平面去截棱锥,底面与 截面之间的部分是棱台.
下底面和上底面:原棱锥的底面和截面
分别叫做棱台的下底面和上底面。
侧面:原棱锥的侧面也叫做棱台的侧面
(截后剩余部分)。 侧棱:原棱锥的侧棱也叫棱台的侧棱
形 状 与 大 小
空间几何体 如果我们只考虑物体的形状和大小,而不考虑其它因素, 那么由这些物体抽象出来的空间图形就叫做空间几何体。
你能把这些几何体 分成两类么?
多面体: 若干个平面多边形围成的几何体
面----围成多面体的各个多边形 棱----相邻两个面的公共边 顶点-----棱与棱的公共点
(截后剩余部分)。
D’
D A’
顶点:上底面和侧面,下底面和侧面
的公共点叫做棱台的顶点。
侧棱 A
上
顶点
底
C’ 面
B’
侧C面
下底面
B
棱台的表示:用表示底面的各顶点的
字母表示。 如:棱台ABCD-
A底’面B是’C三’角D形’,四边形,五边形----的棱台分
别叫三棱台,四棱台,五棱台---
练习:下列几何体是不是棱台,为什么?
B1
C1
B1
C1
A1
B1 A
BC
A1
D1
A
B
A
D
5、判断下列几个命题中的对错
⑴有两个面平行,其余各面都是四边形的几何体叫棱柱 ( × )
⑵有两个面平行,其余各面都是平行四边行的几何体叫棱柱( × )
⑶ 有一个面是多边形,其余各面都是三角形的几何体叫棱锥( × )
空间几何体的立体图超清晰

(一)棱柱1.棱柱:由一个平面多边形沿某一方向平移形成的空间几何体,叫做棱柱。
注意:(1)本节所说的多边形包括它的内部。
(2)一个图形上所有的点,按某一确定的方向移动相同的距离就是平移。
2.棱柱中的相关概念(1)底面:平移起止位置的两个面叫做棱柱的底面。
(2)侧面:多边形的边平移所形成的面叫做棱柱的侧面。
(3)侧棱:两侧面的公共边叫做棱柱的侧棱。
(4)棱柱的对角面:过棱柱不相邻的两条侧棱的截面,叫做棱柱的对角面。
(5)棱柱的顶点:棱柱底面顶点,叫做棱柱的顶点。
(6)棱柱的对角线:不在同一面上的两顶点的连线,叫做棱柱的对角线。
3.棱柱的分类:⎪⎪⎩⎪⎪⎨⎧⋅⋅⋅⋅⋅⋅五棱柱四棱柱三棱柱:棱柱)按底面多边形的边数(1 ⎩⎨⎧斜棱柱直棱柱:棱柱)按侧棱是否垂直底面(2注意:底面是正多边形的直棱柱叫做正棱柱。
4.棱柱的表示方法:用表示底面多边形顶点的字母表示。
如:棱柱/////E D C B A ABCDE -5.棱柱的性质 (1)两底面以及平行于底面的截面是全等多边形;(2)侧棱平行且相等,侧面都是平行四边形。
(3)对角面是平行四边形。
引例:观察下列几何体,它们有什么共同特点?答:上面的几何体,可以看作是当棱柱的一个底面收缩为一个点时,得到的图形。
(二)棱锥1.棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥。
2.棱锥中的相关概念3.棱锥的分类⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅⋅四棱锥三棱锥棱锥4.棱锥的表示方法: 例:棱锥ABCD S -5.棱锥的简单性质:侧面都是有一个公共顶点的三角形。
(三)棱台1.棱台:用一个平行与棱锥底面的平面去截棱锥,得到两个几何体,一个仍是棱锥,另一个叫做棱台。
即截面与底面之间的部分,叫做棱台。
2.棱台中的相关概念3.棱台分类⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅⋅四棱台三棱台棱台4.棱台的表示方法:例如:////D C B A ABCD -棱台 5.棱台的性质: (1)侧面都是梯形;(2)上、下底面互相平行。
常见几何体20个

常见几何体20个几何体是我们日常生活中经常接触到的物体,它们的形状各异,有的是平面的,有的是立体的。
在这篇文章中,我们将介绍20种常见的几何体,包括球体、立方体、圆柱体、圆锥体、棱柱体、棱锥体、正四面体、正八面体、正十二面体、正二十面体、长方体、正方体、六面体、五面体、四面体、三棱锥、四棱锥、五棱锥和六棱锥。
1. 球体球体是一种立体几何体,它的表面是由无数个相等的点组成的。
球体的体积公式为V=4/3πr³,其中r为球体的半径。
2. 立方体立方体是一种六面体,每个面都是正方形。
立方体的体积公式为V=a³,其中a为立方体的边长。
3. 圆柱体圆柱体是一种由两个平行的圆面和一个侧面组成的几何体。
圆柱体的体积公式为V=πr²h,其中r为圆柱体的底面半径,h为圆柱体的高度。
4. 圆锥体圆锥体是一种由一个圆锥面和一个底面组成的几何体。
圆锥体的体积公式为V=1/3πr²h,其中r为圆锥体的底面半径,h为圆锥体的高度。
5. 棱柱体棱柱体是一种由两个平行的多边形和若干个侧面组成的几何体。
棱柱体的体积公式为V=Bh,其中B为棱柱体的底面积,h为棱柱体的高度。
6. 棱锥体棱锥体是一种由一个多边形锥面和一个底面组成的几何体。
棱锥体的体积公式为V=1/3Bh,其中B为棱锥体的底面积,h为棱锥体的高度。
7. 正四面体正四面体是一种四面体,每个面都是正三角形。
正四面体的体积公式为V=1/3a³,其中a为正四面体的边长。
8. 正八面体正八面体是一种八面体,每个面都是正正方形。
正八面体的体积公式为V=1/3a³,其中a为正八面体的边长。
9. 正十二面体正十二面体是一种十二面体,每个面都是正五边形。
正十二面体的体积公式为V=(15+7√5)/4a³,其中a为正十二面体的边长。
10. 正二十面体正二十面体是一种二十面体,每个面都是正三角形。
正二十面体的体积公式为V=(5+5√5)/12a³,其中a为正二十面体的边长。
空间几何体(超级完美版)PPT课件

.
22
5.特殊的四棱柱:
(3)底面是矩 形的直平行六面 体叫做长方体; (4)棱长都相 等的长方体叫做 正方体.
.
23
几种四棱柱(六面体)的关系:
底面是 平行四边形
侧棱与底面 垂直
四棱柱
平行六面体
直平行六面体
底面是 矩形
长方体
底面为 正方形
侧棱与底面 边长相等
正四棱柱
.
正方体
24
思考:棱柱集合、斜棱柱集合、直棱柱 集合、正棱柱集合之间存在怎样的包含 关系?
叫做旋转体
.
5
一.多面体及相关概念
1.多面体:多面体是由若干个平面多边 形所围成的几何体,如下图中的几何体 都是多面体.
.
6
2.相关概念:
(1)围成多面体的各
D`
个多边形叫做多面体 A`
的面;
(2)相邻两个面的公
共边叫做多面体的棱;
D
A
C` B`
C B
.
7
2.相关概念:
(3)棱和棱的公
D`
共点叫做多面体
.
10
▪一.棱柱
.
12
.
13
1.概念:有两个面互相平行,其余各面
都是四边形,每相邻两个面交线都互相
平行,由这些面围成的多面体叫做棱柱.
.
14
棱柱的底面,侧面,侧棱,顶点.
顶点
侧棱
.
侧面 底面
15
D`
C`
A`
侧 棱
D
A 顶点
B`
对 角 线
底
C
高面
侧
B
.
面
16
2.如何理解棱柱?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
②棱柱的特征:
▪ 侧棱平行且相等 ▪ 侧面是平行四边形
直(正)棱柱侧面是全等的矩形
▪ 两底面及平行于底面的截面是全等的多边形
3.棱柱的分类:
(1)按底面多边形的边数分为三棱柱、 四棱柱、五棱柱等(见图)
3.棱柱的分类: (2)按侧棱与底面的关系分类: 侧棱与底面不垂直的棱柱叫做斜棱柱; 侧棱与底面垂直的棱柱叫做直棱柱; 底面是正多边形的直棱柱叫做正棱柱。
侧面展开图 包含最短路程
截面
▪ 1、任意截:截面形状
(正方体)
▪ 2、平行截:中截面 (柱锥台球)
计算点:相似比
▪ 3、垂直截: 轴截面 (正的柱锥台)
计算点:勾股定理
▪ 4、过顶点截:
(正棱锥,圆锥)
最大面积
1、任意截
形状 三角形 四边形 五边形 六边形
特殊情形
等
等
腰
边
三
三
角
角
形
一组三角形 一组梯形
S侧
1 2
ch
S侧
1 2
(c
c)h
圆柱、圆锥、圆台的侧面积
侧面展开图
侧面积
S侧 2 rl
S侧 rl S侧 (r ' r) l
小结:
S三
棱
锥=
1 2
ch'
S圆锥侧= πrl
C’=0
S
正
棱
台=
1(c+c' 2
)h'
C’=C
S直 棱 柱=ch' ch
O
球面被经过球心的平面截得的圆叫做大圆。 球面被不过球心的截面截得的圆叫球的小圆。
想一想:
球、圆柱、圆锥、圆台过轴的截面分别是什么图形?
轴截面
棱柱 棱锥 棱台
(1)棱柱与圆柱统称为柱体。 (2)棱锥与圆锥统称为锥体。
圆柱 圆锥 圆台
(2)棱台与圆台统称为台体。
多面体 旋转体
球
▪ 简单组合体:
练习
将长方体相邻两个面展开有下列三种可能,如图所示. 三个图形甲、乙、丙中AC1的长分别为:
(a + b)2 + c2 = a2 + b2 + c2 + 2ab a2 + (b + c)2 = a2 + b2 + c2 + 2bc (a + c)2 + b2 = a2 + b2 + c2 + 2ac
结构特征
用一个平行于圆 锥底面的平面去截圆 锥,底面与截面之间 的部分是圆台.
O’
O
4. 球的结构特征
以半圆的直径所在的直线为旋转轴,将半圆旋转所 形成的曲面叫作球面,球面所围成的几何体叫作球体, 简称球。
直径
O
球心
半径
想一想:用一个平面去截一个球,截面是什么?
用一个截面去截 一个球,截面是圆面。
棱台用表示上、下底面各顶点的字
母来表示,如右图,棱台ABCD-A1B1C1D1
A1 D1
C B1 1
正棱台:由正棱锥截得的棱台叫做正棱台
D
C
A
O
E
B
D1 O1
C1 E1
A1
B1
旋转体:圆柱、圆锥、圆台和球
这些几何体 是如何形成 的?它们的 结构特征是
什么?
1.圆柱的结构特征
(1)圆柱的形成
(2)圆柱的结构特征
4.棱柱的表示:
(1)用表示各顶点的字母表示棱柱:
如棱柱ABCD-A1B1C1D1; (2)用一条对角线端点的两个字母来
表示,如棱柱AC1.
D1
C1
A1 D
B1 C
A
B
5.特殊的四棱柱:
(1)底面是平行 四边形的棱柱叫做 平行六面体; (2)侧棱与底面 垂直的平行六面体 叫做直平行六面体;
5.特殊的四棱柱:
形
平
长
正
梯
行
方
方
形
四
形
形
边
形
2.平行截
(1)
(3)
(7)
中截面
(5)
2.垂直截
(6)
轴截面
(8)
圆柱、圆锥、圆台轴截面
A
A
B
A
B
C
DB
CC
D
矩形
等腰三角形
等腰梯形
直三棱柱、正三棱锥、正三棱台
C1
A1
B1
C
C
A
B
P
A1
C1
A
B
O
D
B1 D1 C
O D
B
A
正四棱锥V-ABCD,底面面积为16,一条側棱 长为 2 11 ,由此我们可以求出哪些量?
的顶点;
A`
(4)连接不在同
一个面上的两个
顶点的线段叫做
D
多面体的对角线; A
C` B`
C B
2.相关概念:
(5)凸、凹多面体:把一个多面体的任 意一个面延展为平面,如果其余各面都在 这个平面的同一侧,则这样的多面体就叫 做凸多面体,其他的多面体叫做凹多面体; (6)截面:一个几何体和一个平面相交 所得到的平面图形(包括它的内部),叫 做这个几何体的截面;
第一章:
第一部分:
空间几何体
空间几何体学习内容流程
▪ 直观认识多面体和旋转体 ▪ 截面:任意截,横截,竖截,过顶点截 ▪ 侧面展开图
包含最短路程 ▪ 表面积和体积 ▪ 三视图和直观图
顶点
面
由若干个平面
多边形围成的
棱
几何体叫做多
面体 .
轴
由一个平面图形绕它所在平面内的 一条定直线旋转所形成的封闭几何体 叫做旋转体
A’
O’
轴
母
以矩形的一边所在直线 线
侧
为旋转轴,其余边旋转形成
面
的曲面所围成的几何体叫做
圆柱。
A
O
底面
2.圆锥的结构特征 (1)圆锥的形成
2.圆锥的结构特征
母
线
A
以直角三角形的一条直角边所在 直线为旋转轴,其余两边旋转形成的曲 面所围成的几何体叫做圆锥。
顶点
S
轴
侧 面
O B
底面
3.圆台的结构特征
棱锥、四棱锥、五棱锥、……
3、棱锥的表示方法:用表示顶点和底面 的字母表示,如四棱锥S-ABCD。
4.特殊的棱锥 S
(1)正棱锥
正棱锥:如果棱锥的底面 是正多边形,且它的顶点 在过底面中心且与底面垂 直的直线上,则这个棱锥
叫做正棱锥。
A B
E
D
O
M
C
正棱锥性质
1、底面是正多边形; 2、顶点和底面中心的连线与底面垂直; 3、側棱长都相等; 4、各侧面都是全等的等腰三角形; 5、斜高都相等;
一.多面体及相关概念
1.多面体:多面体是由若干个平面多边 形所围成的几何体,如下图中的几何体 都是多面体.
2.相关概念:
(1)围成多面体的 各个多边形叫做多面 体的面; (2)相邻两个面的 公共边叫做多面体的 棱;
D` A`
D A
C` B`
C B
2.相关概念:
(3)棱和棱的公
D`
共点叫做多面体
(3)圆台也可看成是圆锥被平行于底面的平面所截 得截面与底面之间的部分。 其中正确的是___(3_)______
3、下列关于多面体的说法中: (1)底面是矩形的直棱柱是长方体; (2)底面是正方形的棱锥是正四棱锥; (3)两底面都是正方形的棱台是正棱台; (4)正四棱柱就是正方体; 其中正确的是___(1_)_____
r1=0 S圆台侧=π(r1+r2)l
r1=r2 S圆柱侧= 2πrl
侧面展开图的中心角
r 3600
l
最短路程
蚂蚁爬行的最短路线
B
A
如图所示,长方体 ABCD—A1B1C1D1
中,AB=a,BC=b, BB1=c,并且a>b>c> 0.求沿着长方体的表面自 A到C1的最短线路的长.
红
黄
绿
黄
黑
蓝
8、有一个正棱锥所有的棱长都相等,则这个正棱锥 不可能是( D ) A,正三棱锥 B,正四棱锥 C,正五棱锥 D,正六棱锥
9、轴截面是正三角形的圆锥侧面展开图的圆心角的弧
度数为_________
10 甲烷(CH4)分子中,四个H原子恰好在一个正四面体 的顶点处,C原子在这个正四面体的中心,若C原子与
正四棱锥V-ABCD,底面面积为16,一条側棱 长为 2 11 ,由此我们可以求出哪些量?
V
四棱锥V-OBM,有几个面是直角三角形?
D O
C M
A
B
(2)正多面体
A
▪ 正四面体
B
D
E
四个面是全等的正三角形 C
正六面体 正八面体
C1
B1 C1
B1
A1
A1
C
BC
B
A
A
思考:一个三棱柱最少可以分割成几个
1、将一个直角梯形绕其较短的底所在的直线旋转一 周得到一个几何体,关于该几何体的以下描绘中,正 确的是( D)
A、是一个圆台
B、是一个圆柱
C、是一个圆柱和一个圆锥的简单组合体
D、是一个圆柱被挖去一个圆锥后所剩的几何体
2、下列关于简单几何体的说法中:
(1)斜棱柱的侧面中不可能有矩形;
(2)有两个面互相平行,其余各面都是平行四边形 的多面体是棱柱;
5.已知:正三棱锥V -ABC,VO为高, AB=6,VO= 6 ,求侧棱长及斜高。 V
