直角三角形斜边中线等于斜边一半性质
直角三角形斜边的中线等于斜边的一半

一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt△BAC中,∠BAC=,D为BC的中点,则。
2、性质的拓展:如图1:因为D为BC中点,所以,所以AD=BD=DC=,所以∠1=∠2,∠3=∠4,因此∠ADB=2∠3=2∠4,∠ADC=2∠1=2∠2。
因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、求值例1、(2004年江苏省苏州市中考)如图2,CD是Rt△ABC斜边AB上的中线,若CD=4,则AB= .2、证明线段相等例2、(2004年上海市中考)如图4,在△ABC中,∠BAC=90°,延长BA到D 点,使,点E、F分别为边BC、AC的中点。
(1)求证:DF=BE;(2)过点A作AG∥BC,交DF于G。
求证:AG=DG。
3、证明角相等及角的倍分关系例3、已知,如图5,在△ABC中,∠BAC>90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE。
例4、已知:如图6,在△ABC中,AD是高,CE是中线。
DC=BE,DG⊥CE,G为垂足。
4、证明线段的倍分及和差关系例5、如图7,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD 的中点,连AE。
求证:(1)∠AEC=∠C;(2)求证:BD=2AC。
例7、如图8,在梯形ABCD中,AB∥CD,∠A+∠B=90°,E、F分别是AB、CD的中点。
求证:。
5、证明线段垂直例8、如图9,在四边形ABCD中,AC⊥BC,BD⊥AD,且AC=BD,M、N分别是AB、DC边上的中点。
求证:MN⊥DC。
6、证明特殊的几何图形例9、如图10,将Rt△ACB沿直角边AC所在直线翻折180°得到Rt△ACE,点D 与点F分别是斜边AB、AE的中点,连CD、CF,则四边形ADCF为菱形.请给予证明.三、尝试训练1、在△ABC中,∠ACB=90°,AC=6,BC=8,则斜边上中线长为.2、如图11所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6,沿斜边AB的中线把这张纸张剪成△AC1D1和△BC2D2两个三角形(如图12所示),将纸张△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一条直线上),当点D1与点B重合时,停止平移,在平移过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P。
“直角三角形斜边上的中线”的性质及其应用
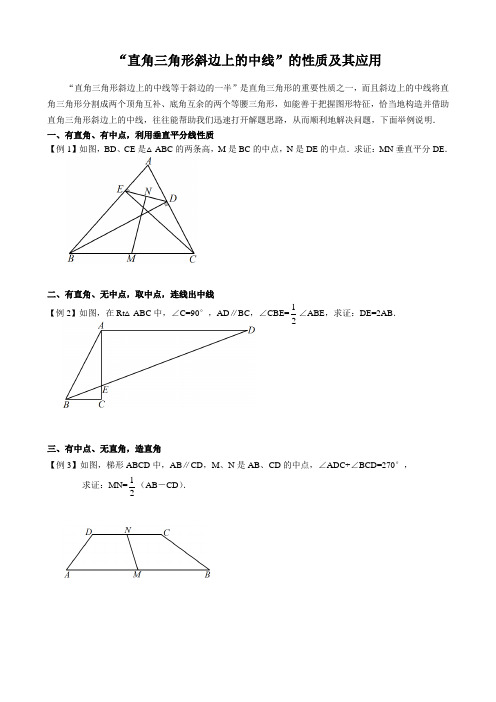
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,利用垂直平分线性质【例1】如图,BD 、CE 是△ABC 的两条高,M 是BC 的中点,N 是DE 的中点.求证:MN 垂直平分DE .二、有直角、无中点,取中点,连线出中线【例2】如图,在Rt △ABC 中,∠C=90°,AD ∥BC ,∠CBE=21∠ABE ,求证:DE=2AB .三、有中点、无直角,造直角【例3】如图,梯形ABCD 中,AB ∥CD ,M 、N 是AB 、CD 的中点,∠ADC+∠BCD=270°,求证:MN=21(AB -CD ).四、逆用性质解题【例4】如图,延长矩形ABCD 的边CB 至E ,使CE=CA ,P 是AE 的中点.求证:BP ⊥DP .【习题练习】1、如图,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E ,求证:CD=21BE .2、如图,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的中点,求证:AB=2DM .3、如图,在四边形ABCD 中,∠DAB=∠DCB=90°,点M 、N 分别是BD 、AC 的中点.确定MN 、AC 的位置关系.直角三角形斜边上中线性质的应用一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图,在Rt △BAC 中,∠BAC=90°,D 为BC 的中点,则BC 21AD =.2、性质的拓展:如图:因为D 为BC 中点,所以BC 21DC BD ==, 所以AD=BD=DC=BC 21, 所以∠1=∠2,∠3=∠4,因此∠ADB=2∠1=2∠2,∠ADC=2∠3=2∠4.因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、21倍关系求值 例1、如图,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、如图,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点.(1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于G .求证:AG=DG .3、证明角相等及角的倍分关系例3、已知,如图,在△ABC中,∠BAC 90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE.例4、已知:如图,在△ABC中,AD是高,CE是中线。
直角三角形斜边中线等于斜边一半的证明方法

直角三角形斜边中线等于斜边一半的证明方法在一个直角三角形中,假设斜边的长度为c,而另外两条直角边分别为a和b。
我们需要证明斜边中线的长度等于斜边长度的一半。
首先,我们知道中线将斜边分成两个长度相等的部分。
因此,我们可以将斜边中线的长度表示为c/2。
接下来,我们将注意力集中在直角三角形的其他两条边上。
我们知道,当这两条边的平方之和等于斜边的平方时,这个三角形就是直角三角形。
因此,我们可以使用勾股定理来计算这两条边的长度。
a +
b = c
现在,我们将斜边中线标记为d,并将直角三角形的底部分成两个等长的部分,如下图所示:
```
/|
/ |
/ |
/___|___
a b
```
我们可以通过将直角三角形中的第一个小三角形翻折到另一边,然后将其放置在第二个小三角形旁边来证明中线长度为c/2。
这样,我们就得到了下面这张图:
```
/|
/ |
/ |
/___|___
a b
/
/ d
/_________
```
现在,我们可以使用勾股定理计算直角三角形的两个小三角形的斜边长度,如下所示:
(c/2) + a = d
(c/2) + b = d
我们可以将这两个等式相加,并使用a + b = c来简化方程,如下所示:
(c/2) + a + (c/2) + b = d + d
c/4 + c/4 + c = 2d
2c/4 = d
c/2 = d
因此,我们可以得出结论:直角三角形斜边中线的长度等于斜边长度的一半,即d = c/2。
直角三角形斜边上中线性质的应用

直角三角形斜边上中线性质的应用一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt△BAC中,∠BAC=,D为BC的中点,则。
2、性质的拓展:如图1:因为D为BC中点,因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、求值例1、(2004年江苏省苏州市中考)如图2,CD是Rt△ABC斜边AB上的中线,若CD=4,则AB= .例2、(2006年上海市中考)已知:如图3,在△ABC中,AD是BC边上的高,E为AC边上的中点,BC=14,AD=12,。
求的值。
2、证明线段相等例3、(2004年上海市中考)如图4,在△ABC中,∠BAC=90°,延长BA到D 点,使,点E、F分别为边BC、AC的中点。
(1)求证:DF=BE;(2)过点A作AG∥BC,交DF于G。
求证:AG=DG。
3、证明角相等及角的倍分关系例4、已知,如图5,在△ABC中,∠BAC>90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE。
例5、(2003年上海市中考题)已知:如图6,在△ABC中,AD是高,CE是中线。
DC=BE,DG⊥CE,G为垂足。
求证:(1)G是CE的中点;(2)∠B=2∠BCE。
4、证明线段的倍分及和差关系例6、(2007年呼和浩特市中考)如图7,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连AE。
求证:(1)∠AEC=∠C;(2)求证:BD=2AC。
例7、(第四届“祖冲之杯”初二竞赛)如图8,在梯形ABCD中,AB∥CD,∠A+∠B=90°,E、F分别是AB、CD的中点。
求证:。
5、证明线段垂直例8、如图9,在四边形ABCD中,AC⊥BC,BD⊥AD,且AC=BD,M、N分别是AB、DC边上的中点。
直角三角形斜边上中线性质的应用

直角三角形斜边上中线性质的应用直角三角形斜边上中线的性质是为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。
一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt△BAC中,∠BAC=,D为BC的中点,则。
二、性质的应用1、求值例、如图2,CD是Rt△ABC斜边AB上的中线,若CD=4,则AB= .解析:由性质可知:CD,所以AB=2CD=8.2、证明线段相等3、证明角相等及角的倍分关系一.智勇大闯关1、已知,如图5,在△ABC中,∠BAC>90°,BD、CE分别为AC、AB上的高,F 为BC的中点,求证:∠FED=∠FDE。
2、(2003年上海市中考题)已知:如图6,在△ABC中,AD是高,CE是中线。
DC=BE,DG⊥CE,G为垂足。
求证:(1)G是CE的中点;(2)∠B=2∠BCE。
3、(2007年呼和浩特市中考)如图7,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连AE。
求证:(1)∠AEC=∠C;(2)求证:BD=2AC。
4、(第四届“祖冲之杯”初二竞赛)如图8,在梯形ABCD中,AB∥CD,∠A+∠B=90°,E、F分别是AB、CD的中点。
求证:。
4、证明线段垂直例、如图9,在四边形ABCD中,AC⊥BC,BD⊥AD,且AC=BD,M、N分别是AB、DC边上的中点。
求证:MN⊥DC。
分析:M是Rt△ADB与Rt△ACB斜边上中点,连DM、CM,由性质可得:,所以△DMC为等腰三角形。
又因为N为CD的中点,所以MN⊥DC。
5、证明特殊的几何图形例、(2007年新疆维吾尔自治区中考)如图10,将Rt△ACB沿直角边AC所在直线翻折180°得到Rt△ACE,点D与点F分别是斜边AB、AE的中点,连CD、CF,则四边形ADCF为菱形.请给予证明.分析:由于△ACE是△ACB沿直角边AC翻折得到的,所以AB=AE,∠ACE=90°.因为D、F分别是Rt△ACB和Rt△ACE斜边上中线,所以,所以AD=DC=AF=FC,所以四边形ADCF为菱形。
斜边中线定理知识点总结

斜边中线定理知识点总结一、斜边中线定理的定义斜边中线定理是指在一个直角三角形中,三角形的斜边上的中线等于斜边的一半。
即斜边中线的长度等于斜边的长度的一半。
这个定理在数学中有着很重要的应用,特别是在直角三角形的计算中。
二、斜边中线定理的证明证明斜边中线定理的过程非常简单,我们可以通过勾股定理和平行线的性质来证明。
首先,我们假设在一个直角三角形ABC中,AB为斜边,C为直角的顶点,M为AB的中点。
我们要证明MC等于AB的一半。
根据勾股定理可知,在直角三角形ABC中,有AB^2=AC^2+BC^2。
根据平行线的性质,可以得出MC平行于BC。
因此,根据斜边中线定理的定义,我们可以得出MC=AB/2。
通过上面的证明过程,我们可以得出斜边中线定理的结论。
三、斜边中线定理的应用1. 直角三角形的计算在解决直角三角形相关问题时,斜边中线定理是一个常用的工具。
通过斜边中线定理,我们可以快速计算出直角三角形中斜边上的中线的长度,从而简化计算过程。
2. 辅助几何问题的解决在解决一些几何问题时,斜边中线定理也是一个重要的工具。
通过斜边中线定理,我们可以快速计算出斜边上的中线的长度,从而解决一些与直角三角形相关的几何问题。
四、斜边中线定理的拓展斜边中线定理在一定条件下也具有拓展的能力。
例如,我们可以将斜边中线定理与其他定理进行结合,从而得出一些更加复杂的几何问题的解决方法。
在解决与直角三角形相关的问题时,我们可以将斜边中线定理与勾股定理、正弦定理、余弦定理等进行结合,从而得出更加复杂的计算方法。
五、斜边中线定理的实际应用1. 在实际测量中,斜边中线定理可以帮助我们快速计算出直角三角形斜边上的中线的长度,从而简化实际测量的过程。
2. 在建筑设计中,斜边中线定理可以帮助我们解决一些关于直角三角形的设计问题,从而提高建筑设计的效率。
3. 在工程测量中,斜边中线定理可以帮助我们解决一些土木工程中的几何问题,从而提高工程测量的准确性。
直角三角形中线等于斜边的一半证明

直角三角形中线等于斜边的一半证明取ac的中点e,连接de。
取bc的中点d。
∵ad是斜边bc的中线,∴bd=cd=1/2bc,∵e是ac的中点,∴de是△abc的中位线,∴de//ab(三角形的中位线平行于底边)∴∠dec=∠bac=90°(两直线平行,同位角相等)∴de垂直平分ac,∴ad=cd=1/2bc。
直角三角形斜边中线定理是数学中关于直角三角形的一个定理,具体内容为:如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。
定理内容:逆命题:其逆命题1:如果一个三角形一条边的中线等同于这条边的一半,那么这个三角形就是直角三角形,且这条边为直角三角形的斜边。
逆命题1是正确的。
以该条边的中点为圆心,以中线长为半径作圆,则该边成为圆的直径,该三角形的另一个顶点在圆上,该顶角为圆周角。
因为直径上的圆周角是直角,所以逆命题1成立。
逆命题2:如果线段bd的一端b就是直角三角形abc的顶点,另一端d在斜边ac上,且bd等同于ac的一半,那么bd就是斜边ac的中线。
逆命题2是不成立的。
举一个反例。
设直角三角形三边长分别为ab=3,bc=4,ac=5。
斜边的一半长为2.5,斜边上的高be=(3*4)/5=2.4,在线段ae上上必能找到一点d,使bd=2.5,但bd并不是ac边的中线,因为ac边的中点在线段ec上。
逆命题3:若直角三角形斜边上一点与直角顶点的连线等同于该点分斜边税金两条线段中任一一条时,该点为斜边中点。
几何叙述:在rt△abc中,∠acb=90°,d就是斜边ab上一点。
若cd=ad或cd=bd,则d就是ab中点。
逆命题3成立,cd=ad则∠a=∠acd,而∠a+∠b=90°,∠acd+∠bcd=90°,因此∠bcd=∠b。
等角对等边,有cd=db,所以ad=bd,即d是斜边中点。
证法:证法1:δabc就是直角三角形,作ab的垂直平分线n交bc于d∴ ad=bd(线段垂直平分线上的点到这条线段两端点的距离相等)以db为半径,d为圆心画弧,与bc在d的另一侧处设c'∴dc’=ad=bd∴∠bad=∠abd ∠c’ad=∠ac’d (等边对等角)又∵∠bad+∠abd+∠c’ad+∠ac’d =°(三角形内角和定理)∴∠bad+∠c’ad=90° 即:∠bac’=90°又∵∠bac=90°∴∠bac=∠bac’∴c与c’在直线ac上又∵c与c’在直线bd上,ac与bd相交∴c与c’重合(也需用横向公理证明:假使c与c’不重合由于ca⊥ab,c’a⊥ab 故过a存有ca、c’a两条直线与ab横向这就与横向公理矛盾∴假设不设立∴c与c’重合)∴dc=ad=bd∴ad是bc上的中线且ad=bc/2这就是直角三角形斜边上的中线定理证法2:δab c是直角三角形,ad是bc上的中线,作ab的中点e,连接de∴bd=cb/2,de就是δabc的中位线∴de‖ac(三角形的中位线平行于第三边)∴∠deb=∠cab=90°(两直线平行,同位角成正比)∴de⊥ab∴de就是ab的垂直平分线∴ad=bd(线段垂直平分线上的点到这条线段两端点的距离相等)∴ad=cb/2证法3:反证法假设 bd != ad1: cd \ue ad =\ue∠cad \ue∠dca (三角形大边对大角)bd \ue ad =\ue∠bad \ue∠abd=\ue∠cad+∠bad \ue∠abd+∠acd=\ue∠abd+∠acd \uc90°=\uecd \ue ad 不成立2:同理可得 cd=\ue cd =ad证法9:设立直角三角形abc,角c就是直角,过a点作ad旋转轴ac,过b点作be旋转轴bcad与be处设f,四边形abcf为矩形,相连接cf,ab与cf处设g,因为矩形对角线成正比且互相平分的性质,所以ag=bg=cg逆命题1几何语言:在△abc中,ad就是中线,且bc=2ad,则∠bac=90°。
直角三角形斜边的中线等于斜边的一半逆定理

直角三角形斜边的中线等于斜边的一半逆定理直角三角形是一种特殊的三角形,它的一个角度为90度,另外两个角度分别为锐角和钝角。
在直角三角形中,斜边是与直角相对的边,而另外两边则被称为直角边。
有一个有趣而又重要的定理与直角三角形的斜边和中线之间的关系密切相关。
这个定理被称为“直角三角形斜边的中线等于斜边的一半”。
首先,让我们来看一下直角三角形中的斜边和中线是如何定义的。
斜边是直角三角形的最长边,它位于直角的对角位置。
中线可以通过连接斜边的两个中点来得到,这条线将斜边分成两个等长的部分。
当我们将斜边切分为两个等长的部分后,我们可以发现这两个部分与直角边的关系非常特殊。
事实上,直角三角形斜边的中线恰好等于斜边的一半长度。
为了更加深入地理解这个定理,我们可以从几何和数学的角度进行解释。
设直角三角形的斜边长度为c,直角边长度分别为a和b。
根据勾股定理,我们可以得到a²+b²=c²,其中a²表示直角边a的平方,b²表示直角边b的平方,c²表示斜边c的平方。
当我们将斜边c划分为两个部分时,每个部分的长度为c/2。
现在,我们可以利用勾股定理来证明斜边的中线等于斜边的一半。
首先,我们可以分别计算两个划分后的斜边部分的平方。
左边的部分为(c/2)²= c²/4,右边的部分为(c-c/2)² = (c/2)²=c²/4。
由于c²/4+c²/4=c²,我们可以看出两个部分的平方之和等于斜边的平方。
也就是说,通过连接斜边的两个中点得到的中线也满足勾股定理。
这个定理在实际应用中具有重要的指导意义。
我们可以利用这个定理来解决各种问题,例如测量无法直接获取的直角三角形边长或角度。
通过知道斜边的长度和中线的关系,我们可以进行精确的计算和推导。
此外,直角三角形斜边的中线等于斜边的一半也反映了数学中的一些重要原理和性质,例如平行线的截距定理和相似三角形的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图4,在△ABC中,∠BAC=90°,延长BA到D 点,使AD= ,点E、F分别为边BC、AC的 中点。
(1)求证:DF=BE; (2)过点A作AG∥BC,交DF于G。求证: AG=DG。
应用:如图1,在△ABC中,点P为BC边中点,直线a绕顶点 A旋转,若B、P在直线a的异侧,BM⊥直线a于点M, CN⊥直线a于点N,连接PM、PN; (1)延长MP交CN于点E(如图2).①求证: △BPM≌△CPE;②求证:PM=PN; (2)若直线a绕点A旋转到图3的位置时,点B、P在直线a 的同侧,其它条件不变,此时PM=PN还成立吗?若成立, 请给予证明:若不成立,请说明理由; (3)若直线a绕点A旋转到与BC边平行的位置时,其它条件 不变,请直接判断四边形MBCN的形状及此时PM=PN还成 立吗?不必说明理由.
如图所示;过矩形ABCD的顶点A作一直线,交BC的延 长线于点E,F是AE的中点,连接FC、FD。 求证:∠FDA=∠FCB
如图2,在Rt△ABC中,∠C=900,AD∥BC, ∠CBE= ∠ABE,求证:DE=2AB
1.如图5,△ABC中,AB=AC,∠ABD=∠CBD, BD⊥DE于D,DE交BC于E, 求证:CD= BE. 2.如图6,△ABC中,∠B=2∠C,AD⊥BC于D, M是BC的 中点,求证:AB=2DM.
直角三角形斜边上的中线等于斜边的一半
已知,如图5,在△ABC中,∠BAC>90°,BD、CE分 别为AC、AB上的高,F为BC的中点,求证: ∠FED=∠FDE。
பைடு நூலகம்
四边形 ABCD 中,BA⊥AC,BD⊥DC,E,F为边上中点。 如图所示, BD 、CE是三角形ABC的两条高,M、N 猜想 EFBC 与AD 的关系。 分别是 、DE 的中点 求证:MN⊥DE 猜想 MN与DE关系
