八年级数学梯形辅助线的做法及应用
梯形中常用辅助线作法优秀获奖科研论文

梯形中常用辅助线作法优秀获奖科研论文梯形是几何平面中一种常见的图形, 它是在三角形和平行四边形的基础上进行研究的.在解决有关梯形知识的问题中, 往往通过添加适当的辅助线, 把梯形转化为平行四边形或三角形.在学生已有的知识体系中利用图形的转换将复杂的问题简单化, 不同条件的梯形转换方式也不尽相同.因此辅助线添加方式也因其而异.下面就自己的教学经验浅谈一下梯形中常见的辅助线作法.1.平移一腰.即从梯形的一个顶点作一腰的平行线, 把梯形分割成一个平行四边形和一个三角形.然后利用平行四边形及三角形的性质解决问题.例1如图1, 在梯形ABCD中, AD∥BC, ∠B=50°, ∠C=80°, AD=10cm, BC=18cm.求CD的长.分析:过A作AE∥CD交BC于点E, 则四边形AECD为平行四边形.欲求CD的长, 只要求出AE即可.2.从上底的两个端点作下底的垂线, 把梯形分成一个矩形和两个直角三角形.如果是等腰梯形, 所得到的两个直角三角形是全等的.例2如图2, 在梯形ABCD中, AD∥BC, AB=CD, AD=4, AB=6, ∠ABC=60°, 求梯形ABCD的面积.分析:根据已知条件知, 欲求梯形面积需先求出下底和高, 故作高AH、DG, 易证BH=GC, HG=AD.进而求出BC.由勾股定理和直角三角形的性质可求出高AH.求等腰梯形的面积一般都要求高, 而求高通常同时作两条高, 把梯形分成一个矩形和两个全等的直角三角形, 结合矩形和直角三角形的有关性质解决问题.3.平移对角线.即从上底的一个端点作一条对角线的平行线, 通过平移对角线可将对角线、上底、下底集中到同一个三角形中.平移后的对角线与另一条对角线及两底之和组成的三角形与原梯形面积相等.例3如图3, 在梯形ABCD中, AD∥BC, AD=1, BC=4, AC=3, BD=4, 求梯形的面积.分析:欲求梯形ABCD的面积, 已知上下底的长, 只要求出梯形ABCD的高.过D作DE∥AC交BC的延长线于E, 则四边形ACED为平行四边形, 从而AD=CE.即得梯形ABCD的面积等于△BDE的面积, 故求出△BDE的面积即可.4.延长梯形的两腰到一点, 得到两个三角形.如果是等腰梯形, 则得到两个分别以梯形的两底为底的等腰三角形.例4如图4, 在四边形ABCD中, AB=CD, ∠B=∠C, AD<BC.求证:四边形ABCD为等腰梯形.分析:欲证四边形ABCD为等腰梯形, 已知∠B=∠C, 故只要证明AD∥BC即可.延长BA、CD交于点E.证得△AED、△BEC均为等腰三角形.从而易得AD∥BC.5.过梯形上底中点作两腰的平行线, 把梯形转化为两个平行四边形和一个三角形.如果是等腰梯形, 得到的三角形是等腰三角形, 再利用等腰三角形的性质解决问题.例5如图5, 已知等腰梯形ABCD, AD∥BC, 点E、F分别为AD、BC的中点, 求证:EF⊥BC.分析:欲证EF⊥BC, 可过E作EM∥AB, EN∥CD, 分别交BC于点M、N.即得BM=AE, CN=DE, MF=NF, ME=NE.利用等腰三角形三线合一的性质可得EF⊥BC.6.旋转上底.以一腰中点为旋转中心, 顺时旋转180°.使上底旋转到下底所在直线的位置.构造出全等三角形.在梯形中出现上底与下底之和等于一腰长时, 利用此种方法添加辅助线, 将分散的线段相对集中, 并构造出等腰三角形, 再运用等腰三角形三线合一的性质解决线段垂直、角相等等问题.例6如图6, 在梯形ABCD中, AD∥BC, 且AB=AD+BC.M为CD的中点, 求证:(1)AM⊥BM.(2)AM平分∠BAD, BM平分∠ABC.分析:欲证AM⊥BM, 先延长AM交BC的延长线与点E(即以点M为中心△ADM顺时旋转180°与△ECM重合), 易证△ADM≌△ECM, 得CE=AD, AM=EM.由AD+BC=AB得AB=BE.利用等腰三角形三线合一的性质得AM⊥BM, 所以BM平分∠ABC.易证AM平分∠BAD.总之, 在解决有关梯形的问题时, 可通过作辅助线——平移线段、延长线段、旋转线段等, 把梯形分割成平行四边形和三角形或构造出全等三角形、等腰三角形, 把有关的线段和角相对集中到一个三角形中, 利用三角形、平行四边形的知识解决梯形问题.“本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文”。
8下梯形中常见辅助线

8下梯形中常见辅助线本文将介绍在8下梯形中常见的辅助线。
平行线在8下梯形中,常见的辅助线是平行线。
平行线是指在同一个平面内,永远不会相交的两条直线。
在梯形中,有以下两组平行线:- 上底和下底:上底和下底是平行的,它们在梯形的上下方分别连接两侧的顶点。
- 两斜边:两斜边是平行的,它们在梯形的两侧连接两个顶点。
这些平行线有助于我们在解答梯形相关的问题时,理解各线段之间的关系,并推导出有用的结论。
等腰梯形的辅助线等腰梯形是指具有两条等长边的梯形。
在等腰梯形中,常见的辅助线是中线。
中线是连接梯形的两个上底顶点与两个下底顶点的线段。
中线满足以下特点:- 中线与上底、下底平行。
- 中线的长度等于上底和下底长度之和的一半。
通过画出中线,我们可以将等腰梯形分成两个等腰三角形。
这样可以帮助我们推导出等腰梯形的性质和解决相关问题。
高线高线是指从梯形的一个顶点到与底边平行的另一条边上的垂直线段。
在梯形中,通过画出高线,我们可以将梯形分割成两个直角三角形。
高线满足以下特点:- 高线与底边垂直。
- 高线与另一条边上的线段平行。
通过计算和利用等腰三角形的性质,我们可以利用高线解决梯形相关的问题。
总结在8下梯形中,常见的辅助线包括平行线、中线和高线。
这些辅助线有助于我们理解梯形各线段之间的关系,并且可以帮助我们解决相关的问题。
在解题时,我们应合理利用这些辅助线,推导出有用的结论和解决方案。
请注意,在实际问题中,可能存在其他类型的辅助线,具体问题具体分析。
初二梯形中常用添加辅助线的方法

初二梯形中常用添加辅助线的方法1.作高:过梯形的顶点作底边上的高线,把梯形问题转化为矩形或直角三角形来解决;例1、已知等腰梯形的上底长为5cm,腰长为7 cm,下底角为600,求这个梯形的周长和面积。
练习:在梯形ABCD中,AB=CD,AD∥BC。
求证:AC2=AB2+BC·AD。
2.平移腰:通过平移梯形的一腰或两腰,使梯形问题转化为平行四边形或三角形来解决;例2、在梯形ABCD中,AD∥BC,∠B+∠C=900,E、F分别是AD和BC边上的中点,求证:EF=(BC-AD)/2。
练习:在梯形ABCD中,AD∥BC,∠B=800,∠C=500,求证:AB=BC-AD。
3.延长两腰:延长梯形的两腰相交于一点,使梯形问题转化为三角形来解决;例3、等腰梯形ABCD,AD∥BC,∠B=600,AD=15,AB=45,求BC的长。
练习:梯形ABCD中,AD∥BC,∠B=∠C。
求证:AB=CD。
4.平移对角线:平移其中的一条对角线,使梯形问题转化为直角三角形来解决,此法适合于已知对角线互相垂直的问题;例4、等腰梯形ABCD中,AB∥CD,AD=BC,且AC⊥BD,CH是高,求证:AB+CD=2CH。
练习:在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD互相垂直,GD⊥BC于G,EF是中位线。
求证:EF=DG。
5.连对角线:连结对角线,将梯形问题转化为平行四边形或三角形来解决;例5、梯形ABCD中,AD=BC,AB∥CD,延长AB到E,使BE=DC,连结AC、CE,求证:AC=CE。
6.取腰的中点:有一腰的中点时,往往取另一腰的中点构成梯形的中位线;例6、梯形ABCD中,AD∥BC,AB=AD+BC,M为CD的中点。
求证:AM、BM平∠分DAB、∠CBA。
7.连结上底与一腰中点并延长与下底的延长线相交,借助于得到的三角形解决梯形问题;例7、梯形ABCD中,AB∥CD,E是腰AD的中点,且AB+CD=BC。
梯形中常见的辅助线
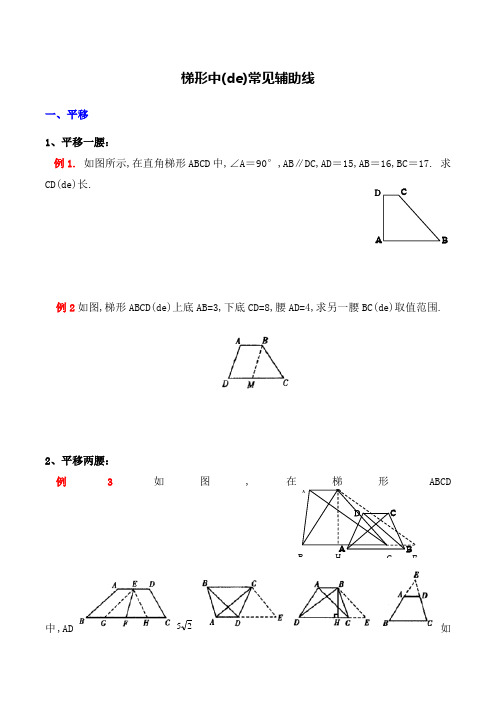
梯形中(de)常见辅助线一、平移 1、平移一腰:例1. 如图所示,在直角梯形ABCD 中,∠A =90°,AB ∥DC,AD =15,AB =16,BC =17. 求CD(de)长.例2如图,梯形ABCD(de)上底AB=3,下底CD=8,腰AD=4,求另一腰BC(de)取值范围.2、平移两腰: 例3如图,在梯形ABCD中,AD25如ABDCEHABCDA BCD图所示,四边形ABCD 中,AD 不平行于BC,AC =BD,AD =BC. 判断四边形ABCD(de)形状,并证明你(de)结论.三、作对角线即通过作对角线,使梯形转化为三角形. 例9如图6,在直角梯形ABCD中,AD )(21AD BC EF -=若等腰梯形(de)锐角是60°,它(de)两底分别为11cm ,35cm ,则它(de)腰长为__________cm .2. 如图所示,已知等腰梯形ABCD 中,AD ∥BC,∠B =60°,AD =2,BC =8,则此等腰梯形(de)周长为( )A. 19B. 20C. 21D. 22AB CDABDCEF ABCDEF3. 如图所示,AB ∥CD,AE ⊥DC,AE =12,BD =20,AC =15,则梯形ABCD(de)面积为( ) A. 130 B. 140 C. 150 D. 160ABCDE4. 如图所示,在等腰梯形ABCD 中,已知AD ∥BC,对角线AC 与BD 互相垂直,且AD =30,BC =70,求BD(de)长.AB CD5. 如图所示,已知等腰梯形(de)锐角等于60°,它(de)两底分别为15cm 和49cm ,求它(de)腰长.AB CD6. 如图所示,已知等腰梯形ABCD 中,AD ∥BC,AC ⊥BD,AD +BC =10,DE ⊥BC 于E,求DE(de)长.ABCDE7. 如图所示,梯形ABCD 中,AB ∥CD,∠D =2∠B,AD +DC =8,求AB(de)长.ABCD8. 如图所示,梯形ABCD 中,AD ∥BC,(1)若E 是AB(de)中点,且AD +BC =CD,则DE 与CE 有何位置关系(2)E 是∠ADC 与∠BCD(de)角平分线(de)交点,则DE 与CE 有何位置关系AB CDE。
全等梯形问题中常见的8种辅助线的作法(有答案解析)

全等梯形问题中常见的8种辅助线的作法(有答案解析)梯形是一种四边形,其中两条边是平行而另外两条边不平行。
在解决全等梯形问题时,我们可以使用一些辅助线的方法来简化问题并找到解答。
以下是常见的8种辅助线的作法,每种方法都附有答案解析。
1. 垂直辅助线法:垂直辅助线法是最基本的辅助线作法之一,它通过引入垂直辅助线来将梯形划分为上下两个小三角形或小梯形,并利用全等三角形的性质来解题。
2. 高度辅助线法:高度辅助线法通过引入高度辅助线来找到梯形的高,并利用相似三角形的性质来解题。
3. 中位线辅助线法:中位线辅助线法通过引入中位线辅助线来将梯形划分为两个全等的平行四边形,并利用平行四边形的性质来解题。
4. 对角线辅助线法:对角线辅助线法通过引入对角线辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
5. 平行边辅助线法:平行边辅助线法通过引入平行边辅助线来将梯形划分为两个全等的梯形,并利用梯形的性质来解题。
6. 外接圆辅助线法:外接圆辅助线法通过引入外接圆辅助线来找到梯形的外接圆,并利用外接圆的性质来解题。
7. 中心对称辅助线法:中心对称辅助线法通过引入中心对称辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
8. 连接线辅助线法:连接线辅助线法通过引入连接线辅助线来划分梯形并利用形成的图形的性质来解题。
这些辅助线的作法可以帮助我们在解决全等梯形问题时更简单而有条理地进行推导和解答。
通过灵活运用这些方法,我们可以提高解决问题的效率和准确性。
请注意:本文档中的答案解析仅供参考,具体解答的正确性应根据实际情况进行确认。
梯形常中的辅助线
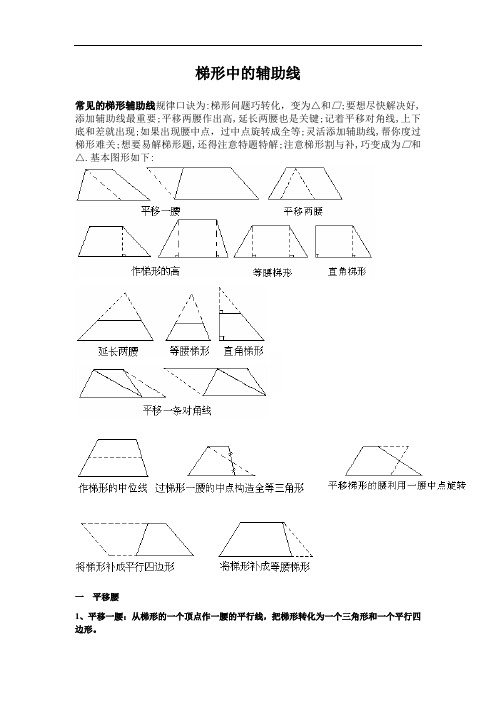
梯形中的辅助线常见的梯形辅助线规律口诀为:梯形问题巧转化,变为△和□;要想尽快解决好,添加辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下:一平移腰1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
例1:梯形两底长分别为14cm 和24cm ,下底与腰的夹角分别是60°和30°,求较短腰长。
DBCA解析:如图,在梯形ABCD 中,AD//BC ,AD=14cm ,BC=24cm ,∠B=60°,∠C=30°。
过点A 作AE//DC 交BC 于E ,得到平行四边形AECD 和△ABE ,故AE=DC ,AD=EC ,∠C=∠AEB=30°。
这样,梯形的两腰,两底之差,下底与腰的两个夹角都集中于Rt △ABE 中,于是得到较短腰巩固练习:如图1,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
析解:过点B 作BM//AD 交CD 于点M ,则梯形ABCD 转化为△BCM 和平行四边形ABMD 。
在△BCM 中,BM=AD=4,CM=CD -DM=CD -AB=8-3=5,所以BC 的取值范围是:5-4<BC<5+4,即1<BC<9。
2.平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
例2:如图,梯形ABCD 中,AD//BC ,E 、F 分别是AD 、BC 的中点,且EF ⊥BC 。
求证:∠B=∠C 。
CFEADB分析:过点E 作EM//AB ,EN//DC ,分别交BC 于点M 、N 。
梯形两腰、下底与腰的两个夹角集中于△EMN 中,由E 、F 分别是AD 、BC 的中点轻易得到,又由EF ⊥BC ,得EM=EN ,故∠EMN=∠ENM ,所以∠B=∠C 。
梯形中添加辅助线的六种常用技巧

梯形中添加辅助线的六种常用技巧Prepared on 22 November 2020梯形中添加辅助线的六种常用技巧浙江唐伟锋梯形是不同于平行四边形的一类特殊四边形,解决梯形问题的基本思路是通过添加辅助线,将梯形进行割补、拼接转化为三角形、平行四边形问题进行解决。
一般而言,梯形中添加辅助线的常用技巧主要有以下几种——一、平移一腰从梯形的一个顶点作一腰的平行线,将梯形转化为平行四边形和三角形,从而利用平行四边形的性质,将分散的条件集中到三角形中去,使问题顺利得解。
例1、如图①,梯形ABCD中AD∥BC,AD=2cm,BC=7cm,AB=4cm,求CD的取值范围。
解:过点D作DE∥AB交BC于E,∵AD∥BC,DE∥AB∴四边形ABED是平行四边形(两组对边分别平行的四边形是平行四边形)∴DE=AB=4cm,BE=AD=2cm∴EC=BC-BE=7-2=5cm在△DEC中,EC-DE<CD<EC+DE(三角形两边之和大于第三边,两边之差小于第三边)∴1cm<CD<9cm。
二、延长两腰将梯形的两腰延长,使之交于一点,把梯形转化为大、小两个三角形,从而利用特殊三角形的有关性质解决梯形问题。
例2、如图②,已知梯形ABCD中,AD∥BC,∠B=∠C,求证:梯形ABCD是等腰梯形。
证明:延长BA、CD,使它们交于E点,∵AD∥BC∴∠EAD=∠B,∠EDA=∠C(两直线平行,同位角相等)又∵B=∠C∴∠EAD=∠EDA∴EA=ED,EB=EC(等角对等边)∴AB=DC∴梯形ABCD是等腰梯形(两腰相等的梯形是等腰梯形)。
三、平移对角线从梯形上底的一个顶点向梯形外作一对角线的平行线,与下底延长线相交构成平行四边形和一特殊三角形(直角三角形、等腰三角形等)。
例3、如图③,已知梯形ABCD中,AD=1.5cm,B C=3.5cm,对角线AC⊥BD,且BD=3cm,AC=4cm,求梯形ABCD的面积。
解:过点D作DE∥AC交BC延长线于E∵AD∥BC,DE∥AC∴四边形ACED是平行四边形(两组对边分别平行的四边形是平行四边形)∴CE=AD=1.5cm,DE=AC=4cm∵AC ⊥BD∴DE ⊥BD∴S 梯形ABCD =111()()222AD BC h CE BC h BE h +⨯=+⨯=⨯(h 为梯形的高) 211346cm 22BD DE =⨯=⨯⨯= 。
梯形的辅助线课件

在几何证明中的应用
证明梯形性质
通过添加适当的辅助线,可以证明梯形的性质,如中位线定理、等腰梯形的性 质等。
证明其他几何定理
在证明其他几何定理时,如平行四边形的性质、勾股定理等,梯形辅助线可以 作为中间步骤。
在数学竞赛中的应用
解决竞赛题目
在数学竞赛中,如奥林匹克数学竞赛、美国数学竞赛等,梯形辅助线是解决某些 题目的关键。
培养解题思维
通过解决涉及梯形辅助线的竞赛题目,可以培养解题思维和创造性解决问题的能 力。
04 梯形辅助线的综合应用
多个辅助线的综合应用
梯形中,除了常见的作高、平移腰等辅助线方法外,还可以 通过作平行线、延长线等手段来解决问题。这些辅助线可以 单独使用,也可以组合使用,以实现更复杂的解题思路。
在解决梯形问题时,有时需要同时使用多种辅助线。例如, 在求梯形的面积时,可以先作高,再作平行于底边的线段, 将梯形划分为更易于计算面积的三角形和平行四边形。
数学证明
梯形的高等于上下底之差的一半,即 $frac{b - a}{2}$,其中 $a$ 和 $b$ 分别是梯形的上 底和下底。
梯形的角平分线
总结词
梯形的角平分线是一条将梯形的一个内角平分的线段。通过作角平分线,可以将梯形划分为一个平行四边形和一个三 角形。
详细描述
首先,找到梯形的一个内角,然后作一条经过该角的平分线。这条平分线将梯形划分为一个平行四边形和一个三角形 。平行四边形的对边相等且平行,三角形的角度被平分。
梯形与其他几何图形的结合
在解决几何问题时,有时需要将梯形与其他几何图形结合。例如,在求梯形的面 积时,可以将梯形划分为一个矩形和一个三角形;在求梯形的周长时,可以将梯 形划分为两个三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:1、AD+BC 怎 ∴ CD=CF 样用一条线段表示? 2、AD+BC跟哪条线 即CD=CB+BF=CB+AD 段有关?
已知,梯形ABCD中,AD∥BC,E是腰AB的中点, ∥ DE ⊥CE, 求证: AD+BC=CD。
一 题 多 证
分析:EF的双重角色
A
D F
证明:(二)构造中位线 E 取CD的中点F,并连结EF 则EF为梯形的中位线。 ∴2EF=AD+BC B Rt∆CDE中,2EF=CD ∴CD=AD+BC
A
D
F
G
B
E
C
HБайду номын сангаас
70°
40° 11
D
E
7
1= C ∴ ∠ 2= ∠1= 70 ° ∴CB=CE=CD─DE=11—4=7(cm)
分析: ∠D =70 °, ∠ C=40°在一个 三角形中结果会如何? 如何才能在一 个三角形中?
一题多解!
70°
解法2:(补三角形)
延长DA与CB交于O 则∠ OAB=∠ D=70 °
F
C
作 A D
高
B
E
F
C
O
补
A D
三
B C
角 形
1、 若梯形ABCD是等腰梯形时, ∆OBC是什么三角形? 2、梯形满足什么条件时, ∆OBC是直 角三角形?
A
D
平 移 对 角 线
B O C E
1、当AC⊥BD时,∆BED是什么三角形? 2、当AC =BD时,∆BED又是什么三角形? 3、哪个命题的证明应用了此法? 对角线相等的梯形是等腰梯形 4 、 ΔBED与梯形ABCD的面积关系如何?
在 梯 形 中 常 用 的 作 辅 助 线 方 法
开动脑筋
转 化 为 三 角 形 或 平 行 四 边
其他方法 平移腰 作 高 补为三角形 平移对角线
形 等
灵 活 应 用
A
D
A
D
平
B E
A D
E
C E O
B A
C D
移
腰
B
C B 1.以上图中相等的线段,相等的角 2.平移腰可将梯形的两腰、两底角放置在一个三角形.
平移腰后, 在Rt∆BDE中计算出 CE=20,则BC=CE+BE=30(cm) B
54º
36º
E
20
C
3、如图,梯形ABCD 中, AD∥BC, ∠B=60 °, ∠ C=45 ° ∥
AB= 2 3 , AD=2,则梯形周长=
A 2 D
2 3
B 60°
3
3 2
45 °
C
3
E` E
3
布置作业:
、求证:对角线垂直的等腰梯形的高等于它的中位线
C
练习:一、填空 1、如图,梯形ABCD中,AD∥BC, AC⊥BD且 ∥ AC=8cm,BD=15cm,则梯形的高 = cm.
先用勾股定理求出BE,再用面积法 求高DF。答案:120/17(cm) B 17 10 A D A D
15
8 F C E
2、梯形ABCD中,AD∥BC, AD∥ ∠B=54 °,∠C=36°, AD=10 AB=12 ,CD=16 则BC= 。
A 构造旋转变换
D O
其 他
B
方 法
证明哪个定理是应用了这个方法
?? 梯形ABCD面积与哪个图形面积相等?
构造中位线
C
E
例题:
1、如图,梯形ABCD 中, AB∥CD, ∠D=70 ° , ∠ C=40 ° ∥
AB=4cm,CD=11cm,求BC.
A
4
B
2
解:(平移腰) 过B作BE∥AD交DC于E 则∠ 1= ∠ D=70°,DE=AB=4 ∵△BCE中, ∠ C=40°∠1=70°
O
A
4
B
7
∵∠C=40°,∠ D=70 ° ∴ ∠O=70 °
70°
40 ° 11
∴ ∠ OAB= ∠O=∠ D=70 °
∴ BC=7
D
C ∴ OB=AB= 4,OC=CD=11
例2:已知,梯形ABCD中,AD∥BC,E是腰AB的中点,
DE ⊥CE, 求证: AD+BC=CD。 A 证明:(一)延长DE交CB延长线于F D ∵ AE=BE,∠A= ∠ ABF,∠ AED= ∠ BEF E ∴ ∆ADE≌∆BFE ∴ DE=FE,AD=BF F B C ∵ DE ⊥CE
