矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案高中数学
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)含答案人教版高中数学高考真题汇编辅导班专用

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.若矩阵A 有特征值122,1λλ=-=,它们所对应的特征向量分别为10i ⎡⎤=⎢⎥⎣⎦
和01j ⎡⎤=⎢⎥⎣⎦
,则矩阵A =______________. 2.函数221log ()2
y x =+的值域为_______________. 关键字:复合函数;求值域;对数 评卷人
得分 二、解答题
3.求使等式
成立的矩阵M 。
4.设M 是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变
换. 求逆矩阵1
M -以及椭圆22
149x y +=在1M -的作用下的新曲线的方程.。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)含答案人教版高中数学高考真题汇编艺考生专用

《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.பைடு நூலகம்题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1.若行列式 ,则 ________
2.已知 是二阶矩阵,且满足满足 ,则 =_____。
评卷人
,则 ,
即曲线 在矩阵MN变换下的函数解析式为 .……………8分
7.由题设得
由 ,可知A1(0,0)、B1(0,-2)、C1( ,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是 ,则由题设知: 。
所以k的值为2或-2。
8.
[解析]本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
8.在平面直角坐标系 中,设椭圆 在矩阵A= 对应的变换作用下得到曲线F,求F的方程.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.理0,文1;
2.
评卷人
得分
二、解答题
3.选修4—2:矩阵与变换
解:矩阵M的特征多项式为 .
令 ,对应的一个特征向量分别为 , .…5分
令 ,得 .
.……………10分
4.命题立意:本题主要考查二阶矩阵的逆矩阵,考查运算求解能力.
解:设 ,则由 得 ,(5分)
解得 所以 .(10分)
5.
6.(选做题)(本小题满分8分)
解:MN= = ,………………4分
设曲线 上的任意一点为 ,变换后的点为
即在矩阵MN变换下 ,………………6分
得分
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案人教版高中数学高考真题汇编艺考生专用

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 评卷人得分 一、填空题1.若行列式112124=-x x,则=x ________2.已知X 是二阶矩阵,且满足满足23321211X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,则X =_____。
4511-⎡⎤⎢⎥-⎣⎦132233223451112111211X ---⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦评卷人得分 二、解答题3.选修4—2:矩阵与变换已知矩阵1221⎡⎤=⎢⎥⎣⎦M ,17⎡⎤=⎢⎥⎣⎦β,计算6M β.4.已知矩阵A 的逆矩阵1A -1002⎡⎤=⎢⎥⎣⎦,求矩阵A .5.已知矩阵1121A ⎡⎤=⎢⎥⎣⎦,向量12β⎡⎤=⎢⎥⎣⎦,求向量α,使得2A αβ=. 设x y α⎡⎤=⎣⎦,由2A αβ=得:32432x y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,32111,43222x y x x y y α+==--⎧⎧⎡⎤∴∴∴=⎨⎨⎢⎥+==⎩⎩⎣⎦6.试求曲线x y sin =在矩阵MN 变换下的函数解析式,其中M =⎥⎦⎤⎢⎣⎡2001,N =⎥⎥⎦⎤⎢⎢⎣⎡10021.7.在平面直角坐标系xOy 中,已知点A(0,0),B(-2,0),C(-2,1)。
设k 为非零实数,矩阵M=⎥⎦⎤⎢⎣⎡100k ,N=⎥⎦⎤⎢⎣⎡0110,点A 、B 、C 在矩阵MN 对应的变换下得到点分别为A 1、B 1、C 1,△A 1B 1C 1的面积是△ABC 面积的2倍,求k 的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。
满分10分。
8.在平面直角坐标系xOy 中,设椭圆2241x y +=在矩阵A=⎣⎡⎦⎤2 00 1对应的变换作用下得到曲线F ,求F 的方程.【参考答案】***试卷处理标记,请不要删除评卷人得分 一、填空题1.理0,文1;2. 评卷人得分 二、解答题3. 选修4—2:矩阵与变换解:矩阵M 的特征多项式为212()2321f λλλλλ--==----. 令12()031f λλλ===-,解得,,对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α,211⎡⎤=⎢⎥-⎣⎦α. …5分 令12m n =+βαα,得4,3m n ==-.6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α.……………10分4.命题立意:本题主要考查二阶矩阵的逆矩阵,考查运算求解能力.解:设a b c d ⎡⎤=⎢⎥⎣⎦A ,则由1-=AA E 得10100201a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,(5分)解得1 0 0 1 2a b c d =⎧⎪=⎪⎨=⎪⎪=⎩,,,,所以10102⎡⎤⎢⎥=⎢⎥⎣⎦A .(10分) 5.6.(选做题)(本小题满分8分)解:MN = ⎥⎦⎤⎢⎣⎡2001⎥⎥⎦⎤⎢⎢⎣⎡10021=⎥⎥⎦⎤⎢⎢⎣⎡20021,……………… 4分 设曲线sin y x =上的任意一点为(),x y ,变换后的点为(),x y ''''即在矩阵MN 变换下⎢⎢⎣⎡⎥⎥⎦⎤=⎢⎣⎡⎥⎦⎤''''→⎢⎣⎡⎥⎦⎤y x y x y x 221,……………… 6分 212x x y y ''=⎧⎪∴⎨''=⎪⎩,则x y ''=''2s in 21, 即曲线x y s in =在矩阵MN 变换下的函数解析式为x y 2sin 2=.…………… 8分7.由题设得0010011010k k MN ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦由00220010001022k k --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,可知A 1(0,0)、B 1(0,-2)、C 1(k ,-2)。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案人教版新高考分类汇编

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 评卷人得分 一、填空题1.若行列式112124=-x x,则=x ________2.方程0c os s in s in c os =xx xx 的解为_____)(,42Z k k x ∈+=ππ______. 评卷人 得分二、解答题3.已知在一个二阶矩阵M 对应变换的作用下,点(1,2)A 变成了点(7,10)A ',点(2,0)B 变成了点(2,4)B ',求矩阵M 的逆矩阵1M -.4.已知矩阵0201,00M N m n ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,若矩阵MN 的对应的变换把直线40x y -+=变成直线40x y ++=,求实数,m n 的值。
5.已知为矩阵属于λ的一个特征向量,求实数a ,λ的值及A 2。
6.在平面直角坐标系xOy 中,已知点A(0,0),B(-2,0),C(-2,1)。
设k 为非零实数,矩阵M=⎥⎦⎤⎢⎣⎡100k ,N=⎥⎦⎤⎢⎣⎡0110,点A 、B 、C 在矩阵MN 对应的变换下得到点分别为A 1、B 1、C 1,△A 1B 1C 1的面积是△ABC 面积的2倍,求k 的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。
满分10分。
7.在平面直角坐标系xOy 中,设椭圆2241x y +=在矩阵A=⎣⎡⎦⎤2 00 1对应的变换作用下得到曲线F ,求F 的方程.8.已知矩阵111A a -⎡⎤=⎢⎥⎣⎦,其中a R ∈,若点(1,1)P 在矩阵A 的变换下得到的点1(0,3)P -(Ⅰ)求实数a 的值;(Ⅱ)求矩阵A 的特征值及特征向量.【参考答案】***试卷处理标记,请不要删除评卷人得分 一、填空题1.理0,文1;2. 评卷人得分 二、解答题3.解:设1a b Mc d -⎡⎤=⎢⎥⎣⎦,依题意有:7122,10240a b a b c d c d ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦------4分 即71017102242240a b c d a b c d +=⎧⎪+=⎪⎨+=⎪⎪+=⎩ ,解之得232112a b c d =-⎧⎪⎪=⎪⎨=⎪⎪=-⎪⎩ ------8分 所以1322112M -⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦------10分 4.5.6.由题设得0010011010k k MN ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦由00220010001022k k --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,可知A 1(0,0)、B 1(0,-2)、C 1(k ,-2)。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案人教版高中数学真题技巧总结提升辅导班专用

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.已知矩阵27b A a -⎡⎤=⎢⎥-⎣⎦的逆矩阵是273a B ⎡⎤=⎢⎥⎣⎦
,则=+b a . 2.设曲线22
:41C x y +=在(,)(2,)x y x y y →-对应的变换下变成另一条曲线'C ,则曲线'C 的方程为______22':(2)41C x y y ++= 评卷人
得分 二、解答题
3.(本小题满分14分)
已知二阶矩阵M 有特征值=8λ及对应的一个特征向量11=1e ⎡⎤⎢⎥⎣⎦,并且矩阵M 对应的变换将点(-1,2)变换成(-2,4)。
(1)求矩阵M ;
(2)求矩阵M 的另一个特征值。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案人教版高中数学辅导班专用

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人得分一、填空题1.直线1+=x y 在矩阵⎢⎣⎡11 ⎥⎦⎤-20作用下变换得到的图形与122=+y x 的位置关系是___.2.若2211x x x y y y =--,则______x y +=(汇编年高考上海卷(理)) 评卷人得分二、解答题3.(选修4—2:矩阵与变换)(本小题满分10分)设矩阵00a b ⎡⎤=⎢⎥⎣⎦M (其中00a b >,>),若曲线C :221x y +=在矩阵M 所对应的变换作用下得到曲线2214x C y '+=:,求a b +的值.4.若圆1:22=+y x C 在矩阵)0,0(00>>⎥⎦⎤⎢⎣⎡=b a b a A 对应的变换下变成椭圆,134:22=+y x E 求矩阵A 的逆矩阵1-A .5.已知M= 1 -23,-2 11α⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,试计算20M α6.已知在一个二阶矩阵M 的变换作用下, 点(12)A ,变成了点(45)A',,点(31)B -,变成了点(51)B',,求矩阵M .7.在直角坐标系中,已知△ABC 的顶点坐标为A (0,0),B (2,0),C (2,1),求△ABC 在矩阵MN作用下变换所得到的图形的面积,这里矩阵:8.已知矩阵⎥⎦⎤⎢⎣⎡-=111a A ,其中R a ∈,若点P (1,1)在矩阵A 的变换下得到点P ’(0,-3),(1)求实数a 的值; (2)求矩阵A 的特征值及特征向量【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1. 2.. 评卷人得分二、解答题3. (选修4-2:矩阵与变换)设曲线C :221x y +=上任意一点(,)P x y ,在矩阵M 所对应的变换作用下得到点111(,)P x y ,则1100x a x b y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即11a x xb y y=⎧⎨=⎩. …………………………………………………………5分又点111(,)P x y 在曲线2214x C y '+=:上,所以221114x y +=,则2214ax by +=为曲线C 的方程.又曲线C 的方程为221x y +=,故24a =,21b =, 因为00a b >,>,所以3a b +=. …………………………………………………………10分4.设点(,)P x y 为圆C :221x y +=上任意一点,经过矩阵A 变换后对应点为(,)P x y ''',则00a x ax x b y by y '⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦,所以,x ax y by '=⎧⎨'=⎩.…………………………………………2分因为点(,)P x y '''在椭圆E :22143x y =+上,所以2222143a x b y =+,………………4分又圆方程为221x y +=,故221,41,3a b ⎧=⎪⎪⎨⎪=⎪⎩,即224,3,a b ⎧=⎪⎨=⎪⎩,又0a >,0b >,所以2a =,3b =.所以2003⎡⎤=⎢⎥⎣⎦A ,……………………………………………………………………6分所以1102303-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A .…………………………………………………………………10分5.解:矩阵M 的特征多次式为212()(1)40,3,1f λλλλ=--===-, 对应的特征向量分别为11⎡⎤⎢⎥-⎣⎦和11⎡⎤⎢⎥⎣⎦,而11211α⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,所以2020202020113232(1)1132M α⎡⎤+⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎢⎥--+⎢⎥⎣⎦⎣⎦⎣⎦6.设a b c d ⎡⎤=⎢⎥⎣⎦M , 则由1425a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,3511a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,···2112⎡⎤=⎢⎥⎣⎦M .7.8.解:(1)4-=a(2)特征值3对应特征向量为 ⎥⎦⎤⎢⎣⎡-21 , 特征值-1对应特征向量为⎥⎦⎤⎢⎣⎡21。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)附答案人教版高中数学高考真题汇编
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
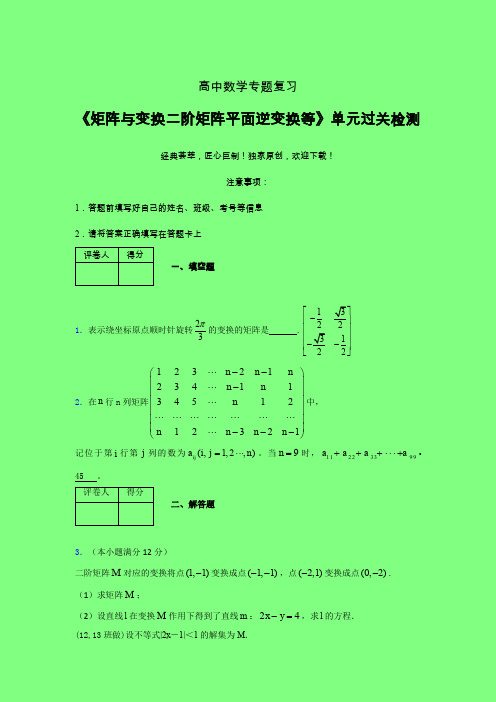
1.表示绕坐标原点顺时针旋转23π的变换的矩阵是 .13223122⎡⎤-⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦
2.在n 行n 列矩阵12321234113451212321n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪
⎪⋅⋅⋅ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭
中, 记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅。
当9n =时,11223399a a a a +++⋅⋅⋅+= 45 。
评卷人
得分 二、解答题
3.(本小题满分12分)
二阶矩阵M 对应的变换将点(1,1)-变换成点(1,1)--,点(2,1)-变换成点(0,2)-.
(1)求矩阵M ;
(2)设直线l 在变换M 作用下得到了直线m :24x y -=,求l 的方程.
(12,13班做)设不等式|2x -1|<1的解集为M .。
矩阵与变换二阶矩阵平面逆变换等单元过关检测卷(六)带答案人教版高中数学新高考指导辅导班专用

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上评卷人得分一、填空题1.坐标平面内某种线性变换将椭圆2212yx+=的上焦点变到直线3y x=上,则该变换对应的矩阵a bc d⎡⎤⎢⎥⎣⎦中的,,,a b c d应满足关系为3d b=12.行列式cos sin36sin cos36ππππ的值是 0 。
评卷人得分二、解答题3.选修4—2:矩阵与变换已知矩阵1221⎡⎤=⎢⎥⎣⎦M,17⎡⎤=⎢⎥⎣⎦β,计算6Mβ.4.已知矩阵⎥⎦⎤⎢⎣⎡=41b aA ,若矩阵A 属于特征值1的一个特征向量为α1=⎥⎦⎤⎢⎣⎡-13,属于特征值5的一个特征向量为α2=⎥⎦⎤⎢⎣⎡11.求矩阵A ,并写出A 的逆矩阵.5.试求曲线x y sin =在先经过矩阵M =1002⎡⎤⎢⎥⎣⎦的变换,再经过矩阵N =10201⎡⎤⎢⎥⎢⎥⎣⎦的变换后所得的新曲线方程.6.若点A (2,2)在矩阵cos sin sin cos αααα-⎡⎤=⎢⎥⎣⎦M 对应变换的作用下得到的点为B (-2,2),求矩阵M 的逆矩阵.7.学校餐厅每天供应1000名学生用餐,每星期一有A 、B 两样菜可供选择,调查资料表明,凡是在本周星期一选A 菜的,下周星期一会有20%改选B ,而选B 菜的,下周星期一则有30%改选A ,若用A n 、B n 分别表示在第n 个星期一选A 、B 菜的人数。
(1)若⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++n n n n B A M B A 11,请你写出二阶矩阵M ; (2)求二阶矩阵M 的逆矩阵。
8.已知曲线C :1=xy(1)将曲线C 绕坐标原点逆时针旋转045后,求得到的曲线'C 的方程; (2)求曲线C 的焦点坐标和渐近线方程.【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1.2.考查行列式运算法则= 评卷人得分二、解答题3. 选修4—2:矩阵与变换 解:矩阵M 的特征多项式为212()2321f λλλλλ--==----. 令12()031f λλλ===-,解得,,对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α,211⎡⎤=⎢⎥-⎣⎦α. …5分令12m n =+βαα,得4,3m n ==-.6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α.……………10分4.选修4—2 矩阵与变换解:由矩阵A 属于特征值1的一个特征向量为α1=⎥⎦⎤⎢⎣⎡-13可得,⎥⎦⎤⎢⎣⎡41b a⎥⎦⎤⎢⎣⎡-13=⎥⎦⎤⎢⎣⎡-13,即33=-b a ; 3分由矩阵A 属于特征值5的一个特征向量为α2=⎣⎢⎡⎦⎥⎤11,可得⎥⎦⎤⎢⎣⎡41b a ⎥⎦⎤⎢⎣⎡11=5⎥⎦⎤⎢⎣⎡11, 即5=+b a , 6分解得⎩⎨⎧==32b a 即A =⎥⎦⎤⎢⎣⎡4312, 7分 A 的逆矩阵是⎥⎥⎥⎦⎤-⎢⎢⎢⎣⎡-5253515410分 5.6.2222-⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦M ,即2cos 2sin 22sin 2cos 2αααα--⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦, (4)分 所以cos sin1,sin cos 1.αααα-=-⎧⎨+=⎩解得cos 0,sin 1.αα=⎧⎨=⎩……………………………………………6分 所以0110M -⎡⎤=⎢⎥⎣⎦.由1M M -=1001⎡⎤⎢⎥⎣⎦,得10110M -⎡⎤=⎢⎥-⎣⎦.………………………10分 另01=M10-=10≠, 10110-⎡⎤=⎢⎥-⎣⎦M . 另01cos90sin 9010sin 90cos90-︒-︒⎡⎤⎡⎤==⎢⎥⎢⎥︒︒⎣⎦⎣⎦M ,看作绕原点O 逆时针旋转90°旋转变换矩阵,于是1cos(90)sin(90)sin(90)cos(90)--︒--︒⎡⎤=⎢⎥-︒-︒⎣⎦M 0110⎡⎤=⎢⎥-⎣⎦. 7.B 解题探究:认真阅读题目,理解题意,得到A n 、B n 与1+n A 、1+n B 之间的关系式,再用矩阵形式表示,根据逆矩阵的定义求之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.若22
11
x x x y y y =--,则______x y +=(汇编年高考上海卷(理)) 2.椭圆1162522=+y x 经过矩阵M 变换后得到的曲线方程为125
162
2=+y x ,试写出一个满足要求的矩阵=M 评卷人
得分 二、解答题
3.已知矩阵⎥⎦⎤⎢⎣⎡=d c A 33,若矩阵A 属于特征值6的一个特征向量为⎥⎦
⎤⎢⎣⎡=111α,属于特征值1的一个特征向量为⎥⎦⎤⎢
⎣⎡-=232α.求矩阵A 的逆矩阵.
4.已知矩阵A =2143-⎡⎤=⎢⎥-⎣⎦
A ,
B =4131-⎡⎤=⎢⎥-⎣⎦B , 求满足AX =B 的二阶矩阵X .
5.求曲线2
2210x xy -+=在矩阵MN 对应的变换作用下得到的曲线方程,其中1002⎡⎤=⎢⎥⎣⎦M ,1011⎡⎤=⎢⎥-⎣⎦
N . 6.试用行列式解二元一次方程组⎩
⎨⎧=-+=++0530142y x y x
7.已知矩阵⎥⎦⎤⎢⎣⎡=d c A 33,若矩阵A 属于特征值6的一个特征向量为⎥⎦
⎤⎢⎣⎡=111α, 属于特征值1的一个特征向量为⎥⎦⎤⎢
⎣⎡-=232α.求矩阵A ,并写出A 的逆矩阵.
8.已知矩阵⎥⎦⎤⎢
⎣⎡-=2112A ,⎥⎦
⎤⎢⎣⎡-=1021B ,记AB C =. (Ⅰ)求1-C ; (Ⅱ)若矩阵B 把直线l :20x y ++=变为直线l ',求直线l '的方程.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分 一、填空题
1..
2. 评卷人
得分 二、解答题
3.由矩阵A 属于特征值6的一个特征向量为⎥⎦⎤
⎢⎣⎡=111α,可得⎥⎦⎤⎢⎣⎡d c 33⎥⎦⎤⎢⎣⎡11=6⎥⎦
⎤⎢⎣⎡11, 即6=+d c ;
由矩阵A 属于特征值1的一个特征向量为⎥⎦
⎤⎢⎣⎡-=232α可得,⎥⎦⎤⎢⎣⎡d c 33⎥⎦
⎤⎢⎣⎡-23=⎥⎦
⎤⎢⎣⎡-23,
即223-=-d c , 解得⎩⎨⎧==,4,2d c 即A =⎥⎦⎤⎢⎣⎡4233,A 逆矩阵是⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡2131-21-32. 4.解:由题意得1312221-⎡⎤⎢⎥=⎢⎥⎣⎦
A ,…………………………5′ =AX
B ,1
319411222312151-⎡⎤⎡⎤--⎡⎤⎢⎥⎢⎥∴===⎢⎥⎢⎥⎢⎥-⎣⎦-⎣⎦⎣⎦X A B …………………………10′
5.
6.
7.解:由矩阵A 属于特征值6的一个特征向量为111α⎡⎤=⎢⎥⎣⎦
可得,
3311611c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
,
即c +d =6; ………………………………………2分
由矩阵A 属于特征值1的一个特征向量为232α⎡⎤=⎢⎥-⎣⎦,可得333322c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦, 即3c -2d =-2, …………………………………………6分
解得233424c A a =⎧⎡⎤⇒=⎨⎢⎥=⎩⎣⎦
…………………………8分 A 的逆矩阵 12/31/21/31/2A c -⎡⎤=⎢⎥⎣⎦
8.已知矩阵⎥⎦⎤⎢
⎣⎡-=2112A ,⎥⎦
⎤⎢⎣⎡-=1021B ,记AB C =. (Ⅰ)求1-C ;
(Ⅱ)若矩阵B 把直线l :x y ++2=0变为直线l ',求直线l '的方程.
解: (Ⅰ)AB C = = 2314-⎡⎤⎢⎥-⎣⎦
, …………2分 =-1C 2314-⎡⎤⎢⎥-⎣⎦; …………5分 (Ⅱ) 任取直线l 上一点P (x ,y )经矩阵B 变换后为点(),P x y ''', 则12201x x x y y y y '--⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦
⎣⎦⎣⎦⎣⎦, 2,,x x y y y '=-⎧∴⎨'=⎩ ∴2,.x x y y y ''=+⎧⎨'=⎩
代入x y ++2=0得:220,x y y '''+++=
∴320,x y ''++=
∴直线l'的方程为320
++=.
x y。
