高一数学立体几何练习题及部分标准答案汇编
高一数学立体几何大题(含答案)

4.in/w).6=4r3.
例 3:如图,PD ⏊ 平面 ABCD,AD ⏊ CD,AB ⎳ CD,PQ ⎳ CD,AD
= CD = DP = 2PQ = 2AB = 2, 点 M 为 BQ 的中点 .
为 的 P Q C -
M-
大小
0 .
Sepm E 却 二
忙=
以 <m (
,
蕊 令 1
二
5 = -
3
※ 琴 㱺 sina.me
㱺 Somc 二 士 心 的 ✗
=r
.
二号 器 Q到 平面 阰 的 距离 为 : d = 2 5
.io
shnoifst.no
,
㱺 VQ-pmc-f-Somc.dk/nEfsio=fs'm0.
PCHEF 进而 1211 平面 ,
在 阳 仲 , PA-E.AE/,PC=0=)PA4AcEpc2=sAc-1A.
所以 又由 题 干 知 : A 4 P B ,
A
C
1
-
平面阳
13
.
13) 易知 SEFG 二 ftp.c , 所以 /7AB=fSopAB-AC.=f-li2nE.iS'm45J-l
1 求二面角 Q - PM - C 的正弦值;
2 若 N 为线段 CQ 上的点,且直线 DN 与平面 PMQ 所成的角为
π 6
,
求线段
QN
的长
.
子 (2) 由 山 知 二面⻆ QPMC 的 大小 为 ,
劝 的平面 PMQ所 成的 ⻆ 为 至
所以 叽 与平面PMC 所 成的 ⻆
高一立体几何试题及答案详解
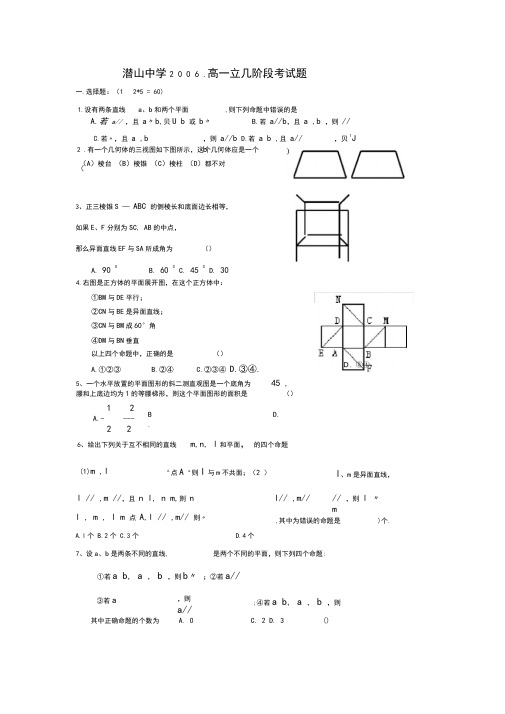
潜山中学2 0 0 6 .高一立几阶段考试题A.若 a// ,且 a 〃b,贝U b 或 b 〃B.若 a//b ,且 a ,b ,则 //l , m , l m 点 A,l // ,m// 则〃A.l 个B.2个C.3个D.4个7、设a 、b 是两条不同的直线,是两个不同的平面,则下列四个命题:①若a b, a , b ,则b 〃 ;②若a//一.选择题:(1 2*5 = 60) 1.设有两条直线a 、b 和两个平面,则下列命题中错误的是C .若〃,且 a ,b ,则 a//bD .若 a b ,且 a// ,贝1Jb 2 .有一个几何体的三视图如下图所示,这个几何体应是一个( (A )棱台 (B )棱锥 (C )棱柱 (D )都不对 3、正三棱锥S — ABC 的侧棱长和底面边长相等, 如果E 、F 分别为SC, AB 的中点, 那么异面直线EF 与SA 所成角为 () A. 90 0 B. 60 0 C. 45 0D. 30 4.右图是正方体的平面展开图,在这个正方体中: ①BM 与DE 平行; ②CN 与BE 是异面直线; ③CN 与BM 成60°角 ④DM 与BN 垂直 以上四个命题中,正确的是 () A.①②③ B.②④ C.②③④ D.③④. 5、一个水平放置的平面图形的斜二测直观图是一个底角为 45 ,腰和上底边均为1的等腰梯形,则这个平面图形的面积是()1 2 A.- --- 2 2 B.D. 6、给出下列关于互不相同的直线 m,n, l 和平面, 的四个命题 (1)m ,l A,点A m,则l 与m 不共面;(2 )l 、m 是异面直线,l // ,m //,且 n l, n m,则 n l// ,m//// ,则 l 〃m③若a,则a//;④若a b, a , b ,则其中正确命题的个数为A. 0C. 2D. 3 (),其中为错误的命题是)个.8 .定点P 不在4ABC 所在平面内,过P 作平面a ,使^ ABC 的三个顶点到a 的距离相等,二.填空题:(4*6 = 2 4)14.106山东•理】如图,在等腰梯形 ABCD 中,AB=2DC=2 , / DAB=60 中点,将 AADE 与4BEC 分别沿ED 、EC 向上折起,使 A 、B 重 合于点P,则三棱锥P —DCE 的外接球的体积为 II 5如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D, E, F ,且知有()(A ) 1 个 (B ) 2 个 9、下列各图是正方体或正四面体, (C) 3 个(D) 4 个P, Q, R, S 分别是所在棱的中点,这四个点中不共面的一个图是SSSSQQQ Q0、如图,在一根长 (B) (C) (D)11cm,外圆周长6cm 的圆柱形柱体外表面,用一根细铁丝缠绕,组成 如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为 (A) 61cm (B) J157 cm (C) J1021 cm1 .(天津卷10)如图,在长方体 ABCD A 1B 1c l D 1中,AB A D 1的两个平行截面将长方体分成三部分, 其体积分别记为 V I V AEA 1 DFD I ,V 3 VB I E I BC 1F 1C 。
高一数学立体几何练习题及部分答案大全

立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 4 3.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( ) A 1个 或2个 B 0个或1个 C 1个 D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直 7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个 8.下列条件中,能判断两个平面平行的是( ) A 一个平面内的一条直线平行于另一个平面; B 一个平面内的两条直线平行于另一个平面 C 一个平面内有无数条直线平行于另一个平面 D 一个平面内任何一条直线都平行于另一个平面 9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( ) A //,,m n n m βα⊥⊂ B //,,m n n m βα⊥⊥ C ,,m n m n αβα⊥=⊂ D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( ) A 1个 B 2个 C 3个 D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
高一数学立体几何练习题及部分答案大全.docx

立体几何试题一.选择题(每题 4 分,共 40 分)1. 已知 AB3003001500空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形, (2)四边相等的四边形是菱形(4)有两边及其夹角对应相等的两个三角(3)平行于同一条直线的两条直线平行 ;形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A平行B相交C在平面内D平行或在平面内4. 已知直线 m过平面外一点,作与平行的平面,则这样的平面可作()A 1 个或 2 个B 0个或1个C1个 D 0个6.如图 , 如果 MC 菱形 ABCD 所在平面 , 那么 MA与 BD的位置关系是 ( )A平行B垂直相交C异面D相交但不垂直7. 经过平面外一点和平面内一点与平面垂直的平面有()A 0 个B 1个C无数个 D 1个或无数个8.下列条件中 , 能判断两个平面平行的是 ( )B一个平面内的两条直线平行于另一个平面C一个平面内有无数条直线平行于另一个平面D一个平面内任何一条直线都平行于另一个平面9. 对于直线m ,n 和平面,, 使成立的一个条件是 ( )A m // n, n, mB m // n, n,mC m n,I m, nD m n, m //, n //)10 . 已知四棱锥 , 则中 , 直角三角形最多可以有 (A 1个B2个 C 3个D4个二.填空题(每题 4 分,共16 分)11. 已知ABC的两边 AC,BC分别交平面于点M,N,设直线AB与平面交于点O,则点 O与直线 MN的位置关系为 _________12.过直线外一点与该直线平行的平面有 ___________个,过平面外一点与该平面平行的直线有_____________条13. 一块西瓜切 3 刀最多能切 _________块14.将边长是 a 的正方形 ABCD沿对角线 AC 折起 , 使得折起后 BD得长为 a, 则三棱锥D-ABC的体积为 ___________三、解答题15(10 分)如图,已知 E,F 分别是正方形ABCD A1B1C1 D1的棱 AA1和棱 CC1上的点,且 AE C1 F 。
高一必修二立体几何练习试题(含答案)

《立体几何初步》练习题一、 选择题1、一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )A 、垂直B 、平行C 、相交不垂直D 、不确定 2. 在正方体1111ABCD A B C D -中, 与1A C 垂直的是( )A. BDB. CDC. BCD. 1CC3、线n m ,和平面βα、,能得出βα⊥的一个条件是( )A.βα//n ,//m ,n m ⊥B.m ⊥n ,α∩β=m ,n ⊂αC.αβ⊆⊥m n n m ,,//D.βα⊥⊥n m n m ,,//4、平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行;B.直线a//α,a//βC.直线a α⊂,直线b β⊂,且a//β,b//αD.α内的任何直线都与β平行 5、设m 、n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n //α,则m n ⊥ ②若αβ//,βγ//,m ⊥α,则m ⊥γ ③若m //α,n //α,则m n // ④若αγ⊥,βγ⊥,则//αβ其中正确命题的序号是( ) A.①和② B.②和③ C.③和④ D.①和④6.点P 为ΔABC 所在平面外一点,PO ⊥平面ABC ,垂足为O,若PA=PB=PC ,则点O 是ΔABC 的( ) A.内心 B.外心 C.重心 D.垂心7. 若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥ C. 若,//l l αβ⊥,则αβ⊥ D .若,l n m n ⊥⊥,则//l m 8. 已知两个平面垂直,下列命题中正确的个数是( ) ①一个平面内的已知直线必垂直于另一个平面的任意一条直线; ②一个平面内的已知直线必垂直于另一个平面的无数条直线; ③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面. A.3 B.2 C.1 D.09.(2013浙江卷)设m.n 是两条不同的直线,α.β是两个不同的平面,( )A .若m ∥α,n ∥α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥n,m ⊥α,则n ⊥αD .若m ∥α,α⊥β,则m ⊥β10.(2013广东卷)设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若//l α,//l β,则//αβ B .若l α⊥,l β⊥,则//αβ C .若l α⊥,//l β,则//αβ D .若αβ⊥,//l α,则l β⊥二、填空题11、在棱长为2的正方体ABCD —A 1B 1C 1D 1中,E ,F 分别是棱AB ,BC 中点,则三棱锥B —B 1EF 的体积为 .12.对于空间四边形ABCD ,给出下列四个命题:①若AB=AC ,BD=CD 则BC ⊥AD ;②若AB=CD ,AC=BD 则BC ⊥AD ;③若AB ⊥AC ,BD ⊥CD 则BC ⊥AD ;④若AB ⊥CD , BD ⊥AC 则BC ⊥AD ;其中真命题序号是 .13. 已知直线b//平面α,平面α//平面β,则直线b 与β的位置关系为 .14. 如图,△ABC 是直角三角形,∠ACB=︒90,PA ⊥平面ABC ,此ABCP图形中有 个直角三角形三、解答题15.如图,PA ⊥平面ABC ,平面PAB ⊥平面PBC 求证:AB ⊥BC16.如图,ABCD 和ABEF 都是正方形,M AC N FB ∈∈,,且AM FN =。
【必刷题】2024高一数学下册立体几何初步专项专题训练(含答案)

【必刷题】2024高一数学下册立体几何初步专项专题训练(含答案)试题部分一、选择题:1. 在空间直角坐标系中,点A(1,2,3)关于x轴的对称点的坐标是()A. (1,2,3)B. (1,2,3)C. (1,2,3)D. (1,2,3)2. 下列关于直线l:x=1,y=2+t,z=32t的描述,正确的是()A. 直线l平行于x轴B. 直线l平行于y轴C. 直线l平行于z轴D. 直线l垂直于x轴3. 一个正方体的对角线长度为6根号3,则其表面积为()A. 216B. 54C. 108D. 1444. 若长方体的长、宽、高分别为2cm、3cm、4cm,则其对角线长度为()A. 5cmB. 6cmC. 7cmD. 9cm5. 下列关于平面α:2x3y+z=6的描述,正确的是()A. 平面α平行于x轴B. 平面α平行于y轴C. 平面α平行于z轴D. 平面α垂直于x轴6. 下列关于点P(2,3,4)到平面α:x+y+z=6的距离,正确的是()A. 1B. 2C. 3D. 47. 若三棱锥的底面是边长为1的正三角形,侧棱长为根号3,则其体积为()A. 1/3B. 1/6C. 1/9D. 1/128. 下列关于球体的描述,正确的是()A. 球体的表面积与半径成正比B. 球体的体积与半径成正比C. 球体的表面积与半径的平方成正比D. 球体的体积与半径的平方成正比9. 若四面体的四个面均为等边三角形,边长为a,则其体积为()A. a^3/6B. a^3/12C. a^3/18D. a^3/2710. 下列关于空间向量夹角的描述,正确的是()A. 向量a与向量b的夹角为90°,则a·b=0B. 向量a与向量b的夹角为0°,则a·b=0C. 向量a与向量b的夹角为180°,则a·b=0D. 向量a与向量b的夹角为60°,则a·b=0二、判断题:1. 在空间直角坐标系中,点A(0,0,0)到点B(1,1,1)的距离等于根号3。
高一立体几何试卷及答案
高一立体几何试卷及答案The document was prepared on January 2, 2021立体几何试题一.选择题每题4分,共40分1.已知AB 0300300150空间,下列命题正确的个数为1有两组对边相等的四边形是平行四边形,2四边相等的四边形是菱形3平行于同一条直线的两条直线平行 ;4有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有A 1个B 2个C 3个D 4个二.填空题每题4分,共16分11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N,设直线AB 与平面α交于点O,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题1510分如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =.求证:四边形1EBFD 是平行四边形1610分如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明:直线PC 与平面ABD 垂直CB1712分如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC1812分如图,长方形的三个面的对角线长分别是a,b,c,求长方体对角线AC'的长C1bC BA答案1三点共线2无数 无数3a 1证明: 1AE C F = 11AB C D =11EAB FC D ∠=∠∴ 11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG 1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++。
高一数学立体几何练习题及部分答案汇编之欧阳法创编
立体几何试题一.选择题(每题4分,共40分)1.已知AB//PQ,BC//QR,则∠PQP等于()A 030B 030C 0150 D 以上结论都不对2.在空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m//平面α,直线n在α内,则m 与n的关系为()A 平行B 相交C 平行或异面D 相交或异面5.经过平面α外一点,作与α平行的平面,则这样的平面可作()A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平面,那么MA 与BD的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有()A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
立体几何经典习题集(含答案)
立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
高一立体几何试卷及答案
立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( )A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂ID ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何试题一.选择题(每题4分,共40分)1.已知AB//PQ,BC//QR,则∠PQP等于()A 030B 030C 0150 D 以上结论都不对2.在空间,下列命题正确的个数为()(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是()A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m//平面α,直线n在α内,则m与n的关系为()A 平行B 相交C 平行或异面D 相交或异面5.经过平面α外一点,作与α平行的平面,则这样的平面可作()A 1个或2个B 0个或1个C 1个D 0个6.如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有()8.下列条件中,能判断两个平面平行的是( )A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( )A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂ID ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( )A 1个B 2个C 3个D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、解答题15(10分)如图,已知E,F 分别是正方形ABCD A B C D -的棱AA 和棱CC 上的点,且1AE C F =。
求证:四边形1EBFD 是平行四边形16(10分)如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明:直线PC 与平面ABD 垂直 PDBA17(12分)如图,正三棱锥A-BCD ,底面边长为a ,则侧棱长为2a ,E,F 分别为AC,AD 上的动点,求截面BEF ∆周长的最小值和这时E,F 的位置.DC18(12分)如图,长方形的三个面的对角线长分别是a,b,c ,求长方体对角线AC '的长C1b CBA答案1.D2.B3.D4.C5.C6.C7.D 8.D 9.A 10.D1三点共线2无数无数 3. 74 123a1证明: 1AE C F =Q11AB C D =11EAB FC D ∠=∠∴11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。
求证:四边形1EBFD 是平行四边形∆所在平面外一点,AP=AC,BP=BC,D为PC的中点,6(10分)如图,P为ABC证明:直线PC与平面ABD垂直B17(12分)如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC18(12分)如图,长方形的三个面的对角线长分别是a,b,c ,求长方体对角线AC '的长C1b CBA答案1证明: 1AE C F =Q11AB C D =11EAB FC D ∠=∠∴11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG∴四边形1EBFD 是平行四边形4 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥5 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++高一数学必修2立体几何测试题试卷满分:100分考试时间:120分钟班级___________姓名__________ 学号_________ 分数___________第Ⅰ卷一、选择题(每小题3分,共30分)A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能4、在正方体1111ABCD A B C D -中,下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45o 角D 、11AC 与1B C 成60o 角5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中:(1)平行于同一直线的两个平面平行;(2)平行于同一平面的两个平面平行;(3)垂直于同一直线的两直线平行;(4)垂直于同一平面的两直线平行.其中正确的个数有A 、1B 、2C 、3D 、47、在空间四边形ABCD 各边AB BC CD DA 、、、上分别取E F G H 、、、四点,如果与EF GH 、能相交于点P ,那么A 、点P 不在直线AC 上B 、点P 必在直线BD 上C 、点P 必在平面ABC 内D 、点P 必在平面ABC 外8、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有A 、0个B 、1个C 、2个D 、3个9、已知二面角AB αβ--的平面角是锐角θ,α内一点C 到β的距离为3,点C 到棱AB 的距离为4,B1C 1A 1D 1BAC D那么tan θ的值等于A 、34 B、35CD 10、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2V B 、3V C 、4V D 、5V二、填空题(每小题4分,共16分)11、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).12、正方体1111ABCD A B C D -中,平面11AB D 和平面1BC D 的位置关系为13、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .14、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD满足条件_________时,有A 1 B ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)第Ⅱ卷一、选择题(每小题3分,共30分)二、填空题(每小题4分,共16分)11、 12、 13、 14、三、解答题(共54分,要求写出主要的证明、解答过程)15、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长. (7分)QP C'B'A'CBA16、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG. 求证:EH ∥BD . (8分)17、已知ABC ∆中90ACB ∠=o ,SA ⊥面ABC ,ADSC ⊥,求证:AD ⊥面SBC .(8分)18、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V 与x 的函数关系式,并求出函数的定义域. (9分)H G F ED BA CSDCBA点.19、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D . (10分)20、已知△BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD , ∠ADB =60°,E 、F 分别是AC 、AD 上的动点,且(01).AE AFAC ADλλ==<< (Ⅰ)求证:不论λ为何值,总有平面BEF ⊥平面ABC ; (Ⅱ)当λ为何值时,平面BEF ⊥平面ACD ? (12分)1A FEDBAC高一立体几何试题一、选择题:(每题5分)1.下列说法中正确的个数为()①以直角梯形的一腰为轴旋转所得的几何体是圆台②用一个平面去截圆锥,得到一个圆锥和一个圆台③各个面都是三角形的几何体是三棱锥④以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥⑤棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥⑥圆锥的顶点与底面圆周上的任意一点的连线都是母线。
A. 0 B. 1 C. 2 D. 3 2.如图,一几何体的三视图如下:则这个几何体是()A. 圆柱B. 空心圆柱C. 圆D. 圆锥3.一梯形的直观图是一个如上图所示的等腰梯形,且梯形OA /B /C /的面积为2,则原梯形的面积为 ( )A. 2B.2 C.D. 4俯视图正 视 图 侧视图4.圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是() A .643πB 1283π C 64π D5. 一个圆台的上、下底面面积分别是12cm 和492cm ,一个平行底面的截面面积为252cm ,则这个截面与上、下底面的距离之比是 ( ) A 2: 1 B. 3: 1C.2: 1 D. 3: 16. 长方体的一个顶点上三条棱的边长分别为3、4、5,且它的八个顶点都在同一个球面上,这个球的表面积是()A. 220πB. 225πC. π50D. π200 7.下列命题中正确的个数是()①若直线l 上有无数个点不在平面α内,则l α∥②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行 ④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点 A. 0 B. 1 C. 2 D. 38.已知直线l α⊥平面,有以下几个判断:①若m l ⊥,则m α//;②若m α⊥,则m l //;③若m α//,则m l ⊥;④若m l //,则m α⊥.上述判断中正确的是()A. ①②③B. ②③④C. ①②④D. ①③④ 9.如图是正方体的展开图,则在这个正方体中,以下四个命题中正确的序号是() ①BM 与ED 平行.②CN 与BE 是异面直线. ③CN 与BM 成60˚角.④DM 与BN 垂直. A. ①②③ B. ③④ C. ②④ D. ②③④E10.在四面体ABCD 中,,E F 分别是,AC BD 的中点,若2,4,AB CD EF AB ==⊥,则AB 与CD 所成的角的度数为() A .030 B .45o C .60o D .90o11.在长方体ABCD-A 1B 1C 1D 1中,B 1B=BC=1,则面BD 1C 与面AD 1D 所成二面角的大小为()A .030B .45oC .60oD .90o12.蚂蚁搬家都选择最短路线行走,有一只蚂蚁沿棱长分别为 1cm,2cm,3cm 的长方体木块的顶点A 处沿表面达到顶点B 处(如图所示),这只蚂蚁走的路程是()A .cm 14B .cm 23C .cm 26D .1+cm 13 二、填空题(每题5分)13.半径为R 的半圆卷成一个圆锥,则它的体积为________________.14.已知a b ,是一对异面直线,且a b ,成70o 角,P 为空间一定点,则在过P 点的直线中与a b ,所成的角为70o 的直线有条。
