2020年高考数学分类汇编:立体几何
全国通用2020_2022三年高考数学真题分项汇编专题06立体几何解答题文(含答案)

高考数学真题分项汇编专题:06 立体几何(解答题)(文科专用)1.【2022年全国甲卷】小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.(1)证明:EF//平面ABCD;(2)求该包装盒的容积(不计包装盒材料的厚度).【答案】(1)证明见解析;√3.(2)6403【解析】【分析】(1)分别取AB,BC的中点M,N,连接MN,由平面知识可知EM⊥AB,FN⊥BC,EM=FN,依题从而可证EM⊥平面ABCD,FN⊥平面ABCD,根据线面垂直的性质定理可知EM//FN,即可知四边形EMNF为平行四边形,于是EF//MN,最后根据线面平行的判定定理即可证出;(2)再分别取AD,DC中点K,L,由(1)知,该几何体的体积等于长方体KMNL−EFGH的体积加上四棱锥B−MNFE体积的4倍,即可解出.(1)如图所示:,分别取AB,BC 的中点M,N ,连接MN ,因为△EAB,△FBC 为全等的正三角形,所以EM ⊥AB,FN ⊥BC ,EM =FN ,又平面EAB ⊥平面ABCD ,平面EAB ∩平面ABCD =AB ,EM ⊂平面EAB ,所以EM ⊥平面ABCD ,同理可得FN ⊥平面ABCD ,根据线面垂直的性质定理可知EM//FN ,而EM =FN ,所以四边形EMNF 为平行四边形,所以EF//MN ,又EF ⊄平面ABCD ,MN ⊂平面ABCD ,所以EF//平面ABCD . (2)如图所示:,分别取AD,DC 中点K,L ,由(1)知,EF//MN 且EF =MN ,同理有,HE//KM,HE =KM ,HG//KL,HG =KL ,GF//LN,GF =LN ,由平面知识可知,BD ⊥MN ,MN ⊥MK ,KM =MN =NL =LK ,所以该几何体的体积等于长方体KMNL −EFGH 的体积加上四棱锥B −MNFE 体积的4倍.因为MN =NL =LK =KM =4√2,EM =8sin60∘=4√3,点B 到平面MNFE 的距离即为点B 到直线MN 的距离d ,d =2√2,所以该几何体的体积V =(4√2)2×4√3+4×13×4√2×4√3×2√2=128√3+2563√3=6403√3.2.【2022年全国乙卷】如图,四面体ABCD 中,AD ⊥CD,AD =CD,∠ADB =∠BDC ,E 为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F−ABC 的体积.【答案】(1)证明详见解析(2)√34【解析】【分析】(1)通过证明AC⊥平面BED来证得平面BED⊥平面ACD.(2)首先判断出三角形AFC的面积最小时F点的位置,然后求得F到平面ABC的距离,从而求得三棱锥F−ABC的体积.(1)由于AD=CD,E是AC的中点,所以AC⊥DE.由于{AD=CD BD=BD∠ADB=∠CDB,所以△ADB≅△CDB,所以AB=CB,故AC⊥BD,由于DE∩BD=D,DE,BD⊂平面BED,所以AC⊥平面BED,由于AC⊂平面ACD,所以平面BED⊥平面ACD.(2)依题意AB=BD=BC=2,∠ACB=60°,三角形ABC是等边三角形,所以AC=2,AE=CE=1,BE=√3,由于AD=CD,AD⊥CD,所以三角形ACD是等腰直角三角形,所以DE=1. DE2+BE2=BD2,所以DE⊥BE,由于AC∩BE=E,AC,BE⊂平面ABC,所以DE⊥平面ABC.由于△ADB≅△CDB,所以∠FBA=∠FBC,由于{BF =BF∠FBA =∠FBC AB =CB ,所以△FBA ≅△FBC ,所以AF =CF ,所以EF ⊥AC ,由于S △AFC =12⋅AC ⋅EF ,所以当EF 最短时,三角形AFC 的面积最小值. 过E 作EF ⊥BD ,垂足为F ,在Rt △BED 中,12⋅BE ⋅DE =12⋅BD ⋅EF ,解得EF =√32,所以DF =√12−(√32)2=12,BF =2−DF =32,所以BF BD =34.过F 作FH ⊥BE ,垂足为H ,则FH//DE ,所以FH ⊥平面ABC ,且FHDE =BFBD =34, 所以FH =34,所以V F−ABC =13⋅S △ABC ⋅FH =13×12×2×√3×34=√34.3.【2021年甲卷文科】已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ⊥. 【答案】(1)13;(2)证明见解析.【解析】 【分析】(1)先证明ABC 为等腰直角三角形,然后利用体积公式可得三棱锥的体积;(2)将所给的几何体进行补形,从而把线线垂直的问题转化为证明线面垂直,然后再由线面垂直可得题中的结论. 【详解】(1)由于11BF A B ⊥,11//AB A B ,所以AB BF ⊥, 又AB ⊥BB 1,1BB BF B ⋂=,故AB ⊥平面11BCC B , 则AB BC ⊥,ABC 为等腰直角三角形, 111221222BCE ABC S S ⎛⎫==⨯⨯⨯= ⎪⎝⎭△△,11111333F EBC BCE V S CF -=⨯⨯=⨯⨯=△. (2)由(1)的结论可将几何体补形为一个棱长为2的正方体1111ABCM A B C M -,如图所示,取棱,AM BC 的中点,H G ,连结11,,A H HG GB ,正方形11BCC B 中,,G F 为中点,则1BF B G ⊥, 又111111,BF A B A B B G B ⊥=,故BF ⊥平面11A B GH ,而DE ⊂平面11A B GH , 从而BF ⊥DE . 【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.对于空间中垂直关系(线线、线面、面面)的证明经常进行等价转化.4.【2021年乙卷文科】如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.【答案】(1)证明见解析;(2 【解析】 【分析】(1)由PD ⊥底面ABCD 可得PD AM ⊥,又PB AM ⊥,由线面垂直的判定定理可得AM ⊥平面PBD ,再根据面面垂直的判定定理即可证出平面PAM ⊥平面PBD ;(2)由(1)可知,AM BD ⊥,由平面知识可知,~DAB ABM ,由相似比可求出AD ,再根据四棱锥P ABCD -的体积公式即可求出. 【详解】(1)因为PD ⊥底面ABCD ,AM ⊂平面ABCD , 所以PD AM ⊥, 又PB AM ⊥,PBPD P =,所以AM ⊥平面PBD , 而AM ⊂平面PAM , 所以平面PAM ⊥平面PBD . (2)[方法一]:相似三角形法 由(1)可知AM BD ⊥. 于是∽ABD BMA ,故=AD ABAB BM.因为1,,12===BM BC AD BC AB ,所以2112BC =,即BC =故四棱锥P ABCD -的体积13=⋅⋅=V AB BC PD . [方法二]:平面直角坐标系垂直垂直法由(2)知⊥AM DB ,所以1⋅=-AM BD k k . 建立如图所示的平面直角坐标系,设2(0)BC a a =>.因为1DC =,所以(0,0)A ,(1,0)B ,(0,2)D a ,()1,M a . 从而2020(2)211001--⋅=⨯=⨯-=-=---AM BD a a k k a a a .所以2a =,即DA =. [方法三]【最优解】:空间直角坐标系法 建立如图所示的空间直角坐标系D xyz -,设||=DA t ,所以(0,0,0)D ,(0,1,0)C ,(0,0,1)P ,(,0,0)A t ,(,1,0)B t . 所以,1,02t M ⎛⎫ ⎪⎝⎭,(,1,1)PB t =-,,1,02t AM ⎛⎫=- ⎪⎝⎭.所以2110(1)1022t t PB AM t ⎛⎫⋅=⋅-+⨯+⨯-=-+= ⎪⎝⎭.所以t ,即||=DA . [方法四]:空间向量法由PB AM ⊥,得0PB AM ⋅=. 所以()0++⋅=PD DA AB AM . 即0⋅+⋅+⋅=PD AM DA AM AB AM .又PD ⊥底面ABCD ,AM 在平面ABCD 内, 因此PD AM ⊥,所以0⋅=PD AM . 所以0⋅+⋅=DA AM AB AM ,由于四边形ABCD 是矩形,根据数量积的几何意义,得221||||02-+=DA AB ,即21||102-+=BC .所以||2BC =,即BC =. 【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长,从而求得该四棱锥的体积; 方法二构建平面直角坐标系,利用直线垂直的条件得到矩形的另一个边长,从而求得该四棱锥的体积;方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法,为最优解;方法四利用空间向量转化求得矩形的另一边长.5.【2020年新课标1卷文科】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC 是底面的内接正三角形,P 为DO 上一点,∠APC =90°.(1)证明:平面PAB ⊥平面PAC ;(2)设DO ,求三棱锥P −ABC 的体积.【答案】(1)证明见解析;(2【解析】 【分析】(1)根据已知可得PA PB PC ==,进而有PAC △≌PBC ,可得90APC BPC ∠=∠=,即PB PC ⊥,从而证得PC ⊥平面PAB ,即可证得结论;(2)将已知条件转化为母线l 和底面半径r 的关系,进而求出底面半径,由正弦定理,求出正三角形ABC 边长,在等腰直角三角形APC 中求出AP ,在Rt APO 中,求出PO ,即可求出结论.【详解】(1)连接,,OA OB OC ,D 为圆锥顶点,O 为底面圆心,OD ∴⊥平面ABC ,P 在DO 上,,OA OB OC PA PB PC ==∴==,ABC 是圆内接正三角形,AC BC ∴=,PAC △≌PBC ,90APC BPC ∴∠=∠=︒,即,PB PC PA PC ⊥⊥,,PA PB P PC =∴⊥平面,PAB PC ⊂平面PAC ,∴平面PAB ⊥平面PAC ;(2)设圆锥的母线为l ,底面半径为r ,圆锥的侧面积为,rl rl π==2222OD l r =-=,解得1,r l ==2sin 603AC r ==在等腰直角三角形APC 中,AP ==在Rt PAO 中,PO ===∴三棱锥P ABC -的体积为11333P ABC ABC V PO S -=⋅==△【点睛】本题考查空间线、面位置关系,证明平面与平面垂直,求锥体的体积,注意空间垂直间的相互转化,考查逻辑推理、直观想象、数学计算能力,属于中档题.6.【2020年新课标2卷文科】如图,已知三棱柱ABC –A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO =AB =6,AO //平面EB 1C 1F ,且∠MPN =π3,求四棱锥B –EB 1C 1F 的体积.【答案】(1)证明见解析;(2)24. 【解析】 【分析】(1)由,M N 分别为BC ,11B C 的中点,1//MN CC ,根据条件可得11//AA BB ,可证1MN AA //,要证平面11EB C F ⊥平面1A AMN ,只需证明EF ⊥平面1A AMN 即可;(2)根据已知条件求得11EB C F S 四边形和M 到PN 的距离,根据椎体体积公式,即可求得11B EB C F V -. 【详解】 (1),M N 分别为BC ,11B C 的中点,1//MN BB ∴又11//AA BB 1//MN AA ∴在等边ABC 中,M 为BC 中点,则BC AM ⊥ 又侧面11BB C C 为矩形, 1BC BB ∴⊥1//MN BBMN BC ⊥由MN AM M ⋂=,,MN AM ⊂平面1A AMN ∴BC ⊥平面1A AMN又11//B C BC ,且11B C ⊄平面ABC ,BC ⊂平面ABC ,11//B C ∴平面ABC又11B C ⊂平面11EB C F ,且平面11EB C F ⋂平面ABC EF =11//B C EF ∴//EF BC ∴又BC ⊥平面1A AMN∴EF ⊥平面1A AMNEF ⊂平面11EB C F∴平面11EB C F ⊥平面1A AMN(2)过M 作PN 垂线,交点为H ,画出图形,如图//AO 平面11EB C FAO ⊂平面1A AMN ,平面1A AMN ⋂平面11EB C F NP =//AO NP ∴ 又//NO AP∴6AO NP ==O 为111A B C △的中心.∴1111sin 606sin 6033ON AC =︒=⨯⨯︒=故:ON AP ==3AM AP ==平面11EB C F ⊥平面1A AMN ,平面11EB C F ⋂平面1A AMN NP =,MH ⊂平面1A AMN∴MH ⊥平面11EB C F 又在等边ABC 中EFAPBC AM =即2AP BCEF AM ⋅===由(1)知,四边形11EB C F 为梯形∴四边形11EB C F 的面积为:111126=62422EB C F EF B C S NP ++=⋅⨯=四边形 111113B EBC F EB C F V S h -∴=⋅四边形,h 为M 到PN 的距离sin 603MH =︒=, ∴1243243V =⨯⨯=. 【点睛】本题主要考查了证明线线平行和面面垂直,及其求四棱锥的体积,解题关键是掌握面面垂直转为求证线面垂直的证法和棱锥的体积公式,考查了分析能力和空间想象能力,属于中档题.7.【2020年新课标3卷文科】如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥;(2)点1C 在平面AEF 内.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】(1)根据正方形性质得AC BD ⊥,根据长方体性质得1AC BB ⊥,进而可证AC ⊥平面11BB D D ,即得结果;(2)只需证明1//EC AF 即可,在1CC 上取点M 使得12CM MC =,再通过平行四边形性质进行证明即可.【详解】(1)因为长方体1111ABCD A B C D -,所以1BB ⊥平面ABCD ∴1AC BB ⊥,因为长方体1111,ABCD A B C D AB BC -=,所以四边形ABCD 为正方形AC BD ∴⊥ 因为11,BB BD B BB BD =⊂、平面11BB D D ,因此AC ⊥平面11BB D D ,因为EF ⊂平面11BB D D ,所以AC EF ⊥;(2)在1CC 上取点M 使得12CM MC =,连,DM MF ,因为111112,//,=D E ED DD CC DD CC =,所以11,//,ED MC ED MC =所以四边形1DMC E 为平行四边形,1//DM EC ∴因为//,=,MF DA MF DA 所以M F A D 、、、四点共面,所以四边形MFAD 为平行四边形, 1//,//DM AF EC AF ∴∴,所以1E C A F 、、、四点共面,因此1C 在平面AEF 内【点睛】本题考查线面垂直判定定理、线线平行判定,考查基本分析论证能力,属中档题.。
2020高考数学题型整理分类《(8)立体几何》解析版(含历年真题)

(八) 大题考法——立体几何1.如图,AC 是圆O 的直径,点B 在圆O 上,∠BAC =30°,BM ⊥AC ,垂足为M .EA ⊥平面ABC ,CF ∥AE ,AE =3,AC =4,CF =1.(1)证明:BF ⊥EM ;(2)求平面BEF 与平面ABC 所成锐二面角的余弦值. 解:(1)证明:∵EA ⊥平面ABC ,∴BM ⊥EA , 又BM ⊥AC ,AC ∩EA =A ,∴BM ⊥平面ACFE , ∴BM ⊥EM .①在Rt △ABC 中,AC =4,∠BAC =30°,∴AB =23,BC =2, 又BM ⊥AC ,则AM =3,BM =3,CM =1.∵FM =MC 2+FC 2=2,EM =AE 2+AM 2=32, EF =42+(3-1)2=25,∴FM 2+EM 2=EF 2,∴EM ⊥FM . ② 又FM ∩BM =M ,③∴由①②③得EM ⊥平面BMF ,∴EM ⊥BF .(2)如图,以A 为坐标原点,过点A 垂直于AC 的直线为x 轴,AC ,AE 所在的直线分别为y 轴,z 轴建立空间直角坐标系.由已知条件得A (0,0,0),E (0,0,3),B (3,3,0),F (0,4,1), ∴BE ―→=(-3,-3,3),BF ―→=(-3,1,1). 设平面BEF 的法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·BE ―→=0,n ·BF ―→=0,得⎩⎨⎧-3x -3y +3z =0,-3x +y +z =0,令x =3,得y =1,z =2,∴平面BEF 的一个法向量为n =(3,1,2). ∵EA ⊥平面ABC ,∴取平面ABC 的一个法向量为AE ―→=(0,0,3). 设平面BEF 与平面ABC 所成的锐二面角为θ, 则cos θ=|cos 〈n ,AE ―→〉|=622×3=22.故平面BEF 与平面ABC 所成的锐二面角的余弦值为22. 2.如图所示,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,PA =2,∠ABC =90°,AB =3,BC =1,AD =23,∠ACD =60°,E 为CD 的中点.(1)求证:BC ∥平面PAE ;(2)求直线PD 与平面PBC 所成角的正弦值. 解:(1)证明:∵AB =3,BC =1,∠ABC =90°, ∴AC =2,∠BCA =60°.在△ACD 中,∵AD =23,AC =2,∠ACD =60°, ∴由余弦定理可得:AD 2=AC 2+CD 2-2AC ·CD ·cos ∠ACD ,∴CD =4, ∴AC 2+AD 2=CD 2,∴△ACD 是直角三角形. 又E 为CD 的中点,∴AE =12CD =CE =2,又∠ACD =60°,∴△ACE 是等边三角形, ∴∠CAE =60°=∠BCA ,∴BC ∥AE . 又AE ⊂平面PAE ,BC ⊄平面PAE , ∴BC ∥平面PAE .(2)由(1)可知∠BAE =90°,以点A 为坐标原点,以AB ,AE ,AP 分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则P (0,0,2),B (3,0,0),C (3,1,0),D (-3,3,0),∴PB ―→=(3,0,-2),PC ―→=(3,1,-2),PD ―→=(-3,3,-2).设n =(x ,y ,z )为平面PBC 的法向量, 则⎩⎪⎨⎪⎧n ·PB ―→=0,n ·PC ―→=0,即⎩⎨⎧3x -2z =0,3x +y -2z =0,取x =1,则y =0,z =32,n =⎝⎛⎭⎫1,0,32,∴cos 〈n ,PD ―→〉=n ·PD ―→|n |·|PD ―→|=-2374·16=-217,∴直线PD 与平面PBC 所成角的正弦值为217.3.如图,在四棱锥S -ABCD 中,AB ∥CD ,BC ⊥CD ,侧面SAB 为等边三角形,AB =BC =2,CD =SD =1.(1)证明:SD ⊥平面SAB ;(2)求AB 与平面SBC 所成角的正弦值.解:(1)证明:以C 为坐标原点,射线CD 为x 轴正半轴建立如图所示的空间直角坐标系C -xyz ,则D (1,0,0),A (2,2,0),B (0,2,0).设S (x ,y ,z ),显然x >0,y >0,z >0,则AS ―→=(x -2,y -2,z ),BS ―→=(x ,y -2,z ),DS ―→=(x -1,y ,z ).由|AS ―→|=|BS ―→|,得 (x -2)2+(y -2)2+z 2=x 2+(y -2)2+z 2,解得x =1.由|DS ―→|=1,得y 2+z 2=1. ① 由|BS ―→|=2,得y 2+z 2-4y +1=0.②由①②,解得y =12,z =32.∴S ⎝⎛⎭⎫1,12,32,AS ―→=⎝⎛⎭⎫-1,-32,32,BS ―→=⎝⎛⎭⎫1,-32,32,DS ―→=⎝⎛⎭⎫0,12,32, ∴DS ―→·AS ―→=0,DS ―→·BS ―→=0,∴DS ⊥AS ,DS ⊥BS , 又AS ∩BS =S ,∴SD ⊥平面SAB .(2)设平面SBC 的法向量为n =(x 1,y 1,z 1), 则n ⊥BS ―→,n ⊥CB ―→,∴n ·BS ―→=0,n ·CB ―→=0. 又BS ―→=⎝⎛⎭⎫1,-32,32,CB ―→=(0,2,0),∴⎩⎪⎨⎪⎧x 1-32y 1+32z 1=0,2y 1=0,取z 1=2,得n =(-3,0,2). ∵AB ―→=(-2,0,0),∴cos 〈AB ―→,n 〉=AB ―→·n | AB ―→||n |=-2×(-3)2×7=217.故AB 与平面SBC 所成角的正弦值为217. 4.(2018·诸暨高三适应性考试)如图,四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,△PAD 是边长为2的等边三角形,底面ABCD 是直角梯形,∠BAD =∠CDA =90°,AB =2DC =22,E 是CD 的中点.(1)求证:AE ⊥PB ;(2)设F 是棱PB 上的点,EF ∥平面PAD ,求EF 与平面PAB 所成角的正弦值. 解:(1)证明:取AD 的中点G ,连接PG ,BG ,∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PG ⊥AD , ∴PG ⊥平面ABCD ,∵AE ⊂平面ABCD ,∴AE ⊥PG . 又∵tan ∠DAE =tan ∠ABG =24, ∴∠ABG +∠EAB =∠DAE +∠EAB =∠DAB =90°, ∴AE ⊥BG .∵BG ∩PG =G ,BG ⊂平面PBG ,PG ⊂平面PBG , ∴AE ⊥平面PBG , ∴AE ⊥PB .(2)法一:作FH ∥AB 交PA 于H ,连接DH ,则HF ∥DC . ∵EF ∥平面PAD ,平面FHDE ∩平面PAD =DH , ∴EF ∥DH ,∴四边形FHDE 为平行四边形, ∴HF =DE .易知DC ∥AB ,DC =12AB ,∴HF =14AB ,即H 为PA 的一个四等分点.取PA 的中点K ,连接DK ,则DK ⊥PA .∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,AB ⊥AD , ∴AB ⊥平面PAD . ∵DK ⊂平面PAD , ∴AB ⊥DK , ∵PA ∩AB =A , ∴DK ⊥平面PAB .∴∠DHK 为EF 与平面PAB 所成的角, 由已知得DK =3,DH =DK 2+HK 2=132, ∴sin ∠DHK =DK DH =3132=23913,∴EF 与平面PAB 所成角的正弦值为23913.法二:以A 为坐标原点,AB ,AD 所在直线为x 轴,y 轴建立如图所示的空间直角坐标系.则A (0,0,0),B (22,0,0),P (0,1,3),E ⎝⎛⎭⎫22,2,0,PB ―→=(22,-1,-3),EP―→=⎝⎛⎭⎫-22,-1,3. 设PF ―→=λPB ―→,则EF ―→=EP ―→+λPB ―→=⎝⎛⎭⎫22λ-22,-1-λ,3-3λ.由(1)知PG ⊥平面ABCD ,∴PG ⊥AB . ∵AD ⊥AB ,PG ⊥AD =G , ∴AB ⊥平面PAD ,∴AB ―→=(22,0,0)为平面PAD 的一个法向量. ∵EF ∥平面PAD ,∴EF ―→·AB ―→=22×⎝⎛⎭⎫22λ-22=0,解得λ=14. ∴EF ―→=⎝⎛⎭⎫0,-54,334.设平面PAB 的一个法向量为n =(x ,y ,z ), 又AB ―→=(22,0,0),PB ―→=(22,-1,-3), 则⎩⎪⎨⎪⎧n ·AB ―→=0,n ·PB ―→=0,即⎩⎨⎧22x =0,22x -y -3z =0,取y =3,得z =-1,∴n =(0,3,-1). ∴|cos 〈n ,EF ―→〉|=⎪⎪⎪⎪-534-3342×132=23913,∴EF 与平面PAB 所成角的正弦值为23913.5.(2019届高三·镇海中学检测)如图,在三棱柱ABC -A 1B 1C 1中,平面A 1ACC 1⊥平面ABC ,AB =BC =2,∠ACB =30°,∠C 1CB =60°,BC 1⊥A 1C ,E 为AC 的中点,CC 1=2.(1)求证:A 1C ⊥平面C 1EB ;(2)求直线CC 1与平面ABC 所成角的余弦值. 解:(1)证明:因为AB =BC =2,E 为AC 的中点, 所以AC ⊥BE .又因为平面A 1ACC 1⊥平面ABC ,平面A 1ACC 1∩平面ABC =AC , 所以BE ⊥平面A 1ACC 1,所以BE ⊥A 1C .又因为BC 1⊥A 1C ,BC 1∩BE =B ,BC 1⊂平面C 1EB ,BE ⊂平面C 1EB , 所以A 1C ⊥平面C 1EB .(2)法一:因为平面A 1ACC 1⊥平面ABC , 所以直线CC 1与平面ABC 所成角为∠C 1CA . 因为∠ACB =30°,AB =BC =2,E 为AC 的中点, 所以EC =3,EB =1.因为CC 1=BC =2,∠C 1CB =60°,所以BC 1=2, 因为BE ⊥平面A 1ACC 1,所以BE ⊥EC 1,所以EC 1= 3. 在△CC 1E 中,根据余弦定理可知,cos ∠C 1CE =33. 所以直线CC 1与平面ABC 所成角的余弦值为33. 法二:以E 为坐标原点,EC 为x 轴,EB 为y 轴建立如图所示的空间直角坐标系.因为∠ACB =30°,AB =BC =2,E 为AC 的中点, 所以EC =3,EB =1.因为CC 1=CB =2,∠C 1CB =60°,所以BC 1=2, 因为BE ⊥平面AA 1CC 1,所以BE ⊥EC 1,所以EC 1= 3. 所以|CC 1―→|=2,|C 1E ―→|=3, 设C 1(x,0,y ),又C (3,0,0),所以⎩⎨⎧(x -3)2+y 2=4,x 2+y 2=3,解得⎩⎨⎧x =33,y =263,所以C 1⎝⎛⎭⎫33,0,263,则CC 1―→=⎝⎛⎭⎫-233,0,263, 易知平面ABC 的一个法向量为n =(0,0,1), 设直线CC 1与平面ABC 所成的角为α, 则sin α=|cos 〈CC 1―→,n 〉|=63,所以cos α=33.即直线CC 1与平面ABC 所成角的余弦值为33.6.如图所示,四棱锥P -ABCD 的底面ABCD 为矩形,PA ⊥平面ABCD ,点E 是PD 的中点,点F 是PC 的中点.(1)证明:PB ∥平面AEC ;(2)若底面ABCD 为正方形,探究在什么条件下,二面角C -AF -D 的大小为60°?解:易知AD ,AB ,AP 两两垂直,建立如图所示的空间直角坐标系A -xyz ,设AB =2a ,AD =2b ,AP =2c ,则A (0,0,0),B (2a,0,0),C (2a,2b,0),D (0,2b,0),P (0,0,2c ).连接BD 交AC 于点O ,连接OE ,则O (a ,b,0),又E 是PD 的中点,所以E (0,b ,c ).(1)证明:因为PB ―→=(2a,0,-2c ),EO ―→=(a,0,-c ), 所以PB ―→=2EO ―→,所以PB ―→∥EO ―→, 即PB ∥EO .因为PB ⊄平面AEC ,EO ⊂平面AEC , 所以PB ∥平面AEC .(2)因为四边形ABCD 为正方形,所以a =b ,则A (0,0,0),B (2a,0,0),C (2a,2a,0),D (0,2a,0),P (0,0,2c ),E (0,a ,c ),F (a ,a ,c ),因为z 轴⊂平面CAF ,所以设平面CAF 的一个法向量为n =(x,1,0),而AC ―→=(2a,2a,0),所以AC ―→·n =2ax +2a =0,得x =-1,所以n =(-1,1,0). 因为y 轴⊂平面DAF ,所以设平面DAF 的一个法向量为m =(1,0,z ), 而AF ―→=(a ,a ,c ),所以AF ―→·m =a +cz =0,得z =-a c ,所以m =⎝⎛⎭⎫1,0,-ac ∥m ′=(c,0,-a ). 所以cos 60°=|n ·m ′||n ||m ′|=c 2(a 2+c 2)=12,得a =c .故当AP 与正方形ABCD 的边长相等时,二面角C -AF -D 的大小为60°.。
北京市高考数学联考试题分类大汇编(8)立体几何试题解析.doc

北京市 2020 年高考数学最新联考试题分类大汇编一、选择题:(3) ( 北京市东城区 2020 年 1 月高三考试文科)一个几何体的三视图如图所示,则该几何体的体积为( A)(B)( C)(D)【答案】 C【解析】该几何体为底面是直角边为的等腰直角三角形,高为的直三棱柱,其体积为。
7. ( 北京市西城区2020 年 1 月高三期末考试理科) 某几何体的三视图如图所示,该几何体的体积是()(A)(B)(C)(D)【答案】 D【解析】将三视图还原直观图,可知是一个底面为正方形(其对角线长为2),高为 2 的四棱锥,其体积为A.且,则B.且,则C.且,则D.且,则【答案】 C体的体积为.(9) ( 北京市城区 2020 年 4 月高考一模文科 ) 已知一个四棱的三如所示,四棱的体是 .10. (2020 年 4 月北京市房山区高三一模理科一个几何体的三如所示,个几何体的体 .三、解答:(17) ( 北京市城区2020 年 1 月高三考文科)(本小共14 分)如,在四棱中,底面是正方形,平面,是中点,段上一点.(Ⅰ)求:;(Ⅱ)确定点在段上的位置,使// 平面,并明理由.【命分析】本考垂直和面探索性等合。
考学生的空想象能力。
明垂直的方法:(1)异面直所成的角直角;( 2)面垂直的性定理;( 3)面面垂直的性定理;( 4)三垂定理和逆定理;( 5)勾股定理;( 6)向量垂直 . 要注意面、面面垂直的性定理的成立条件 . 解程中要特体会平行关系性的性,垂直关系的多性 . 本第一利用方法二行明;探求某明(Ⅰ)因平面,所以.又四形是正方形,所以,,所以平面 ,又平面,所以 .⋯⋯⋯⋯⋯⋯7分. ⋯⋯⋯⋯⋯⋯ 14 分(16) ( 2020 年 4 月北京市海淀区高三一模理科)(本小分14 分)在四棱中,//,,,平面,.(Ⅰ)平面平面,求://;(Ⅱ)求:平面;(Ⅲ)点段上一点,且直与平面所成角的正弦,求的.(16)(本小分 14 分)所以,,,所以,.所以, .因,平面,平面,所以平面 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分由(Ⅱ)知平面的一个法向量 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分17. (2020 年 3 月北京市朝阳区高三一模文科⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分zPA D⋯⋯ ⋯yCBx⋯⋯ ⋯) (本分13 分)在如所示的几何体中,四形平行四形,,平面,,,,,且是的中点 .(Ⅰ)求:平面;(Ⅱ)在上是否存在一点,使得最大?若存在,求出的正切;若不存在,明理由 .(17)(本小分 13 分)(Ⅱ)解:假在上存在一点,使得最大. 因平面,所以 .又因,所以平面.⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分在中, .17. ( 北京市西城区 2020 年 4 月高三第一次模文 ) (本小分 14 分)如,矩形中,,.,分在段和上,∥,将矩形沿折起.折起后的矩形,且平面平面.(Ⅰ)求:∥平面;(Ⅱ)若,求:;(Ⅲ)求四面体体的最大.17.(本小分 14 分)(Ⅰ)明:因四形,都是矩形,所以∥∥,.所以四形是平行四形,⋯⋯⋯⋯⋯ 2 分所以∥,⋯⋯⋯⋯⋯⋯ 3 分因平面,所以∥平面.⋯⋯⋯⋯⋯⋯ 4 分(Ⅱ)明:接,.因平面平面,且,所以平面,⋯⋯ 5 分所以.⋯⋯⋯⋯ 6 分9 分(Ⅲ)解:,,其中.由(Ⅰ)得平面,所以四面体的体.⋯⋯⋯ 11 分所以.⋯⋯⋯⋯⋯13 分当且当,即,四面体的体最大.(17) ( 北京市城区2020 年 4 月高考一模理科⋯⋯⋯⋯⋯⋯) (本小共14 分13 分)1(17)(共 13 分)(Ⅰ)明:取中点,.因,,所以,而,即△是正三角形又因 ,所以.⋯⋯⋯⋯2分所以在 2 中有, . ⋯⋯⋯⋯ 3 分所以二面角.的平2面角.1又二面角直二面角,所以. ⋯⋯⋯⋯ 5 分又因 ,所以⊥平面 , 即⊥平面 .⋯⋯⋯⋯6分(Ⅱ)解:由(Ⅰ)可知⊥平面,,如,以原点,建立空直角坐系,,,,.在1中,.因,所以∥,且 .所以四形平行四形.所以∥,且 .故点的坐(1,, 0) . 2 所以,, .⋯⋯⋯⋯8分不妨平面的法向量,即令,得 .⋯⋯⋯⋯10分所以 .⋯⋯⋯⋯12分故直与平面所成角的大小.⋯⋯⋯⋯13分(17) ( 北京市城区 2020 年 4 月高考一模文科 ) (本小共 14 分)如,在的正三角形中,,,分,,上的点,且足 . 将△沿折起到△的位置,使平面平面,,. (如)(Ⅰ)若中点,求:∥平面;(Ⅱ)求: .1 2(17)(共 14 分)明:(Ⅰ)取中点, .在△中,分 的中点,所以∥,且.因 ,所以∥ , 且,所以∥,且.所以四 形 平行四 形.所以∥.⋯⋯⋯⋯ 5 分又因 平面,且平面, 所以∥平面.(Ⅱ)取中点, .因 ,,所以,而,即△是正三角形 又因 , 所以 .所以在2 中有 . 因 平面平面,平面平面,.⋯⋯⋯⋯ 9 分⋯⋯⋯⋯ 7 分所以⊥平面 .⋯⋯⋯⋯ 12 分17. (2020又平面, 所以⊥ .年 3 月北京市丰台区高三一模文科) (本小 共⋯⋯⋯⋯ 14 分)14 分如 ,四棱 P-ABCD 中,底面 ABCD 是菱形, PA =PD ,∠ BAD =60o , E 是 AD 的中点,点Q在 棱 PC 上.(Ⅰ)求 : AD ⊥平面 PBE ; (Ⅱ)若 Q 是 PC 的中点,求 : PA // 平面 BDQ ;(Ⅲ)若 V P-BCDE =2 V Q - ABCD , 求的 .17. 明:(Ⅰ)因E 是 AD 的中点, PA =PD ,所以AD⊥PE .⋯⋯⋯⋯⋯⋯⋯⋯ 1 分因 底面 ABCD 是菱形,∠ BAD =60o ,所以 = ,又因 E 是 的中点,AB BD AD所以⊥.⋯⋯⋯⋯⋯⋯⋯⋯ 2 分AD BE因 PE∩BE=E,⋯⋯⋯⋯⋯⋯⋯⋯ 3 分所以 AD⊥平面 PBE.⋯⋯⋯⋯⋯⋯⋯⋯ 4 分(Ⅱ)接 AC交 BD于点 O, OQ.⋯⋯⋯⋯⋯⋯⋯⋯ 5 分因O 是中点,Q 是的中点,AC PC所以 OQ△ PAC中位.所以 OQ //因,所以.⋯⋯⋯⋯⋯⋯⋯⋯14分17. (2020年4月北京市房山区高三一模理科(本小共14 分)在直三棱柱中,=2 ,.点分是,的中点,是棱上的点.(I )求:平面;(II)若 // 平面,确定点的位置,并出明;(III)求二面角的余弦 .17.(本小共 14 分)(I)明:∵在直三棱柱中,,点是的中点,∴⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分, ,∴⊥平面⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分平面∴,即⋯⋯⋯⋯⋯⋯⋯ 3 分又∴平面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分( II )当是棱的中点, // 平面 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分明如下 :, 取的中点H,接 ,的中位∴∥,⋯⋯⋯⋯⋯⋯⋯ 6 分∵由已知条件,正方形∴∥,∵ 的中点,(III)∵ 直三棱柱且又平面的法向量,==,⋯⋯⋯⋯⋯⋯⋯⋯13 分二面角的平面角,且角.⋯⋯⋯⋯⋯⋯⋯⋯14 分。
2020高考数学分类汇编--立体几何

2020年普通高等学校招生全国统一考试理科数学3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .14B .12C .14D .1210.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π16.如图,在三棱锥P –ABC 的平面展开图中,AC =1,AB AD =AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB = .18.(12分)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC △是底面的内接正三角形,P 为DO 上一点,PO .(1)证明:PA ⊥平面PBC ; (2)求二面角B PC E --的余弦值. 3.C 10.A16.14-18.解:(1)设DO a =,由题设可得,,63PO a AO a AB a ===,2PA PB PC ===. 因此222PA PB AB +=,从而PA PB ⊥. 又222PA PC AC +=,从而PA PC ⊥. 所以PA ⊥平面PBC .(2)以O 为坐标原点,OE 的方向为y 轴正方向,||OE 为单位长,建立如图所示的空间直角坐标系O xyz -.由题设可得1(0,1,0),(0,1,0),(,0),(0,0,)22E A C P -.所以31(,,0),(0,2EC EP =--=-.设(,,)x y z =m 是平面PCE 的法向量,则00EP EC ⎧⋅=⎪⎨⋅=⎪⎩m m ,即2023102y z x y⎧-+=⎪⎪⎨⎪--=⎪⎩,可取3(,1,2)=-m . 由(1)知2(0,1,)2AP =是平面PCB 的一个法向量,记AP =n , 则25cos ,|||5⋅==n m n m n m |. 所以二面角B PC E --的余弦值为25.2020年普通高等学校招生全国统一考试理科数学4.北京天坛的圆丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)A .3699块B .3474块C .3402块D .3339块7.右图是一个多面体的三视图,这个多面体某条棱的一个断点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为ME F GHA .EB .FC .GD .H10. 已知ABC △是面积为439的等边三角形,且其顶点都在球O 的表面上,若球O 的表面积为π16,则球O 到平面ABC 的距离为( ) A .3B .23 C .1 D .23 16.设有下列四个命题: 1P :两两相交且不过同一点的三条直线必在同一平面内. 2P :过空间中任意三点有且仅有一个平面. 3P :若空间两条直线不相交,则这两条直线平行. 4P :若直线⊂l 平面α,直线⊥m 平面α,则l m ⊥.则下述命题中所有真命题的序号是________. ①41p p ∧②21p p ∧③32p p ∨⌝④ 43p p ⌝∨⌝20.(12分)如图,已知三棱柱111C B A ABC -的底面是正三角形,侧面C C BB 11是矩形,M ,N 分别为BC ,11C B 的中点,P 为AM 上一点,过11C B 和P 的平面交AB 于E ,交AC 于F .(1)证明:MN AA ∥1,且平面F C EB AMN A 111平面⊥;(2)设O 为△111C B A 的中心,若F C EB AO 11平面∥,且AB AO =,求直线E B 1与平面AMN A 1所成角的正弦值.2020年普通高等学校招生全国统一考试理科数学8.下图为某几何体的三视图,则该几何体的表面积是A .B .C .D .15.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为__________.19.(12分)如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 在平面AEF 内;(2)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.8.C15 19.解:设AB a =,AD b =,1AA c =,如图,以1C 为坐标原点,11C D 的方向为x 轴正方向,建立空间直角坐标系1C xyz -.(1)连结1C F ,则1(0,0,0)C ,(,,)A a b c ,2(,0,)3E a c ,1(0,,)3F b c ,1(0,,)3EA b c =,11(0,,)3C F b c =,得1EA C F =.因此1EA C F ∥,即1,,,A E F C 四点共面,所以点1C 在平面AEF 内. (2)由已知得(2,1,3)A ,(2,0,2)E ,(0,1,1)F ,1(2,1,0)A ,(0,1,1)AE =--,(2,0,2)AF =--,1(0,1,2)A E =-,1(2,0,1)A F =-.设1(,,)x y z =n 为平面AEF 的法向量,则 110,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,220,y z x z --=⎧⎨--=⎩可取1(1,1,1)=--n . 设2n 为平面1A EF 的法向量,则 22110,0,A E A F ⎧⋅=⎪⎨⋅=⎪⎩n n 同理可取21(,2,1)2=n .因为121212cos ,||||⋅〈〉==⋅n n n n n n ,所以二面角1A EF A --.2020年普通高等学校招生全国统一考试文科数学3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .14B .12C .14D .1211.设12,F F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P 在C 上且||2OP =,则12PF F △的面积为 A .72B .3C .52D .212.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π19.(12分)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC △是底面的内接正三角形,P 为DO 上一点,∠APC =90°.(1)证明:平面PAB ⊥平面PAC ;(2)设DO ,求三棱锥P −ABC 的体积. 3.C11.B12.A19.解:(1)由题设可知,PA =PB = PC .由于△ABC 是正三角形,故可得△PAC ≌△PAB . △PAC ≌△PBC .又∠APC =90°,故∠APB =90°,∠BPC =90°.从而PB ⊥PA ,PB ⊥PC ,故PB ⊥平面PAC ,所以平面PAB ⊥平面PAC . (2)设圆锥的底面半径为r ,母线长为l .由题设可得rl 222l r ==.解得r =1,l从而AB 1)可得222PA PB AB +=,故PA PB PC ===所以三棱锥P -ABC 的体积为311113232PA PB PC ⨯⨯⨯⨯=⨯⨯=.2020年普通高等学校招生全国统一考试文科数学11.已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为AB .32C .1D 16.设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内. p 2:过空间中任意三点有且仅有一个平面. p 3:若空间两条直线不相交,则这两条直线平行. p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l . 则下述命题中所有真命题的序号是__________. ① 14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝20.(12分)如图,已知三棱柱ABC –A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO =AB =6,AO //平面EB 1C 1F ,且∠MPN =π3,求四棱锥B –EB 1C 1F 的体积. 12.A16.①③④20.解:(1)因为M ,N 分别为BC ,B 1C 1的中点,所以MN ∥CC 1.又由已知得AA 1∥CC 1,故AA 1∥MN .因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N .又B 1C 1⊥MN ,故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)AO ∥平面EB 1C 1F ,AO ⊂平面A 1AMN ,平面A 1AMN ⋂平面EB 1C 1F = PN , 故AO ∥PN ,又AP ∥ON ,故四边形APNO 是平行四边形,所以PN =AO =6,AP = ON =13AM PM =23AM EF =13BC =2.因为BC ∥平面EB 1C 1F ,所以四棱锥B -EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离.作MT ⊥PN ,垂足为T ,则由(1)知,MT ⊥平面EB 1C 1F ,故MT =PM sin ∠MPN =3.底面EB 1C 1F 的面积为1111()(62)624.22B C EF PN ⨯+⨯=+⨯=所以四棱锥B -EB 1C 1F 的体积为1243243⨯⨯=.2020年普通高等学校招生全国统一考试文科数学9.如图为某几何体的三视图,则该几何体的表面积是A .B .C .D .16.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________. 19.(12分)如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥;(2)点1C 在平面AEF 内. 9.C16.2π 19.解:(1)如图,连结BD ,11B D .因为AB BC =,所以四边形ABCD 为正方形,故AC BD ⊥.又因为1BB ⊥平面ABCD ,于是1AC BB ⊥.所以AC ⊥平面11BB D D . 由于EF ⊂平面11BB D D ,所以EF AC ⊥.(2)如图,在棱1AA 上取点G ,使得12AG GA =,连结1GD ,1FC ,FG ,因为1123D E DD =,123AG AA =,11DD AA =∥,所以1ED AG =∥,于是四边形1ED GA 为平行四边形,故1AE GD ∥.因为1113B F BB =,1113AG AA =,11BB AA =∥,所以11FG A B =∥,11FG C D =∥,四边形11FGD C 为平行四边形,故11GD FC ∥.于是1AE FC ∥.所以1,,,A E F C 四点共面,即点1C 在平面AEF 内. 2020年普通高等学校招生全国统一考试(北京卷)(3)某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为(A )63+(B )623+(C )123+(D )1223+(16)(本小题13分) 如图,在正方体1111ABCD A B C D -中,E 为1BB 的中点.(Ⅰ)求证:1BC ∥平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.2020年普通高等学校招生全国统一考试(江苏卷)9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是 cm.15.(本小题满分14分)在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点. (1)求证:EF ∥平面AB 1C 1; (2)求证:平面AB 1C ⊥平面ABB 1.9.1232π 15.满分14分.证明:因为,E F 分别是1,AC B C 的中点,所以1EF AB ∥. 又/EF ⊂平面11AB C ,1AB ⊂平面11AB C , 所以EF ∥平面11AB C .(2)因为1B C ⊥平面ABC ,AB ⊂平面ABC , 所以1B C AB ⊥.又AB AC ⊥,1B C ⊂平面11AB C ,AC ⊂平面1AB C ,1,B C AC C =所以AB ⊥平面1AB C .又因为AB ⊂平面1ABB ,所以平面1AB C ⊥平面1ABB . 22.(本小题满分10分)在三棱锥A —BCD 中,已知CB =CD 5,BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值. 2020年普通高等学校招生全国统一考试(天津卷)5.若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为 A .12π B .24πC .36πD .144π17.(本小题满分15分)如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且2,1,AD CE M ==为棱11A B 的中点.(Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值. 5.C17.满分15分.依题意,以C 为原点,分别以1,,CA CB CC 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图),可得1(0,0,0),(2,0,0),(0,2,0),(0,0,3)C A B C ,11(2,0,3),(0,2,3),(2,0,1),(0,0,2)A B D E ,(1,1,3)M .(Ⅰ)证明:依题意,1(1,1,0)C M =,1(2,2,2)B D =--,从而112200C M B D ⋅=-+=,所以11C M B D ⊥.(Ⅱ)解:依题意,(2,0,0)CA =是平面1BB E 的一个法向量,1(0,2,1)EB =,(2,0,1)ED =-.设(,,)x y z =n 为平面1DB E 的法向量,则10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,20.y z x z +=⎧⎨-=⎩不妨设1x =,可得(1,1,2)=-n . 因此有|||6cos ,6|A CA C CA ⋅〈〉==n n n ,于是30sin ,CA 〈〉=n . 所以,二面角1B B E D --的正弦值为306. (Ⅲ)解:依题意,(2,2,0)AB =-.由(Ⅱ)知(1,1,2)=-n 为平面1DB E 的一个法向量,于是3cos ,3||||AB AB AB ⋅==-n n n .所以,直线AB 与平面1DB E 32020年普通高等学校招生全国统一考试新高考4.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为A.20°B.40°C.50°D.90°D16.已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以1的球面与侧面BCC1B1的交线长为________.20.(12分)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.4.B 1620.解:(1)因为PD⊥底面ABCD,所以PD AD⊥.⊥,因此AD⊥底面PDC.又底面ABCD为正方形,所以AD DC∥,AD⊄平面PBC,所以AD∥平面PBC.因为AD BC∥.因此l⊥平面PDC.由已知得l AD(2)以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D xyz -.则(0,0,0),(0,1,0),(1,1,0),(0,0,1)D C B P ,(0,1,0)DC =,(1,1,1)PB =-. 由(1)可设(,0,1)Q a ,则(,0,1)DQ a =.设(,,)x y z =n 是平面QCD 的法向量,则0,0,DQ DC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0.ax z y +=⎧⎨=⎩ 可取(1,0,)a =-n . 所以cos ,||||3PB PB PB ⋅〈〉==⋅n nn . 设PB 与平面QCD 所成角为θ,则sin θ==当且仅当1a =时等号成立,所以PB 与平面QCD 所成角的正. 2020年普通高等学校招生全国统一考试(浙江卷)5.某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是A .73B.143C .3D .614.已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______. 19.(本题满分15分)如图,在三棱台ABC —DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC . (Ⅰ)证明:EF ⊥DB ;(Ⅱ)求直线DF 与平面DBC 所成角的正弦值.5.A 14.119.满分15分。
2020年高考数学专题讲解:立体几何(一)
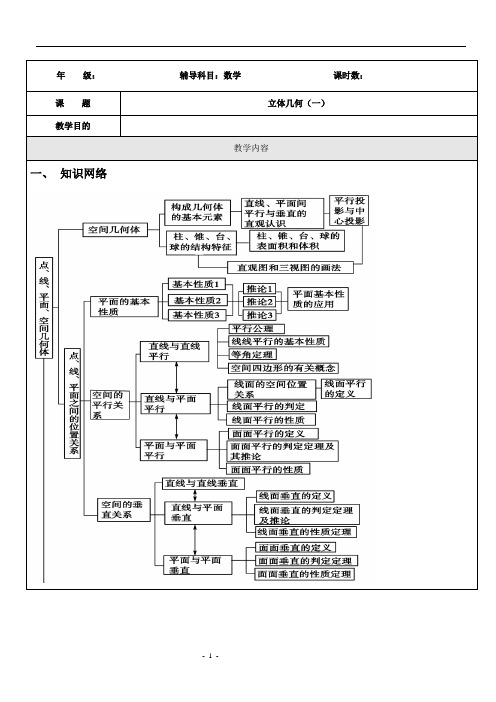
年级:辅导科目:数学课时数:课题立体几何(一)教学目的教学内容一、知识网络二、命题分析立体几何在高考中考查的主要内容有:空间几何体的性质、线面关系的判定与证明、表面积与体积的运算、空间几何体的识图,空间中距离、角的计算等.从近几年高考来看,一般以2~3个客观题来考查线面关系的判定、表面积与体积、空间中的距离与角、空间几何体的性质与识图等,以1个解答题来考查线面关系的证明以及距离、角的计算.在高考中属于中档题目.而三视图作为新课标的新增内容,在2011年高考中,有多套试卷在此知识点命题,主要考查三视图和直观图,特别是通过三视图来确定原图形的相关量.预计今后高考中,三视图的考查不只在选择题、填空题中出现,很有可能在解答题中与其他知识点结合在一起命题.三、复习建议在2012年高考复习中注意以下几个方面:(1)从命题形式来看,涉及立体几何内容的命题形式最为多变,除保留传统的“四选一”的选择题外,还尝试开发了“多选填空”、“完型填空”、“构造填空”等题型,并且这种命题形式正在不断完善和翻新;解答题则设计成几个小问题,此类题目往往以多面体为依托,第一小问考查线线、线面、面面的位置关系,后面几问考查面积、体积等度量关系,其解题思路也都是“作——证——求”,强调作图、证明和计算相结合.在2012年高考复习中注意以下几个方面:(1)从命题形式来看,涉及立体几何内容的命题形式最为多变,除保留传统的“四选一”的选择题外,还尝试开发了“多选填空”、“完型填空”、“构造填空”等题型,并且这种命题形式正在不断完善和翻新;解答题则设计成几个小问题,此类题目往往以多面体为依托,第一小问考查线线、线面、面面的位置关系,后面几问考查面积、体积等度量关系,其解题思路也都是“作——证——求”,强调作图、证明和计算相结合.(3)从方法上来看,着重考查公理化方法,如解答题注重理论推导和计算相结合,考查转化的思想方法,如要把立体.4.空间几何体的直观图画空间几何体的直观图常用画法,基本步骤是:(1)在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′= .(2)已知图形中平行于x轴、y轴的线段,在直观图中分别画成平行于的线段.(3)已知图形中平行于x轴的线段,在直观图中保持原长度,平行于y轴的线段,长度变为.(4)在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的z′轴也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直观图中仍平行于z′轴且长度.5.中心投影与平行投影(1)平行投影的投影线互相,而中心投影的投影线相交于一点.(2)从投影的角度看,三视图和用斜二测画法画出的直观图都是在投影下画出来的图形.(三)基础自测1.(2010·北京理)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为( )[答案] C[解析] 本题考查了三视图知识,解题的关系是掌握三视图与直观图的知识,特别是应明确三视图是从几何体的哪个方向看到的.由三视图中正(主)视图、侧(左)视图得到几何体的直观图如图所示,所以该几何体的俯视图为C.2.(2010·福建理)如图,若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确...的是( ) A.EH∥FG B.四边形EFGH是矩形 C.Ω是棱柱 D.Ω是棱台[答案] D[解析] ∵EH∥A1D1,∴EH∥B1C1∴B1C1∥面EFGH,B1C1∥FG,∴Ω是棱柱,故选D.3.右图为水平放置的正方形ABCO,它在直角坐标系xOy中点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( )A.12B.22C.1 D. 2[答案] B[解析] 如图,在平面直观图中,B′C′=1,∠B′C′D′=45°,∴B′D′=2 2 .4.已知某物体的三视图如图所示,那么这个物体的形状是( )A.六棱柱 B.四棱柱 C.圆柱 D.五棱柱[答案] A[解析] 由俯视图可知,该物体的形状是六棱柱,故选A.5.用小正方体搭成一个几何体,如图是它的主视图和左视图,搭成这个几何体的小正方体最多为________个.[答案] 7[解析] 由主视图和左视图知,该几何体由两层组成,底层最多有3×2=6个,上层只有1个,故最多为7个.6.(2010·新课标理)正(主)视图为一个三角形的几何体可以是________.(写出三种)[答案] 三棱锥、三棱柱、圆锥(其他正确答案同样给分).[解析] 本题考查空间几何体的三视图.本题属于开放性题目,答案不唯一.正视图是三角形的几何体,最容易想到的是三棱锥,其次是四棱锥、圆锥;对于五棱锥、六棱锥等,正视图也可以是三角形.7.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .[分析] 由三视图的形状大小,还原成几何体;再利用体积公式和表面积公式求解.[解析] (1)由该几何体的俯视图、主视图、左视图可知,该几何体是四棱锥.且四棱锥的底面ABCD 是边长为6和8的矩形,高VO =4,O 点是AC 与BD 的交点.∴该几何体的体积V =13×8×6×4=64. (2)如图所示,OE ⊥AB ,OF ⊥BC ,侧面VAB 中,VE =VO 2+OE 2=42+32=5,∴S △VAB =12×AB ×VE =12×8×5=20, 侧面VBC 中,VF =VO 2+OF 2=42+42=42,∴S △VBC =12×BC ×VF =12×6×42=12 2. ∴该几何体的侧面积S =2(S △VAB +S △VBC )=40+24 2.[点评] 由三视图还原成几何体,需要对常见的柱、锥、台、球的三视图非常熟悉,有时还可根据三视图的情况,还原成由常见几何体组合而成的组合体.(四)典型例题1.命题方向:空间几何体的结构特征[例1] 下列命题中,成立的是( )A .各个面都是三角形的多面体一定是棱锥B .四面体一定是三棱锥C .棱锥的侧面是全等的等腰三角形,该棱锥一定是正棱锥D .底面多边形既有外接圆又有内切圆,且侧棱相等的棱锥一定是正棱锥[分析] 结合棱锥、正棱锥的概念逐一进行考查.[解析] A 是错误的,只要将底面全等的两个棱锥的底面重合在一起,所得多面体的每个面都是三角形,但这个多面体不是棱锥;B 是正确的,三个面共顶点,另有三边围成三角形是四面体也必定是个三棱锥;对于C ,如图所示,棱锥的侧面是全等的等腰三角形,但该棱锥不是正棱锥;D 也是错误的,底面多边形既有内切圆又有外接圆,如果不同心,则不是正多边形,因此不是正棱锥.[答案] B[点评] 本题考查棱锥、正棱锥的概念以及四面体与三棱锥的等价性,当三棱锥的棱长都相等时,这样的三棱锥叫正四面体.判断一个命题为真命题要考虑全面,应特别注意一些特殊情况.跟踪练习1:以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥、得到一个圆锥和一个圆台.其中正确命题的个数为( )A.0 B.1 C.2 D.3[答案] A[解析] ①应以直角三角形的一条直角边为轴旋转才可以得到圆锥;②以直角梯形垂直于底边的一腰为轴旋转可得到圆台;③它们的底面为圆面,④用平行于圆锥底面的平面截圆锥,可得到一个圆锥和圆台.应选A.2.命题方向:直观图[例2] 若已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,那么原△ABC的面积为( )A.32a2 B.34a2 C.62a2 D.6a2[解析] 如图是△ABC的平面直观图△A′B′C′.作C′D′∥y′轴交x′轴于D′,则C′D′对应△ABC的高CD,∴CD=2C′D′=2·2·C′O′=22·32a=6a.而AB=A′B′=a,∴S△ABC=12·a·6a=62a2[答案] C[点评] 解决这类题的关键是根据斜二测画法求出原三角形的底和高,将水平放置的平面图形的直观图,还原成原来的图形,其作法就是逆用斜二测画法,也就是使平行于x轴的线段的长度不变,而平行于y轴的线段长度变为直观图中平行于y′轴的线段长度的2倍.跟踪练习2已知正三角形ABC 的边长为a ,那么△ABC 的平面直观图△A ′B ′C ′的面积为( )A.34a 2B.38a 2C.68a 2D.616a 2 [分析] 先根据题意画出直观图,然后根据直观图△A ′B ′C ′的边长及夹角求解.[答案] D[解析] 如图①、②所示的实际图形和直观图.由②可知,A ′B ′=AB =a ,O ′C ′=12OC =34a , 在图②中作C ′D ′⊥A ′B ′于D ′,则C ′D ′=22O ′C ′=68a . ∴S △A ′B ′C ′=12A ′B ′·C ′D ′=12×a ×68a =616a 2. 3.命题方向:三视图[例3] 下列图形中的图(b)是根据图(a)中的实物画出的主视图和俯视图,你认为正确吗?若不正确请改正并画出左视图.[解析] 主视图和俯视图都不正确.主视图的上面的矩形中缺少中间小圆柱形成的轮廓线(用虚线表示);左视图的轮廓是两个矩形叠放在一起,上面的矩形中有2条不可视轮廓线.下面的矩形中有一条可视轮廓线(用实线表示),该几何体的三视图如图所示:[点评] 简单几何体的三视图的画法应从以下几个方面加以把握:(1)搞清主视、左视、俯视的方向,同一物体由放置的位置不同,所画的三视图可能不同.(2)看清简单组合体是由哪几个基本元素组成.(3)画三视图时要遵循“长对正,高平齐,宽相等”的原则,还要注意几何体中与投影垂直或平行的线段及面的位置关系.跟踪练习3(2010·浙江文)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )A.3523cm 3B.3203cm 3C.2243cm 3D.1603cm 3 [答案] B[解析] 本题考查了三视图及几何体体积的求解.由三视图可知,该几何体是由一个正四棱台和一个长方体构成的一个组合体,V 台=13×2×(16+42×82+64)=2243cm 3, V 长方体=4×4×2=32cm 3 ∴V 总=V 台+V 长方体=2243+32=3203cm 3.(五)思想方法点拨:1.要注意牢固把握各种几何体的结构特点,利用它们彼此之间的联系来加强记忆,如棱柱、棱锥、棱台为一类;圆柱、圆锥、圆台为一类;或分成柱体、锥体、台体三类来分别认识.只有对比才能把握实质和不同,只有联系才能理解共性和个性.2.要适当与平面几何的有关概念、图形和性质进行对比,通过平面几何与立体几何相关知识的比较,丰富自己的空间想象力.对组合体可通过把它们分解为一些基本几何体来研究.3.画图时要紧紧把握住一斜——在已知图形中垂直于x 轴的线段,在直观图中均与x 轴成45°;二测——两种度量形式,即在直观图中,平行于x 轴的线段长度不变,平行于y 轴的线段变为原长度的一半.4.三视图(1)几何体的三视图的排列规则:俯视图放在主视图的下面,长度与主视图一样,左视图放在主视图右面,高度与主视图一样,宽度与俯视图一样,即“长对正,高平齐,宽相等”.注意虚、实线的区别.(2)应用:在解题的过程中,可以根据三视图的形状及图中所涉及到的线段的长度,推断出原几何图形中的点、线、面之间的关系及图中的一些线段的长度,这样我们就可以解出有关的问题.5.本节常涉及一些截面问题,它把空间图形的性质、画法及有关论证、计算融为一体,常见的、基本的截面问题,如直截面、对角截面、中截面等,要求熟知并掌握.要知道这些截面的形状、位置,并能画出其图形,这常常可以将较难的问题变得简单,如“用一个平面截一个球,截面是圆面”这一点很重要,它把有关球的一些问题转化为圆的问题来解决.(六)课后强化作业一、选择题1.(2010·陕西理)若某空间几何体的三视图如图所示,则该几何体的体积是( )A.13B.23 C .1 D .2[答案] C[解析] C 该几何体是如图所示的直三棱柱V =12×1×2×2=1. 2.下列命题中:①与定点的距离等于定长的点的集合是球面;②球面上三个不同的点,一定都能确定一个圆;③一个平面与球相交,其截面是一个圆,其中正确命题的个数为( )A .0B .1C .2D .3[答案] C[解析] 命题①、②都对,命题③一个平面与球相交,其截面是一个圆面,故选C.[点评] 要注意球与球面的区别.3.(2009·上海文,16)如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )[答案] B[解析] 本题考查三视图的基本知识及空间想象能力.由题可知,选B.4.如果一个空间几何体的主视图与左视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )A.33πB.233πC.3πD.π3- 11 - [答案] A[解析] 由三视图知,该几何体是底半径为1的圆锥,轴截面是边长为2的正三角形,∴高为3,体积V =33π. 5.如图,△O ′A ′B ′是△OAB 水平放置的直观图,则△OAB 的面积为( )A .6B .3 2C .6 2D .12[答案] D[解析] 若还原为原三角形,则易知OB =4,OA ⊥OB ,OA =6,∴S △AOB =12×4×6=12. 6.棱长为1的正方体ABCD -A 1B 1C 1D 1的8个顶点都在球O 的表面上,E 、F 分别是棱AA 1、DD 1的中点,则直线EF 被球O 截得的线段长为( )A.22 B .1 C .1+22 D. 2 [答案] D[解析] 由条件知球O 半径为32,球心O 到直线EF 的距离为12,由垂径定理可知直线EF 被球O 截得的线段长d =2⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫122= 2. 7.(2010·广东)如图所示,△ABC 为正三角形,AA ′∥BB ′∥CC ′,CC ′⊥平面ABC 且3AA ′=32BB ′=CC ′=AB ,则多面体ABC -A ′B ′C ′的正视图(也称主视图)是( )[答案] D[解析] 本小题考查线面垂直的判定方法及三视图的有关概念.由于AA ′∥BB ′∥CC ′及CC ′⊥平面ABC ,知BB ′⊥平面ABC ,又CC ′=32BB ′,且△ABC 为正三角形,故正(主)视图为D.8.用单位正方体搭一个几何体,使它的主视图和俯视图如图所示,则它的体积的最小值与最大值分别为( )A .9与13B .7与10C .10与16D .10与15[答案] C [解析] 由俯视图知几何体有三行和三列,且第三列的第一行,第二行都没有小正方体,其余各列各行都有小正- 12 -。
2020年高考试题分类汇编(立体几何)

2020年高考试题分类汇编(立体几何)考法1空间中的点、线、面的位置关系1.(2020·全国卷Ⅰ·文理科)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状科视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥的一个侧面三角形的面积,则其侧面三角形底边上的高于底面正方形的边长的比值为 A .514- B .512- C .514+ D .512+2.(2020·全国卷Ⅰ·理科)如图,在三棱锥P ABC -的平面展开图中,1AC =,3AB AD ==,AB AC ⊥,AB AD ⊥, 30CAE ∠=,则cos FCB ∠= .3.(2020·全国卷Ⅱ·文理科)设有下列四个命题:1p :两两相交且不过同一点的三条直线必在同一个平面内. 2p :过空间任意三点有且仅有一个平面.3p :若空间两条直线不相交,则这两条直线平行. 4p :若直线l ⊂平面α,直线m ⊥平面α,则l m ⊥.则下列命题中所以真命题的序号是 .①14p p ∧ ②12p p ∧ ③23()p p ⌝∨ ④34()()p p ⌝∨⌝ 4.(2020·浙江卷)已知空间中不过同一点的三条直线m ,n ,l ,则“m ,n ,ABCD (P )E (P )F (P )l 在同一平面”是“m ,n ,l 两两相交”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 考法2三视图1.(2020·全国卷Ⅱ·理科)右图是一个多面体的三视图,这个多面体某天棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为A .EB .FC .GD .H2.(2020·全国卷Ⅲ·文理科)右图为某几何体的三视图,则该几何体的表面积为A .642+B .442+C .623+D .423+3.(2020·浙江卷)某几何体的三视图(单位:cm )如图所示,则该几 何体的体积(单位:3cm )是A .73B .143C .3D .64.(2020·北京卷)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱M N EF GH222的表面积为A .63+B .623+C .123+D .1223+考法3与球的组合体1.(2020·全国卷Ⅰ·文理科)已知A ,B ,C 为球O 的球面上三点,1O 为ABC ∆的外接圆,若1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为 A .64π B .48π C .36π D .32π2.(2020·山东卷)日冕是中国古代用来测定时间的仪器,利用与冕面垂直的冕针投射到冕面的影子来测定时间,把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成的角,点A 处的水平面是指过点A 且与OA 垂直的平面,在点A 处放置一个日冕,若冕面与赤道所在的平面平行,点A 的纬度为北纬40,则冕针与点A 处的水平面所成的角为A .20B .40C .50D .903.(2020·全国卷Ⅱ·文理科)已知ABC ∆是面积为934的等边三角形,且其顶点都在球O 的球面上,若球O 的表面积为16π,则O 到平面ABC 的面积112正(主)视图 侧(左)视图俯视图AB .32C .1 D.24.(2020·全国卷Ⅲ·文理科)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .5.(2020·山东卷)已知直四棱柱1111ABCD A B C D -的棱长均为2,60BAD ∠=.以1D11BCC B 的交线长为 .6.(2020·天津卷)若棱长为则该球的表面积为A .12πB .24πC .36πD .144π考法4解答题1.(2020·全国卷Ⅰ·理科)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC ∆是底面的内角正三角形,P 为DO上一点,6PO DO =. (Ⅰ)证明:PA ⊥平面PBC ; (Ⅱ)求二面角B PC E --的余弦值.2.(2020·全国卷Ⅰ·文科)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC ∆是底面的内角正三角形,P 为DO 上一点,90ABC ∠=. (Ⅰ)证明:平面PAB ⊥平面PAC ;(Ⅱ)设DO =,求三棱锥P ABC -的体积.P ABO E CDP ABO C D3.(2020·全国卷Ⅱ·理科)如图,已知三棱柱111ABC A B C -的底面是正三角形,侧面11BCC B 是矩形,M ,N 分别为的BC ,11B C 的中点,P 为AM 上一点,过11B C 和P 的平面交AB 于E ,交AC 于F .(Ⅰ)证明:1AA MN ∥,且平面1A AMN ⊥平面11EB C F ;(Ⅱ)设O 为111A B C ∆的中心,若AO ∥平面11EB C F ,且AO AB =,求直线1B E 与平面1A AMN 所成角的正弦值.4.(2020·全国卷Ⅱ·文科)如图,已知三棱柱111ABC A B C -的底面是正三角形,侧面11BCC B 是矩形,M ,N 分别为的BC ,11B C 的中点,P 为AM 上一点,过11B C 和P 的平面交AB 于E ,交AC 于F .(Ⅰ)证明:1AA MN ∥,且平面1A AMN ⊥平面11EB C F ;(Ⅱ)设O 为111A B C ∆的中心,若6AO AB ==,AO ∥平面11EB C F ,且3MPN π∠=,求四棱锥11B EB C F -的体积.5.(2020·全国卷Ⅲ·理科)如图,在长方体1111ABCD A B C D -中,点E 、F 分别在棱1DD ,1BB 上,且2DE =1ED ,12BF FB =. (Ⅰ)证明:点1C 在平面AEF 内;ABC E F O MNA 1B 1C 1PABC E FO MNA 1B 1C 1P(Ⅱ)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.6.(2020·全国卷Ⅲ·文科)如图,在长方体1111ABCD A B C D -中,点E 、F 分别在棱1DD ,1BB 上,且2DE =1ED ,12BF FB =.(Ⅰ)当AB BC =时,EF AC ⊥. (Ⅱ)证明:点1C 在平面AEF 内;7.(2020·山东卷)如图,四棱锥P ABCD -的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l . (Ⅰ)证明:l ⊥平面PDC ;(Ⅱ)已知1PD AD ==,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值.A BCDEF A 1B 1C 1D 1ABCDEFA 1B 1C 1D 1PABCD8.(2020·天津卷)如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,AC BC ⊥,2AC BC ==,13CC =,点D ,E 分别在棱1AA 和棱1CC 上,且1AD =,2CE =,M 为棱11A B 的中点. (Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.9.(2020·浙江卷)如图,三棱台DEF ABC -中,面ADFC ⊥面ABC ,45ACB ACD ∠=∠=,DC =2BC .(Ⅰ)证明:EF DB ⊥;(Ⅱ)求DF 与面DBC 所成角的正弦值.A BCDEMB 1A 1C 1ABCDEF10.(2020·北京卷)如图,在正方体1111ABCD A B C D 中,E 为1BB 的中点. (Ⅰ)求证:1BC ∥平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.ABCDE A 1B 1C 1D 1。
2020-2022年高考数学真题分类汇编专题05 平面解析几何+立体几何(教师版+学生版)

专题05 平面解析几何1.【2021年新高考1卷】已知1F ,2F 是椭圆C :22194x y+=的两个焦点,点M 在C 上,则12MF MF ⋅的最大值为( )A .13B .12C .9D .6【答案】C【分析】本题通过利用椭圆定义得到1226MF MF a +==,借助基本不等式212122MF MF MF MF ⎛+⎫⋅≤ ⎪⎝⎭即可得到答案.【解析】由题,229,4a b ==,则1226MF MF a +==,所以2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭(当且仅当123MF MF ==时,等号成立). 故选:C .2.【2021年新高考2卷】抛物线22(0)y px p =>的焦点到直线1y x =+的距离为2,则p =( ) A .1 B .2 C .22 D .4【答案】B【分析】首先确定抛物线的焦点坐标,然后结合点到直线距离公式可得p 的值. 【解析】抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭,其到直线10x y -+=的距离:012211pd -+==+,解得:2p =(6p =-舍去).故选:B. 3.【2022年新高考1卷】已知O 为坐标原点,点在抛物线上,过点的直线交C 于P ,Q 两点,则( )A .C 的准线为B .直线AB 与C 相切 C .D .【答案】BCD【分析】求出抛物线方程可判断A ,联立AB 与抛物线的方程求交点可判断B ,利用距离公式及弦长公式可判断C、D.【解析】将点的代入抛物线方程得,所以抛物线方程为,故准线方程为,A错误;,所以直线的方程为,联立,可得,解得,故B正确;设过的直线为,若直线与轴重合,则直线与抛物线只有一个交点,所以,直线的斜率存在,设其方程为,,联立,得,所以,所以或,,又,,所以,故C正确;因为,,所以,而,故D正确.故选:BCD 4.【2022年新高考2卷】已知O为坐标原点,过抛物线焦点F的直线与C交于A,B两点,其中A在第一象限,点,若,则()A.直线的斜率为B.C.D.【答案】ACD【分析】由及抛物线方程求得,再由斜率公式即可判断A选项;表示出直线的方程,联立抛物线求得,即可求出判断B选项;由抛物线的定义求出即可判断C选项;由,求得,为钝角即可判断D选项.【解析】对于A,易得,由可得点在的垂直平分线上,则点横坐标为,代入抛物线可得,则,则直线的斜率为,A 正确;对于B ,由斜率为可得直线的方程为,联立抛物线方程得,设,则,则,代入抛物线得,解得,则,则,B 错误;对于C ,由抛物线定义知:,C 正确;对于D ,,则为钝角, 又,则为钝角,又,则,D 正确.故选:ACD.5.【2021年新高考1卷】已知点P 在圆()()225516x y -+-=上,点()4,0A 、()0,2B ,则( )A .点P 到直线AB 的距离小于10 B .点P 到直线AB 的距离大于2C .当PBA ∠最小时,32PB =D .当PBA ∠最大时,32PB =【答案】ACD【分析】计算出圆心到直线AB 的距离,可得出点P 到直线AB 的距离的取值范围,可判断AB 选项的正误;分析可知,当PBA ∠最大或最小时,PB 与圆M 相切,利用勾股定理可判断CD 选项的正误.【解析】圆()()225516x y -+-=的圆心为()5,5M ,半径为4,直线AB 的方程为142x y +=,即240x y +-=,圆心M 到直线AB 的距离为2252541111545512+⨯-==>+,所以,点P 到直线AB 的距离的最小值为115425-<,最大值为1154105+<,A 选项正确,B 选项错误;如下图所示:当PBA ∠最大或最小时,PB 与圆M 相切,连接MP 、BM ,可知PM PB ⊥,()()22052534BM =-+-4MP =,由勾股定理可得2232BP BM MP =-=CD 选项正确.故选:ACD.【点睛】结论点睛:若直线l 与半径为r 的圆C 相离,圆心C 到直线l 的距离为d ,则圆C 上一点P 到直线l 的距离的取值范围是[],d r d r -+.6.【2021年新高考2卷】已知直线2:0l ax by r +-=与圆222:C x y r +=,点(,)A a b ,则下列说法正确的是( )A .若点A 在圆C 上,则直线l 与圆C 相切B .若点A 在圆C 内,则直线l 与圆C 相离 C .若点A 在圆C 外,则直线l 与圆C 相离D .若点A 在直线l 上,则直线l 与圆C 相切 【答案】ABD【分析】转化点与圆、点与直线的位置关系为222,a b r +的大小关系,结合点到直线的距离及直线与圆的位置关系即可得解. 【解析】圆心()0,0C 到直线l的距离2d =若点(),A a b 在圆C 上,则222a b r +=,所以2d r =,则直线l 与圆C 相切,故A 正确;若点(),A a b 在圆C 内,则222a b r +<,所以2d r =,则直线l 与圆C 相离,故B 正确;若点(),A a b 在圆C 外,则222a b r +>,所以2d r =,则直线l 与圆C 相交,故C 错误;若点(),A a b 在直线l 上,则2220a b r +-=即222=a b r +,所以2d r ,直线l 与圆C 相切,故D 正确.故选:ABD.7.【2020年新高考1卷(山东卷)】已知曲线22:1C mx ny +=.( ) A .若m >n >0,则C 是椭圆,其焦点在y 轴上 B .若m =n >0,则CC .若mn <0,则C是双曲线,其渐近线方程为y = D .若m =0,n >0,则C 是两条直线 【答案】ACD【分析】结合选项进行逐项分析求解,0m n >>时表示椭圆,0m n =>时表示圆,0mn <时表示双曲线,0,0m n =>时表示两条直线.【解析】对于A ,若0m n >>,则221mx ny +=可化为22111x y m n +=, 因为0m n >>,所以11m n<, 即曲线C 表示焦点在y 轴上的椭圆,故A 正确;对于B ,若0m n =>,则221mx ny +=可化为221x y n+=, 此时曲线C 表示圆心在原点,半径为nn的圆,故B 不正确; 对于C ,若0mn <,则221mx ny +=可化为22111x y m n +=,此时曲线C 表示双曲线, 由220mx ny +=可得my x n=±-,故C 正确; 对于D ,若0,0m n =>,则221mx ny +=可化为21y n=, ny n=±,此时曲线C 表示平行于x 轴的两条直线,故D 正确; 故选:ACD.【点睛】本题主要考查曲线方程的特征,熟知常见曲线方程之间的区别是求解的关键,侧重考查数学运算的核心素养. 8.【2022年新高考1卷】写出与圆和都相切的一条直线的方程________________. 【答案】或或【分析】先判断两圆位置关系,分情况讨论即可. 【解析】圆的圆心为,半径为,圆的圆心为,半径为,两圆圆心距为,等于两圆半径之和,故两圆外切,如图,当切线为l时,因为,所以,设方程为O到l的距离,解得,所以l的方程为,当切线为m时,设直线方程为,其中,,由题意,解得,当切线为n时,易知切线方程为,故答案为:或或.9.【2022年新高考1卷】已知椭圆,C的上顶点为A,两个焦点为,,离心率为.过且垂直于的直线与C交于D,E两点,,则的周长是________________.【答案】13【分析】利用离心率得到椭圆的方程为,根据离心率得到直线的斜率,进而利用直线的垂直关系得到直线的斜率,写出直线的方程:,代入椭圆方程,整理化简得到:,利用弦长公式求得,得,根据对称性将的周长转化为的周长,利用椭圆的定义得到周长为.【解析】∵椭圆的离心率为,∴,∴,∴椭圆的方程为,不妨设左焦点为,右焦点为,如图所示,∵,∴,∴为正三角形,∵过且垂直于的直线与C交于D,E两点,为线段的垂直平分线,∴直线的斜率为,斜率倒数为,直线的方程:,代入椭圆方程,整理化简得到:,判别式,∴,∴,得,∵为线段的垂直平分线,根据对称性,,∴的周长等于的周长,利用椭圆的定义得到周长为.故答案为:13.10.【2022年新高考2卷】设点,若直线关于对称的直线与圆有公共点,则a的取值范围是________.【答案】【分析】首先求出点关于对称点的坐标,即可得到直线的方程,根据圆心到直线的距离小于等于半径得到不等式,解得即可;【解析】解:关于对称的点的坐标为,在直线上,所以所在直线即为直线,所以直线为,即;圆,圆心,半径,依题意圆心到直线的距离,即,解得,即;故答案为:11.【2022年新高考2卷】已知直线l 与椭圆在第一象限交于A ,B 两点,l 与x轴,y 轴分别交于M ,N 两点,且,则l 的方程为___________.【答案】【分析】令的中点为,设,,利用点差法得到,设直线,,,求出、的坐标,再根据求出、,即可得解; 【解析】解:令的中点为,因为,所以,设,,则,,所以,即所以,即,设直线,,,令得,令得,即,,所以, 即,解得或(舍去),又,即,解得或(舍去),所以直线,即;故答案为:12.【2021年新高考1卷】已知O 为坐标原点,抛物线C :22y px =(0p >)的焦点为F ,P为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则C 的准线方程为______. 【答案】32x =-【分析】先用坐标表示P Q ,,再根据向量垂直坐标表示列方程,解得p ,即得结果. 【解析】抛物线C :22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点,PF 与x 轴垂直, 所以P 的横坐标为2p ,代入抛物线方程求得P 的纵坐标为p ±,不妨设(,)2pP p ,因为Q 为x 轴上一点,且PQ OP ⊥,所以Q 在F 的右侧, 又||6FQ =,(6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥,所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=,所以C 的准线方程为32x =-故答案为:32x =-.【点睛】利用向量数量积处理垂直关系是本题关键.13.【2021年新高考2卷】若双曲线22221x y a b -=的离心率为2,则此双曲线的渐近线方程___________.【答案】y =【分析】根据离心率得出2c a =,结合222+=a b c 得出,a b 关系,即可求出双曲线的渐近线方程.【解析】由题可知,离心率2ce a==,即2c a =,又22224a b c a +==,即223b a =,则ba=故此双曲线的渐近线方程为y =.故答案为:y =.14.【2020年新高考1卷(山东卷)C :y 2=4x 的焦点,且与C 交于A ,B 两点,则AB =________. 【答案】163【分析】先根据抛物线的方程求得抛物线焦点坐标,利用点斜式得直线方程,与抛物线方程联立消去y 并整理得到关于x 的二次方程,接下来可以利用弦长公式或者利用抛物线定义将焦点弦长转化求得结果.【解析】∵抛物线的方程为24y x =,∴抛物线的焦点F 坐标为(1,0)F , 又∵直线AB 过焦点F 且斜率为3,∴直线AB 的方程为:3(1)y x =- 代入抛物线方程消去y 并化简得231030x x -+=,解法一:解得121,33x x == ,所以212116||1||13|3|33AB k x x =+-=+⋅-=解法二:10036640∆=-=>,设1122(,),(,)A x y B x y ,则12103x x +=, 过,A B 分别作准线1x =-的垂线,设垂足分别为,C D 如图所示. 12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为:163【点睛】本题考查抛物线焦点弦长,涉及利用抛物线的定义进行转化,弦长公式,属基础题. 15.【2022年新高考1卷】已知点在双曲线上,直线l 交C 于P ,Q 两点,直线的斜率之和为0.(1)求l 的斜率; (2)若,求的面积.【答案】(1);(2).【分析】(1)由点在双曲线上可求出,易知直线l的斜率存在,设,,再根据,即可解出l的斜率;(2)根据直线的斜率之和为0可知直线的倾斜角互补,再根据即可求出直线的斜率,再分别联立直线与双曲线方程求出点的坐标,即可得到直线的方程以及的长,由点到直线的距离公式求出点到直线的距离,即可得出的面积.【解析】(1)因为点在双曲线上,所以,解得,即双曲线易知直线l的斜率存在,设,,联立可得,,所以,,.所以由可得,,即,即,所以,化简得,,即,所以或,当时,直线过点,与题意不符,舍去,故.(2)不妨设直线的倾斜角为,因为,所以,因为,所以,即,即,解得,于是,直线,直线,联立可得,,因为方程有一个根为,所以,,同理可得,,.所以,,点到直线的距离,故的面积为.16.【2022年新高考2卷】已知双曲线的右焦点为,渐近线方程为.(1)求C的方程;(2)过F的直线与C的两条渐近线分别交于A,B两点,点在C上,且.过P且斜率为的直线与过Q且斜率为的直线交于点M.从下面①②③中选取两个作为条件,证明另外一个成立:①M在上;②;③.注:若选择不同的组合分别解答,则按第一个解答计分.【答案】(1);(2)见解析【分析】(1)利用焦点坐标求得的值,利用渐近线方程求得的关系,进而利用的平方关系求得的值,得到双曲线的方程;(2)先分析得到直线的斜率存在且不为零,设直线AB的斜率为k,M(x0,y0),由③|AM|=| BM|等价分析得到;由直线和的斜率得到直线方程,结合双曲线的方程,两点间距离公式得到直线PQ的斜率,由②等价转化为,由①在直线上等价于,然后选择两个作为已知条件一个作为结论,进行证明即可.【解析】(1)右焦点为,∴,∵渐近线方程为,∴,∴,∴,∴,∴.∴C的方程为:;(2)由已知得直线的斜率存在且不为零,直线的斜率不为零,若选由①②推③或选由②③推①:由②成立可知直线的斜率存在且不为零;若选①③推②,则为线段的中点,假若直线的斜率不存在,则由双曲线的对称性可知在轴上,即为焦点,此时由对称性可知、关于轴对称,与从而,已知不符;总之,直线的斜率存在且不为零.设直线的斜率为,直线方程为,则条件①在上,等价于;两渐近线的方程合并为,联立消去y并化简整理得:设,线段中点为,则,设,则条件③等价于,移项并利用平方差公式整理得:,,即,即;由题意知直线的斜率为, 直线的斜率为,∴由,∴,所以直线的斜率,直线,即,代入双曲线的方程,即中,得:,解得的横坐标:,同理:,∴∴, ∴条件②等价于,综上所述:条件①在上,等价于;条件②等价于;条件③等价于;选①②推③:由①②解得:,∴③成立;选①③推②:由①③解得:,,∴,∴②成立;选②③推①:由②③解得:,,∴,∴,∴①成立.17.【2021年新高考1卷】在平面直角坐标系xOy 中,已知点()117,0F -、()21217,02F MF MF -=,,点M 的轨迹为C .(1)求C 的方程; (2)设点T 在直线12x =上,过T 的两条直线分别交C 于A 、B 两点和P ,Q 两点,且TA TB TP TQ ⋅=⋅,求直线AB 的斜率与直线PQ 的斜率之和.【答案】(1)()221116y x x -=≥;(2)0. 【分析】(1) 利用双曲线的定义可知轨迹C 是以点1F 、2F 为左、右焦点双曲线的右支,求出a 、b 的值,即可得出轨迹C 的方程;(2)方法一:设出点的坐标和直线方程,联立直线方程与曲线C 的方程,结合韦达定理求得直线的斜率,最后化简计算可得12k k +的值. 【解析】(1) 因为12122217MF MF F F -=<=,所以,轨迹C 是以点1F 、2F 为左、右焦点的双曲线的右支,设轨迹C 的方程为()222210,0x y a b a b -=>>,则22a =,可得1a =,2174b a =-=,所以,轨迹C 的方程为()221116y x x -=≥.(2)[方法一] 【最优解】:直线方程与双曲线方程联立,如图所示,设1(,)2T n ,设直线AB 的方程为112211(),,(2,(),)y n k x A x y B x y -=-.联立1221()2116y n k x y x ⎧-=-⎪⎪⎨⎪-=⎪⎩,化简得22221111211(16)(2)1604k x k k n x k n k n -+---+-=.则22211112122211111624,1616k n k n k k n x x x x k k +-+-+==--.故12,11||)||)22TA x TB x --.则222111221(12)(1)11||||(1)()()2216n k TA TB k x x k ++⋅=+--=-.设PQ 的方程为21()2y n k x -=-,同理22222(12)(1)||||16n k TP TQ k ++⋅=-. 因为TA TB TP TQ ⋅=⋅,所以22122212111616k k k k ++=--,化简得22121717111616k k +=+--,所以22121616k k -=-,即2212k k =.因为11k k ≠,所以120k k +=.[方法二] :参数方程法设1(,)2T m .设直线AB 的倾斜角为1θ,则其参数方程为111cos 2sin x t y m t θθ⎧=+⎪⎨⎪=+⎩,联立直线方程与曲线C 的方程2216160(1)x y x --≥=,可得222221111cos 116(cos )(sin 2sin )1604t m t t mt θθθθ+-++-=+,整理得22221111(16cos sin )(16cos 2sin )(12)0t m t m θθθθ-+--+=.设12,TA t TB t ==,由根与系数的关系得2212222111(12)12||||16cos sin 117cos t m m TA TB t θθθ-++⋅===--⋅.设直线PQ 的倾斜角为2θ,34,TP t TQ t ==,同理可得2342212||||117cos m T T t P Q t θ+⋅==-⋅ 由||||||||TA TB TP TQ ⋅=⋅,得2212cos cos θθ=.因为12θθ≠,所以12s o o s c c θθ=-.由题意分析知12θθπ+=.所以12tan tan 0θθ+=, 故直线AB 的斜率与直线PQ 的斜率之和为0. [方法三]:利用圆幂定理因为TA TB TP TQ ⋅=⋅,由圆幂定理知A ,B ,P ,Q 四点共圆.设1(,)2T t ,直线AB 的方程为11()2y t k x -=-,直线PQ 的方程为21()2y t k x -=-,则二次曲线1212()()022k kk x y t k x y t --+--+=. 又由22116y x -=,得过A ,B ,P ,Q 四点的二次曲线系方程为:221212()()(1)0(0)2216k k y k x y t k x y t x λμλ--+--++--=≠,整理可得:[]2212121212()()()()16k x y k k xy t k k k k k x μμλλλλ++--+++-12(2)02y k k t m λ++-+=,其中21212()42k k t m t k k λμ⎡⎤=+-+-⎢⎥⎣⎦. 由于A ,B ,P ,Q 四点共圆,则xy 项的系数为0,即120k k +=.【整体点评】(2)方法一:直线方程与二次曲线的方程联立,结合韦达定理处理圆锥曲线问题是最经典的方法,它体现了解析几何的特征,是该题的通性通法,也是最优解; 方法二:参数方程的使用充分利用了参数的几何意义,要求解题过程中对参数有深刻的理解,并能够灵活的应用到题目中.方法三:圆幂定理的应用更多的提现了几何的思想,二次曲线系的应用使得计算更为简单.18.【2021年新高考2卷】已知椭圆C 的方程为22221(0)x y a b a b +=>>,右焦点为F ,(1)求椭圆C 的方程;(2)设M ,N 是椭圆C 上的两点,直线MN 与曲线222(0)x y b x +=>相切.证明:M ,N ,F 三点共线的充要条件是||MN =【答案】(1)2213x y +=;(2)证明见解析.【分析】(1)由离心率公式可得a =2b ,即可得解;(2)必要性:由三点共线及直线与圆相切可得直线方程,联立直线与椭圆方程可证MN充分性:设直线():,0MN y kx b kb =+<,由直线与圆相切得221b k =+,联立直线与椭圆方=1k =±,即可得解.【解析】(1)由题意,椭圆半焦距c =c e a ==,所以a = 又2221b a c =-=,所以椭圆方程为2213x y +=;(2)由(1)得,曲线为221(0)x y x +=>,当直线MN 的斜率不存在时,直线:1MN x =,不合题意; 当直线MN 的斜率存在时,设()()1122,,,M x y N x y , 必要性:若M ,N ,F三点共线,可设直线(:MN y k x =即0kx y --=,由直线MN 与曲线221(0)x y x +=>1=,解得1k =±,联立(2213y x x y ⎧=±⎪⎨⎪+=⎩可得2430x -+=,所以1212324x x x x +=⋅=,所以MN 所以必要性成立;充分性:设直线():,0MN y kx b kb =+<即0kx y b -+=, 由直线MN 与曲线221(0)x y x +=>1=,所以221b k =+,联立2213y kx b x y =+⎧⎪⎨+=⎪⎩可得()222136330k x kbx b +++-=, 所以2121222633,1313kb b x x x x k k -+=-⋅=++,所以MN ==()22310k -=,所以1k =±, 所以1k b =⎧⎪⎨=⎪⎩或1k b =-⎧⎪⎨=⎪⎩:MN y x=y x =-,所以直线MN 过点F ,M ,N ,F 三点共线,充分性成立; 所以M ,N ,F 三点共线的充要条件是||MN = 【点睛】关键点点睛:解决本题的关键是直线方程与椭圆方程联立及韦达定理的应用,注意运算的准确性是解题的重中之重.19.【2020年新高考1卷(山东卷)】已知椭圆C :22221(0)x y a b a b +=>>过点()2,1A . (1)求C 的方程:(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得DQ 为定值.【答案】(1)22163x y +=;(2)详见解析.【分析】(1)由题意得到关于,,a b c 的方程组,求解方程组即可确定椭圆方程.(2)方法一:设出点M ,N 的坐标,在斜率存在时设方程为y kx m =+, 联立直线方程与椭圆方程,根据已知条件,已得到,m k 的关系,进而得直线MN 恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q 的位置. 【解析】(1)由题意可得:22222411c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得:2226,3a b c ===,故椭圆方程为:22163x y +=.(2)[方法一]:通性通法 设点()()1122,,,M x y N x y ,若直线MN 斜率存在时,设直线MN 的方程为:y kx m =+, 代入椭圆方程消去y 并整理得:()222124260kxkmx m +++-=,可得122412km x x k +=-+,21222612m x x k -=+,因为AM AN ⊥,所以·0AM AN =,即()()()()121222110x x y y --+--=, 根据1122,kx m y kx m y =+=+,代入整理可得:()()()()22121212140x x km k x x km ++--++-+=,所以()()()22222264121401212m km k km k m k k -⎛⎫++---+-+= ⎪++⎝⎭, 整理化简得()()231210k m k m +++-=,因为(2,1)A 不在直线MN 上,所以210k m +-≠,故23101k m k ++=≠,,于是MN 的方程为2133y k x ⎛⎫=-- ⎪⎝⎭()1k ≠,所以直线过定点直线过定点21,33P ⎛⎫- ⎪⎝⎭.当直线MN 的斜率不存在时,可得()11,N x y -, 由·0AM AN =得:()()()()111122110x x y y --+---=, 得()1221210x y -+-=,结合2211163x y +=可得:2113840x x -+=, 解得:123x =或22x =(舍).此时直线MN 过点21,33P ⎛⎫- ⎪⎝⎭. 令Q 为AP 的中点,即41,33Q ⎛⎫⎪⎝⎭,若D 与P 不重合,则由题设知AP 是Rt ADP △的斜边,故12DQ AP =, 若D 与P 重合,则12DQ AP =,故存在点41,33Q ⎛⎫⎪⎝⎭,使得DQ 为定值. [方法二]【最优解】:平移坐标系将原坐标系平移,原来的O 点平移至点A 处,则在新的坐标系下椭圆的方程为22(2)(1)163x y +++=,设直线MN 的方程为4mx ny .将直线MN 方程与椭圆方程联立得224240x x y y +++=,即22()2()0x mx ny x y mx ny y +++++=,化简得22(2)()(1)0n y m n xy m x +++++=,即2(2)()(1)0y y n m n m x x ⎛⎫⎛⎫+++++= ⎪ ⎪⎝⎭⎝⎭.设()()1122,,,M x y N x y ,因为AM AN ⊥则1212AM AN y y k k x x ⋅=⋅112m n +==-+,即3m n =--. 代入直线MN 方程中得()340n y x x ---=.则在新坐标系下直线MN 过定点44,33⎛⎫-- ⎪⎝⎭,则在原坐标系下直线MN 过定点21,33P ⎛⎫- ⎪⎝⎭.又AD MN ⊥,D 在以AP 为直径的圆上.AP 的中点41,33⎛⎫⎪⎝⎭即为圆心Q .经检验,直线MN 垂直于x 轴时也成立.故存在41,33Q ⎛⎫ ⎪⎝⎭,使得1||||2DQ AP =.[方法三]:建立曲线系 A 点处的切线方程为21163x y ⨯⨯+=,即30x y +-=.设直线MA 的方程为11210k x y k --+=,直线MB 的方程为22210k x y k --+=,直线MN 的方程为0kx y m -+=.由题意得121k k .则过A ,M ,N 三点的二次曲线系方程用椭圆及直线,MA MB 可表示为()()22112212121063x y k x y k k x y k λ⎛⎫+-+--+--+= ⎪⎝⎭(其中λ为系数). 用直线MN 及点A 处的切线可表示为()(3)0kx y m x y μ-+⋅+-=(其中μ为系数).即()()22112212121()(3)63x y k x y k k x y k kx y m x y λμ⎛⎫+-+--+--+=-++- ⎪⎝⎭. 对比xy 项、x 项及y 项系数得()()()121212(1),4(3),21(3).k k k k k m k k k m λμλμλμ⎧+=-⎪++=-⎨⎪+-=+⎩①②③将①代入②③,消去,λμ并化简得3210m k ++=,即2133m k =--.故直线MN 的方程为2133y k x ⎛⎫=-- ⎪⎝⎭,直线MN 过定点21,33P ⎛⎫- ⎪⎝⎭.又AD MN ⊥,D 在以AP 为直径的圆上.AP 中点41,33⎛⎫⎪⎝⎭即为圆心Q .经检验,直线MN 垂直于x 轴时也成立.故存在41,33Q ⎛⎫ ⎪⎝⎭,使得1||||2DQ AP ==.[方法四]:设()()1122,,,M x y N x y .若直线MN 的斜率不存在,则()()1111,,,M x y N x y -. 因为AM AN ⊥,则0AM AN ⋅=,即()1221210x y -+-=.由2211163x y +=,解得123x =或12x =(舍).所以直线MN 的方程为23x =.若直线MN 的斜率存在,设直线MN 的方程为y kx m =+,则()()()222122()6120x kx m k x x x x ++-=+--=.令2x =,则()()1222(21)(21)2212k m k m x x k +-++--=+.又()()221221262y m y y y y y k k -⎛⎫⎛⎫+-=+-- ⎪ ⎪⎝⎭⎝⎭,令1y =,则()()122(21)(21)1112k m k m y y k +--+---=+.因为AM AN ⊥,所以()()()()12122211AM AN x x y y ⋅=--+--2(21)(231)12k m k m k +-++=+0=,即21m k =-+或2133m k =--.当21m k =-+时,直线MN 的方程为21(2)1y kx k k x =-+=-+.所以直线MN 恒过(2,1)A ,不合题意;当2133m k =--时,直线MN 的方程为21213333y kx k k x ⎛⎫=--=-- ⎪⎝⎭,所以直线MN 恒过21,33P ⎛⎫- ⎪⎝⎭.综上,直线MN 恒过21,33P ⎛⎫- ⎪⎝⎭,所以||3AP =又因为AD MN ⊥,即AD AP ⊥,所以点D 在以线段AP 为直径的圆上运动.取线段AP 的中点为41,33Q ⎛⎫ ⎪⎝⎭,则1||||2DQ AP =.所以存在定点Q ,使得||DQ 为定值.【整体点评】(2)方法一:设出直线MN 方程,然后与椭圆方程联立,通过题目条件可知直线过定点P ,再根据平面几何知识可知定点Q 即为AP 的中点,该法也是本题的通性通法; 方法二:通过坐标系平移,将原来的O 点平移至点A 处,设直线MN 的方程为4mx ny ,再通过与椭圆方程联立,构建齐次式,由韦达定理求出,m n 的关系,从而可知直线过定点P ,从而可知定点Q 即为AP 的中点,该法是本题的最优解;方法三:设直线:MN y kx m =+,再利用过点,,A M N 的曲线系,根据比较对应项系数可求出,m k 的关系,从而求出直线过定点P ,故可知定点Q 即为AP 的中点;方法四:同方法一,只不过中间运算时采用了一元二次方程的零点式赋值,简化了求解()()1222--x x 以及()()1211y y --的计算.20.【2020年新高考2卷(海南卷)】已知椭圆C :22221(0)x y a b a b +=>>过点M (2,3),点A 为其左顶点,且AM 的斜率为12 , (1)求C 的方程;(2)点N 为椭圆上任意一点,求△AMN 的面积的最大值.【答案】(1)2211612x y +=;(2)18.【分析】(1)由题意分别求得a ,b 的值即可确定椭圆方程;(2)首先利用几何关系找到三角形面积最大时点N 的位置,然后联立直线方程与椭圆方程,结合判别式确定点N 到直线AM 的距离即可求得三角形面积的最大值. 【解析】(1)由题意可知直线AM 的方程为:13(2)2y x -=-,即24-=-x y .当y =0时,解得4x =-,所以a =4,椭圆()2222:10x y C a b a b+=>>过点M (2,3),可得249116b +=,解得b 2=12.所以C 的方程:2211612x y +=.(2)设与直线AM 平行的直线方程为:2x y m -=,如图所示,当直线与椭圆相切时,与AM 距离比较远的直线与椭圆的切点为N ,此时△AMN 的面积取得最大值.联立直线方程2x y m -=与椭圆方程2211612x y +=,可得:()2232448m y y ++=, 化简可得:2216123480y my m ++-=,所以()221444163480m m ∆=-⨯-=,即m 2=64,解得m =±8,与AM 距离比较远的直线方程:28x y -=, 直线AM 方程为:24-=-x y ,点N 到直线AM 的距离即两平行线之间的距离, 利用平行线之间的距离公式可得:12514d ==+由两点之间距离公式可得||AM =.所以△AMN 的面积的最大值:1182⨯=.【点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.【】专题05 平面解析几何1.【2021年新高考1卷】已知1F ,2F 是椭圆C :22194x y+=的两个焦点,点M 在C 上,则12MF MF ⋅的最大值为( )A .13B .12C .9D .62.【2021年新高考2卷】抛物线22(0)y px p =>的焦点到直线1y x =+的距离为2,则p =( ) A .1B .2C .22D .43.【2022年新高考1卷】已知O 为坐标原点,点在抛物线上,过点的直线交C 于P ,Q 两点,则( )A .C 的准线为B .直线AB 与C 相切 C .D .4.【2022年新高考2卷】已知O 为坐标原点,过抛物线焦点F 的直线与C 交于A ,B 两点,其中A 在第一象限,点,若,则( ) A .直线的斜率为B .C .D .5.【2021年新高考1卷】已知点P 在圆()()225516x y -+-=上,点()4,0A 、()0,2B ,则( )A .点P 到直线AB 的距离小于10 B .点P 到直线AB 的距离大于2C .当PBA ∠最小时,32PB =D .当PBA ∠最大时,32PB =6.【2021年新高考2卷】已知直线2:0l ax by r +-=与圆222:C x y r +=,点(,)A a b ,则下列说法正确的是( )A .若点A 在圆C 上,则直线l 与圆C 相切B .若点A 在圆C 内,则直线l 与圆C 相离 C .若点A 在圆C 外,则直线l 与圆C 相离D .若点A 在直线l 上,则直线l 与圆C 相切7.【2020年新高考1卷(山东卷)】已知曲线22:1C mx ny +=.( ) A .若m >n >0,则C 是椭圆,其焦点在y 轴上 B .若m =n >0,则C nC .若mn <0,则C 是双曲线,其渐近线方程为my x n=±- D .若m =0,n >0,则C 是两条直线 8.【2022年新高考1卷】写出与圆和都相切的一条直线的方程________________. 9.【2022年新高考1卷】已知椭圆,C 的上顶点为A ,两个焦点为,,离心率为.过且垂直于的直线与C 交于D ,E 两点,,则的周长是________________. 10.【2022年新高考2卷】设点,若直线关于对称的直线与圆有公共点,则a 的取值范围是________.11.【2022年新高考2卷】已知直线l 与椭圆在第一象限交于A ,B 两点,l 与x轴,y 轴分别交于M ,N 两点,且,则l 的方程为___________.12.【2021年新高考1卷】已知O 为坐标原点,抛物线C :22y px =(0p >)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则C 的准线方程为______.13.【2021年新高考2卷】若双曲线22221x y a b -=的离心率为2,则此双曲线的渐近线方程___________.14.【2020年新高考1卷(山东卷)】斜率为3的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则AB =________. 15.【2022年新高考1卷】已知点在双曲线上,直线l 交C 于P ,Q 两点,直线的斜率之和为0.(1)求l 的斜率; (2)若,求的面积.16.【2022年新高考2卷】已知双曲线的右焦点为,渐近线方程为.(1)求C 的方程;(2)过F 的直线与C 的两条渐近线分别交于A ,B 两点,点在C 上,且.过P 且斜率为的直线与过Q 且斜率为的直线交于点M .从下面①②③中选取两个作为条件,证明另外一个成立: ①M 在上;②;③.注:若选择不同的组合分别解答,则按第一个解答计分.17.【2021年新高考1卷】在平面直角坐标系xOy 中,已知点()1F 、)2122F MF MF -=,,点M 的轨迹为C .(1)求C 的方程; (2)设点T 在直线12x =上,过T 的两条直线分别交C 于A 、B 两点和P ,Q 两点,且TA TB TP TQ ⋅=⋅,求直线AB 的斜率与直线PQ 的斜率之和.18.【2021年新高考2卷】已知椭圆C 的方程为22221(0)x y a b a b +=>>,右焦点为F ,(1)求椭圆C 的方程;(2)设M ,N 是椭圆C 上的两点,直线MN 与曲线222(0)x y b x +=>相切.证明:M ,N ,F 三点共线的充要条件是||MN =19.【2020年新高考1卷(山东卷)】已知椭圆C :22221(0)x y a b a b +=>>过点()2,1A . (1)求C 的方程:(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得DQ 为定值.20.【2020年新高考2卷(海南卷)】已知椭圆C :22221(0)x y a b a b +=>>过点M (2,3),点A 为其左顶点,且AM 的斜率为12 , (1)求C 的方程;(2)点N 为椭圆上任意一点,求△AMN 的面积的最大值.【】三年专题05 立体几何(选择题、填空题)(理科专用)1.【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()()A.B.C.D.【答案】C【解析】【分析】根据题意只要求出棱台的高,即可利用棱台的体积公式求出.【详解】依题意可知棱台的高为(m),所以增加的水量即为棱台的体积.棱台上底面积,下底面积,∴.故选:C.2.【2022年新高考1卷】已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为,且,则该正四棱锥体积的取值范围是()A.B.C.D.【答案】C【解析】【分析】设正四棱锥的高为,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围. 【详解】 ∵ 球的体积为,所以球的半径,设正四棱锥的底面边长为,高为,则,,所以,所以正四棱锥的体积,所以,当时,,当时,,所以当时,正四棱锥的体积取最大值,最大值为, 又时,,时,,所以正四棱锥的体积的最小值为, 所以该正四棱锥体积的取值范围是.故选:C.3.【2022年新高考2卷】已知正三棱台的高为1,上、下底面边长分别为和,其顶点都在同一球面上,则该球的表面积为( ) A .B .C .D .【答案】A 【解析】 【分析】根据题意可求出正三棱台上下底面所在圆面的半径,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积. 【详解】设正三棱台上下底面所在圆面的半径,所以,即,设球心到上下底面的距离分别为,球的半径为,所以,,故或,即或,解得符合题意,所以球的表面积为.故选:A .4.【2021年甲卷理科】2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45AC B ∠'''=︒,。
2020年高考数学分类汇编:立体几何

2020年高考数学分类汇编:立体几何4.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为A.20°B.40°C.50°D.90°8.右图为某几何体的三视图,则该几何体的表面积是A. 6+42+B. 442+C. 623+D. 4239.右图为某几何体的三视图,则该几何体的表面积是A. 6+42B. 4+42C. 6+23D. 4+237.右图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为A .EB .FC .GD .H16.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的切球表面积为11.已知△ABC 的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为AB .32C .1D 16.设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内. p 2:过空间中任意三点有且仅有一个平面. p 3:若空间两条直线不相交,则这两条直线平行. p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l . 则下述命题中所有真命题的序号是__________. ① 14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为②③ A B C D3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .14B .12C .14D .1212.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π16.设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内. p 2:过空间中任意三点有且仅有一个平面. p 3:若空间两条直线不相交,则这两条直线平行. p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l . 则下述命题中所有真命题的序号是__________. ① 14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝5.某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是A .73B .143C .3D .66.已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件10.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π15.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为____.10.已知△ABC 的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为AB .32C .1D 9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm ,高为2cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是▲ cm.4.某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A .6+B .6+C .12+D .12+5.若棱长为A.12πB.24πC.36πD.144πD为半径的球面与侧面BCC1B1 16.已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以1的交线长为________.16.如图,在三棱锥P–ABC的平面展开图中,AC=1,AB AD=AB⊥AC,AB⊥AD,∠CAE=30°,则cos ∠FCB=.14.已知圆锥的侧面积(单位:cm2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是_______.19.(本题满分15分)如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.(Ⅰ)证明:EF⊥DB;(Ⅱ)求直线DF与平面DBC所成角的正弦值.如图,在长方体ABCD -1111A B C D 中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =. (1)证明:点1C 在平面AEF 内;(2)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.19.(12分)如图,在长方体1111ABCD A B C D -中,在E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =,证明:(1) 当AB BC =时,EF AC ⊥; (2) 点1C 在平面AEF 内.如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.20.(12分)如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=π3,求四棱锥B–EB1C1F的体积.如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥EB1C1F;(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.18.(12分)△是底面的内接正如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE AD=.ABC三角形,P为DO上一点,PO=.(1)证明:PA⊥平面PBC;--的余弦值.(2)求二面角B PC E如图,D为圆锥的顶点,O是圆锥底面的圆心,ABC△是底面的内接正三角形,P为DO上一点,∠APC=90°.(1)证明:平面PAB⊥平面PAC;(2)设DO,求三棱锥P−ABC的体积.22.(本小题满分10分)在三棱锥A—BCD中,已知CB=CD,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.(1)求直线AB与DE所成角的余弦值;(2)若点F在BC上,满足BF=14BC,设二面角F—DE—C的大小为θ,求sinθ的值.15.(本小题满分14分)在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点. (1)求证:EF ∥平面AB 1C 1; (2)求证:平面AB 1C ⊥平面ABB 1.16.(本小题13分)如图,在正方体1111ABCD A B C D 中,E 为1BB 的中点.(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.17.(本小题满分15分)如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E分别在棱1AA 和棱1CC 上,且2,1,AD CE M ==为棱11A B 的中点.(Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高考数学分类汇编:立体几何
4.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为
A.20°B.40°
C.50°D.90°
8.右图为某几何体的三视图,则该几何体的表面积是
A. 6+42
B. 442
C. 623
D. 423
9.右图为某几何体的三视图,则该几何体的表面积是
A. 6+42
B. 4+42
C. 6+23
D. 4+23
7.右图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为
A .
E
B .
F C .G
D .
H
16.已知圆锥的底面半径为
1,母线长为3,则该圆锥内半径最大的切球表面积为
11.已知△ABC 是面积为
934
的等边三角形,且其顶点都在球
O 的球面上.若球
O 的表面积为16π,则O
到平面ABC 的距离为A .
3
B .32
C .1
D .
32
16.设有下列四个命题:
p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l
平面α,直线m ⊥平面α,则m ⊥l .
则下述命题中所有真命题的序号是__________.
①
14p p ②12p p ③
23
p p ④
34
p p 3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
②
③A .
514
B .
512
C .
514
D .
512
3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方
形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
A .
514
B .
512
C .
514
D .
512
12.已知,,A B C 为球O 的球面上的三个点,⊙
1O 为ABC △的外接圆,若⊙1O 的面积为4π
,1AB
BC AC
OO ,则球O 的表面积为
A .
64πB .48π
C .36π
D .
32π
16.设有下列四个命题:
p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l
平面α,直线m ⊥平面α,则m ⊥l .
则下述命题中所有真命题的序号是__________.
①
14p p ②12p p ③
23
p p ④
3
4
p p 5.某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:
cm 3
)是
A .
73
B .
143
C .3
D .6
6.已知空间中不过同一点的三条直线
l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
10.已知,,A B C 为球
O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,
1AB
BC AC
OO ,则球O 的表面积为
A .
64πB .48π
C .36π
D .
32π
15.已知圆锥的底面半径为
1,母线长为3,则该圆锥内半径最大的球的体积为
____.
10.已知△ABC 是面积为
934
的等边三角形,且其顶点都在球
O 的球面上.若球
O 的表面积为16π,则O
到平面ABC 的距离为A .
3
B .32
C .1
D .
32
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为
2cm ,
高为2cm ,内孔半轻为
0.5 cm ,则此六角螺帽毛坯的体积是
▲
cm.
4.某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为().
A .63
B .
623C .123D .1223
5.若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为
A.12πB.24πC.36πD.144π
D为球心,5为半径的球面与侧面BCC1B1 16.已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以
1
的交线长为________.
AB AD,AB⊥AC,AB⊥AD,∠CAE=30°,则cos 16.如图,在三棱锥P–ABC的平面展开图中,AC=1,3
∠FCB=.
14.已知圆锥的侧面积(单位:cm2)为2,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是_______.
19.(本题满分15分)
如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
如图,在长方体ABCD -1111A B C D 中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED ,12BF
FB .
(1)证明:点1C 在平面AEF 内;(2)若2AB
,1AD
,1
3AA ,求二面角1A
EF
A 的正弦值.
19.(12分)如图,在长方体1111ABCD A B C D 中,在E ,F 分别在棱1DD ,1BB 上,且12DE
ED ,12BF
FB ,
证明:
(1)当AB BC 时,EF AC ;
(2)点1C 在平面AEF 内.
如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
20.(12分)
如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=π
3
,求四棱锥B–EB1C1F的体
积.
如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1∥MN,且平面A1AMN⊥EB1C1F;
(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
18.(12分)
△是底面的内接正如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE AD.ABC
三角形,P为DO上一点,6
PO DO.
6
(1)证明:PA平面PBC;
(2)求二面角B PC E的余弦值.
如图,D为圆锥的顶点,O是圆锥底面的圆心,ABC
△是底面的内接正三角形,P为DO上一点,∠APC=90°.
(1)证明:平面PAB⊥平面PAC;
(2)设DO=2,圆锥的侧面积为3π,求三棱锥P-ABC的体积.
22.(本小题满分10分)
在三棱锥A—BCD中,已知CB=CD=5,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.(1)求直线AB与DE所成角的余弦值;
(2)若点F在BC上,满足BF=1
4
BC,设二面角F—DE—C的大小为θ,求sinθ的值.
15.(本小题满分14分)
在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面
AB 1C ⊥平面ABB 1.
16.(本小题13分)如图,在正方体
1111ABCD
A B C D 中,E 为1BB 的中点.
(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线
1AA 与平面1AD E 所成角的正弦值.
17.(本小题满分15分)
如图,在三棱柱111ABC A B C 中,1CC 平面,,2ABC AC BC AC BC ,13CC ,点,D E 分别在棱1AA 和棱1CC 上,且2,1,AD CE M 为棱11A B 的中点.(Ⅰ)求证:11C M
B D ;(Ⅱ)求二面角
1B B E D 的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.。
