化工热力学课件第1章流体pvt关系
合集下载
高等热力学课件第1章流体pVT关系
3
等温与绝热
可用于描述理想气体的扩张和压缩过程，探索其热力学性质。
流体的比热容和焓
比热容
衡量流体在吸收或释放热量时的 温度变化。
焓
描述了系统的内能和对外界做功 的总和性 质和能量转化。
麦克斯韦方程和吉布斯-杜亨方程
1 麦克斯韦方程
热力学函数之间的偏导数关系，揭示了系统 的性质。
理想气体与实际气体
1 理想气体
遵循理想气体定律，分子之间无相互作用。
2 实际气体
分子之间有相互作用，需要使用状态方程来描述。
3 真实气体状态方程
包括艾伦-富根方程和范德华方程。
等温过程和绝热过程
1
等温过程
温度保持不变，内能转化为热量与环境交换。
2
绝热过程
热量不从或不向环境交换，内能转化为功或由功转化为内能。
2 吉布斯-杜亨方程
描述了多组分体系的平衡条件。
相图和临界点
相图
展示了物质在不同温度和压 力条件下的各种相态。
临界点
温度和压力达到临界值时， 物质不再存在液态和气态之 分。
临界温度和临界压力
定义了物质转变为超临界流 体的条件。
流体在工程中的应用
1 流体动力学
用于设计飞行器、汽车和船只的空气动力学 和水动力学。
2 能源转换
涉及流体的燃烧、蒸汽发电和涡轮机等领域。
3 化工过程
4 环境工程
流体在化学工程中的传热、传质和反应过程。
涉及水力学、水污染和废水处理等流体问题。
高等热力学课件第1章流 体pVT关系
流体力学的核心概念之一是流体的pVT关系。通过深入研究这些关系，我们可 以更好地理解流体的特性和行为。
流体的性质
第1章_流体的p-V-T关系
化工热力学标准化作业一流体的压力p、温度T、体积V和数量(质量或摩尔量)是可以通过实验测量的，利用这些可测得的量和流体的热容数据，可计算其它不能直接从实验测得的热力学性质，如焓H、熵、热力学能(内能)U、Gibbs自由焓G等。
流体pVT关系可采用两种方式来描述：一是图形法；二是解析法，如状态方程法与对应状态原理法等。
1 本章学习要求本章的核心内容是流体的pVT关系。
要求学生掌握纯物质的p-V-T立体相图中，点、线、面所代表的物理意义及在pT面和pV面上投影所形成的p-T相图和p-V相图。
认识物质的气、液、固三类常见状态和气-液、气-固、液-固相平衡等在相图中的表征方法；掌握临界点的物理意义及其数学特征。
要求掌握理想气体的基本概念及其基本的数学表达方法；明确在真实条件下，物质都是以非理想状态存在的，掌握采用立方型状态方程和多项级数展开式，如Virial方程进行非理想气体pVT计算的方法。
2 重点与难点(1) p-V-T相图(2) 状态方程(Equations of State，EOS)(3) 对应状态原理(Corresponding State Principle)(4) 混合物pVTx关系一、是否题（正确划√号，错误划×号，并写清正确与错误的原因）1、纯物质由蒸汽变成液体，必须经过冷凝的相变化过程。
答：2、当压力大于临界压力时，纯物质就以液态存在。
答：3、由于分子间相互作用力的存在，实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积，所以，理想气体的压缩因子Z=1，实际气体的压缩因子Z＜1。
答：4、纯物质的三相点随着所处的压力或温度不同而改变。
答：5、在同一温度下，纯物质的饱和液体与饱和蒸汽的吉氏函数相等。
答：6、纯物质的平衡气化过程，摩尔体积、焓、热力学能、吉氏函数的变化值均大于零，答：7、气体混合物的virial系数，如B、C…，是温度的函数。
答：8*、virial方程和RK方程既可以应用于汽相，又可以用于液相。
《流体的PVT关系 》课件
流量计
用于测量流体的流 量。
搅拌器
用于混合流体。
实验步骤与操作方法
准备实验设备与器材，确保其完好无损。
01
按照实验要求，向储液罐中加入适量的流 体，并搅拌均匀。
03
02
将压力表、温度计、流量计等测量仪器连接 到实验设备上。
04
启动实验设备，观察并记录压力、温度和 流量等参数的变化。
在实验过程中，保持环境温度和压力恒定 ，以减小误差。
03
pvt关系的表现形式
压力与体积的关系
压力与体积的负相关关系
在恒温条件下，流体的压力增大，体积将减小；压力减小，体积将增大。这是因 为压力的增加会导致流体分子间的平均距离减小，从而体积减小。
等温压缩系数
描述压力变化时体积变化的程度。等温压缩系数越大，表示压力变化引起的体积 变02
气体定律
气体在一定条件下遵循pvt关系，如理想气体定律和范德华方程等。这 些定律可以帮助我们预测和解释气体在不同压力、温度和体积下的行为 。
流体的压缩性
流体的压缩性是指流体在压力变化下体积的变化程度。通过pvt关系， 我们可以了解流体的压缩性，进而研究流体在管道中的流动特性。
压力对pvt关系的影响
总结词
压力是影响流体pvt关系的另一个重要因素 。
详细描述
在高压下，流体的分子间的距离变小，相互 作用力增强，导致流体的密度和粘度增加。 同时，压力的变化也可能影响流体的蒸气压
和溶解度等物性参数。
物质种类对pvt关系的影响
要点一
总结词
要点二
详细描述
不同物质具有不同的分子结构和相互作用力，因此其pvt关 系也不同。
不同物质的pvt关系曲线存在差异，这是因为不同物质的分 子间相互作用力和分子结构不同。此外，同一种物质在不 同温度和压力下的pvt关系也可能存在差异。
第1章流体pVT关系
RT a p 2 V b V
对van der Walls方程作了很多改进，其中比较成功地改进 包括Redlich和Kwong改进的RK方程、Soave的进一步改进 （Soave方程，1972年），Peng和Robinson（1976年） 这些立方型状态方程中的参数基本上可用临界性质表示， 但也包括对温度和其他性质如压缩因子Z或偏心因子的修 正，这些方程的改进大都是经验的或者任意的。 近来一些统计力学理论已用于改进立方型状态方程。流体的p –V -T关系
主要内容
流体pVT关系发展概况 维里方程 立方型状态方程 流体的非理想性 混合物的pVT行为 总结
流体的p –V –T关系的发展概况
一、理想气体
1662年 Boyle定律
1834年 理想气体状态方程 二、维里方程
B C Z 1 Bp C p 1 2 V V
b 0.07780 RTc / pc
(T ) 1 k(1 T )
0.5 r
2
k 0.3746 1.54226 0.26992
a( T )＝f (Tc，pc，T, ω)
2
方程使用情况：
（1）RK方程和RKS方程在计算临界压缩因子Zc和
液体密度时都会出现较大的偏差，PR方程弥补这一
a T RT p V b V V b
方程参数：
a T a T 0.4278 R 2Tc2 / pc T
b 0.08664 RTc / pc
(T ) 1 m(1 T )
0.5 r
2
m 0.480 1.574 0.176 2 式中，ω为偏心因子
2
化工热力学第三版第1章绪论与第2章流体的pVT关系
混合物的状态方程
2.4.3 混合物的状态方程
（3）Martin-Hou方程 温度函数混合规则的通式为
若L代表方程常数b，则n＝１
2.4.3 混合物的状态方程
2.4.4 状态方程混合规则的发展
（1）单流体混合规则的改进
2.4.4 状态方程混合规则的发展
1.3.1 体系与环境
1. 孤立体系：体系与环境之间既无物质的交换又无能量 的交换
2. 封闭体系：体系与环境之间只有能量的交换而无物质 的交换
3. 敞开体系：体系与环境之间可以有能量与物质的交换。
1.3.2 平衡状态与状态函数
状态是指体系在某一瞬间所呈现的宏观物理状况。热 力学中，一般说体系处于某个状态， 即指平衡状态。
2.1 纯物质的p-V-T关系
2.1 纯物质的p-V-T关系
2.1 纯物质的p-V-T关系
等温线在两相区中的水平线段随着温度升高而缩短，最 后在临界温度时缩成一点犆。从图2-3上看出，临界等温 线在临界点上的斜率和曲率都等于零。数学上表示为
2.1 纯物质的p-V-T关系
2.2 气体的状态方程
对比态原理认为，在相同的对比状态下，所有的物质表 现出相同的性质。 令 将这些关系代入van der Waalls方程，得
这种关系在数学上可表示为
因为
2.3.2 以偏心因子为第三参数 的对比态原理
物质的对比蒸气压的对数与绝对温度有近似线性关系， 即
对比蒸气压方程可以表示为
2.3.2 以偏心因子为第三参数 的对比态原理
2.2.1 理想气体方程
理想气体方程是最简单的状态方程，即
2.2.2 立方型状态方程
所谓立方型状态方程是因为方程可展开为体积 （ 或密 度）的三次多项式。Vander Waals方程 （1873年）是第 一个适用真实气体的立方型方程，是对理想气体方程 （2-4）的校正。
2.4.3 混合物的状态方程
（3）Martin-Hou方程 温度函数混合规则的通式为
若L代表方程常数b，则n＝１
2.4.3 混合物的状态方程
2.4.4 状态方程混合规则的发展
（1）单流体混合规则的改进
2.4.4 状态方程混合规则的发展
1.3.1 体系与环境
1. 孤立体系：体系与环境之间既无物质的交换又无能量 的交换
2. 封闭体系：体系与环境之间只有能量的交换而无物质 的交换
3. 敞开体系：体系与环境之间可以有能量与物质的交换。
1.3.2 平衡状态与状态函数
状态是指体系在某一瞬间所呈现的宏观物理状况。热 力学中，一般说体系处于某个状态， 即指平衡状态。
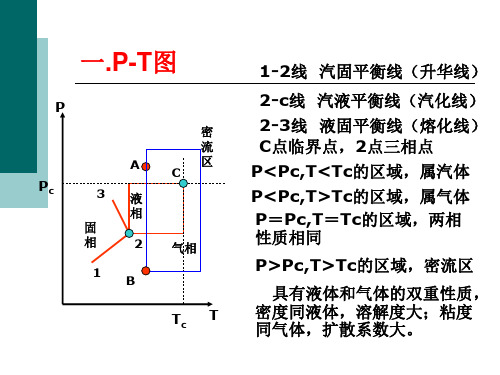
2.1 纯物质的p-V-T关系
2.1 纯物质的p-V-T关系
2.1 纯物质的p-V-T关系
等温线在两相区中的水平线段随着温度升高而缩短，最 后在临界温度时缩成一点犆。从图2-3上看出，临界等温 线在临界点上的斜率和曲率都等于零。数学上表示为
2.1 纯物质的p-V-T关系
2.2 气体的状态方程
对比态原理认为，在相同的对比状态下，所有的物质表 现出相同的性质。 令 将这些关系代入van der Waalls方程，得
这种关系在数学上可表示为
因为
2.3.2 以偏心因子为第三参数 的对比态原理
物质的对比蒸气压的对数与绝对温度有近似线性关系， 即
对比蒸气压方程可以表示为
2.3.2 以偏心因子为第三参数 的对比态原理
2.2.1 理想气体方程
理想气体方程是最简单的状态方程，即
2.2.2 立方型状态方程
所谓立方型状态方程是因为方程可展开为体积 （ 或密 度）的三次多项式。Vander Waals方程 （1873年）是第 一个适用真实气体的立方型方程，是对理想气体方程 （2-4）的校正。
化工热力学-流体的 p-V-T 关系
Z
Z
Z
1
q
Z
或
Z
0.026196
Z
Z
0.026196
1.026196 Z 6.6060 0.026196
将 Z= 代入上式右边，迭代计算后得到收敛值Z=0.04331。
V l ZRT 0.043318.314350 133.3 cm3mol1
p
0.9457
为了比较计算结果，在例2/5-1的情况下，运用四种立方型状态 方程所计算得到的V v及V l 值列表如下：
第二章 流体的 p-V-T 关系
（一）纯流体的三维相图
自由度与相律
（二）纯流体的二维相图
异戊烷的p-V图
p-T相图
T-V图
（三）纯流体 pVT 行为的模型化
→ 什么是状态方程？
f p,V,T 0
dV
V T
p
dT
V p
T
dp
V=V(T,p)
p=p(T,V )
（四）理想气体
只有在Zc相等的条件下，对比态原理才能成立
以ω为第三参数的对应状态原理
Z f pr ,Tr ,
偏心因子
Pitzer： 物质对比饱和蒸汽压的对数，与对比温度的倒数呈 下列线性关系
log
prS
a 1
1 Tr
prS
pS pc
球形分子虽然临界参数相差很大，但在Tr=0.7时，对比蒸气压 logprS = -1 。
ZC 3/8 1/3 1/3 0.30740
临界压缩因子Zc
VDW: 3/8 RK/SRK: 1/3 PR: 0.3047
立方型状态方程的数值求解
p
RT
V b
V
化工热力学 流体的P-V-T关系
P>Pc,T>Tc的区域，压缩流体 区（密流区，超临界流体区）
Tc T
超临界流体既不同于液体，又不同于气体，密度可以接近液体，但又具有气体的
体积可变性和传递性质，可以作为特殊的萃取溶剂和反应介质。开发超临界流体 区的分离技术和反应技术已成为目前研究的热点。
二.P-V图
T2 T1 T3 Tc
气
T4 C P T5
D、D’——……
注意：B≠B’ C ≠C’ D ≠D’
B' B RT
C'
C B2
RT 2
(近似式)
D 3BC 2B3
D' RT3
2.两项维里方程
维里方程式中,保留前两项,忽略掉第三项之 后的所有项,得到:
Z=PV/RT=1+B’P
Z=PV/RT=1+B/V
把这个式子代入用压力表示的两项维里方程中， 就得到常用的两项维里方程。
1.试差法解题
8.314106 273.15 v - 26.8026
101.33106
1.55881012 (273.15)0.5 v(v 26.8026)
2270.9691 101.33 1.5588106
v - 26.8026
16.5277v(v 26.8026)
试差法： 假定v值
方程左边
2.通过作图得出结果
若令 y1=方程左边＝f1(v) y2=方程右边＝f2(v) Y
V求
V
2.迭代法 :
A a 4.934 4.934 4.934 1.549
B
bRT1.5
(T/Tc )1.5
273.15 1.5
2.1641.5
126.2
B 0.08664Pr Tr
Tc T
超临界流体既不同于液体，又不同于气体，密度可以接近液体，但又具有气体的
体积可变性和传递性质，可以作为特殊的萃取溶剂和反应介质。开发超临界流体 区的分离技术和反应技术已成为目前研究的热点。
二.P-V图
T2 T1 T3 Tc
气
T4 C P T5
D、D’——……
注意：B≠B’ C ≠C’ D ≠D’
B' B RT
C'
C B2
RT 2
(近似式)
D 3BC 2B3
D' RT3
2.两项维里方程
维里方程式中,保留前两项,忽略掉第三项之 后的所有项,得到:
Z=PV/RT=1+B’P
Z=PV/RT=1+B/V
把这个式子代入用压力表示的两项维里方程中， 就得到常用的两项维里方程。
1.试差法解题
8.314106 273.15 v - 26.8026
101.33106
1.55881012 (273.15)0.5 v(v 26.8026)
2270.9691 101.33 1.5588106
v - 26.8026
16.5277v(v 26.8026)
试差法： 假定v值
方程左边
2.通过作图得出结果
若令 y1=方程左边＝f1(v) y2=方程右边＝f2(v) Y
V求
V
2.迭代法 :
A a 4.934 4.934 4.934 1.549
B
bRT1.5
(T/Tc )1.5
273.15 1.5
2.1641.5
126.2
B 0.08664Pr Tr
流体的PVT关系PPT课件
3. 81型
在55型方程的基础上增加了常数Ｂ４，这样就得到了我 们讲义P12式（2-33）,此式称为81型Ｍ-Ｈ方程。
优点： ａ：计算精度高，误差：气相１％，液相<５％ ｂ：常数易确定，只需两点实测数据（临界点，常压下数 据）
c：可用于极性气体ＰＴＶ性质计算 ｄ：可用于ＶＬＥ和液相性质的计算
问题：对液相极性物质计算误差大,最大误差达16% 参考文献：化工学报, (1). 1981
实际气体的等温线
将范德华方程整理后得到： P（V-b）V2=RTV2-a（V-b） PV3-（bP+RT）V2+aV+ab=0
由这个方程可以看出，当温度不变时，是一个关于V的 三次方程，其解有三种情况:
P
• 三个不等的实根。 • 三个相等的实根 • 一个实根，两个虚根
L
DH
V
• R-K Equation (1949年，Redlich and Kwong)
b 0.08664RTc Pc
a(T) a(Tc)(T) 0.42748R2Tc2 (T)
Pc
(T) 0.5 1 m'(1 Tr0.5)
m' 0.481.574 - 0.1752
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
关于两常数（立方型）状态方程，除了我们介绍的 范德华、R－K、SRK Eq以外，还有许多方程，包括我们 讲义上的P－R Eq和P-T Eq
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C V2
Onnes：1901年以一种经验的关系式开发出了维 里方程；
Ursell：1927年 维里方程的进一步理论发展；
Mayer：1937年 维里方程的进一步理论发展
三、立方型状态方程
1873年van der Waals（范德华） 首次提出了能表达从气 态到液态连续性的状态方程 ：
RT a pV bV2
再如：研究四氯化碳CCl4～丙酮及氯仿CHCl3～丙 酮之间的作用力非常不同。
2
1
混合焓，
KJ/mol0
-1
-2
CCl4～丙酮 丙酮摩尔分数
-20
冰点
-100 -60
-100
丙酮摩尔分数
1. 丙酮和四氯化碳的混合热是正的（吸热），而丙酮和氯仿 的混合热是负的，数值上也差别很大。
四氯化碳混合热的数据表明，物理的分子力的影响只造成少量 的吸热。但在氯仿混合物中，化学效应之大不仅抵消了物理作 用对混合热应有的贡献，而且造成放热。因为破坏氢键需要能 量，所以形成氢键时，自然需要放出能量。
➢氯仿和二异丁基甲酮也形成氢键，但由于存在空间障碍， 络合的趋势小得多。
Cl Cl C H
Cl
CH3C
O CH3CO源自CC C C CC C C
比较同分异构体C2H6O的某些热力学性质，便可 以很好地说明氢键对于物化性质的强烈影响。
乙醇 CH3CH2OH;二甲醚 CH3OCH3
乙醇
二甲醚
正常沸点，℃
Jones 12-6位能函数。
ur
4
12
6
r r
分子的缔合和氢键
极性物质的分子趋向于形成基团，因为它们的氢 原子表现出好像有剩余价，这种作用称为氢键。 其趋势是随着组成原子的电负性减小而减小。
例如(HF)6；而乙酸、甲酸的气体在略高于沸点时 是双分子；醇类、酯类、醛类和其他物质，在正 常压力和温度下，也表现出明显的缔合。这种缔 合的程度随压力和浓度减小而降低，缺随着温度 的升高而降低。
流体的p –V -T关系
主要内容
流体pVT关系发展概况 流体的非理想性 混合物的pVT行为 维里方程 立方型状态方程 总结
流体的p –V –T关系的发展概况
一、理想气体
1662年 Boyle定律
pV 常数
1834年 理想气体状态方程
pV RT
二、维里方程
Z
1
Bp
C p 2
1
B V
78
-25
沸点下蒸发焓
42.6
18.6
8 ℃、1bar下在
无穷
7.12
水中的溶解度
g/100g
当形成氢键的物质溶于相对惰性的非极性溶剂中， 然后研究溶液的热力学性质，往往可以发现同种分 子的氢键。
如：乙醇溶于过量的非极性溶剂（如己烷或环己烷） 时，其混合体积有明显膨胀（超额体积大于0）。这 是由于氢键不断地断裂，直至无限稀释时，二聚体、 三聚体、高聚体等都消失，所有的分子都以单体存 在。
2. 氯仿和四氯化碳有两个低共熔点，之间有一段上凸的曲线， 极值点在50％处，这表明在固态中存在络合物，不过液态时解 离了。
存在络合物充分证明了两种不同分子间的强烈作用。极值点出 现在组成轴的中点。因此我们推知络合物化学计量比为1：1
缔合存在时的pVT行为
其转换分数为
nA An
Z
平初衡始时的的分分子子数数＝表观压缩因子＝1－＋
对van der Walls方程作了很多改进，其中比较成功地改进 包括Redlich和Kwong改进的RK方程、Soave的进一步改进 （Soave方程，1972年），Peng和Robinson（1976年）
这些立方型状态方程中的参数基本上可用临界性质表示， 但也包括对温度和其他性质如压缩因子Z或偏心因子的修 正，这些方程的改进大都是经验的或者任意的。
此外，实际气体与理想气体之间的另一个重要差别是 它们的热行为。如
C
ig p
f T
Cp f T, p
二、分子间作用力
分子的大小、形状和结构确定了它们之间的力和最终的 pVT行为。引力使分子结合在一起，斥力使分子分开。前者 在分子距离大时起作用，后者在近距离范围内有影响。 根据分子的电性质，分子可以分为三种： （1）电中性和对称性，通常维非极性分子 （2）电中性而非对称性，即具有偶极距，称为极性分子； （3）有剩余价，可产生缔合和氢键。 在所有分子中都存在斥力和引力，但在缔合和极性分子中， 它们以不寻常的形式出现。 目前pVT关系和方程最成功地描述非极性物质的行为，包括 重要的烃类。
氢键
➢例如氟化氢 H FH FH- F
➢两个电负性足够大的原X和Y，在适当的条件下可以按的 形式和氢连接。 H XY 因而，分子如果含有和电负性 原子连接的氢（如在醇、酸、胺中），它就显示出互相缔 合以及和其他具有可接近的电负性原子的分子生成溶剂化 物的强烈趋势。
➢再如：醋酸主要以二聚体组成，这是存在氢键的作用。 ➢氯仿CHCl3和丙酮CH3COCH3有溶剂化的趋势，这是因 为氯仿中的伯氢原子和丙酮中的羰基氧之间形成氢键，这 种溶剂化作用对于氯仿－丙酮溶液的性质有显著影响。
近来一些统计力学理论已用于改进立方型状态方程。
四、液体
对于液体，虽然在理论上和关联方面已做了很多工作，但 了解仍然比气体少得多。
有一些经验关联式专门用于液体密度的计算，如 Hankinson 和Thomson提出的饱和液体密度计算关联式是 典型代表；
一些复杂的方程，如PR方程、BWR方程、Harmens－ Knapp方程，可作为较好的液体密度表达式。
特别值得推荐的是ASOG和UNIFAC方法，通过流体的分
子结构去预测液体的混合物行为。
基团贡献法
流体的非理想性
一、与理想性的偏差
理想气体
分子的大小如同几何点 分子间不存在相互作用力
极低的压力下真实气体非常接近理想气体
许多实际物质的性质可以通过与理想气体的偏差，这 也是热力学研究的一个重要方法。如压缩因子Z，剩余 性质MR
分子极性
极性：当一个键的电中心与其质量中心不重合时，就产生 偶极距。极性是以偶极距的大小来定义的。偶极距的单位 为Debye。
极性分子特点：极性分子与非极性分子相比，具有较大的 黏度和较高的沸点和熔点；极性分子还更能溶解于水。特 别重要的是极性分子表现出更大的超额热力学性质。
分子之间的作用力可以使用位能函数来描述。例如Lennard-