全国大学生建模大赛论文
数学建模竞赛优秀大学生论文

数学建模竞赛优秀大学生论文随着科学技术的高速发展,数学的应用价值越来越得到众人的重视,因此数学建模也被逐渐的引起重视了。
下面是店铺为大家整理的数学建模优秀论文,供大家参考。
数学建模优秀论文篇一:《数学建模用于生物医学论文》1数学建模的过程1.1模型准备首先要了解实际背景,寻找内在规律,形成一个比较清晰的轮廓,提出问题。
1.2模型假设在明确目的、掌握资料的基础上,抓住问题的本质,舍弃次要因素,对实际问题做出合理的简化假设。
1.3模型建立在所作的假设条件下,用适当的数学方法去刻画变量之间的关系,得出一个数学结构,即数学模型。
原则上,在能够达到预期效果的基础上,选择的数学方法应越简单越好。
1.4模型求解建模后要对模型进行分析、求解,求解会涉及图解、定理证明及解方程等不同数学方法,有时还需用计算机求数值解。
1.5模型分析、检验、应用模型的结果应当能解释已存的现象,处理方法应该是最优的决策和控制方案,所以,对模型的解需要进行分析检验。
把求得的数学结果返回到实际问题中去,检验其合理性。
如果理论结果符合实际情况,那么就可以用它来指导实践,否则需再重新提出假设、建模、求解,直到模型结果与实际相符,才能进行实际应用。
总之,数学建模是一项富有创造性的工作,不可能用一些条条框框的规则规定的十分死板,只要是能够做到全面兼顾、能抓住问题的本质、最终检验结果合理,都是一个好的数学模型。
2数学建模在生物医学中的应用2.1DNA序列分类模型DNA分子是遗传信息存储的基本单位,许多生命科学中的重大问题都依赖于对这种特殊分子的深入了解。
因此,关于DNA分子结构与功能的问题,成为二十一世纪最重大的课题之一。
DNA序列分类问题是研究DNA分子结构的基础,它常用的方法是聚类分析法。
聚类分析是使用数据建模简化数据的一种方法,它将数据分成不同的类或者簇,同一个簇中的数据有很大的同质性,而不同的簇中的数据有很大的相异性。
在对DNA序列进行分类时,需首先引入样品变量,比如说单个碱基的丰度、两碱基丰度之比等;然后计算出每条DNA序列的样品变量值,存入到向量中;最后根据相似度度量原理,计算出所有序列两两之间的Lance与Williams距离,依据距离的远近进行分类。
全国大学生数学建模大赛国家一等奖论文A题

=
− − ( − 1)′
, = 1, 2, · · ·, 210
当逐渐增大,锚链受到的竖直向下方向的合力与支持力之差先逐渐接近于0,
再等于0,直至小于0。当合力小于0时,锚链以海床接触,此时海床提供向上的支持
力,其大小与′ 相等。因此可将小于0 的值都作零处理,故锚链接触海床时,
对于问题二,首先考虑第一个子问题,将风速36/直接代入问题一的模型中,
得出此条件下的吃水深度为0.723,各钢管倾斜角度(度)依次为8.960、9.014、9.068
、9.123,钢桶倾斜角(度)为9.179,锚链链接处的切线方向与海床的夹角(度)为18.414,
游动区域半径为18.80。发现此条件下,水声通讯系统设备的工作效果较差,且锚被
计与应用对海上科学发展有重要意义。
1.2 问题的提出
已知某近浅海传输节点(如图1所示),将浮标视作底面直径2为、高为2、质量
为1000的圆柱体,锚的质量为600,钢管共4节,每节长度为1,直径为50,
每节钢管的质量为10。水声通讯系统安装在一个长为1、外径为30的密封圆
柱形钢桶内,设备和钢桶总质量为100。
Step1: 遍历求解
令吃水深度ℎ的初始值为0.1,以0.0005为单位逐步增加至2。( 浮标高度为2,
完全浸没时吃水深度ℎ则为2 ),记录对应的数据,选取水下物体竖直方向高度和
与海域水深最接近的组别,进一步进行计算,结果如下表所示(具体程序见附录):
表 1: 不同风速的相关结果表
以风速24/的情况为例,绘制游动区域图:
题意的变量临界值。以水深16、系统各部分递推关系式和钢桶与竖直方向夹角小
于5°为约束条件,将多目标优化转化为单目标优化。通过调节决策变量中锚链的型
优秀的数学建模论文范文(通用8篇)

优秀的数学建模论文范文第1篇摘要:将数学建模思想融入高等数学的教学中来,是目前大学数学教育的重要教学方式。
建模思想的有效应用,不仅显著提高了学生应用数学模式解决实际问题的能力,还在培养大学生发散思维能力和综合素质方面起到重要作用。
本文试从当前高等数学教学现状着手,分析在高等数学中融入建模思想的重要性,并从教学实践中给出相应的教学方法,以期能给同行教师们一些帮助。
关键词:数学建模;高等数学;教学研究一、引言建模思想使高等数学教育的基础与本质。
从目前情况来看,将数学建模思想融入高等教学中的趋势越来越明显。
但是在实际的教学过程中,大部分高校的数学教育仍处在传统的理论知识简单传授阶段。
其教学成果与社会实践还是有脱节的现象存在,难以让学生学以致用,感受到应用数学在现实生活中的魅力,这种教学方式需要亟待改善。
二、高等数学教学现状高等数学是现在大学数学教育中的基础课程,也是一门必修的课程。
他能为其他理工科专业的学生提供很多种解题方式与解题思路,是很多专业,如自动化工程、机械工程、计算机、电气化等必不可少的基础课程。
同时,现实生活中也有很多方面都涉及高数的运算,如,银行理财基金的使用问题、彩票的概率计算问题等,从这些方面都可以看出人们不能仅仅把高数看成是一门学科而已,它还与日常生活各个方面有重要的联系。
但现在很多学校仍以应试教育为主,采取填鸭式教学方式,加上高数的教材并没有与时俱进,将其与生活的关系融入教材内,使学生无法意识到高数的重要性以及高数在日常生活中的魅力,因此产生排斥甚至对抗的心理,只是在临考前突击而已。
因此,对高数进行教学改革是十分有必要的,而且怎么改,怎么让学生发现高数的魅力,并积极主动学习高数也是作为教师所面临的一个重大问题。
三、将数学建模思想融入高等数学的重要性第一,能够激发学生学习高数的兴趣。
建模思想实际上是使用数学语言来对生活中的实际现象进行描述的过程。
把建模思想应用到高等数学的学习中,能够让学生们在日常生活中理解数学的实际应用状况与解决日常生活问题的方便性,让学生们了解到高数并不只是一门课程,而是整个日常生活的基础。
数学建模竞赛优秀大学生论文.doc

数学建模竞赛优秀大学生论文医学论文》1数学建模的过程1.1模型准备首先要了解实际背景,寻找内在规律,形成一个比较清晰的轮廓,提出问题。
1.2模型假设在明确目的、掌握资料的基础上,抓住问题的本质,舍弃次要因素,对实际问题做出合理的简化假设。
1.3模型建立在所作的假设条件下,用适当的数学方法去刻画变量之间的关系,得出一个数学结构,即数学模型。
原则上,在能够达到预期效果的基础上,选择的数学方法应越简单越好。
1.4模型求解建模后要对模型进行分析、求解,求解会涉及图解、定理证明及解方程等不同数学方法,有时还需用计算机求数值解。
1.5模型分析、检验、应用模型的结果应当能解释已存的现象,处理方法应该是最优的决策和控制方案,所以,对模型的解需要进行分析检验。
把求得的数学结果返回到实际问题中去,检验其合理性。
如果理论结果符合实际情况,那么就可以用它来指导实践,否则需再重新提出假设、建模、求解,直到模型结果与实际相符,才能进行实际应用。
总之,数学建模是一项富有创造性的工作,不可能用一些条条框框的规则规定的十分死板,只要是能够做到全面兼顾、能抓住问题的本质、最终检验结果合理,都是一个好的数学模型。
2数学建模在生物医学中的应用2.1DNA序列分类模型DNA分子是遗传信息存储的基本单位,许多生命科学中的重大问题都依赖于对这种特殊分子的深入了解。
因此,关于DNA分子结构与功能的问题,成为二十一世纪最重大的课题之一。
DNA序列分类问题是研究DNA分子结构的基础,它常用的方法是聚类分析法。
聚类分析是使用数据建模简化数据的一种方法,它将数据分成不同的类或者簇,同一个簇中的数据有很大的同质性,而不同的簇中的数据有很大的相异性。
在对DNA序列进行分类时,需首先引入样品变量,比如说单个碱基的丰度、两碱基丰度之比等;然后计算出每条DNA序列的样品变量值,存入到向量中;最后根据相似度度量原理,计算出所有序列两两之间的Lance与Williams距离,依据距离的远近进行分类。
全国大学生数学建模竞赛b题全国优秀论文

基于打车软件的出租车供求匹配度模型研究与分析摘要目前城市“出行难”、“打车难”的社会难题导致越来越多的线上打车软件出现在市场上。
“打车难”已成为社会热点。
以此为背景,本文将要解决分析的三个问题应运而生。
本文运用主成分分析、定性分析等分析方法以及部分经济学理论成功解决了这三个问题,得到了不同时空下衡量出租车资源供求匹配程度的指标与模型以及一个合适的补贴方案政策,并对现有的各公司出租车补贴政策进行了分析。
针对问题一,根据各大城市的宏观出租车数据,绘制柱形图进行重点数据的对比分析,首先确定适合进行分析研究的城市。
之后,根据该市不同地区、时间段的不同特点选择多个数据样本区,以数据样本区作为研究对象,进行多种数据(包括出租车分布、出租车需求量等)的采集整理。
接着,通过主成分分析法确定模型的目标函数、约束条件等。
最后运用spss软件工具对数据进行计算,求出匹配程度函数F与指标的关系式,并对结果进行分析。
针对问题二,在各公司出租车补贴政策部分已知的情况下,综合考虑出租车司机以及顾客两个方面的利益,分别就理想情况与实际情况进行全方位的分析。
在问题一的模型与数据结果基础上,首先分别从给司机和乘客补贴两个角度定性分析了补贴的效果。
重点就给司机进行补贴的方式进行讨论,定量分析了目前补贴方案的效果,得出了如果统一给每次成功的打车给予相同的补贴无法改善打车难易程度的结论,并对第三问模型的设计提供了启示,即需要对具有不同打车难易程度和需求量的区域采取分级的补贴政策。
针对问题三,在问题二的基础上我们设计了一种根据不同区域打车难易程度和需求量来确定补贴等级的方法。
设计了相应的量化指标,以极大化各区域打车难易程度降低的幅度之和作为目标,建立该问题的规划模型。
目的是通过优化求解该模型,使得通过求得的优化补贴方案,能够优化调度出租车资源,使得打车难区域得到缓解。
通过设计启发式原则和计算机模拟的方法进行求解,并以具体案例分析得到,本文方法相对统一的补贴方案而言的确可以一定程度缓解打车难的程度。
全国大学生数学建模大赛D题优秀论文(精)
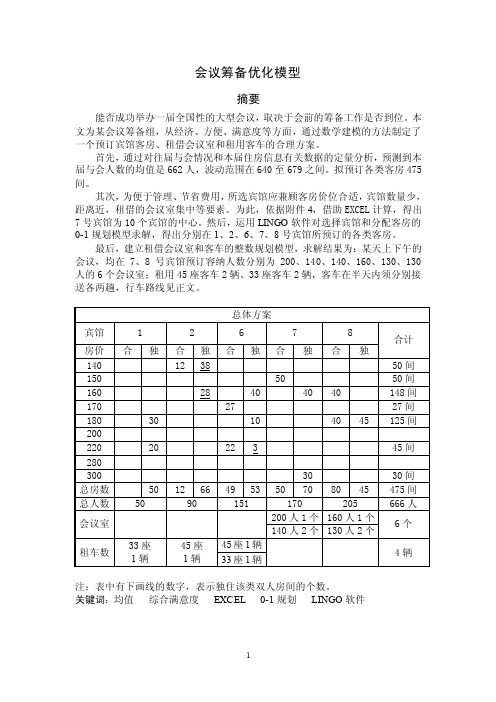
会议筹备优化模型摘要能否成功举办一届全国性的大型会议,取决于会前的筹备工作是否到位。
本文为某会议筹备组,从经济、方便、满意度等方面,通过数学建模的方法制定了一个预订宾馆客房、租借会议室和租用客车的合理方案。
首先,通过对往届与会情况和本届住房信息有关数据的定量分析,预测到本届与会人数的均值是662人,波动范围在640至679之间。
拟预订各类客房475间。
其次,为便于管理、节省费用,所选宾馆应兼顾客房价位合适,宾馆数量少,距离近,租借的会议室集中等要素。
为此,依据附件4,借助EXCEL计算,得出7号宾馆为10个宾馆的中心。
然后,运用LINGO软件对选择宾馆和分配客房的0-1规划模型求解,得出分别在1、2、6、7、8号宾馆所预订的各类客房。
最后,建立租借会议室和客车的整数规划模型,求解结果为:某天上下午的会议,均在7、8号宾馆预订容纳人数分别为200、140、140、160、130、130人的6个会议室;租用45座客车2辆、33座客车2辆,客车在半天内须分别接送各两趟,行车路线见正文。
注:表中有下画线的数字,表示独住该类双人房间的个数。
关键词:均值综合满意度EXCEL 0-1规划LINGO软件1.问题的提出1.1基本情况某一会议服务公司负责承办某专业领域的一届全国性会议。
本着经济、方便和代表满意的原则,从备选10家宾馆中的地理位置、客房结构、会议室的规模(费用)等因素出发,同时,依据会议代表回执中的相关信息,初步确定代表总人数并预定宾馆和客房;会议期间在某一天上下午各安排6个分组会议,需合理分配和租借会议室;为保证代表按时参会,租用客车接送代表是必需的(现有45座、36座、33座三种类型的客车,租金分别是半天800元、700元和600元)。
1.2相关信息(见附录)附件1 10家备选宾馆的有关数据。
附件2 本届会议的代表回执中有关住房要求的信息(单位:人)。
附件3 以往几届会议代表回执和与会情况。
附件4 宾馆平面分布图。
全国大学生数学建模竞赛论文1

目录一 问题重述问题重述......................................................... ......................................................... 1 二 问题分析问题分析......................................................... ......................................................... 2 三 模型假设模型假设......................................................... ......................................................... 2 四 符号说明符号说明......................................................... ......................................................... 2 五 模型的建立与求解模型的建立与求解................................................. ................................................. 3 六结果分析六结果分析......................................................... (12)一 问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,等数据,通过预先标定的罐容表通过预先标定的罐容表通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)(即罐内油位高度与储油量的对应关系)(即罐内油位高度与储油量的对应关系)进行实进行实时计算,以得到罐内油位高度和储油量的变化情况。
大学生数学建模论文(专业推荐范文10篇)

大学生数学建模是一项基础性得学科竞赛,可以交流更多得经验,学习更多得知识,所以大学生数学建模很受学者们得欢迎,本篇文章就向大家介绍一些大学生数学建模论文,供给大家作为一个参考。
大学生数学建模论文专业推荐范文10篇之第一篇:数学建模对大学生综合素质影响得调查研究---------------------------------------------------------------------------------------------------------------------感谢使用本套资料,希望本套资料能带给您一些思维上的灵感和帮助,个人建议您可根据实际情况对内容做适当修改和调整,以符合您自己的风格,不太建议完全照抄照搬哦。
---------------------------------------------------------------------------------------------------------------------摘要:文章通过问卷网以调查问卷得形式和线下访谈得方法 ,对笔者所在学校参加过数学建模竞赛得同学和未参加过数学建模竞赛得同学对数学建模对自身综合素质得影响进行了调查研究。
调查表明,大部分学生都能认识到数学建模学习和竞赛对其自身综合素质得提升是有帮助得,但是大多数学生对数学建模得意义认识还不到位。
文章对调查结果进行分析,结合笔者得切身体会对地方高校数学建模课程教学及学生参加竞赛提出某些建议。
关键词:数学建模; 大学生; 综合素质; 研究;一、前言随着社会得不断进步和发展,大学生想要在激烈得人才竞争中脱颖而出,就必须要不断提高自己得综合素质,而良好得综合素质不仅应具有坚实得理论基础,扎实得专业知识,还应该具有较强得创新能力、与他人合作得能力、较强得语言表达能力、以及稳定得心理状态。
许多科学家断言未来科学技术得竞争是数学技术得竞争,这无疑对数学能力提出了更高得要求,不可否认数学建模课程教学及建模竞赛是提升大学生数学能力得有效途径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):B题我们的参赛报名号为(如果赛区设置报名号的话):010084所属学校(请填写完整的全名):内蒙古科技大学包头师范学院参赛队员(打印并签名) :1. 李小彦2. 闫文朕3. 樊玉波指导教师或指导教师组负责人(打印并签名):数模教研组日期: 2011 年 9 月 12日赛区评阅编号(由赛区组委会评阅前进行编号):2011高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):交巡警服务平台的设置与调度动态规划模型摘要本文以动态规划模型解决了交巡警服务平台的最优化设置与调度问题,为警察更好的刑事执法、治安管理、交通管理、服务群众四大职能提供大前提,也为政府部门提高工作效率解决了一大难题。
问题一:(一)根据动态规划的最优化分配该市A区20个交巡警服务平台的管辖范围。
(二)通过对A区20个交巡警服务平台与13条交通要道位置的具体分析,对比,找出合理的调度方案。
(三)根据A区各交巡警服务平台的个数、节点、发案率及人口与面积等信息的分析,找出“盲区”,将2-5个平台分配到A区的具体位置。
问题二:(一)综合ABCDEF六个区的交巡警服务平台个数、每个区的平均发案率和人口密度的分析,从交巡警服务平台设置方案合理性与不合理性两方面具体评价了该城市个区交巡警服务平台分布情况。
(二)对ABCDEF六个区17个进出该市的路口及六个区80个交巡警服务平台位置的分析及逃犯,按两套方案解决此问题,即方案一:逃犯未逃出A区;方案二:逃犯已经逃出A区但未逃出该市区,全面综合的调度全市交巡警服务平台警力资源并给出最优围堵方案。
关键词:动态分配最优化(opt) 调度交警服务平台一、问题重述每个平台全市联网,单独的一个平台比一个派出所的功能还要强大,交巡警制度整合了警力资源,将刑事执法、治安管理、交通管理、服务群众四大职能有机融合的新型防控体系,代表了未来的发展方向,是脱离原始,改变粗放,走向动态警务运行模式的显著标志,必将产生强大的司法制衡力、社会治安的驾驭力、打击犯罪的冲击力。
现给出了某市区的示意图以及该市意图,并且给出了全市路口结点的坐标、交通路口路线、交巡警平台、全市出入口的位置、以及六城区的相关数据。
该市现要增加2-~5个平台,又已知了警车的时速为60hkm/。
交巡警平台的设置以及调动方案要尽量满足以下要求:A1. 巡警平台所管辖的范围内出现突发事件时,要求该平台的交巡警尽量能在3分钟内出现事发地。
A2.对于重大突发事件,需要电镀全区20个交巡警服务平台的警力资源,对进出该区的13条交通要到实现快速封锁。
A3.根据交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟定在该区内再增加2至5个平台。
A4.平台的利用得到"opt"是optimization(最优化)的缩写,尽量避免浪费。
A5.在已知的P点出现发生了重大刑事案件,在案发3分钟后接到报警,犯罪嫌疑人已驾车逃跑。
为了快速搜捕嫌疑犯,请给出围堵的最佳方案。
现在我们需要解决一下几个问题:一.若满足要求A1,该市至少需要设置多少个平台以及设置的具体位置。
二.若满足要求A2,在A1的基础上给出平台的设置以及调动方案。
三.若满足A3, 在A1,A2的基础上,需给出相关的额数据说明以及图示。
四.根据附件2给出的数据,以及每个平台所能管辖的最大范围,给出方案以及评价的指标值。
五.对于P点的具体问题而言,给出具体的围堵方案。
二、问题分析(1)首先,针对A区20个交巡警服务平台分配管辖范围。
然后,当出现重大突发事故,合理调度20个服务台迅速封锁进出A区的13个交通要道。
最后,根据交巡警服务台工作量不均衡和出警时间过长的情况,增加2-5个交台。
需满足条件:一、3分钟内到达事发地;二、一个平台的警力最多封锁一个路口;(2)针对全市六个城区的具体情况,分析研究该市交巡警服务平台设置的合理性和不合理性,并给出解决方案;当P点出现重大刑事案件时,请给出调度全市交巡警服务平台警力资源的最佳围堵方案。
三、问题求解问题一(一)交巡警服务台管辖范围分配 1.1模型假设与符号说明假设城区A 的交通网络现有的20个交巡警服务平台及其坐标分别为:)394,444(),364,418(),371,432(),335,415(),328,337()335,290(),292,280(),270,225(),316,219(),301,247()325,283(),342,333(),5.353,5.334(),362,317(),383,335()376,339(),5.377,381(),351,5.383(),343,403()359,413(2019181716151413121110987654321AA A A A A A A A A A A A A A A A A A A ,交巡警服务平台管辖范围的最大半径为R,其中交巡警出警的平均速度为V ,出警所用时间为t 。
1.2、模型建立与求解按理论上建立的模型,以交巡警服务平台所在地点为圆心,以要求尽量能在3分钟内有交警到达事发地R=v*t 为半径的圆(其中v=60km/h,t=3min,)的面积为该平台管辖范围。
1.3、模型的检验及部分模型评价与改进:因为具体到A 区的街道路线,交巡警到达事发地点所走路线为“折线”路线,而非理想直线,所以,交巡警可能在3分钟内到达不了所管辖范围的任意一点,尤其是圆域中离交巡警服务平台较远的边缘地带,而本模型不足之处在于由于交巡警警力有限,平台少的原因,会出现盲区,如上图所示, 未被覆盖的区域,交巡警一定在3分钟到达不了的区域(称之为“盲区”)而对于那些部分交巡警所管辖范围有重叠的部分发生事故时该指挥中心指派最近靠近事故发生地的交巡警到达现场更为益。
改进交巡警管辖漏洞,可以将交巡警平台管辖区重叠严重的地带将交巡警平台移动,使其更合理的覆盖盲区,还可以将发案率低而交巡警服务平台密集的抽调到案发率高的地区,再就是添加部分交巡警平台以解决警力不足的缺陷。
(二)A 区重大突发事件二十个交警平台分配到十三条交通要道 2.1、模型假设与符号说明①A 区现有的20个交巡警服务平台,记为:(i A 同上) ②进出A 区的13个路口节点,记为:271,234(),227,251(),328,337(),292,280(),316,219(2221161412a a a a a )367,314(),337,246(),328,243(),290,212(),265,225(3029282423a a a a a)381,381(),374,315(),330,317(624838a a a③警力调度时经过的交叉路口节点,记为:)339,336(),350,327(),335,326(),301,256(),300,227(3533322625c c c c c )372,325(),5.327,411(),5.330,5.388(),333,371(),334,336(4741403936c c c c c④根据上题已分配好的各平台管辖范围,找出所在范围内距离该平台最近的路口交叉点,进行精力调度;另外,对于警力分配明显不均衡的地区,当发生重大事件时,对各个平台警力资源平行调度,不再就近封锁:2.2、模型建立、求解与结果 ①警力分配原则:1>就近原则;2>警力分布不均衡,平行调度原则; ②警力分配方案:1> A12不动;2>平行调度(见下图表):比较对象 比较过程 比较结果所走路线 总路程(km ) 22a22112610a A c A →→→ 7.708甲乙目的地1目的地210A 24a24252610a c c A →→→8.243 2210a →A22a11A 24a2211a A →3.2702411a A →242511a c A →→3.805 382a A → 3817a A → 3839402a c c A →→→3.982 382a A →384117a c A →→ 4.858 485a A → 486a A → 48475a c A →→ 2.476 485a A →48476a c A →→2.552305a A → 306a A → 306a A → 3048475a a c A →→→ 3.2573048476a a c A →→→3.287 3076a A A →→3.344 308a A → 488a A → 30732338a A c c A →→→→ 3.056 308a A →2048478a a c A →→→3.879 624a A → 624a A →0.350624a A → 297a A →29307a a A →→8.015 297a A → 169a A → 1636359a c c A →→→1.532 169a A →2313a A →2313a A →0.500 2313a A →2114a A →2114a A →3.265 2114a A →2815a A → 2815a A → 4.725 2815a A → 1416a A →1416a A →6.742 1416a A →1212A A → 1212A A → 01212A A →③距离求解:将每两个节点间的距离近似为直线段,利用公式:d=()()221221y y x x -+-算出距离,再将个线段长度相加,对于有多条路线的调度方案,通过计算比较取得最优解(见上表)。
2.3、模型评价方案等级划分 优(s ≤3km ) 良(3km<s ≤5km ) 差(s>5km )624a A → 0.350 382a A → 3.982 1416a A →6.742485a A →2.476 308a A →3.056 297a A → 8.015 169a A → 1.532 2411a A → 3.270 2210a →A7.708 2313a A →0.500 2114a A →3.265 1212A A →2815a A →4.725对于等级为“差”的调度方案,由于距离太大,当突发重大事件时,明显不能实现对路口的快速封锁,而且A 区发案率相对较高,这就要求警力调度有更好的灵活性和速度,而对于等级为“优”与“良”的调度方案可以尽量在3分钟到达封锁路口。
