第10章静电场8-2
大学物理授课教案 第八章 静电场中的导体和电介

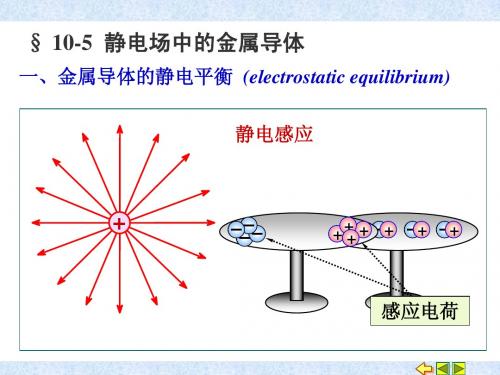
第八章 静电场中的导体和电介质§8-1 静电场中的导体一、静电感应 导体的静电平衡条件 1、静电感应2、导体静电平衡条件(1)导体的静电平衡:当导体上没有电荷作定向运动时,称这种状态为导体的静电平衡。
(2)静电平衡条件从场强角度看:①导体内任一点,场强0=E;②导体表面上任一点E与表面垂直。
从电势角度也可以把上述结论说成: ①⇒导体内各点电势相等; ②⇒导体表面为等势面。
用一句话说:静电平衡时导体为等势体。
二、静电平衡时导体上的电荷分布 1、导体内无空腔时电荷分布如图所示,导体电荷为Q ,在其内作一高斯面S ,高斯定理为:∑⎰=•内S Sq s d E 01ε 导体静电平衡时其内0=E,∴ 0=•⎰s d E S, 即0=∑内S q 。
S 面是任意的,∴导体内无净电荷存在。
结论:静电平衡时,净电荷都分布在导体外表面上。
2、导体内有空腔时电荷分布(1)腔内无其它电荷情况如图所示,导体电量为Q ,在其内作一高斯面S ,高斯定理为:∑⎰=•内S Sq s d E 01ε 静电平衡时,导体内0=E∴ 0=∑内S q ,即S 内净电荷为0,空腔内无其它电荷,静电平衡时,导体内又无净电荷∴ 空腔内表面上的净电荷为0。
但是,在空腔内表面上能否出现符号相反的电荷,等量的正负电荷?我们设想,假如有在这种可能,如图所示,在A 点附近出现+q ,B 点附近出现-q ,这样在腔内就分布始于正电荷上终于负电荷的电力线,由此可知,B A U U >,但静电平衡时,导体为等势体,即BAU U =,因此,假设不成立。
结论:静电平衡时,腔内表面无净电荷分布,净电荷都分布在外表面上,(腔内电势与导体电势相同)。
(2)空腔内有点电荷情况如图所示,导体电量为Q ,其内腔中有点 电荷+q ,在导体内作一高斯面S ,高斯定理为∑⎰=•内S Sq s d E 01ε 静电平衡时0=E, ∴ 0=∑内S q 。
又因为此时导体内部无净电荷,而腔内有电荷+q ,∴ 腔内表面必有感应电荷-q ,。
人教版高中物理必修第三册精品课件 分层作业 第10章 静电场中的能量 分层作业9 电势差

面2的电势为+3 V,求:
(1)电子从等势面1运动至等势面4过程静电力做的功;
(2)等势面1的电势。
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析 (1)由动能定理得,电子从等势面1运动至等势面4的过程静电力做的
意得Uab>Ubc,又静电力做功W=qU,则Wab>Wbc,由动能定理得粒子由a点到b
点的动能变化大于由b点到c点的动能变化,D正确。
1 2 3 4 5 6 7 8 9 10 11 12 13 14
13.(2023陕西宝鸡中学校考)如图所示,虚线为某电场的5个等势面,相邻等
势面间电势差相等。一电子只在静电力作用下在电场中运动(轨迹未画
为等势面,C、D、G、E点电势相等,A、C错误; D、G两点中G点距离AB近,
电场强度矢量和大,方向均从A指向B,B正确;E点电势为0,F点的电势小于
0,E点为连线中点,电场强度大于F点电场强度,并且方向不同,D错误。
1 2 3 4 5 6 7 8 9 10 11 12 13 14
11.(2023江苏南通一中校考)两个位于纸面内的点电荷产生的电场的等势
A.C、D两点的电势相等,电场强度大小相等、方向不同
B.D、G两点的电势相等,电场强度大小不等、方向相同
C.E、G两点的电势不等,电场强度大小不等、方向相同
D.E、F两点的电势不等,电场强度大小相等、方向不同
1 2 3 4 5 6 7 8 9 10 11 12 13 14
根据对称性知,C、D两点的电场强度大小相等,方向均从A指向B,AB中垂面
A.电势φA>φB,电场强度EA>EB
人教版高中物理必修第三册精品课件 分层作业 第10章 静电场中的能量 带电粒子在电场中运动的四种题型

5mg,方向竖直向下 (2)mg,方向竖直向下
1 2 3 4 5 6 7 8 9 10 11 12
12.(2023河南济源高级中学测试)足够长的带电平行金属板MN、PQ与竖
直方向夹角θ=30°,相距d=1.0 m,板间电场强度大小E=3.0×103 N/C,带电情
错误。
1 2 3 4 5 6 7 8 9 10 11 12
10.如图所示,充电后的平行板电容器水平放置,电容为C,极板间距离为d,上
极板正中有一小孔,质量为m、电荷量为+q的小球从小孔正上方高h处由
静止开始下落,穿过小孔到达下极板处时速度恰为零(空气阻力忽略不计),
极板间电场可视为匀强电场,重力加速度为g,求:
4.相距10 cm的平行板A和B之间存在匀强电场,电场强度大小E=4×104
V/m,方向竖直向下,如图所示。电场中C点距B板3 cm,D点距A板2 cm。有
一个质量为m=2×10-8 kg的带电微粒沿图中所示的虚线从C点运动至D点。
若重力加速度g取10 m/s2,则下列说法正确的是( C )
A.该微粒在D点时的电势能最大
度地将小球释放,g取10 m/s2。求:
(1)小球通过最高点B时速度的大小;
(2)小球通过最高点B时,丝线对小球拉力的大小。
1 2 3 4 5 6 7 8 9 10 11 12
解析 (1)小球由A运动到B,其初速度为零,静电力对小球做正功,重力对小球
做负功,丝线拉力不做功,则由动能定理有
2
若小球获得初速度恰能绕O点在竖直平面内做圆周运动,取小球静止时的
位置为电势能零点和重力势能零点,cos 37°=0.8,g取10 m/s2。下列说法正
大学物理第10章 电荷和静电场-2
例如 孤立的导体球的电容
Q
Q C V
地球
Q Q 4π 0 R
4π 0 R
6
R
4
RE 6.4 10 m, CE 7 10 F
二 电容器
导体组合,使之不受周 围导体的影响 ——电容器
电容器的电容:
当电容器的两极板分
别带有等值异号电荷Q时 ,电量Q与两极板间相应 的电势差VA-VB的比值。
详细说明如下
二、导体表面的电荷和电场 导体表面电荷的分布与导体本身的形状以及附近 带电体的状况等多种因素有关。
孤立导体的电荷面密度与其表面的曲率有关,曲率越大 电荷面密度越大。 表面突出尖锐部分曲率大, 电荷面密度大;
表面比较平坦部分曲率小, 电荷面密度小; 表面凹进部分曲率为负, 电荷面密度最小。
S
–q'
说明空腔内表面所带总电量与空腔内带电体的电量 相等、符号相反。导体空腔是等势体,腔内场强不 为零,不是等电势区间。
四、导体静电平衡性质的应用
1. 静电屏蔽 (electrostatic shielding)
+q +q +q
-q
-q
利用导体静电平衡的性质,使导体空腔内部空 间不受腔外电荷和电场的影响,或者将导体空腔 接地,使腔外空间免受腔内电荷和电场影响,这 类操作都称为静电屏蔽。无线电技术中有广泛应 用,例如,常把测量仪器或整个实验室用金属壳 或金属网罩起来,使测量免受外部电场的影响。
Cn
VB
等效
VA
C
VB
令 U VA VB
q1 C1U
q2 C2U
•导导体表面外附近的场强 E 0
★ 注意:
E 仅由 S 处电荷产生而与其它电荷无关吗?为什么?
人教版高中物理必修第三册精品课件 第10章 静电场中的能量 2 电势差

(2)电场中任意两点的电势差,与是否放入试探电荷有关。
( × )
(3)若电场中两点间的电势差UAB=1 V,则将单位电荷从A点
移到B点,静电力做功为1 J。( × )
(4)若UAB>0,说明φA>φB,但无法判断φA、φB的正负。( √ )
(5)将电荷量为q的电荷从A点移到B点与将电荷量为-q的电
课前•基础认知
一、电势差
1.电势差:电场中两点之间电势的 差值 。电势差也叫作
电压。
2.表达式:UAB= φA-φB 。
3.矢标性:电势差是 标量 ,其正负表示两点电势的 高
低 。
,用符号V表示。
4.单位:在国际单位制中,单位为 伏特
5.静电力做功与电势差的关系:UAB=
。
微判断 (1)电场中A、B两点的电势差,不仅与A、B两点的
点要克服静电力做功4×10-8 J,则M点电势φM为多少?若将该
电荷从M点移到N点,静电力做功14×10-8 J,则N点电势φN为
多少?M、N两点间的电势差UMN为多少?
答案:-2 V 5 V -7 V
解析:由
WSM=qUSM 得,USM=
=
-×-
-
V=2 V
-×
而 USM=φS-φM,所以 φM=φS-USM=(0-2) V=-2 V
垂直距离,也就是海拔,也称为绝对高度,而地面上某一点高出
另一点的垂直距离称为相对高度。
(1)选择不同的测量起点时,不同地方的高度和两个地方的
高度差会有怎样的变化?
(2)与等高线类似,在电场中选择不同的零电势点时,不同位
置的电势和两个位置的电势差又会有怎样的变化?
§8-2 电通量 高斯定理

∑q
i
i内
根据高斯定理列方程,解方程得 第4步:根据高斯定理列方程,解方程得E
∫
S
r r E ⋅ dS = E ∫ dS = E.S =∑ q内 / ε 0
∑q E=
内
Sε 0
......( A)
7
应用举例: 4、应用举例:
均匀带电体的场强分布 的场强分布(点 球面、球体) 例8.6P13:求球对称均匀带电体的场强分布 点、球面、球体 求
2
高斯定理 定理: 三. 高斯定理:
(K.F.Gauss——德国物理学家、数学家、天文学家) 德国物理学家、数学家、天文学家 德国物理学家
1、表述 168):在真空中的任何静电场中 通过任 、表述(P :在真空中的任何静电场中, 闭合曲面的电通量等于该闭合曲面所包围的电荷的 的电通量等于该闭合曲面所包围的电荷的代 一闭合曲面的电通量等于该闭合曲面所包围的电荷的代 数和的1/ε0倍, 即 数和的 ε
R P2
∴ E2 =
q 4πε0r
...(2)# ⇒ 球面外与点电 2
荷电场相同
(2)、 求均匀带电球体 的场强分布:P14 、 的场强分布: r 已知R, 求球内外P 已知 q, 求球内外 1、P2处的 E 作与带电球体同心半径为 半径为r的 作与带电球体同心半径为 的 球面为高斯面 球面为高斯面 r r 高斯面: 2 ∫S1E ⋅ dS = 4πr E =∑ q内 / ε 0 ∑ q内 ......( A) E= S 2 4πε 0 r
ε0 i 式中:闭合面s 式中:闭合面s——高斯面 高斯面 r r 通过s 通过 ∫ E ⋅ dS ——通过s的电通量
S i内
Φe =
∫
S
r r 1 E ⋅ dS =
8-(2-3)静电场的高斯定理

一、电场线
为了形象和直观地描述电场,在电场中画出的一系列 有指向的虚拟曲线,称为电场线。
(1)电场线描述电场
① E方向: 电场线各点的切线方向
② E大小:
E
电场线的疏密反映电场的强弱。
E lim e de 电 场 线 密 度 S0 S dS
电场线密度:(定量描述电力线疏密与电场的强弱的关系)
Φ e
E dS
S
1
ε 0
qi
(λ为沿轴线方向单位长度带电量)
解: r R 高
E dS
S
E dS E dS E dS
斯 面
r
S上
S下
S侧
l
E dS E 2πrl
S侧
E
q r 2l
E r
2 0
§8-3 静电场的环路定理 电势
一、电场力做功
b
Aab q0 E dl
θ
π
2
θ
π
2
Φ e
0
Φ e
0
[例]求均匀电场中一半球面的电通量。
nE
n
n
S1
oR
n
S2
Φ S1
E
dS
S1
E S2
Φ S1
EπR 2
三、高斯定理
在真空中的任意静电场中,通过任一闭合曲面S
的电通量e ,等于该闭合曲面所包围的电荷电量的
代数和除以0 而与闭合曲面外的电荷无关。
Φ e
E
S
dS
ε1 0
a
当带电体在静电场中移动时,静电场力对带电体
要作功,这说明静电场具有能量。
dA F dl q0 E dl q0E cosθdl
高二上学期物理人教版必修第三册课件:电势差

提示:UAB=φA-φB。 活动 2:试探电荷 q 在 A、B 两点的电势能是多少? 提示:EpA=φAq,EpB=φBq。 活动 3:点电荷 q 从 A 点到 B 点静电力做的功是多少? 提示:WAB=EpA-EpB=φAq-φBq=(φA-φB)q=UABq。 活动 4:由活动 3 你能得出电势差与静电力做功有什么关系? 提示:UAB=WqAB。
高二上学期物理人教版必修第三册课 件: 10.2电势差
规范解答
高二上学期物理人教版必修第三册课 件: 10.2电势差
(1)对电势差要注意角标的排序,如:UAB=-UBA,UAB+UBC=UAC。 (2)若求某点的电势,必须明确规定零电势点在哪里,但两点间电势差 的数值与零电势点的选取无关。
高二上学期物理人教版必修第三册课 件: 10.2电势差
课前自主学习
高二上学期物理人教版必修第三册课 件: 10.2电势差
一、电势差 1.定义:在电场中,两点之间 01 _电__势___的差值,也叫作电压。 2.定义式:设电场中 A 点的电势为 φA,B 点的电势为 φB,则它们之 间的电势差 UAB= 02 ___φ_A_-__φ_B____,UBA= 03 __φ_B_-__φ_A__,显然 UAB= 04 __-__U__B_A__。 3.电势差可以是 05 _正__值,也可以是 06 _负__值。当 A 点电势比 B 点电 势高时,UAB 为 07 _正__值,UBA 则为 08 _负__值。 4.选择不同的位置作为零电势点,电场中某点电势的数值可能 09 __改__变__,但电场中某两点之间电势的差值 10 __保__持__不__变____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
+ +
en
+ + +
侧面
E dS
上、下底面的电场强度方向 与面平行,电通量为零。
侧面
E
EdS cos 0 E dS E 2rh
侧面
q
i
h
1 n qi SE dS o i 1
h
r
o y
e n en
E 2 0 r
x
例;无限大均匀带电平面的电场分布。设电荷面密度 为σ 。
E dS
s
解 对称性分析: E 垂直平面 作如图所示圆柱形高斯面。
侧面
E d S E dS E d S
左 右
0 Edscos0 Edscos0
第10章 真空中的静电场 七、高斯定理应用(2) 计算特殊带电体的电场强度
1
场源电荷具有某种对称性时才能用高斯定理求场强。
常见的具有某种对称性的场源电荷有:
球对称分布: 包括均匀带电 的球面、球体 和多层同心球 壳等。
轴对称分布: 包括无限长均 匀带电的直线、 圆柱面、圆柱 体等。
面对称分布: 包括无限大的 均匀带电平面、 平板等。
用高斯定理计算场强的主要步骤 1、根据电通量定义式计算出通 过高斯面的电通量
1 E dS
S
o
q
i 1
n
i
关键:根据场强分布的特点,选取适当的高斯面。
即能计算出 E dS ?
S
2)计算高斯面所包围的电量代数和qi 1ni?
3)上述结果代入高斯定理表达式求出场强。
左 右
ES' ES' 2ES'
E
q S '
1 n qi SE dS o i 1
S'
S'
S'
E
S' 2 S' E 0
E 2 0
下一讲:静电场的环路定理
7
当场点在球面外时 当场点在球面内时
q0
E =0
4
例:无限长均匀带电直线的电场分布。设电荷线密度 为λ。 解 对称性分析:轴对称 以带电直导线为轴,作如图 所示圆柱形高斯面S。
E dS
s 侧面
E dS
上底
E dS
下底
E dS
3
例:求均匀带电球面的电场分布。球面半径为R,总电 量为Q。
解:球对称,作球面高斯面 e E dS E dS cos0
S S
高斯面
r
R
E
Q
E dS 4 r 2 E
S
根据高斯定律 4r E
2
1
0
q
E= Q
均匀带电球面
高斯面
4 0 r 2
