lec09 3.4~3.6
LEC准则综合打分法

LEC准则综合打分法————————————————————————————————作者:————————————————————————————————日期:1、工作危害性分析法(LEC法)LEC分值表分数值事故发生的可能性(L)10 6 3 1 0.5 0.2 0.1完全可以预料相当可能可能,但不经常可能性小,完全意外很不可能,可以设想极不可能实际不可能分数值暴露于危险环境的频繁程度(E)10 6 3 2 1 0.5连续暴露每天工作时间内暴露每周一次或偶然暴露每月一次暴露每年几次暴露非常罕见的暴露分数值发生事故产生的后果(C)100 40 15 7 3 1大灾难,许多人死亡灾难,数人死亡非常严重,一人死亡严重,重伤重大,致残引人关注,不利于基本的安全卫生要求分数值危险程度(D)危险等级>320 160~320 70~160 20~70 <20极其危险,不能继续作业高度危险,需立即整改显著危险,需要整改一般危险,需要注意稍有危险,可以接受54321注:D=L*E*C2、矩阵法对照表(1)从人员伤亡程度、财产损失、停工时间和对声誉的影响等四个方面,对后果的严重程度进行评价取值,取四项得分最高的分值作为其最终的S 值。
S是四项因素之中最高分值的任何一项;表(1)评估后果的严重性(S)分数人员伤亡程度财产损失停工时间对声誉的影响5 ·死亡·终身残废·丧失劳动能力≥50万元≥30天引起公众的反应;持续不断的指责;国家级媒体的大量负面报道。
4 ·部分丧失劳动能力·职业病·慢性病·住院治疗≥5万元≥5天引起整个区域公众的关注;大量的指责,当地媒体大量的反面报道;国内媒体负面报道,当地或国家政策的可能限制措施。
3 需要去医院治疗,但不需住院≥1万元≥1天一些当地公众表示关注,受到一些指责;一些媒体有报道和政治上的重视2 ·皮外伤·短时间身体不适小于1万元半天公众对事件有反应,但是没有表示关注1 没有受伤无没有误时没有公众反应对照表(2)从发生偏差的频率、安全检查的频率、操作规程的执行情况、员工的胜任程度、现有防范和控制措施的有效性等方面,评价危害事件发生的可能性,取五项中分值最高的分值作为其最终的L值。
lec评价法

LEC评价法(美国安全专家K.J.格雷厄姆和K.F.金尼提出)用于评
价操作人员在具有潜在危险性环境中作业时的危险性、危害性。
LEC法不适用于重大危险源的辨识,重大危险源的辨识请参照GB18218-2009《危险化zhi学品重大危险源辨识》。
LEC评价法
用于评价操作人员在具有潜在危险性环境中作业时的危险性、危害性。
该方法用与系统风险有关的三种因素指标值的乘积来评价操作
人员伤亡风险大小,这三种因素分别是:L(likelihood,事故发生的可能性)、E(exposure,人员暴露于危险环境中的频繁程度)
和C(consequence,一旦发生事故可能造成的后果)。
给三种因素的不同等级分别确定不同的分值,再以三个分值的乘积(danger,危险性)来评价作业条件危险性的大小。
风险分值D=LEC。
D值越大,说明该系统危险性大,需要增加
安全措施,或改变发生事故的可能性,或减少人体暴露于危险环境
中的频繁程度,或减轻事故损失,直至调整到允许范围内。
该方法以与系统风险率有关的三种因素指标值之积来评价系统人员伤亡风险的大小,并将所得作业条件危险性数值与规定的作业条件危险性等级相比较,从而确定作业条件的危险程度。
当前有些企业在理解和运用LEC风险评价法时存在一定的误区,导致不能准确地对危险源进行风险评价。
根据经验,总分在20以下是被认为低危险的,这样的危险比日常生活中骑自行车去上班还要安全些;如果危险分值到达70~160之间,那就有显著的危险性,需要及时整改;如果危险160~320之间,那么这是一种必须立即采取措施进行整改的高度危险环境;分值在320以上的高分值表示环境非常危险,应立即停止生产直到环境得
到改善为止。
LEC法标准(可编辑修改word版)

《危险源辨识和风险评价表》填表说明危险源辨识和风险评价是职业健康安全管理体系建立的基础,评价出重点风险并有效控制是体系运行的关键,为此我们必须充分辨识危险源,认真填写《危险源辨识和风险评价表》。
1、设备设施/ 场所/ 岗位:根据实际确定,将所使用的设备设施或场所(填具体的设备设施名称,如果是多种设备设施,也可填场所,如锅炉房、变电站、空压张、污水站等)、人员的岗位等描述清楚。
如“拆箱机/操作工”、“制丝冷端/操作工”、“卷接包装机/操作工”、“变电站/维修电工”;“车间维修组/机修工”、“叉车/驾驶员”、“成品库/保管员”、“分拣机/操作工”、运输车辆/司机”、“各办公室/管理和技术人员”等。
2、作业活动:该工序或工种所从事的具体作业活动。
如“卷接包装机/操作工”可能涉及到的具体作业有装卡材料、加工操作、排除故障、清理设备等;“维修电工”可能涉及到的具体作业活动有“登高作业”、“检修电气设备”等、“电焊作业”可能涉及到的具体作业活动有“开关焊机设备”、“焊接加工”等。
3、第一类危险源:该作业活动中可能接触的第一类危险源,即“存在的、可能发生意外释放的能量(能源或能量载体)或危险物质”,如带电导体、遇水自燃物质、运动的机械、奔驰的汽车、压力容器、悬吊物的势能、有毒品、烟草粉尘、机械噪声 --- 等;一种作业活动中可能有一种或几种第一类危险源。
4、第二类危险源 -- 危险源描述:根据第一类危险源,描述可能引发事故或伤害的人的不安全行为、物的不安全状态、作业环境的不良因素等第二类危险源及其后果,并参考《生产过程危险和有害因素分类与代码》(GB/T13861-1992)填写第二类危险源的代码;如“维修电工” 在进行“检修电气设备”时,第一类危险源是“带电导体”,第二类危险源可能有“外露线路绝缘层破损”,后果是“触电”(物,代码11505)、“设备漏电”,后果是“触电”(物,代码11510)、“不按规定监控,停电检修过程中合闸通电”,后果是“触电”(人,代码515)。
LEC法危险源辨识方法和标准

LEC法危险源辨识方法和标准危险源辨识方法和标准1 危险源辨识的范围1.1 所属区域的一切生产经营活动。
1.2 所有进入工作场所人员(包括合同方人员和参观者)的活动。
1.3 工作场所的所有设施,无论是本公司提供的还是他人提供的。
2 危险源辨识应考虑如下方面:2.1 三种时态人身伤害事故,并延续到现在的。
维护、改进、报废等活动时产生的安全控制状态。
2.2三种状态件。
2.3六种危险和有害因素类型2.4作业活动的划分3 危险源的辨识方法询问交流:与某项工作具有经验的人交谈工作中的危险源。
现场观察:现场观察可发现存在的危险源。
获取外部信息:从有关生产厂家、文献资料获取有关危险源的信息,加以分析研究。
4各单位进行危险源辨识、风险评价时应有员工代表的参与。
5风险评价5.1评价原则风险评价首先用“定性法”进行评价,对不能用“定性法”评价的,用“半定量法(DLEC法)”进行评价。
5.2风险评价方法不符合法律法规及其他要求(按A级管理);曾经发生过事故,仍未采取有效控制措施(按A级管理);直接观察到的危险,且无适当控制措施(按A级管理);相关方合理抱怨或要求(按A级管理);对属《重大危险源辨识》GB18218-2000中所规定的重大危险源(按A级管理);满足上列任意一项时,可直接判断为不可容许风险。
对国家级重大危险源申报范围的危险源其临界量或危险性接近判定标准的(按B级管理)。
L—发生事故的可能性大小;E—人体暴露在这种风险环境中的频繁程度;C—一旦发生事故会造成后果的严重程度;D—危险性分值。
L:发生事故的可能性大小E:人体暴露在这种危险环境的频繁程度C:一旦发生事故会造成后果的严重程度D:危险性分值C的取值如下表D—危险性分值a法规和其他要求;b企业的方针、目标;c事故、事件、不符合项和预防措施记录;d检查/审核结果;e相关方要求;f类似事故、事件信息;g与企业的设施、工艺流程和运行活动有关的信息;h半定量评价(LEC法, D=LEC)。
LEC安全风险等级评估

LEC安全风险等级评估
LEC安全风险等级评估是一个评估LEC系统(Local Exchange Carrier System)中安全风险的等级的过程。
LEC系统是指一
个电话运营商或者互联网供应商的局域网环境。
评估LEC安全风险等级的目的是为了识别和评估潜在的安全
威胁和漏洞,以便采取相应的安全措施来保护系统免受攻击和数据泄露的风险。
评估LEC安全风险等级的步骤通常包括以下几个方面:
1. 收集信息:收集关于LEC系统的基本信息,包括网络拓扑、硬件和软件配置、用户权限和访问控制等。
2. 风险识别:通过对LEC系统进行扫描和漏洞测试,识别系
统中存在的潜在安全威胁和漏洞。
3. 风险评估:评估每个识别的安全威胁和漏洞的潜在风险程度,根据其可能性和影响等因素进行评估。
4. 等级划分:根据风险评估的结果,将安全威胁和漏洞划分为不同的等级,如高风险、中风险和低风险。
5. 安全措施建议:根据风险等级,提出相应的安全措施建议,包括修复漏洞、加强访问控制、加密通信等。
6. 风险追踪和监控:建立风险追踪和监控机制,定期检查和评
估LEC系统的安全状况,以及对新的安全威胁和漏洞进行监控和应对。
通过进行LEC安全风险等级评估,可以帮助组织及时识别和应对潜在的安全威胁和漏洞,提高LEC系统的安全性和可靠性。
LEC法取值标准对照表
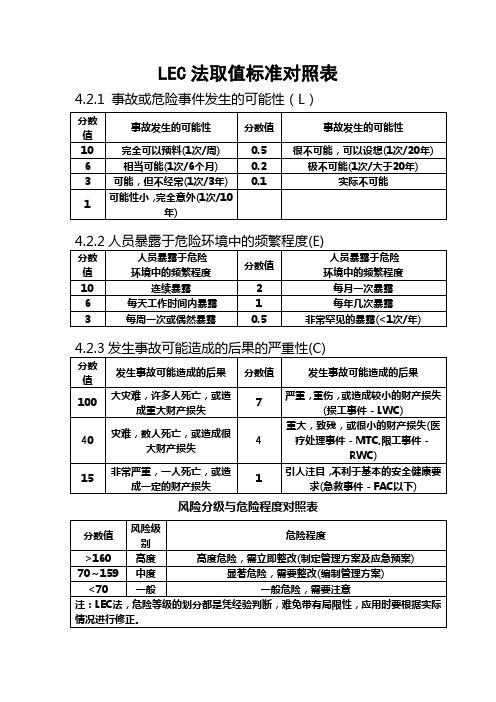
LEC法取值标准对照表4.2.1 事故或危险事件发生的可能性(L)分数值事故发生的可能性分数值事故发生的可能性10 完全可以预料(1次/周) 0.5 很不可能,可以设想(1次/20年) 6 相当可能(1次/6个月) 0.2 极不可能(1次/大于20年)3 可能,但不经常(1次/3年) 0.1 实际不可能1 可能性小,完全意外(1次/10年)4.2.2人员暴露于危险环境中的频繁程度(E)分数值人员暴露于危险环境中的频繁程度分数值人员暴露于危险环境中的频繁程度10 连续暴露 2 每月一次暴露6 每天工作时间内暴露 1 每年几次暴露3 每周一次或偶然暴露0.5 非常罕见的暴露(<1次/年)4.2.3发生事故可能造成的后果的严重性(C)分数值发生事故可能造成的后果分数值发生事故可能造成的后果100 大灾难,许多人死亡,或造成重大财产损失7严重,重伤,或造成较小的财产损失(损工事件-LWC)40 灾难,数人死亡,或造成很大财产损失4重大,致残,或很小的财产损失(医疗处理事件-MTC,限工事件-RWC)15 非常严重,一人死亡,或造成一定的财产损失1引人注目,不利于基本的安全健康要求(急救事件-FAC以下)风险分级与危险程度对照表分数值风险级别危险程度>160 高度高度危险,需立即整改(制定管理方案及应急预案) 70~159 中度显著危险,需要整改(编制管理方案)<70 一般一般危险,需要注意注:LEC法,危险等级的划分都是凭经验判断,难免带有局限性,应用时要根据实际情况进行修正。
LEC计算参数表

极不可能
实际不可能
表A.1.2 暴露于危险环境的频繁程度(E )
分数值 频繁程度 连续暴露
每天工作时间 内暴露
每周一次,或 偶然暴露
每月一次暴露 每年几次暴露 非常罕见地暴
露
表A.1.3 发生事故产生的后果(C )
分数值 后果 大灾难,许多 人死亡 灾难,数人死 亡
非常严重,一 人死亡 重伤
8
井下消防
消防设施
消防器材
火灾报警
……
9
排土场
运输
排土
平整
……
表A.1.1 事故发生的可能性(L )
分数值
事故发生的可 能性
完全可能预料
相当可能
可能,但不经 常
可能性小,完 全意外
附表5-1
LEC计算参数表
序号
主单元
岗位(设备设施 /作业活动)单
元
危险有害因素
1 开拓运输与开采
凿岩
1、凿岩机保护装置失效; 2、顶板未按规定及时支护;
事故类型 触电、顶板
L(事故可能性)
E(暴露于危险环境频 率)
C(事故后果)
完全可能预料
非常罕见地暴露
大灾难,许多人死亡
爆破
1、爆破前未检查有毒有害气 体; 2、警戒距离不符合规定;
中毒窒息、爆 破伤人
相当可能
每周一次,或偶然暴露 非常严重,一人死亡
铲装
机械伤人 很不可能,可能设想
连续暴露
轻伤
破碎
可能,但不经常 每周一次,或偶然暴露 非常严重,一人死亡
运输
可能,但不经常
每月一次暴露
非常严重,一人死亡
装卸
可能,但不经常 每周一次,或偶然暴露 非常严重,一人死亡
LECD风险评价等级

LECD风险评价等级
LECD是一种风险评估方法,它考虑了事故或危害事件的可能性、暴露于危害事件环境的频率以及事故或危害事件的可能结果。
根据D值风险等级,我们可以对不同等级的风险采取不同的措施。
对于D值超过320的非常高风险,我们需要立即停止作业,以避免事故的发生。
对于D值在1160至320之间的高风险,我们需要立即整改,以降低风险。
对于D值在270至160之间的中等风险,我们需要采取措施进行整改。
对于D值在320至70之间的可能风险,我们需要注意风险并采取必要的预防措施。
对于D值在420以下的可接受风险,我们可以容忍并继续作业。
在LECD方法中,事故或危害事件发生可能性(L)分数根据其可能性的程度进行评估,从完全会被预料到到实际上不可能,分别对应不同的分数值。
暴露于危害事件环境的情况(E)分数值根据暴露的频率进行评估,从每天在工作时间内暴露到非常罕见地暴露,分别对应不同的分数值。
事故或危害
事件的可能结果(C)也根据其严重程度进行评估,从大灾难到引人注目,分别对应不同的分数值。
LECD方法可以帮助我们全面评估风险,并根据不同的风险等级采取相应的措施来预防事故的发生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15
(4) P(4 X 7) b( x;15,.2) B(7;15,.2) B(3;15,.2) .348
x4
7
Example 3.32
An electronics manufacturer claims that at most 10% of its power supply units need service during the warranty period. To investigate this claim, technicians at a testing laboratory purchase 20 units and subject each one to accelerated testing to simulate use during the warranty period. Let p denote the probability that a power supply unit needs repair during the period (the proportion of all such units that need repair).The laboratory technicians must decide whether the data resulting from the experiment supports the claim that p≤0.1. Let X denote the number among the 20 sampled that need repair, so X~Bin(20, p).Consider the decision rule
X= the number of S’s among the n trials Possible values for X in an n-trial experiment are x = 0,1,2,…,n. we will often write X~Bin(n,p) to indicate that X is a binomial rv based on n trials with success probability p.
k 1 k 1
n
np C in1 p i (1 p)( n1)i np( p 1 p) n1 np
i 0
n 1
Another solution: Suppose
k nk k f ( x) (q px) C k p q x n n k 0
Solution :
6 3 3 6 P( X 3) b(3;6,.5) (.5) (.5) 20(.5) .313 3
6 x 6 x P(3 X ) b( x;6,.5) (.5) (.5) .656 x 3 x 3 x
x
P( X x) B( x; n, p) b( y; n, p)
y 0
x 0,1,2,...,n
Example 3.31 Suppose that 20% of all copies of a particular textbook
fail a certain binding strength test. Let X denote the number among 15 randomly selected copies that fail the test. Then X has a binomial distribution with n=15 and p=.2. Determine the following probability
Reject the claim that p≤0.1 in favor of the conclusion that p>.10 if x≥5 and consider the claim plausible if x≤4
Solution:
The probability that the claim is rejected when p=.10 (an incorrect conclusion) is
The Binomial Random Variable and Distribution
Definition: Given a binomial experiment consisting of n trials, the
binomial random variable X associated with this experiment is defined as
n
n k k n k k 1 Derivation for two sides f ( x) np(q px)n1 kCn p q x k 0
Let x=1, then
np kC n p k q n k E ( X )
k k 0
n
Example 2: Let X have the binomial distribution with parameters n, p, determine V(X) .
P( X 5 when p .10) 1 B(4;20,.1) 1 .957 .043
The probability that the claim is not rejected when p=.20 (a different type of incorrect conclusion) is
One might think that the probability of this second type of erroneous conclusion could be made smaller by changing the cutoff value 5 in the decision rule to something else. However, although replacing 5 by a smaller number would yield a probability smaller than .630, the other probability would then increase. The only way to make both “error probabilities” small is to base the decision rule on an experiment involving many more units.
(1) the probability that at most 8 fail the test;
(2) The probability that exactly 8 fail (3) The probability that at least 8 fail (4) The probability that between 4 and 7, inclusive, fail
Example 3.30
Each of six randomly selected cola drinkers is given a glass containing cola S and one containing cola F ,The glasses are identical in appearance except for a code on the bottom to identify the cola. Suppose there is actually no tendency among cola drinkers to prefer one cola to the other. Then p=P(a selected individual prefers S)=.5, so with X= the number among the six who prefer S, X~Bin(6,.5). Determine the probability P(X=3), P(3≤X), P(X ≤1)
Solution :
(1) P( X 8) b( x;15,.2) B(8;15,.2) .009
x 0 8
15 8 158 (2) P( X 8) b(8;15,.2) (.2) (.8) .003 8
(3) P( X 8) b( x;15,.2) B(15;15,.2) B(7;15,.2) .004
The Mean and Variance of X
Proposition: If X~Bin(n,p), then E(X)=np, V(X)=np(1-p)=npq, and
X npq
Example 2: If X is a binomial rv with parameters p and n, determine the expectation.
Solution: because a binomial distribution is n Bernoulli distribution, and a Bernoulli distribution is x p(x) 0 q 1 p
E( X i ) p, E( X i 2 ) p, V ( X i ) p p2 p(1 p) pq
P( X 4 when p .) B(4;20,.2) .630
The first probability is rather small, but the second is intolerably large. When p=.20, so that the manufacturer has grossly understate the percentage of units that need service, and the stated decision rule is used, 63% of all samples will result in the manufacturer’s claim being judges plausible!
