人教版必修一数学2-2-2-3
人教版高中数学必修一-第二章-基本初等函数知识点总结
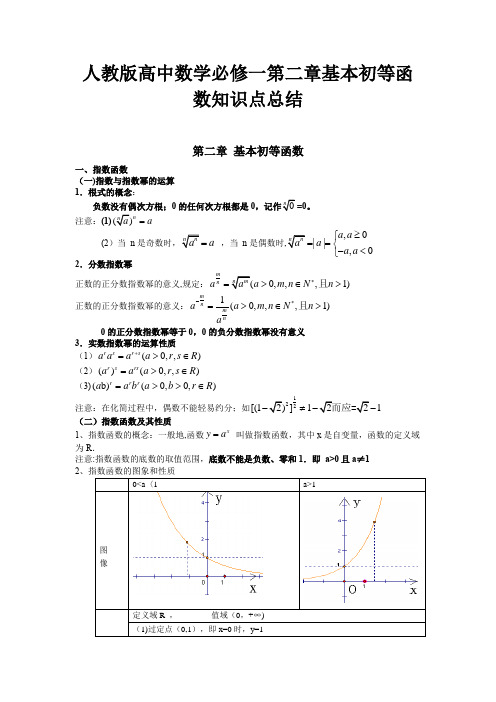
人教版高中数学必修一第二章基本初等函数知识点总结第二章 基本初等函数一、指数函数(一)指数与指数幂的运算 1.根式的概念:负数没有偶次方根;0的任何次方根都是0=0。
注意:(1)na =(2)当 n a = ,当 n 是偶数时,0||,0a a a a a ≥⎧==⎨-<⎩2.分数指数幂正数的正分数指数幂的意义,规定:0,,,1)m na a m n N n *=>∈>且正数的正分数指数幂的意义:_1(0,,,1)m nm naa m n N n a*=>∈>且0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)(0,,)rsr s a a aa r s R +=>∈(2)()(0,,)r s rsa a a r s R =>∈ (3)(b)(0,0,)rrra ab a b r R =>>∈注意:在化简过程中,偶数不能轻易约分;如122[(1]11≠ (二)指数函数及其性质1、指数函数的概念:一般地,函数xy a = 叫做指数函数,其中x 是自变量,函数的定义域为R .注意:指数函数的底数的取值范围,底数不能是负数、零和1.即 a>0且a ≠1 2a>1注意: 指数增长模型:y=N (1+p)指数型函数: y=ka 3 考点:(1)a b =N, 当b>0时,a,N 在1的同侧;当b 〈0时,a,N 在1的 异侧.(2)指数函数的单调性由底数决定的,底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小,同底找对应的指数函数,底数不同指数也不同插进1(=a 0)进行传递或者利用(1)的知识。
(3)求指数型函数的定义域可将底数去掉只看指数的式子,值域求法用单调性. (4)分辨不同底的指数函数图象利用a 1=a ,用x=1去截图象得到对应的底数。
(5)指数型函数:y=N (1+p)x 简写:y=ka x 二、对数函数 (一)对数1.对数的概念:一般地,如果x a N = ,那么数x 叫做以a 为底N 的对数,记作:log a x N = ( a - 底数, N — 真数,log a N — 对数式)说明:1。
人教A版数学必修一2-2-1-3换底公式

(金戈铁骑 整理制作)
1.(1)计算log48,log42与log28的值,看它们之间有什 么关系?
答案:32,12,3,log28=lloogg4482. (2)计算log1000100的值,看它们与lg100,lg1000的值有 何联系?
答案:log1000100=llgg1100000.
a·log63=2b·log62=2. 所以2a=log63,1b=log62. 所以2a+1b=log63+log62=log66=1.
设3a=5b= 15,则1a+1b=________. [答案] 2 [解析] 将3a=5b= 15的两边取常用对数得, alg3=blg5=12lg15,∴a=l2gl1g53,b=l2gl1g55, ∴1a+1b=2lgl1g35+2lgl1g55=2llgg1155=2.
)
1
5ቤተ መጻሕፍቲ ባይዱ
A.3
B.3
C.3 [答案] A
D.-23
[解析] 因为lg12-lg58+lg12.5-log89·log278 =lg2-1-(lg5-lg8)+lg25-lg2-llgg98·llgg287 =-lg2-lg5+3lg2+2lg5-lg2-23llgg33 =lg5+lg2-23=1-23=13.故选A.
[答案]
n m+n
[解析] lg5=lloogg33150=logl3o(g23×5 5) =log3l2o+g3l5og35=m+n n.
三、解答题 6.已知log32=a,3b=5,试用a、b表示log3 30.
[解析] 根据题意得:b=log35 ∴log3 30=12log3(3×10)=12(1+log310) =12(1+log32+log35)=12(1+a+b).
人教版高中数学必修1课件全册

因此,函数就是表达了两个变量之间变化关系的一个表达式。其准 确定义如下:
设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集 合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么 就称f:A→B为集合A到集合B的一个函数(function),记作y=f(x), x∈A。
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相 对应的y值叫做函数值(因变量),函数值的集合{f(x)|x ∈A}叫做函数 的值域。而对应的关系f则成为对应法则,则上面两个例子中,对应法则 分别是“乘以10再加20”和“平方后乘以4.9”
{ 例题、不等式组
2x-1>0 3x-6 0
的解集为A,U=R,试求A及CUA,并把它们
分别表示在数轴上。
A={x|1/2<x<2},CuA={x|x≤1/2,x≥2}
思考:
1、CUA在U中的补集是什么?
A
2、U=Z,A={x|x=2k,k∈Z}, B={x|x=2k+1,K∈Z},则CUA=_B__, CUB=__A__。
解: A∪B={x|-1<x<2} ∪ {x|1<x<3} ={x|-1<x<3}
-1 1 2 3
并集的运算性质:
(1) A A A (2) A A (3) A B B A (4) A A B, B A B, A B A B (5) A B则A B B
注意:计算并集和交集的时候尽可能的转化为图像,减少 犯错的几率,常用的图像有Venn图,数轴表示法,坐标表 示法。尤其是涉及到不等式和坐标点的时候。
6、已知A {x | x 2 3x 2 0},B {x | x 2 ax a 1 0}若A B A,求实数a的值.
人教版高中数学选修2-3知识点汇总

人教版高中数学必修2-3知识点第一章计数原理1.1分类加法计数与分步乘法计数分类加法计数原理:完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法。
分类要做到“不重不漏”。
分步乘法计数原理:完成一件事需要两个步骤。
做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法。
分步要做到“步骤完整”。
n元集合A={a1,a2⋯,a n}的不同子集有2n个。
1.2排列与组合1.2.1排列一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement)。
从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数,用符号表示。
排列数公式:n个元素的全排列数规定:0!=11.2.2组合一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合(combination)。
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号或表示。
组合数公式:∴规定:组合数的性质:(“构建组合意义”——“殊途同归”)1.3二项式定理1.3.1二项式定理(binomial theorem)*注意二项展开式某一项的系数与这一项的二项式系数是两个不同的概念。
1.3.2“杨辉三角”与二项式系数的性质*表现形式的变化有时能帮助我们发现某些规律!(1)对称性(2)当n 是偶数时,共有奇数项,中间的一项取得最大值;当n 是奇数时,共有偶数项,中间的两项,同时取得最大值。
(3)各二项式系数的和为(4)二项式展开式中,奇数项二项式系数之和等于偶数项二项式系数之和:(5)一般地,第二章随机变量及其分布2.1离散型随机变量及其分布(n ∈N *)其中各项的系数(k ∈{0,1,2,⋯,n})叫做二项式系数(binomial coefficient);2.1.1离散型随机变量随着试验结果变化而变化的变量称为随机变量(random variable)。
人教版(2019)数学选择性必修一 2_2_2直线的两点式方程课件

截距式,故解决问题过程中要注意分类讨论.
跟踪训练
4
2.直线l过点P ,2 ,且与x轴、y轴的正半轴分别交于3ຫໍສະໝຸດ A、B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程.
(2)当△AOB的面积为6时,求直线l的方程.
4
2.直线l过点P ,2 ,且与x轴、y轴的正半轴分别交于
3
A、B两点,O为坐标原点.
用截距式方程解决问题的优点及注意事项
技
法
点
拨
(1)由截距式方程可直接确定直线与x轴和y轴的交点的坐标,
因此用截距式画直线比较方便.
(2)在解决与截距有关或直线与坐标轴围成的三角形面积、
周长等问题时,经常使用截距式.
(3)但当直线与坐标轴平行时,有一个截距不存在;当直线
通过原点时,两个截距均为零.在这两种情况下都不能用
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
(1)求BC边的方程;
∵BC边过两点B(5,-4),C(0,-2),
∴由两点式得
− −4
−2 − −4
=
−5
0−5
,
即2x+5y+10=0.
故BC边的方程为2x+5y+10=0(0≤x≤5).
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
用两点式表示;
(3)如果将直线两点式转化为:(x2-x1)(y-y1)=(y2-y1)(x-
x1),此时只要直线上两点不重合,都可以用它表示出来(即
这个变形方程可以表示过任意已知两点的直线).
跟踪训练
1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中,
高中数学必修1(人教B版)第二章_2-3知识点总结配同步练习及答案

描述:例题:高中数学必修1(人教B版)知识点总结含同步练习题及答案
第二章 函数 2.3 函数的应用(I)
一、学习任务
了解一次函数、二次函数模型的意义,并能进行简单应用.
二、知识清单
函数模型的应用
三、知识讲解
1.函数模型的应用
函数模型的概念
函数模型就是用函数知识对日常生活中普遍存在的成本最低、利润最高、产量最大、收益最好、用料最省等实际问题进行归纳加工,建立相应的目标函数,确定变量的取值范围,运用函数的方法进行求解,最后用其解决实际问题.
几种函数模型的增长速度比较
在区间 上,尽管函数 , 和 都是增函数,但它们的增长速度不同,随着 的增大,指数函数 的增长速度会越来越快,会超过并远远大于幂函数 的增长速度,而 的增长则会越来越慢,因此总会存在一个 ,当 时,就有 .
(0,+∞)y =(a >1)a x y =x (a >1)log a y =(a >0)x a x y =(a >1)a x y =(a >0)x a y =x (a >1)log a x 0x >x 0x <<log a x a a
x
向高 为的水瓶内注水,注满为止,如果注水量 与水深 的函数关系的图像如图所示,那
么水瓶的形状是( )
解:B
取 的中点 作 轴的垂线,由图可知,当水深 达到容量高度的一半时,体积大于一
H V
h OH E h h
高考不提分,赔付1万元,关注快乐学了解详情。
答案:A . 分钟B . 分钟C . 分钟D . 分钟B
3.50 3.75
4.00
4.25。
2020-2021学年新教材数学人教B版必修第一册:2-2-3 一元二次不等式的解法

类型二
配方法解一元二次不等式
[例 2] 用配方法解下列不等式:
(1)4x2+4x-5≤0;
(2)14x2+x+2≥0.
[解] (1)4x2+4x-5=(2x+1)2-6≤0,
即(2x+1)2≤6,- 6≤2x+1≤ 6,
-1+2
6≤x≤
6-1 2.
所以不等式的解集为x|-1+2
6≤x≤
6-1
2
.
(2)14x2+x+2=(12x+1)2+1≥0, 因为不等式恒成立,所以不等式的解集为 R.
中的不等号也可以是“<”“≥”“≤”等.
知识点二
一元二次不等式的解法
[填一填]
1.因式分解法
(1)一般地,如果 x1<x2,则不等式(x-x1)(x-x2)<0 的解集是
(x1,x2),不等式(x-x1)(x-x2)>0 的解集是(-∞,x1)∪(x2,+∞).
(2) 解 一 元 二 次 不 等 式 , 先 把 不 等 式 化 成 定 义 形 式 __a_x_2+__b_x_+__c_>_0_ (其中不等号也可以是“<”“≥”“≤”等),若 ax2+bx+c 比较容易因式分解,可先将其进行_因__式__分__解___,然后
第二章
等式与不等式法
[课程目标] 1.掌握一元二次不等式的概念;2.会用因式分解 法和配方法解一元二次不等式.
要点整合夯基础 课堂达标练经典
典例讲练破题型 课时作业
知识点一
一元二次不等式的概念
[填一填] 一般地,形如__a_x_2+__b_x_+__c_>_0______的不等式称为一元二次不 等式,其中 a,b,c 均为常数,而且__a_≠__0____.一元二次不等式
高中数学 2-2-3待定系数法课件 新人教版必修1

解:(1)设所求函数解析式为y=ax2+bx+c(a≠0),其 中a、b、c待定,根据已知条件得:
9c=a+-33b,+c=0, 4a-2b+c=5,
解得ba==-1 2 c=-3
因此所求函数解析式为y=x2-2x-3.
(2)设所求函数为 y=a(x-4)2+2(a≠0),其中 a 待定. 根据已知条件得:a(2-4)2+2=0,解得 a=-12. 因此所求函数为 y=-12(x-4)2+2=-12x2+4x-6. (3)y=x2-4x+h=(x-2)2+h-4,∴顶点 A(2,h-4). 由已知得:-4×2-1=h-4,即 h=-5,因此所求函 数为 y=x2-4x-5.
B(x2,0),且x1,x2的倒数和为
2 3
,求这个二次函数的解析
式.
(1)证明:和这个二次函数对应的一元二次方 程是x2-2(m-1)x+m2-2m-3=0.
∵Δ=4(m-1)2-4(m2-2m-3)
=4m2-8m+4-4m2+8m+12=16>0,
∴方程x2-2(m-1)x+m2-2m-3=0必有两 个不相等的实数根.
∴对称轴为x=-1.
∴可设计:已知二次函数y=x2+bx+c的图象经过点
(1,0),对称轴为x=-1,求它的解析式等等.
评析:(1)本题属于开放性问题,答案不唯一,能够较 好地考查学生的思维能力.
(2)用待定系数法求函数解析式的一般步骤: ①设出含有待定系数的函数解析式; ②把已知条件(自变量与函数的对应值)代入解析式, 得到关于待定系数的方程组; ③解方程(组),求出待定系数; ④将求得的待定系数的值代回所设的解析式.
由已知顶点为(1,-3),可得h=1,k=-3.
即所求的二次函数为y=a(x-1)2-3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1.若log2x=3,则x的值为()
A.4B.6
C.8D.9
[答案] C
2.log(n+1-n)(n+1+n)=()
A.1 B.-1
C.2 D.-2
[答案] B
3.(2010·浙江,文科)已知函数f(x)=log2(x+1),若f(a)=1,则a =()
A.0 B.1
C.2 D.3
[答案] B
4.以下函数中,在区间(-∞,0)上为单调增函数的是()
A.y=-log1
2(-x) B.y=2+
x
1-x
C.y=x2-1 D.y=-(x+1)2
[答案] B
[解析]y=-log1
2
(-x)=log2(-x)在(-∞,0)上为减函数,否定A;y=x2-1在(-∞,0)上也为减函数,否定C;y=-(x+1)2在(-∞,0)上不单调,否定D,故选B.
5.(2010·山东文,3)函数f(x)=log2(1-3x)的值域为()
A.(0,+∞) B.[0,+∞)
C.(-∞,0) D.[-∞,0)
[答案] C
[解析]3x>0⇒0<1-3x<1⇒log2(3x+1)<log21=0,选C.
6.(2012~2013山东梁山一中期中试题)已知a=log20.3,b=20.3,c=0.32则a、b、c三者之间的大小关系为()
A.a>b>c B.b>a>c
C.b>c>a D.c>b>a
[答案] C
[解析]a=log20.3<log21=0,b=20.3>20=1,
c=0.32<0.30=1,又0.32>0,
∴b>c>a,故选C.
7.(2012~2013衡水二中月考试题)若f(x)=|lg x|,0<a<b且f(a)>f(b)则下列结论正确的是()
A.ab>1 B.ab<1
C.ab=1 D.(a-1)(b-1)>0
[答案] B
[解析]由y=|lg x|图象可知,a<1<b,否定D.
∵f(a)>f(b),∴|lg a|>|lg b|即-lg a>lg b
∴lg a+lg b<0,∴lg(ab)<0,∴0<ab<1.故选B.
8.已知函数f (x )=log 12
(3x 2-ax +5)在[-1,+∞)上是减函数,
则实数a 的取值范围是( )
A .-8≤a ≤-6
B .-8<a <-6
C .-8<a ≤-6
D .a ≤-6
[答案] C [解析]
⎩⎨⎧
3-a ×(-1)+5>0a
6≤-1
⇒-8<a ≤-6,故选C.
[点评] 不要只考虑对称轴,而忽视了定义域的限制作用. 二、填空题
9.(2012·全国高考数学江苏卷)函数f (x )=1-2log 6x 的定义域为________.
[答案] (0,6]
[解析] 由题意⎩⎨⎧
x >01-2log 6x ≥0
,所以x ∈(0,6].
10.y =log a x 的图象与y =log b x 的图象关于x 轴对称,则a 与b 满足的关系式为________.
[答案] ab =1
11.若a =log 3π、b =log 76、c =log 20.8,则a 、b 、c 按从小到大顺序用“<”连接起来为________.
[答案] c <b <a
[解析] a =log 3π>log 33=1,b =log 76<log 77=1, log 76>log 71=0,c =log 20.8<log 21=0, ∴c <b <a .
12.已知log a 1
2<1,那么a 的取值范围是__________. [答案] 0<a <1
2或a >1
[解析] 当a >1时,log a 1
2<0成立, 当0<a <1时,log a 12<log a a ,∴1
2>a >0. 三、解答题
13.计算下列各式的值. (1)log 2
748+log 212-12log 242;
(2)lg52+2
3lg8+lg5·lg20+lg 22;
[解析] (1)原式=log 2(743×12×17×6)
=log 2(12
)=log 22-12=-1
2.
(2)原式=2lg5+2lg2+lg5(1+lg2)+lg 22 =2(lg5+lg2)+lg5+lg2(lg2+lg5) =2+lg5+lg2=3.
14.讨论函数f (x )=lg(1+x )+lg(1-x )的奇偶性与单调性. [分析] 按照奇偶性与单调性的定义进行讨论,注意要先求函数的定义域.
[解析] 由题意,得⎩
⎪⎨⎪⎧
1+x >0,1-x >0,
解得-1<x <1,
∴f (x )的定义域为(-1,1).
又∵f (-x )=lg(1-x )+lg(1+x )=f (x ),
∴f (x )为偶函数.
f (x )=lg(1-x )+lg(1+x )=lg[(1-x )(1-x )] =lg(1-x 2).
设x 1,x 2∈(-1,0)且x 1<x 2, ∴x 2-x 1>0,x 1+x 2<0,
∴(1-x 21)-(1-x 2
2)=(x 2-x 1)(x 1+x 2)<0, 即1-x 21<1-x 22, ∴lg(1-x 21)<lg(1-x 22),
即f (x 1)<f (x 2),
∴f (x )=lg(1+x )+lg(1-x )在(-1,0)内单调递增. 又∵f (x )是偶函数,
∴f (x )=lg(1+x )+lg(1-x )在(0,1)内单调递减.
[点评] 判断函数奇偶性,必须先求出定义域,单调性的判断在定义域内用定义判断.
15.(2012~2013山东淄博一中期中试题)已知f (x )=log a 1+x 1-x (a >0
且a ≠1).
(1)求f (x )的定义域; (2)判断y =f (x )的奇偶性; (3)求使f (x )>0的x 的取值范围.
[解析] (1)依题意有1+x
1-x >0,即(1+x )(1-x )>0,所以-1<x <1,
所以函数的定义域为(-1,1).
(2)f (x )为奇函数.因为函数的定义域为(-1,1), 又f (-x )=log a 1-x 1+x =log a (1+x 1-x
)-1
=-log a 1+x
1-x =-f (x ),
因此y =f (x )为奇函数.
(3)由f (x )>0得,log a 1+x
1-x >0(a >0,a ≠1),①
当0<a <1时,由①可得0<1+x
1-x <1,②
解得-1<x <0;
当a >1时,由①知1+x
1-x >1,③
解此不等式得0<x <1.
16.已知函数y =log 12
(-x 2+ax +3)在区间(-3,-2]上单调递
减,求实数a 的取值范围.
[解析] 令t =-x 2+ax +3,则y =log 12
t .
∵y =log 12
t 是减函数,
∴要使题设函数在区间(-3,-2]上单调递减,只要t =-x 2+ax +3在区间(-3,-2]上单调递增,
好a
2≥-2.①
又单调区间必须使函数有意义,
∴-x 2+ax +3>0在(-3,-2]上恒成立. 又t =-x 2+ax +3在(-3,-2]上单调递增, ∴-(-3)2+a (-3)+3≥0.②
由①②可得,-4≤a ≤-2即为所求.。
