四边形难题
平行四边形难题

平行四边形1.(2014•祁阳县校级模拟)如图,在平行四边形ABCD中,点E、F是对角线AC上两点,且AE=CF.试说明:∠EBF=∠FDE.2.(2014•滕州市校级模拟)(1)如图1,点P是平行四边形ABCD对角线AC、BD的交点,若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4.请你说明理由;(2)变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD.若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,则S1、S2、S3、S4的关系为;(3)变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,则S1、S2、S3、S4的关系为.请你说明理由.3.(2014•博白县模拟)如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM 上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.(1)求证:BF=FD;(2)点D在运动过程中能否使得四边形ACFE为平行四边形?如不能,请说明理由;如能,求出此时∠A的度数.4.(2014春•太仓市期中)△ABC中E是AB的中点,CD平分∠ACB,AD⊥CD与点D,求证:DE=(BC﹣AC).5.(2013•常德)已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;(3)如图2,当∠BCE=45°时,求证:BM=ME.6.(2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.7.(2011•贵阳)[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为.(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.8.(2011•吉林)如图,四边形ABCD是平行四边形,点E 在BA 的延长线上,且BE=AD,点F在AD上,AF=AB,求证:△AEF≌△DFC.9.(2011•厦门)如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.(1)求证:四边形ABCD是平行四边形;(2)若AB=3cm,BC=5cm,AE=AB,点P从B点出发,以1cm/s的速度沿BC→CD→DA 运动至A点停止,则从运动开始经过多少时间,△BEP为等腰三角形?10.(2011•大田县质检)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A 同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).(1)当t为何值时,四边形PQDC是平行四边形;(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.平行四边形参考答案与试题解析1.(2014•祁阳县校级模拟)如图,在平行四边形ABCD中,点E、F是对角线AC上两点,且AE=CF.试说明:∠EBF=∠FDE.考点:平行四边形的性质;全等三角形的判定与性质.专题:证明题.分析:通过三角形全等得出DE=BF与BE=DF,即四边形EBFD是平行四边形,即可得出结论.解答:证明:在平行四边形ABCD中,则AD=BC,∠DAE=∠BCF,在△ADE和△CBF中,,∴△ADE≌△CBF(SAS),∴DE=BF,同理BE=DF,∴四边形EBFD是平行四边形,∴∠EBF=∠FDE.点评:本题主要考查平行四边形的性质及全等三角形的判定及性质问题,应熟练掌握.2.(2014•滕州市校级模拟)(1)如图1,点P是平行四边形ABCD对角线AC、BD的交点,若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4.请你说明理由;(2)变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD.若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,则S1、S2、S3、S4的关系为S1+S3=S2+S4;(3)变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,则S1、S2、S3、S4的关系为S1•S3=S2•S4.请你说明理由.考点:平行四边形的性质;三角形的面积.分析:(1)根据平行四边形的对角相互相平分与如果三角形等底等高面积相同,得解;(2)可以根据△ABD≌△CDB求得;(3)由△ABP中AP边上的高与△BCP中CP边上的高相同与△PAD中AP边上的高与△PCD中CP边上的高相同,可得即,即,所以,即S1•S3=S2•S4.解答:解:(1)∵四边形ABCD是平行四边形,∴AP=CP,又∵△ABP中AP边上的高与△BCP中CP边上的高相同,∴S△PAB=S△PBC,即S1=S2,同理可证S2=S3S3=S4,∴S1=S2=S3=S4;(2)S1+S3=S2+S4;(3)S1•S3=S2•S4;理由:∵△ABP中AP边上的高与△BCP中CP边上的高相同,∴即,∵△PAD中AP边上的高与△PCD中CP边上的高相同,∴即,∴,∴S1•S3=S2•S4.点评:此题考查了平行四边形的性质.解题的关键是注意:等底等高的三角形面积相等,等底的三角形的面积比等于高的比,等高的三角形面积的比等于底的比.3.(2014•博白县模拟)如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM 上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.(1)求证:BF=FD;(2)点D在运动过程中能否使得四边形ACFE为平行四边形?如不能,请说明理由;如能,求出此时∠A的度数.考点:平行四边形的判定;等腰三角形的判定.专题:动点型.分析:(1)欲证BF=FD,可证BF=EF,FD=EF.欲证BF=EF,在△BEF中,可证∠BEF=∠EBF,由于CE为直角△ABE斜边AB的中线,所以CB=CE,根据等边对等角,得出∠CEB=∠CBE,又∠CEF=∠CBF=90°,由等角的余角相等得出∠BEF=∠EBF;欲证FD=EF,在△FED中,可证∠FED=∠EDF,由于∠BEF+∠FED=90°,∠EBD+∠EDB=90°,而∠BEF=∠EBF,故∠FED=∠EDF.(2)假设点D在运动过程中能使四边形ACFE为平行四边形,则AC∥EF,AC=EF,由(1)知AC=CB=AB,EF=BF=BD,则BC=EF=BF,即BA=BD,∠A=45°.解答:解:(1)在Rt△AEB中,∵AC=BC,∴,∴CB=CE,∴∠CEB=∠CBE.∵∠CEF=∠CBF=90°,∴∠BEF=∠EBF,∴EF=BF.∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,∴∠FED=∠EDF,∵EF=FD.∴BF=FD.(2)能.理由如下:若四边形ACFE为平行四边形,则AC∥EF,AC=EF,∴BC=BF,∴BA=BD,∠A=45°.∴当∠A=45°时四边形ACFE为平行四边形.点评:本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.4.(2014春•太仓市期中)△ABC中E是AB的中点,CD平分∠ACB,AD⊥CD与点D,求证:DE=(BC﹣AC).考点:三角形中位线定理.专题:证明题.分析:延长AD交BC于F,证明AC=CF,DE是△ABF的中位线,即可求证.解答:解:延长AD交BC于F,说明AC=CF,DE是△ABF的中位线.∵CD平分∠ACB,AD⊥CD,∴∠ACD=∠BCD,CD是公共边,∠ADC=∠FDC=90°,∴△ADC≌△FDC(ASA)∴AC=CF,AD=FD又∵△ABC中E是AB的中点,∴DE是△ABF的中位线,∴DE=BF=(BC﹣CF)=(BC﹣AC).点评:此题主要考查三角形的中位线定理,综合利用了三角形全等的知识,证出DE是△ABF 的中位线是关键.5.(2013•常德)已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;(3)如图2,当∠BCE=45°时,求证:BM=ME.考点:三角形中位线定理;全等三角形的判定与性质;等腰直角三角形.专题:压轴题.分析:(1)证法一:如答图1a所示,延长AB交CF于点D,证明BM为△ADF的中位线即可;证法二:如答图1b所示,延长BM交EF于D,根据在同一平面内,垂直于同一直线的两直线互相平行可得AB∥EF,再根据两直线平行,内错角相等可得∠BAM=∠DFM,根据中点定义可得AM=MF,然后利用“角边角”证明△ABM和△FDM全等,再根据全等三角形对应边相等可得AB=DF,然后求出BE=DE,从而得到△BDE是等腰直角三角形,根据等腰直角三角形的性质求出∠EBM=45°,从而得到∠EBM=∠ECF,再根据同位角相等,两直线平行证明MB∥CF即可,(2)解法一:如答图2a所示,作辅助线,推出BM、ME是两条中位线;解法二:先求出BE的长,再根据全等三角形对应边相等可得BM=DM,根据等腰三角形三线合一的性质可得EM⊥BD,求出△BEM是等腰直角三角形,根据等腰直角三角形的性质求解即可;(3)证法一:如答图3a所示,作辅助线,推出BM、ME是两条中位线:BM=DF,ME=AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME;证法二:如答图3b所示,延长BM交CF于D,连接BE、DE,利用同旁内角互补,两直线平行求出AB∥CF,再根据两直线平行,内错角相等求出∠BAM=∠DFM,根据中点定义可得AM=MF,然后利用“角边角”证明△ABM和△FDM全等,再根据全等三角形对应边相等可得AB=DF,BM=DM,再根据“边角边”证明△BCE和△DFE 全等,根据全等三角形对应边相等可得BE=DE,全等三角形对应角相等可得∠BEC=∠DEF,然后求出∠BED=∠CEF=90°,再根据等腰直角三角形的性质证明即可.解答:(1)证法一:如答图1a,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,∴点B为线段AD的中点,又∵点M为线段AF的中点,∴BM为△ADF的中位线,∴BM∥CF.证法二:如答图1b,延长BM交EF于D,∵∠ABC=∠CEF=90°,∴AB⊥CE,EF⊥CE,∴AB∥EF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=MF,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,∵BE=CE﹣BC,DE=EF﹣DF,∴BE=DE,∴△BDE是等腰直角三角形,∴∠EBM=45°,∵在等腰直角△CEF中,∠ECF=45°,∴∠EBM=∠ECF,∴MB∥CF;(2)解法一:如答图2a所示,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,∴AB=BC=BD=a,AC=CD=a,∴点B为AD中点,又点M为AF中点,∴BM=DF.分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=GE=2a,CG=CF=a,∴点E为FG中点,又点M为AF中点,∴ME=AG.∵CG=CF=a,CA=CD=a,∴AG=DF=a,∴BM=ME=×a=a.解法二:如答图1b.∵CB=a,CE=2a,∴BE=CE﹣CB=2a﹣a=a,∵△ABM≌△FDM,∴BM=DM,又∵△BED是等腰直角三角形,∴△BEM是等腰直角三角形,∴BM=ME=BE=a;(3)证法一:如答图3a,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,AC=CD,∴点B为AD中点,又点M为AF中点,∴BM=DF.延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=EG,CF=CG,∴点E为FG中点,又点M为AF中点,∴ME=AG.在△ACG与△DCF中,,∴△ACG≌△DCF(SAS),∴DF=AG,∴BM=ME.证法二:如答图3b,延长BM交CF于D,连接BE、DE,∵∠BCE=45°,∴∠ACD=45°×2+45°=135°∴∠BAC+∠ACF=45°+135°=180°,∴AB∥CF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=FM,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,BM=DM,∴AB=BC=DF,在△BCE和△DFE中,,∴△BCE≌△DFE(SAS),∴BE=DE,∠BEC=∠DEF,∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°,∴△BDE是等腰直角三角形,又∵BM=DM,∴BM=ME=BD,故BM=ME.点评:本题考查了三角形中位线定理、全等三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出中位线、全等三角形和等腰直角三角形是解题的关键,也是本题的难点.6.(2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.考点:平行四边形的性质;全等三角形的性质;全等三角形的判定与性质;直角三角形斜边上的中线.分析:(1)由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,又由M、N分别是AD,BC的中点,即可利用SAS证得△ABN≌△CDM;(2)易求得∠MND=∠CND=∠2=30°,然后由含30°的直角三角形的性质求解即可求得答案.解答:(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠CDM,∵M、N分别是AD,BC的中点,∴BN=DM,∵在△ABN和△CDM中,,∴△ABN≌△CDM(SAS);(2)解:∵M是AD的中点,∠AND=90°,∴MN=MD=AD,∴∠1=∠MND,∵AD∥BC,∴∠1=∠CND,∵∠1=∠2,∴∠MND=∠CND=∠2,∴PN=PC,∵CE⊥MN,∴∠CEN=90°,∠END+∠CNP+∠2=180°﹣∠CEN=90°又∵∠END=∠CNP=∠2∴∠2=∠PNE=30°,∵PE=1,∴PN=2PE=2,∴CE=PC+PE=3,∴CN==2,∵∠MNC=60°,CN=MN=MD,∴△CNM是等边三角形,∵△ABN≌△CDM,∴AN=CM=2.点评:此题考查了平行四边形的性质、等边三角形的判定与性质、直角三角形的性质、全等三角形的判定与性质以及三角函数等性质.此题难度较大,注意掌握数形结合思想的应用.7.(2011•贵阳)[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.考点:平行四边形的性质;坐标与图形性质;矩形的性质.专题:几何综合题;压轴题.分析:(1)根据矩形的对角线互相平分及点E的坐标即可得出答案.(2)根据题意画出图形,然后可找到点D的坐标.解答:解:(1)M(,),即M(2,1.5).(2)如图所示:根据平行四边形的对角线互相平分可得:设D点的坐标为(x,y),∵以点A、B、C、D构成的四边形是平行四边形,①当AB为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴BC=,∴AD=,∵﹣1+3﹣1=1,2+1﹣4=﹣1,∴D点坐标为(1,﹣1),②当BC为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴AC=2,BD=2,D点坐标为(5,3).③当AC为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴AB=,CD=,D点坐标为:(﹣3,5),综上所述,符合要求的点有:D'(1,﹣1),D″(﹣3,5),D″′(5,3).点评:本题考查了平行四边形的性质及矩形的性质,关键是掌握已知两点求其中点坐标的方法.8.(2011•吉林)如图,四边形ABCD是平行四边形,点E 在BA 的延长线上,且BE=AD,点F在AD上,AF=AB,求证:△AEF≌△DFC.考点:平行四边形的性质;全等三角形的判定.专题:证明题.分析:根据平行四边形的性质结合题目条件可得出AE=DF及∠EAF=∠D,AF=CD,利用SAS即可证明两三角形的全等.解答:证明:∵四边形ABCD是平行四边形,∴AB=CD且AB∥CD,∴AF=CD,∠EAF=∠ADC,又∵AF=AB,∴AF=CD,AE=DF,在△AEF和△DFC中,∴△AEF≌△DFC.点评:此题考查了平行四边形的性质及全等三角形的证明,熟练掌握并运用平行四边形对边相等且平行的性质是解答本题的关键,另外要熟练掌握全等三角形的判定定理.9.(2011•厦门)如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.(1)求证:四边形ABCD是平行四边形;(2)若AB=3cm,BC=5cm,AE=AB,点P从B点出发,以1cm/s的速度沿BC→CD→DA 运动至A点停止,则从运动开始经过多少时间,△BEP为等腰三角形?考点:平行四边形的判定与性质;全等三角形的判定与性质;等腰三角形的性质;勾股定理;相似三角形的判定与性质.专题:几何综合题;压轴题.分析:(1)推出AD∥BC,AB∥DC,根据平行四边形的判定推出即可;(2)求出AC,当P在BC上时,①BP=EB=2,②BP=PE,作PM⊥AB于M,根据cosB求出BP,③BE=PE=2cm,作EN⊥BC于N,根据cosB求出BN;当P在CD 上不能得出等腰三角形;当P在AD上时,过P作PQ⊥BA于Q,证△QAP∽△ABC,推出PQ:AQ:AP=4:3:5,设PQ=4xcm,AQ=3xcm,在△EPN中,由勾股定理得出方程(3x+1)2+(4x)2=22,求出方程的解即可.解答:(1)证明:∵∠BAC=∠ACD=90°,∴AB∥CD,∵∠B=∠D,∠B+∠BAC+∠ACB=∠D+∠ACD+∠DAC=180°,∴∠DAC=∠ACB,∴AD∥BC,∴四边形ABCD是平行四边形.(2)解:∵∠BAC=90°,BC=5cm,AB=3cm,′由勾股定理得:AC=4cm,即AB、CD间的最短距离是4cm,∵AB=3cm,AE=AB,∴AE=1cm,BE=2cm,设经过ts时,△BEP是等腰三角形,当P在BC上时,①BP=EB=2cm,t=2时,△BEP是等腰三角形;②BP=PE,作PM⊥AB于M,∴BM=ME=BE=1cm∵cos∠ABC===,∴BP=cm,t=时,△BEP是等腰三角形;③BE=PE=2cm,作EN⊥BC于N,则BP=2BN,∴cosB==,∴=,BN=cm,∴BP=,∴t=时,△BEP是等腰三角形;当P在CD上不能得出等腰三角形,∵AB、CD间的最短距离是4cm,CA⊥AB,CA=4cm,当P在AD上时,只能BE=EP=2cm,过P作PQ⊥BA于Q,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠QAD=∠ABC,∵∠BAC=∠Q=90°,∴△QAP∽△ABC,∴PQ:AQ:AP=4:3:5,设PQ=4xcm,AQ=3xcm,在△EPQ中,由勾股定理得:(3x+1)2+(4x)2=22,∴x=,AP=5x=cm,∴t=5+5+3﹣=,答:从运动开始经过2s或s或s或s时,△BEP为等腰三角形.点评:本题主要考查对平行四边形的性质和判定,相似三角形的性质和判定.全等三角形的性质和判定,勾股定理,等腰三角形的性质,勾股定理等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.10.(2011•大田县质检)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A 同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).(1)当t为何值时,四边形PQDC是平行四边形;(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.考点:平行四边形的性质;等腰三角形的性质;直角梯形.专题:压轴题;动点型.分析:(1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC 即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间;(2)要使以C、D、Q、P为顶点的梯形面积等于60cm2,可以分为两种情况,点P、Q分别沿AD、BC运动或点P返回时,再利用梯形面积公式,即(QD+PC)×AB÷2=60,因为Q、P点的速度已知,AD、AB、BC的长度已知,用t可分别表示QD、BC的长,即可求得时间t;(3)使△PQD是等腰三角形,可分三种情况,即PQ=PD、PQ=QD、QD=PD;可利用等腰三角形及直角梯形的性质,分别用t表达等腰三角形的两腰长,再利用两腰相等即可求得时间t.解答:解:(1)∵四边形PQDC是平行四边形∴DQ=CP当P从B运动到C时,∵DQ=AD﹣AQ=16﹣t,CP=21﹣2t∴16﹣t=21﹣2t解得t=5当P从C运动到B时,∵DQ=AD﹣AQ=16﹣t,CP=2t﹣21∴16﹣t=2t﹣21,解得t=,∴当t=5或秒时,四边形PQDC是平行四边形;(2)若点P、Q分别沿AD、BC运动时,即解得t=9(秒)若点P返回时,CP=2(t﹣),则解得t=15(秒).故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;(3)当PQ=PD时作PH⊥AD于H,则HQ=HD∵QH=HD=QD=(16﹣t)由AH=BP得解得秒;当PQ=QD时QH=AH﹣AQ=BP﹣AQ=2t﹣t=t,QD=16﹣t,∵QD2=PQ2=t2+122∴(16﹣t)2=122+t2解得(秒);当QD=PD时DH=AD﹣AH=AD﹣BP=16﹣2t,∵QD2=PD2=PH2+HD2=122+(16﹣2t)2∴(16﹣t)2=122+(16﹣2t)2即3t2﹣32t+144=0∵△<0,∴方程无实根,综上可知,当秒或秒时,△PQD是等腰三角形.点评:本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.。
(完整版)平行四边形难题讲解
平行四边形综合题选讲四边形的知识是三角形的有关知识自然而然的延伸和扩展。
在整个初中平面几何中占有重要的地位。
此外四边形这一章蕴含着丰富的图形变化思想,是历年中考命题关注的焦点.所以,学好四边形这一章对于几何能力的提升和中考成绩的提高有着重要的意义。
本周结合四边形的综合题对有关四边形的知识进行梳理,对方法进行总结,提高分析问题解决问题的能力。
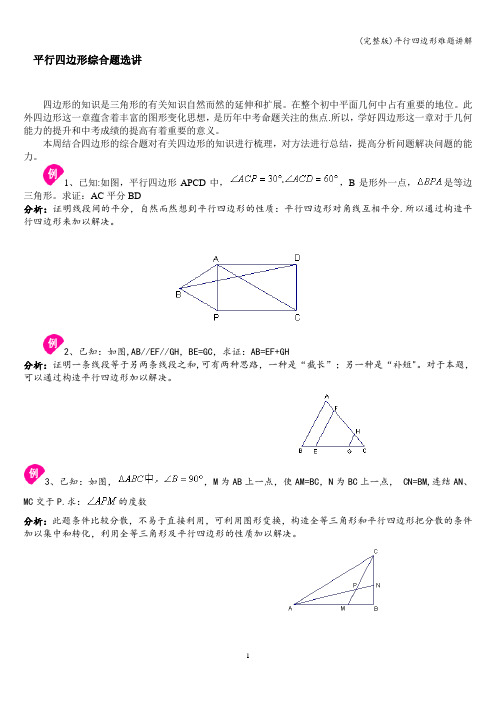
1、已知:如图,平行四边形APCD中,,B是形外一点,是等边三角形。
求证:AC平分BD分析:证明线段间的平分,自然而然想到平行四边形的性质:平行四边形对角线互相平分.所以通过构造平行四边形来加以解决。
2、已知:如图,AB//EF//GH,BE=GC,求证:AB=EF+GH分析:证明一条线段等于另两条线段之和,可有两种思路,一种是“截长”;另一种是“补短"。
对于本题,可以通过构造平行四边形加以解决。
3、已知:如图,,M为AB上一点,使AM=BC,N为BC上一点, CN=BM,连结AN、MC交于P.求:的度数分析:此题条件比较分散,不易于直接利用,可利用图形变换,构造全等三角形和平行四边形把分散的条件加以集中和转化,利用全等三角形及平行四边形的性质加以解决。
4、已知:如图求证:AF与EG互相平分分析:要证明AF与EG互相平分,只需证明四边形AGFE是平行四边形即可。
5、已知:如图,是等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为边作等边。
求证:(1)≌(2)四边形CDEF为平行四边形分析:证明≌相对比较简单,用SAS证明即可.要证明四边形CDEF为平行四边形,可证明四边形一组对边平行且相等即可。
1。
证明:连结PD交AC于M,边结BM平行四边形APCD在和中在2、证明:过F点作FD//BC交AB于D∴四边形DBEF是平行四边形∴∴∴∴∴∴3、解:过M点,作4、证明:5、证明:(1)∴≌(2)∵≌。
平行四边形难题讲解

平行四边形综合题选讲四边形的知识是三角形的有关知识自然而然的延伸和扩展。
在整个初中平面几何中占有重要的地位。
此外四边形这一章蕴含着丰富的图形变化思想,是历年中考命题关注的焦点。
所以,学好四边形这一章对于几何能力的提升和中考成绩的提高有着重要的意义。
本周结合四边形的综合题对有关四边形的知识进展梳理,对方法进展总结,提高分析问题解决问题的能力。
1、:如图,平行四边形APCD中,,B是形外一点,是等边三角形。
求证:AC平分BD分析:证明线段间的平分,自然而然想到平行四边形的性质:平行四边形对角线互相平分。
所以通过构造平行四边形来加以解决。
2、:如图,AB//EF//GH,BE=GC,求证:AB=EF+GH分析:证明一条线段等于另两条线段之和,可有两种思路,一种是“截长〞;另一种是“补短〞。
对于此题,可以通过构造平行四边形加以解决。
3、:如图,,M为AB上一点,使AM=BC,N为BC上一点, CN=BM,连结AN、MC交于P。
求:的度数分析:此题条件比拟分散,不易于直接利用,可利用图形变换,构造全等三角形和平行四边形把分散的条件加以集中和转化,利用全等三角形及平行四边形的性质加以解决。
4、:如图求证:AF与EG互相平分分析:要证明AF与EG互相平分,只需证明四边形AGFE是平行四边形即可。
5、:如图,是等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为边作等边。
求证:〔1〕≌〔2〕四边形CDEF为平行四边形分析:证明≌相比照拟简单,用SAS证明即可。
要证明四边形CDEF为平行四边形,可证明四边形一组对边平行且相等即可。
1. 证明:连结PD交AC于M,边结BM平行四边形APCD在和中在2、证明:过F点作FD//BC交AB于D∴四边形DBEF是平行四边形∴∴∴∴∴∴3、解:过M点,作4、证明:5、证明:〔1〕∴≌〔2〕∵≌。
四边形难题50道

1.如图,正方形ABCD中,AB= 3,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.(1)求证:DF+BE=EF;(2)则∠EFC的度数为度;(3)则△AEF的面积为.2.如图,将矩形ABCD沿对角线BD折叠,C点与E点重合,若AB=3,BC=9,则折叠后重叠部分(△BDF)的面积是.3.如图①E、F、G、H为正方形ABCD各边延长线上的点,CE=BC,DF=CD,AG=DA,BH=AB,若正方形ABCD的面积等于1.(1)则四边形EFGH的面积为;(2)如图②,图③,若将正方形ABCD变为矩形和菱形,其他条件仍然不变,则四边形EFGH的面积分别为,.(3)如图④,若将正方形ABCD变为任意四边形,其他条件仍然不变,请你猜想四边形EFGH的面积为,并说明理由.4.(1)如图1矩形ABCD中,AB=8,AD=5,M为AB中点,则S阴影=,S矩形ABCD=.(2)如图2,在直角梯形ABCD中,AD⊥AB,BC⊥BA,AB=8,BC=4,AD=5,M为AB中点,S阴影= ,S梯形ABCD=.(3)如图3在平行四边形ABCD中,∠A=120°,∠B=60°,AB=8,AB的中点为M,AD=5,S阴影=,S四边形ABCD=.解决问题:如图4有一四边形菜地ABCD,其中AD∥BC,在AB的中点M处有一口井,现要将这块地等分给两家,且都能用井浇地,请你设计方案并说明理由.5.已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,则AE=.6.(1998•台州)如图,矩形ABCD的长、宽分别为5和3,将顶点C折过来,使它落在AB上的C′点(DE为折痕),那么,阴影部分的面积是.7.如图,将矩形ABCD折叠,使A与C重合,折痕为EF,若AB=3,AD=4,则折痕EF=.8.如图所示,在平行四边形ABCD中,∠ABC的角平分线分别交AC,AD于E,F点,EG⊥BC,若BA=6,AC=8,AD=10.(1)则FD为;(2)则△BEC的面积为.9.在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,(1)AC与EF互相平分吗?;(2)若∠B=60°,BE=2CE,AB=4,则四边形AECF的周长为,面积为.10.如图,等边△ABC以2m/s的速度沿直线l向菱形DCEF移动,直到AB与CD重合,其中∠DCE=60°,设x s时,三角形与菱形重叠部分的面积为y m2.(1)则y与x的关系表达式是.(2)当x=0.5时,y=;当x=1时,y=.(3)当重叠部分的面积是菱形面积一半时,三角形移动了s.11.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠DBC=45°,点F 在AB边上,点E在BC边上,将△BFE沿折痕EF翻折,使点B落在点D处.若AD=1,BC=5.则:(1)BD的长为;(2)∠C的正切值是.12.(2005•新疆)如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E 为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈cm.(结果精确到0.1cm)13.(2010•吉林)如图,在等腰梯形ABCD中,AD∥BC,AE⊥BC于点E.EF⊥BC于点F.AD=2cm,BC=6cm,AE=4cm.点P、Q分别在线段AE、DF上,顺次连接B、P、Q、C,线段BP、PQ、QC、CB所围成的封闭图形记为M,若点P在线段AE上运动时,点Q也随之在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FG=ycm.解答下列问题:(1)直接写出当x=3时y的值是;(2)y与x之间的函数关系式是,并写出自变量x的取值范围;(3)当x取时,图形M成为等腰梯形;(4)线段PQ在运动过程中所能扫过的区域的面积为cm2.14.(2001•黑龙江)如图,在平行四边形ABCD中,AB=4cm,BC=1cm,E 是CD边上一动点,AE、BC的延长线交于点F.设DE=x(cm),BF=y(cm).(1)y(cm)与x(cm)之间的函数关系式为,自变量x的取值范围是;(2)画出此函数的图象.15.如图,正方形纸片ABCD的边BC上有一点E,AE=8cm,若把纸片对折,使点A与点E重合,则纸片折痕的长是cm.16.如图,在梯形ABCD中,AD∥BC,AD=1,BC=4,AC=3,BD=4,则梯形ABCD的面积为17.(2010•北京)阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD中,AD=8cm,AB=6cm.现有一动点P按下列方式在矩形内运动:它从A点出发,沿着AB边夹角为45°的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45°的方向作直线运动,并且它一直按照这种方式不停地运动,即当P点碰到BC边,沿着BC边夹角为45°的方向作直线运动,当P点碰到CD边,再沿着与CD边夹角为45°的方向作直线运动,…,如图1所示,问P点第一次与D点重合前与边相碰几次,P点第一次与D点重合时所经过的路径的总长是多少.小贝的思考是这样开始的:如图2,将矩形ABCD沿直线CD折迭,得到矩形A1B1CD,由轴对称的知识,发现P2P3=P2E,P1A=P1E.请你参考小贝的思路解决下列问题:(1)P点第一次与D点重合前与边相碰次;P点从A点出发到第一次与D点重合时所经过的路径的总长是cm;(2)近一步探究:改变矩形ABCD中AD、AB的长,且满足AD>AB,动点P从A点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上.若P点第一次与B点重合前与边相碰7次,则AB:AD的值为.18.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD上,AH=2,连接CF.(1)当四边形EFGH为正方形时,则DG的长为;(2)当△FCG的面积为1时,则DG的长为(3)当△FCG的面积最小时,则DG的长为.19.如图①,平面直角坐标系中的▱AOBC,∠AOB=60°,OA=8cm,OB=10cm,点P从A点出发沿AC 方向,以1cm/s速度向C点运动;点Q从B点同时出发沿BO方向,以3cm/s的速度向原点O运动.其中一个动点到达端点时,另一个动点也随之停止运动.(1)则A点的坐标是,C点的坐标是;(2)如图②,从运动开始,经过s,四边形AOQP是平行四边形;(3)在点P、Q运动的过程中,四边形AOQP成为直角梯形.此时t=s(若能,求出运动时间;若不能,填不存在).(图③供解题时用)20.用同样大小的平行四边形按下列图案中的规律摆放:第1个图案有平行四边形3个,第2个图案有平行四边形11个,第3个图案有平行四边形21个,…(1)第4个图案中平行四边形的个数是;(2)第n个(n是大于1的正整数)图案中平行四边形的个数是.21.(2010•汕头)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G、∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.(1)求证:△EGB是等腰三角形;(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小度时,四边形ACDE成为以ED为底的梯形(如图(2)).则此梯形的高为.22.如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.连接DE,若BE=4CE,CD=2,则DE=.23.(2005•无锡)已知正方形ABCD的边长AB=k(k是正整数),正△PAE的顶点P在正方形内,顶点E在边AB上,且AE=1.将△PAE在正方形内按图1中所示的方式,沿着正方形的边AB、BC、CD、DA、AB、…连续地翻转n次,使顶点P第一次回到原来的起始位置.(1)如果我们把正方形ABCD的边展开在一直线上,那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动.图2是k=1时,△PAE沿正方形的边连续翻转过程的展开示意图.请你探索:若k=1,则△PAE沿正方形的边连续翻转的次数n=时,顶点P第一次回到原来的起始位置.(2)若k=2,则n=时,顶点P第一次回到原来的起始位置;若k=3,则n=时,顶点P第一次回到原来的起始位置.(3)请你猜测:使顶点P第一次回到原来的起始位置的n值与k之间的关系是(请用含k的代数式表示n).24.如图,以平行四边形ABCD的对称中心为坐标原点,建立平面直角坐标系,A点坐标为(-4,3),且AD与x轴平行,AD=6,则B点、C点、D点坐标分别是、、25.如图,在等腰梯形ABCD中,AB∥DC,AB=9cm,CD=3cm,AD=6cm.点P从点A出发,以2cm/s 的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒.(1)当DQ=AP时,四边形APQD是平形四边形,则t=s;(2)当PQ将梯形ABCD分成一个平形四边形和一个等边三角形时,则t=s;(3)当t=s时,四边形PBCQ的面积是梯形ABCD面积的一半.26.(2010•河源)如图,△ABC中,点P是边AC上的一个动点,过P作直线MN∥BC,设MN交∠BCA 的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:PE=PF;(2)当点P在边AC上运动时,四边形AECF可能是矩形吗?说明理由;(3)若在AC边上存在点P,使四边形AECF是正方形,且APBC=2.此时∠A的度数为度.27.如图,正方形ABCD中,E、F分别在边BC、CD上,∠EAF=45°,BE=2,CF=3,则正方形的边长为.28.已知:如图,点P是平行四边形ABCD的边DC上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求证:AP⊥PB(2)如果AD=5,AP=8,那么△APB的面积是.29.如图,有两条笔直的公路(BD和EF,其宽度不计)从一块矩形的土地ABCD中穿过,已知:EF是BD的垂直平分线,有BD=400m,EF=300m,则这块矩形土地ABCD的面积为m2.30.如图,在梯形ABCD,AD∥BC,AB=CD,上底AD=227),(1)则C坐标为,D坐标;(2)将梯形ABCD向左平移2个单位长度,所得四边形的四个顶点的坐标为:A,B,C,D;(3)梯形ABCD的面积为.31.(2004•三明)动手操作:将一张边长为10cm的正方形纸片ABCD,按如图去折叠,使D点与AB的中点E重合,度量出有关线段的长度(精确到1cm)后,算出图中阴影部分四边形EFGH的面积为cm2.32.如图,在梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,E是CD的中点,AB=2AD=4,则BE=.33.如图,直角梯形的两底为AD=17cm,BC=25cm,斜腰AB=10cm,AB的垂直平分线EF交DC的延长线于F,则EF的长为cm.34.如图,四边形ABCD为直角梯形,∠C=90°,CD=10cm,AD=30 cm,BC=36 cm,点P从D出发,以2 cm/s的速度向A运动,点Q从B同时出发,以4 cm/s的速度向C运动.其中一个点到达端点时,另一个动点也随之停止运动.(1)从运动开始,经过s,四边形PQBA为平行四边形;(2)从运动开始,经过s,四边形PQBA为等腰梯形.35.试画出如图所示的图案,则阴影部分的面积为.36.如图,在正方形ABCD中,对角线AC与BD相交于点O,AF平分∠BAC,交BD于点F.(1)求证:AB-OF=12AC;(2)点A1、点C1分别同时从A、C两点出发,以相同的速度运动相同的时间后同时停止,如图,A1F1平分∠BA1C1,交BD于点F1,过点F1作F1E⊥A1C1,垂足为E,请猜想EF1,AB与12A1C1三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当A1E1=6,C1E1=4时,则BD的长为.37.如图,等腰梯形ABCD中,AD∥BC,AB=CD,AD=10cm,BC=30cm,动点P从点A开始沿AD边向点以每秒1cm的速度运动,同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(1)当t=s时,四边形ABQP是平行四边形;(2)当t=s时,四边形ABQP能成为等腰梯形.38.如图,已知AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB=43,则BC=.39.如图所示的直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).四边形ABCD的面积是.40.已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF=1cm,CE=2cm,BE,DF 相交于点G,则四边形CEGF的面积为cm2.41.(2006•邵阳)如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.(1)则EF=;(2)则梯形ABCE的面积是.42.如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,则FC= cm,EF=43.(2002•青海)已知:如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在D点处,则D点坐标是(,).44.如图:在△ABC中,点D、E、F分别在边AB、BC、CA上,已知AB=12,AC=8,四边形ADEF是菱形,则菱形ADEF的边长为.45.已知:AC是矩形ABCD的对角线,延长CB至E,使CE=CA,F是AE的中点,连接DF、CF分别交AB于G、H点,若∠E=60°,且AE=8时,则梯形AECD的面积是.46.现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE 折叠,点B落在四边形AECD内,记为点B′.则线段B′C=47.(2003•随州)已知:如图,梯形ABCD中,AD∥BC,DC⊥BC.沿对角线BD折叠,点A恰好落在DC上,记为A′.若AD=4,BC=6,则A′B=.48.如图,在直角梯形ABCD中.AB∥CD,AB=12cm,CD=6cm,DA=3cm,∠D=∠A=90°,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D 开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t表示移动的时间(单位:秒),并且0≤t≤3.(1)当t=s时,△QAP为等腰三角形;(2)不论t取何值,四边形QAPC的面积是一个定值,则这个定值为cm2;(3)当t=s时,△PBC是直角三角形.49.如图,要设计一个等腰梯形的花坛,花坛上底长12米,下底长18米,高8米.(1)梯形的中位线的长是米;(2)在梯形两腰中点连线(虚线)处有一条横向通道,上下底之间有两条纵向通道,各条通道的宽度均为x米.①若通道的总面积等于42平方米,通道的宽是米;②按要求通道的宽不能超过1米,且修建三条通道应付的工资合计为2533元,当通道的宽度为米时,所建花坛应付的总工资最少,最少工资是元.50.如图,在矩形ABCD中,AB=6,BC=12.动点M、N分别从点B、D同时出发,以每秒1个单位长度的速度运动.其中点M沿BC向终点C运动,点N沿DA向终点A运动,过点N作NP⊥BC于点Q,交AC于点P,连接MP.设动点运动的时间为t秒.(1)当t=6时,PM=;(2)t=时,△PMC的面积等于矩形ABCD面积的19.。
特殊平行四边形难题综合训练含参考答案

第五章特殊平行四边形难题综合训练1、正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为()A.10 B.12 C.14 D.162、如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形的边长为.第1题第2题第3题第4题3、如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1、l4上,该正方形的面积是平方单位.4、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是.5、如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.6、如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=()A.2 B.3 C.222D.3第5题第6题第7题第8题7、如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为()A 、(2,2-)B 、(2,2-)C 、(3,3-)D 、(2,2--)8、如图,正方形ABCD 中,AB =3,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连接AG ,CF .下列结论:①点G 是BC 中点;②FG =FC ;③S △FGC =9/10.其中正确的是( ) A .①② B .①③ C .②③ D .①②③9、如图,在正方形ABCD 中,点O 为对角线AC 的中点,过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ,且∠EOF =90°,BO 、EF 交于点P .则下列结论中:(1)图形中全等的三角形只有两对;(2)正方形ABCD 的面积等于四边形OEBF 面积的4倍;(3)BE +BF =20A ;(4)AE 2+CF 2=20P ?OB .正确的结论有( )个. A .1 B .2 C .3 D .410、如图,在矩形ABCD 中,由8个面积均为1的小正方形组成的L 型模板如图放置,则矩形ABCD 的周长为.11、在边长为6的菱形ABCD 中,动点M 从点A 出发,沿A →B →C 向终点C 运动,连接DM 交AC 于点N .(1)如图11-1,当点M 在AB 边上时,连接BN .求证:ABN ADN △≌△; (2)如图11-2,若∠ABC =90°,记点M 运动所经过的路程为x (6≤x ≤12).试问:x 为何值时,△ADN 为等腰三角形.12、如图所示,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接BE DG ,. (1)求证:BE DG =.(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.CM BN AD(图11-2)CB M AND(图11-1)E FGDA B13、请阅读,完成证明和填空.数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:(1)如图13-1,正三角形ABC 中,在AB AC 、边上分别取点M N 、,使BM AN =,连接BN CM 、,发现BN CM =,且60NOC ∠=°.请证明:60NOC ∠=°.(2)如图13-2,正方形ABCD 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN DM 、,那么AN =,且DON ∠=度.(3)如图13-3,正五边形ABCDE 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN EM 、,那么AN =,且EON ∠=度.(4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论. 请大胆猜测,用一句话概括你的发现:.14、ABC △是等边三角形,点D 是射线BC 上的一个动点(点D 不与点B C 、重合),ADE △是以AD 为边的等边三角形,过点E 作BC 的平行线,分别交射线AB AC 、于点F G 、,连接BE .(1)如图(a )所示,当点D 在线段BC 上时.①求证:AEB ADC △≌△;②探究四边形BCGE 是怎样特殊的四边形?并说明理由;(2)如图(b )所示,当点D 在BC 的延长线上时,直接写出(1)中的两个结论是否成立?(3)在(2)的情况下,当点D 运动到什么位置时,四边形BCGE 是菱形?并说明理由.A A ABB C C CDDO OOM M M NNN E 图13-1图13-2图13-3…15、如图,ABC △中,点O 是边AC 上一个动点,过O 作直线MN BC ∥,设MN 交BCA∠的平分线于点E ,交BCA ∠的外角平分线于点F .(1)探究:线段OE 与OF 的数量关系并加以证明;(2)当点O 在边AC 上运动时,四边形BCFE 会是菱形吗?若是,请证明,若不是,则说明理由;(3)当点O 运动到何处,且ABC △满足什么条件时,四边形AECF 是正方形? 16、如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1与EF 的长;17、在120ABC =°,将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A 1△11C 分别交AC BC 、于D F 、两点.(1)如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系?并证明你的结论; (2)如图2,当α30=°时,试判断四边形1BC DA 的形状,并说明理由18、在菱形ABCD 中,对角线AC 与BD 相交于点O ,56AB AC ==,.过点D 作DE AC ∥交BC 的延长线于点E . (1)求BDE △的周长;(2)点P 为线段BC 上的点,连接PO 并延长交AD 于点Q .求证:BP DQ =.A G CD BFE 图 ADCBE G图AM EAD BE CF ADBECFAQ D E BP CO19、如图,在平面直角坐标系中,矩形AOBC 在第一象限内,E 是边OB 上的动点(不包括端点),作∠AEF =90?,使EF 交矩形的外角平分线BF 于点F ,设C (m ,n ). (1)若m =n 时,如图,求证:EF =AE ;(2)若m ≠n 时,如图,试问边OB 上是否还存在点E ,使得EF =AE ?若存在,请求出点E 的坐标;若不存在,请说明理由.(3)若m =tn (t >1)时,试探究点E 在边OB 的何处时,使得EF =(t +1)AE 成立?并求出点E 的坐标.20、形恰.(1)画出拼成的矩形的简图; (2)求x y的值.21、如图所示,在矩形ABCD 中,1220AB AC ==,,两条对角线相交于点O .以OB 、OC 为邻边作第1个平行四边形1OBB C ;对角线相交于点1A ;再以11A B 、1A C 为邻边作第2个平行四边形111A B C C ,对角线相交于点1O ;再以11O B 、11O C 为邻边作第3个平行四边形1121O B B C ……依次类推. (1)求矩形ABCD 的面积;(2)求第1个平行四边形11OBB C 、第2个平行四边形111A B C C 和第6个平行四边形的面积.22、如图(22),直线l 的解析式为4y x =-+,它与x 轴、y 轴分别相交于A B 、两点.平行于直线l 的直线m 从原点O 出发,沿x 轴的正方形以每秒1个单位长度的速度运动,它与x 轴、y 轴分别相交于M N 、两点,设运动时间为t 秒(04t <≤). (1)求A B 、两点的坐标;(2)用含t 的代数式表示MON △的面积1S ;(3)以MN 为对角线作矩形OMPN ,记MPN △和OAB △重合部分的面积为2S , ①当2t <≤4时,试探究2S 与t 之间的函数关系式; ②在直线m 的运动过程中,当t 为何值时,2S 为OAB △面积的516? 23、如图15,在四边形ABCD 中,E 为AB 上一点,△ADE 和△BCE 都是等边三角形,AB 、BC 、CD 、DA 的中点分别为P 、Q 、M 、N ,试判断四边形PQMN 为怎样的四边形,并证明你的结论.24、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:A 1A 2B 2C 2 C 1 B 1O 1 DABC OO M A PN yl mxB OM AP Nyl m xB E P F 图22(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.25、如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于E ,BF DE ∥,交AG 于F .求证:AF BF EF =+.参考答案1、D2、1043、5或94、2010052355+ 5、156、C 7、A 8、B 9、C 10、5811、(1)证明:∵四边形ABCD 是菱形∴AB =AD ,∠1=∠2又∵AN =AN ∴△ABN ≌△ADN (2)解:∵∠ABC =90°,∴菱形ABCD 是正方形此时,∠CAD =45°. 下面分三种情形:Ⅰ)若ND =NA ,则∠ADN =∠NAD =45°.此时,点M 恰好与点B 重合,得x =6; Ⅱ)若DN =DA ,则∠DNA =∠DAN =45°.此时,点M 恰好与点C 重合,得x =12; Ⅲ)若AN =AD =6,则∠1=∠2,由AD ∥BC ,得∠1=∠4,又∠2=∠3,∴∠3=∠4,从而CM =CN ,易求AC =62,∴CM =CN =AC -AN =62-6, 故x =12-CM =12-(62-6)=18-62 综上所述:当x =6或12或18-62时,△ADN是等腰三角形12、(1)因为ABCD 是正方形,所以BC =CD 。
利用平行四边形性质巧解生活难题

方法技巧栏目 可以安排在总复习使用利用平行四边形的性质 巧解生活难题平行四边形是特殊的四边形,在实际生活中着广泛的应用,对于生活中的一些实际问题,同学们可以巧借平行四边形的相关性质加以解决。
下面撷取几个生活实例说明如下.一、比较线路长短图1是某区部分街道示意图,其中CE 垂直平分AF ,BC=DA ,BC ∥DF ,FD//BC .从B 站乘车到E 站只有两条路线有直接到达的公交车,路线1是B -D -A -E ,路线2是B -C -F -E ,请比较两条路线路程的长短,并说明理由.【分析】本题是一道设计比较新颖的实际问题,要比较两条线段的长短,首先要从实际问题构建数学模型。
实际上线路1,可用线段BD 、DA 、AE 的和来表示;线路2可用线段BC 、CF 、FE 的和来表示,本题就可以通过比较BD+DA+AE和BC+CF+FE 的大小即可.解:两条线路相等.理由:因为DE 垂直平分AF ,所以DF=DA ,FE=AE.又BC ∥DF ,FD//BC ,所以四边形FDBC 是平行四边形,所以BD=CF ,CB=DF=DA , 所以BD+DA+AE=CF+BC+FE ,所以线路1与线路2的路程相等.二、扩大池塘的面积如图2,一口呈四边形的池塘,在它的四周A 、B 、C 、D 处各有一棵桃树,如果想把池塘扩大一倍,而保住四棵桃数不动,并要求扩建的池塘为平行四边形的形状,请你判断这一想法能否实现?【分析】由于四棵桃树分别在四边形的顶点,所以要想把池塘改成平行四边形,切面积扩大一倍,则四棵桃树应在平行四边形的边上,且每条边上都有一棵桃树.为此只要过四边形的顶点A 、C 两点作对角线BD 的平行线,过顶点B 、D 作对角线AC 的平行线即可.解:如图1,分别过点A 、C 作BD 的平行线,过点B 、D 作AC 的平行线,四条线分别相交于点E 、F 、G 、H 。
由作图可知四边形AEBO 、BFCO 、CGDO 、DHAO 均为平行四边形,且△ABO 、△BOC 、△COD 、△DOA 的面积分别为平行四边形AEBO 、BFCO 、CGDO 、DHAO 面积的一半,所以平行四边形EFGH 为四边形ABCD 面积的一半.三、计算影子的面积如图3,阳光透过长方形玻璃投射到地面上,地面上出现了一个明亮的四边形,小刚用量角器量出了一条对角线与一边垂直,,用直尺量出了四边形的四条边分别是30cm ,50cm ,30cm ,50cm ,小刚说用这些数据就能计算出四边形的面积,你知道小刚是如何计算的吗?这样计算的根据是什么?【分析】根据小明测量的数据可知这个四边形的对边相等,由此可确定该四边形为平行四边形,可画出如图所示的图形,根据已知可得AB ⊥AC ,AB=30cm ,BC =50cm ,根据勾股定理可以计算出△ABC 的面积和△ACD 的面积,所以计算四边形ABCD 的面积. 解:如图4,根据已知条件可四边形ABCD 是平行四边形,所以AB//CD ,因为AB ⊥AC ,所图 1 图2 图4图3以CD ⊥AC ,所以△ACD 为直角三角形.在Rt △ABC 中,因为AB2+AC2=BC2,所以AC2=502-302=402,所以AC =40,所以△ABC 的面积为21×40×30=600(cm 2).同样△ACD 的面积为600cm 2,所以四边形ABCD 的面积为1200cm 2. 四、等分地块的面积 如图5,ABCD 是老王家的一块平行四边形田地,P 为水井,现要把这块田平均分给两个儿子,为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由.【分析】 我们说只要满足所分的两块地面积相等,且都与水井相邻就可以。
平行四边形超级难题学霸挑战2

2018年05月22日y冬夏y的初中数学组卷一.选择题(共9小题)1.如图所示,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为()A.1cm2B.C.2cm2D.3cm22.如图,▱ABCD中,点O是对角线BD上的任意一点,过点O作MN∥AB,PQ∥BC,则下列结论中正确的是()A.S△MOD =S△NOBB.S四边形BNOP=S四边形DMOQC.S△ABD =2S四边形AMOPD.S四边形AMOP=S四边形CNOQ3.如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB∥DC,EF∥DA∥CB,则有()A.S1=S4B.S1+S4=S2+S3C.S1S4=S2S3D.都不对4.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=,则△ABC的周长是()A.28 B.32 C.18 D.255.根据如图所示的三个图所表示的规律,依次下去第n个图中平行四边形的个数是()A.3n B.3n(n+1)C.6n D.6n(n+1)6.在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为()A.2 B .C .D.157.AD是△ABC中BC边上的中线,若AB=2,AC=4,则AD的取值范围是()A.AD<6 B.AD>2 C.2<AD<6 D.1<AD <38.如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,FG=3,线段DG,EF的交点为O,当线段FG在线段BC上移动时,三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是()A.15 B.12 C.9 D.69.△ABC 与平行四边形DEFG 如图放置,点D ,G 分别在边AB ,AC 上,点E ,F 在边BC 上.已知BE=DE ,CF=FG ,则∠A 的度数( )A .等于80°B .等于90°C .等于100°D .条件不足,无法判断二.选择题(共7小题)10.如图,△ABC 中,BD 平分∠ABC ,AD ⊥BD 于D ,F 为AC 中点,AB=5,BC=7,则DF= .11.在▱ABCD 中,两对角线交于点O ,点E ,F ,G ,H 分别是AO ,BO ,CO ,DO 的中点,那么以图中的点为顶点的平行四边形共有 个.12.在△ABC 中,BC=10,B 1、C 1分别是图①中AB 、AC 的中点,在图②中,B 1,B 2,C 1,C 2分别是AB ,AC 的三等分点,在图③中B 1,B 2…B 9;C 1C 2…C 9分别是AB 、AC 的10等分点,则B 1C 1+B 2C 2+…+B 9C 9的值是 .13.已知四边形ABCD 中,AC 交BD 于点O ,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:(1)如果再加上条件“BC=AD”,那么四边形ABCD 一定是平行四边形;(2)如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD 一定是平行四边形;(3)如果再加上条件“AO=OC”,那么四边形ABCD 一定是平行四边形;(4)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD 一定是平行四边形 其中正确的说法是 .14.已知△ABC 周长为1,连接△ABC 三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2010个三角形的周长为 .15.如图,对面积为1的平行四边形ABCD 逐次进行以下操作:第一次操作,分别延长AB ,BC ,CD ,DA 至点A 1,B 1,C 1,D 1,使得A 1B=2AB ,B 1C=2BC ,C 1D=2CD ,D 1A=2AD ,顺次连接A 1,B 1,C 1,D 1,得到平行四边形A 1B 1C 1D 1,记其面积为S 1;第二次操作,分别延长A 1B 1,B 1C 1,C 1D 1、D 1A 1至点A 2,B 2,C 2,D 2,使得A 2B 1=2A 1B 1,B 2C 1=2B 1C 1,C 2D 1=2C 1D 1,D 2A 1=2A 1D 1,顺次连接A 2,B 2,C 2,D 2记其面积为S 2;…;按此规律继续下去,可得到平行四边形A 5B 5C 5D 5,则其面积S 5= .16.如图,平行四边形ABCD中,E是AB上一点,DE与AC交于点F,且S△AEF =6cm2,S△DCF=54cm2,则S平行四边形ABCD= cm2.三.选择题(共23小题)17.如图,平行四边形ABCD中,M是BC的中点,AM=9,BD=12,AD=10,求平行四边形ABCD的面积.18.如图,AB∥CD,∠ACB=90°,E是AB的中点,CE=CD,DE和AC相交于点F.求证:(1)DE⊥AC;(2)∠ACD=∠ACE.19.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;问题二:如图3,在△ABC中,AC>AB,D点在AC 上,AB=CD,E、F分别是BC、AD的中点,连接EF 并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.20.已知:如图,AD∥BC,AC⊥BD于O,AD+BC=5,AC=3,AE ⊥BC于E.求AE的长.21.已知:如图,在△ABC中,AD平分∠BAC,CN ⊥AD于E交AB于N,F是AC的中点,FE的延长线交BC于M.试判断BM=MC的正确性.如果正确,请给出证明过程;若不正确,请说明理由.22.已知:如图在▱ABCD中,AC,BD交于O,CE ⊥BD于E,AF⊥BD于F,连接AE,CF.(1)判断四边形AFCE的形状;(2)证明你的结论.23.已知:如图,四边形ABCD中,对角线AC、BD 交于O,AD∥BC,AC=4,BO=,AB=5,BC=3.(1)判断四边形ABCD的形状并说明理由;(2)求四边形ABCD的边AB上的高.24.已知:如图(1),AC是▱ABCD的对角线,直线MN过点D,且MN∥AC,分别交BA、BC的延长线于点M、N,我们容易得到MD=DN.探究:(1)如图(2),若将MN向左平移,MN分别交AD、CD于P、Q,在直线MN上相等的线段有(只写一组);(2)如图(3),若将MN向右平移,MN分别交AD、CD的延长线于P、Q,在直线MN上相等的线段有(只写一组).请在探究(1)、(2)中任选一结论加以证明.25.如图,在△ABC中,AB=6cm,BC=8cm.线段BC 所在直线(即动点E)以每秒2cm的速度沿BA方向运动,并始终保持与原位置平行,运动过程中与AB的交点为E,与AC的交点为D.(1)经过多少秒后ED是△ABC的中位线此时ED 的长为多少(2)经过多少秒后ED的长为2cm26.如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.(1)△ACD和△CBF全等吗请说明理由;(2)判断四边形CDEF的形状,并说明理由;(3)当点D在线段BC上移动到何处时,∠DEF=30°.27.如图,在▱ABCD中,E,F分别是AD、BC上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N,求证:MN∥AD,MN=AD.28.如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.29.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;(2)判断四边形ABDF是怎样的四边形,并说明理由;(3)若AB=6,BD=2DC,求四边形ABEF的面积.30.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类直接写出构成图形的类型和相应的条件.31.如图,在平行四边形ABCD中,点E是边AD 的中点,BE的延长线与CD的延长线相交于点F.(1)求证:△ABE≌△DFE;(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.32.在△HBC中,∠B=∠C,在边HC上取点D,在边BH上取点A,使HD=BA,连接AD.求证:AD ≥BC.33.如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.(1)求证:PA=PC.(2)若AD=12,AB=15,∠DAB=60°,求四边形ABCD 的面积.34.(1)如图,如果四边形ABCD是任意四边形(不是梯形或平行四边形)的纸片,E、F、G、H分别是AB、BC、CD、AD的中点.依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH.请判断四边形纸片EFGH的形状,并说明理由.(2)你能将上述四边形纸片ABCD经过恰当地剪切后拼合(无重叠无缝隙)成一个平行四边形纸片吗请在图上画出对应的示意图.(3)如图,E,F,G,H分别是四边形ABCD各边的中点,若△AEH,△BEF,△CFG,△DGH的面积分别为S1,S2,S3,S4,且S1=2,S3=5,则四边形ABCD是面积是.(不要求说明理由)35.操作1:如图1,一三角形纸片ABC,分别取AB、AC的中点D、E,连接DE,沿DE将纸片剪开,并将其中的△ADE纸片绕点E旋转180°后可拼合(无重叠无缝隙)成平行四边形纸片BCFD.操作2:如图2,一平行四边形纸片ABCD,E、F、G、H分别是AB、BC、CD、AD边的中点,沿EF剪开并将其中的△BFE纸片绕点E旋转180°到△AF1E位置;沿HG剪开并将其中的△DGH纸片绕点H旋转180°到△AG1H位置;沿FG剪开并将△CFG纸片放置于△AF1G1的位置,此时四张纸片恰好拼合(无重叠无缝隙)成四边形FF1G1G.则四边形FF1G1G 的形状是.36.如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.求证:(1)DE∥BC ;(2).37.已知:如图,点P是平行四边形ABCD的边DC 上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求证:AP⊥PB;(2)如果AD=5,AP=8,求△APB的面积.38.在平行四边形ABCD中,AE,CF分别平分∠BAD 和∠BCD,(1)AC与EF互相平分吗试说明理由.(2)若∠B=60°,BE=2CE,AB=4,求四边形AECF 的周长和面积.39.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.(1)求证:CD∥AB;(2)求证:△BDE≌△ACE;(3)若O为AB中点,求证:OF=BE.四.解答题(共1小题)40.如图所示,在▱ABCD中,AB>BC,∠A与∠D 的平分线交于点E,∠B与∠C的平分线交于F点,连接EF.(1)延长DE交AB于M点,则图中与线段EM一定相等的线段有哪几条说明理由;(不再另外添加字母和辅助线)(2)EF、BC与AB之间有怎样的数量关系为什么(3)如果将条件“AB>BC”改为“AB<BC”,其它条件不变,EF 、BC与AB的关系又如何请画出图形并证明你的结论.2018年05月22日y冬夏y的初中数学组卷参考答案与试题解析一.选择题(共9小题)1.如图所示,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为()A.1cm2B.C.2cm2D.3cm2【解答】解:连接MN,作AF⊥BC于F.∵AB=AC,∴BF=CF=BC=×8=4,在Rt△ABF中,AF==,∵M、N分别是AB,AC的中点,∴MN是中位线,即平分三角形的高且MN=8÷2=4,∴NM=BC=DE,∴△MNO≌△EDO,O也是ME,ND的中点,∴阴影三角形的高是AF÷2=÷2=,∴S阴影=4×÷2=.故选B.2.如图,▱ABCD中,点O是对角线BD上的任意一点,过点O作MN∥AB,PQ∥BC,则下列结论中正确的是()A.S△MOD=S△NOBB.S四边形BNOP=S四边形DMOQC.S△ABD=2S四边形AMOPD.S四边形AMOP=S四边形CNOQ【解答】解:∵平行四边形中,MN∥AB,PQ∥BC,∴S△BOP=S△BON,S△MOD=S△QOD,S(△BOP+▱APOM+△MOD)=S(△BON+▱CQON+△QOD).∴S▱APOM=S▱CQON∴A、B、C说法都不正确,故选D.3.如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB ∥DC,EF∥DA∥CB,则有()A.S1=S4B.S1+S4=S2+S3C.S1S4=S2S3D.都不对【解答】解:设红、紫四边形的高相等为h1,黄、白四边形的高相等,高为h2,则S1=DE•h1,S2=AF•h2,S3=EC•h1,S4=FB•h2,因为DE=AF,EC=FB,故A错误;S1+S4=DE•h1+FB•h2=AF•h1+FB•h2,S2+S3=AF•h2+EC•h1=AF•h2+FB•h1,故B错误;S1S4=DE•h1•FB•h2=AF•h1•FB•h2,S2S3=AF•h2•EC•h1=AF•h2•FB•h1,所以S1S4=S2S3,故C正确;故选:C.4.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=,则△ABC的周长是()A.28 B.32 C.18 D.25【解答】解:延长线段BN交AC于E.∵AN平分∠BAC,∴∠BAN=∠EAN,AN=AN,∠ANB=∠ANE=90°,∴△ABN≌△AEN,∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25,故选:D.5.根据如图所示的三个图所表示的规律,依次下去第n个图中平行四边形的个数是()A.3n B.3n(n+1)C.6n D.6n(n+1)【解答】解:从图中我们发现(1)中有6个平行四边形,6=1×6,(2)中有18个平行四边形,18=(1+2)×6,(3)中有36个平行四边形,36=(1+2+3)×6,∴第n个中有3n(n+1)个平行四边形.故选:B.6.在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为()A.2 B .C .D.15【解答】解:设平行四边形ABCD的面积是S,设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y.则S=5a•3x=3b•5y.即ax=by=.△AA4D2与△B2CC4全等,B2C=BC=b,B2C边上的高是•5y=4y.则△AA4D2和△B2CC4的面积是2by=.同理△D2C4D与△A4BB2的面积是.则四边形A4B2C4D2的面积是S ﹣﹣﹣﹣=,即=1,解得S=.故选:C.7.AD是△ABC中BC边上的中线,若AB=2,AC=4,则AD的取值范围是()A.AD<6 B.AD>2 C.2<AD<6 D.1<AD <3【解答】解:延长AD至E,使AD=DE,连接BE、CE,∵AD=DE∵AD是△ABC中BC边上的中线∴BD=DC∴四边形ABEC为平行四边形∴BE=AC=4∴在△ABE中:BE﹣AB<AE<BE+AB即2<2AD<6∴1<AD<3故选:D.8.如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,FG=3,线段DG,EF的交点为O,当线段FG在线段BC上移动时,三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是()A.15 B.12 C.9 D.6【解答】解:如图:连接DE,过A向BC作垂线,H为垂足,∵△ABC中,D、E分别是AB、AC的中点,∴DE,AH分别是△ABC的中位线和高,BH=CH=BC=×6=3,∵AB=AC=5,BC=6,由勾股定理得AH===4,∴S△ADE=BC •=×3×=3,设△DOE的高为a,△FOG的高为b,则a+b==2,∴S△DOE+S△FOG=DE•a+FG•b=×3(a+b)=×3×2=3,∴三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是S△ADE+S△DOE+S△FOG=3+3=6.故选:D.9.△ABC与平行四边形DEFG如图放置,点D,G 分别在边AB,AC上,点E,F在边BC上.已知BE=DE,CF=FG,则∠A的度数()A.等于80°B.等于90°C.等于100°D.条件不足,无法判断【解答】解:∵BE=DE∴∠B=∠BDE∵四边形DEFG是平行四边形∴∠ADG=∠B∴∠ADG=∠BDE同理:∠AGD=∠CGF∵∠AGD+∠CGF+∠DGF=180°,∠DGF+∠GDE=180°∴∠AGD+∠CGF=∠GDE∵∠ADG+∠BDE+∠GDE=180°∴∠ADG+∠BDE+∠AGD+∠CGF=180°∴∠ADG+∠AGD=90°∴∠B+∠C=90°∴∠A=90°故选:B.二.选择题(共7小题)10.如图,△ABC中,BD平分∠ABC,AD⊥BD于D,F为AC中点,AB=5,BC=7,则DF= 1 .【解答】解:延长AD交BC于E∵AD⊥BD,BD平分∠ABC∴△ABD≌△EBD∴BE=AB=5又∵BC=7∴EC=BC﹣BE=7﹣5=2∵DF为△AEC的中位线∴DF=EC=×2=1.故答案为1.11.在▱ABCD中,两对角线交于点O,点E,F,G,H分别是AO,BO,CO,DO的中点,那么以图中的点为顶点的平行四边形共有 4 个.【解答】解:根据对角线互相平分的四边形是平行四边形,可判定四边形EFGH是平行四边形;根据SAS可分别证明:△AHD≌△CFB,△AFB≌△CGD,可得,AH=CF,AF=CH,所以AHCF是平行四边形;同理可得BGDE是平行四边形,则以图中的点为顶点的平行四边形是四边形EFGH、ABCD、AHCF、BGDE,故有4个.故答案为4.12.在△ABC中,BC=10,B1、C1分别是图①中AB、AC的中点,在图②中,B1,B2,C1,C2分别是AB,AC的三等分点,在图③中B1,B2…B9;C1C2…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是45 .【解答】解:当B1、C1是AB、AC的中点时,B1C1=BC;当B1,B2,C1,C2分别是AB,AC的三等分点时,B1C1+B2C2=BC+BC;…当B1,B2,C1,…,Cn分别是AB,AC的n等分点时,B1C1+B2C2+…+Bn﹣1Bn﹣1=BC+BC+…+BC=BC=5(n﹣1);当n=10时,5(n﹣1)=45;故B1C1+B2C2+…+B9C9的值是45.故答案为45.13.已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD 为平行四边形,给出以下四种说法:(1)如果再加上条件“BC=AD”,那么四边形ABCD 一定是平行四边形;(2)如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;(3)如果再加上条件“AO=OC”,那么四边形ABCD 一定是平行四边形;(4)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形其中正确的说法是(2)(3).【解答】解:其中正确的说法是(2)、(3).因为再加上条件“∠BAD=∠BCD”,即可求得另一组对角相等,那么四边形ABCD一定是平行四边形;如果再加上条件“AO=OC”,即可证明△AOB≌△COD,所以,AB=DC,那么四边形ABCD一定是平行四边形.故答案为:(2)(3).14.已知△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2010个三角形的周长为.【解答】解:∵连接△ABC三边中点构成第二个三角形,∴新三角形的三边与原三角形的三边的比值为1:2,∴它们相似,且相似比为1:2,同理:第三个三角形与第二个三角形的相似比为1:2,即第三个三角形与第一个三角形的相似比为:1:22,以此类推:第2010个三角形与原三角形的相似比为1:22009,∵△ABC周长为1,∴第2010个三角形的周长为.故答案为:.15.如图,对面积为1的平行四边形ABCD逐次进行以下操作:第一次操作,分别延长AB,BC,CD,DA至点A1,B1,C1,D1,使得A1B=2AB,B1C=2BC,C1D=2CD,D1A=2AD,顺次连接A1,B1,C1,D1,得到平行四边形A1B1C1D1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1D1、D1A1至点A2,B2,C2,D2,使得A2B1=2A1B1,B2C1=2B1C1,C2D1=2C1D1,D2A1=2A1D1,顺次连接A2,B2,C2,D2记其面积为S2;…;按此规律继续下去,可得到平行四边形A5B5C5D5,则其面积S5= 135.【解答】解:如图,连接BD,B1D,∵B1C=2BC,∴△B1DC的面积是△DBC的面积的两倍,又∵C1D=2DC,△B1C1D的面积是△B1DC的两倍,∴△B1C1C的面积是△DBC的面积的6倍,也就是平行四边形ABCD的面积的三倍,以此类推,其余三个三角形的面积都是平行四边形面积的三倍,∴新的平行四边形的面积是原来平行四边形面积的13倍,按此规律继续下去,那么平行四边形A5B5C5D5的面积是135.故填空答案135.16.如图,平行四边形ABCD中,E是AB上一点,DE与AC交于点F,且S△AEF =6cm2,S△DCF=54cm2,则S平行四边形ABCD= 144 cm2.【解答】解:设S△AEF 的高为h1,S△DCF的高为h2,平行四边形的高为h ∵平行四边形ABCD ∴△AEF∽△CDF∵S△AEF =6cm2,S△DCF=54cm2∴AE:DC=AE:AB=1:3,h 1:h2=1:3∴AB=3AE∵h=h1+h2∴h=4h1∵S△AEF=AE•h1=6∴AE•h1=12∴S平行四边形ABCD =AB•h=3AE•4h1=12AE•h1=144cm2三.选择题(共23小题)17.如图,平行四边形ABCD中,M是BC的中点,AM=9,BD=12,AD=10,求平行四边形ABCD的面积.【解答】解:过D作DE∥AM交BC的延长线于E.∵四边形ABCD是平行四边形,∴AD∥BC,∵DE∥AM,∴四边形AMED是平行四边形,∴AD=ME,AM=DE,∵M 是BC的中点,AD=10,∴MB==5,∴BE=BM+ME=15,∵四边形AMED是平行四边形,∴AM=DE=9,∵BD=12,∴92+122=152,即BD2+DE2=BE2,∴△DBE为直角三角形.∴BE边上的高为=,∴平行四边形ABCD的面积为10×=72.18.如图,AB∥CD,∠ACB=90°,E是AB的中点,CE=CD,DE和AC相交于点F.求证:(1)DE⊥AC;(2)∠ACD=∠ACE.【解答】证明:(1)直角三角形ACB中,∵CE是斜边AB的中线,∴CE=AE=BE=CD,又∵AB∥CD,∴BCDE为平行四边形,∴BC∥DE,∵AC⊥BC,∴DE⊥AC.(2)∵CD∥AB,∴∠ACD=∠CAE.由(1)知EC=EA,∴∠A=∠ACE.∴∠ACD=∠ACE.19.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;问题二:如图3,在△ABC中,AC>AB,D点在AC 上,AB=CD,E、F分别是BC、AD的中点,连接EF 并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.【解答】解:(1)取AC中点P,连接PF,PE,可知PE=,PE∥AB,∴∠PEF=∠ANF,同理PF=,PF∥CD,∴∠PFE=∠CME,又PE=PF,∴∠PFE=∠PEF,∴∠OMN=∠ONM,∴△OMN为等腰三角形.(2)判断出△AGD是直角三角形.证明:如图连接BD,取BD的中点H,连接HF、HE,∵F是AD的中点,∴HF∥AB,HF=AB,同理,HE∥CD,HE=CD,∵AB=CD∴HF=HE,∵∠EFC=60°,∴∠HEF=60°,∴∠HEF=∠HFE=60°,∴△EHF是等边三角形,∴∠3=∠EFC=∠AFG=60°,∴△AGF是等边三角形.∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°∴∠AGD=90°即△AGD是直角三角形.20.已知:如图,AD ∥BC ,AC ⊥BD 于O ,AD+BC=5,AC=3,AE ⊥BC 于E .求AE 的长.【解答】解:过点A 作AF ∥DB 交CB 的延长线于点F ,(1分) ∵AD ∥BC ,∴四边形AFBD 是平行四边形. ∴FB=AD . ∵AD+BC=5,∴FC=FB+BC=AD+BC=5.(2分) ∵AC ⊥BD , ∴FA ⊥AC .(3分)在△FAC 中,∠FAC=90°,AC=3,FC=5, ∴AF=4.(4分) ∵AE ⊥BC 于E , ∴AF •AC=FC •AE . ∴AE=.(5分)21.已知:如图,在△ABC 中,AD 平分∠BAC ,CN ⊥AD 于E 交AB 于N ,F 是AC 的中点,FE 的延长线交BC 于M .试判断BM=MC 的正确性.如果正确,请给出证明过程;若不正确,请说明理由.【解答】解:结论BM=MC 正确.证明过程如下: ∵AD 平分∠BAC , ∴∠NAE=∠CAE . ∵CE ⊥AD ,∴∠AEN=∠AEC=90°. ∵AE=AE , ∴△ANE ≌△ACE . ∴NE=CE .∵F 为AC 的中点, ∴AF=CF . ∴EF ∥AB . ∵AF=CF , ∴BM=MC .22.已知:如图在▱ABCD 中,AC ,BD 交于O ,CE ⊥BD 于E ,AF ⊥BD 于F ,连接AE ,CF . (1)判断四边形AFCE 的形状;(2)证明你的结论.【解答】解:(1)四边形AFCE 是平行四边形.(2)∵在△ABE和△CDF中∠ABE=∠CDF,∠AEB=∠CFD=90°,AB=CD,∴△ABE≌△CDF.∴BE=DF.又∵ABCD是平行四边形,∴OA=OC,OB=OD.∴OE=OF.∴AECF是平行四边形.23.已知:如图,四边形ABCD中,对角线AC、BD 交于O,AD∥BC,AC=4,BO=,AB=5,BC=3.(1)判断四边形ABCD的形状并说明理由;(2)求四边形ABCD的边AB上的高.【解答】解:(1)四边形ABCD为平行四边形.∵AC=4,BC=3,AB=5,∴AC2+BC2=AB2∴∠ACB=90°在Rt△OBC中,OB=,BC=3,∴.∵AC=4,∴OA=2,∴OA=OC.∵AD∥BC,∴∠DAO=∠BCO.又∵∠AOD=∠COB,∴△AOD≌△COB.∴BC=AD.∵BC∥AD,∴四边形ABCD为平行四边形.(2)设AB边上的高为h,∵S平行四边形ABCD=BC•AC=AB•h,∴3×4=5h,∴h=.即AB边上的高为.24.已知:如图(1),AC是▱ABCD的对角线,直线MN过点D,且MN∥AC,分别交BA、BC的延长线于点M、N,我们容易得到MD=DN.探究:(1)如图(2),若将MN向左平移,MN分别交AD、CD于P、Q,在直线MN上相等的线段有MP=NQ (只写一组);(2)如图(3),若将MN向右平移,MN分别交AD、CD的延长线于P、Q,在直线MN上相等的线段有MP=NQ (只写一组).请在探究(1)、(2)中任选一结论加以证明.【解答】解:探究(1):如图(2),在直线MN上相等的线段有MP=NQ.探究(2):如图(3),在直线MN上相等的线段有MP=NQ.选择探究(1):如图(2),证明MP=NQ.理由:如图(2)∵四边形ABCD是平行四边形,∴AD∥BC;又MN∥AC,∵四边形ACNP是平行四边形,∴NP=AC.同理可证MQ=AC,∴NP=MQ∴PQ+QN=MP+PQ,∴MP=NQ.25.如图,在△ABC中,AB=6cm,BC=8cm.线段BC 所在直线(即动点E)以每秒2cm的速度沿BA方向运动,并始终保持与原位置平行,运动过程中与AB的交点为E,与AC的交点为D.(1)经过多少秒后ED是△ABC的中位线此时ED 的长为多少(2)经过多少秒后ED的长为2cm【解答】解:(1)ED是△ABC的中位线即E、D分别为AB、AC的中点,则ED=BC=4cm,∴BE=AB=3cm,∵动点速度为每秒2cm,∴时间为t==;(2)ED的长为2cm,即ED=BC,∴AE=AB=,∴BE=6cm﹣=故时间t==秒,答:(1)经过秒后ED是△ABC的中位线,此时ED 的长为4cm,(2)经过秒后ED的长为2cm.26.如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.(1)△ACD和△CBF全等吗请说明理由;(2)判断四边形CDEF的形状,并说明理由;(3)当点D在线段BC上移动到何处时,∠DEF=30°.【解答】解:(1)△ACD≌△CBF证:∵△ABC为等边三角形∴AC=BC∠ACD=∠B=60°∵CD=BF∴△ACD≌△CBF(SAS)(2)四边形CDEF为平行四边形∵△ACD≌△CBF∴∠DAC=∠BCF,CF=AD∵△AED是等边三角形∴AD=DE∴CF=DE①∵∠ACG+∠BCF=60°∴∠ACG+∠DAC=60°∴∠AGC=180°﹣(∠ACG+∠DAC)=120°∴∠DGF=∠AGC=120°∵△AED是等边三角形∴∠ADE=60°∴∠DGF+∠ADE=180°∴CF∥DE②综合①②可得四边形CDEF是平行四边形.(3)∵AC=BC,当点D是BC中点时,BF=CD=BC=AB,∴CF为AB边上的中线,CF平分∠ACB,∴∠DEF=∠ACB=30°,∴当点D是BC中点时,∠DEF=30°.27.如图,在▱ABCD中,E,F分别是AD、BC上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N,求证:MN∥AD,MN=AD.【解答】证明:连接EF,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵DE=CF,∴AE=BF.∴四边形ABFE和四边形CDEF都是平行四边形.∴BM=ME,CN=NE.∴MN是△BCE的中位线.∴MN∥AD,MN=AD.28.如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.【解答】解:连接BD,取BD的中点G,连接MG,NG∵G、N、M分别是BD、BC、AD的中点,∴GN是△ADB的AB对的中位线,GM是△BCD的CD 对的中位线∴NG∥AB,NG=AB,GM∥CD,GM=CD∴∠1=∠GNM,∠2=∠GME又∵AB=CD∴MG=NG∴∠GNM=∠GME∴∠1=∠2.29.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;(2)判断四边形ABDF是怎样的四边形,并说明理由;(3)若AB=6,BD=2DC,求四边形ABEF的面积.【解答】解:(1)(选证一)△BDE≌△FEC.证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60度.∵CD=CE,∴△EDC是等边三角形.∴DE=EC,∠CDE=∠DEC=60°∴∠BDE=∠FEC=120度.又∵EF=AE,∴BD=FE.∴△BDE≌△FEC.(选证二)△BCE≌△FDC.证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60度.又∵CD=CE,∴△EDC是等边三角形.∴∠BCE=∠FDC=60°,DE=CE.∵EF=AE,∴EF+DE=AE+CE.∴FD=AC=BC.∴△BCE≌△FDC.(选证三)△ABE≌△ACF.证明:∵△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=60度.∵CD=CE,∴△EDC是等边三角形.∴∠AEF=∠CED=60度.∵EF=AE,△AEF是等边三角形.∴AE=AF,∠EAF=60度.∴△ABE≌△ACF.(2)四边形ABDF是平行四边形.理由:由(1)知,△ABC、△EDC、△AEF都是等边三角形.∴∠CDE=∠ABC=∠EFA=60度.∴AB∥DF,BD∥AF.∴四边形ABDF是平行四边形.(3)由(2)知,四边形ABDF是平行四边形.∴EF∥AB,EF≠AB.∴四边形ABEF是梯形.过E作EG⊥AB于G,则EG=.∴S四边形ABEF=EG•(AB+EF)=(6+4)=10.30.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类直接写出构成图形的类型和相应的条件.【解答】(1)证明:∵△ABE、△BCF为等边三角形,∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.∴∠CBA=∠FBE.∴△ABC≌△EBF.∴EF=AC.又∵△ADC为等边三角形,∴CD=AD=AC.∴EF=AD.同理可得AE=DF.∴四边形AEFD是平行四边形.(2)解:构成的图形有四类,一类是菱形,一类是线段.当图形为菱形时,∠BAC≠60°(或A与F不重合、△ABC不为正三角形);当图形为线段时,∠BAC=60°(或A与F重合、△ABC为正三角形).31.如图,在平行四边形ABCD中,点E是边AD 的中点,BE的延长线与CD的延长线相交于点F.(1)求证:△ABE≌△DFE;(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CF.∴∠1=∠2,∠3=∠4∵E是AD的中点,∴AE=DE.∴△ABE≌△DFE.(2)解:四边形ABDF是平行四边形.∵△ABE≌△DFE,∴AB=DF又∵AB∥DF∴四边形ABDF是平行四边形.32.在△HBC中,∠B=∠C,在边HC上取点D,在边BH上取点A,使HD=BA,连接AD.求证:AD ≥BC.【解答】(1)证明:如图,当A、D为BH、CH的中点时,AD=BC.(2)证明:如图,当A,D不是BH、CH的中点时.∵∠B=∠C,∴BH=HC.∵DH=AB,∴AH=CD.过B作BE∥AD,过D作DE∥BH,BE与DE交于E点,连接EC∴四边形ABED为平行四边形,∠EDC=∠H.∴DE=AB,BE=AD.∴DH=DE.又∵CD=AH∴△ADH≌△CED.∴CE=AD.∴BE=CE.在△BEC中,BE+EC>BC,∴2AD>BC.∴AD >BC.综合(1),(2)可得,AD ≥BC.33.如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.(1)求证:PA=PC.(2)若AD=12,AB=15,∠DAB=60°,求四边形ABCD 的面积.【解答】(1)证明:在PA和PC的延长线上分别取点M、N,使AM=AE,CN=CF.∵AP+AE=CP+CF,∴PN=PM.∵PE=PF,∴四边形EMFN是平行四边形.∴ME=FN,∠EMA=∠CNF.又∵∠AME=∠AEM,∠CNF=∠CFN,∴△EAM≌△FCN.∴AM=CN.∵PM=PN,∴PA=PC.(2)解:∵PA=PC,EP=PF,∴四边形AFCE为平行四边形.∴AE∥CF.∵∠PED=∠PFB,∠EPD=∠FPB,EP=PF,∴△PED≌△PFB.∴DP=PB.由(1)知PA=PC,∴四边形ABCD为平行四边形.∵AB=15,AD=12,∠DAB=60°,∴四边形ABCD的面积为90.34.(1)如图,如果四边形ABCD是任意四边形(不是梯形或平行四边形)的纸片,E、F、G、H分别是AB、BC、CD、AD的中点.依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH.请判断四边形纸片EFGH的形状,并说明理由.(2)你能将上述四边形纸片ABCD经过恰当地剪切后拼合(无重叠无缝隙)成一个平行四边形纸片吗请在图上画出对应的示意图.(3)如图,E,F,G,H分别是四边形ABCD各边的中点,若△AEH,△BEF,△CFG,△DGH的面积分别为S1,S2,S3,S4,且S1=2,S3=5,则四边形ABCD是面积是28 .(不要求说明理由)【解答】解:(1)四边形EFGH的形状是平行四边形.连接AC.在△ABC中,因为E、F分别是AB、BC 的中点,即EF是△ABC的中位线,所以EF∥AC,EF=AC.在△ADC中,同样可以得到HG∥AC,HG=AC.所以四边形EFGH是平行四边形.(2)如图,(3)四边形ABCD是面积是28.35.操作1:如图1,一三角形纸片ABC,分别取AB、AC的中点D、E,连接DE,沿DE将纸片剪开,并将其中的△ADE纸片绕点E旋转180°后可拼合(无重叠无缝隙)成平行四边形纸片BCFD.操作2:如图2,一平行四边形纸片ABCD,E、F、G、H分别是AB、BC、CD、AD边的中点,沿EF剪开并将其中的△BFE纸片绕点E旋转180°到△AF1E位置;沿HG剪开并将其中的△DGH纸片绕点H旋转180°到△AG1H位置;沿FG剪开并将△CFG纸片放置于△AF1G1的位置,此时四张纸片恰好拼合(无重叠无缝隙)成四边形FF1G1G.则四边形FF1G1G的形状是平行四边形.【解答】解:操作2:四边形FF1G1G的形状是平行四边形连接AC.在△ABC中,因为E、F分别是AB、BC的中点,即EF 是△ABC的中位线,所以EF∥AC,EF=AC.在△ADC中,同样可以得到HG∥AC,HG=AC.又△BFE纸片绕点E旋转180°到△AF1E位置所以EF1∥AC,EF1=AC同理HG1∥AC,HG1=AC∴FF1∥GG1且FF1=GG1四边形FF1G1G是平行四边形.36.如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.求证:(1)DE∥BC ;(2).【解答】证明:(1)延长AD、AE,交BC于F、G;∵BE⊥AG,∴∠AEB=∠BEG=90°;∵BE平分∠ABG,∴∠ABE=∠GBE;∴∠BAE=∠BGE;∴△ABG是等腰三角形;∴AB=BG,E是AG中点;同理可得:AC=CF,D是AF中点;∴DE是△AFG的中位线;∴DE∥BC.(2)由(1)知DE是△AFG的中位线,∴DE=FG;∵FG=BG+CF﹣BC,且AB=BG,AC=CF;∴FG=AB+AC﹣BC,即DE=(AB+AC﹣BC).37.已知:如图,点P是平行四边形ABCD的边DC 上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求证:AP⊥PB;(2)如果AD=5,AP=8,求△APB的面积.【解答】(1)证明:∵AP和BP分别平分∠DAB和∠CBA,∴.又∵四边形ABCD是平行四边形,∴AD∥BC.∴∠PAB+∠PBA=90°.∴∠APB=180°﹣90°=90°.从而AP⊥PB.(2)解:∵四边形ABCD是平行四边形,∴BC=AD=5.又∵AP和BP分别平分∠DAB和∠CBA,∴∠PAB=∠PAD=∠DPA.∴DP=AD=5.同理PC=BC=5.∴AB=DC=DP+PC=10.∴在Rt△APB中,应用勾股定理得:.∴△APB 的面积是.38.在平行四边形ABCD中,AE,CF分别平分∠BAD 和∠BCD,(1)AC与EF互相平分吗试说明理由.(2)若∠B=60°,BE=2CE,AB=4,求四边形AECF 的周长和面积.【解答】解:(1)AC,EF互相平分.证明如下:∵四边形ABCD为平行四边形∴∠BAD=∠BCD,AD∥BC,∴∠DAE=∠BEA又∵AE,CF分别平分∠BAD,和∠BCD.∴∠BAE=∠DAE=,∠BCF=∠DCF=,∵∠BAD=∠BCD,∴∠DAE=∠BCF。
中考数学平行四边形(大题培优 易错 难题)附详细答案

中考数学平行四边形(大题培优易错难题)附详细答案一、平行四边形1.已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.【答案】(1)见解析;(2)存在,理由见解析;(3)不成立.理由如下见解析.【解析】试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD 是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;(2)由∠BMC=90°,易证得△ABM∽△DMC,设AM=x,根据相似三角形的对应边成比例,即可得方程:x2﹣bx+a2=0,由b>2a,a>0,b>0,即可判定△>0,即可确定方程有两个不相等的实数根,且两根均大于零,符合题意;(3)由(2),当b<2a,a>0,b>0,判定方程x2﹣bx+a2=0的根的情况,即可求得答案.试题解析:(1)∵b=2a,点M是AD的中点,∴AB=AM=MD=DC=a,又∵在矩形ABCD中,∠A=∠D=90°,∴∠AMB=∠DMC=45°,∴∠BMC=90°.(2)存在,理由:若∠BMC=90°,则∠AMB+∠DMC=90°,又∵∠AMB+∠ABM=90°,∴∠ABM=∠DMC,又∵∠A=∠D=90°,∴△ABM∽△DMC,∴AM ABCD DM=,设AM=x,则x aa b x =-,整理得:x 2﹣bx+a 2=0,∵b >2a ,a >0,b >0,∴△=b 2﹣4a 2>0,∴方程有两个不相等的实数根,且两根均大于零,符合题意,∴当b >2a 时,存在∠BMC=90°,(3)不成立.理由:若∠BMC=90°,由(2)可知x 2﹣bx+a 2=0,∵b <2a ,a >0,b >0,∴△=b 2﹣4a 2<0,∴方程没有实数根,∴当b <2a 时,不存在∠BMC=90°,即(2)中的结论不成立.考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质2.问题发现:(1)如图①,点P 为平行四边形ABCD 内一点,请过点P 画一条直线l ,使其同时平分平行四边形ABCD 的面积和周长.问题探究:(2)如图②,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴正半轴上,点B 坐标为(8,6).已知点(6,7)P 为矩形外一点,请过点P 画一条同时平分矩形OABC 面积和周长的直线l ,说明理由并求出直线l ,说明理由并求出直线l 被矩形ABCD 截得线段的长度.问题解决:(3)如图③,在平面直角坐标系xOy 中,矩形OABCD 的边OA 、OD 分别在x 轴、y 轴正半轴上,DC x ∥轴,AB y ∥轴,且8OA OD ==,2AB CD ==,点(1052,1052)P --为五边形内一点.请问:是否存在过点P 的直线l ,分别与边OA 与BC 交于点E 、F ,且同时平分五边形OABCD 的面积和周长?若存在,请求出点E 和点F 的坐标:若不存在,请说明理由.【答案】(1)作图见解析;(2)25y x =-,353)(0,0)E ,(5,5)F .【解析】试题分析:(1)连接AC 、BD 交于点O ,作直线PO ,直线PO 将平行四边形ABCD 的面积和周长分别相等的两部分.(2)连接AC ,BD 交于点O ',过O '、P 点的直线将矩形ABCD 的面积和周长分为分别相等的两部分.(3)存在,直线y x =平分五边形OABCD 面积、周长.试题解析:(1)作图如下:(2)∵(6,7)P ,(4,3)O ',∴设:6PO y kx =+',67{43k b k b +=+=,2{5k b ==-, ∴25y x =-,交x 轴于5,02N ⎛⎫ ⎪⎝⎭, 交BC 于11,62M ⎛⎫ ⎪⎝⎭, 2211563522MN ⎛⎫=+-= ⎪⎝⎭.(3)存在,直线y x =平分五边形OABCD 面积、周长.∵(1052,102)P --在直线y x =上,∴连OP 交OA 、BC 于点E 、F ,设:BC y kx b =+,(8,2)(2,8)B C ,82{28k b k +=+=,1{10k b =-=, ∴直线:10BC y x =-+,联立10{y x y x =-+=,得55x y =⎧⎨=⎩, ∴(0,0)E ,(5,5)F .3.如图,△ABC 是等边三角形,AB=6cm ,D 为边AB 中点.动点P 、Q 在边AB 上同时从点D 出发,点P 沿D→A 以1cm/s 的速度向终点A 运动.点Q 沿D→B→D 以2cm/s 的速度运动,回到点D 停止.以PQ 为边在AB 上方作等边三角形PQN .将△PQN 绕QN 的中点旋转180°得到△MNQ .设四边形PQMN 与△ABC 重叠部分图形的面积为S (cm 2),点P 运动的时间为t (s )(0<t <3).(1)当点N 落在边BC 上时,求t 的值.(2)当点N 到点A 、B 的距离相等时,求t 的值.(3)当点Q 沿D→B 运动时,求S 与t 之间的函数表达式.(4)设四边形PQMN 的边MN 、MQ 与边BC 的交点分别是E 、F ,直接写出四边形PEMF 与四边形PQMN 的面积比为2:3时t 的值.【答案】(1)(2)2(3)S=S 菱形PQMN =2S △PNQ =t 2;(4)t=1或【解析】 试题分析:(1)由题意知:当点N 落在边BC 上时,点Q 与点B 重合,此时DQ=3; (2)当点N 到点A 、B 的距离相等时,点N 在边AB 的中线上,此时PD=DQ ;(3)当0≤t≤时,四边形PQMN 与△ABC 重叠部分图形为四边形PQMN ;当≤t≤时,四边形PQMN 与△ABC 重叠部分图形为五边形PQFEN .(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题4.如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.求证:AF=BF+EF.【答案】详见解析.【解析】【分析】由四边形ABCD为正方形,可得出∠BAD为90°,AB=AD,进而得到∠BAG与∠EAD互余,又DE垂直于AG,得到∠EAD与∠ADE互余,根据同角的余角相等可得出∠ADE=∠BAF,利用AAS可得出△ABF≌△DAE;利用全等三角的对应边相等可得出BF=AE,由AF-AE=EF,等量代换可得证.∵ABCD 是正方形,∴AD=AB ,∠BAD=90°∵DE ⊥AG ,∴∠DEG=∠AED=90°∴∠ADE+∠DAE=90°又∵∠BAF+∠DAE=∠BAD=90°,∴∠ADE=∠BAF .∵BF ∥DE ,∴∠AFB=∠DEG=∠AED .在△ABF 与△DAE 中,AFB AED ADE BAF AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABF ≌△DAE (AAS ).∴BF=AE .∵AF=AE+EF ,∴AF=BF+EF .点睛:此题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,熟练掌握判定与性质是解本题的关键.5.菱形ABCD 中、∠BAD =120°,点O 为射线CA 上的动点,作射线OM 与直线BC 相交于点E ,将射线OM 绕点O 逆时针旋转60°,得到射线ON ,射线ON 与直线CD 相交于点F . (1)如图①,点O 与点A 重合时,点E ,F 分别在线段BC ,CD 上,请直接写出CE ,CF ,CA 三条段段之间的数量关系;(2)如图②,点O 在CA 的延长线上,且OA =13AC ,E ,F 分别在线段BC 的延长线和线段CD 的延长线上,请写出CE ,CF ,CA 三条线段之间的数量关系,并说明理由; (3)点O 在线段AC 上,若AB =6,BO =27,当CF =1时,请直接写出BE 的长.【答案】(1)CA=CE+CF .(2)CF-CE=43AC .(3)BE 的值为3或5或1. 【解析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,∴CA=CE+CF.(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵OB=27,∴OH=22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∵OC=4,CF=1,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.6.现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.(1)求AE、EF的位置关系;(2)求线段B′C的长,并求△B′EC的面积.【答案】(1)见解析;(2)S△B′EC=108 25.【解析】【分析】(1)由折线法及点E是BC的中点,可证得△B'EC是等腰三角形,再有条件证明∠AEF=90°即可得到AE⊥EF;(2)连接BB′,通过折叠,可知∠EBB′=∠EB′B,由E是BC的中点,可得EB′=EC,∠ECB′=∠EB′C,从而可证△BB′C为直角三角形,在Rt△AOB和Rt△BOE中,可将OB,BB′的长求出,在Rt△BB′C中,根据勾股定理可将B′C的值求出.【详解】(1)由折线法及点E是BC的中点,∴EB=EB′=EC,∠AEB=∠AEB′,∴△B'EC是等腰三角形,又∵EF⊥B′C∴EF为∠B'EC的角平分线,即∠B′EF=∠FEC,∴∠AEF=180°﹣(∠AEB+∠CEF)=90°,即∠AEF=90°,即AE⊥EF;(2)连接BB'交AE于点O,由折线法及点E是BC的中点,∴EB=EB′=EC,∴∠EBB′=∠EB′B,∠ECB′=∠EB′C;又∵△BB'C三内角之和为180°,∴∠BB'C=90°;∵点B′是点B关于直线AE的对称点,∴AE垂直平分BB′;在Rt△AOB和Rt△BOE中,BO2=AB2﹣AO2=BE2﹣(AE﹣AO)2将AB=4cm,BE=3cm,AE=5cm,∴AO=165cm,∴BO22AB AO125cm,∴BB′=2BO=245cm,∴在Rt △BB 'C 中,B ′C =22BC BB '-=518cm , 由题意可知四边形OEFB ′是矩形,∴EF =OB ′=125, ∴S △B ′EC =*111812108225525B C EF '⨯=⨯⨯=.【点睛】考查图形的折叠变化及三角形的内角和定理勾股定理的和矩形的性质综合运用.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.7.如图,在正方形ABCD 中,对角线AC 与BD 交于点O ,在Rt △PFE 中,∠EPF=90°,点E 、F 分别在边AD 、AB 上.(1)如图1,若点P 与点O 重合:①求证:AF=DE ;②若正方形的边长为23,当∠DOE=15°时,求线段EF 的长;(2)如图2,若Rt △PFE 的顶点P 在线段OB 上移动(不与点O 、B 重合),当BD=3BP 时,证明:PE=2PF .【答案】(1)①证明见解析,②2;(2)证明见解析.【解析】【分析】(1)①根据正方形的性质和旋转的性质即可证得:△AOF ≌△DOE 根据全等三角形的性质证明;②作OG ⊥AB 于G ,根据余弦的概念求出OF 的长,根据勾股定理求值即可;(2)首先过点P 作HP ⊥BD 交AB 于点H ,根据相似三角形的判定和性质求出PE 与PF 的数量关系.【详解】(1)①证明:∵四边形ABCD 是正方形,∴OA=OD ,∠OAF=∠ODE=45°,∠AOD=90°,∴∠AOE+∠DOE=90°,∵∠EPF=90°,∴∠AOF+∠AOE=90°,∴∠DOE=∠AOF ,在△AOF 和△DOE 中,OAF ODE OA ODAOF DOE ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AOF ≌△DOE ,∴AF=DE ;②解:过点O 作OG ⊥AB 于G ,∵正方形的边长为23, ∴OG=12BC=3, ∵∠DOE=15°,△AOF ≌△DOE ,∴∠AOF=15°,∴∠FOG=45°-15°=30°,∴OF=OG cos DOG∠=2, ∴EF=22=22OF OE +;(2)证明:如图2,过点P 作HP ⊥BD 交AB 于点H ,则△HPB 为等腰直角三角形,∠HPD=90°,∴HP=BP ,∵BD=3BP ,∴PD=2BP ,∴PD=2HP ,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,∴∠HPF=∠DPE ,又∵∠BHP=∠EDP=45°,∴△PHF ∽△PDE , ∴12PF PH PE PD ==, ∴PE=2PF .【点睛】 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.8.如图1,在正方形ABCD 中,AD=6,点P 是对角线BD 上任意一点,连接PA ,PC 过点P 作PE ⊥PC 交直线AB 于E .(1) 求证:PC=PE;(2) 延长AP 交直线CD 于点F.①如图2,若点F 是CD 的中点,求△APE 的面积;②若ΔAPE 的面积是21625,则DF 的长为 (3) 如图3,点E 在边AB 上,连接EC 交BD 于点M,作点E 关于BD 的对称点Q ,连接PQ ,MQ ,过点P 作PN ∥CD 交EC 于点N ,连接QN ,若PQ=5,MN=723,则△MNQ 的面积是【答案】(1)略;(2)①8,②4或9;(3)56【解析】【分析】(1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;(2)作出△ADP 和△DFP 的高,由面积法容易求出这个高的值.从而得到△PAE 的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;(3)根据已经条件证出△MNQ 是直角三角形,计算直角边乘积的一半可得其面积.【详解】(1) 证明:∵点P 在对角线BD 上,∴△ADP ≌△CDP ,∴AP=CP , ∠DAP =∠DCP ,∵PE ⊥PC ,∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP =90°-∠DCP ,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;(2)①如图2,过点P 分别作PH ⊥AD,PG ⊥CD,垂足分别为H 、G.延长GP 交AB 于点M.∵四边形ABCD 是正方形,P 在对角线上,∴四边形HPGD 是正方形,∴PH=PG,PM ⊥AB,设PH=PG=a,∵F 是CD 中点,AD =6,则FD=3,ADF S n =9,∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4,又∵PA=PE,∴AM=EM,AE=4,∵APE S n =1144822EA MP ⨯=⨯⨯=, ②设HP =b,由①可得AE=2b,MP=6-b,∴APE S n =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或, ∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯, ∴当b=2.4时,DF=4;当b =3.6时,DF =9,即DF 的长为4或9; (3)如图,∵E 、Q 关于BP 对称,PN ∥CD,∴∠1=∠2,∠2+∠3=∠BDC=45°,∴∠1+∠4=45°, ∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC,∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC,∴∠6+∠7=90°,∴△MNQ 是直角三角形,设EM=a,NC=b 列方程组222252372 a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56, ∴MNQ 56S V =, 【点睛】本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.要注意运用数形结合思想.9.△ABC 为等边三角形,AF AB =.BCD BDC AEC ∠=∠=∠.(1)求证:四边形ABDF 是菱形.(2)若BD 是ABC ∠的角平分线,连接AD ,找出图中所有的等腰三角形.【答案】(1)证明见解析;(2)图中等腰三角形有△ABC ,△BDC ,△ABD ,△ADF ,△ADC ,△ADE .【解析】【分析】(1)先求证BD ∥AF ,证明四边形ABDF 是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD 平分∠ABC ,得到BD 垂直平分线段AC ,进而证明△DAC 是等腰三角形,根据BD ⊥AC,AF ⊥AC ,找到角度之间的关系,证明△DAE 是等腰三角形,进而得到BC =BD =BA =AF =DF ,即可解题,见详解.【详解】(1)如图1中,∵∠BCD =∠BDC ,∴BC =BD ,∵△ABC 是等边三角形,∴AB =BC ,∵AB =AF ,∴BD =AF ,∵∠BDC =∠AEC ,∴BD ∥AF ,∴四边形ABDF 是平行四边形,∵AB =AF ,∴四边形ABDF 是菱形.(2)解:如图2中,∵BA =BC ,BD 平分∠ABC ,∴BD 垂直平分线段AC ,∴DA =DC ,∴△DAC 是等腰三角形,∵AF ∥BD ,BD ⊥AC∴AF ⊥AC ,∴∠EAC =90°,∵∠DAC =∠DCA ,∠DAC +∠DAE =90°,∠DCA +∠AEC =90°,∴∠DAE=∠DEA,∴DA=DE,∴△DAE是等腰三角形,∵BC=BD=BA=AF=DF,∴△BCD,△ABD,△ADF都是等腰三角形,综上所述,图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.【点睛】本题考查菱形的判定,等边三角形的性质,等腰三角形的判定等知识,属于中考常考题型,熟练掌握等腰三角形的性质是解题的关键.10.问题探究(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM =CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;问题解决(3)如图③,AC为边长为23的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.【答案】(1)AM⊥BN,证明见解析;(2)△APB周长的最大值2;(3)△PAB的周长最大值3.【解析】试题分析:根据全等三角形的判定SAS证明△ABM≌△BCN,即可证得AM⊥BN;(2)如图②,以AB为斜边向外作等腰直角△AEB,∠AEB=90°,作EF⊥PA于E,作EG⊥PB于G,连接EP,证明PA+PB=2EF,求出EF的最大值即可;(3)如图③,延长DA到K,使得AK=AB,则△ABK是等边三角形,连接PK,取PH=PB,证明PA+PB=PK,求出PK的最大值即可.试题解析:(1)结论:AM⊥BN.理由:如图①中,∵四边形ABCD是正方形,∴AB=BC,∠ABM=∠BCN=90°,∵BM=CN,∴△ABM≌△BCN,∴∠BAM=∠CBN,∵∠CBN+∠ABN=90°,∴∠ABN+∠BAM=90°,∴∠APB=90°,∴AM⊥BN.(2)如图②中,以AB为斜边向外作等腰直角三角形△AEB,∠AEB=90°,作EF⊥PA于E,作EG⊥PB于G,连接EP.∵∠EFP=∠FPG=∠G=90°,∴四边形EFPG是矩形,∴∠FEG=∠AEB=90°,∴∠AEF=∠BEG,∵EA=EB,∠EFA=∠G=90°,∴△AEF≌△BEG,∴EF=EG,AF=BG,∴四边形EFPG是正方形,∴PA+PB=PF+AF+PG﹣BG=2PF=2EF,∵EF≤AE,∴EF的最大值=AE=2,∴△APB周长的最大值=4+4.(3)如图③中,延长DA到K,使得AK=AB,则△ABK是等边三角形,连接PK,取PH=PB.∵AB=BC,∠ABM=∠BCN,BM=CN,∴△ABM≌△BCN,∴∠BAM=∠CBN,∴∠A PN=∠BAM+∠ABP=∠CBN+∠ABN=60°,∴∠APB=120°,∵∠AKB=60°,∴∠AKB+∠APB=180°,∴A、K、B、P四点共圆,∴∠BPH=∠KAB=60°,∵PH=PB,∴△PBH是等边三角形,∴∠KBA=∠HBP,BH=BP,∴∠KBH=∠ABP,∵BK=BA,∴△KBH≌△ABP,∴HK=AP,∴PA+PB=KH+PH=PK,∴PK的值最大时,△APB的周长最大,∴当PK是△ABK外接圆的直径时,PK的值最大,最大值为4,∴△PAB的周长最大值=2+4.11.在矩形纸片ABCD中,AB=6,BC=8,现将纸片折叠,使点D与点B重合,折痕为EF,连接DF.(1)说明△BEF是等腰三角形;(2)求折痕EF的长.【答案】(1)见解析;(2).【解析】【分析】(1)根据折叠得出∠DEF=∠BEF,根据矩形的性质得出AD∥BC,求出∠DEF=∠BFE,求出∠BEF=∠BFE即可;(2)过E作EM⊥BC于M,则四边形ABME是矩形,根据矩形的性质得出EM=AB=6,AE=BM,根据折叠得出DE=BE,根据勾股定理求出DE、在Rt△EMF中,由勾股定理求出即可.【详解】(1)∵现将纸片折叠,使点D与点B重合,折痕为EF,∴∠DEF=∠BEF.∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠BFE,∴∠BEF=∠BFE,∴BE=BF,即△BEF 是等腰三角形;(2)过E作EM⊥BC于M,则四边形ABME是矩形,所以EM=AB=6,AE=BM.∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE==DE=BF,AE=8﹣DE=8﹣==BM,∴FM=﹣=.在Rt△EMF中,由勾股定理得:EF==.故答案为:.【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点,能熟记折叠的性质是解答此题的关键.12.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC(1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE P ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.13.如图1所示,(1)在正三角形ABC 中,M 是BC 边(不含端点B 、C )上任意一点,P 是BC 延长线上一点,N 是∠ACP 的平分线上一点,若∠AMN=60°,求证:AM=MN . (2)若将(1)中“正三角形ABC”改为“正方形ABCD”,N 是∠DCP 的平分线上一点,若∠AMN=90°,则AM=MN 是否成立?若成立,请证明;若不成立,说明理由.(3)若将(2)中的“正方形ABCD”改为“正n 边形A 1A 2…A n “,其它条件不变,请你猜想:当∠A n ﹣2MN=_____°时,结论A n ﹣2M=MN 仍然成立.(不要求证明)【答案】0(2)180n n- 【解析】分析:(1)要证明AM=MN ,可证AM 与MN 所在的三角形全等,为此,可在AB 上取一点E ,使AE=CM ,连接ME ,利用ASA 即可证明△AEM ≌△MCN ,然后根据全等三角形的对应边成比例得出AM=MN .(2)同(1),要证明AM=MN ,可证AM 与MN 所在的三角形全等,为此,可在AB 上取一点E ,使AE=CM ,连接ME ,利用ASA 即可证明△AEM ≌△MCN ,然后根据全等三角形的对应边成比例得出AM=MN .详(1)证明:在边AB 上截取AE=MC ,连接ME .在正△ABC 中,∠B=∠BCA=60°,AB=BC .∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE ,BE=AB-AE=BC-MC=BM ,∴∠BEM=60°,∴∠AEM=120°.∵N是∠ACP的平分线上一点,∴∠ACN=60°,∴∠MCN=120°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(2)解:结论成立;理由:在边AB上截取AE=MC,连接ME.∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE,BE=AB-AE=BC-MC=BM,∴∠BEM=45°,∴∠AEM=135°.∵N是∠DCP的平分线上一点,∴∠NCP=45°,∴∠MCN=135°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(3)由(1)(2)可知当∠A n-2MN等于n边形的内角时,结论A n-2M=MN仍然成立;即∠A n-2MN=()02180nn-时,结论A n-2M=MN仍然成立;故答案为[()02180nn-].点睛:本题综合考查了正方形、等边三角形的性质及全等三角形的判定,同时考查了学生的归纳能力及分析、解决问题的能力.难度较大.14.已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.【答案】(1)10;(2)12-a;(3)不能【解析】解:(1)过点G作GM⊥BC于M.在正方形EFGH中,∠HEF=90°,EH=EF,∴∠AEH+∠BEF=90°.∵∠AEH+∠AHE=90°,∴∠AHE=∠BEF.又∵∠A=∠B=90°,∴△AHE≌△BEF.同理可证△MFG≌△BEF.∴GM=BF=AE=2.∴FC=BC-BF=10.∴.(2)过点G作GM⊥BC交BC的延长线于M,连接HF.∵AD∥BC,∴∠AHF=∠MFH.∵EH∥FG,∴∠EHF=∠GFH.∴∠AHE=∠MFG.又∵∠A=∠GMF=90°,EH=GF,∴△AHE≌△MFG.∴GM=AE=2.∴.(3)△GFC的面积不能等于2.说明一:∵若S△GFC=2,则12-a=2,∴a=10.此时,在△BEF中,.在△AHE中,,∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.说明二:△GFC的面积不能等于2.∵点H在AD上,∴菱形边EH的最大值为,∴BF的最大值为.又∵函数S△GFC=12-a的值随着a的增大而减小,∴S△GFC的最小值为.又∵,∴△GFC的面积不能等于2.15.数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC 剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.请你阅读下面交流信息,解决所提出的问题.展示交流:小敏:满足条件的图形如图甲所示图形,延长BQ与AD交于点H.我们可以证明△BCQ≌△ACD,从而易得BQ=AD,BQ⊥AD.小慧:根据图甲,当点F在线段BC上时,我们可以验证小慧的说法是正确的.但当点F在线段CB的延长线上(如图乙)或线段CB的反向延长线上(如图丙)时,我对小慧说法的正确性表示怀疑.(1)请你帮助小慧进行分析,小敏的结论在图乙、图丙中是否成立?请说明理由.(选择图乙或图丙的一种情况说明即可).(2)小慧思考问题的方式中,蕴含的数学思想是.拓展延伸:根据你上面选择的图形,分别取AB、BD、DQ、AQ的中点M、N、P、T.则四边形MNPT 是什么样的特殊四边形?请说明理由.【答案】成立;分类讨论思想;正方形.【解析】试题分析:利用等腰直角三角形的性质结合全等三角形的判定与性质得出BQ=AD,BQ⊥AD;利用已知条件分类得出,体现数学中的分类讨论思想,拓展延伸:利用三角形中位线定理结合正方形的判定方法,首先得出四边形MNPT是平行四边形进而得出它是菱形,再求出一个内角是90°,即可得出答案.试题解析:(1)、成立,理由:如图乙:由题意可得:∠FDE=∠QDC=∠ABC=∠BAC=45°,则DC=QC,AC=BC,在△ADC和△BQC中∵,∴△ADC≌△BQC(SAS),∴AD=BQ,∠DAC=∠QBC,延长AD交BQ于点F,则∠ADC=∠BDF,∴∠BFD=∠ACD=90°,∴AD⊥BQ;(2)、小慧思考问题的方式中,蕴含的数学思想是:分类讨论思想;拓展延伸:四边形MNPT是正方形,理由:∵取AB、BD、DQ、AQ的中点M、N、P、T,∴MN AD,TP AD,∴MN TP,∴四边形MNPT是平行四边形,∵NP BQ,BQ=AD,∴NP=MN,∴平行四边形MNPT 是菱形,又∵AD⊥BQ,NP∥BQ,MN∥AD,∴∠MNP=90°,∴四边形MNPT是正方形.考点:几何变换综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).
请解答以下问题:
(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论.
(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?
(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系. 设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F 分别为AB、CD中点)?为什么?
练习1:如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AH=6,点D为AB边上的任意一点,过点D作DE∥BC,交AC于点E.设△ADE的高AF为x(0<x<6),以DE为折线将△A DE翻折,所得的△A′DE与梯形DBCE重叠部分的面积记为y(点A关于DE的对称点A′落在AH所在的直线上).
(1)分别求出当0<x≤3与3<x<6时,y与x的函数关系式;
(2)当x取何值时,y的值最大?最大值是多少?
练习2:如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C (0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.
设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.
四边形ABCD 是正方形,点E ,K 分别在BC ,AB 上,点G 在BA 的延长线上,且CE=BK=AG .
(1)求证:①DE=DG ; ②DE ⊥DG
(2)尺规作图:以线段DE ,DG 为边作出正方形DEFG (要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF ,猜想并写出四边形CEFK 是怎样的特殊四边形,并证明你的猜想:
(4)当
CE 1
CB n
时,请直接写出
ABCD DEFG S S 正方形正方形的值. 如图,四边形ABCD 中,对角
线相交于点O,E 、F 、G 、H 分别是AD 、BD 、BC 、AC 的中点。
(1)求证:四边形EFGH 是平行四边形;
(2)当四边形ABCD 满足一个什么条件时,四边形EFGH 是菱形?并证明你的结论。
用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的
三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转. (1)当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时(如图所示),通过观察或测量BE 、CF 的长度,你能得出什么结论?并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时(如图所示),你在(1)中得到的结论还成立吗?说明理由。
O
H
G
F
E
C
D B
A
已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(!)求证:BF =AC ; (2)求证:CE =
1
2
BF ; (3)CE 与BC 的大小关系如何?试证明你的结论。
)如图甲,在△ABC 中,∠ACB 为锐角.点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF . 解答下列问题:
(1)如果AB=AC ,∠BAC=90º.
①当点D 在线段BC 上时(与点B 不重合),如图乙,线段CF 、BD 之间的位置关系为 ,数量关系为 .
②当点D 在线段BC 的延长线上时,如图丙,①中的结论是否仍然成立,为
什么?
(2)如果AB ≠AC ,∠BAC ≠90º,点D 在线段BC 上运动.
试探究:当△ABC 满足一个什么条件时,CF ⊥BC (点C 、F 重合除外)?画出相应图形,并说明理由.(画图不写作法)
A
B
C
D
E F 第28题图
图甲
图乙 F E
B
A
F E
D
C
B A 图丙
如图(1),已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG . (1)连接GD ,求证:△ADG ≌△ABE ;
(2)连接FC ,观察并猜测∠FCN 的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD 改为矩形ABCD ,AB =a ,BC =b (a 、b 为常数),E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请用含a 、b 的代数式表示tan ∠FCN 的值;若∠FCN 的大小发生改变,请举例说明.
如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG ⊥EB ,垂足为G ,AG 交BD 于F ,则OE=OF . (1)请证明0E=OF
(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.
1如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(-3,4),
点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H .
(1)求直线AC 的解析式;
(2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB
N M B E A C D
F G
图(1)
图(2) M B E A C D
F G
N
的面积为S (S ≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);
2.已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,
A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P
从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒. (1)求直线BC 的解析式;
(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的
27
? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请
直接写出S 与t 的函数关系式,并指出自变量t 的取值范围;
已知:如图4-56A .,直线l 通过正方形ABCD 的顶点D EC=AC ,并且EC 与边AD 相交于点F .求证:AE=AF .
本例中,点E 与A 位于BD 同侧.如图4-56B .,点E 与A 位于BD 异侧,直线EC 与DA 的延长线交于点F ,这时仍有AE=AF .请自己证明.。
