苏科版七年级上册数学第5章 走进图形世界检测题
苏教版初一数学第五章《走进图形世界》检测卷(含答案)
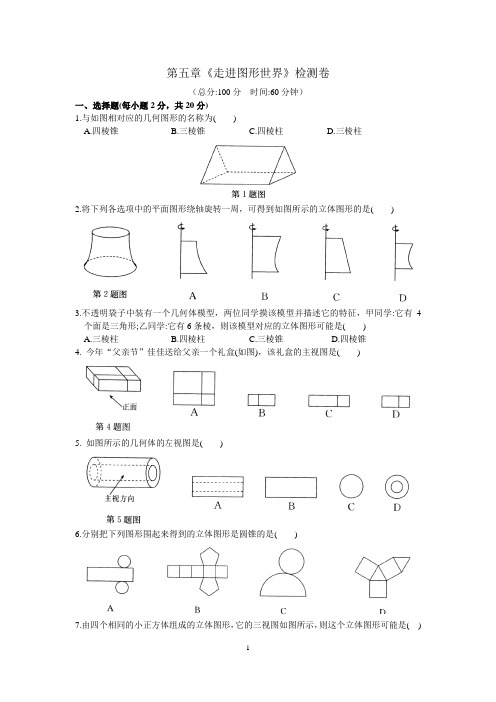
第五章《走进图形世界》检测卷(总分:100分时间:60分钟)一、选择题(每小题2分,共20分)1.与如图相对应的几何图形的名称为( )A.四棱锥B.三棱锥C.四棱柱D.三棱柱2.将下列各选项中的平面图形绕轴旋转一周,可得到如图所示的立体图形的是( )3.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有6条棱,则该模型对应的立体图形可能是( )A.三棱柱B.四棱柱C.三棱锥D.四棱锥4. 今年“父亲节”佳佳送给父亲一个礼盒(如图),该礼盒的主视图是( )5. 如图所示的几何体的左视图是( )6.分别把下列图形围起来得到的立体图形是圆锥的是( )7.由四个相同的小正方体组成的立体图形,它的三视图如图所示,则这个立体图形可能是( )8.毕业前夕,同学们准备了一份礼物送给自己的母校,现用一个正方体盒子(如图)进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上,则此包装盒的展开图(不考虑文字方向)不可能是( )9.如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )A. 12 cm2B.(12+π) cm2C. 6π cm2D. 8π cm210.有一个正方体木块,每一块的各面都写上不同的数字,现把它们分别摆放成如图所示的位置.请你判断数字4对面的数字是( )A. 6B. 3C. 2D. 1二、填空题(每小题3分,共24分)11.若一个棱柱的底面是一个七边形,则它的侧面必须有个长方形,它一共有个面. 12一个直角三角形绕其中一条直角边旋转一周所形成的几何体是.13.如图,该图形是立体图形的展开图.14.如图是由若干个相同的小正方体组合而成的几何体,则三个视图中面积最小的是.15.长方体的主视图与俯视图如图所示,则这个长方体的体积是.16.如图,木工师傅把一个长为1.6 m的长方体木料锯成3段后,表面积比原来增加了80 cm2,那么这根木料原来的体积是cm3 .17.一个由16个完全相同的小正方体搭成的几何体,其最下面一层摆放了9个小正方体,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.18.如图,在一次数学活动课上,张明用17个棱长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要个小正方体,王亮所搭几何体的表面积为.三、解答题(本大题共6小题,共56分)19.(8分)如图是一个无盖的正方体纸盒,下底面标有字母M,沿图中的粗实线将该纸盒剪开,请画出它的平面展开图.20.(8分)如图是由若干个小正方体搭成的几何体,试画出该几何体的主视图、俯视图、左视图.21. (10分)如图所示是一个正方体的平面展开图,请回答下列问题:(1)与面,B C相对的面分别是,;(2)若32135A a a b =++,2312B a b a =+,31C a =-,21(15)5D a b =-+,且相对两个面所表示的代数式的和都相等,求,E F 分别代表的代数式.22. (10分)已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.23. (10分) (1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图①所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子;(添加的正方形用阴影表示)(2)如图②所示的几何体是由几个相同的正方体搭成的,请画出它的主视图;(3)如图③是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体的左视图.24. (10分)如图①是由一些大小相同的小正方体组合成的简单几何体,并放在墙角. (1)该几何体的主视图如图③所示.请在图④方格纸中画出它的右视图;(2)若将其外面涂一层漆,则其涂漆面积为 cm 2 ;(正方体的棱长为1 cm)(3)一个全透明的正方体玻璃(如图②),上面嵌有一根黑色的金属丝,在图⑤中画出金属丝在俯视图中的形状.参考答案一、选择题1. D2. A3. C4. C5. D6. C7. A8. C9. C 10. B 二、填空题 11. 7 9 12. 圆锥 13. 三棱柱 14. 左视图 15. 24 16. 3200 17. 1018. 19 48 三、解答题 19. 如图所示20. 如图所示21. (1) F E (2) 212F a b =-,1E = 22. 解:该几何体为三棱柱. 表面积:1862(1086)41442⨯⨯⨯+++⨯=(cm 2) 体积:1864962⨯⨯⨯=(cm 3) 23. 解:(1)如图①所示.(答案不唯一) (2)如图②所示. (3)如图③所示.24. (1) (3)如图所示(2)涂漆面积为67411++=(cm 2)。
苏教版七年级数学 第五章走进图形世界检测试卷含答案

第五章走进图形世界检测卷(总分100分时间60分钟)一、选择题(每小题3分,共30分)1.将如图所示的图案通过平移后可以得到的图案是( )2.长方体的顶点数、棱数、面数分别是( )A.8、10、6 B.6、12、8 C.6、8、10 D.8、12、6 3.把一张正方形纸片如图中图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )4.如图所示的几何体的俯视图是( )5.将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是( )A.文B.明C.城D.市6.三视图表示的可能是宜昌四种特产:西瓜、蜜橘、梨、土豆中的( )7.下图是由两个相同的正方体和一个圆锥体组成的立体图形,其主视图是( )8.如图给定的是纸盒的外表面,下面能由它折叠而成的是( )9.如图是一个由6个大小相同、棱长为1的小正方体搭成的几何体,关于它的下列说法中正确的是( )A.主视图的面积为6 B.左视图的面积为2C.俯视图的面积为5 D.三种视图的面积都是510.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有( )A.9箱B.10箱C.11箱D.12箱二、填空题(每小题3分,共30分)11.一个直角三角形绕其中一条直角边旋转一周所形成的几何体是_______.12.在圆柱、棱柱、球、圆锥中,表面不能展开成平面图形的是_______.13.如图,在方格纸中有四个图形(1)、(2)、(3)、(4),其中面积相等的图形是_______.14.三棱锥的展开图是由_______个_______形组成的.15.一个直棱柱有15条棱,则这个直棱柱有_______个面.16.一个无盖的正方体纸盒,将它展开成平面图形,可能的情况有_______种.17.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是. 18.如图,长方形ABCD的长AB=4,宽BC=3,以AB所在直线为轴,将长方形旋转一周后所得几何体的主视图的面积是_______.19.如图,从边长为10的正方体的一顶点处挖去一个边长为1的小正方体,则剩下图形的表面积为_______.20.用八个大小相同的立方体粘成一个大立方体如图5-13中图①,得到的几何体的三视图如图②所示,若小明从八个小立方体中,取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图②,则他取走的小立方体最多可以是_______个. 三、解答题(本题共6小题,共40分) 21.(6分)请在下图所示图形符号中找出它们所蕴含的内在规律,并在横线上的空白处填上恰当的图形:22.(6分)画出如图所示物体的三视图.23.(6分)如图,在一个五棱柱的萝卜块上,切下一个三棱柱,剩下的部分仍是一个棱柱,那么剩下部分的棱柱可能有哪几种情况?它们的棱数、面数与原棱柱相比,发生了怎样的变化? 24.(6分)如图所示,图①为一个长方体,AD =AB =10,AE =6,图②为图①的表面展开图(字在外表面上),请根据要求回答问题: (1)面“扬”的对面是面_______;(2)如果面“丽”是右面,面“美”在后面,哪一面会在上面?(3)图①中,M 、N 为所在棱的中点,试在图②中画出点M 、N 的位置;并求出图②中三角形ABM 的面积;左视图俯视图主视图26(第17题)25.(6分)一个正方体,六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数为16、19和20,问这六个数的和为多少?26.(10分)(1)图①是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数.请搭出这个物体,并画出相应几何体的主视图、左视图;(2)图②是由几个小立方块所搭成的几何体的左视图,小正方形中的数字表示该位置小立方块的个数,请搭出这个几何体,并画出相应几何体的主视图、俯视图,这样的几何体唯一吗?参考答案1—10 ADCBB BBBCA11.圆锥12.球13.(1)(2)14.四;三角15.716.817.7218.2419.60020.421.22.如图23.分3种情况:(1)剩下部分为四棱柱,则棱少3条,面少1个;(2)剩下部分为五棱柱,则棱数与面数均不变;(3)剩下部分为六棱柱,则棱多3条,面多1个.24.(1)“爱”;(2)由图可知,如果面“丽”是右面,面“美”在后面,“爱”面会在上面;(3)105.25.解:六个数为16,17,18,19,20,21;其和为11126.解:(1)图①所搭几何体的主视图、左视图分别如图;(2)由图②可知有8个小立方块.分小组进行摆放、组合、调整,会发现这样的几何体不唯一.选取其中两种几何体,画出它的主视图、俯视图为如图.第一种:第二种:。
苏科版七年级上册数学第5章 走进图形世界 含答案

苏科版七年级上册数学第5章走进图形世界含答案一、单选题(共15题,共计45分)1、用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱. ()A.①②③④B.①③④C.①④D.①②2、下列各图中,经过折叠能围成一个立方体的是()A. B. C. D.3、下图是某个几何体的三视图,该几何体是()A.长方体B.正方体C.圆柱D.三棱柱4、如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是()A. B. C. D.5、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有()种画法.A.2B.3C.4D.56、如图是一个几何体的三视图,根据图中数据计算这个几何体的表面积是()A.16πB.12πC.10πD.4π7、如图的几何体的主视图是()A. B. C. D.8、如图所示的三棱柱的正视图是()A. B. C.D.9、已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为()A.48B.48+9C.32+6D.48+1210、下图是由大小相同的5个小正方体搭成的几何体,则它的主视图是()A. B. C. D.11、如图,该立体图形的主视图为()A. B. C. D.12、如图是一个由5个相同的正方体组成的立体图形,它的主视图是()A. B. C. D.13、用一个平面去截正方体,截面的形状不可能是()A.四边形B.五边形C.六边形D.七边形14、如图所示的几何体,它的主视图是()A. B. C. D.15、一个物体的外形是长方体,其内部构造不详.用5个水平的平面纵向平均截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是()A.球体B.圆柱C.圆锥D.球体或圆锥二、填空题(共10题,共计30分)16、画三视图是有一定要求的,首先确定________的位置,画出主视图,然后在主视图的下面画出________,在主视图的右面画出________.17、“夜晚的流星划过天空时留下一条明亮的光线,汽车的雨刷在挡风玻璃上画出一个扇面.”上面两句话用几何知识可以解释为________.18、若一直棱柱有10个顶点,那么它共有________ 条棱.19、如图,长方体中,,,,一只蚂蚁从点出发,以秒的速度沿长方体表面爬行到点,至少需要________分钟。
苏科版七年级上册数学第5章 走进图形世界 含答案

苏科版七年级上册数学第5章走进图形世界含答案一、单选题(共15题,共计45分)1、小林同学在一个正方形盒子的每个面都写有一个字,分别是:每、天、进、步、一、点,其平面展开图如图所示,那么在该正方体盒子中,和“每”相对的面所写的字是()A.进B.步C.一D.点2、下列图中,左边的图形是立方体的表面展开图,把它折叠成立方体,它会变右边的()A. B. C. D.3、在下列的四个几何体中,其主视图与俯视图相同的是()A. 圆柱B.圆锥 C. 三棱柱 D. 球4、用一个平面去截一个正方体,截面不可能是()A.梯形B.五边形C.六边形D.七边形5、如图是某个几何体的展开图,该几何体是()A.圆锥B.圆柱C.三棱柱D.四棱柱6、如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )A.主视图会发生改变B.俯视图会发生改变C.左视图会发生改变 D.三种视图都会发生改变7、如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对的面上的汉字是( )A.数B.活C.学D.的8、下列说法中,正确的是()A.棱柱的侧面可以是三角形B.由六个大小一样的正方形所组成的图形是正方体的展开图C.正方体的各条棱都相等D.棱柱的各条棱都相等9、如图所示的一个六角螺帽毛坯底面正六边形的边长、高和内孔直径都相等,其主视图是()A. B. C. D.10、如图所示的几何体是由以下四个图形中的哪一个图形绕着虚线旋转一周得到的()A. B. C. D.11、三个大小相同的正方体搭成的几何体如图所示,其俯视图是()A. B. C. D.12、如图所示的正六棱柱的左视图是()A. B. C. D.13、下列四个图形中是三棱柱的表面展开图的是()A. B. C. D.14、是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.文德中学初一年级学习小组送给医务工作者的正方体6面上都有一个汉字,如图所示是它的一种展开图,那么在原正方体中,与“最”字所在面相对的面上的汉字是()A. 美B.的C.逆D.人15、如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)()A.40πcm 2B.65πcm 2C.80πcm 2D.105πcm 2二、填空题(共10题,共计30分)16、一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图,左视图如图所示要摆成这样的图形,至少需用________块小正方体.17、有如图四张卡片,除卡片上的图案不同其余完全相同,现把这些卡片有图案的一面朝下搅匀,随机抽出一张,上面的图案能够围成一个正方体的概率是________.18、任意放置以下几何体:正方体、圆柱、圆锥、球体,则三视图都完全相同的几何体是________ .19、已知一个几何体的三视图如图所示,则这个几何体的侧面积是________.20、________是画三视图必须遵循的法则.21、将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的________(只填序号).22、第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.图1旋转形成________ 图2旋转形成________ 图3旋转形成________ ,图4旋转形成________ ,图5旋转形成________ ,图6旋转形成________23、如图所示,一个长方体的长为4cm,宽为3cm,高为5cm.则长方体所有棱长的和为________;长方体的表面积为________ .24、如图是某几何体的展开图,那么这个几何体是________25、一个容积是125dm3的正方体棱长是________dm.三、解答题(共5题,共计25分)26、已知有一个长为5cm,宽为3cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?27、如图是一个正方形盒的展开图,若在其中的三个正方形A、B、C、内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为多少?28、如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.(1)请你画出它的从正面看和从左面看的形状图.(2)如果每个立方体的棱长为2cm,则该几何体的表面积是多少?29、如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2,那么这根木料本来的体积是多少?30、一个几何体从前面看及从上面看的视图如图所示。
苏科版七年级上册数学第5章 走进图形世界含答案(各地真题)

苏科版七年级上册数学第5章走进图形世界含答案一、单选题(共15题,共计45分)1、如图几何体的俯视图是()A. B. C. D.2、如图所示的圆锥的主视图是()A. B. C. D.3、如图所示,该几何体的主视图是()A. B. C. D.4、一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是()A.和B.谐C.凉D.山5、一个几何体的三视图如图所示,则该几何体的表面积是()A.24+2πB.16+4πC.16+8πD.16+12π6、如图,小亮用6个相同的小正方体搭成一个立体图形,研究几何体的三视图的变化情况,若由图①变到图②,其三视图中不改变的是()A.主视图B.主视图和左视图C.主视图和俯视图D.左视图和俯视图7、下图中的几何体的左视图是()A. B. C. D.8、如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是()A. B. C. D.9、如图,有一个无盖的正方体纸盒,的下底面标有字母“ ”,若沿图中的粗线将其剪开展成平面图形,这个平面图形是()A. B. C.D.10、如图是正方体的表面展开图,则与“前”字相对的字是()A.认B.真C.复D.习11、一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为()A.66B.48C.48 +36D.5712、一个立方体的体积为64立方米,将此立方体的棱长增加2米,那么新立方体的体积变为()A.72立方米B.216立方米C.66立方米D.128立方米13、下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是()A.圆锥B.圆柱C.三棱柱D.球14、下列几何体中,主视图和俯视图都为矩形的是()A. B. C. D.15、一个几何体的三视图如图所示,则该几何体可能是()A. B. C. D.二、填空题(共10题,共计30分)16、一个几何体的三种视图如图所示,这个几何体的表面积是________.(结果保留π)17、(1)侧面可以展开成一长方形的几何体有________;(2)圆锥的侧面展开后是一个________;(3)各个面都是长方形的几何体是________;18、如图中,请在横线上直接写出相应的几何体的名称;图1________.图2________.图3________.19、由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是________.20、一个几何体的三视图如图,很据图示的数据计算该几何体的表面积为________(结果保留π).21、李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为________22、如图,是一个正方体的平面展开图,原正方体中“考”的对面的字是________.23、如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是________.24、如图,扇形A的圆心角的度数为________.25、如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为________ .三、解答题(共5题,共计25分)26、我们知道,将一个长方形绕它的一边旋转一周得到的几何体是圆柱,现有一个长是5cm,宽是3cm的长方形,分别绕它的长和宽所在的直线旋转一周,得到不同的圆柱几何体,分别求出它们的体积.27、如图是一个由小立方体搭成的几何体.请你分别从正面、左面和上面看,试把你看到的形状图面出来.28、一个正方体六个面分别标有字母A、B、C、D、E、F,其展开如图所示,已知:A=x2﹣2xy、B=A﹣C,C=3xy+y2,若该正方体相对两个面上的多项式的和相等,试用x、y的代数式表示多项式D,并求当x=﹣1,y=﹣2时,多项式D 的值.29、如图是一个正方体的表面展开图,请回答下列问题:(1)与面B、C相对的面分别是;(2)若A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=﹣(a2b﹣6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.30、仔细数一数图中有几个直角三角形,几个正方形,几个长方形.参考答案一、单选题(共15题,共计45分)1、D2、A3、D4、D5、D6、D7、B8、A9、A10、B11、A12、B14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
2022学年第I学期苏科版七年级数学上册第五章《走进图形世界》过关检测题附答案
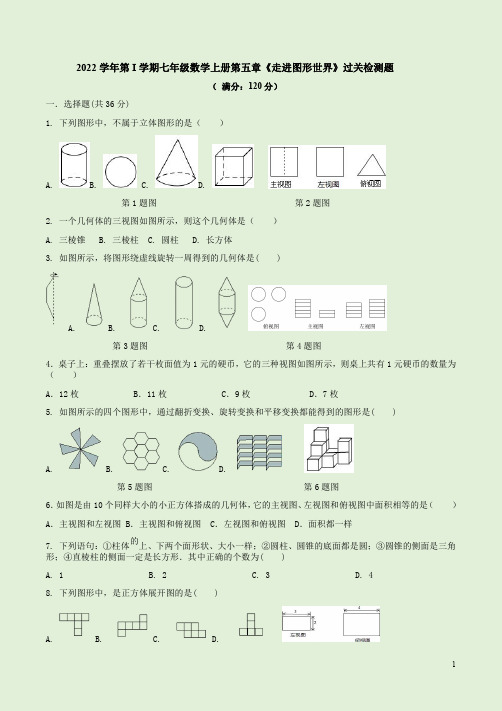
2022学年第I学期七年级数学上册第五章《走进图形世界》过关检测题(满分:120分)一.选择题(共36分)1.下列图形中,不属于立体图形的是()A. B. C. D.第1题图第2题图2.一个几何体的三视图如图所示,则这个几何体是()A.三棱锥B.三棱柱C.圆柱D.长方体3.如图所示,将图形绕虚线旋转一周得到的几何体是()A. B. C. D.第3题图第4题图4.桌子上:重叠摆放了若干枚面值为1元的硬币,它的三种视图如图所示,则桌上共有1元硬币的数量为()A.12枚B.11枚C.9枚D.7枚5.如图所示的四个图形中,通过翻折变换、旋转变换和平移变换都能得到的图形是()A. B. C. D.第5题图第6题图6.如图是由10个同样大小的小正方体搭成的几何体,它的主视图、左视图和俯视图中面积相等的是()A.主视图和左视图B.主视图和俯视图C.左视图和俯视图D.面积都一样7.下列语句:①柱体的上、下两个面形状、大小一样;②圆柱、圆锥的底面都是圆;③圆锥的侧面是三角形;④直棱柱的侧面一定是长方形.其中正确的个数为()A.1B.2C.3D.48.下列图形中,是正方体展开图的是()A. B. C. D.第8题图第9题图9.如图一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为()A.6B.8C.12D.1610.用一个平面取截一个几何体,得到的截面是四边形,这个几何体可能是()A.圆柱B.球体C.圆锥D.以上都有可能11.图1、图2均是正方体,图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图,小敏同学经过研究得到如下结论:(1)若将图1中正方体的表面沿某些棱剪开,展成一个平面图形,需要剪开7条棱;(2)用一个平面从不同方向去截图1中的正方体,得到的截面可能是三角形、四边形、五边形或六边形;(3)用一个平面去截图1中的正方体得到图2,截面三角形ABC中∠ABC=45°;(4)如图3,要搭成该几何体的正方体的个数最少是a,最多是b,则a+b=19其中正确结论的个数有()A.1个B.2个C.3个D.4个第11题图第12题图12.如图1,是一个正方体的侧面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格、这时小正方体朝上面的字是()A.和B.谐C.社D.会二.填空题(共39分)13.三棱锥是由________个面围成的,有________个顶点,有________条棱.14.如图所示是一个由6个大小相同、棱长为1的小正方体搭成的几何体,那么它的俯视图的面积是________.第14题图第15题图第16题图第17题图第18题图15.一个正方体的每个面上都有一个汉字,其表面展开图如图所示,那么在该正方体中和“毒”字相对的字是________.16.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面__________.(填字母)17.如图是一个长方体纸盒的表面展开图,纸片厚度忽略不计,按图中数据,这个盒子容积为__________.18.将如图所示的平面展开图折叠成正方体后,相对面上两个数的和都相等,则x y+=____.19.如图,该平面展开图折叠成正方体后,相对面上两个数之和为10,则m+n=________.第19题图第20题图第21题图第22题图20.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的垫片的周长是________cm.21.如图,线段AB和CD分别是正方体两个面的对角线,将此正方体沿部分棱剪开展开成一个平面图形.观察AB和CD所在的直线,下列情况:①AB⊥CD,②AB∥CD,③AB和CD在同一条直线上,其中可能出现的是______.22.如下图是一个物体的表面展开图(单位:cm),则这个物体的体积为________cm3.23.如图1是边长为18cm的正方形纸板,剪掉阴影部分后将其折叠成如图2所示的长方体盒子.已知该长cm.方体的宽是高的2倍,则它的体积是______324.一个长方体包装盒展开后如图所示(单位:cm),则其容积为_____cm3.25.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.三.解答题(共45分)26.(4分)画出如图18所示的几何体的三视图.27.(8分)如图长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:(1)如图①,绕着它的宽所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)(2)如图②,绕着它的长所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)28.(10分)18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在着一个有趣的关系式,这个关系式被称为欧拉公式.请你观察如图所示的几种简单多面体模型,解答下列问题.(1)根据上面的多面体模型,补全表格:多面体顶点数(V)面数(F)棱数(E)四面体44长方体8612正八面体812正十二面体201230顶点数(V)、面数(F)、棱数(E)之间存在的关系式是;(2)一个多面体的顶点数比面数大8,且有30条棱,则这个多面体的面数是;(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面的三角形的个数为x,八边形的个数为y,求x+y的值.29.(11分)如图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成.(1)请在上面方格纸中,画出图(2)几何体的俯视图和左视图;(2)按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是______,第n个叠放的图形中,小正方体木块总数应是______;(3)若露在外面的面都涂上颜色(底面不涂),小正方体的边长为1,则第(3)个叠放的图形中,涂上颜色的面积是__________.30.(12分)如图1,边长为cm a 的正方形硬纸板的4个角上剪去相同的小正方形,这样可制作一个无盖的长方体纸盒,设底面边长为cm x.(1)这个纸盒的底面积是______2cm ,高是______cm (用含a 、x 的代数式表示).(2)x 的部分取值及相应的纸盒容积如表所示:①请通过表格中的数据计算:m =_____,n =______;②猜想:当x 逐渐增大时,纸盒容积的变化情况:_______.(3)若将正方形硬纸板按图2方式裁剪,亦可制作一个无盖的长方体纸盒.①若为该纸盒制作一个长方形盖子,则该长方形的两边长分别是______cm ,_____cm (用含a 、y 的代数式表示):②已知A ,B ,C ,D 四个面上分别标有整式2(2)m +,m ,3-,6,且该纸盒的相对两个面上的整式的和相等,求m 的值./cm x 123456789纸盒容积3/cm m72n答案1.B2.B3.D4.B5.B6.D7.C8.B9.B10.A11.B12.D13.4,4,614.515.防16.E17.618.219.1220.21021.①②22.250π.:23.216【解析】设该长方体的高为x,则长方体的宽为2x,利用展开图得到2x+2x+x+x=18,然后解方程得到x的值,从而得到该长方体的高、宽、长,于是可计算出它的体积.设该长方体的高为x,则长方体的宽为2x,2x+2x+x+x=18,解得x=3,所以该长方体的高为3,则长方体的宽为6,长为18−6=12,所以它的体积为3×6×12=216(cm3),故答案为216.24.6000解:由题意可得,该长方体的高为:42﹣32=10(cm),宽为:32﹣10=20(cm),长为:(70﹣10)÷2=30(cm),故其容积为:30×20×10=6000(cm3),故答案为:6000.257【解析】从图形进行分析,结合正方体的基本性质,得到对面的数字,即可求得结果.一个正方体已知1,4,6,第二个正方体已知1,2,3,第三个正方体已知2,5,6,且不同的面上写的数字各不相同,可求得1的对面数字为5,6的对面数字为3,2的对面数字为4∴a+b=7故答案为:7.三.解答题(共45分)26.(4分)画出如图18所示的几何体的三视图.【答案】27.解:(1)得到的是底面半径是7cm,高是3cm的圆柱,V≈3.14×72×3=461.58(cm3),即得到的几何体的体积约是461.58cm3.(2)得到的是底面半径是3cm,高是7cm的圆柱,V≈3.14×32×7=197.82(cm3),即得到的几何体的体积约是197.82cm3.28.(10分)18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在着一个有趣的关系式,这个关系式被称为欧拉公式.请你观察如图所示的几种简单多面体模型,解答下列问题.(1)根据上面的多面体模型,补全表格:多面体顶点数(V)面数(F)棱数(E)四面体44长方体8612正八面体812正十二面体201230顶点数(V)、面数(F)、棱数(E)之间存在的关系式是;(2)一个多面体的顶点数比面数大8,且有30条棱,则这个多面体的面数是;(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面的三角形的个数为x,八边形的个数为y,求x+y 的值.解:(1)四面体的棱数为6;正八面体的顶点数为6;V+F-E=2.(2)12.(3)这个多面体的面数为x+y,棱数为24×32=36,根据V+F-E=2可得24+(x+y)-36=2,所以x+y=14.29.(11分)如图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成.(1)请在上面方格纸中,画出图(2)几何体的俯视图和左视图;(2)按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是______,第n 个叠放的图形中,小正方体木块总数应是______;(3)若露在外面的面都涂上颜色(底面不涂),小正方体的边长为1,则第(3)个叠放的图形中,涂上颜色的面积是__________.解:(1)如图所示,(2)第一个叠放的图形,小正方体木块总数为1;第二个叠放的图形,小正方体木块总数为156+=;第三个叠放的图形,小正方体木块总数为15915++=;第四个叠放的图形,小正方体木块总数为1591328+++=;第五个叠放的图形,小正方体木块总数为159131745++++=;……第n 个叠放的图形,小正方体木块总数为()1591317114n +++++++-⨯⎡⎤⎣⎦159131743n =++++++- ()1432n n +-⨯=()21n n =-22n n =-当7n =时,227798791⨯-=-=故答案为:91,22n n-(3)第一个图形,其涂色面积为1415⨯+=第二个图形,其涂色面积为()()1341421+⨯++=第三个图形,其涂色面积为()()135414445++⨯+++=故答案为:4530.(12分)如图1,边长为cm a 的正方形硬纸板的4个角上剪去相同的小正方形,这样可制作一个无盖的长方体纸盒,设底面边长为cm x .(1)这个纸盒的底面积是______2cm ,高是______cm (用含a 、x 的代数式表示).(2)x 的部分取值及相应的纸盒容积如表所示:①请通过表格中的数据计算:m =_____,n =______;②猜想:当x 逐渐增大时,纸盒容积的变化情况:_______.(3)若将正方形硬纸板按图2方式裁剪,亦可制作一个无盖的长方体纸盒.①若为该纸盒制作一个长方形盖子,则该长方形的两边长分别是______cm ,_____cm (用含a 、y 的代数式表示):②已知A ,B ,C ,D 四个面上分别标有整式2(2)m +,m ,3-,6,且该纸盒的相对两个面上的整式的和相等,求m 的值.解:(1)这个纸盒的底面积是22cm x ,高是cm 2a x-,故答案为:2x ,2a x -;(2)①由题意得:当6x =时,纸盒的容积为372cm ,2722a x x -∴⋅=,636722a -∴⋅=,10a ∴=,∴当2x =时,1024162m -=⨯=,当9x =时,109818122m -=⨯=,故答案为:16,812;②当1x =时,1019122m -=⨯=,当2x =时,1024162m -=⨯=,当3x =时,10363922m -=⨯=,当4x =时,10416482m -=⨯=,当5x =时,1051252522m -=⨯=,当6x =时,10636722m -=⨯=,当7x =时,1071474922m -=⨯=,当8x =时,10864642m -=⨯=,当9x =时,109818122m -=⨯=,猜想:当x 逐渐增大时,纸盒容积的变化情况:先随着x 的增大而增大,后随着x 的增大而减小,故答案为:先随着x 的增大而增大,后随着x 的增大而减小;(3)①若为该纸盒制作一个长方形盖子,则该长方形的两边长分别是cm y ,(2)cm a y -,故答案为:y ,2a y -,②由图可知:A 与C 相对,B 与D 相对,由题意得:2(2)(3)6m m ++-=+,2436m m +-=+,5m =,m ∴的值为5./cmx 123456789纸盒容积3/cm m72n。
《新新练案系列》苏科版七年级数学(上册)《第5章 走进图形世界》单元检测题(含答案解析)

第5章 走进图形世界检测题【本试卷满分100分,测试时间90分钟】一、选择题(每小题3分,共30分)1.在棱柱中( )A.只有两个面平行B.所有的棱都平行C.所有的面都是平行四边形D.两底面平行,且各侧棱也互相平行2.下列平面图形不能够围成正方体的是( )3.下列图形是四棱柱的侧面展开图的是( )4.将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是( )A.5B.6C.7D.85.下列图形中,不是三棱柱的表面展开图的是( )6.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列左图是以下四个图中的哪一个绕着直线旋转一周得到的( )7.如图是一个立体图形的三视图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是( )A.4B.5C.6D.78.若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个立体图形可能 是( )A.圆锥B.三棱柱C.圆柱D.三棱锥9.一个四棱柱被一刀切去一部分,剩下的部分是( )A.三棱柱B.四棱柱C.五棱柱D.以上都有可能10.如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是( )A.蓝色、绿色、黑色B.绿色、蓝色、黑色C.绿色、黑色、蓝色D.蓝色、黑色、绿色二、填空题(每小题3分,共24分)11.下列表面展开图的立体图形的名称分别是:______、______、______、______.12.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去____(填序号).13.如果一个几何体的三种视图之一是三角形,这个几何体可能是 (写出3个即可).14.几何体中主视图是圆,左视图和俯视图都是长方形,该几何体是 .15.在桌上摆有一些大小相同的正方体木块,其主视图和左视图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.16.一个棱锥有7个面,这是 棱锥,有 个侧面.A B DC17.用六根长度相等的火柴棒搭等边三角形,最多搭成个.18.下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应填空.①:_____________;②:_____________;③:_____________;④:_____________;⑤:_____________.三、解答题(共46分)19.(6分)如图是一个正方体骰子的表面展开图,请根据要求回答问题:(1)如果1点在上面,3点在左面,几点在前面?(2)如果5点在下面,几点在上面?20.(6分)画出如图所示的三棱锥的三视图.21.(6分)如图是一个由若干个小正方体搭成的几何体的俯视图,其中小正方形格内的数字是该位置小正方体的层数,请你画出它的主视图和左视图.22.(7分)画出下列几何体的三视图:23.(7分)如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你有几种画法,在图上用阴影注明.24.(7分)如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求的值.25.(7分)一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B处,如图所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条?第5章走进图形世界检测题参考答案一、选择题1.D 解析:对于A,如果是长方体,可能不止有两个面平行,故错;对于B,如果是长方体,不可能所有的棱都平行,只是所有的侧棱都平行,故错;对于C,如果是底面为梯形的棱柱,不是所有的面都是平行四边形,故错;对于D,根据棱柱的定义知其正确,故选D.2.B 解析:利用自己的空间想象能力或者自己动手实践一下,可知答案选B.3.A4.C 解析:如果把一个正方体剪开展平的图画出来,发现有5条棱没剪(没剪的棱为两个正方形的公共边),正方体总共12条棱,∴12-5=7(条)即为所需剪的棱.5.D 解析:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故D不能围成三棱柱.6.A 解析:根据选项中图形的特点,A.可以通过旋转得到两个圆柱,故本选项正确;B.可以通过旋转得到一个圆柱,一个圆筒,故本选项错误;C.可以通过旋转得到一个圆柱,两个圆筒,故本选项错误;D.可以通过旋转得到三个圆柱,故本选项错误.7.D 解析:如图,由已知中的俯视图,我们可得:该立体图形共有五摞小正方体组成,由主视图我们可知,第1摞只有一个小正方体,由左视图我们可知,第3和第5摞也只有一个小正方体,只有2、4两摞有两个小正方体.故这些相同的小正方体共有7个.8.A 解析:A.圆锥的三视图分别是等腰三角形、等腰三角形、圆及一点,符合题意;B.三棱柱的三视图分别是长方形、长方形、三角形,不符合题意;C.圆柱的三视图分别是长方形、长方形、圆,不符合题意;D.三棱锥的三视图分别为三角形、三角形、三角形及中心与顶点的连线,不符合题意.故选A.9.D 解析:三棱柱、四棱柱、五棱柱都有可能,故选D.10.B 解析:分析可知黄色的对面是绿色,白色的对面是蓝色,红色的对面是黑色.二、填空题11.圆柱圆锥四棱锥三棱柱12.1或2或6 解析:根据有“田”字格的展开图都不是正方体的表面展开图可知,应剪去1或2或6,答案不唯一.13.圆锥,三棱柱,三棱锥等14.圆柱解析:几何体的左视图和俯视图都是长方形,主视图是圆,符合这个条件的几何体只有圆柱.15.6 16 解析:易得第一层最少有4块正方体,最多有12块正方体;第二层最少有2块正方体,最多有4块正方体,故总共至少有6块正方体,至多有16块正方体.16.六,6解析:一个棱锥有7个面,这是六棱锥,有6个侧面.17.4解析:如图,用六根长度相等的火柴棒可以搭成如图中三棱锥的形状,所以最多搭成4个等边三角形.18.D,E,A,B,C三、解答题19.解:(1)如果1点在上面,3点在左面,那么2点在前面.(2)如果5点在下,那么2点在上.20.解:三视图如图所示.21.分析:从俯视图可以看出该几何体有三行、四列,以及每行(每列)的最高层数.因而在主视图中共四列,(自左到右数)第一列最高一层,第二列最高两层,第三列最高三层,第四列最高一层,从而确定主视图的形状.在左视图中共三行,(自左到右数)第一行最高三层,第二行最高两层,第三行最高一层,从而确定左视图的形状.解:主视图和左视图如图所示.22.解:三视图如下:23.解:画图如图所示,共有四种画法.24.解:由于正方体的平面展开图共有六个面,其中面“”与面“3”相对,面“”与面“-2”相对,面“”与面“10”相对,则,,,解得,,.故.25.分析:欲求从A点到B点的最短路线,在立体图形中难以解决,可以考虑把正方体展开成平面图形来考虑.如图所示,我们都有这样的实际经验,在两点之间,走直线路程最短,因而沿着从A到B的虚线走路程最短.然后再把展开图折叠起来.解:所走的最短路线是正方体平面展开图中从A点到B点的连线,在正方体上,像这样的最短路线一共有六条,如图所示.。
(考试直接用)苏科版七年级上册数学第5章 走进图形世界 含答案

苏科版七年级上册数学第5章走进图形世界含答案一、单选题(共15题,共计45分)1、如图是一个几何体的俯视图,则该几何体可能是()A. B. C. D.2、以下几种图形:①三角形②正方体③圆④圆锥⑤圆柱⑥正方形⑦梯形⑧球⑨等腰三角形,其中不属于平面图形的是()A.②③④⑧B.②④⑤C.④⑤⑧⑨D.②④⑤⑧3、下列几何体的主视图是三角形的是()A. B. C. D.4、如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 ( )A.①②B.②③C.②④D.③④5、下列图形中不可能拼成正方体的是()A. B. C. D.6、如图所示的支架是由两个长方体构成的组合体,则它的主视图是()A. B. C. D.7、如图所示的几何体是由六个小正方体组合而成的,它的左视图是().A. B. C. D.8、如图是一个几何体的主视图和俯视图,则这个几何体是()A.三棱柱B.正方体C.三棱锥D.长方体9、如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于()A.108°B.114°C.126°D.129°10、如图,正方体的平面展开图,每个面上都标有一个汉字,与“中”字相对的面上的字为()A.宜B.居C.城D.市11、如图,由三个小立方块搭成的俯视图是()A. B. C. D.12、如图所示几何图形中,是棱柱的是()A. B. C. D.13、如图是某几何体的三视图,其侧面积()A.6B.4πC.6πD.12π14、如图是一个正方体的表面展开图,则原正方体中,与“安”字所在面相对的面上标的字是()A.重B.泰C.山D.于15、从上面看如图所示的几何体,得到的图形是()A. B. C. D.二、填空题(共10题,共计30分)16、若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是________.17、一个几何体的面数为12,棱数为30,它的顶点数为________.18、有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,再将水全部倒入A容器,结果为________.(填“溢出”“刚好”或“未装满”)19、如图,是由一些大小相同的小正方体搭成的几何体分别从左面看和从上面看得到的平面图形,则搭成该几何体的小正方体最少是________个.20、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 走进图形世界检测题
【本试卷满分100分,测试时间90分钟】
一、选择题(每小题3分,共30分)
1.在棱柱中( )
A.只有两个面平行
B.所有的棱都平行
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也互相平行
2.下列平面图形不能够围成正方体的是( )
3.下列图形是四棱柱的侧面展开图的是( )
4.将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是( )
A.5
B.6
C.7
D.8
5.下列图形中,不是三棱柱的表面展开图的是( )
6.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列左图是以下四个图中A B D C
的哪一个绕着直线旋转一周得到的()
7.如图是一个立体图形的三视图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是()
A.4
B.5
C.6
D.7
8.若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个立体图形可能是()
A.圆锥
B.三棱柱
C.圆柱
D.三棱锥
9.一个四棱柱被一刀切去一部分,剩下的部分是()
A.三棱柱
B.四棱柱
C.五棱柱
D.以上都有可能
10.如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是()
A.蓝色、绿色、黑色
B.绿色、蓝色、黑色
C.绿色、黑色、蓝色
D.蓝色、黑色、绿色
二、填空题(每小题3分,共24分)
11.下列表面展开图的立体图形的名称分别是:______、______、______、______.
12.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应
剪去____(填序号).
13.如果一个几何体的三种视图之一是三角形,这个几何体可能是(写出3
个即可).
14.几何体中主视图是圆,左视图和俯视图都是长方形,该几何体是 .
15.在桌上摆有一些大小相同的正方体木块,其主视图和左视图如图所示,则要摆出这样的图形至少需要块正方体木块,至多需要块正方体木块.
16.一个棱锥有7个面,这是棱锥,有个侧面.
17.用六根长度相等的火柴棒搭等边三角形,最多搭成个.
18.下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应填空.
①:_____________;②:_____________;③:_____________;④:_____________;⑤:_____________.
三、解答题(共46分)
19.(6分)如图是一个正方体骰子的表面展开图,请根据要求回答问题:
(1)如果1点在上面,3点在左面,几点在前面?
(2)如果5点在下面,几点在上面?
20.(6分)画出如图所示的三棱锥的三视图.
21.(6分)如图是一个由若干个小正方体搭成的几何体的俯视图,其中小正方形格内的数字是该位置小正方体的层数,请你画出它的主视图和左视图.
22.(7分)画出下列几何体的三视图:
23.(7分)如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你有几种画法,在图上用阴影注明.
24.(7分)如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求错误!未找到引用源。
的值.
25.(7分)一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B处,如图所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条?
第5章走进图形世界检测题参考答案
一、选择题
1.D 解析:对于A,如果是长方体,可能不止有两个面平行,故错;
对于B,如果是长方体,不可能所有的棱都平行,只是所有的侧棱都平行,故错;
对于C,如果是底面为梯形的棱柱,不是所有的面都是平行四边形,故错;
对于D,根据棱柱的定义知其正确,故选D.
2.B 解析:利用自己的空间想象能力或者自己动手实践一下,可知答案选B.
3.A
4.C 解析:如果把一个正方体剪开展平的图画出来,发现有5条棱没剪(没剪的棱为两个正方形的公共边),正方体总共12条棱,∴12-5=7(条)即为所需剪的棱.
5.D 解析:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故D不能围成三棱柱.
6.A 解析:根据选项中图形的特点,
A.可以通过旋转得到两个圆柱,故本选项正确;
B.可以通过旋转得到一个圆柱,一个圆筒,故本选项错误;
C.可以通过旋转得到一个圆柱,两个圆筒,故本选项错误;
D.可以通过旋转得到三个圆柱,故本选项错误.
7.D 解析:如图,由已知中的俯视图,我们可得:
该立体图形共有五摞小正方体组成,
由主视图我们可知,第1摞只有一个小正方体,
由左视图我们可知,第3和第5摞也只有一个小正方体,只有2、4两摞有两个小正方体.
故这些相同的小正方体共有7个.
8.A 解析:A.圆锥的三视图分别是等腰三角形、等腰三角形、圆及一点,符合题意;
B.三棱柱的三视图分别是长方形、长方形、三角形,不符合题意;
C.圆柱的三视图分别是长方形、长方形、圆,不符合题意;
D.三棱锥的三视图分别为三角形、三角形、三角形及中心与顶点的连线,不符合题意.
故选A.
9.D 解析:三棱柱、四棱柱、五棱柱都有可能,故选D.
10.B 解析:分析可知黄色的对面是绿色,白色的对面是蓝色,红色的对面是黑色.
二、填空题
11.圆柱圆锥四棱锥三棱柱
12.1或2或6 解析:根据有“田”字格的展开图都不是正方体的表面展开图可知,应剪去1或2或6,答案不唯一.
13.圆锥,三棱柱,三棱锥等
14.圆柱解析:几何体的左视图和俯视图都是长方形,主视图是圆,符合这个条件的几何体只有圆柱.
15.6 16 解析:易得第一层最少有4块正方体,最多有12块正方体;第二层最少有2块正方体,最多有4块正方体,故总共至少有6块正方体,至多有16块正方体.
16.六,6 解析:一个棱锥有7个面,这是六棱锥,有6个侧面.
17.4 解析:如图,用六根长度相等的火柴棒可以搭成如图中三棱锥的形状,所以最
多搭成4个等边三角形.
18.D,E,A,B,C
三、解答题
19.解:(1)如果1点在上面,3点在左面,那么2点在前面.
(2)如果5点在下,那么2点在上.
20.解:三视图如图所示.
21.分析:从俯视图可以看出该几何体有三行、四列,以及每行(每列)的最高层数.因而在主视图中共四列,(自左到右数)第一列最高一层,第二列最高两层,第三列最高三层,第四列最高一层,从而确定主视图的形状.在左视图中共三行,(自左到右数)第一行最高三层,第二行最高两层,第三行最高一层,从而确定左视图的形状.
解:主视图和左视图如图所示.
22.解:三视图如下:
23.解:画图如图所示,共有四种画法.
24.解:由于正方体的平面展开图共有六个面,
其中面“错误!未找到引用源。
”与面“3”相对,面“错误!未找到引用源。
”与面“-2”相
对,面“错误!未找到引用源。
”与面“10”相对,
则错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,
解得错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
.
故错误!未找到引用源。
.
25.分析:欲求从A点到B点的最短路线,在立体图形中难以解决,可以考虑把正方体展开成平面图形来考虑.如图所示,我们都有这样的实际经验,在两点之间,走直线路程最短,因而沿着从A到B的虚线走路程最短.然后再把展开图折叠起来.
解:所走的最短路线是正方体平面展开图中从A点到B点的连线,
在正方体上,像这样的最短路线一共有六条,如图所示.
初中数学试卷金戈铁制卷。
