例3-4-1
《网店开设》项目3-4测试一2

《网店开设》项目3-4测试一2班级:姓名:一、单选题1. 店铺页头,默认有店铺招牌和()两个模块。
A、店铺标志B、店铺海报C、宝贝推荐D、导航2. 自定义模块在设计上也要注意与整体风格统一,可放一些()。
A、宝贝推荐B、消费者保障信息C、宝贝排行D、友情链接3. ()是首页的主体部分。
A、店铺页头B、店铺页中C、商品分类D、店铺页尾4. 网页设计中用的最广泛的一种布局方式是()A、“T”结构布局B、“口”型布局C、“三”型布局D、对称对比布局5. POP布局的优点是()。
A、信息量大B、视觉冲击力强C、主次分明D、漂亮吸引人6. 页中部分最多可以添加()通栏或者左右两栏的布局单元。
A、3个B、4个C、5个D、6个7. ()可以通过编辑器输入文字、图片等信息,也可以单击工具栏上的“源代码按钮”,通过输入HTML代码的形式编辑内容。
A、店铺招牌B、宝贝推荐C、自定义区D、宝贝排行8. 对店铺装修模块描述不正确的一项是()A、具有不同功能的页面展示模板B、设置结构要合理C、视觉设计要吸引人D、以上都不正确9. 下列关于页头的说法不正确的是()A、页头在网店装修中可有可无B、页头会在详情页中显示C、页头是淘宝店铺中暴光度最高的部分D、页头的好坏也会影响店铺转化率10. 店招模块的宽度为()A、750像素B、950像素C、920像素D、720像素11. 店招支持上传()以内的图片。
A、50KB、80KC、100KD、150K12. 运费的计价方式不包括()A、件数B、价格C、重量D、体积13. 新旺铺专业版通栏图片轮播模块的宽度为()A、720像素B、750像素C、920像素D、950像素14. 图片轮播“模块高度”设置的范围为()A、100-500像素B、100-600像素C、100-700像素D、100-800像素15. 宝贝推荐模块的展示方式不包括()A、一行展示3个宝贝B、一行展示4个宝贝C、一行展示5个宝贝D、一行展示6个宝贝16. 下列关于图片轮播正确的是()A、图片轮播一般位于详情页中B、图片轮播最多可以设计10张图片C、新旺铺专业版图片轮播的宽度为950像素D、轮播的图片越大越好17. 关于选择宝贝分类页的描述哪一项是不正确的? ()A.选择“推广新页面”后,选择“店内宝贝集合页面”,可在“选择分类”中选择想要推广的分类页B.推广分类页面后,当买家点击推广信息进入店铺后,即可看到该店铺的所有宝贝C.推广分类页面后,当买家点击推广信息进入店铺后,即可看到该分类页面下的所有宝贝D.选择“推广新页面”后,选择“自定义页面”,填入想要推广的店内分类页的URL18. 淘宝宝贝的运送方式不包括()A.快递B.EMSC.平邮D.包邮19. 宝贝分类是开店的掌柜们什么时候的一项重要操作项目()A.前期布置B.中期布置C.后期布置D.临时布置20. 淘宝装修中的宝贝分类,与发布产品时选择的()毫无关系。
数学课本习题整理(完整版 )

(4)P (-3,-8) L1:2y-7=0
2.已知三角形ABC三个顶点坐标分别为A(2,1)B(5,3)C(-1,5)求三角形ABC,BC边上的高h.
3.已知三角形ABC三个顶点坐标分别为A(1,1)B(9,3)C(2,5)求角BAC的角平分线所在的直线方程。
例4求经过A(1,0) B(3,0) C(2,2)三点的圆的方程.
例5求过点M(2,2 )且与圆 + =4相切的直线的方程.
练习12.2(2)
1.判断下列方程是否表示圆,并说明理由.
(1) + -2x -4y + 6 = 0
(2) + -2x -4y = 0
(3) + -2x -4y + 5 = 0
3.已知直线l:y=ax+2和A(1,4)B(3,1)两点。当l与线段AB相交时,求实数a的取值范围。
4.直线l经过点P(-2,1)且点A(-1,-2)到l的距离等于1,求直线l方程。
12.1曲线和方程
例1已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线ℓ的方程是2x-y-2=0。
例3已知三角形ABC三个顶点坐标分别为A(1,3) B(3,1)C(-1,0),求△ABC面积。
例4已知直线l:y=kx+1与两点A(-1.5)B(4,-2)若直线l与线段AB相交,求k取值范围.
11.4(2)
1.求两条平行线x+y-1=0与2x+2y+1=0得距离
2.已知直线x-y+3平行且距离等于2的直线的方程。
例2造船时,在船体放样中,要画出甲板圆弧线.由于这条圆弧线的半径很大,无法在钢板上用圆规画出,因此需要先求出这条圆弧线的方程,再用描点法画出圆弧线.已知圆弧AB的半径r=29米,圆弧AB所对的弦长l=12米,以米为单位,建立适当的坐标系,并求圆弧AB的方程(答案中的数据精确到0.001米)
3-1 土石方工程(4)-1:挖沟槽土方

1-1(2-2)
解答:1、基数计算 挖土深度=-0.3-(-1.7)=1.4m 2、按顺序计算: (2)内墙基础沟槽2-2剖面段 如左图所示: 内墙基槽净长 8-1.2=6.8m
内墙基础沟槽2-2剖面段体积= V=(6.8*1.4)*1.4=13.33m3
1-1(2-2)
解答:1、基数计算 挖土深度=-0.3-(-1.7)=1.4m 2、按顺序计算: (3)内墙基础沟槽1-1剖面段 如左图所示: 内墙基槽净长= 5-(0.5+0.1+0.6+0.1)=3.7m 内墙基础沟槽1-1剖面段体积= V=(3.7*1.2)*1.4=6.216m3
2、挖沟槽土方工程量计算
B-4 例题: 例:某工程如图1—6、1—7所示,土质为三类土,试计算条 形基础土石方工程量,确定定额项目。(K取0.3。)
图1—6 基础平面图
-0.03
基础大样图 (含土方放坡)
1)开挖深度:H=0.7+0.35+0.35+0.35+0.15=1.90m 2)放坡深度:h=1.9-0.15=1.75m>1.70m 所以需要放坡。 3)沟槽断面积S= [1.54×0.15+(1.54+0.3×1.75)×1.75]=3.845m2 4)沟槽长: L中=(7.2+14.4+5.4+13.7)×2=81.40m
注意:工作面宽度由施工组织设计确定,当施工组织设计中无规定
时,按预算定额规定计算。
2、挖沟槽土方工程量计算
B-2 挖沟槽断面积(S断):
(3)S断的表达式:
基本思路,将等腰梯形转变成长方形。(板书)
S断 = H(a + 2c + KH)
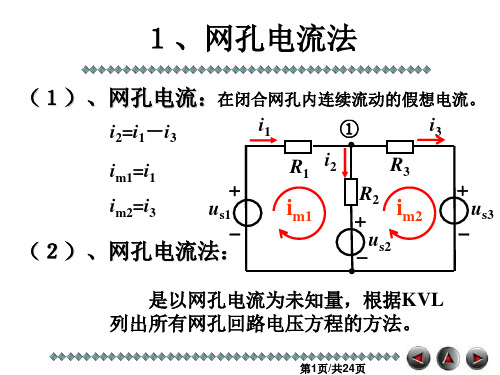
回路电流法和结点电压法
6
① 4② 5 ③
2
1
3
G11un1+ G12 un2 + G13 un3 +- - - + G1(n-1)un(n-1)= is11
0
G21un1+ G22un2 + G23 un3 + - - +G2(n-1)un(n-1) = iS22
------------------------
3、举例 例3-8
gmU
解:这是含有受控源的电路 ①
R1 I1② +RmI1_
③
Un1=US Un2-Un3=RmI1
++
_US
U _
R2
R3
U n2 - U n1 R1
+ Un2 R1
- gmU
+ Un3 R3
0
0
U Un2
I1
U n1
-Un2 R1
受控电流源作独立电流源处理
第19页/共24页
4、结点电压法的解题步骤
1、网孔电流法
(1)、网孔电流:在闭合网孔内连续流动的假想电流。
i2=i1-i3
i1
①
i3
im1=i1 +
im2=i3
us1
-
(2)、网孔电流法:
R1 i2
im1
R3
R2 +
im2
-us2
+ us3
-
是以网孔电流为未知量,根据KVL 列出所有网孔回路电压方程的方法。
第1页/共24页
2、公式
R11im1+R12im2=us11
-G4un1 +( G2+G4+G5) un2 -G5un3=0
牛津阅读树自然拼 3(1-4)单词翻译

下雨
又、再
den
窝棚
疼痛、痛苦
pail
木桶、铁桶
fix the roof
修理屋顶
nail
钉子
wait
等等
boot
靴子
hair
头发
尾巴
his tip to his tail 从头到尾
Book 3
3-4 The Red Coat
国王
外套
took chip to a shop 带Chip去商店
Book 3
3-1 The Moon Jet
喷气式飞机
翻筋斗
环、圈
急速上升,嗡嗡声
发隆隆声
nod off
打瞌睡,犯困
冲、扑、射,飞驰
(赶走鸟等时发出的声音) 嘘声
soon
不久以后,很快
讨厌的,可恶的
好吃的
Book 3
3-2 Wet Feet
竿、杆、棒
河流
deep
深的
钓鱼
in that bit
在那个池塘
get fishing
开始钓鱼
feed the fish
喂鱼
feel a fish
觉得有鱼来了
reel…in
往卷轴上绕起
need to
需要做…
杂草,野草
got his feet wet
把脚打湿了
嘻嘻,嬉笑声
鳗鱼,鳝鱼
呀(表示突然的惊恐)
Book 3
稍微,有一点
an odd smell
一股奇怪的味道
pong/pongs
发出臭味
smell odd
闻起来很怪
soap
数字推理1--12

数字推理1--12第一期:【1】1/2,1,1,(),9/11,11/13A.2B.3C.1D.7/9【2】95,88,71,61,50,()A.40B.39C.38D.37【3】4,2,2,3,6,()A.6B.8C.10D.15【4】1,7,8,57,()A.123B.122C.121 D、120【5】4,12,8,10,()A.6B.8C.9D.24参考答案:【1】1/2,1,1,(C),9/11,11/13 A.2 B.3 C.1 D.7/91/25/57/79/1111/13【2】95,88,71,61,50,( A )A.40B.39C.38D.3795-9-5=8188-8-8=7271-7-1=6361-6-1=5450-5-0=4540-4-0=36【3】4,2,2,3,6,(D)A.6B.8C.10D.15B/A=1/213/225/2【4】1,7,8,57,( C )A.123B.122C.121 D、1202 A^2+B=C 【5】4,12,8,10,( C )A.6B.8C.9A+B)/2=C第二期:1. 157 ,65 ,27 ,11 ,5,()A.4 B.3 C.2 D.12. -26,6,2,4,6,()A.8 B. 12 C. 20 D. 103. 0,1,4,15,56,()A.203B.205C.207D.2094.3/2 , 8/11 , 27/35 ,( )A. 89/116B. 75/116C. 39/74D. 105/745.1234,1360,1396,2422, 2458,( )A.2632B. 2584C.2864D.2976参考答案:1.D解析:第一项等于第二项乘以2加第三项,依次类推。
(选自08年国考第41题。
)2.D解析:多次方数列变式。
(-3)3+1=-26(-2)2+2=6(-1)3+3=202+4=422+6=(10)3. C解析:(1-0)×5-1=4,(4-1) ×5+0=15,(15-4) ×5+1=56,(56-15) ×5+2=207另解:1*4-0=44*4-1=1515*4-4=5656*4-15=209有的同学是这么算的,个人认为是可以的,故做一个补充。
第4章j交通规划 算例
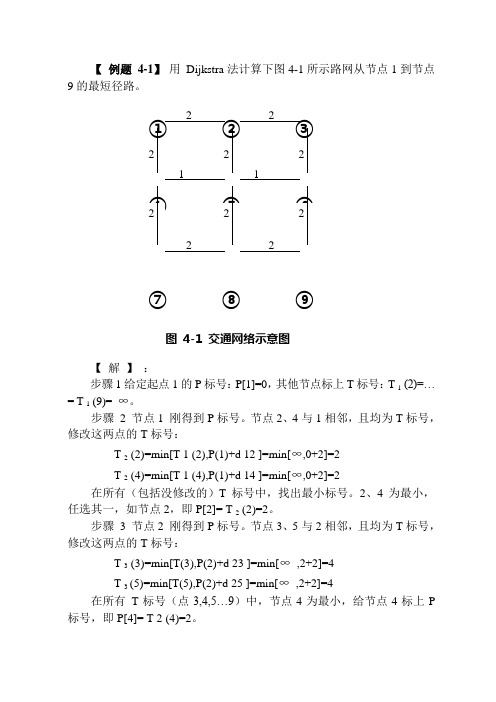
【例题4-1】用Dijkstra法计算下图4-1所示路网从节点1到节点9的最短径路。
⑦⑧⑨图4-1 交通网络示意图【解】:步骤1给定起点1的P标号:P[1]=0,其他节点标上T标号:T 1(2)=… = T 1 (9)= ∞。
步骤2 节点1 刚得到P标号。
节点2、4与1相邻,且均为T标号,修改这两点的T标号:T 2 (2)=min[T 1 (2),P(1)+d 12 ]=min[∞,0+2]=2T 2 (4)=min[T 1 (4),P(1)+d 14 ]=min[∞,0+2]=2在所有(包括没修改的)T标号中,找出最小标号。
2、4为最小,任选其一,如节点2,即P[2]= T 2 (2)=2。
步骤3 节点2 刚得到P标号。
节点3、5与2相邻,且均为T标号,修改这两点的T标号:T 3 (3)=min[T(3),P(2)+d 23 ]=min[∞,2+2]=4T 3 (5)=min[T(5),P(2)+d 25 ]=min[∞,2+2]=4在所有T标号(点3,4,5…9)中,节点4为最小,给节点4标上P 标号,即P[4]= T 2 (4)=2。
步骤4 节点4 刚得到P标号。
节点5、7与4相邻,且为T标号,修改这两点的T标号:T 4 (5)=min[T(5),P(4)+d 45 ]=min[4,2+1]=3T 4 (7)=min[T(7),P(4)+d 47 ]=min[∞,2+2]=4在所有T标号中,节点5为最小,给节点5标上P标号,即P[5]= T 4 (5)=3。
步骤5 节点5 刚得到P标号。
节点6、8与5相邻,且为T标号,修改这两点的T标号:T 5 (6)=min[T(6),P(5)+d 56 ]=min[∞,3+1]=4T 5 (8)=min[T(8),P(5)+d 58 ]=min[∞,3+2]=5在所有T标号中,节点3为最小,给节点3标上P标号,即P[3]=T 3 (3)=4。
步骤6 节点3 刚得到P标号。
鸡兔同笼全解

鸡兔同笼问题全解鸡兔同笼是我国古代著名趣题之一。
大约在1500年前,《孙子算经》中就记载了这个有趣的问题。
书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。
问笼中各有几只鸡和兔?一、用画图凑数法解鸡兔同笼例1一只鸡有一个头2只脚,一只兔有一个头4只脚.如果一个笼子里关着的鸡和兔共有10个头和26只脚,你知道笼子里有几只鸡、有几只兔吗?解:这是古代的民间趣题,叫“鸡兔同笼”问题.见图15-1(1)、(2)、(3).①先画10个②每个头下画上两条腿:数一数,共有20条腿,比题中给出的腿数少26-20=6条腿.③给一些鸡添上两条腿,叫它变成兔.边添腿边数,凑够26条腿.每把一只鸡添上两条腿,它就变成了兔,显然添6条腿就变出来3只兔.这样就得出答案,笼中有3只兔和7只鸡.例2一辆自行车有2个轮子,一辆三轮车有3个轮子.车棚里放着自行车和三轮车共10辆,数数车轮共有26个.问自行车几辆,三轮车几辆?解:发挥想像力和创造力,你可以画一个简图代表车身,见图15-2(1)、(2)、(3).①先画10个车身:②在每个车身下配上两个轮子,它就成了自行车:③数一数共20个车轮,比题中给出的轮子数少26-20=6个轮子,在自行车下面添轮子,每添一个轮子,这个自行车就成了三轮车.边添边凑数,凑出26个轮子出来.最后数一数,共有6辆三轮车,4辆自行车.注意,用这种画图凑数法解题,很直观,也比较快,为了使解题速度更快,可以把三个步骤合起来,就能得出答案.例3一只蛐蛐6条腿,一只蜘蛛8条腿.现有蛐蛐和蜘蛛共10只,共有68条腿.问蛐蛐几只,蜘蛛几只?解:此题要想个更简单的办法,见图15-3(1)、(2).①先画10个头,在每个头下写上数字“6”,代表6只腿,--即先假设10只都是蛐蛐,则如:②数一数,算一算,6×10=60,即共有60条腿,比题中给出的腿数少68-60=8条腿,所以就要在下面再添腿,每在一个头下添2条腿(写个“2”),它就变成了一只蜘蛛,共添上8条腿,就使总腿数凑够68条腿了.最后数一数,共有4只蜘蛛,6只蛐蛐.解这道题时,我们用数字代表腿数,使我们省去了画“腿”的麻烦.其实,也可以完全省去画图,我们只要把解题想法和算式摘出来就行了!第一步,先把10只全部看成是蛐蛐,那么一共就有:6×10=60条腿.第二步,算一算少了多少条腿?少了68-60=8条腿.第三步,把一个蛐蛐给它添上2条腿,使它变成了蜘蛛,可以变成几只蜘蛛呢?8÷2=4只(蜘蛛),第四步,再算出蛐蛐的只数出来:10-4=6只(蛐蛐).这样一来,我们就不必借助于画图的直观形象,也可以解这类题目了.如果能这样,我们的思维能力就又提高一步了!特别重要的是,我们这样就可以不用“凑数”的尝试方法了.例4笼中有兔又有鸡,数数腿36,数数脑袋11,问几只兔子几只鸡?解:方法1:先用画图凑数法解,见图15-4(1)、(2)、(3).①先画11个头:②再在头下填腿:③数一数,共有2×11=22条腿.还少36-22=14条腿,每添2条腿,就使一只鸡变成兔.数一数,共变出了7只兔:14÷2=7.最后数一数,笼中共有7只兔,4只鸡.方法2:①把11只全部看成鸡,共有2×11=22条腿.②比题中给出的腿数少了36-22=14条腿.③给一只鸡添2条腿使它变成一只兔,共变成:14÷2=7只(兔).③再算出鸡数为:11-7=4只(鸡).④例5今有五分的和一角的两种汽车票,共10张,总钱数是七角五分.问每种各几张?习题十五1.笼中有兔又有鸡,数数腿三十整,数数脑袋一十一,几只兔子几只鸡?2.今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?(这是一道古代趣题.雉,即野鸡,“各几何”是各多少的意思.)3.有一首中国民谣:“一队猎手一队狗,二队排着一起走,数头一共三百六,数腿一共八百九,多少猎手多少狗?”二、列举法解鸡兔同笼例1一只鸡有一个头2只脚,一只兔有一个头4只脚.如果一个笼子里关着的鸡和兔共有10个头和26只脚,你知道笼子里有几只鸡、有几只兔吗?练习例2一辆自行车有2个轮子,一辆三轮车有3个轮子.车棚里放着自行车和三轮车共10辆,数数车轮共有26个.问自行车几辆,三轮车几辆?例3一只蛐蛐6条腿,一只蜘蛛8条腿.现有蛐蛐和蜘蛛共10只,共有68条腿.问蛐蛐几只,蜘蛛几只?三、用假设法解鸡兔同笼问题例1(古典题)鸡兔同笼,头共46,足共128,鸡兔各几只?解法一:先假设它们全是鸡。
